Как найти область значений дробной функции

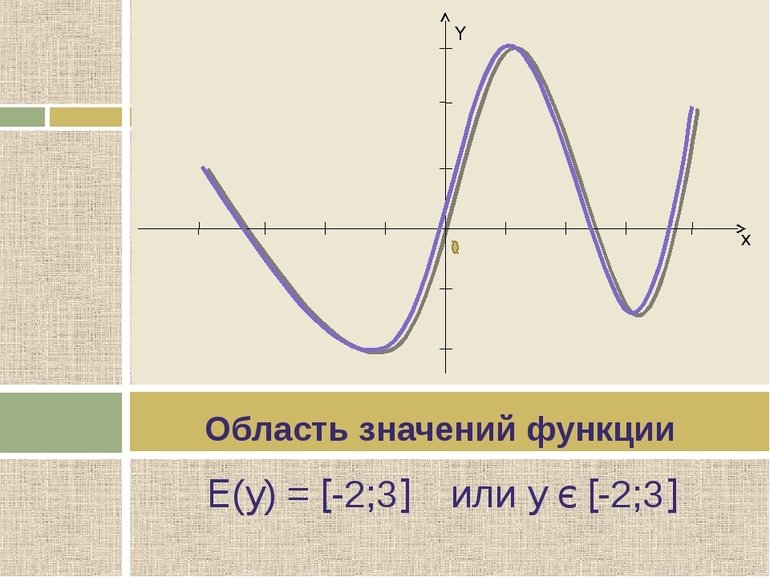
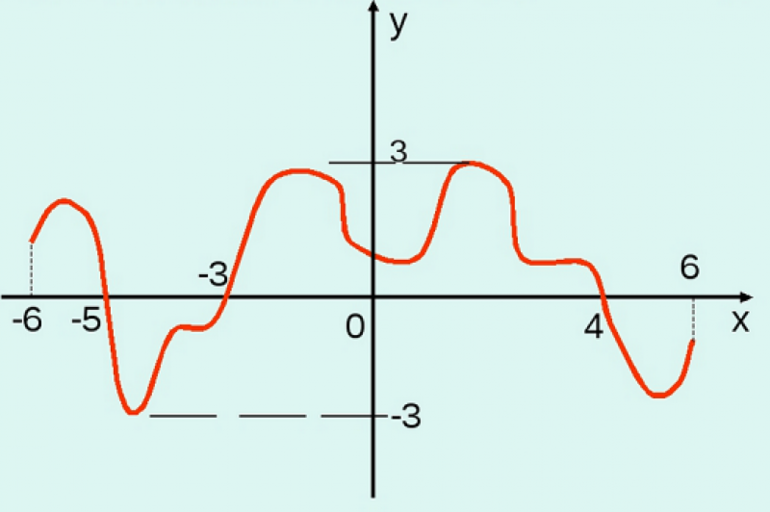
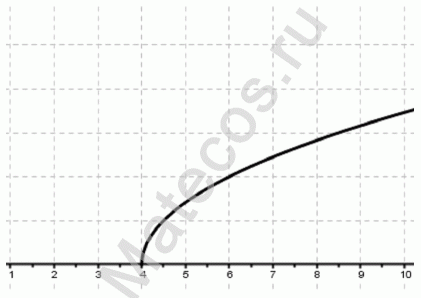
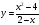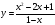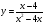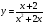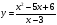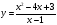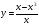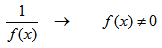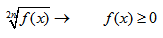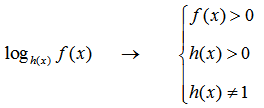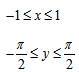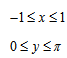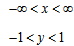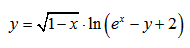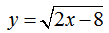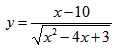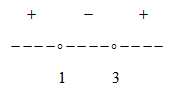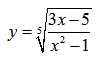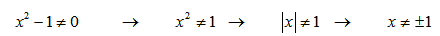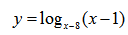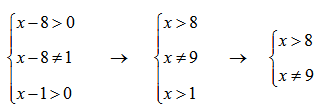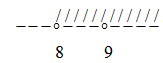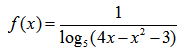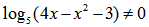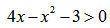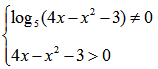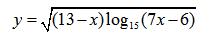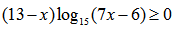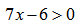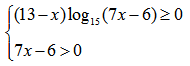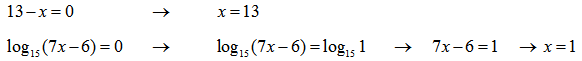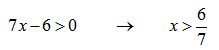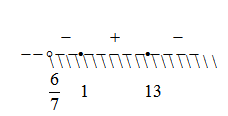НАХОЖДЕНИЕ ОБЛАСТИ ЗНАЧЕНИЙ ДРОБНО-РАЦИОНАЛЬНОЙ ФУНКЦИИ

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

 

ВВЕДЕНИЕ

К свойствам функции относится область значений функции. Проблема нахождения области значений, например, дробно-рациональной функции, привела к необходимости ознакомиться со способами ее нахождения.

Цель исследования: найти различные методы нахождения области значений дробно-рациональных функций. Задачи исследования:1). Ознакомиться со способами решения задач на нахождение области значений функции;

2). Изучить инверсию функций;

3). Использовать алгебраические неравенства для нахождения области значений функции;

4). Составить банк функций с нахождением области значений функций различными методами. Сравнить эти методы с точки зрения затрат времени и трудоёмкости;

5). Использовать программу Graphи различные свойства функций для построения графиков функций.При ознакомлении с некоторыми методами нахождения области значений функции в различных источниках, указанных ниже, не нашлось таких примеров решения, в которых бы использовались различные методы. В данной исследовательской работе сопоставляются разные, возможные, методы нахождения области значений функции для выделения самого рационального.ГЛАВА I.ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

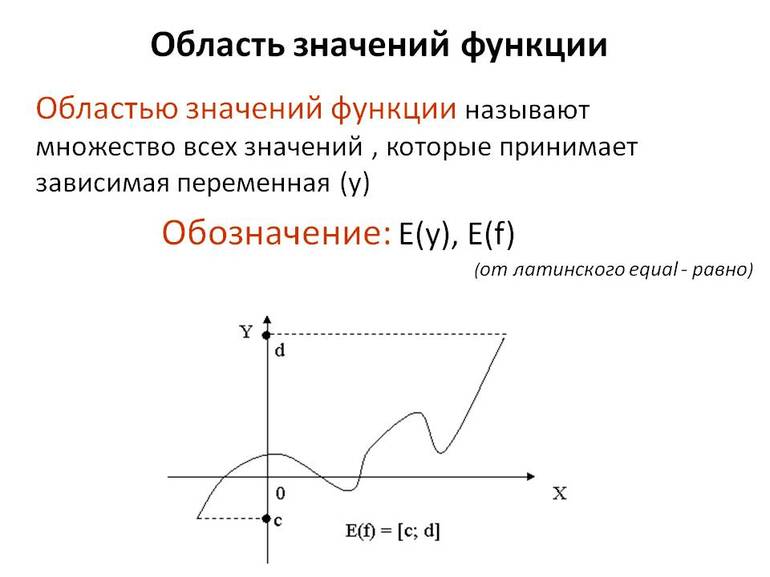
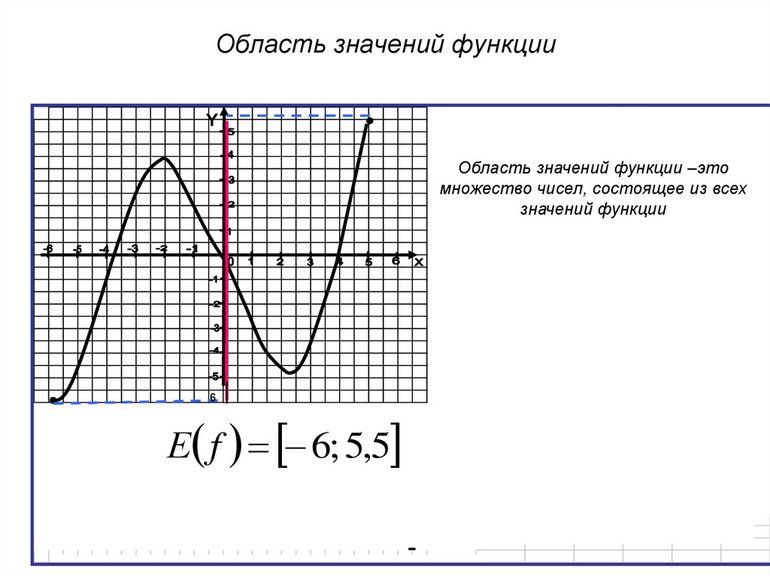
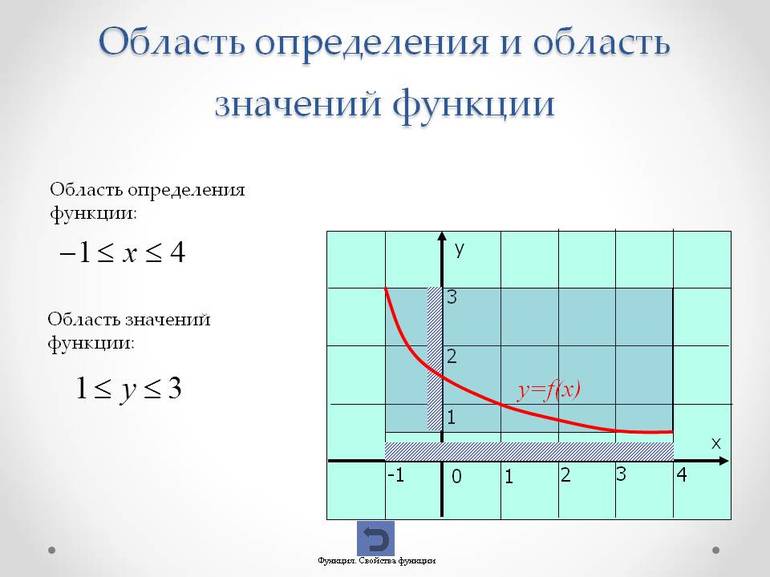
§1. Некоторые сведения об области значений функции.Определение области значений функции.Областью (множеством) значений E(у) функции y = f(x) называется множество таких чисел y₀, для каждого из которых найдётся такое число x₀, что: f(x₀) = y₀.

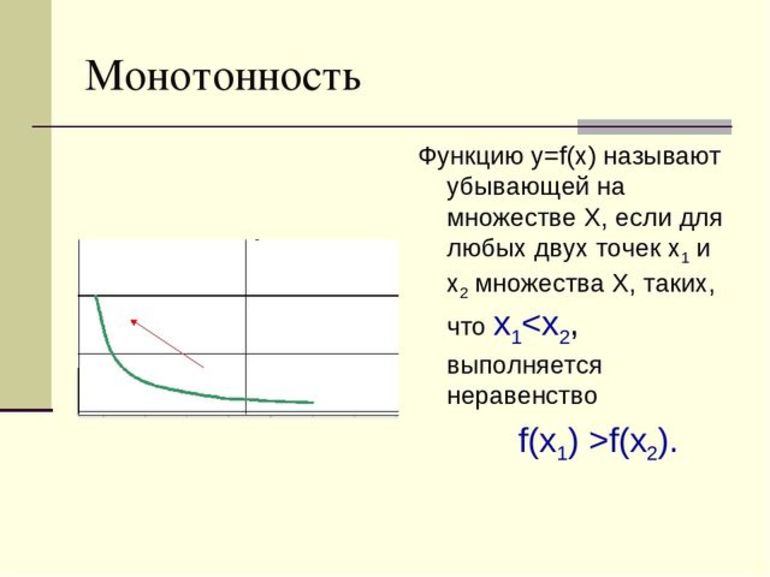
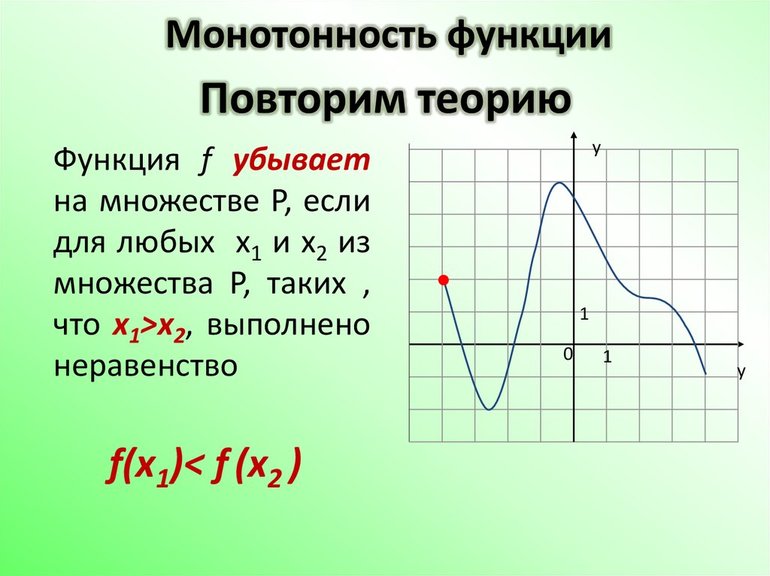
Свойства функций, используемые при нахождении области значений функцииДля успешного нахождения области значений функции надо хорошо знать свойства основных элементарных функций, особенно их области определения и характер монотонности. Приведём свойства функции, которые учитываются при нахождении Е(у):непрерывность;монотонность;дифференцируемость;чётность, нечётность;обратимость;периодичность и т.д.Известны следующие способы нахождения областей значений функций:а) последовательное нахождение значений сложных аргументов функции;б) метод оценок;в) использование свойств непрерывности и монотонности функции;г) использование производной;д) использование наибольшего и наименьшего значений функции;е) графический метод;ж) метод введения параметра;з) метод обратной функции. Определение.Параметром называется независимая переменная, значение которой в задаче считается задан­ным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренно­му множеству.Определение. Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. {displaystyle f^{-1}}§2. Инверсия. Известна теорема о том, что если функция возрастает и принимает только положительные значения, то функция убывает.

Целесообразно рассматривать преобразования плоскости, при которых точки с координатами переходят в точки с координатами , ибо легко заметить, что именно с помощью такого преобразования можно построить рассмотренный график.

Определение. Точка В называется инвертной точке А относительно данной прямой (оси) l, если:

1. эти точки лежат по одну сторону относительно оси l;

2. отрезок, их соединяющий, перпендикулярен оси l;

3. произведение расстояний от этих точек до оси lравно 1.

У точек оси инвертных точек нет.

Определение. Преобразование плоскости, при котором каждая точка переходит в инвертную ейотносительно данной прямой, называется инверсией. Для точек этой прямой преобразование не определяется.

Замечание. При инверсии относительно осиОх точка А с координатами , , переходит в точку В с координатами , где

В самом деле, , так как отрезок АВ перпендикулярен осиОх, должны быть одного знака, так как А и В лежат в одной полуплоскости относительно оси Ох, наконец, так как произведение расстояний от А и В до оси равно единице, т.е.

Свойства инверсии. Построение графиков.

А — неподвижная точка инверсии относительно осиОх тогда и только тогда, когда т.е. — неподвижная точка инверсии относительно оси Оутогда и только тогда, когда т.е.

Чем дальше от оси инверсии точка, тем ближе к ней инвертная ей точка.

Теорема.График функции получается из графика функции инверсией относительно осиОх.

Теорема.График функции получается из графика функции преобразованием инверсии относительно оси Оу.

§3. Некоторые неравенства, используемые в работе.

Доказательства некоторых неравенств (проведенные самостоятельно).Неравенство 1. .Доказательство.

Теорема о высоте: CD =.в частном случае, если,ч.т.д.

Неравенство 2. Доказательство.

Преобразуем выражение: . По теореме катета:. ПотеоремеПифагора:

В частности, если Ч. т. д.

Неравенство 3. Доказательство.

Значит, , ч. т. д.

ГЛАВА II.ПРАКТИЧЕСКАЯ ЧАСТЬ§1.Примеры нахождения области значений функций, графики которых можно построить с помощью инверсии, представив в виде или представив в виде .

Пример 1.Построить график функции и найти область значений E(f) данной функции.

Решение. Строится график функции , отмечаются точки с ординатой, равной 1, замечается, что искомый график имеет асимптоты так как график функции при абсциссах, «близких» к , все ближе подходит к оси инверсии, а при «больших» абсциссах уходит от неё неограниченно далеко. Показывается, что надо, таким образом, от точки (0,1) «вести вправо и вверх» к прямой и «влево и вниз» к прямой и т.п.

Ответ:.

Пример 2.Построить график функции и найти область значений E(f) данной функции.

Решение.

График функции получается из графика функции смещением на 1 единицу вправо. Для построения графика функции заменим значения абсцисс графика функции на обратные числа. . Прямаяявляется асимптотой. Если сравнить выражение с единицей: то оно меньше ее при , значит, точки графика функции не поднимутся выше прямой которая является асимптотой графика рассматриваемой функции. Эта функция является неотрицательной, значит ниже осиОх точки графика не появятся.

Ответ:.

§2. Метод введения параметра для нахождения области значений функции.

Пример 3.Найти область значений E(f) функции.

Решение.Решим пример методом введения параметра, согласно которому E(f) совпадает с множеством значений параметра а, для которых уравнениеимеет хотя бы один корень.

Если_,уравнение является линейным с ненулевым коэффициентом при неизвестной, поэтому имеет решение. Если _, уравнение является квадратным, поэтому оно разрешимо тогда и только тогда, когда его дискриминант.

Так как точка принадлежит отрезку, то искомым множеством значений параметра а, значит, и областью значений E(f) будет весь отрезок.

Ответ:.

§3. Метод обратной функции. Как непосредственное развитие метода введения параметра при нахождении множества значений функции, можно рассматривать метод обратной функции, для нахождения которой надо решить относительно х уравнение f(x)= y, считая y параметром. Если это уравнение имеет единственное решение x =g(y), то область значений E(f) исходной функции f(x) совпадает с областью определения D(g) обратной функции g(y). Если же уравнение f(x)= y имеет несколько решений x =g₁(y), x =g₂(y) и т.д., то E(f) равна объединению областей определений функции g₁(y), g₂(y) и т.д.Пример4. (самостоятельное решение).Найдите область значений E(f) функции.

Решение.Решим уравнение относительно , учитывая, что

Неравенство методом интервалов, получаем, что

Ответ:.

§4. Использованиепроизводной, непрерывности и монотонности функции и графика функции

Пример 5. (самостоятельное решение с применением программы Grahf).Найти область значений E(f) функции .

Решение.График функции не пересекает ось абсцисс, т.к. уравнение не имеет решения.

Функция непрерывна на, значит, дифференцируема. Найдем производную функции:

Найдем критические точки первого рода:

Выясним характер монотонности функции:

Найдем асимптоты функции:

Вертикальных асимптот нет, т.к. .Наклонная асимптота:. Получили горизонтальную асимптоту .

Найдём

Заметим, что последний метод является наглядным, однако времяёмким и трудоемким.

Ответ:.

§ 5. Задачи на нахождение области значений функций с помощью алгебраических неравенств

Пример 6. Найти область значений E(f) функции(используя неравенство).

Решение.

Учитывая, что заданная функция является нечетной, получаем

Ответ:.

Пример 7. Найти область значений E(f) функции(используя неравенство).

Решение. Учитывая, что заданная функция является нечетной, получаем

А так у функции один нуль, , и она меняет монотонность от убывания к возрастанию, а затем от возрастания к убыванию, то можно определить, как меняются ее значения: .

Ответ:.

Пример 8. Найти область значений E(f) функции(используя неравенство).

Решение.

График имеет вертикальную асимптоту , не пересекает ось абсцисс.

Найдем производную функции

Найдем критические точки первого рода:

Выясним характер монотонности функции:

Ответ:.

§ 6. Нахождение области значений функций разными способами

Ранее решённые Примеры 3, 4, 5 указывают на то, что найти область значений функции можно было тремя способами: методом введения параметра, методом обратной функции, а также с использованием производной, непрерывности функции, монотонности и графика. Применить инверсию для построения графика этой функции не удается, так как она не представима в виде или в виде . Также не получится представить эту функцию в виде суммы двух слагаемых, к которой можно было бы применить одно из указанных алгебраических свойств. Наиболее рациональными являются первые два метода.

Решим и другие Примерыразличнымидоступнымиметодами и способами.Пример 1.Построить график функции и найти область значений E(f) данной функции. (См. стр. I-IIПРИЛОЖЕНИЕ 1)Пример 2.Построить график функции и найти область значений E(f) данной функции. (См. стр. II-IIIПРИЛОЖЕНИЕ 2)Пример 6.Найти область значений E(f) функции(См. стр. III-VПРИЛОЖЕНИЕ 3)Пример 7. Найти область значений E(f) функции(См. стр. V-VIIПРИЛОЖЕНИЕ 4)Пример 8. Найти область значений E(f) функции(См. стр. VII-VIIIПРИЛОЖЕНИЕ 5)

ЗАКЛЮЧЕНИЕ

Данная тема имеет практическое применение, так как при изучении тех или иных процессов из реальной жизни, описываемых математическими формулами, чаще всего вычисляют значения функций. В школьном курсе математики изучается тема «Область значения функции». Такие задачи обязательно содержатся в заданиях различных математических тестов, в частности в заданиях единого государственного экзамена.Если выбирать универсальный способ нахождения области значений функции, то это графический с применением производной, таких свойств как четность, асимптоты, нули функции. Удобно использовать инверсию для построения график функций, но не все функции инвертируются. Если есть выбор способов, то к рациональным способам можно отнести и введение параметра и метод обратной функции. Знание различных способов решения одной и той же задачи позволяет осуществить проверку полученных результатов.СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ

1. Сильвестров В.В. Множество значений функции: Учебное пособие./Сильвестров В.В. – Чебоксары: 2004. — 200-204 с.2. Карп А.П. Даю урокипо математике /Карп А.П. — М.: Просвещение, 1992. — 21-31с.3. Райский В. Математика: Сборник задач и упражнений для VI класса./Райский В. — Кишинёв:PrutInternaţional, 2002.- 25-33 с.4. Щербаков П.А. Нахождение области значений функции (Электронный ресурс) http://pandia.ru/text/77/355/6329.php (дата обращения 29.10.2016)5. Сикорский К.П. Факультатив. Математика 7-8 класс./Сикорский К.П. — М.: Просвещение, 1969.- 256-263 с.

Просмотров работы: 3598

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Нахождение
  области значений
  дробно-рациональных функций

• 

  2 слайд

  Областью (множеством) значений E(у) функции y = f(x) называется множество таких чисел y0, для каждого из которых найдётся такое число x0, что: f(x0) = y0.

• 

  3 слайд

  Свойства функций, используемые при нахождении области значений функции:

  непрерывность;

  монотонность;

  дифференцируемость;

  чётность, нечётность;

  обратимость.

• 

  4 слайд

  Способы нахождения областей значений функций:

  а) последовательное нахождение значений сложных аргументов функции;
  б) метод оценок;
  в) использование свойств непрерывности и монотонности функции;
  г) использование производной;
  д) использование наибольшего и наименьшего значений функции;
  е) графический метод;
  ж) метод введения параметра;
  з) метод обратной функции.

• 

  5 слайд

  Определение. Параметром называется независимая переменная, значение которой в задаче считается задан­ным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренно­му множеству.

  Определение. Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x.

• 

  6 слайд

  Определение. Точка В называется инвертной точке А относительно данной прямой (оси) l, если:
  эти точки лежат по одну сторону относительно оси l;
  отрезок, их соединяющий, перпендикулярен оси l;
  произведение расстояний от этих точек до оси lравно 1.
  Определение. Преобразование плоскости, при котором каждая точка переходит в инвертную ей относительно данной прямой, называется инверсией. Для точек этой прямой преобразование не определяется.
  Свойства инверсии:

  График функции получается из графика функции инверсией относительно оси Ох.

  График функции получается из графика функции преобразованием инверсии относительно оси Оу.

  Чем дальше от оси инверсии точка, тем ближе к ней инвертная ей точка.

• 

  7 слайд

  Некоторые неравенства, используемые в работе

• 

  8 слайд

  Пример 1.
  Асимптоты:
  Ответ:
  .
  (1. Строим график, используя инверсию)
  Решение.

• 

  9 слайд

  Пример 1.
  Ответ:
  .
  ( 2. Метод введения параметра)
  Решение.

• 

  10 слайд

  Пример 1.
  Ответ:
  .
  ( 3. Метод обратной функции)
  Решение.

• 

  11 слайд

  Пример 1.
  Ответ:
  .
  ( 4. Метод применения производной)
  Решение.
  Вертикальная асимптота , график не пересекает ось абсцисс.

  Критическиx точек первого рода нет.

• 

  12 слайд

  Применить алгебраические неравенства к Примеру 1 невозможно

• 

  13 слайд

  Пример 2.
  Асимптоты:
  Ответ:
  .
  (1. Строим график, используя инверсию)
  Решение.

• 

  14 слайд

  Пример 2.
  Ответ:
  .
  (2. Введение параметра)
  Решение.

• 

  15 слайд

  Пример 2.
  Ответ:
  .
  (3. Метод обратной функции)
  Решение.

• 

  16 слайд

  Пример 2.
  Ответ:
  .
  (4. Метод применения производной)
  Решение.
  График имеет вертикальную асимптоту,
  не пересекает ось абсцисс.
  Горизонтальная асимптота:

• 

  17 слайд

  Применить алгебраические неравенства к Примеру 2 невозможно

• 

  18 слайд

  Пример 6.
  Ответ:
  .
  (1.
  Решение.
  Функция нечетная:

• 

  19 слайд

  Пример 6.
  Ответ:
  .
  (2. Метод введения параметра)
  Решение.

• 

  20 слайд

  Пример 6.
  Ответ:
  .
  (3. Метод обратной функции)
  Решение.

• 

  21 слайд

  Пример 6.
  Ответ:
  .
  (4. Метод применения производной)
  Решение.
  Вертикальная асимптота:
  График не пересекает ось абсцисс.
  Наклонная асимптота:

• 

  22 слайд

  Применить инверсию к функции Примера 6 невозможно

• 

  23 слайд

  ВЫВОД

  Нахождение области значений функции имеет практическое применение.

  2. Универсальный способ нахождения области значений функции — графический с применением производной, таких свойств как четность, асимптоты, нули функции.

  3. Удобно использовать инверсию для построения график функций, но не все функции инвертируются.

  4. Если есть выбор способов, то к рациональным способам можно отнести и введение параметра и метод обратной функции.

  5. Знание различных способов решения одной и той же задачи позволяет осуществить проверку полученных результатов.

Краткое описание документа:

Презентация «Нахождение области значений дробно-рациональных функций» содержит информацию о параметре, инверсии, о способах нахождения области значений дробно-рациональных функций (на конкретных примерах некоторые способы применены).

Способы нахождения областей значений функций:

а) последовательное нахождение значений сложных аргументов функции;
б) метод оценок;
в) использование свойств непрерывности и монотонности функции;
г) использование производной;
д) использование наибольшего и наименьшего значений функции;
е) графический метод;
ж) метод введения параметра;
з) метод обратной функции.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 263 983 материала в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Организация маркетинга в туризме»

• Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс профессиональной переподготовки «Организация деятельности специалиста оценщика-эксперта по оценке имущества»

• Курс профессиональной переподготовки «Эксплуатация и обслуживание общего имущества многоквартирного дома»

Общая информация

У каждой функции y = f (x) есть два типа переменных: зависимые и независимые. Переменная «х» является независимой, поскольку она может принимать любые значения, кроме тех, которые «превращают» функцию в пустое множество (этого необходимо избегать). Они бывают с одной или несколькими независимыми переменными. Необходимо выяснить все значения зависимой переменной.

Существует несколько методов решения задач такого типа. К ним относятся следующие способы: автоматизированный и ручной. Решение первым подразумевает использование специальных программных оболочек и web-приложений, позволяющих найти область значения функции. Онлайн-калькулятор с решением применяется для тех, кто выполняет большое количество вычислений или проверку вычислений.

В различных дисциплинах необходимо исследовать поведение функций. Например, при проектировании какого-либо программного продукта. Программисты занимаются поиском «багов», при которых происходит некорректная работа приложения. Если заданы недопустимые параметры независимой переменной, то произойдет ошибка. Это называется исключением, и его всегда следует обрабатывать. При проектировании различных устройств нужно также уметь находить область значения функции.

Основные понятия

Руководствуясь некоторыми данными, можно сделать вывод: областью значений некоторой функции называются все ее допустимые значения. Обозначается она буквой «E», т. е. E (f) или E (y). Когда y = f (x) является сложной (w = f (x, y, z)), тогда можно ее обозначить «E (w)».

Независимая переменная, принимающая некоторые значения, называется аргументом. Для конкретного случая существует определенный алгоритм. Можно сразу определить E (f), но в некоторых ситуациях нужно выполнить некоторые преобразования.

Например, нужно найти область значений квадратичной функции y = 3x ² — 2x — 1. Следует записать уравнение 3x ² — 2x — 1 = 0. Ордината вычисляется таким образом: y0 = -D / 4a = -[b ² — 4ac] / 4a = -[(-2)^2 — 4 * 3 * (-1)] / (4 * 3) = -16 / 12 = -4/3. Если коэффициент а>0, то ветви параболы направлены вверх. Следовательно, E (y) = (-4/3;+бесконечность).

Специалисты-математики утверждают, что важным аспектом является определение типа функции. Следовательно, следует разобраться в их классификации. Для этого необходимо знать их графики и названия.

Типы функций

Перед тем, как найти все допустимые значения, нужно знать область значения некоторых элементарных функций. Для каждой из них существует свой промежуток:

1. (-бесконечность;+бесконечность): y =kx + b, y = x^(2n+1), y = x^(1/(2n+1)), y = log (x) с основанием а, y = tg (x) и y = ctg (x).
2. [0;+бесконечность): y = x^(2n), y = x^(1/(2n)) и y = a^x.
3. (-бесконечность;0] U [0;+бесконечность) только для y = k / x (гипербола).
4. [-1;1]: y = sin (x) и y = cos (x).
5. [0;Pi]: y = arccos (x) и arcsin (x).
6. [-Pi/2;Pi/2]: y = arctg (x) и arcsin (x).

Если функция является многочленом четной степени, то для нее существует интервал [m;+бесконечность). Значение «m» — наименьшее значение многочлена. На промежутке (-бесконечность;n) число n — наибольшее его значение.

Довольно сложной задачей считается нахождение области значений тригонометрических функций. Примером одной из них считается y = cos (2x) + 2cos (x). Кроме того, при нахождении E (f) необходимо руководствоваться не только табличными значениями. Этих данных мало, поскольку нужно также знать о свойствах некоторых функций и способы нахождения E.

Важные свойства

Для качественного исследования нужно знать свойства простых функций: монотонность, непрерывность, дифференцируемость, четность или нечетность, периодичность, область определения и значения. Среди свойств можно выделить несколько основных:

1. В случае, когда функция f (x) является непрерывной, и наблюдается ее возрастание или убывание на отрезке [a;b], то множество значений — интервал [f (a);f (b)].
2. Если y = f (x) обладает непрерывностью на промежутке [a;b], и существует некоторое минимальное m и максимальное М ее значения, то множеством ее значений является интервал [m;M].
3. При непрерывности и дифференцируемости функции на промежутке [a;b], она имеет минимальное и максимальное значения на данном промежутке.

Последние два свойства применяются для непрерывных функций. Простое решение позволяет получить первое свойство. При этом очень важно доказать ее монотонность. Задача существенно упрощается, когда удается доказать четность или нечетность функции, а также ее периодичность. По необходимости следует проверять и использовать некоторые ее свойства: непрерывность (при разрыве нужно определить его точку или интервал), монотонность, дифференцируемость, периодичность, четность или нечетность и т. д.

Методы нахождения

Существует много способов нахождения области значений. Однако для решения задач нужно подбирать оптимальный метод, поскольку следует избегать лишних вычислений. Например, если функция является простой, то нет необходимости применять сложные алгоритмы решения. К методам нахождения относятся следующие:

1. Отдельное нахождение значений элементов сложной функции.
2. Оценочный.
3. Учет непрерывности и монотонности.
4. Взятие производной.
5. Использование max и min функции.

Для каждого из методов существует определенный алгоритм. Хотя встречаются случаи, когда целесообразно применить два простых метода. Нужно руководствоваться минимальным количеством вычислений и затраченным временем.

Для каждого элемента

Иногда в задачах следует найти E (f) при условии, когда функция является сложной. Очень распространенная методика разбиения задачи на подзадачи, которая применяется не только в дисциплинах с физико-математическим уклоном, но в экономике, бизнесе и других направлениях. Решение с помощью метода последовательного нахождения E (f) каждой из функций. Алгоритм имеет такой вид:

1. Выполнить необходимые преобразования — упростить выражение.
2. Разбить выражение на элементы.
3. Выполнить поиск E (f) для каждого элемента.
4. Произвести замену.
5. Анализ.
6. Результат решения.

Однако довольно сложно ориентировать по данному алгоритму, поскольку нужно разобрать решение примера с его помощью. Дана функция y = log0.5 (4 — 2 * 3^x — 9^x). Решается задача таким образом:

1. Упростить (выделить квадрат): y = log0.5 (4 — 2 * 3^x — 9^x) = log0.5 [5 — (1 — 2 * 3^x — 9^x)] = log0.5 [5 — (3^x + 1)].
2. Разбить на элементарные функции: y = 3^x, y = 3^x + 1, y = [-(3^x + 1)]^2 и y = [5 — (3^x + 1)]^2.
3. Определить для каждого элемента E (f): E (3^x) = (0;+бесконечность), E (3^x + 1) = (1;+бесконечность), E ([-(3^x + 1)]^2) = (-бесконечность;-1) и E ([5 — (3^x + 1)]^2) = (-бесконечность;4).
4. Произвести замену: t = 5 — (3^x + 1)]^2 (-бесконечность <= t <=4).
5. Анализ: поскольку E (f) на луче (-бесконечность;4) совпадает с интервалом (0;4), то функция непрерывна и убывает. Необходимо отметить, что интервал (0;4) получен при пересечении луча (-бесконечность;4) с областью определения функции логарифмического типа (0;+бесконечность). На интервале (0;4) эта функция непрерывна и убывает. Если t>0, то она стремится к бесконечности. Когда t = 4, ее значение равно -2.
6. Результат решения — искомый интервал: E (f) = (-2;+бесконечность).

Необходимо обратить внимание на пункты 1, 3 и 5. Они являются очень важными, поскольку от них зависит правильность решения. Очень важно уметь анализировать полученную функцию в 4 пункте.

Оценочный способ

Еще одним методом определения E (f) является способ оценки. Необходимо оценить непрерывную функцию в нижнем и верхнем направлениях. Еще следует доказать достижение нижней и верхней границ. Для этой цели существует также алгоритм. Он немного проще предыдущего. Суть его заключается в следующем:

1. Доказать непрерывность.
2. Составить неравенство или неравенства для нескольких функций.
3. Узнать оценку.
4. Записать интервал.

Необходимо разобрать алгоритм на примере функции y = cos (7x) + 5 * cos (x). Следует учитывать, что известен только один знак неравенства. Второй нужно доказать оценочным методом. Решение задачи имеет такой вид:

1. Функция вида y = cos (x) является непрерывной.
2. Неравенства: -1<=cos (7x)?1 и -5<=5 * cos (x)?5.
3. Оценка получает при объединении неравенств: -6<=y?6. При значениях независимой переменной x = Pi и x = 0 функция принимает значения -6 и 6 соответственно (нижняя и верхняя границы). Функция состоит из двух элементов, следовательно, она является линейной и непрерывной.
4. Интервал: E (y) = [-6;6].

Метод позволяет найти решение без использования дополнительных вычислений. Но при его использовании легко ошибиться.

Учет непрерывности и монотонности

Одним из простых способов решения, который специалисты рекомендуют новичкам, является метод учета непрерывности и монотонности. Для этого существует специальный алгоритм:

1. Упростить выражение.
2. Выполнить замену при необходимости.
3. Найти вершину графика.
4. Определить промежуток.
5. Вычислить максимальное и минимальное значения.
6. Записать E (f).

Например, существует некоторая функция y = cos (2x) + 2cos (x). Необходимо найти ее E. Искать следует по алгоритму решения методом учета монотонности и непрерывности:

1. Упростить (по формуле двойного угла): y = 2 * (cos (x))^2 + 2cosx — 1.
2. Замена t = cos (x): y = 2 * t ² + 2 * t — 1 = 2 * (t + 0,5)^2 — 1,5.
3. Показательная функция является параболой. Она монотонна, непрерывна и имеет вершину по оси ОУ -1,5. Промежуток, который рассматривается — [-1;1], поскольку E (cos (x)) = [-1;1].
4. Минимальное значение равно -1,5, так как ветви направлены вверх. Максимальное на промежутке [-1;1] — MAX (y) = 3. Для его нахождения нужно построить график параболы y = 2 * (t + 0,5)^2 — 1,5.
5. Искомый интервал — E (cos (2x) + 2cos (x)) = [-1,5;3].

Чтобы построить график параболы, нужно найти ее вершину и точки пересечения с осью абсцисс. Последние находятся при решении уравнения 2 * (t + 0,5)^2 — 1,5 = 0. Однако существует способ намного проще. Для этого следует привести выражение к виду 2 * (t + 0,5)^2 = 1,5. Отсюда t = — 0,5. Следовательно, координаты вершины — (-0,5;-1,5). Корни уравнения при его решении: t1 = -[(1 + (3)^0.5)] / 2 и t2 = -[(1 — (3)^0.5)] / 2.

Производная, min и max

Одним из простейших способов нахождения E (f) является взятие производной функции. Этот метод можно комбинировать с определением максимального и минимального значений. Математики рекомендуют простейший алгоритм:

1. Найти производную.
2. Анализ.
3. Указать MAX (f) и MIN (f).
4. Запись интервала в формате (MIN (f);MAX (f)).

Практическое применение алгоритма — решение задачи этим методом. Например, нужно найти E (arcsin (x)). Решение выполняется по нескольким этапам:

1. Производная: y’ = [arcsin (x)]’ = 1 / [(1 — x ² )^0.5].
2. Функция возрастает на интервале (-1;1).
3. Минимум и максимум на отрезке (-1;1): MIN (arcsin (-1)) = -Pi/2 MAX (arcsin (1)) = Pi/2.
4. Интервал: E (arcsin (x)) = [-Pi/2;Pi/2].

В некоторых случаях рекомендуется вычислять пределы, поскольку часть задач решается только с их применением. Существует определенный тип задач, в которых нужно доказать, что отрезок является E (f) конкретной функции. Например, следует выяснить принадлежность [-1;1] функции sin (x). Для этого необходимо воспользоваться вышеописанным алгоритмом:

1. Производная: y’ = [sin (x)]’ = cos (x).
2. Период функции равен 2Pi. Следует взять отрезок [0;2Pi]. Для нахождения множества значений на нем нужно приравнять производную функции к 0, т. е. cos (x) = 0. Найти х = Pi/2 + Pi * к, где «к» принадлежит Z. Точки экстремума равны Pi/2 и 3Pi/2.
3. Минимум и максимум на отрезке [0;2Pi): MIN ([sin (3Pi/2)]) = -1 и MAX ([sin (3Pi/2)]) = 1.
4. E (sin (x)) = [-1;1].

Отрезок [-1;1] является E (sin (x)). Оптимальный метод — нахождение производной и определение E (f). В этом примере необходимо знать и проверить периодичность.

Таким образом, существует несколько способов нахождения E (f), но всегда необходимо выбирать метод, приводящий к минимуму вычислений. Нет смысла усложнять решение, поскольку большинство алгоритмов направлены на оптимизацию вычислений.

Дробно-рациональная функция — это функция вида , где f(x) и g(x) — некоторые функции.
График дробно-рациональной функции представляет собой гиперболу.
Функция имеет две асимптоты — вертикальную и горизонтальную.
Определение.Прямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность:
x=a уравнение вертикальной асимптоты
y=b уравнение горизонтальной асимптоты
y=kx+b уравнение наклонной асимптоты

Дробно-линейная функция представляет собой частный случай дробно-рациональной функции.
Дробно-линейная функция – это такая алгебраическая дробь , у которой числитель и знаменатель представляют собой линейные функции.
Во всякой дробно-линейной функции можно выделить целую часть.
Построим график функции y=1/x:
D(y): х≠0
E(y): у≠0
y = k/x — нечетная

Построим график функции y=k/x:
При k=2 y=-2/x:
ООФ: х≠0
МЗФ: у≠0
y=k/x – нечетная

Пример1 . Построим график функции , т.е. представим ее в виде : выделим целую часть дроби, разделив числитель на знаменатель, мы получим:

.

Итак, . Мы видим, что график этой функции может быть получен из графика функции у=5/х с помощью двух последовательных сдвигов: сдвига гиперболы у=5/х вправо на 3 единицы, а затем сдвига полученной гиперболы  вверх на 2 единицы.

При этих сдвигах асимптоты гиперболы у=5/х также переместятся: ось х на 2 единицы вверх, а ось у на 3 единицы вправо.

Для построения графика проведем в координатной плоскости пунктиром асимптоты: прямую у=2 и прямую х=3. Так как гипербола состоит из двух ветвей, то для построения каждой из них составим две таблицы: одну для х3 (т. е. первую слева от точки пересечения асимптот, а вторую справа от нее):

x	-7	-2	-1	0	1	2	2,5
y	1,5	1	0,75	0,33	-0,5	-3	-8

x	3,5	4	5	6	7	8	13
y	12	7	4,5	3,33	3,25	3	2,52

Отметив в координатной плоскости точки, координаты которых указаны в первой таблице, и соединив их плавной линией, получим одну ветвь гиперболы. Аналогично (используя вторую таблицу) получим вторую ветвь гиперболы. График функции  изображен на рисунке 3.

Любую дробь  можно записать аналогичным образом, выделив ее целую часть. Следовательно, графики всех дробно-линейных функций являются гиперболами, различным образом сдвинутыми параллельно координатным осям и растянутыми по оси Оу.

Пример 2.

Построим график функции .

Поскольку мы знаем, что график есть гипербола, достаточно найти прямые, к которым приближаются ее ветви (асимптоты), и еще несколько точек.

Найдем сначала вертикальную асимптоту. Функция не определена там, где 2х+2=0, т.е. при х=-1. Стало быть, вертикальной асимптотой служит прямая х=-1.

Чтобы найти горизонтальную асимптоту, надо посмотреть, к чему приближаются значения функций, когда аргумент возрастает (по абсолютной величине), вторые слагаемые в числителе и знаменателе дроби  относительно малы. Поэтому

.

Стало быть, горизонтальная асимптота – прямая у=3/2.

Определим точки пересечения нашей гиперболы с осями координат. При х=0 имеем у=5/2. Функция равна нулю, когда 3х+5=0, т.е. при х=-5/3.

Отметив на чертеже точки (-5/3;0) и (0;5/2) и проведя найденные горизонтальную и вертикальную асимптоты, построим график (рис.4).

Вообще, чтобы найти горизонтальную асимптоту, надо разделить числитель на знаменатель, тогда y=3/2+1/(x+1), y=3/2 – горизонтальная асимптота.

Алгоритм построения графика дробно-рациональной функции, содержащей квадратный трехчлен.

1. Найти область определения функции.

2. Разложить на множители квадратный трехчлен.

3. Сократить дробь.

4. Построить график (параболу, гиперболу, кубическую параболу).

5. Исключить из графика точки, не входящие в область определения («выколотые» точки).

6. Найти значение функции в «выколотых» точках.

7. Определить, при каких значениях b прямая y=b имеет с графиком ровно одну общую точку.

ЗАДАНИЕ

Построить график функции (D(y), на графике – выколотые точки):

1. 

2. 

3. 

4. 

5. 

6. 

7. 

Дробно-рациональные уравнения

Что такое дробно-рациональные уравнения

Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:

при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.

Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.

9 x 2 — 1 3 x = 0

1 2 x + x x + 1 = 1 2

6 x + 1 = x 2 — 5 x x + 1

Уравнения, которые не являются дробно-рациональными:

Как решаются дробно-рациональные уравнения

В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.

Алгоритм действий при стандартном способе решения:

1. Выписать и определить ОДЗ.
2. Найти общий знаменатель для дробей.
3. Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
4. Записать уравнение со скобками.
5. Раскрыть скобки для приведения подобных слагаемых.
6. Найти корни полученного уравнения.
7. Выполним проверку корней в соответствии с ОДЗ.
8. Записать ответ.

Пример 1

Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:

x x — 2 — 7 x + 2 = 8 x 2 — 4

Начать следует с области допустимых значений:

x 2 — 4 ≠ 0 ⇔ x ≠ ± 2

Воспользуемся правилом сокращенного умножения:

x 2 — 4 = ( x — 2 ) ( x + 2 )

В результате общим знаменателем дробей является:

Выполним умножение каждого из членов выражения на общий знаменатель:

x x — 2 — 7 x + 2 = 8 x 2 — 4

x ( x — 2 ) ( x + 2 ) x — 2 — 7 ( x — 2 ) ( x + 2 ) x + 2 = 8 ( x — 2 ) ( x + 2 ) ( x — 2 ) ( x + 2 )

После сокращения избавимся от скобок и приведем подобные слагаемые:

x ( x + 2 ) — 7 ( x — 2 ) = 8

x 2 + 2 x — 7 x + 14 = 8

Осталось решить квадратное уравнение:

Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:

Примеры задач с ответами для 9 класса

Требуется решить дробно-рациональное уравнение:

x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0

x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0

Определим область допустимых значений:

О Д З : x + 2 ≠ 0 ⇔ x ≠ — 2

x 2 + 7 x + 10 ≠ 0

D = 49 — 4 · 10 = 9

x 1 ≠ — 7 + 3 2 = — 2

x 2 ≠ — 7 — 3 2 = — 5

Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:

a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 )

x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0

Заметим, что общим знаменателем для дробей является: ( x + 2 ) ( x + 5 ) . Умножим на этот знаменатель уравнение:

x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0

Сократим дроби, избавимся от скобок, приведем подобные слагаемые:

x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 —

— ( 7 — x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0

x ( x + 5 ) + ( x + 1 ) ( x + 2 ) — 7 + x = 0

x 2 + 5 x + x 2 + 3 x + 2 — 7 + x = 0

2 x 2 + 9 x — 5 = 0

Потребуется решить квадратное уравнение:

2 x 2 + 9 x — 5 = 0

Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.

Дано дробно-рациональное уравнение, корни которого требуется найти:

4 x — 2 — 3 x + 4 = 1

В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:

4 ( x + 4 ) x — 2 — 3 ( x — 2 ) x + 4 — 1 ( x — 2 ) ( x + 4 ) = 0

4 ( x + 4 ) — 3 ( x — 2 ) — ( x — 2 ) ( x + 4 ) ( x — 2 ) ( x + 4 ) = 0

4 x + 16 — 3 x + 6 — ( x 2 + 4 x — 2 x — 8 ) ( x — 2 ) ( x + 4 ) = 0

x + 22 — x 2 — 4 x + 2 x + 8 ( x — 2 ) ( x + 4 ) = 0

Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:

— x 2 — x + 30 ( x — 2 ) ( x + 4 ) = 0 ⇔ — x 2 — x + 30 = 0 ( x — 2 ) ( x + 4 ) ≠ 0

Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:

( x — 2 ) ( x + 4 ) ≠ 0

Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:

— x 2 — x + 30 = 0 _ _ _ · ( — 1 )

Получилось квадратное уравнение, которое можно решить:

Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.

Нужно решить дробно-рациональное уравнение:

x + 2 x 2 — 2 x — x x — 2 = 3 x

На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:

x + 2 1 x ( x — 2 ) — x x x — 2 — 3 ( x — 2 ) x = 0

x + 2 — x 2 — 3 ( x — 2 ) x ( x — 2 ) = 0

x + 2 — x 2 — 3 x + 6 x ( x — 2 ) = 0

— x 2 — 2 x + 8 x ( x — 2 ) = 0 ⇔ — x 2 — 2 x + 8 = 0 x ( x — 2 ) ≠ 0

Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.

— x 2 — 2 x + 8 = 0 _ _ _ · ( — 1 )

Корни квадратного уравнения:

x 1 = — 4 ; x 2 = 2

Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.

Найти корни уравнения:

x 2 — x — 6 x — 3 = x + 2

Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:

x 2 — x — 6 1 x — 3 — x ( x — 3 ) — 2 ( x — 3 ) = 0

x 2 — x — 6 — x ( x — 3 ) — 2 ( x — 3 ) x — 3 = 0

x 2 — x — 6 — x 2 + 3 x — 2 x + 6 x — 3 = 0

0 x x — 3 = 0 ⇔ 0 x = 0 x — 3 ≠ 0

Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:

Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.

Ответ: х — любое число, за исключением 3.

Требуется вычислить корни дробно-рационального уравнения:

5 x — 2 — 3 x + 2 = 20 x 2 — 4

На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:

5 ( x + 2 ) x — 2 — 3 ( x — 2 ) x + 2 — 20 1 ( x — 2 ) ( x + 2 ) = 0

5 ( x + 2 ) — 3 ( x — 2 ) — 20 ( x — 2 ) ( x + 2 ) = 0

5 x + 10 — 3 x + 6 — 20 ( x — 2 ) ( x + 2 ) = 0

2 x — 4 ( x — 2 ) ( x + 2 ) = 0 ⇔ 2 x — 4 = 0 ( x — 2 ) ( x + 2 ) ≠ 0

( x — 2 ) ( x + 2 ) ≠ 0

Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.

Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.

Ответ: корни отсутствуют

Нужно найти корни уравнения:

x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )

Начнем с определения ОДЗ:

— 5 ≠ 0 x ≠ 0 x ( x — 5 ) ≠ 0 x ≠ 5 x ≠ 0

При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:

x — 3 x — 5 + 1 x = x + 5 x ( x — 5 ) · x ( x — 5 )

( x — 3 ) x ( x — 5 ) x — 5 + x ( x — 5 ) x = ( x + 5 ) x ( x — 5 ) x ( x — 5 )

( x — 3 ) x + x = x + 5

Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:

x 2 — 3 x + x — 5 = x + 5 → x 2 — 2 x — 5 — x — 5 = 0 → x 2 — 3 x — 10 = 0

Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x 2 , который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:

x 1 · x 2 = — 10 x 1 + x 2 = 3

В этом случае подходящими являются числа: -2 и 5.

Второе значение не соответствует области допустимых значений.

Как найти область определения функции?

Синонимы: область допустимых значений или сокращенно ОДЗ. Первое, с чем Вы сталкиваетесь при изучении различных функций или же при построении графиков — это область определения функции.

Определение:

Областью определения называется множество значений, которые может принимать x. Обозначение D(f).

Как же это правило применить к заданной Вам функции?

В математике имеется достаточно небольшое количество элементарных функций, область определения которых ограничена. Все остальные «сложные» функции — это всего лишь их сочетания и комбинации.

1. Дробная функция — ограничение на знаменатель.

2. Корень четной степени — ограничение на подкоренное выражение.

3. Логарифмы — ограничение на основание логарифма и подлогарифмическое выражение.

3. Тригонометрические tg(x) и ctg(x) — ограничение на аргумент.

Для тангенса:

Для котангенса:

4. Обратные тригонометрические функции.

Пример нахождения области определения функции №1

Нахождение области определения любой линейной функции, т.е. функции первой степени:

y = 2x + 3 — уравнение задает прямую на плоскости.

Посмотрим внимательно на функцию и подумаем, какие же числовые значения мы сможем подставить в уравнение вместо переменной х?

Попробуем подставить значение х=0

Так как y = 2·0 + 3 = 3 — получили числовое значение, следовательно функция существует при взятом значении переменной х=0.

Попробуем подставить значение х=10

так как y = 2·10 + 3 = 23 — функция существует при взятом значении переменной х=10 .

Попробуем подставить значение х=-10

так как y = 2·(-10) + 3 = -17 — функция существует при взятом значении переменной х=-10 .

Уравнение задает прямую линию на плоcкости, а прямая не имеет ни начала ни конца, следовательно она существует для любых значений х.

Заметим, что какие бы числовые значения мы не подставляли в заданную функцию вместо х, всегда получим числовое значение переменной y.

Следовательно, функция существует для любого значения x ∈ R или запишем так: D(f) = R

Формы записи ответа: D(f)=R или D(f)=(-∞:+∞)или x∈R или x∈(-∞:+∞)

Для любой функции вида y = ax + b областью определения является множество действительных чисел.

Пример нахождения области определения функции №2

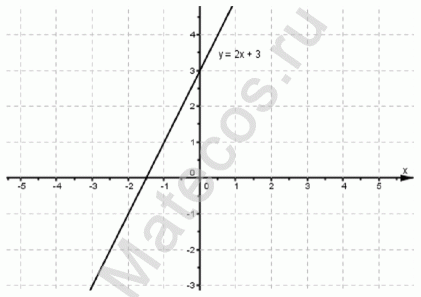
Задана функция вида:

y = 10/(x + 5) — уравнение гиперболы

Имея дело с дробной функцией, вспомним, что на ноль делить нельзя. Следовательно функция будет существовать для всех значений х, которые не

обращают знаменатель в ноль. Попробуем подставить какие-либо произвольные значения х.

При х = 0 имеем y = 10/(0 + 5) = 2 — функция существует.

При х = 10 имеем y = 10/(10 + 5) = 10/15 = 2/ 3 — функция существует.

При х = -5 имеем y = 10/(-5 + 5) = 10/0 — функция в этой точке не существует.

Т.е. если заданная функция дробная, то необходимо знаменатель приравнять нулю и найти такую точку, в которой функция не существует.

x + 5 = 0 → x = -5 — в этой точке заданная функция не существует.

Для наглядности изобразим графически:

На графике также видим, что гипербола максимально близко приближается к прямой х = -5 , но самого значения -5 не достигает.

Видим, что заданная функция существует во всех точках действительной оси, кроме точки x = -5

Формы записи ответа: D(f)=R <-5>или D(f)=(-∞;-5) ∪ (-5;+∞) или x ∈ R <-5>или x ∈ (-∞;-5) ∪ (-5;+∞)

Если заданная функция дробная, то наличие знаменателя накладывает условие неравенства нулю знаменателя.

Пример нахождения области определения функции №3

Рассмотрим пример нахождения области определения функции с корнем четной степени:

Так как квадратный корень мы можем извлечь только из неотрицательного числа, следовательно, функция под корнем — неотрицательна.

Решим простое неравенство:

2х — 8 ≥ 0 → 2х ≥ 8 → х ≥ 4

Заданная функция существует только при найденных значениях х ≥ 4 или D(f)=[4 ;+∞) или x ∈ [4 ;+∞) .

На графике видим, что функция существует для найденных значений х : х ≥ 4 или D(f)=[4 ;+∞) или x ∈ [4 ;+∞) .

При попытке подставить вместо х значения, отличные от найденных, под корнем получим отрицательное число, те в этих точках функция не существует.

Если заданная функция содержит квадратный корень (или корень любой четной степени), то обязательно накладывается условие неотрицательности (≥0) на подкоренное выражение. Если квадратный корень находится в знаменателе функции, у которой мы находим область определения, то на подкоренное выражение накладывается условие положительности (>0), так как знаменатель всегда должен быть отличен от нуля.

Пример нахождения области определения функции №4

Рассмотрим пример нахождения области определения функции с корнем четной степени в знаменателе:

В числителе имеем линейную функцию, область определения которой множество всех действительных чисел. (см. пример 1)

В знаменателе — квадратный корень, накладывает условие на подкоренное выражение, не забывая о том, что знаменатель всегда отличен от нуля.

x 2 — 4x + 3 > 0 → (x — 1)(x — 3) > 0

Решим строгое неравенство методом интервалов:

Видим, что функция положительна на следующих интервалах: x∈(-∞;1)∪(3;+∞)

Нашли такие значения переменной х, при которых функция существует — нашли ОДЗ функции.

Пример нахождения области определения функции №5

Рассмотрим пример нахождения области определения функции с корнем нечетной степени:

Имеем дело с корнем нечетной степени. Так как корень нечетной степени существует при любых значениях подкоренного выражения, то заданная дробная функция под корнем может принимать любые значения.

В числителе дробной функции — уравнение первой сnепени, которое существует при любых значениях переменной. Знаменатель любой дроби отличен от нуля. Следовательно, при нахождении ОДЗ заданного выражения имеем дело лишь с одним ограничением — ограничение на знаменатель дроби.

Пример нахождения области определения функции №6

Рассмотрим пример нахождения области определения логарифма:

Простенький пример на область определения логарифмической функции.

Помним, что основание логарифма положительно и отлично от нуля. Подлогарифмическое выражение положительно:

Покажем на числовой прямой:

Получили ОДЗ: x∈(8;9)∪(9;+∞)

Пример нахождения области определения функции №7

Задана функция вида:

1 ограничение основывается на наложении ограничения на знаменатель дроби (отличен от нуля):

Второе ограничение — подлогарифмическое выражение положительно:

Т.е. для определения области определения заданной функции необходимо решить систему:

Необходимо решить каждое из ограничений системы по отдельности и пересечь получившиеся результаты.

Допускаю, что читатель самостоятельно может это проделать и перехожу к разбору следующего примера.

Пример нахождения области определения функции №8

Рассмотрим следующий пример:

Имеем дело с корнем четной степени, следовательно первое ограничение на подкоренное выражение:

Имеем дело с логарифмом, следовательно ограничение на подлогарифмическую функцию:

Таким образом для определения области определения исходной функции необходимо решить систему неравенств:

Каждое из неравенств решим по отдельности.

Первое неравенство будем решать методом интервалов: найдем корни каждого из выражений неравенства, вынесем их на координатную плоскость и расставим знаки неравенства в каждом из полученных интервалов.

Выносим на координатную прямую:

Объясню как расставлены знаки в каждом из интервалов:

Значения левее 6/7 нет смысла рассматривать, так как логарифм для этих значений не существует.

1-ый интервал: (6/7;1]

Основание логарифма больше единицы, следовательно функция возрастающая. В корне x=1 логарифм меняет свое значение с » — » на » + «.

Как найти область определения функции

Что такое область определения функции?

Начнём с краткого определения. Область определения функции y=f(x) — это множество значений X, для которых существуют значения Y.

Войдём в тему более основательно. Каждой точке графика функции соответствуют:

• определённое значение «икса» — аргумента функции;
• определённое значение «игрека» — самой функции.

Верны следующие факты.

• От аргумента — «икса» — вычисляется «игрек» — значения функции.
• Область определения функции — это множества всех значений «икса», для которых существует, то есть может быть вычислен «игрек» — значение функции. Иначе говоря, множество значений аргумента, на котором «функция работает».

Можно понимать область определения функции и как проекцию графика функции на ось Ox.

Что требуется, чтобы уверенно находить область определения функции? Во-первых, нужно различать виды функций (корень, дробь, синус и др.). Во-вторых, решать уравнения и неравенства с учетом вида функции (например, на что нельзя делить, какое выражение не может быть под знаком корня и тому подобное). Согласитесь, не так уж много и не так сложно. При изучении темы области определения функции поможет материал Свойства и графики элементарных функций. А поскольку областью определения функции служат различные множества, а также их объединения и пересечения, то пригодится и материал Множества и операции над множествами.

Итак, чтобы находить области определения распространённых функций, порешаем уравнения и неравенства с одной переменной.

После этого экскурса в важную составную матанализа многие согласятся, что найти область определения функции не очень сложно.

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы. Приступаем к практике.

Общий принцип на самых простых примерах

Пример 1. На рисунке изображён график функции . Знаменатель дроби не может быть равен нулю, так как на нуль делить нельзя. Поэтому, приравнивая знаменатель нулю

и решая это уравнение:

получаем значение, не входящее в область определения функции: 1. То есть, область определения заданной функции — это все значения «икса» от минус бесконечности до единицы и от единицы до плюс бесконечности. Это хорошо видно на графике. Приведённый здесь пример функции относится к виду дробей. На уроке разберём решения всех распространённых видов функций.

Пример 2. Как найти область определения функции игрек равен квадратному корню из икса минус пять (подкоренное выражение икс минус пять) ()? Так как подкоренное выражение должно быть неотрицательным, нужно решить неравенство

Если перенести какое-либо слагаемое в другую часть неравенства с противоположным знаком, то мы получим равносильное неравенство с тем же знаком неравенства. Переносим минус 5 и получаем неравенство

Получаем решение: область определения функции — все значения икса больше или равно пяти (или икс принадлежит промежутку от пяти включительно до плюс бесконечности).

На чертеже сверху — фрагмент числовой оси. На ней область опредения рассмотренной функции заштрихована, при этом в «плюсовом» направлении штриховка продолжается бесконечно вместе с самой осью.

Область определения корня n-й степени

В случае, функции корня n-й степени, то есть когда функция задана формулой и n — натуральное число:

если n — чётное число, то областью определения функции является множество всех неотрицательных действительных чисел, то есть [0; + ∞[ ;

если n — нечётное число, то областью определения функции является множество всех действительных чисел, то есть ]- ∞; + ∞[ .

Пример 3. Найти область определения функции .

Решение. Как следует из определения, корень чётной степени имеет смысл, если подкоренное выражение неотрицательно. Поэтому решаем неравенство

.

Это квадратное неравенство

,

По формуле находим дискриминант:

.

По формуле находим корни квадратного трёхчлена:

.

Найденные точки разбивают числовую прямую на три промежутка:

и .

При этом знак квадратного трёхчлена (больше или меньше нуля) совпадает со знаком коэффициента a во всех точках промежутков

и

и противоположен знаку коэффициента a во всех точках промежутка .

В нашем случае имеем отрицательный коэффициент a=-1 , поэтому квадратный трёхчлен неотрицателен во всех точках промежутка .

Следовательно, область определения данной функции — [- 1; 1] .

Заштрихованная область числовой прямой на чертеже сверху — это область определения данной функции.

Область определения степенной функции

Область определения степенной функции находится в зависимости от вида степени в выражении.

Область определения степенной функции с дробным показателем степени

В случае, когда функция задана формулой :

если — положительное, то областью определения функции является множество [0; + ∞[ , то есть нуль входит в область определения;

если — отрицательное, то областью определения функции является множество (0; + ∞[ , то есть нуль не входит в область определения.

Пример 4. Найти область определения функции .

Решение. Выражение функции можно представить так:

Квадратный трёхчлен в скобках в знаменателе должен быть строго больше нуля (ещё и потому, что дробный показатель степени данной степенной функции — отрицательный). Поэтому решим строгое неравенство, когда квадратный трёхчлен в скобках строго больше нуля:

.

.

Дикриминант получился отрицательный. Следовательно сопряжённое неравенству квадратное уравнение не имеет корней. А это значит, что квадратный трёхчлен ни при каких значениях «икса» не равен нулю. Таким образом, область определения данной функции — вся числовая ось, или, что то же самое — множество R действительных чисел, или, что то же самое — ]- ∞; + ∞[ .

Пример 5. Найти область определения функции .

Решение. Оба слагаемых в выражении функции — степенные функции с положительными дробными показателями степеней. Следовательно, область определения данной функции — множество [0; + ∞[ .

На чертеже сверху заштрихована часть числовой прямой от нуля (включительно) и больше, причём штриховка продолжается вместе с самой прямой до плюс бесконечности.

Область определения степенной функции с целым показателем степени

В случае, когда функция задана формулой :

если a — положительное, то областью определения функции является множество всех действительных чисел, то есть ]- ∞; + ∞[ ;

если a — отрицательное, то областью определения функции является множество ]- ∞; 0[ ∪ ]0 ;+ ∞[ , то есть вся числовая прямая за исключением нуля.

На соответствующем чертеже сверху вся числовая прямая заштрихована, а точка, соответствующая нулю, выколота (она не входит в область определения функции).

Пример 6. Найти область определения функции .

Решение. Первое слагаемое целой степенью икса, равной 3, а степень икса во втором слагаемом можно представить в виде единицы — так же целого числа. Следовательно, область определения данной функции — вся числовая прямая, то есть ]- ∞; + ∞[ .

Область определения показательной и логарифмической функции

Область определения показательной функции

В случае, когда функция задана формулой , областью определения функции является вся числовая прямая, то есть ]- ∞; + ∞[ . Подробнее о графике такой функции.

Область определения логарифмической функции

Логарифмическая функция определена при условии, если её аргумент положителен, то есть, областью её определения является множество ]0; + ∞[ . Подробнее о графике такой функции.

Найти область определения функции самостоятельно, а затем посмотреть решение

Пример 7. Найти область определения функции .

Пример 8. Найти область определения функции .

Область определения тригонометрических функций

Область определения функции y = cos(x) — так же множество R действительных чисел.

Область определения функции y = tg(x) — множество R действительных чисел, кроме чисел .

Область определения функции y = ctg(x) — множество R действительных чисел, кроме чисел .

Пример 9. Найти область определения функции .

Решение. Внешняя функция — десятичный логарифм и на область её определения распространяются условия области определения логарифмической функции вообще. То есть, её аргумент должен быть положительным. Аргумент здесь — синус «икса». Пользуясь тригонометической таблицей (или поворачивая воображаемый циркуль по окружности), видим, что условие sin x > 0 нарушается при «иксе» равным нулю, «пи», два, умноженном на «пи» и вообще равным произведению числа «пи» и любого чётного ( 2kπ ) или нечётного целого числа ( (2k+1)π ).

Таким образом, область определения данной функции задаётся выражением

,

где k — целое число.

Область определения обратных тригонометрических функций

Область определения функции y = arcsin(x) — множество [-1; 1] .

Область определения функции y = arccos(x) — так же множество [-1; 1] .

Область определения функции y = arctg(x) — множество R действительных чисел.

Область определения функции y = arcctg(x) — так же множество R действительных чисел.

Пример 10. Найти область определения функции .

Решение. Решим неравенство:

Решение получили, основываясь на свойстве неравенств: если все части верного неравенства умножить на одно и то же положительное число, то получится также верное неравество. В данном случае умножали на 4.

Таким образом, получаем область определения данной функции — отрезок [- 4; 4] .

Пример 11. Найти область определения функции .

Решение. Решим два неравенства:

Решение первого неравенства:

Решение получили, основываясь на свойстве неравенств: если обе части верного неравенства умножить на одно и то же отрицательное число изменить знак неравенства на противоположный, то получится верное неравенство. В данном случае умножали на минус 2.

Аналогично и решение второго неравенства:

Таким образом, получаем область определения данной функции — отрезок [0; 1] .

Область определения дроби

Если функция задана дробным выражением, в котором переменная находится в знаменателе дроби, то областью определения функции является множество R действительных чисел, кроме таких x , при которых знаменатель дроби обращается в нуль.

Пример 12. Найти область определения функции .

Решение. Решая равенство нулю знаменателя дроби:

находим область определения данной функции — множество ]- ∞; — 2[ ∪ ]- 2 ;+ ∞[ , то есть все числа, кроме минус 2.

Пример 13. Найти область определения функции .

Решение. Решим уравнение:

Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 1[ ∪ ]1 ;+ ∞[ , то есть все числа, кроме минус единицы и единицы.

Пример 14. Найти область определения функции .

Решение. Область определения первого слагаемого — данной функции — множество R действительных чисел, второго слагаемого — все действительные числа, кроме -2 и 2 (получили, решая равенство нулю знаменателя, как в предыдущем примере). В этом случае область определения функции должна удовлетворять условиями определения обоих слагаемых. Следовательно, область определения данной функции — ]- ∞; — 2[ ∪ ]- 2 ; 2[ ∪ ]2 ;+ ∞[ , то есть все числа, кроме -2 и 2.

Пример 15. Найти область определения функции .

Решение. Решим уравнение:

Уравнение не имеет действительных корней. Но функция определена только на действительных числах. Таким образом, получаем область определения данной функции — вся числовая прямая или, что то же самое — множество R действительных чисел или, что то же самое — ]- ∞; + ∞[ .

То есть, какое бы число мы не подставляли вместо «икса», знаменатель никогда не будет равен нулю.

Пример 16. Найти область определения функции .

Решение. Решим уравнение:

Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 0[ ∪ ]0 ; 1[ ∪ ]1 ;+ ∞[ .

Пример 17. Найти область определения функции .

Решение. Кроме того, что знаменатель не может быть равным нулю, ещё и выражение под корнем не может быть отрицательным. Сначала решим уравнение:

График квадратичной функции под корнем представляет собой параболу, ветви которой направлены вверх. Как следует из решения квадратного уравнения, парабола пересекает ось Ox в точках 1 и 2. Между этими точками линия параболы находится ниже оси Ox, следовательно значения квадратичной функции между этими точками отрицательное. Таким образом, исходная функция не определена на отрезке [1; 2] .

Найти область определения функции самостоятельно, а затем посмотреть решение

Пример 18. Найти область определения функции .

Пример 19. Найти область определения функции .

Область определения постоянной

Постоянная (константа) определена при любых действительных значениях x , следовательно, данная функция определена на всём множестве R действительных чисел. Это можно записать и так: областью определения данной функции является вся числовая прямая ]- ∞; + ∞[ .

Пример 20. Найти область определения функции y = 2 .

Решение. Область определения функции не указана, значит, в силу выше приведённого определения имеется в виду естественная область определения. Выражение f(x) = 2 определено при любых действительных значениях x , следовательно, данная функция определена на всём множестве R действительных чисел.

Поэтому на чертеже сверху числовая прямая заштрихована на всём протяжении от минус бесконечности до плюс бесконечности.

Область определения линейной функции

Если функция задана формулой вида y = kx + b , то область определения функции — множество R действительных чисел.