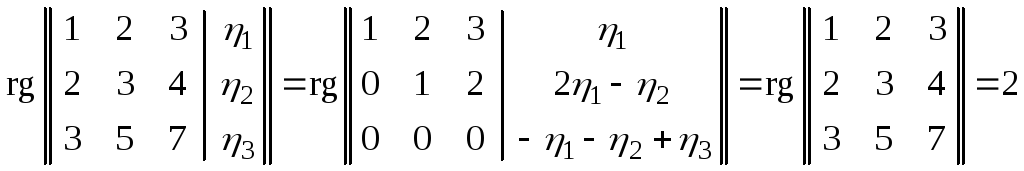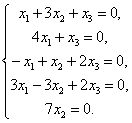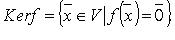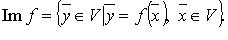Трактуя
линейный оператор, действующий в линейном
пространстве, как некоторое обобщение
понятия функции, естественно рассмотреть
вопрос об области определения и области
значений линейных операторов.
Под
областью
значений линейного оператора
будем понимать множество образоввсех
элементов
,
то есть элементов вида.
В этом случае очевидно, что для любого
линейного оператора его область
определения совпадает с.
Ответ
на вопрос “Что
представляет собой область значений
линейного оператора?”
дает
|
Теорема 8.4.1. |
Пусть
1.
2. |
|
Доказательство: Пусть Пусть |
|
линейности Выделим Теорема |
|
Определение 8.4.1. |
Рангом |
Ранг
линейного оператора линейного оператора
обозначается как
.
|
Следствие 8.4.1. |
|
|
Следствие 8.4.2. |
Размерность |
|
Доказательство: Поскольку Следствие |
|
Теорема 8.4.2. |
Ранг |
|
Доказательство: Рассмотрим |
|
С Теорема |
|
Теорема 8.4.3. |
Если
|
|
Доказательство: Будем Если
Теорема |
Замечания:
1.
Если матрица
не квадратная, но существует одно из
произведений
или
,
то при
также верны равенства
или, соответственно,
.
В этом можно убедиться, заменив матрицу
матрицей
,
являющейся дополнением нулевыми
столбцами или нулевыми строками
до квадратной так, чтобы существовали
или
,
ибо очевидно, что
.
2.
Ранг произведения матриц может быть
меньше рангов каждого из сомножителей.
Например:
.
Другой
важной характеристикой линейного
оператора является совокупность
элементов линейного пространства
,
называемаяядром
линейного оператора и обозначаемая
.
|
Определение 8.4.2. |
Ядро |
|
Теорема 8.4.4. |
Если |
|
Доказательство: Непосредственной Пусть С Теорема |
Линейные
отображения
Как
было отмечено в §8.1., в тех случаях, когда
область значений оператора не принадлежит
области определения, следует говорить
об отображении.
В
§7.5. было использовано понятие взаимно
однозначного отображения, называемого
иногда биекцией.
Для отображений также выделяются
специальные случаи так называемых
инъективных
и сюръективных
отображений. Рассмотрим эти случаи
подробнее.
|
Определение 8.4.3. |
Отображение |
В
случае инъекции множество всех значений
оператора
может не совпадать с.
|
Определение 8.4.4. |
Отображение |
В
случае сюръекции прообраз любого
элемента из
всегда существует в ,
но, вообще говоря, он не единственен.
В
таблице 8.4.1. приведены сравнительные
примеры отображений различных типов.
|
Тип |
Инъективное |
Неинъективное |
|
Сюръективное |
|
|
|
Несюръективное |
|
|
Таблица
8.4.1.
Рассмотрим
теперь линейный оператор
,
отображающий элементы
в элементы
,
то есть отображение, для которого
,
а
.
Допустим, что
есть
базис
в
,
а
— базис в
.
Тогда можно сделать следующее обобщение
определения 8.3.1.
|
Определение 8.4.5. |
Матрица |
Отметим,
что в конечномерном случае сюръективность
отображения означает выполнение условия
,
а инъективность — условия
.
Отсюда следует, что ранг матрицы линейного
оператора, являющегося сюръективным
отображением, равен числу ее строк, а
ранг матрицы инъективного отображения
равен числу ее столбцов. Наконец,
отображение, являющееся одновременно
и инъективным и сюръективным, будет
взаимно однозначным — или биекцией (см.
определение 5.2.4.).
Из
определения 8.4.5. следует, что матрица
линейного отображения зависит как от
выбора базиса
,
так и от выбора базиса.
Правило изменения этой матрицы при
замене базисов дает
|
Теорема 8.4.5. |
Матрица где |
|
Доказательство: |
В
общем случае, исследование свойств
оператора, у которого область значений
не содержится в области его определения,
может оказаться достаточно сложной
задачей. Если же область значений имеет
конечную размерность, не превышающую
размерность области определения, то,
пользуясь теоремой 7.5.1. (об изоморфизме),
можно попытаться свести исследование
отображения к исследованию преобразования,
установив изоморфизм между областью
значений отображения и некоторым
подпространством области его определения.
|
Пример 8.4.1. |
1. Оператор Отметим, Например,
2. Исследование |
|
|
|
Задача 8.4.1. |
Линейное |
Решение:
1.
Пусть координатное представление
прообраза преобразования
есть

а координатное представление образа —
Тогда ядро — множество элементовx
таких, что
,
задается в координатном представлении
системой линейных уравнений
или

общее решение которой есть

Отсюда заключаем, что ядро линейного
отображения
есть линейная оболочка элемента

и поскольку оно не состоит только из
нулевого элемента, то данное отображение
неинъективное.
Заметим,
что к этому же заключению можно прийти,
приняв во внимание, что
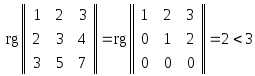
2.
Область значений линейного отображения
состоит из элементов
таких, что
.
В координатной форме принадлежность
элемента
к множеству значений означает совместность
системы линейных уравнений

следовательно,
нам необходимо выяснить, при каких
значениях
данная система линейных уравнений
совместна. Это можно сделать, например,
при помощи теоремы 6.6.1. (Кронекера-Капелли),
сравнив ранги основной и расширенной
матриц данной системы.
Из
условия
найдем,
что для совместности необходимо и
достаточно, чтобы
,
что, в свою очередь, означает, что
множество значений отображения
состоит из элементов вида

являющихся
решениями уравнения
.
Заметим,
наконец, что поскольку не каждый элемент
имеет прообраз в
,
то данное отображение не является и
сюръективным.
Пусть J: Ln → Lm линейный оператор.
Определение 33. Областью значений Оператора J Называется множество J (Ln) образов всех элементов из Ln .
Теорема 32. Область значений линейного оператора J: Ln → Lm есть линейное подпространство в Lm
Доказательство. По определению линейного оператора J (Ln) включает Lm. Пусть в и С – любые два вектора из J (Ln). Тогда существуют такие векторы А1 и А2 Из Ln , что J(А1) = В, J (А2) = С. Тогда, по определению 311, J(AА1 + BА2) = AJ(А1) + BJ(А2) = AВ + BС. Так как AА1 + BА2 Î Ln, То J(AА1 + BА2) Î J (Ln), т. е. AВ + BС Î J (Ln). Отсюда следует, что J (Ln) – линейное подпространство в Lm .
Определение 34. Ядром Линейного оператора J: Ln → Lm называется множество всех векторов из Ln , отображающихся в нулевой вектор пространства Lm.
Теорема 33. Ядро линейного оператора J: Ln → Lm является линейным подпространством в пространстве Ln . (Обозначение ядра Ker(J) )
Доказательство. По определению ядра Ker(J) Ì Ln. Если А1 и А2 Î Ker(J), то J (А1) = 0, J (А2) = 0. Но тогда J(AА1 + BА2) = AJ(А1) + BJ(А2) = A×0 + B×0 = 0 Þ AА1 + BА2 Î Ker(J). Итак, Ker(J) – линейное подпространство в пространстве Ln.
Примеры. 1. Даны два линейных пространства L3 И L5 . Пусть Е = (Е1, Е2, е3) и F = (f1, f2, f3 , f4 , f5 ) – базисы в L3 И L5 соответственно. Пусть А1 = (1, 4, –1, 3, 0), А2 = (3, 0, 1, –3, 7), А3 = (1, 1, 2, 2, 0) – три вектора из L5 . Пусть линейный оператор J: L3 ® L5 задан по правилу J(Х1Е1 + Х2Е2 + Х3Е3 ) = Х1А1 + Х2А2 + Х3А3. Найти J(L3) и Ker(J).
Решение. Так как Х1, х2, х3 – любые элементы поля коэффициентов Р, то Х1А1 + Х2А2 + Х3А3 – любой вектор из линейной оболочки < а1, а2, а3 >. Итак, J(L3) = < а1, а2, а3 >.
J(Х1Е1 + Х2Е2 + Х3Е3 ) = 0 Û Х1А1 + Х2А2 + Х3А3 = 0 Û Х1(1, 4, –1, 3, 0) + Х2(3, 0, 1, –3, 7)+ + Х3(1, 1, 2, 2, 0) = (Х1 + 3Х2 + Х3 , 4Х1 + Х3 , –Х1 + Х2 + 2Х3 , 3Х1 –3Х2 + 2Х3 , 7Х2 ) = 0 Û
|
|
Для нахождения Х1, х2. х3 получили систему пяти уравнений с тремя неизвестными. Решая её, получим Х1 = х2 = х3 = 0. Следовательно, ядро данного линейного оператора состоит только из нулевого вектора. |
2. Даны два линейных пространства L3 И L5 . Пусть Е = (Е1, Е2, е3) и F = (f1, f2, f3 , f4 , f5) – реперы в L3 И L5 соответственно. Пусть линейный оператор J : L5 ® L3 задан правилом J( х1F1 + Х2F2 + Х3 F3 + Х4F4 + Х5F5) = Х1Е1 + Х2Е2 + Х3Е3. Найти J(L5) и Ker(J).
Решение. Очевидно, J(L5) = < е1, Е2, е3 > = L3. Найдём ядро.
J( х1F1 + Х2F2 + Х3 F3 + Х4F4 + Х5F5) = 0 равносильно Х1Е1 + Х2Е2 + Х3Е3 равносильно Х1 = х2 = х3 = 0. Итак, ядро состоит из векторов вида А = (0, 0, 0, Х4, х5 ), где Х4, х5 – любые элементы поля Р.
| < Предыдущая | Следующая > |
|---|
01.Образ и ядро линейного оператора. Ранг и дефект линейного оператора
Определение: Совокупность всевозможных векторов вида называется образом оператора A и обозначается ImA. Таким образом .
Определение: Совокупность всевозможных векторов для которых называется ядром оператора A и обозначается KerA. Таким образом .
Утверждение: образ и ядро линейного оператора А являются подпространствами линейного пространства V.
Доказательство: В самом деле в силу линейности оператора А имеем:
1) тогда и т. к то
и т. к. , то является подпространством пространства V.
является подпространством пространства V. #
Пусть V – n мерное комплексное или вещественное линейное пространство.
1) Тождественный оператор , при этом Ax = Ix = X, тогда ImA=ImI=V, KerA=KerI=θ>
/ ядро состоит из единственного нулевого элемента /
2) Нулевой оператор, тогда
3) Рассмотрим оператор дифференцирования на пространстве многочленов степени не выше N, тогда отсюда. Видно, что во всех приведенных примерах справедливо:
, что не является случайным.
Теорема (о сумме размерностей образа и ядра линейного оператора) :
Пусть A — линейный оператор, действующий в линейном пространстве V. Тогда сумма размерностей образа и ядра оператора равна размерности данного линейного пространства, т. е.
Доказательство:
Выберем в пространстве V произвольный базис . Поскольку по определению , то можно записать, что линейная оболочка, порождаемая совокупностью образов базисных векторов , причем , где R – максимальное число л. н.з. векторов в системе. Но координаты именно этих векторов стоят в столбцах матрицы линейного оператора А в базисе, поэтому .
Рассмотрим ядро оператора А: .
В выбранном базисе равенству соответствует однородная СЛАУ:, которая, как известно, имеет (N—R) л. н.з. решений, образующих ФСР. Поскольку неизвестными данной системы являются координаты векторов, составляющих KerA, то отсюда заключаем, что dim(KerA)=N—R. В результате получаем, что
Определение: Размерность образа оператора называется рангом оператора, размерность ядра оператора называется дефектом оператора.
Определение: Линейный оператор называется невырожденным, если в произвольном базисе (E) данного линейного пространства V Оператор А имеет невырожденную матрицу .
Следствие: Если А – невырожденный линейный оператор, то его образ совпадает со всем пространством, в котором этот оператор действует.
Доказательство: Если , то по предыдущей теореме запишем . По Свойству 40 невырожденных операторов (докажем позже в параграфе 12 главе 7) равенство возможно только при отсюда откуда . Т. к. , то отсюда следует, что .
Определение: Подпространство L пространства V называется инвариантным относительно линейного оператора А, если .
Теорема (об инвариантности образа и ядра линейного оператора):
Образ и ядро линейного оператора А являются подпространствами инвариантными относительно оператора А.
Доказательство:
1) Пусть , т. к. то и поэтому , т. е. подпространство ImA является инвариантным относительно оператора А.
2) Пусть . Тогда, т. у. а значит подпространство KerA инвариантно относительно оператора А.
Как найти дефект матрицы
Определение 2. Пусть — линейный оператор, действующий в пространстве Совокупность всевозможных векторов вида где называется областью значений оператора или образом пространства при преобразовании а множество всевозможных векторов х, для которых — ядром оператора
Покажем, что область значений и ядро линейного оператора являются подпространствами в
Действительно, для области значений это вытекает из теоремы 1, если рассматриваемое в ней подпространство совпадает со всем пространством
С другой стороны, если т. е. если то и и значит, — подпространство.
Размерность области значений оператора совпадает с рангом матрицы А (и называется рангом оператора Действительно, подпространство порождается векторами
где — любой базис пространства и значит, размерность равна максимальному числу линейно независимых векторов в системе (6), т. е. равна максимальному числу линейно независимых столбцов матрицы
Размерность ядра называется дефектом линейного оператора
Теорема 4. Сумма ранга и дефекта линейного оператора равна размерности пространства.
Доказательство. Если ранг линейного оператора равен то среди векторов найдется линейно независимых, через которые линейно выражаются все остальные. Пусть, для определенности, это будут
Обозначим через подпространство, порожденное в векторами и покажем, что (r-мерное) подпространство и ядро пересекаются только по нулевому вектору. Действительно, если то Но так как векторы линейно независимы, то
Покажем теперь, что подпространства и порождают все (т. е. что их сумма совпадает с Пусть х — произвольный вектор из Тогда , следовательно, Вектор принадлежит, очевидно, а разность так как Мы нашли, что где
Таким образом, пространство равно прямой сумме подпространств и а значит, его размерность равна сумме размерностей этих подпространств.
В дальнейшем нам понадобится еще такое
Определение 2. Пусть — линейный оператор, отображающий пространство в пространство (вообще говоря, другой размерности). Тогда множество всех векторов у из вида где называется областью значений оператора (или образом пространства при отображении а множество всех векторов х из таких, что его ядром.
Нетрудно видеть, что область значений оператора заявляется подпространством в а его ядро — подпространством в (докажите это),
Линейное пространство
Пусть L- это некоторое множество, элементы которого мы удем называть «векторами», P- некоторое(числовое поле). Пусть так же выполняются следующие условия.
1. В L определена операция сложения элементов.
2. В Lопределена операция умножения элемента на число из P.
3. Эти операции удовлетворяют законам дистрибутивности.
Тогда говорим, что L образует линейное пространство над полем P относительно операций сложений и умножней.
Произведение линейных операторов: определение и свойства.
Критерии невырожденности линейного оператора.
Ядро, образ, ранг и дефект линейного оператора. Связь ранга и дефекта
ВНИМАНИЕ, ДЛЯ ПОЛНОГО ОЗНАКОМЛЕНИЕ ПРОСМОТРИТЕ ВОПРОС 33!
Ядро и область значений линейного оператора
Ядро оператора: 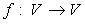
Область значений (образ) оператора 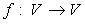
Множества Ker f и Im f являются подпространствами пространства V.
Ранг оператора 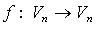
dim Im f = rank A.
Дефектом оператора 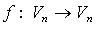
dim Im f + dim Ker f = n.
Матрица линейного оператора. Теорема о координатах образа вектора при линейном преобразовании
-Матрица линейного оператора.
Линейный оператор A действует из n-мерного линейного пространства X в m-мерное линейное пространство Y .
В этих пространствах определены базисы e = 1, . en> и f = 1, . fm>.
Пусть A(ei ) = a1i·f1 + a2i·f2 + . + ami·fm — разложение образа i-го базисного вектора базиса e пространства X по базису f пространства Y, i = 1, 2, . n.
Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f , A = aij>= A(ej )i>:
Координаты образа y = A(x) и прообраза x связаны соотношеннием:
y =A· x,
-Теорема о координатах образа вектора при линейном преобразовании.
Образ вектора х равен произведению матрицы линейного оператора на столбец его координат: если у = А(х), то

 ядру оператора
ядру оператора


















 ,
,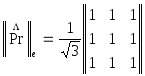 .
. .
.