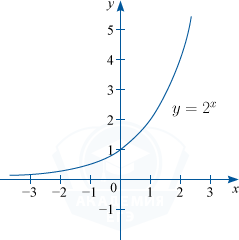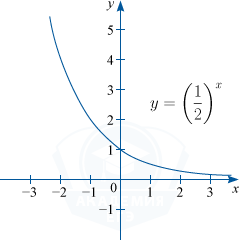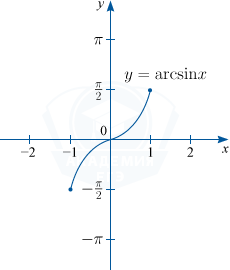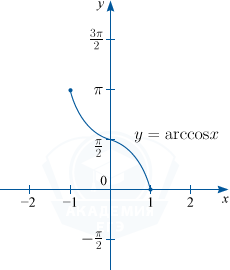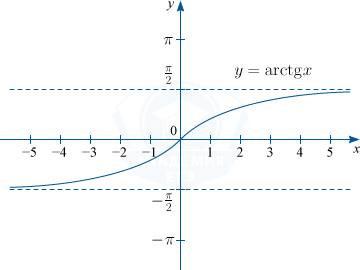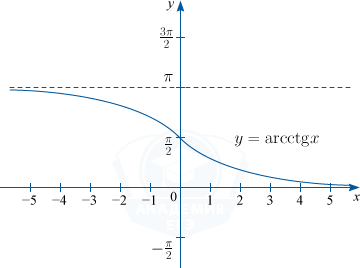Линейная функция
Но сначала официальное определение «Функции» – теперь ты его поймешь. Держи в уме: деньги – зарплата, вес – круассаны, расстояние – время.
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция ( y=fleft( x right)), это значит что каждому допустимому значению переменной ( x) (которую называют «аргументом») соответствует одно значение переменной ( y) (называемой «функцией»).
Что значит «допустимому»?
Все дело в понятии «область определения»: для некоторых функций не все аргументы «одинаково полезны» — не все можно подставить в зависимость.
Например, для функции ( y=sqrt{x}) отрицательные значения аргумента ( x) – недопустимы.
Ну и вернемся, наконец, к теме данной статьи.
Линейной называется функция вида ( y=kx+b), где ( k) и ( b) – любые числа (они называются коэффициентами).
Другими словами, линейная функция – это такая зависимость, что функция прямо пропорциональна аргументу.
Как думаешь, почему она называется линейной?
Все просто: потому что графиком этой функции является прямая линия. Но об этом чуть позже.
Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения ( Dleft( y right)) и область значений ( Eleft( y right)).
Область значений линейной функции
Тут тоже все просто: поскольку функция прямо пропорциональна аргументу, то чем больше аргумент ( x), тем больше значение функции ( y).
Значит, ( y) так же как и ( x) может принимать все возможные значения, то есть ( Eleft( y right)=mathbb{R}), верно?
Верно, да не всегда. Есть такие линейные функции, которые не могут принимать любые значения. Как думаешь, в каком случае возникают ограничения?
Вспомним формулу: ( y=kx+b). Какие нужно выбрать коэффициенты ( k) и ( b), чтобы значение функции y не зависело от аргумента ( x)?
А вот какие: ( b) – любое, но ( k=0). И правда, каким бы ни был аргумент ( x), при умножении на ( k=0) получится ( 0)!
Тогда функция станет равна ( y=0cdot x+b=b), то есть она принимает одно и то же значение при всех ( x):
( y = kx + b:{rm{ }}left[ begin{array}{l}Eleft( y right) = mathbb{R}{rm{ при }}k ne 0\Eleft( y right) = left{ b right}{rm{ при }}k = 0.end{array} right.)
Теперь рассмотрим несколько задач на линейную функцию.
График линейной функции
Как я уже упоминал ранее, график такой функции – прямая линия.
Как известно из геометрии, прямую можно провести через две точки (то есть, если известны две точки, принадлежащие прямой, этого достаточно, чтобы ее начертить).
Предположим, у нас есть функция линейная функция ( y=2x+1). Чтобы построить ее график, нужно вычислить координаты любых двух точек.
То есть нужно взять любые два значения аргумента ( x) и вычислить соответствующие два значения функции.
Затем для каждой пары ( left( x;y right)) найдем точку в системе координат, и проведем прямую через эти две точки.
Проще всего найти функцию, если аргумент ( x=0:yleft( 0 right)=2cdot 0+1=1).
Итак, первая точка имеет координаты ( left( 0;1 right)).
Теперь возьмем любое другое число в качестве ( x), например, ( x=1:yleft( 1 right)=2cdot 1+1=3).
Вторая точка имеет координаты ( left( 1;3 right)).
Ставим эти две точки на координатной плоскости:
Теперь прикладываем линейку, и проводим прямую через эти две точки:
Вот и все, график построен!
Давай теперь на этом же рисунке построим еще два графика: ( y={x} -1) и ( y=-x+2).
Построй их самостоятельно так же: посчитай значение y для любых двух значений ( x), отметь эти точки на рисунке и проведи через них прямую.
Должно получиться так:
Коэффициенты линейной функции
Для начала выясним, что делает коэффициент ( displaystyle b). Рассмотрим функцию ( displaystyle y=x+b), то есть ( displaystyle k=1).
Меняя ( displaystyle b) будем следить, что происходит с графиком.
Итак, начертим графики для разных значений ( displaystyle b:b=-2,text{ -}1,text{ }0,text{ }1,text{ }2):
Что ты можешь сказать о них? Чем отличаются графики?
Это сразу видно: чем больше ( displaystyle b), тем выше располагается прямая.
Более того, заметь такую вещь: график пересекает ось ( displaystyle mathbf{y}) в точке с координатой, равной ( displaystyle mathbf{b})!
И правда. Как найти точку пересечения графика с осью ( displaystyle y)? Чему равен ( displaystyle x) в такой точке?
В любой точке оси ординат (это название оси ( displaystyle y), если ты забыл) ( displaystyle x=0).
Значит достаточно подставить ( displaystyle x=0) в функцию, и получим ординату пересечения графика с осью ( displaystyle y):
( displaystyle y=kcdot 0+b=b)
Теперь по поводу ( displaystyle k). Рассмотрим функцию ( displaystyle left( b=0 right).) Будем менять ( displaystyle k) и смотреть, что происходит с графиком.
Построим графики для ( displaystyle k=-3,text{ -}1,text{ }0,text{ }1,text{ }2:)
Так, теперь ясно: ( displaystyle k) влияет на наклон графика.
Чем больше ( displaystyle k) по модулю (то есть несмотря на знак), тем «круче» (под большим углом к оси абсцисс – ( displaystyle Ox)) расположена прямая.
Если ( displaystyle k>0), график наклонен «вправо», при ( displaystyle k<0) – «влево». А когда ( displaystyle k=0), прямая располагается вдоль оси абсциссс.
Давай разбираться. Начертим новый график ( displaystyle y=kx+b):
Выберем на графике две точки ( displaystyle A) и ( displaystyle B). Для простоты выберем точку ( displaystyle A) на пересечении графика с осью ординат. Точка ( displaystyle B) – в произвольном месте прямой, пусть ее координаты равны ( displaystyle left( x;y right)).
Рассмотрим прямоугольный треугольник ( displaystyle ABC), построенный на отрезке ( displaystyle AB) как на гипотенузе.
Из рисунка видно, что ( displaystyle AC=x), ( displaystyle BC=y-b).
Подставим ( displaystyle y=kx+b) в ( displaystyle BC:BC=y-b=kx+b-b=kx).
Получается, что ( BC = k cdot AC{rm{ }} Rightarrow {rm{ }}k = frac{{BC}}{{AC}} = {mathop{rm tg}nolimits} alpha ).
Итак, коэффициент ( displaystyle k) равен тангенсу угла наклона графика, то есть угла между графиком и осью абсциссс.
Именно поэтому его (коэффициент ( displaystyle k)) обычно называют угловым коэффициентом.
В случае, когда ( k < 0,{mathop{rm tg}nolimits} alpha < 0,) что соответствует тупому углу:
Если же ( displaystyle k=0), тогда и ( {mathop{rm tg}nolimits} alpha = 0,) следовательно ( displaystyle alpha =0), то есть прямая параллельна оси абсцисс.
Понимать геометрическое значение коэффициентов очень важно, оно часто используется в различных задачах на линейную функцию.
Свойства линейной функции
1) Найдем область определения и область значений функции
Так как область определения функции — это допустимые значения независимой переменной, то задача заключается в том, чтобы понять есть ли у линейной функции ограничения на значение переменной «х» . Давайте обратим внимание на аналитическое задание y=kx+b, проанализировав данное выражение можно сделать вывод: «х» может принимать любые действительные значения, следовательно:
D(f)=(-∞;+∞).
Аналогично найдем область значений функции — «у» может принимать любые действительные значения, следовательно:
Е(f)=(-∞;+∞).
2) Найдем нули функции
Если y=0, то получим уравнение kx+b=0, откуда
x=-b/k
Значит функция пересекает ось ОХ в точке (-b/k ; 0)
3) Определим промежутки знакопостоянства
Для определения промежутков знакопостоянства воспользуемся алгоритмом выведенным ранее ( Свойства функций → Знакопостоянства):
а) Функция принимает положительные значения: kx+b>0
x>-b/k
б) Функция принимает отрицательные значения: kx+b<0
x<-b/k
4) Определим промежутки монотонности линейной функции
Рассмотрим 2 случая:
1 случай: k>0
Функция возрастает при x ∈ (-∞; +∞)
2 случай: k<0
Функция убывает при x ∈ (-∞; +∞)
5) Проверим функцию на четность и нечетность
f(-x)=-kx+b
Функция не является четной и не является нечетной если k ≠ 0 и b ≠ 0
Если k=0, то функция является четной
Если k ≠ 0 и b=0, то функция является нечетной
Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.
Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.
Число k называется угловым коэффициентом прямой.
Свойства линейной функции
- Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
- Областью значений также является множество всех действительных чисел.
- Функция не имеет ни наибольших, ни наименьших значений.
- При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
- При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
- При k=0 прямая параллельна оси х.
- Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.
Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.
Пример №1
Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:
Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).
Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:
у=2х – 1=2×0 – 1= –1;
у=2х – 1=2×3 – 1= 5.
Вписываем в таблицу значения у:
Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5), проводим через эти две точки прямую.
Итак, по формуле мы видим, что угловой коэффициент – положительный, значит, график – возрастает, что мы и видим на нашем графике.
Пример №2.
Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.
По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).
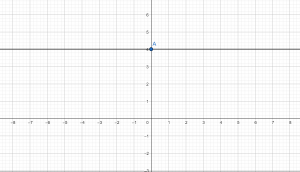
Пример №3
Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:
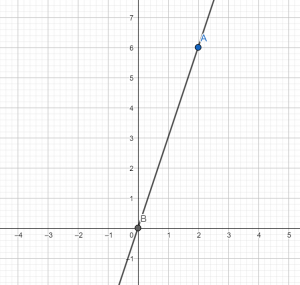
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.
Задание OM1106o
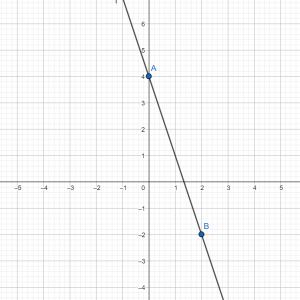
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ:
КОЭФФИЦИЕНТЫ:
1) k>0, b<0 2) k>0, b>0 3) k<0, b<0
ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<900). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
Ответ: 213
pазбирался: Даниил Романович | обсудить разбор
Задание OM1103o
Установите соответствие между функциями и их графиками.
Функции:
A) y = 3x
Б) y = -3x
В) y = (1/3)x
Графики:
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
y = kx + b
График данной функции зависит от k и b.
- если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1
Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.
Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 6.2k
Графики элементарных функций
Линейная функция
Линейная функция — это функция вида y=kx+b, где k и b некоторые действительные числа.
Если b=0, то функция примет вид y=kx и будет называться прямой пропорциональностью.
D(f) : x in R;enspace E(f) : y in R
График линейной функции — прямая.
Угловой коэффициент k прямой y=kx+b вычисляется по следующей формуле:
k= tg alpha , где alpha — угол наклона прямой к положительному направлению оси Ox.
1) Функция монотонно возрастает при k > 0.
Например: y=x+1
2) Функция монотонно убывает при k < 0.
Например: y=-x+1
3) Если k=0, то придавая b произвольные значения, получим семейство прямых параллельных оси Ox.
Например: y=-1
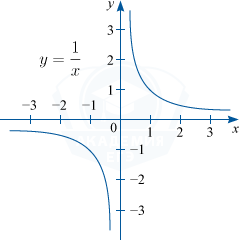
Обратная пропорциональность
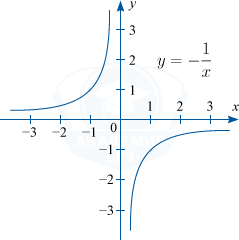
Обратной пропорциональностью называется функция вида y=frac {k}{x}, где k — отличное от нуля, действительное число
D(f) : x in left { R/x neq 0 right }; : E(f) : y in left {R/y neq 0 right }.
Графиком функции y=frac {k}{x} является гипербола.
1) Если k > 0, то график функции будет располагаться в первой и третьей четверти координатной плоскости.
Например: y=frac{1}{x}
2) Если k < 0, то график функции будет располагаться во второй и четвертой координатной плоскости.
Например: y=-frac{1}{x}
Степенная функция
Степенная функция — это функция вида y=x^n, где n — отличное от нуля, действительное число
1) Если n=2, то y=x^2. D(f) : x in R; : E(f) : y in [0; +infty) .
Графиком функции y=x^2 является парабола.
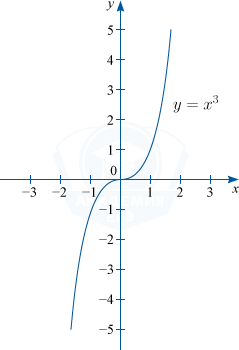
2) Если n=3, то y=x^3. D(f) : x in R; : E(f) : y in R .
Графиком функции y=x^3 является кубическая парабола.
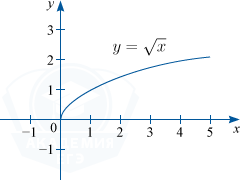
3) Если n=frac{1}{2}, то y=x^tfrac{1}{2} или y=sqrt{x}. D(f) : x in [0; +infty ); : E(f) : y in [0; +infty )
4) Если n=frac{1}{3}, то y=x^tfrac{1}{3} или y=sqrt[3]{x}. D(f) : x in R; : E(f) : y in R
Показательная функция
Показательная функция — это функция вида y=a^x, где a=const, a > 0, a neq 1
D(f) : x in R; : E(f) : y in (0; +infty ).
Графиком показательной функции является экспонента.
1) Функция будет монотонно возрастать при a > 1.
Например: y=2^x
2) Функция монотонно убывает при 0 < a < 1.
Например: y=left (frac{1}{2} right )^{x}
Логарифмическая функция
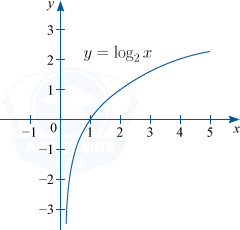
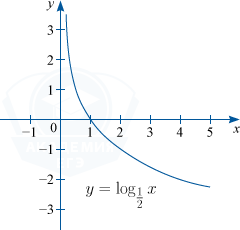
Логарифмическая функция — это функция вида y=log_{a}x, где a — действительное число, a > 0, : a neq 1
D(f) : x in (0; +infty ); : E(f) : y in R.
1) Функция монотонно возрастает при a > 1.
Например: y=log_{2}x
2) Функция будет монотонно убывать при 0 < a < 1.
Например: y=log_{tfrac{1}{2}}x
Тригонометрическая функция
К тригонометрическим функциям относят функции вида:
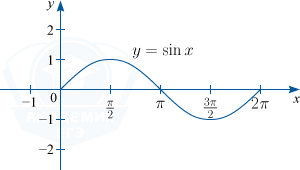
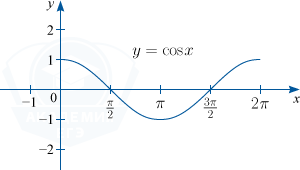
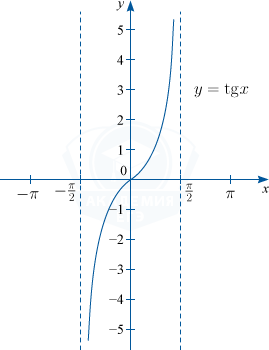
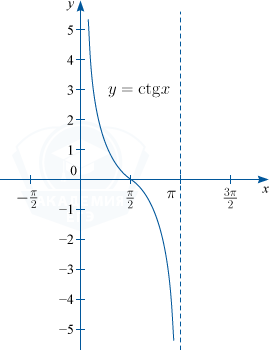
1) y=sin x. D(f) : x in R; : E(f) : y in [-1; 1]; основной период функции T=2 pi
2) y = cos x. D(f) : x in R; : E(f) : y in [-1; 1]; основной период функции T=2 pi
3) y = tg x. D(f) : x in left { R /x neq frac{pi}{2}+pi nright }, n in mathbb{Z}; : E(f) : y in R; основной период функции T= pi
4) y = ctg x. D(f) : x in left { R /x neq 0+pi nright }, n in mathbb{Z}; : E(f) : y in R; основной период функции T= pi
Обратные тригонометрические функции
К обратным тригонометрическим функциям относят функции вида:
1) y=arcsin x. D(f) : x in [-1; 1], : E(f) : y in left [ -frac{pi}{2}; frac{pi}{2} right ]
2) y=arccos x. D(f) : x in [-1; 1], : E(f) : y in [0; pi]
3) y=arctg x. D(f) : x in R, : E(f) : y in left (-frac{pi}{2}; frac{pi}{2} right )
4) y= arcctg x. D(f) : x in R, : E(f) : y in left (0; pi right )
На этой странице вы узнаете:
- За что отвечают коэффициенты в записи линейной функции?
- Как пронумерованы четверти на координатной плоскости?
- Чем отличается график функции квадратного корня от графика квадратичной функции и почему?
Линейная функция
Любую функцию можно изобразить на графике (рисунке) и наглядно определить многие её свойства. Этим пользуются люди, составляя графики движения транспорта, посещения соцсетей или просмотра видеороликов на канале.

Вспомним, что функция – это зависимость одной переменной от другой, а график функции – это представление данной зависимости на координатной плоскости.
С помощью графика функции можно изучать поведение функции: возрастает или убывает, имеет ли нули, на каких промежутках значения положительные, а на каких отрицательные, наибольшее и наименьшее значение, является ли симметричной относительно OY.
Теперь давайте рассмотрим основные элементарные функции.
Что же такое линейная функция?
Линейная функция – это функция вида y=kx+b, где k и b – известные числа, графиком которой является прямая.
y = kx + b, где
k – коэффициент
b – свободный член
x – переменная
С линейной функцией мы встречаемся, когда оплачиваем проезд в общественном транспорте.
Коэффициент и переменная определяют стоимость билета в зависимости от дальности поездки. Свободным членом может выступать доплата за комфортное место или за поезд-экспресс.
| Пункт назначения | Станция 200 км | Станция 300 км | Станция 400 км |
| Цена поездки в обычном вагоне (kx) | 500 руб. | 750 руб. | 1000 руб. |
| Цена за вагон “Люкс” (kx + b) | 750 руб. | 1000 руб. | 1250 руб. |
Рассмотрим пример такой функции и ее график:
y = 2x + 3
Составим таблицу значений.

Теперь отметим найденные точки на координатной плоскости и проведём через них прямую.

Полученный нами график является графиком данной линейной функции.
Также можно составить уравнение линейной функции самостоятельно при наличии графика.
Коэффициент b – это длина отрезка по оси OY, на который происходит сдвиг от начала координат (может быть отрицательным, если пересечение графика с осью Y в точке с отрицательным значением).
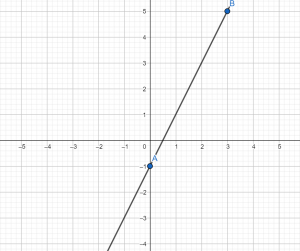
Коэффициент k – это угол наклона прямой, он равен отношению разностей координат двух произвольных точек.

На графике найдем сначала коэффициент b , после определим координаты двух произвольных точек прямой и вычислим коэффициент k.

Подставим найденные коэффициенты в формулу линейной функции и получим
(y = frac{1}{2}x + 2)
Свойства линейной функции:
- Область определения: D(y) = (-∞; +∞)
- Область значений функции: E(y) = (-∞; +∞)
- Наименьшего и наибольшего значения не существует.
- Непериодическая.
- Возрастает при k > 0, убывает при k < 0.
Квадратичная функция
Квадратичная функция – это функция вида y = ax2, где a – известное число и a ≠ 0, графиком которой является парабола.
y = ax2, где
a – известное число
a ≠ 0
x – переменная
Для примера построим график функции y = 2x2


Параболой можно описать полет мяча в баскетбольную корзину.

Какой вид имеет парабола в зависимости от коэффициента a ?
При a > 0 – ветви параболы вверх

При a < 0 – ветви параболы вниз

Сдвиг параболы по оси Y
y = ax2 + c
При c > 0 – сдвиг параболы вверх

При c < 0 – сдвиг параболы вниз

Сдвиг параболы по оси X
y = a(x — n)2
При n > 0 – сдвиг параболы вправо

При n < 0 – сдвиг параболы влево

Свойства квадратичной функции:
- Область определения: D(y) = (-∞; +∞)
- Область значений функции: E(y) = [0; +∞)
- При a > 0 – наименьшее значение y = 0.
При a < 0 – наибольшее значение y=0. - Непериодическая.
- На (-∞; 0] – убывает при a > 0 и возрастает при a < 0.
На [0; +∞) — убывает при a < 0 и возрастает при a > 0. - Нуль функции x=0.
- Четная (симметричная относительно OY).
Функция обратной пропорциональности
Функция обратной пропорциональности – это функция вида y = (frac{k}{x}), где k – известное число и k ≠ 0, графиком которой является гипербола.
(y = frac{k}{x}), где
k – известное число
k ≠ 0
x – переменная
Рассмотрим пример такой функции (y = frac{2}{x})


Как коэффициент k влияет на расположение гиперболы?
Вспомним четверти плоскостей. Они идут против часовой стрелки начиная с четверти, где и x, и y — положительные.

Гипербола при k > 0 – в первой и третьей плоскостях

Гипербола при k< 0 – во второй и четвертой плоскостях

Гипербола может также двигаться по оси X или по оси Y
Движение графика по оси Y
(y = frac{k}{x} + n) при k> 0
При n < 0, сдвиг вниз
При n > 0, сдвиг вверх

По графику выше можно сделать вывод, что n = 3.
Движение графика по оси X
(y = frac{k}{x + c}) при k> 0
При c < 0, сдвиг вправо
При c > 0, сдвиг влево

По графику выше можно сделать вывод, что c = 3.
Свойства функции обратной пропорциональности:
- Область определения: D(y) = (-∞; 0) U (0; +∞)
- Область значений функции: E(y) = (-∞; 0) U (0; +∞)
- Наименьшего и наибольшего значений не существует.
- Непериодическая.
- При k > 0 убывает на (-∞;0) и (0; +∞).
При k < 0 возрастает на (-∞; 0) и (0; +∞). - Нулей нет.
- Нечетная.
Где же в реальной жизни мы можем встретить эту функцию?
Самый простой пример – движение автомобиля: чем выше его скорость, тем меньше времени потребуется, чтобы преодолеть одно и то же расстояние.
Функция квадратного корня
Функция квадратного корня – это функция вида (y = sqrt{x}), где x ≥ 0 .
(y = sqrt{x}), где
x – переменная
x ≥ 0
В жизни такая функция часто используется для определения стороны квадрата при известной площади. Например: при проектировании дома или разбиения участка земли на квадраты.
Рассмотрим график такой функции.


По графику квадратного корня уже видно, что это половина параболы, изображенной вдоль оси х. А график квадратичной функции — это целая парабола, изображенная вдоль оси y.
Так как корень всегда положительный, у функции квадратного корня (y = sqrt{x}) , всегда y ≥ 0. А значит не будет части параболы, где y < 0.
Если возвести обе части функции квадратного корня в квадрат, то получим y2 = x. Получившаяся функция будет уже квадратичной функцией относительно y, следовательно, будет строиться относительно х.
Какие бывают сдвиги функции квадратного корня?
Сдвиг по оси Y
(y = sqrt{x} + n)
При n < 0, сдвиг вниз
При n > 0, сдвиг вверх

По графику выше можно утверждать, что n = -2.
Сдвиг по оси X
(y = sqrt{x + c})
При c < 0, сдвиг вправо
При c > 0, сдвиг влево

Сделаем вывод, что для рисунка выше c = -2.
Свойства функции квадратного корня:
- Область определения: D(y) = [0; +∞)
- Область значений функции: E(y) = [0; +∞)
- Наименьшее значение при y = 0.
- Непериодическая.
- Возрастает на всей области определения.
- Нуль функции x = 0.
Фактчек
- Линейная функции y = kx + b.
- Квадратичная функции y = ax2.
- Функция обратной пропорциональности (y = frac{k}{x}).
- Функция квадратного корня (y = sqrt{x}).
Термины
Элементарная функция – это функция вида y = f(x) , где f(x) – это формула, содержащая конечное число арифметических операций.
Парабола – это незамкнутая линия, точки на которой равноудалены от оси ординат.
Проверь себя
Задание 1.
Определите какая из функций является линейной
- (y = 2x^2 + frac{1}{2})
- (y = sqrt{x + 2})
- (y = frac{1}{2}x + 3)
- (y = frac{1}{x — 2})
Задание 2.
Определите какая из функций является квадратичной
- y = 4(x — 1)2
- y = 2x + 11
- (y = frac{x}{2} + 1)
- (y = sqrt{x} + 3)
Задание 3.
Определите какая функция является обратной пропорциональностью
- (y = frac{x}{2} + 5)
- (y = frac{1}{x + 2})
- (y = sqrt{x + 1})
- y = x2
Задание 4.
Определите какая функция является функцией квадратного корня
- y = x2
- (y = sqrt{x — 1} — 4)
- (y = 6x + frac{1}{3})
- y = 2x2 + 3
Задание 5.
В какую сторону будет сдвиг у параболы y = (x + 4)2?
- Вправо
- Вниз
- Вверх
- Влево
Ответы: 1. – 3; 2. – 1; 3. – 2; 4. – 2; 5. – 4



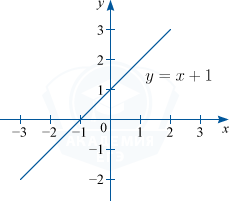
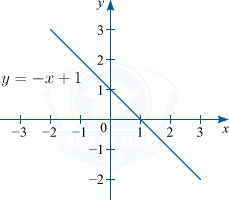
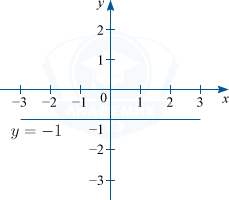
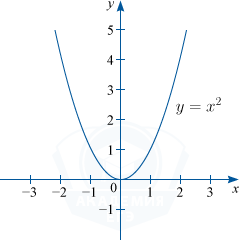
![График степенной функции y=x^{frac 13} или y=sqrt[3]x](https://egeguru.com/i/grafik-stepennoj-funkcii-yxfrac-13-ili-ysqrt3x.png)