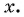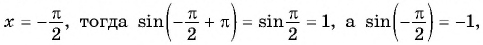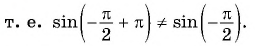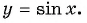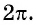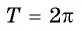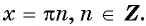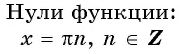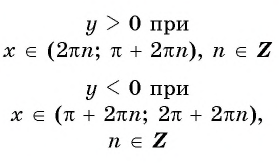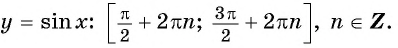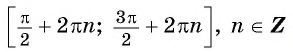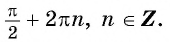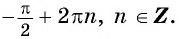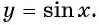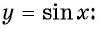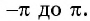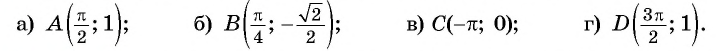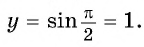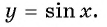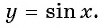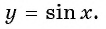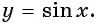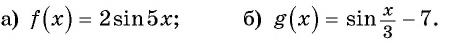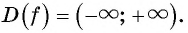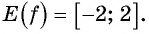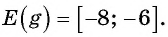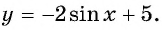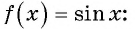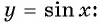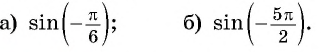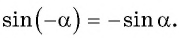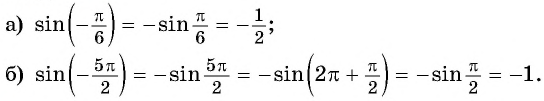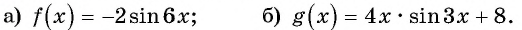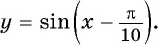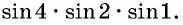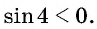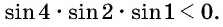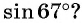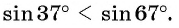ВИДЕО УРОК
Области определения
тригонометрических функций.
Всякая функция имеет свою
собственную совокупность значений аргумента, при которых она определена, то
есть существует. Эта совокупность всех допустимых значений аргумента, при
которых функция определена, называется областью определения или областью существования функции.
Функции sin α и соs α определены при любом значении α. В самом деле, любая точка М, лежащая на единичной окружности, имеет вполне
определённые координаты х и у, первая из которых
есть косинус угла α, составленного с
осью Ох подвижным радиусом ОМ, а вторая – синус угла α.
Функция tg α определена
при всех значениях α, за исключением
случая, когда подвижной радиус перпендикулярен к оси Ох, то есть кроме значений α, равных
± π/2, ± 3π/2, ± 5π/2,
…
И вообще кроме значений α, равных
π/2 + kπ,
где k – любое целое
число.
В самом деле, при этих (и
только при этих) значениях α подвижной радиус лежит на оси Оу, абсцисса х конца подвижного радиуса равна нулю (х = 0) и поэтому
делить у на х нельзя.
Функция сtg α определена
при всех значениях α, за исключением
следующих:
0, ±π,
±2π, ±3π,
…
И вообще – за исключением
значений α, равных kπ, где k – любое целое
число, так как при этих (и только при этих) значениях α подвижной радиус лежит на оси Ох, ордината у его конца равна нулю (у = 0) и поэтому
делить х на у нельзя.
ПРИМЕР:
Найдите область определения функции
f(x) = tg 2x.
РЕШЕНИЕ:
В область определения не войдут следующие точки:
2х ≠ π/2 + kπ.
или
В
результате получим:
х ≠ π/4 + πk/2, k ∈ Z.
Отразим графически.
ОТВЕТ:
Область определения функции tg 2x все
действительные числа за исключением
х ≠ π/4 + πk/2, k ∈ Z.
Области значения
тригонометрических функций.
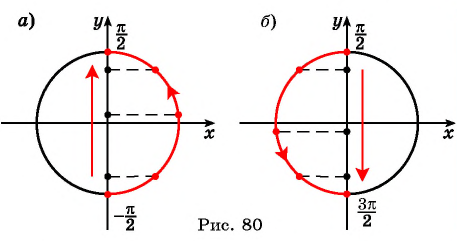
Функции sin α и соs α принимают все значения между –1 и +1, включая и эти числа. В самом деле, синус угла α, составленного с осью Ох подвижным
радиусом ОМ единичной окружности, есть ордината у точки М единичной
окружности, которая, как легко видеть, принимает все значения между –1 и +1, включая и эти числа.
Задача нахождения угла α, имеющего данный синус у, при условии, что число у заключено в
пределах от –1 до +1, имеет бесконечное множество решений.
И действительно,
построим на оси Оу точку Р,
ордината
которой равна у, и через эту точку
проведём прямую параллельную оси Ох. Пусть М1 и М2 – точки, в которых эта прямая пересекает единичную
окружность. Если обозначим через α любой угол, составленный с осью Ох любым из
подвижных радиусов ОМ1 и ОМ2, то sin α =
у.
На чертеже
отмечено несколько углов,
составленных с осью Ох одним из подвижных радиусов ОМ1 и ОМ2.
Аналогично убеждаемся в том,
что соs α принимает
все значения от –1 до +1, включая и эти числа.
В самом деле, косинус
угла α, составленного с осью Ох подвижным
радиусом ОМ единичной окружности, есть абсцисса х конца М подвижного
радиуса ОМ, а абсцисса х точки
единичной окружности, принимает все значения от
–1 до +1, включая и эти числа.
Так же как и для функции sin α, для заданного числового значения косинуса
соs α = х,
при условии, что число х по
абсолютной величине не больше единицы,
–1 ≤ х ≤ +1,
существует бесконечное
множество углов, косинус которых равен х.
И действительно, построим на
оси Ох точку Q, абсцисса которой
равна х, и проведя через эту точку
прямую, параллельную оси Оу. Пусть М1 и М2 – точки, в которых эта прямая пересекает единичную
окружность. Если через α мы обозначим любой угол, составленный с
осью Ох любым из подвижных радиусов ОМ1 или ОМ2, то соs α = х.
На чертеже
отмечено несколько углов,
составленных с осью Ох одним из подвижных радиусов ОМ1 или ОМ2.
На чертеже
мы взяли 0 < у
< 1.
На чертеже
мы берём
–1 < х
< 0.
Функция tg α принимает
все действительные значения. В самом деле, пусть р – любое действительное число. Докажем, что
существует и притом бесконечное множество углов, тангенсы которых равны р.
Построим на оси
тангенсов точку Р,
ордината которой равна р. Соединим точку
Р с началом
координат и продолжим РО за центр до пересечения с единичной
окружностью. Пусть М1 и
М2 – точки, в которых прямая РО пересекает
окружность. Тогда, если α – угол, составленный
с осью Ох любым из подвижных радиусов ОМ1 или ОМ2, то
tg α = р.
На чертеже
мы считали, что р ˃ 0. На этом же чертеже отмечено несколько углов,
составленных с осью Ох радиусами
ОМ1 или ОМ2. Тангенсы всех этих углов равны р.
Наконец, функция сtg α, как и tg α, принимает все действительные значения.
В самом деле, пусть q – любое число. Построим на оси котангенсов
точку Q, абсцисса которой
равна q, соединим эту точку Q с началом
координат и продолжим QО за центр до
пересечения с единичной окружностью.
Обозначим через М1 и М2 точки пересечения прямой QО с единичной окружностью. Тогда котангенс
любого из углов, составленных с осью Ох радиусом
ОМ1 или ОМ2, будет равен q.
ПРИМЕР:
Найти область значений функции:
у = 5 – 4 sin х.
РЕШЕНИЕ:
Из определения синуса следует,
–1 ≤ sin х ≤ 1.
Далее воспользуемся свойствами числовых неравенств.
Умножим все три части двойного неравенства на –4.
–4 ≤ –4 sin х ≤ 4.
Прибавим к трём частям двойного неравенства 5.
1 ≤ 5 – 4 sin х ≤ 9.
Так как данная функция непрерывна на всей области определения, то
множество её значений заключено между наименьшим и наибольшим её значением на
всей области определения, если таковые существуют. В данном случае множество
значений функции
у = 5 – 4 sin х
есть множество [1; 9].
ОТВЕТ: [1; 9]
ПРИМЕР:
Найти область определения и область значений функции:
y = tg x.
РЕШЕНИЕ:
Функция y = tg x определяется формулой
Эта функция определена при значениях х, для которых соs х ≠ 0.
Известно, что соs х = 0 при
х = π/2 + πn, n ∈ Z.
Следовательно, областью определения функции y = tg x является множество чисел кроме
х = π/2 + πn, n ∈ Z.
Так как уравнение tg x = а имеет корни при любом
действительном значении а, то множеством значений функции y = tg x является множество R всех действительных чисел.
ПРИМЕР:
Найти область определения функции:
y = sin 3х + tg 2x.
РЕШЕНИЕ:
Нужно выяснить, при каких значениях
х выражение
y = sin х + tg 2x
имеет смысл. Выражение sin 3х имеет
смысл при любом значении х, а выражение tg 2x – при всех значениях
х кроме
2х = π/2 + πn, n ∈ Z или
х = π/4 + πn/2, n ∈ Z.
Следовательно, областью определения данной функции является множество
действительных чисел, кроме
х = π/4 + πn/2, n ∈ Z.
ПРИМЕР:
Найти
область значения тригонометрической функции:
у = 3 соs х – 2.
РЕШЕНИЕ:
Для нахождения
области значения функции
у = 3 соs х – 2
используем
тот факт, что функция у = соs х изменяет своё значение от –1 до 1, то есть имеет место двойное неравенство:
–1 ≤ соs х ≤ 1.
Умножим
все части этого неравенства на 3:
–3 ≤ 3 соs х ≤ 3.
Вычтем
из всех частей полученного неравенства 2, получим:
–3 – 2 ≤ 3 соs х – 2 ≤ 3 – 2,
–5 ≤ 3 соs х – 2 ≤ 1.
Таким
образом, область значений функции будет промежуток
[–5; 1].
ОТВЕТ: [–5; 1]
ПРИМЕР:
Найти
область значения тригонометрической функции:
у = 3 соs х – 4 sin х.
РЕШЕНИЕ:
Для нахождения
области значения функции
у = 3 соs х – 4 sin х
воспользуемся следующей формулой:
В нашем случае
а = 3, b = –4, то есть:
Следовательно,
областью значений является промежуток:
[–5; 5].
ОТВЕТ: [–5; 5]
Задания к уроку 6
- Задание 1
- Задание 2
- Задание 3
ДРУГИЕ УРОКИ
- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 5. Периодичность тригонометрических функций
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 11. Основные тригонометрические тождества
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 15. Теорема косинусов
- Урок 16. Решение косоугольных треугольников
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 28. Основные тождества обратных тригонометрических функций
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований
Алгебра и начала математического анализа, 11 класс
Урок №1. Область определения и множество значений тригонометрических функций.
Перечень вопросов, рассматриваемых в теме
- Овладение понятиями «область определения», «область определения тригонометрических функций», «множество значений функции», «множество значений тригонометрических функций»;
- Нахождение области определения и множества значений тригонометрических функций вида y=af(kx+b)+c и y=|f(k|x|+b)|, где f(x) — косинус, синус, тангенс или котангенс действительного числа от значения коэффициентов a, k, b.;
- Объяснение зависимости области определения и множества значений функции вида y=af(kx+b)+c и y=|f(k|x|+b)|, где f(x) — косинус, синус, тангенс или котангенс действительного числа от значения коэффициентов a, k, b.
Глоссарий по теме
Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.
Множеством значений функции y = sin x и y = cos x является отрезок -1 ≤ y ≤ 1. Данные функции ограничены сверху и снизу.
Областью определения функции y = tg x является множество чисел x ≠ π/2 + πk, kЄ Z.
Областью определения функции y = сtg x является множество чисел x ≠ πk, kЄ Z.
Множеством значений функции y = tg x и y =сtg x является множество R всех действительных чисел, т.к. уравнения tg x = a и сtg x = a имеют корни при любом действительном значении a. Функции неограниченные.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Дополнительная литература:
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Актуализация знаний
Вопросы:
- Что такое функция?
- Что такое область определения функции? Чем является область определения функции геометрически?
- Что такое множество значений функции? Чем является множество значений функции геометрически?
Ответы на вопросы:
- Если каждому значению x из некоторого множества чисел поставлено в соответствие по определенному правилу число y, то говорят, что на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у – зависимой переменной или функцией. Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают y=f(x).
- Областью определения функции называют множество всех допустимых значений переменной x. Геометрически – это проекция графика функции на ось Ох.
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически – это проекция графика функции на ось Оy.
Найдите область определения функции и множество значений функции:
1) 


Ответы:
D(f): 1) 

E(f): 1)


Объяснение нового материала
С помощью единичной окружности сделайте выводы об области определения и множестве значений тригонометрических функций.
Заполните таблицу:
|
Функция |
Область определения |
Множество значений |
|
|
||
|
|
||
|
|
||
|
|
Ответ:
|
Функция |
Область определения |
Множество значений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.
Множеством значений функции y = sin x и y = cos x является отрезок -1 ≤ y ≤ 1. Данные функции ограничены сверху и снизу.
Областью определения функции y = tg x является множество чисел x ≠ π/2 + πk, kЄ Z.
Областью определения функции y = сtg x является множество чисел x ≠ πk, kЄ Z.
Множеством значений функции y = tg x и y =сtg x является множество R всех действительных чисел, т.к. уравнения tg x = a и сtg x = a имеют корни при любом действительном значении a. Функции неограниченные.
Примеры и разборы решения заданий тренировочного модуля:
Пример 1. Найти область определения функции 



Ответ: −
Пример 2. Найти все решения уравнения


Ответ:

Содержание:
Рассматривая произвольное действительное число
Таким образом, мы установим соответствие между множеством действительных чисел и множеством значений синусов углов. Каждому действительному числу соответствует единственное значение синуса. Такое соответствие определяет тригонометрическую функцию
Определение функция y=sin x
Определение:
Зависимость, при которой каждому действительному числу 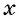
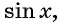
Рассмотрим свойства функции 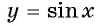
Область определения функции y=sin x
Областью определения функции 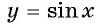
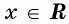
Графически это означает, что для любой абсциссы найдется точка графика функции
Множеством значений функции y=sin x
Множеством значений функции 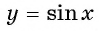
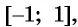
Графически это означает, что график функции 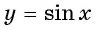
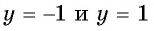
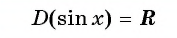
Периодичность функции y=sin x
Периодичность функции 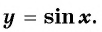
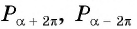
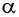
Говорят, что число 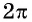
Определение:
Функция 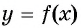
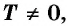
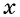
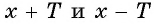
Чтобы определить, является ли функция периодической с периодом 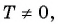
- принадлежат ли области определения функции числа
если
принадлежит области определения функции;
- выполняется ли равенство
Определим, верно ли, что число 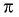
- Числа
принадлежат области определения функции, так как
- Проверим, выполняется ли равенство
для всех
Пусть
Значит, число 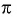
Периодом функции 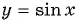
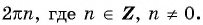
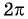
Функция 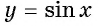
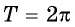
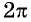
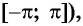
Четность (нечетность) функции y=sin x
Четность (нечетность) функции y=sin x 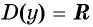
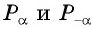
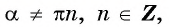
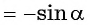
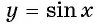
Для построения ее графика достаточно построить его часть для неотрицательных значений аргумента и отобразить эту часть симметрично относительно начала координат.
Нули функции y=sin x
Нули функции. Ординаты точек 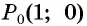
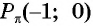
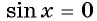
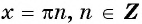
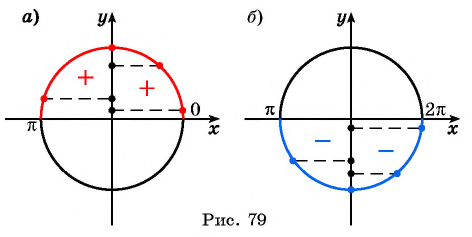
Промежутки знакопостоянства функции y=sin x
На промежутках 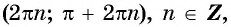
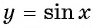
На промежутках 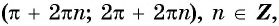
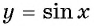
Монотонность функции y=sin x
Монотонность функции. Так как ординаты точек единичной окружности увеличиваются от -1 до 1 при изменении угла от 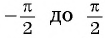
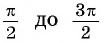
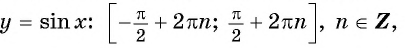
Функции 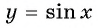
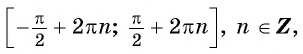
Наибольшее значение функции 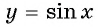
Наименьшее значение функции 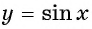
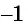
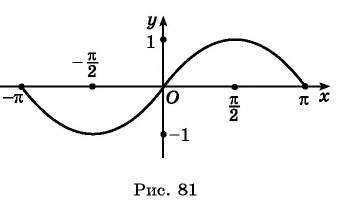
На основании проведенного исследования построим график функции 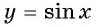
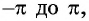
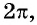
На этом периоде функция
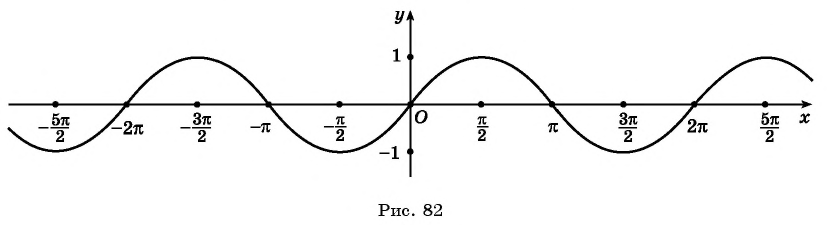
На рисунке 81 изображена часть графика функции 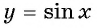
Перенесем эту часть на другие периоды и получим график функции 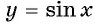
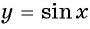
Примеры заданий и их решения
Пример №1
Определите, принадлежит ли графику функции 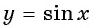
Решение:
а) Подставим в формулу 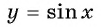
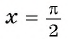
Полученное значение функции равно ординате точки 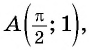
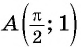
б) При 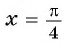
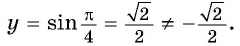
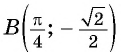
в) При 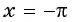
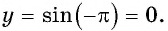
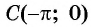
г) При 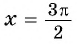
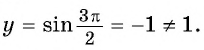
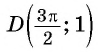
Пример №2
Найдите область определения и множество значений функции:
Решение:
а) Так как область определения функции 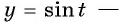
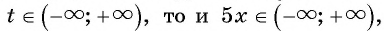
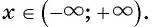
Множеством значений функции 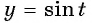
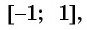
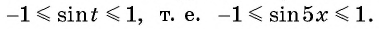
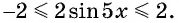
б) 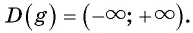
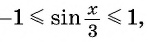
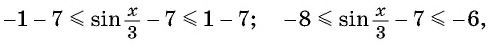
Пример №3
Найдите наибольшее значение функции
Решение:
Так как 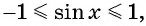
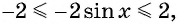
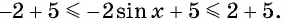
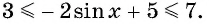
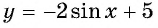
- Заказать решение задач по высшей математике
Пример №4
Найдите значение выражения, используя свойство периодичности функции
Решение:
Так как число 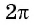
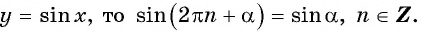
Пример №5
Найдите значение выражения, используя свойство нечетности функции
Решение:
Так как функция 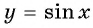
Тогда:
Пример №6
Исследуйте функцию на четность (нечетность):
Решение:
a) 
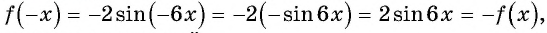
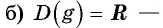
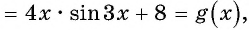
Пример №7
Найдите нули функции:
Решение:
а) Пусть 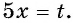
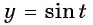
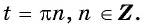
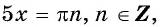
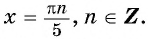
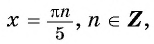
б) Пусть 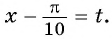
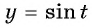
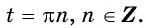
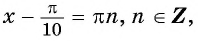
Таким образом, числа 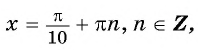
Пример №8
Определите знак произведения
Решение:
Так как 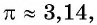
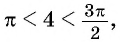
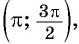
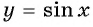
Углы 2 радиана и 1 радиан принадлежат промежутку 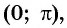
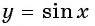
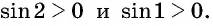
Пример №9
Что больше: 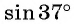
Решение. Так как функция 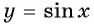
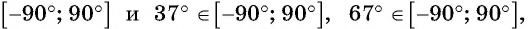
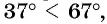
Пример №10
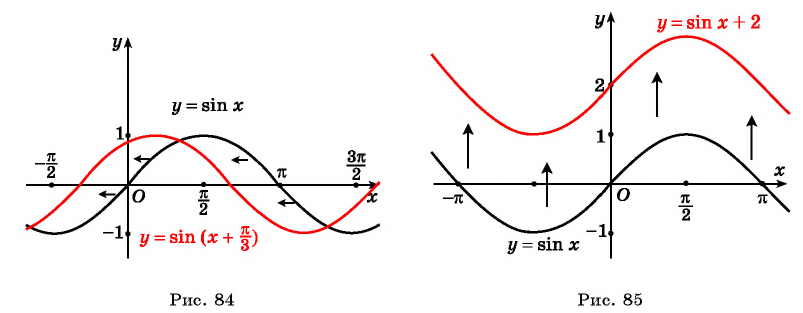
Постройте график функции:
Решение:
а) График функции 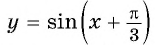
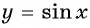
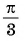
б) График функции 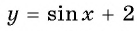
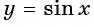
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
Каждому действительному числу
x
соответствует единственная точка единичной окружности
A
, получаемая поворотом точки ((1;0)) на угол
x
рад.
Значит, каждому действительному числу
x
соответствует число, равное
sinx
, и каждому действительному числу
x
соответствует число, равное
cosx
. Так заданы функции
y=sinx
и
y=cosx
на множестве
ℝ
.





































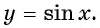
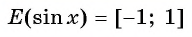
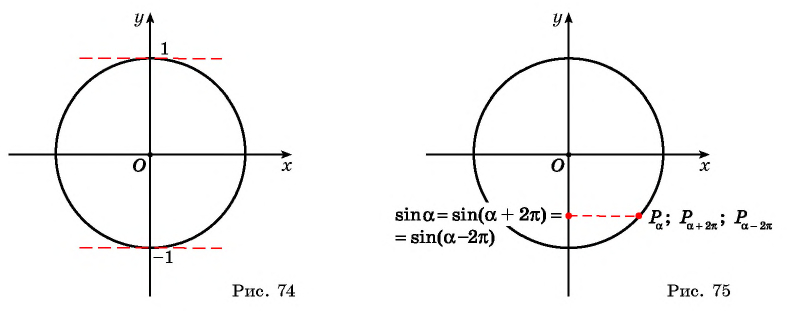
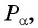
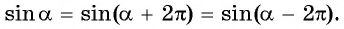
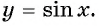
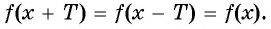
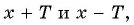 если
если 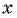 принадлежит области определения функции;
принадлежит области определения функции;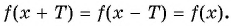
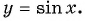
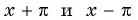 принадлежат области определения функции, так как
принадлежат области определения функции, так как 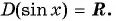
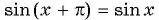 для всех
для всех