Общая информация
У каждой функции y = f (x) есть два типа переменных: зависимые и независимые. Переменная «х» является независимой, поскольку она может принимать любые значения, кроме тех, которые «превращают» функцию в пустое множество (этого необходимо избегать). Они бывают с одной или несколькими независимыми переменными. Необходимо выяснить все значения зависимой переменной.
Существует несколько методов решения задач такого типа. К ним относятся следующие способы: автоматизированный и ручной. Решение первым подразумевает использование специальных программных оболочек и web-приложений, позволяющих найти область значения функции. Онлайн-калькулятор с решением применяется для тех, кто выполняет большое количество вычислений или проверку вычислений.
В различных дисциплинах необходимо исследовать поведение функций. Например, при проектировании какого-либо программного продукта. Программисты занимаются поиском «багов», при которых происходит некорректная работа приложения. Если заданы недопустимые параметры независимой переменной, то произойдет ошибка. Это называется исключением, и его всегда следует обрабатывать. При проектировании различных устройств нужно также уметь находить область значения функции.
Основные понятия
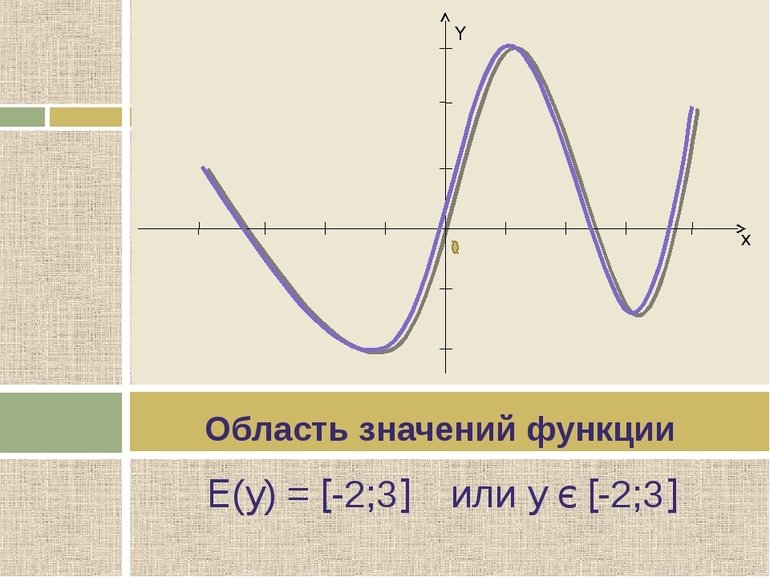
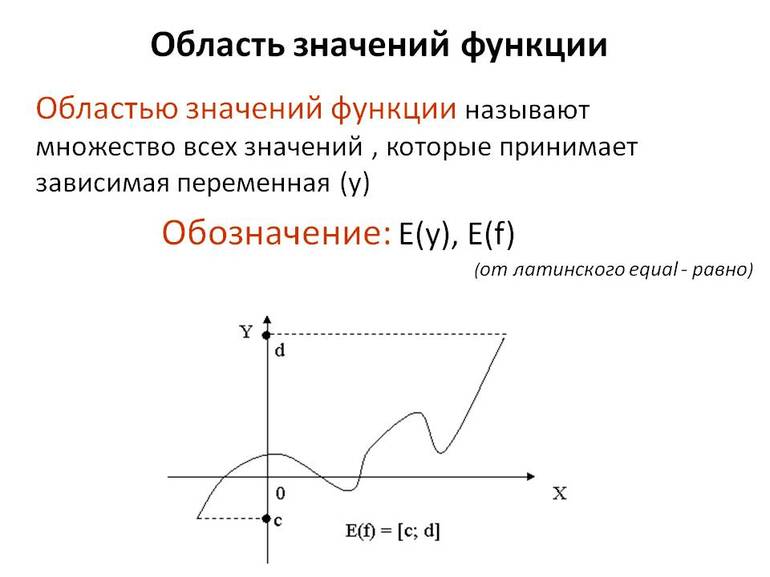
Руководствуясь некоторыми данными, можно сделать вывод: областью значений некоторой функции называются все ее допустимые значения. Обозначается она буквой «E», т. е. E (f) или E (y). Когда y = f (x) является сложной (w = f (x, y, z)), тогда можно ее обозначить «E (w)».
Независимая переменная, принимающая некоторые значения, называется аргументом. Для конкретного случая существует определенный алгоритм. Можно сразу определить E (f), но в некоторых ситуациях нужно выполнить некоторые преобразования.
Например, нужно найти область значений квадратичной функции y = 3x 2 — 2x — 1. Следует записать уравнение 3x 2 — 2x — 1 = 0. Ордината вычисляется таким образом: y0 = -D / 4a = -[b 2 — 4ac] / 4a = -[(-2)^2 — 4 * 3 * (-1)] / (4 * 3) = -16 / 12 = -4/3. Если коэффициент а>0, то ветви параболы направлены вверх. Следовательно, E (y) = (-4/3;+бесконечность).
Специалисты-математики утверждают, что важным аспектом является определение типа функции. Следовательно, следует разобраться в их классификации. Для этого необходимо знать их графики и названия.
Типы функций
Перед тем, как найти все допустимые значения, нужно знать область значения некоторых элементарных функций. Для каждой из них существует свой промежуток:
- (-бесконечность;+бесконечность): y =kx + b, y = x^(2n+1), y = x^(1/(2n+1)), y = log (x) с основанием а, y = tg (x) и y = ctg (x).
- [0;+бесконечность): y = x^(2n), y = x^(1/(2n)) и y = a^x.
- (-бесконечность;0] U [0;+бесконечность) только для y = k / x (гипербола).
- [-1;1]: y = sin (x) и y = cos (x).
- [0;Pi]: y = arccos (x) и arcsin (x).
- [-Pi/2;Pi/2]: y = arctg (x) и arcsin (x).
Если функция является многочленом четной степени, то для нее существует интервал [m;+бесконечность). Значение «m» — наименьшее значение многочлена. На промежутке (-бесконечность;n) число n — наибольшее его значение.
Довольно сложной задачей считается нахождение области значений тригонометрических функций. Примером одной из них считается y = cos (2x) + 2cos (x). Кроме того, при нахождении E (f) необходимо руководствоваться не только табличными значениями. Этих данных мало, поскольку нужно также знать о свойствах некоторых функций и способы нахождения E.
Важные свойства
Для качественного исследования нужно знать свойства простых функций: монотонность, непрерывность, дифференцируемость, четность или нечетность, периодичность, область определения и значения. Среди свойств можно выделить несколько основных:
- В случае, когда функция f (x) является непрерывной, и наблюдается ее возрастание или убывание на отрезке [a;b], то множество значений — интервал [f (a);f (b)].
- Если y = f (x) обладает непрерывностью на промежутке [a;b], и существует некоторое минимальное m и максимальное М ее значения, то множеством ее значений является интервал [m;M].
- При непрерывности и дифференцируемости функции на промежутке [a;b], она имеет минимальное и максимальное значения на данном промежутке.
Последние два свойства применяются для непрерывных функций. Простое решение позволяет получить первое свойство. При этом очень важно доказать ее монотонность. Задача существенно упрощается, когда удается доказать четность или нечетность функции, а также ее периодичность. По необходимости следует проверять и использовать некоторые ее свойства: непрерывность (при разрыве нужно определить его точку или интервал), монотонность, дифференцируемость, периодичность, четность или нечетность и т. д.
Методы нахождения
Существует много способов нахождения области значений. Однако для решения задач нужно подбирать оптимальный метод, поскольку следует избегать лишних вычислений. Например, если функция является простой, то нет необходимости применять сложные алгоритмы решения. К методам нахождения относятся следующие:
- Отдельное нахождение значений элементов сложной функции.
- Оценочный.
- Учет непрерывности и монотонности.
- Взятие производной.
- Использование max и min функции.
Для каждого из методов существует определенный алгоритм. Хотя встречаются случаи, когда целесообразно применить два простых метода. Нужно руководствоваться минимальным количеством вычислений и затраченным временем.
Для каждого элемента
Иногда в задачах следует найти E (f) при условии, когда функция является сложной. Очень распространенная методика разбиения задачи на подзадачи, которая применяется не только в дисциплинах с физико-математическим уклоном, но в экономике, бизнесе и других направлениях. Решение с помощью метода последовательного нахождения E (f) каждой из функций. Алгоритм имеет такой вид:
- Выполнить необходимые преобразования — упростить выражение.
- Разбить выражение на элементы.
- Выполнить поиск E (f) для каждого элемента.
- Произвести замену.
- Анализ.
- Результат решения.
Однако довольно сложно ориентировать по данному алгоритму, поскольку нужно разобрать решение примера с его помощью. Дана функция y = log0.5 (4 — 2 * 3^x — 9^x). Решается задача таким образом:
- Упростить (выделить квадрат): y = log0.5 (4 — 2 * 3^x — 9^x) = log0.5 [5 — (1 — 2 * 3^x — 9^x)] = log0.5 [5 — (3^x + 1)].
- Разбить на элементарные функции: y = 3^x, y = 3^x + 1, y = [-(3^x + 1)]^2 и y = [5 — (3^x + 1)]^2.
- Определить для каждого элемента E (f): E (3^x) = (0;+бесконечность), E (3^x + 1) = (1;+бесконечность), E ([-(3^x + 1)]^2) = (-бесконечность;-1) и E ([5 — (3^x + 1)]^2) = (-бесконечность;4).
- Произвести замену: t = 5 — (3^x + 1)]^2 (-бесконечность <= t <=4).
- Анализ: поскольку E (f) на луче (-бесконечность;4) совпадает с интервалом (0;4), то функция непрерывна и убывает. Необходимо отметить, что интервал (0;4) получен при пересечении луча (-бесконечность;4) с областью определения функции логарифмического типа (0;+бесконечность). На интервале (0;4) эта функция непрерывна и убывает. Если t>0, то она стремится к бесконечности. Когда t = 4, ее значение равно -2.
- Результат решения — искомый интервал: E (f) = (-2;+бесконечность).
Необходимо обратить внимание на пункты 1, 3 и 5. Они являются очень важными, поскольку от них зависит правильность решения. Очень важно уметь анализировать полученную функцию в 4 пункте.
Оценочный способ
Еще одним методом определения E (f) является способ оценки. Необходимо оценить непрерывную функцию в нижнем и верхнем направлениях. Еще следует доказать достижение нижней и верхней границ. Для этой цели существует также алгоритм. Он немного проще предыдущего. Суть его заключается в следующем:
- Доказать непрерывность.
- Составить неравенство или неравенства для нескольких функций.
- Узнать оценку.
- Записать интервал.
Необходимо разобрать алгоритм на примере функции y = cos (7x) + 5 * cos (x). Следует учитывать, что известен только один знак неравенства. Второй нужно доказать оценочным методом. Решение задачи имеет такой вид:
- Функция вида y = cos (x) является непрерывной.
- Неравенства: -1<=cos (7x)?1 и -5<=5 * cos (x)?5.
- Оценка получает при объединении неравенств: -6<=y?6. При значениях независимой переменной x = Pi и x = 0 функция принимает значения -6 и 6 соответственно (нижняя и верхняя границы). Функция состоит из двух элементов, следовательно, она является линейной и непрерывной.
- Интервал: E (y) = [-6;6].
Метод позволяет найти решение без использования дополнительных вычислений. Но при его использовании легко ошибиться.
Учет непрерывности и монотонности
Одним из простых способов решения, который специалисты рекомендуют новичкам, является метод учета непрерывности и монотонности. Для этого существует специальный алгоритм:
- Упростить выражение.
- Выполнить замену при необходимости.
- Найти вершину графика.
- Определить промежуток.
- Вычислить максимальное и минимальное значения.
- Записать E (f).
Например, существует некоторая функция y = cos (2x) + 2cos (x). Необходимо найти ее E. Искать следует по алгоритму решения методом учета монотонности и непрерывности:
- Упростить (по формуле двойного угла): y = 2 * (cos (x))^2 + 2cosx — 1.
- Замена t = cos (x): y = 2 * t 2 + 2 * t — 1 = 2 * (t + 0,5)^2 — 1,5.
- Показательная функция является параболой. Она монотонна, непрерывна и имеет вершину по оси ОУ -1,5. Промежуток, который рассматривается — [-1;1], поскольку E (cos (x)) = [-1;1].
- Минимальное значение равно -1,5, так как ветви направлены вверх. Максимальное на промежутке [-1;1] — MAX (y) = 3. Для его нахождения нужно построить график параболы y = 2 * (t + 0,5)^2 — 1,5.
- Искомый интервал — E (cos (2x) + 2cos (x)) = [-1,5;3].
Чтобы построить график параболы, нужно найти ее вершину и точки пересечения с осью абсцисс. Последние находятся при решении уравнения 2 * (t + 0,5)^2 — 1,5 = 0. Однако существует способ намного проще. Для этого следует привести выражение к виду 2 * (t + 0,5)^2 = 1,5. Отсюда t = — 0,5. Следовательно, координаты вершины — (-0,5;-1,5). Корни уравнения при его решении: t1 = -[(1 + (3)^0.5)] / 2 и t2 = -[(1 — (3)^0.5)] / 2.
Производная, min и max
Одним из простейших способов нахождения E (f) является взятие производной функции. Этот метод можно комбинировать с определением максимального и минимального значений. Математики рекомендуют простейший алгоритм:
- Найти производную.
- Анализ.
- Указать MAX (f) и MIN (f).
- Запись интервала в формате (MIN (f);MAX (f)).
Практическое применение алгоритма — решение задачи этим методом. Например, нужно найти E (arcsin (x)). Решение выполняется по нескольким этапам:
- Производная: y’ = [arcsin (x)]’ = 1 / [(1 — x 2 )^0.5].
- Функция возрастает на интервале (-1;1).
- Минимум и максимум на отрезке (-1;1): MIN (arcsin (-1)) = -Pi/2 MAX (arcsin (1)) = Pi/2.
- Интервал: E (arcsin (x)) = [-Pi/2;Pi/2].
В некоторых случаях рекомендуется вычислять пределы, поскольку часть задач решается только с их применением. Существует определенный тип задач, в которых нужно доказать, что отрезок является E (f) конкретной функции. Например, следует выяснить принадлежность [-1;1] функции sin (x). Для этого необходимо воспользоваться вышеописанным алгоритмом:
- Производная: y’ = [sin (x)]’ = cos (x).
- Период функции равен 2Pi. Следует взять отрезок [0;2Pi]. Для нахождения множества значений на нем нужно приравнять производную функции к 0, т. е. cos (x) = 0. Найти х = Pi/2 + Pi * к, где «к» принадлежит Z. Точки экстремума равны Pi/2 и 3Pi/2.
- Минимум и максимум на отрезке [0;2Pi): MIN ([sin (3Pi/2)]) = -1 и MAX ([sin (3Pi/2)]) = 1.
- E (sin (x)) = [-1;1].
Отрезок [-1;1] является E (sin (x)). Оптимальный метод — нахождение производной и определение E (f). В этом примере необходимо знать и проверить периодичность.
Таким образом, существует несколько способов нахождения E (f), но всегда необходимо выбирать метод, приводящий к минимуму вычислений. Нет смысла усложнять решение, поскольку большинство алгоритмов направлены на оптимизацию вычислений.
Что такое функция в алгебре
Определение
Функция в алгебре — некое математическое выражение y=f(x), где каждому значению переменной x соответствует одно значение переменной y.
Из этого следует, что решений у функции может быть много. Для обозначения совокупностей таких решений вводятся особые термины.
Определние
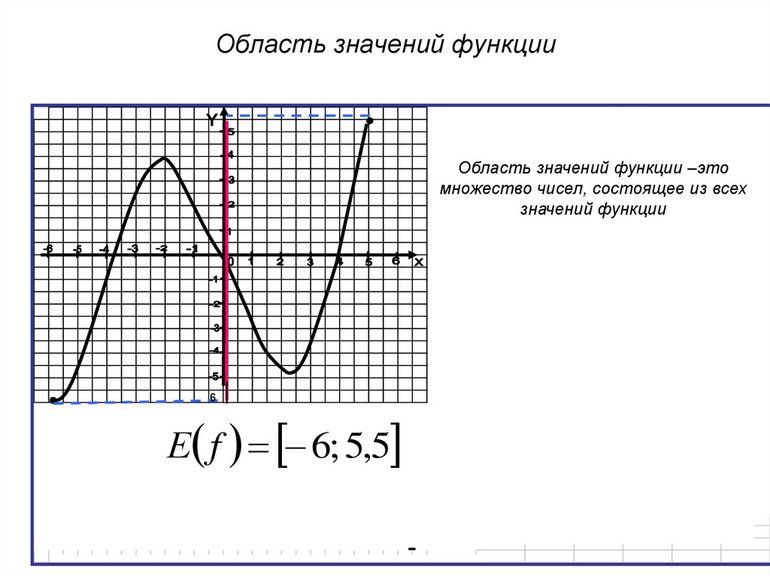
Множество значений функции y=f(x) — совокупность значений переменной y, которые она принимает при переборе всех значений переменной x на заданном отрезке X.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Областью значений функции y=f(x) называется такое множество значений, которые функция y принимает при переборе всех значений аргумента x из области определения. Область значений обозначается как E(f).
Определение
Область допустимых значений (область определения) функции — такое множество всех значений переменных, при которых функция имеет смысл, то есть решается.
Область значений функции вместе с областью ее определения формирует границы для отображения данной функции в виде графика.
Виды функций
Для каждой функции, в зависимости от ее структуры, область значений будет своя. Рассмотрим основные виды элементарных математических функций.
Линейная
(y=kcdot x+b)
Область значений включает в себя все действительные числа: (E(f)=(-infty;;+infty).)
Обратная пропорциональность
(y=frac kx)
Согласно свойств данной функции, (kneq0), так как в этом случае ее график вместо гиперболы приобретает вид прямой линии, проходящей по оси ординат за исключением точки (0; 0). Исходя из этого, условия, область значений функции обратной пропорциональности включает в себя все действительные числа, кроме нуля:
(E(f)=(-infty;;0)cup(0;;+infty).)
Квадратичная (квадратная)
(y=acdot x^2+bcdot x+c)
В ее основе лежит стандартный квадратный трехчлен (acdot x^2+bcdot x+c), причем ( aneq0), так как иначе функция сокращается до линейной. В общем виде область значений квадратичной функции ограничивается вершиной параболы, которая является ее графиком.
Координата вершины (y_0) рассчитывается так:
(y_0=-frac{b^2-4cdot acdot c}{4cdot a}.)
Область значений зависит от коэффициента a:
- если a>0: (E(f)=lbrack y_0;;+infty))
- если a<0: (E(f)=(-infty;;y_0rbrack)
Квадратную функцияю y=x^2 можно рассматривать как частный случай квадратичной или степенной функций. Так как при возведении числа в четную степень результат будет всегда положительным, область значений для нее следующая:
(mathrm E(mathrm f)=lbrack0;;+infty) )
Степенная
(y=x^n)
Область значений степенной функции зависит от того, к какому числовому множеству относится показатель степени n:
- Если (mathrm ninmathbb{N}), то есть является натуральным числом (за исключением нуля), то область значений включает в себя все действительные числа: ( mathrm E(mathrm f)=(-infty;;+infty).)
- Если (mathrm ninmathbb{R}), то есть относится к действительным числам, то область значений степенной функции сужается: (mathrm E(mathrm f)=(0;;+infty)).
Показательная
(mathrm y=mathrm a^{mathrm x})
Для показательной функции существует одно определяющее условие: (mathrm a>0). В связи с этим область ее значений включает в себя все положительные числа:
(mathrm E(mathrm f)=(0;;+infty) )
Логарифмическая
(mathrm y=log_{mathrm a}left(mathrm xright))
По своим свойствам логарифмическая функция обратна показательной. Для данных функций область определения и область значений меняются местами соответственно. ОЗ логарифмической функции включает в себя все действительные числа:
(mathrm E(mathrm f)=(-infty;;+infty))
Тригонометрические
Рассмотрим четыре базовые тригонометрические функции:
- синус;
- косинус;
- тангенс;
- котангенс.
Первые две периодически повторяются в промежутке между -1 и 1:
(mathrm E(mathrm f)=(-1;;1))
Область значения тангенса и котангенса включает в себя все действительные числа:
(mathrm E(mathrm f)=(-infty;;+infty))
Типы функций
При определении области значений функции необходимо учитывать ее фундаментальные особенности. Обозначенная выше классификация — не единственная. У математических функций есть некоторые параметры, которые влияют как на саму область значений, так и на выбор методики ее нахождения.
Важные свойства
К наиболее важным для поиска области значений функции относят следующие ее свойства:
- Непрерывность. Непрерывной называется функция, на графике которой нет «точек разрыва». Таким точкам соответствуют значения переменной, при которых функция не имеет смысла, то есть — исключенные из области определения.
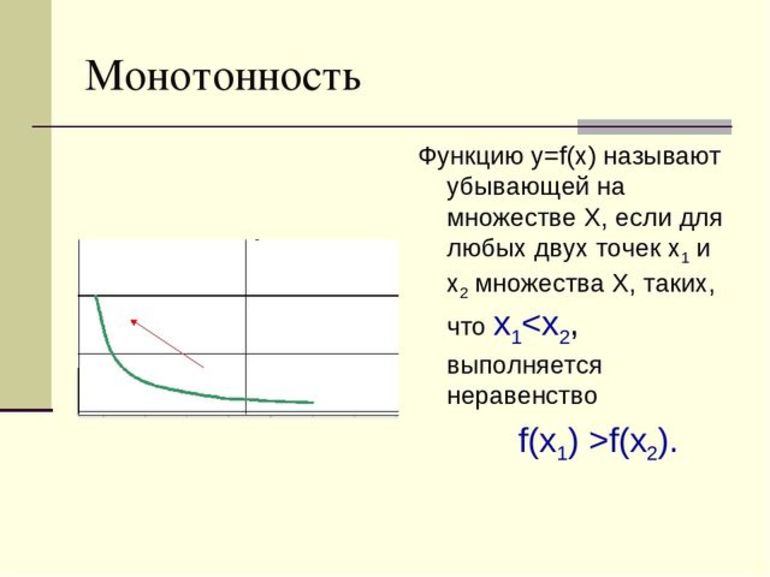
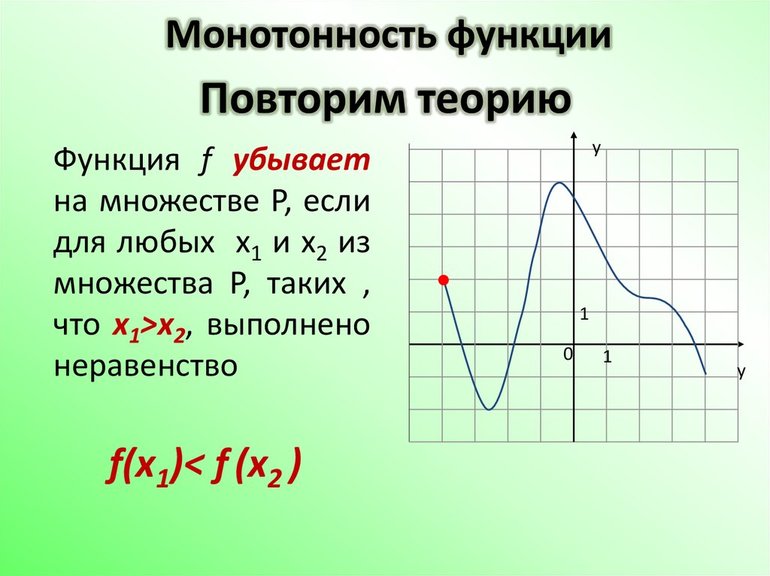
- Монотонность. Монотонной называется функция, которая не возрастает или не убывает на всей области определения.
- Четность. Четной называется функция, не меняющая своего значения при смене знака переменной. То есть, f(-x)=f(x). Соответственно, нечетная функция меняет значение. Выделяют также функции общего вида, которые не симметричны относительно центра или оси координат.
- Периодичность. Периодическая функция повторяет свои значения через определенные равные интервалы значений переменной.
Методы нахождения
Поиск области значений функции несколько сложнее, чем определение ОДЗ. В зависимости от вида и типа функции, а также условий задачи для этого могут применяться различные методы.
Перебор значений
Самый простой и ограниченный способ. При его помощи можно находить область значений на небольшом промежутке целых чисел (xin(a;;b)). В таком случае заданные значения переменной поочередно подставляются в уравнение и вычисляются значения функции, соответствующие им.
Графический метод
Как ясно из названия способа, для его реализации необходимо построить график исследуемой функции. По внешнему виду кривой уже можно делать некоторые выводы. Если линия графика соответствует одному из видов элементарных функций, например, является параболой, то в качестве области значений берется промежуток, соответствующий данному графику.
Примечание
Если по условию задачи необходимо найти область значений функции на определенном промежутке значений переменной x, то на графике максимальные и минимальные точки становятся очевидными. Это могут быть как общие точки экстремума, так и локальные максимальные и минимальные значения.
Учет непрерывности и монотонности
Данный метод вытекает из предыдущего и позволяет делать некоторые прогнозы об области значений функции исходя из ее свойств. Если на графике видно, что функция не прерывается и монотонно убывает или возрастает на определенном промежутке, можно предположить, что эта тенденция сохранится и дальше.
Например, график квадратичной функции f(x)=x^2 имеет вид параболы с точкой перегиба с координатами (0, 0). Кривая непрерывна, то есть не имеет разрывов в области определения. Для того, чтобы определить область значений данной функции, достаточно построить ее график на ограниченном промежутке. Для примера возьмем (xinlbrack-4;;4rbrack):
Рисунок 1. Значение непрерывности и монотонности функции для области определения
На графике видно, что функция монотонно убывает на промежутке (lbrack-4;;0rbrack) и монотонно возрастает на промежутке( lbrack0;;4rbrack). Исходя из этого и непрерывности функции, можно экстраполировать данную закономерность на всю область определения. Так как минимальное значение данной функции равняется нулю, область значений будет следующей:
(mathrm E(mathrm f)=lbrack0;;+infty))
Производная, min и max
Описанные выше способы подходят не для всех ситуаций. В общем случае, задача по определению области значений функции всегда сводится к нахождению ее минимального и максимального значения или точек экстремума.
Определение
Согласно теореме Ферма, в точках локального экстремума производная исследуемой функции равняется нулю.
Важно понимать, что сами локальный экстремум не обязательно является максимумом или минимумом для функции в целом. Такие точки называются критическими или стационарными. Поэтому, кроме самих точек необходимо определять промежутки возрастания и убывания:
- если при переходе через критическую точку производная функции меняет знак с (+) на (-), то эта точка является максимумом;
- если при переходе через критическую точку производная меняет знак с (-) на (+), то такая точка является минимумом;
- если при переходе знак производной не меняется, то экстремума в данной точке нет.
Кроме того, экстремумы функции можно определять по второй производной. Предположим, при исследовании функции обнаружилась некая критическая точка x_1. Для нее справедливы следующие неравенства:
Если (f»(x_1)>0), то (x_1) — точка минимума.
Если (f»(x_1)<0), то (x_1) — точка максимума.
Пример решения
Задача
Дана функция (y=x^4-2cdot x^2-5). Найти область ее значений.
Решение:
Так как функция не относится к элементарным и по условию задачи область поиска не ограничена, воспользуемся методом нахождения точек минимума и максимума.
Найдем производную данной функции y’, воспользовавшись формулами из таблицы производных:
(y’=4cdot x^3-4cdot x)
Согласно теореме Ферма, в точках экстремума производная равняется нулю.
Начнем решать полученное уравнение:
(4cdot x^3-4cdot x=0)
(4cdot xcdot(x^2-1)=0)
(4cdot xcdot(x-1)cdot(x+1)=0)
Так как уравнение равняется нулю, если хотя бы один из множителей равен нулю, разобьем его на три составляющие:
- (4cdot x=0)
- (x-1=0)
- (x+1=0)
Получим следующие результаты:
(x_1=0)
(x_2=1)
(x_3=-1)
Данные точки являются критическими. В итоге мы имеем четыре промежутка:
((-infty;;-1rbrack,;lbrack-1;;0rbrack,;lbrack0;;1rbrack;и;lbrack1;;+infty).)
Чтобы понять, какие из точек являются минимальными и максимальными, необходимо взять по числу из каждого промежутка и решить производную (y’=4cdot x^3-4cdot x )относительно них. Сам результат вычислений не важен, учитывать нужно только знак: (+) или (-).
Возьмем (x_1^ast=-2;;x_2^ast=-0.5;;x_3^ast=0.5;;x_4^ast=2.)
На первом и третьем промежутках производная принимает отрицательное значение, на втором и четвертом — положительное. Следовательно, найденные ранее точки (x_1=-1;и;x_3=1) являются точками минимума, а точка (x_2=1) — точкой максимума. Это еще не окончательный результат, так как необходимо понять, на каких промежутках функция возрастает, а на каких — убывает.
Согласно определению, в точка минимума функция переходит от убывания к возрастанию, а в точке максимума — наоборот. Таким образом, на промежутке ((-infty;;-1rbrack ) функция монотонно убывает и монотонно возрастает на промежутке (lbrack1;;+infty)). Из этого следует, что точка (x_2=1) является лишь локальным экстремумом. Значит, область значений функции (y=x^4-2cdot x^2-5) не ограничивается ей.
Чтобы вычислить минимальное значение, подставляем полученные точки минимума в изначальное выражение. Получаем (y_{min}=-6).
Область определения функции (y=x^4-2cdot x^2-5) следующая:
(E(y)=lbrack-6;;+infty).)
Содержание материала
- Что такое функция в алгебре
- Видео
- Область определения показательной функции
- Области определения основных элементарных функций
- Как найти область значений функции по уравнению
- Методы нахождения
- Перебор значений
- Графический метод
- Учет непрерывности и монотонности
- Производная, min и max
- Дробная функция
- Разница между областью значения и областью определения функции
Что такое функция в алгебре
Определение
Функция в алгебре — некое математическое выражение y=f(x), где каждому значению переменной x соответствует одно значение переменной y.
Из этого следует, что решений у функции может быть много. Для обозначения совокупностей таких решений вводятся особые термины.
Определние
Множество значений функции y=f(x) — совокупность значений переменной y, которые она принимает при переборе всех значений переменной x на заданном отрезке X.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Областью значений функции y=f(x) называется такое множество значений, которые функция y принимает при переборе всех значений аргумента x из области определения. Область значений обозначается как E(f).
Определение
Область допустимых значений (область определения) функции — такое множество всех значений переменных, при которых функция имеет смысл, то есть решается.
Область значений функции вместе с областью ее определения формирует границы для отображения данной функции в виде графика.
Видео
Область определения показательной функции
Показательная функция записывается как: y=kx
где значение x — показатель степени;
k — число, которое обязательно больше нуля и не равно единице.
Область определения показательной функции — это множество значений R.
Основные примеры показательных функций:
Область определения, для этих функций, записывается следующим образом: (−∞, +∞).
Области определения основных элементарных функций
Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.
На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = xy и другие.
А области их определения изучаем, как свойства.
Как найти область значений функции по уравнению
Нахождение области значений функции по заданному уравнению также сводится к вычислению экстремумов.
Рассмотрим два случая:
- Нахождение области значений функции, непрерывной на некотором заданном отрезке.
- Нахождение области значений функции, непрерывной на некотором интервале. Сюда же отнесем случаи, когда функция не существует в какой-либо точке. Например, точка нуля знаменателя, в которой функция не существует, а область определения терпит разрыв.
Алгоритм поиска области значений для первого случая:
- Находим производную функции.
- Приравниваем производную к нулю, находим корни уравнения f′(x)=0 и точки, в которых производная не существует — критические точки.
- Отмечаем корни, критические точки и границы заданного интервала на прямой и определяем знаки производной на каждом получившемся промежутке.
- Находим минимумы и максимумы функции. Если в некоторой точке x1 производная меняет знак с «+» на «-», то точка x1 — максимум, если с «-» на «+» — минимум.
- Подставляя значения аргументов для минимума и максимума функции в выражение f(x), находим минимальное и максимальное значения функции. В том случае, если имеются точки, в которых производная не существует, значение функции вычисляем через пределы по формулам: limx→x1—f(x) и limx→x1+f(x).
- Записываем область значений функции.
Для второго случая:
- Находим производную, приравниваем ее к нулю и определяем знаки производной на каждом промежутке.
- Определяем значение функции в каждой из точек. Для определения значения функции в граничных точках, а также в точках разрыва или точках, в которых производная не существует, вычисляем пределы функции аналогично указанным в пункте 5 для первого случая.
- Определяем и записываем область значений.
Методы нахождения
Поиск области значений функции несколько сложнее, чем определение ОДЗ. В зависимости от вида и типа функции, а также условий задачи для этого могут применяться различные методы.
Перебор значений
Самый простой и ограниченный способ. При его помощи можно находить область значений на небольшом промежутке целых чисел (xin(a;;b)). В таком случае заданные значения переменной поочередно подставляются в уравнение и вычисляются значения функции, соответствующие им.
Графический метод
Как ясно из названия способа, для его реализации необходимо построить график исследуемой функции. По внешнему виду кривой уже можно делать некоторые выводы. Если линия графика соответствует одному из видов элементарных функций, например, является параболой, то в качестве области значений берется промежуток, соответствующий данному графику.
Примечание
Если по условию задачи необходимо найти область значений функции на определенном промежутке значений переменной x, то на графике максимальные и минимальные точки становятся очевидными. Это могут быть как общие точки экстремума, так и локальные максимальные и минимальные значения.
Учет непрерывности и монотонности
Данный метод вытекает из предыдущего и позволяет делать некоторые прогнозы об области значений функции исходя из ее свойств. Если на графике видно, что функция не прерывается и монотонно убывает или возрастает на определенном промежутке, можно предположить, что эта тенденция сохранится и дальше.
Например, график квадратичной функции f(x)=x^2 имеет вид параболы с точкой перегиба с координатами (0, 0). Кривая непрерывна, то есть не имеет разрывов в области определения. Для того, чтобы определить область значений данной функции, достаточно построить ее график на ограниченном промежутке. Для примера возьмем (xinlbrack-4;;4rbrack):
Рисунок 1. Значение непрерывности и монотонности функции для области определения
На графике видно, что функция монотонно убывает на промежутке (lbrack-4;;0rbrack) и монотонно возрастает на промежутке( lbrack0;;4rbrack). Исходя из этого и непрерывности функции, можно экстраполировать данную закономерность на всю область определения. Так как минимальное значение данной функции равняется нулю, область значений будет следующей:
(mathrm E(mathrm f)=lbrack0;;+infty))
Производная, min и max
Описанные выше способы подходят не для всех ситуаций. В общем случае, задача по определению области значений функции всегда сводится к нахождению ее минимального и максимального значения или точек экстремума.
Определение
Согласно теореме Ферма, в точках локального экстремума производная исследуемой функции равняется нулю.
Важно понимать, что сами локальный экстремум не обязательно является максимумом или минимумом для функции в целом. Такие точки называются критическими или стационарными. Поэтому, кроме самих точек необходимо определять промежутки возрастания и убывания:
- если при переходе через критическую точку производная функции меняет знак с (+) на (-), то эта точка является максимумом;
- если при переходе через критическую точку производная меняет знак с (-) на (+), то такая точка является минимумом;
- если при переходе знак производной не меняется, то экстремума в данной точке нет.
Кроме того, экстремумы функции можно определять по второй производной. Предположим, при исследовании функции обнаружилась некая критическая точка x_1. Для нее справедливы следующие неравенства:
Если (f»(x_1)>0), то (x_1) — точка минимума.
Если (f»(x_1)<0), то (x_1) — точка максимума.
Дробная функция
Определение:рациональной $f(x)=dfrac{a_nx^n+cdots+a_1x+a_0}{b_nx^n+cdots+b_1x+b_0}=dfrac{P(x)}{Q(x)}$ $D_f=mathbb{R} — lbrace x| Q(x)=0 rbrace$ Пример:Решение: $x^2-1=0 rightarrow x=pm 1$ $D_f=mathbb{R}- lbrace pm 1 rbrace$ $y(x^2-1)=x^2+1 rightarrow yx^2-x^2=y+1 rightarrow x^2=dfrac{y+1}{y-1} \ rightarrow x= pm sqrt{dfrac{y+1}{y-1}} rightarrow dfrac{y+1}{y-1} geq 0 \ rightarrow y leq -1 ,, or ,, y > 1 rightarrow R_f=(-infty,-1] cup (1,+infty).$ 

Разница между областью значения и областью определения функции
Стоит обратить внимание, что область значений функции — не одно и то же с термином «область определения функции».
Определение 3
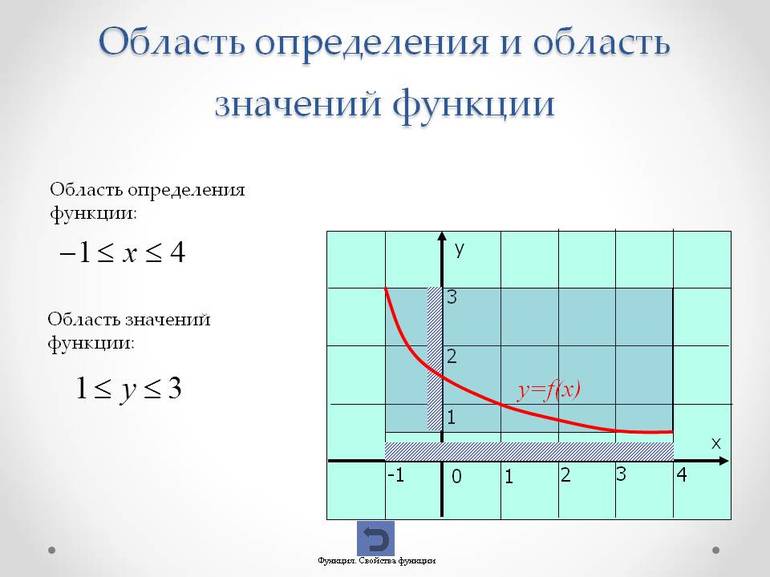
Область определения функции $D(y)$ — это диапазон таких значений переменной $x$, при которых существует функция $y(x)$.
Например, рассмотрим функцию $y(x)=x^2$. В данном случае область определения этой функции будет множеством вещественных (действительных) чисел $mathbb{R}$, а сама функция будет принимать значения только положительных действительных чисел $mathbb{R}^+$, так как вещественное число, возведённое в квадрат, не может давать отрицательное значение. То есть, в этом примере множество значений функции — это множество положительных вещественных чисел $mathbb{R}^+$.
Также имеют место случаи, когда область определения функции совпадает с областью значений. В качестве иллюстрации можно рассмотреть функцию $y(x)=2x$. За аргумент $x$ данная функция может принимать любое действительное число из множества $mathbb{R}$, а значения, которые будет принимать сама функция — это удвоенные числа из множества всех действительных чисел. То есть, в данном случае областью значений $E(y)$ будет также всё множество вещественных чисел $mathbb{R}$.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Теги
Всем здравствуйте! Тренируемся находить область значений функции! Кто еще не понял, что такое область определения (а она нам тоже понадобится непременно), тому сюда.
Что же такое область значений функции? Это та «часть» оси ординат, та область, где можно наткнуться на какие-либо точки, принадлежащие функции. То есть можно сказать, что если область значений найдена, то все точки функции находятся в ней, не выше и не ниже. Это почти тоже самое, что и область определения, только теперь это «область определения по оси ординат». Здесь никаких особых ограничений нет, поэтому, чтобы найти область значений, нужно иметь представление об элементарных функциях — например, как выглядят парабола или гипербола, как определить, направлены ли ветви параболы вверх или вниз и т.п. Все это рассказано и показано здесь.
Ну, поехали!
Примеры.
1. Найдите область значений функции
Решение: функция – квадратичная, представляет собой параболу с положительным старшим коэффициентом, ветви направлены вверх. Понятно тогда, что весь график располагается выше координаты своей вершины (вершина — самая низшая точка). Ордината вершины: 

2. Найдите область значений функции
Решение: область определения функции 



В точках (-7) и (3) двучлен обращается в ноль. Поскольку результат извлечения корня — величина положительная, то вся функция располагается выше оси абсцисс, и ее область значений 

3. Найти область значений функции
Область определения – вся числовая ось, кроме ноля. Можем подставить любое число из области определения, при этом функция всегда отрицательна.
Из графика также видно, что
4. Найти область значений функции:
Решение. Область определения:


На концах отрезка функция принимает значение 1, под корнем имеем квадратный двучлен, наибольшее значение он принимает в вершине, при 
Подставив 1, получаем
Ответ:
5. Найдите область значений функции:
Очевидно, что график данной функции может быть получен из графика обычной параболы 
Область значений нашей функции 

6. Найдите область значений функции:
Очевидно, что график данной функции может быть получен из графика обычной параболы 


7. Найдите область значений функции:
Данная функция получена преобразованием обычной гиперболы. Данная функция не существует при 



Ответ:
8. Найти область значений функции:
Решение. Область определения:


При 

При x, стремящемся к бесконечности, функция стремится к нулю. Но мы запишем область значений от меньшего к большему:
Ответ: 

Понятие функции и всё, что с ним связано, относится к традиционно сложным, не
до конца понятым. Особым камнем преткновения при изучении функции и подготовке к
ЕГЭ являются область определения и область значений (изменения) функции.
Нередко учащиеся не видят разницы между областью определения функции и областью
её значений.
И если задачи на нахождение области определения функции учащимся удаётся
освоить, то задачи на нахождение множества значений функции вызывают у них
немалые затруднения.
Цель данной статьи: ознакомление с методами нахождения значений функции.
В результате рассмотрения данной темы был изучен теоретический материал,
рассмотрены способы решения задач на нахождение множеств значений функции,
подобран дидактический материал для самостоятельной работы учащихся.
Данная статья может быть использована учителем при подготовке учащихся к
выпускным и вступительным экзаменам, при изучении темы “Область значения
функции” на факультативных занятиях элективных курсах по математике.
Приложение 1, Приложение 2
I. Определение области значений функции.
Областью (множеством) значений E(у) функции y = f(x) называется множество
таких чисел y0, для каждого из которых найдётся такое число x0,
что: f(x0) = y0.
Напомним области значений основных элементарных функций.
Рассмотрим таблицу.
| Функция | Множество значений |
| y = kx+ b | E(y) = (-∞;+∞) |
| y = x2n | E(y) = [0;+∞) |
| y = x2n +1 | E(y) = (-∞;+∞) |
| y = k/x | E(y) = (-∞;0)u(0;+∞) |
| y = x1/2n | E(y) = [0;+∞) |
| y = x1/2n+1 | E(y) = (-∞;+∞) |
| y = ax | E(y) = (0;+∞) |
| y = logax | E(y) = (-∞;+∞) |
| y = sin x | E(y) = [-1;1] |
| y = cos x | E(y) = [-1;1] |
| y = tg x | E(y) = (-∞;+∞) |
| y = ctg x | E(y) = (-∞;+∞) |
| y = arcsin x | E(y) = [-π/2; π/2] |
| y = arcos x | E(y) = [0; π] |
| y = arctg x | E(y) = (-π/2; π/2) |
| y = arcctg x | E(y) = (0; π) |
Заметим также, что областью значения всякого многочлена чётной степени
является промежуток [m;+∞) , где m – наименьшее значение этого многочлена, либо
промежуток
(-∞;n] , где n – наибольшее значение этого многочлена.
II. Свойства функций, используемые при нахождении области значений функции
Для успешного нахождения множества значений функции надо хорошо знать
свойства основных элементарных функций, особенно их области определения, области
значений и характер монотонности. Приведём свойства непрерывных, монотонных
дифференцируемых функций, наиболее часто используемые при нахождении множества
значений функций.
- Если функция f(x) непрерывна и возрастает на отрезке [a;b], то множество
значений функции на этом отрезке есть отрезок [f(a),f(b)]. При этом каждое
значение А
[f(a),f(b)] функция принимает ровно при одном значении x принадлежит [a,b],
т.е уравнение f(x) = А имеет единственный корень на отрезке [a,b]. Если же f(x)
– непрерывная и убывающая на отрезке [a,b] функция, то её множество значений
на [a,b] есть отрезок [f(a),f(b)]. - Если функция f(x) непрерывна на отрезке [a,b] и m = min f(x), M = max f(x)
– её наименьшее и наибольшее значение на этом отрезке, то множество значений
f(x) на [a,b] есть отрезок [m;M]. - Если функция непрерывна на отрезке [a,b] и дифференцируема (имеет
производную) в интервале (a,b), то наибольшее и наименьшее значения функции
на отрезке [a,b] существуют и достигаются либо на концах отрезка, либо в
критических точках функции, расположенных на отрезке
Свойства 2 и 3, как правило, используются вместе свойством элементарной
функции быть непрерывной в своей области определения. При этом наиболее простое
и краткое решение задачи на нахождение множества значений функции достигается на
основании свойства 1, если несложными методами удаётся определить монотонность
функции. Решение задачи ещё упрощается, если функция, вдобавок, – чётная или
нечётная, периодическая и т.д. Таким образом, при решении задач на нахождение
множеств значений функции следует по мере надобности проверять и использовать
следующие свойства функции:
- непрерывность;
- монотонность;
- дифференцируемость;
- чётность, нечётность, периодичность и т.д.
Несложные задачи на нахождение множества значений функции в большинстве своём
ориентированны:
а) на использование простейших оценок и ограничений: (2х>0,
-1≤sinx?1, 0≤cos2x?1 и т.д.);
б) на выделение полного квадрата: х2 – 4х + 7 = (х – 2)2+
3;
в) на преобразование тригонометрических выражений: 2sin2x – 3cos2x
+ 4 = 5sin2x +1;
г) использование монотонности функции x1/3 + 2x-1
возрастает на R.
III. Рассмотрим способы нахождения областей значений функций.
а) последовательное нахождение значений сложных аргументов функции;
б) метод оценок;
в) использование свойств непрерывности и монотонности функции;
г) использование производной;
д) использование наибольшего и наименьшего значений функции;
е) графический метод;
ж) метод введения параметра;
з) метод обратной функции.
Раскроем суть этих методов на конкретных примерах.
Пример 1. Найдите область значений E(y) функции y = log0,5(4
– 2·3x – 9x).
Решим этот пример методом последовательного нахождения значений сложных
аргументов функции. Выделив полный квадрат под логарифмом, преобразуем функцию
y = log0,5(5 – (1 + 2·3x – 32x)) = log0,5(5
– (3x + 1)2)
И последовательно найдём множества значений её сложных аргументов:
E(3x) = (0;+∞), E(3x+ 1) = (1;+∞), E(-(3x+
1)2 = (-∞;-1), E(5 – (3x+1)2) = (-∞;4)
Обозначим t = 5 – (3x+1)2, где -∞≤t≤4.
Тем самым задача сводится к нахождению множества значений функции y = log0,5t
на луче (-∞;4). Так как функция y = log0,5t определена лишь
при, то её множество значений на луче (-∞;4) совпадает со множеством значений
функции на интервале (0;4), представляющем собой пересечение луча (-∞;4) с
областью определения (0;+∞) логарифмической функции. На интервале (0;4) эта
функция непрерывна и убывает. При t > 0 она стремится к +∞, а при t =
4 принимает значение -2, поэтому E(y) = (-2, +∞).
Пример 2. Найдите область значений функции
y = cos7x + 5cosx
Решим этот пример методом оценок, суть которого состоит в оценке непрерывной
функции снизу и сверху и в доказательстве достижения функцией нижней и верхней
границы оценок. При этом совпадение множества значений функции с промежутком от
нижней границы оценки до верхней обуславливается непрерывностью функции и
отсутствием у неё других значений.
Из неравенств -1≤cos7x?1, -5≤5cosx?5 получим оценку -6≤y?6. При x = р и x = 0
функция принимает значения -6 и 6, т.е. достигает нижней и верхней границы
оценки. Как линейная комбинация непрерывных функций cos7x и cosx, функция y
непрерывна на всей числовой оси, поэтому по свойству непрерывной функции она
принимает все значения с -6 до 6 включительно, и только их, так как в силу
неравенств -6≤y?6 другие значения у неё невозможны. Следовательно, E(y) =
[-6;6].
Пример 3. Найдите область значений E(f) функции f(x) =
cos2x + 2cosx.
По формуле косинуса двойного угла преобразуем функция f(x) = 2cos2x
+ 2cosx – 1 и обозначим t = cosx. Тогда f(x) = 2t2 + 2t
– 1. Так как E(cosx) =
[-1;1], то область значений функции f(x) совпадает со множеством
значений функции g(t) = 2t2 + 2t – 1 на отрезке [-1;1],
которое найдём графическим методом. Построив график функции y = 2t2 +
2t – 1 = 2(t + 0,5)2 – 1,5 на промежутке [-1;1], находим E(f)
= [-1,5; 3].
Замечание – к нахождению множества значений функции сводятся многие задачи с
параметром, связанные, в основном, с разрешимостью и числом решений уравнения и
неравенств. Например, уравнение f(x) = а разрешимо тогда и только тогда,
когда
a
E(f) Аналогично, уравнение f(x) = а имеет хотя бы один корень,
расположенный на некотором промежутке Х, или не имеет ни одного корня на этом
промежутке тогда и только тогда, когда а принадлежит или не принадлежит
множеству значений функции f(x) на промежутке Х. Также исследуются с
привлечением множества значений функции и неравенства f(x)≠ а, f(x)>а
и т.д. В частности, f(x)≠ а для всех допустимых значений х, если
a
E(f)
Пример 4. При каких значениях параметра а уравнение (x + 5)1/2
= a(x2 + 4) имеет единственный корень на отрезке [-4;-1].
Запишем уравнение в виде (x + 5)1/2 / (x2 + 4) = a .
Последнее уравнение имеет хотя бы один корень на отрезке [-4;-1] тогда и только
тогда, когда а принадлежит множеству значений функции f(x) = (x + 5)1/2
/ (x2 + 4) на отрезке [-4;-1]. Найдём это множество, используя
свойство непрерывности и монотонности функции.
На отрезке [-4;-1] функция y = xІ + 4 непрерывна, убывает и положительна,
поэтому функция g(x) = 1/(x2 + 4) непрерывна и возрастает на
этом отрезке, так как при делении на положительную функцию характер монотонности
функции меняется на противоположный. Функция h(x) = (x + 5)1/2
непрерывна и возрастает в своей области определения D(h) = [-5;+∞) и, в
частности на отрезке [-4;-1], где она, кроме того, положительна. Тогда функция
f(x)=g(x)·h(x), как произведение двух непрерывных, возрастающих и
положительных функций, также непрерывна и возрастает на отрезке [-4;-1], поэтому
её множество значений на [-4;-1] есть отрезок [f(-4); f(-1)] = [0,05;
0,4]. Следовательно, уравнение имеет решение на отрезке [-4;-1], причём
единственное (по свойству непрерывной монотонной функции), при 0,05 ≤ a ≤ 0,4
Замечание. Разрешимость уравнения f(x) = a на некотором промежутке Х
равносильна принадлежности значений параметра а множеству значений
функции f(x) на Х. Следовательно, множество значений функции f(x)
на промежутке Х совпадает с множеством значений параметра а, для которых
уравнение f(x) = a имеет хотя бы один корень на промежутке Х. В
частности, область значений E(f) функции f(x)совпадает с
множеством значений параметра а, для которых уравнение f(x) = a
имеет хотя бы один корень.
Пример 5. Найдите область значений E(f) функции
Решим пример методом введения параметра, согласно которому E(f)
совпадает с множеством значений параметра а, для которых уравнение
имеет хотя бы один корень.
При а=2 уравнение является линейным – 4х – 5 = 0 с ненулевым коэффициентом
при неизвестной х , поэтому имеет решение. При а≠2 уравнение является
квадратным, поэтому оно разрешимо тогда и только тогда, когда его дискриминант
Так как точка а = 2 принадлежит отрезку
то
искомым множеством значений параметра а, значит, и областью значений E(f)
будет весь отрезок.
Как непосредственное развитие метода введения параметра при нахождении
множества значений функции, можно рассматривать метод обратной функции, для
нахождения которой надо решить относительно х уравнение f(x)= y, считая y
параметром. Если это уравнение имеет единственное решение x =g(y), то
область значений E(f) исходной функции f(x) совпадает с областью
определения D(g) обратной функции g(y). Если же уравнение f(x)=
y имеет несколько решений x =g1(y), x =g2(y)
и т.д., то E(f) равна объединению областей определений функции g1(y),
g2(y) и т.д.
Пример 6. Найдите область значений E(y) функции y = 52/(1-3x).
Из уравнения
найдём обратную функцию x = log3((log5y – 2)/(log5y))
и её область определения D(x):
Так как уравнения относительно х имеет единственное решение, то
E(y) = D(x) = (0; 1)(25;+∞).
Если область определения функции состоит из нескольких промежутков или
функция на разных промежутках задана разными формулами, то для нахождения
области значений функции надо найти множества значений функции на каждом
промежутке и взять их объединение.
Пример 7. Найдите области значений f(x) и f(f(x)), где
Найдём сначала множество значений функции f(x) на луче (-∞;1], где она
совпадает с выражением 4x + 9·4-x + 3. Обозначим t = 4x
. Тогда f(x) = t + 9/t + 3, где 0 < t ≤ 4 , так как показательная
функция непрерывно возрастает на луче (-∞;1] и стремится к нулю при х → -∞. Тем
самым множество значений функции f(x) на луче (-∞;1] совпадает с
множеством значений функции g(t) = t + 9/t + 3, на промежутке
(0;4], которое найдём, используя производную g’(t) = 1 – 9/t2.
На промежутке (0;4] производная g’(t) определена и обращается там в нуль
при t = 3. При 0<t<3 она отрицательна, а при 3<t<4
положительна. Следовательно, в интервале (0;3) функция g(t) убывает, а в
интервале (3;4) она возрастает, оставаясь непрерывной на всём промежутке (0;4),
поэтом g(3)= 9 – наименьшее значений этой функции на промежутке (0;4], в
то время как её наибольшее значение не существует, так при t→0 справа
функция g(t)→+∞. Тогда, по свойству непрерывной функции, множеством
значений функции g(t) на промежутке (0;4], а значит, и множеством
значений f(x) на (-∞;-1], будет луч [9;+∞).
При х >1 функция f(x) совпадает с выражением 2cos(x-1)1/2
+ 7. Квадратный корень (x-1)1/2 при x > 1 определён и
принимает все положительные значения, поэтому cos(x-1)1/2
принимает все значения от -1 до 1 включительно, а выражение 2cos(x-1)1/2
+ 7 принимает все значения от 5 до 9 включительно. Следовательно, множеством
значений функции f(x) на луче (1;+∞) будет отрезок [5;9].
Теперь, объединив промежутки [9;+∞) и [5;9] – множества значений функции f(f(x)),
обозначим t = f(x). Тогда f(f(x)) = f(t), где
При указанных t функция f(t) = 2cos(x-1)1/2 + 7
и она снова принимает все значения от 5 до 9 включительно, т.е. область значений
E(fІ) = E(f(f(x))) = [5;9].
Аналогично, обозначив z = f(f(x)), можно найти область значений E(f3)
функции f(f(f(x))) = f(z), где 5 ≤ z ≤ 9 и т.д. Убедитесь, что E(f3)
= [2cos81/2 + 7; 2cos2 + 7].
Наиболее универсальным методом нахождения множества значений функции является
использование наибольшего и наименьшего значений функции на заданном промежутке.
Пример 8. При каких значениях параметра р неравенcтво 8x—р
≠ 2x+1 – 2x выполняется для всех -1 ≤ x < 2.
Обозначив t = 2x, запишем неравенство в виде р ≠ t3
– 2t2 + t. Так как t = 2x – непрерывная
возрастающая функция на R, то при -1 ≤ x < 2 переменная
2-1 ≤ t <22 ↔
0,5 ≤ t < 4, и исходное неравенство выполняется для всех -1 ≤ x < 2 тогда и
только тогда, когда р отлична от значений функции f(t) = t3
– 2t2 + t при 0,5 ≤ t < 4.
Найдём сначала множество значений функции f(t) на отрезке [0,5;4], где
она всюду имеет производную f’(t) =3t2 – 4t + 1.
Следовательно, f(t) дифференцируема, значит, и непрерывна на отрезке
[0,5;4]. Из уравнения f’(t) = 0 найдём критические точки функции t =
1/3, t = 1, первая из которых не принадлежит отрезку [0,5;4], а вторая
принадлежит ему. Так как f(0,5) = 1/8, f(1) = 0, f(4) = 36, то, по
свойству дифференцируемой функции, 0 – наименьшее, а 36 – наибольшее значение
функции f(t) на отрезке [0,5;4]. Тогда f(t), как непрерывная
функция, принимает на отрезке [0,5;4] все значения от 0 до 36 включительно,
причём значение 36 принимает только при t = 4, поэтому при 0,5 ≤ t < 4,
она принимает все значения из промежутка [0;36). Тем самым
Заключение.
Данная тема имеет практическое значение. В школьном курсе математики
изучается тема “Область значения функции”. Такие задачи обязательно содержатся в
заданиях различных математических тестов, в частности в заданиях единого
государственного экзамена.
Результаты работы можно использовать на уроках и дополнительных занятиях при
подготовке учащихся выпускным и вступительным экзаменам, при самостоятельной
подготовке учащихся по данной теме.
Литература.
- Сильвестров В.В. Множество значений функции: Учебное пособие.–
Чебоксары, 2004. - Амелькин В.В., Рабцевич В.Л. Задачи с параметрами.– Минск, 1996.
- Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. –
Москва – Харьков, 1998. - Мочалов В.В., Сильвестров В.В. Уравнения и неравенства с
параметрами: Учебное пособие. 4-е изд., доп., перераб. – М., 2006. - Сильвестров В.В. Неравенства с параметром на едином
государственном экзамене // Математика для школьников. 2008. №
2.













![E(f)=[{1/3};1] E(f)=[{1/3};1]](https://easy-physic.ru/img_formuls/math_985.5_1886f49c79f1ee64a352b2c46dc2c867.png)













