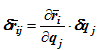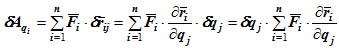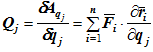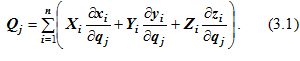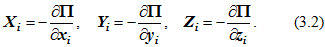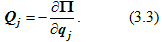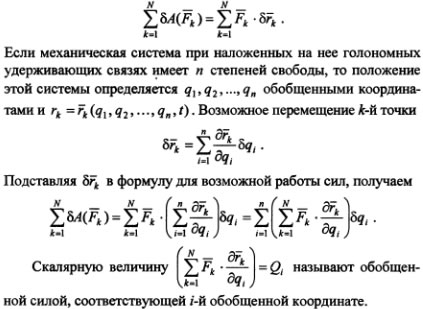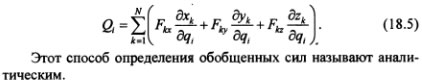Обобщенные силы и способы их вычисления
Рассмотрим
механическую систему с идеальными
связями. Пусть
активные силы системы. Дадим механической
системе виртуальное перемещение и
вычислим элементарную работу сил системы
на этом перемещении:
.
Используя
равенство (17.2) выразим вариацию
радиусавектора
точкиMk
через вариации
обобщенных координат:
и,
следовательно,
. (17.6)
Поменяем в равенстве
(17.6) порядок суммирования:
. (17.7)
Обозначим в
выражении (17.7)
. (17.8)
Получим
.
Обобщенными
силами Qj
называют
коэффициенты при вариациях обобщенных
координат в выражении элементарной
работы сил системы.
В
зависимости от размерности вариаций
обобщенных координат
обобщенные силыQj
могут иметь размерность силы, момента
и др.
Способы вычисления обобщенных сил
Рассмотрим три
способа вычисления обобщенных сил.
1.
Определение
обобщенных сил по основной формуле
(17.8)
. (17.9)
Формула (17.9) на
практике применяется редко. При решении
задач чаще применяется второй способ.
2.
Способ
«замораживания» обобщенных координат.
Дадим
механической системе такое виртуальное
перемещение, при котором все вариации
обобщенных координат кроме
равны нулю:
.
Вычислим
на это перемещение работу
всех активных сил, приложенных к системе
.
По
определению множитель при вариации
равен первой обобщенной силеQ1.
Далее дадим системе
виртуальное перемещение
и
определим вторую обобщенную силу Q2,
вычислив виртуальную работу всех сил
системы
.
Аналогично вычислим
все остальные обобщенные силы системы.
3.
Случай
потенциального силового поля.
Предположим,
известна потенциальная энергия
механической системы
.
Тогда
и по формуле (32.8)
.
(17.10)
Принцип виртуальных перемещений статики в обобщенных координатах
Согласно принципу
виртуальных перемещений статики для
равновесия системы с идеальными
удерживающими голономными, стационарными
связями необходимо и достаточно является
условие
при
нулевых начальных скоростях.
Переходя к
обобщенным координатам, получим
. (17.11)
Так как вариации
обобщенных координат независимы, то
равенство нулю выражения (17.11) возможно
только в том случае, когда все коэффициенты
при вариациях обобщенных координат
равны нулю:
. (17.12)
Таким
образом, для
того, чтобы механическая система с
идеальными, голономными, стационарными
и удерживающими связями находилась в
равновесии необходимо и достаточно,
чтобы все обобщенные силы системы
равнялись нулю (при нулевых начальных
скоростях системы).
Уравнения Лагранжа в обобщенных координатах (уравнения Лагранжа второго рода)
Уравнения Лагранжа
выводятся из общего уравнения динамики
заменой виртуальных перемещений их
выражениями через вариации обобщенных
координат. Они представляют собой
систему дифференциальных уравнений
движения механической системы в
обобщенных координатах:
. (17.13)
где
обобщенные скорости,
Т
кинетическая энергия системы,
представленная как функция обобщенных
координат и обобщенных скоростей
,
Qj
обобщенные силы.
Число уравнений
системы (17.13) определяется числом степеней
свободы и не зависит от количества тел
входящих в систему. При идеальных связях
в правые части уравнений войдут только
активные силы. Если связи неидеальны,
то их реакции следует отнести к активным
силам.
В случае потенциальных
сил, действующих на механическую систему
уравнения (17.13) примут вид
.
Если
ввести функцию Лагранжа L
= Т
П,
то учитывая, что потенциальная энергия
не зависит от обобщенных скоростей,
получим уравнения Лагранжа второго
рода для случая потенциальных сил в
следующей форме
.
При составлении
уравнений Лагранжа второго рода нужно
выполнить следующие действия:
-
Установить число
степеней свободы механической системы
и выбрать ее обобщенные координаты. -
Составить выражение
кинетической энергии системы и
представить ее как функцию обобщенных
координат и обобщенных скоростей. -
Пользуясь
изложенными выше способами найти
обобщенные активные силы системы. -
Выполнить все
необходимые в уравнениях Лагранжа
операции дифференцирования.
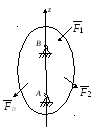
Пример.
|
Рис.17.3 |
Составим
1.
q
2. Кинетическая
|
где
Jz
момент инерции тела относительно оси
вращения z,
угловая скорость тела.
3.
Определим обобщенную силу. Дадим телу
виртуальное перемещение
и вычислим виртуальную работу всех
активных сил системы:
.
Следовательно,
Q
= Mz
главный момент активных сил системы
относительно оси вращения тела.
4. Выполним операции
дифференцирования в уравнении Лагранжа
:
(17.14)
.
(17.15)
Подставляя
равенства (17.15) в уравнение (173
.14) получим
дифференциальное уравнение вращательного
движения тела
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обобщенной силой Qi, соответствующей обобщенной координате qj, называют скалярную величину, определяемую отношением элементарной работы действующих сил на перемещении механической системы, вызванную изменением обобщенной координаты qj, к величине приращения этой координаты δqj:
Qi = δAj / δqj
или
δAj = Qi ∙ δqj.
Размерность обобщенной силы зависит от размерности обобщенной координаты и может выражаться в единицах силы [Н], момента [Н∙м]. Число обобщенных сил для данной системы соответствует числу обобщенных координат.
При необходимости можно сосчитать обобщенные силы от внешних сил QiF, обобщенные силы реакций связей QiR, обобщенные силы от сил инерции QiΦ.
Радиус-вектор произвольной точки механической системы есть функция обобщенных координат:
ri = ri (q1, q2 … qj … qs),
поэтому приращение радиуса-вектора, вызванное изменением, например, обобщенной координаты qj, будет
тогда работа приложенных к системе сил на малом перемещении будет
То есть обобщенная сила может быть выражена соотношением
Расписав скалярное произведение, получим
Для консервативной системы силы поля, действующие на точки механической системы, выражаются соотношениями
Учитывая, что радиус-вектор любой точки и потенциальная энергия системы есть функция координат и, следовательно, обобщенных координат, можно получить из выражения (3.1):
Примеры решения задач >
Общее уравнение динамики в обобщенных силах >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Обобщенные силы. Способы вычисления обобщенных сил.
В аналитической механике наряду с понятием о силе как векторной величине, характеризующей воздействие на данное тело со стороны других материальных тел, используют понятие об обобщенной силе. Для определения обобщенной силы рассмотрим возможную работу сил, приложенных к точкам системы,
Таким образом, обобщенной силой, соответствующей i-й обобщенной координате, называется величина, равная коэффициенту при вариации данной обобщенной координаты в выражении возможной работы сил, действующих на механическую систему.
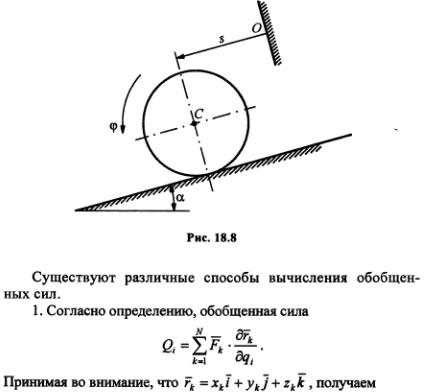
В общем случае обобщенная сила является функцией обобщенных координат, скоростей точек системы и времени. Из определения следует, что обобщенная сила — скалярная величина, которая зависит от выбранных для данной механической системы обобщенных координат. Это значит, что при изменении набора обобщенных координат, определяющих положение данной системы, изменятся и обобщенные силы. Так, для диска радиусом r и массой m, который катится без скольжения по наклонной плоскости (рис. 18.8), за обобщенные координаты можно принять либо s — координата центра масс диска, либо «фи» — угол поворота диска. Если пренебречь сопротивлением качению, то в пер-
2. Обобщенные силы для механических систем с n > 1 целесообразно вычислять последовательно, учитывая, что обобщенные координаты, а значит, и их вариации независимы между собой. Системе всегда можно сообщить такое возможное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не варьируются. В этом случае:
Из лекций:
Из интернета:
————-
Суммируя виртуальные работы по всем обобщенным координатам, найдем виртуальную работу сил системы в обобщенных координатах:
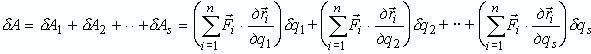 |
(3) |
Обозначая коэффициенты при приращениях или вариациях обобщенных координат как Q1, Q2, …, Qs, выражаем виртуальную работу сил системы в обобщенных координатах в виде
| (4) |
————-
Обобщенные силы и способы их вычисления. В аналитической механике обобщенными силами называются коэффициенты Q1, Q2, …, Qs при приращениях или вариациях обобщенных координат в выражении (4) виртуальной работы сил системы в обобщенных координатах.
Обобщенная сила Qj в общем случае не является силой в обычном понимании. Ее размерность зависит от размерности обобщенной координаты qj и определяется равенством [Qj] = [A] / [qj], где [A] — размерность работы. Так, если обобщенная координата — линейная величина, то обобщенная сила имеет размерность силы. Если обобщенная координата — угловая величина, то обобщенная сила имеет размерность момента, а если обобщенная координата является, например, объемом камеры сгорания над поршнем двигателя, то обобщенная сила имеет размерность давления.
Рассмотрим основные способы вычисления обобщенных сил.
Первый способ аналогичен тому, что мы применяли для вычисления виртуальной работы сил системы в обобщенных координатах. Системе дается виртуальное перемещение так, чтобы изменялась только первая обобщенная координата при фиксированных остальных обобщенных координатах. На этом виртуальном перемещении подсчитывается виртуальная работа сил системы. Коэффициент при вариации первой обобщенной координаты в выражении этой работы будет обобщенной силой по первой обобщенной координате. Аналогично поступают и для остальных обобщенных координат, определяя каждый раз коэффициенты при вариациях обобщенных координат в выражениях виртуальной работы, которые будут представлять собой обобщенные силы по соответствующей обобщенной координате.
Второй способ используется для голономных систем со стационарными связями, когда обобщенные скорости могут совпадать с виртуальными обобщенными скоростями, то есть
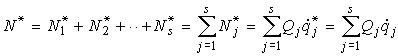 |
(7) |
Из (7) видим, что обобщенными силами будут коэффициенты при обобщенных скоростях в выражениях виртуальной мощности сил системы по каждой обобщенной координате, вычисляемой при не равной нулю обобщенной скорости по данной обобщенной координате (qj’ <> 0), когда остальные обобщенные скорости равны нулю (qk’ = 0 (k <> j)).
Третий способ основан на выражении обобщенных сил в координатной форме. Записав (3) в виде
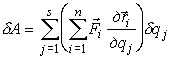 |
(8) |
выразим обобщенную силу по соответствующей обобщенной координате как
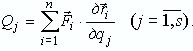 |
(9) |
Выразив (9) в аналитической форме записи, получаем формулу для вычисления обобщенных сил в координатной форме:
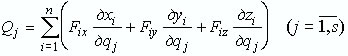 |
(10) |
где Fix, Fiy, Fiz — проекции силы Fi на оси координат.
Четвертый способ применяется тогда, когда большинство сил системы потенциальны. В этом случае потенциальная энергия системы является функцией обобщенных координат, то есть П = П(q1, q2, …, qs), а
| (11) |
Примечание: при вычислении обобщенных сил первым или вторым способами приращения (вариации) обобщенных координат или обобщенные скорости нужно направлять в сторону увеличения обобщенных координат.
Используются технологии uCoz
Обобщенные силы
Каждой обобщенной координате 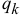
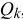
Чтобы определить обобщенную силу 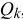
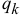
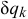
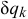
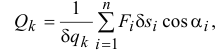
где 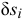
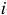
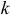
Обобщенная сила определяется с помощью элементарных работ. Поэтому эту силу можно вычислить иначе (см. выражения (15.3) и (15.4))
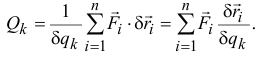
И так как 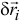
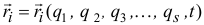
за счет приращения координаты 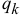
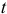
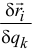
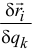
Тогда
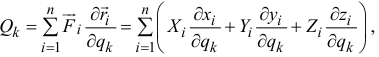
где координаты точек — функции обобщенных координат (18.1).
Если система консервативная, то есть движение происходит под действием сил потенциального поля (15.14), проекции которых
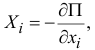
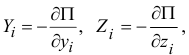
где
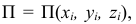
а координаты точек — функции обобщенных координат, то
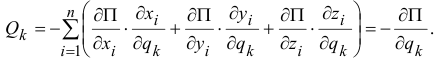
Обобщенная сила консервативной системы есть частная производная от потенциальной энергии по соответствующей обобщенной координате со знаком минус.
Конечно, при вычислении этой обобщенной силы потенциальную энергию следует определять как функцию обобщенных координат
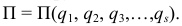
Замечания.
Первое. При вычислении обобщенных сил реакции идеальных связей не учитываются.
Второе. Еденица измерения обобщенной силы зависит от размерности обобщенной координаты. Так, если 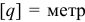
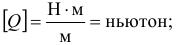
если
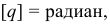
то
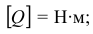
если
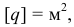
то
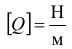
и т.п.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
Описание презентации по отдельным слайдам:
-
1 слайд
УРАВНЕНИЯ ЛАГРАНЖА II РОДА.
ОБОБЩЁННЫЕ КООРДИНАТЫ,
СКОРОСТИ И СИЛЫ.
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
ДинамикаЛЕКЦИЯ 12
-
2 слайд
Определять положение любой точки механической системы
Научиться описывать движение механической системы с несколькими степенями свободыЦель введения обобщенных координат, скоростей и сил
2 -
3 слайд
Обобщенные координаты
Обобщенные координаты – это независимые между собой параметры любой размерности, однозначно определяющие положение механической системы в пространстве.
3
ОБОБЩЕННЫЕ КООРДИНАТЫ -
4 слайд
ПОНЯТИЕ СТЕПЕНИ СВОБОДЫ
Число независимых между собой возможных перемещений МС называется числом степеней свободы системы.
4
У механической системы с голономными связями число обобщенных координат совпадает с числом её степеней свободы
Обобщенные координаты -
5 слайд
В несвободной механической системе декартовых координат ее точек должны удовлетворять уравнениям связей, поэтому независимыми среди них будут только координат.
5
Если бы система была свободной, то все декартовых координат ее точек были бы независимыми.
КОЛИЧЕСТВО СТЕПЕНЕЙ СВОБОДЫ
Обобщенные координаты
1
2 -
6 слайд
6
КОЛИЧЕСТВО СТЕПЕНЕЙ СВОБОДЫ
Обобщенные координаты
У свободного твёрдого тела 6 степеней свободы:
3 поступательных вдоль осей координат и 3 вращательных вокруг этих осей. -
7 слайд
ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ТОЧЕК МС
Тогда радиус-векторы всех точек системы можно определить как функцию обобщенных координат
Обобщенные координаты будем обозначать буквой —
7
Обобщенные координаты -
8 слайд
ОБОБЩЁННЫЕ СКОРОСТИ
Обобщенные скорости
8
При движении системы её обобщённые координаты будут меняться со временем по закону— кинематическое уравнение движения в обобщённых координатах.
Размерность обобщённой скорости зависит от размерности соответствующей обобщённой координаты.
Производные от обобщённых координат по времени называются обобщёнными скоростями -
9 слайд
ОБОБЩЁННЫЕ СИЛЫ
Обобщенные силы
9
Рассмотрим МС, состоящую из n материальных точек, на которые действуют силы
Пусть система имеет S степеней свободы и ее положение определяется обобщенными координатами
Сообщим системе такое независимое возможное перемещение, при котором координата получает приращение а остальные координаты не изменяются.
Тогда каждый из радиус-векторов точек системы получит элементарное приращение -
10 слайд
ОБОБЩЁННЫЕ СИЛЫ
Обобщенные силы
10
Поскольку изменяется только координата , то вычисляется как частный дифференциал
Тогда вычислим сумму элементарных работ всех действующих сил на рассматриваемом перемещении. -
11 слайд
ОБОБЩЁННЫЕ СИЛЫ
Обобщенные силы
11
— обобщённая сила, соответствующая координате -
12 слайд
12
Обобщённые силы – это величины, равные коэффициентам при приращениях обобщённых
координат в выражении полной элементарной работы
действующих на систему сил.
Размерность обобщённой силы равна размерности работы, деленной на размерность соответствующей обобщённой координаты.
Обобщенные силы
Если системе сообщить такое возможное перемещение, при котором одновременно меняются все обобщенные координаты, то сумма элементарных работ приложенных сил на этом перемещении равна: -
13 слайд
13
Обобщенные силы
ПРИМЕР (ДВОЙНОЙ МАЯТНИК) -
14 слайд
13
Обобщенные силы
ПРИМЕР (ДВОЙНОЙ МАЯТНИК) -
15 слайд
14
Обобщенные силы