Калькулятор для вычисления обратного элемента по модулю ниже, теория под ним.
Обратный элемент в кольце по модулю
Обратным к числу a по модулю m называется такое число b, что:
,
Обратный элемент обозначают как .
Для нуля обратного элемента не существует никогда, для остальных же элементов обратный элемент может как существовать, так и нет.
Утверждается, что обратный элемент существует только для тех элементов a, которые взаимно просты с модулем m.
Для нахождения обратного элемента по модулю можно использовать Расширенный алгоритм Евклида.
Для того, чтобы показать это, рассмотрим следующее уравнение:
Это линейное диофантово уравнение с двумя переменными, см. Линейные диофантовы уравнения с двумя переменными. Посколько единица может делиться только на единицу, то уравнение имеет решение только если .
Решение можно найти с помощью расширенного алгоритма Евклида. При этом, если мы возьмём от обеих частей уравнения остаток по модулю m, то получим:
Таким образом, найденное x и будет являться обратным к a.
Пусть K – некоторое
коммутативное кольцо.
Определение.
Стандартным
многочленом (или полиномом) степени
от
переменной
x
над
коммутативным кольцом K называется
выражение вида
, (23)
где
.
Элементы
называются коэффициентами многочлена.
Все они,
или часть из них, могут быть нулевыми.
Каноническая
форма многочлена (23)
определяется следующим образом.
Находим
наибольшее
,
такое, что
,
скажем
и запишем
(24)
Степенью
многочлена
называется
число
,
если оно существует. Если же все
обращаются в нуль, то канонической
формой многочлена является 0,
а его
степень –
.
Степень
обозначается
.
Пусть
и
— два
многочлена.
В
зависимости от того, какому из множеств
принадлежат коэффициенты
,
различаются следующие типы многочленов:
-
с
булевыми коэффициентами
; -
с
целочисленными коэффициентами
; -
с
вещественными коэффициентами
; -
с
рациональными коэффициентами
; -
с
комплексными коэффициентами
.
;
;
;
;
.
Лемма. Многочлены
и
равны тогда и только тогда, когда
,
при которых
определены, а все остальные
,
равны нулю.
Пусть
имеется два многочлена
степени
и
степени
.
Определение. Суммой
многочленов
и
называется многочлен
(25)
где
и
(26)
Определение. Произведением
двух многочленов
и
называется многочлен
, (27)
где
.
Пример. Пусть
заданы два многочлена с булевыми
коэффициентами т.е.
.
Суммой
многочленов
является
многочлен
вида:
,
а
произведением – многочлен
:
Можно показать,
что введенная операция умножения
многочленов ассоциативна, следовательно
многочлены образуют по операции умножения
полугруппу, и эта полугруппа коммутативна.
Вывод. Многочлены
с целочисленными коэффициентами образуют
коммутативное кольцо. Можно показать,
что многочлены с рациональными,
вещественными и комплексными коэффициентами
также образуют соответствующие кольца
многочленов. В общем случае говорят о
«кольцах многочленов
над кольцом
.
3. Кольцо целостности.
Пусть
– произвольное кольцо. Как было показано
ранее, для любого элемента
выполняются равенства:
.
Отсюда
следует, что нулевой – 0 и единичный –
элементы являются различными элементами
кольца.
Если
для элемента
в кольце
существует обратный элемент
,
то он единственный,
для которого выполняется условие
.
Единичный
элемент кольца
является обратным для самого себя:
.
Из
равенства
следует, что элемент
также являетсяобратным
для самого себя.
Нулевой
элемент 0 кольца
не имеет обратного элемента, поскольку
,
для любого элемента
.
Определение. Элемент
,
для которого в кольце
существует,
и притом только единственный, обратный
элемент
,
называют
обратимым
или делителем
единицы.
Кольцо
целых чисел
является
самым простым примером коммутативного
кольца, в котором только 1 и –1 являются
делителями единицы
.
Теорема. Множество
всех делителей единицы
кольца
является группой по умножению.
Доказательство. Действительно,
если
,
т.е. являются делителями единицы
кольца
,
то
и, следовательно,
.
А
это означает, что
и
также являются делителями единицы
и, следовательно, содержатся в множестве
.
Поэтому множество
является группой по умножению.
Определение. Группа
называется группой делителей единичного
элемента
кольца
.
Так
как для любого элемента
выполняется
равенство
,
то по определению делителей элементов
кольца, каждый элемент является делителем
нуля. В теории колец для произвольных
элементов
используют следующее определение
делителей нуля.
Определение. Элементы
называются делителями нуля, если
,
а
;
при этом
называют левым, а
– правым делителем нуля.
Пример. 1. В
кольце классов вычетов по mod m существуют
делители нуля:
:
,
:
.
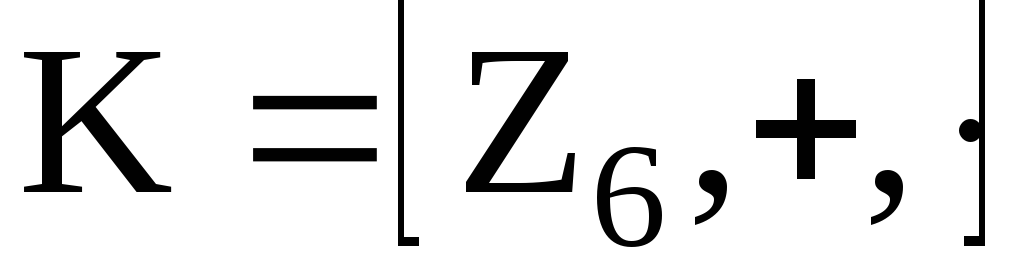
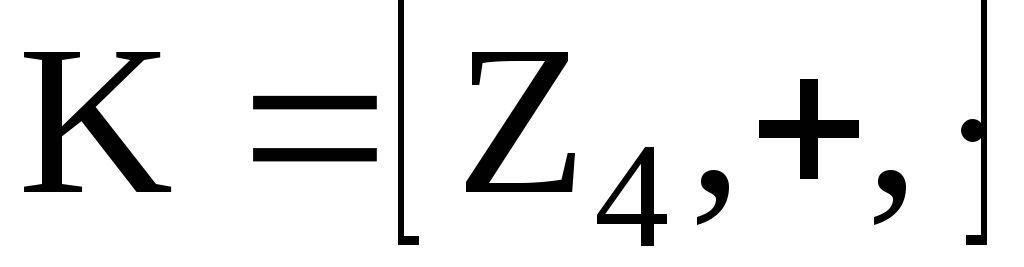
2. В кольце
квадратных матриц второго порядка также
существуют делители нуля:
пусть
,
тогда
.
Определение. Кольцом
(областью) целостности называется
коммутативное кольцо без делителей
нуля.
Пример. 1.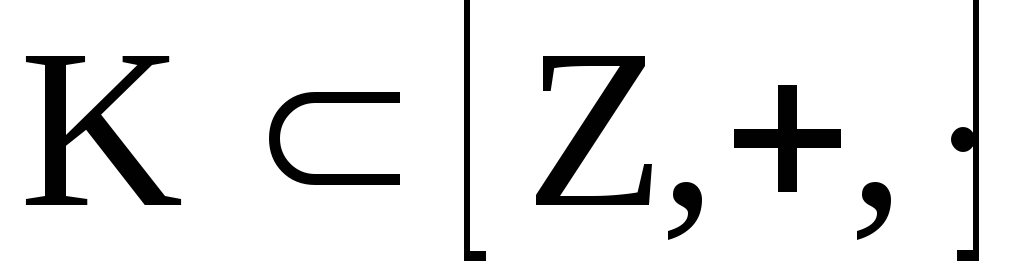 
–
кольцо целых чисел является кольцом
целостности.
2. Кольцо
является
кольцом целостности в том и только в
том случае, если
– простое число.
Рассмотрим
произвольное кольцо
.
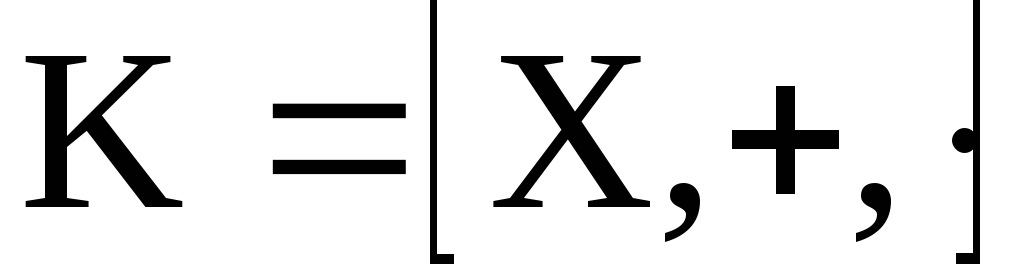
Если
,
и
,
т.е. кольцо не содержит делителей нуля,
то такое кольцо называется телом.
Более строго.
Определение. Кольцо
K , в котором для всех отличных от нуля
элементов существуют обратные, называется
телом.
Тело
не содержит делителей нуля,
т.е. если
и
– тело, то, если
.
Это означает, что
отличные от нуля элементы тела образуют
полугруппу по умножению.
Более того, т.к.
тело содержит единичный элемент и для
каждого отличного от нуля элемента в
теле существует обратный элемент, то
элементы тела, отличные от нуля образуют
группу по умножению.
Примеры. 1. Тело
рациональных чисел
.
Действительно, если
,
где
.
Если
.
Важно,
чтобы обратный элемент
.
Для
любого целого числа, например
,
обратный элемент существует и равен
,
но он не принадлежит
.
2. Тело
вещественных чисел.
3. Тело комплексных
чисел.
Кольцом
целостности, с которым наиболее часто
приходится встречаться, является кольцо
целых чисел
.
В
теории колец особую роль играют кольца,
которые по своим свойствам достаточно
близки к кольцу целых чисел. В частности,
для этих колец можно развить теорию
делимости, аналогичную теории делимости
целых чисел. Эти кольца получили название
колец главных идеалов. Пусть
– кольцо целостности с единицей –
коммутативное кольцо без делителей
нуля, в котором понятие правого и левого
делителя элемента совпадают. Определение
делимости элементов этого кольца можно
сформулировать так:
Определение.
Если для
элементов
кольца
целостности
в
существует такой элемент
,
что
,
то говорят, что элемент
делится на
,
и пишут
или
делит
–
,
или
.
Из
определения делимости двух элементов
вытекают следующие свойства делимости
в кольце целостности
:
Эти
свойства являются распространением на
кольцо целостности
соответствующих свойств делимости в
кольце целых чисел.
5. Каждый
элемент
делится на любой делитель
единицы
.
Действительно, если
– делитель единицы, то и
– также делитель единицы, а это означает,
что
,
тогда
и, следовательно,
.
6. Если
делится на
,
то
делится и на
,
где
– любой делитель единицы.
Действительно,
из равенства
следует равенство
и, следовательно,
.
7. Каждый
элемент из делителей
и
,
где
– любой делитель единицы, является
делителем и другого.
Действительно,
из равенства
следует равенство
,
а из равенства
– равенство
.
Следовательно, если
,
то
,
и наоборот.
В
дальнейшем будем рассматривать элементы
кольца целостности
,
отличные от нуля.
Определение. Элементы
кольца целостности
называютсяассоциированными,
если каждый из них является делителем
другого:
. (55)
Из
равенства (55) следует, что
.
Отсюда, сократив обе части полученного
равенства на
,
получаем
.
Следовательно,
и
являются делителями единицы. Таким
образом, если
и
– ассоциированные элементы, то
,
где
– некоторый делитель единицы. С другой
стороны, какой бы мы не взяли делитель
единицы
,
элементы
и
ассоциированные между собой, поскольку
.
Определение. Элементы
кольца целостности
называютсяассоциированными,
если
,
где
– некоторый делитель единицы.
Пример. В
кольце целых чисел
ассоциированными являются пары чисел
.
Если
и
ассоциированные элементы кольца
целостности
,
то
.
Отсюда следует, что
– главный идеал, порожденный элементом
является подмножеством
– главного идеала, порожденного элементом
и наоборот:
Это
означает, что два ассоциированных
элемента
,
кольца целостности
порождают один и тот же главный идеал.
Пусть
– произвольные элементы кольца
целостности
.
Определение. Элемент
называется общим делителем элементов
и
,
если каждый из этих элементов делится
на
.
По
свойству 5 все делители единицы
кольца целостности
являются общими делителями элементов
и
.
Но у элементов
и
могут быть и другие общие делители.
Введем понятие наибольшего общего
делителя (НОД) этих элементов. Определение
НОД двух целых чисел, по которому НОД
называютнаибольший
из общих делителей, распространить на
кольцо целостности нельзя, т.к. в
произвольном кольце целостности
нет отношения порядка. Однако можно
ввести и другое определение НОД двух
чисел
и
,
а именно: НОД двух чисел
и
называется такой общий делитель этих
чисел, который делится на любой другой
их общий делитель. Именно это определение
НОД и распространяется на элементы
кольца целостности
.
Определение. Наибольшим
общим делителем двух элементов
кольца целостности
называется такой элемент
,
обозначаемый символом
и обладающий двумя свойствами:
-
; -
.
;
.
Замечание. Ясно,
что вместе с
свойствами 1., 2. Обладает любой
ассоциированный с ним элемент.
Действительно, если
– НОД элементов
,
то формально это записывается в виде
или
.
Если также и
,
то элементы
и
делятся друг на друга и, следовательно,
являются ассоциированными. С другой
стороны, если
,
то, очевидно,
,
где
– любой делитель единицы. Таким образом
НОД элементов
определяется с точностью до сомножителя
,
который является делителем единицы.
С учетом этого
замечания к свойствам 1., 2. Наибольшего
общего делителя добавляются следующие:
-
; -
; -
; -
.
;
;
;
.
Свойство
6. позволяет распространить понятие НОД
на произвольное конечное число элементов
кольца целостности
.
По
аналогии с
вводится дуальное понятиенаименьшего
общего кратного
элементов
кольца целостности
определенного с точностью до
ассоциированности и обладающее также
двумя свойствами:
;
.
В
частности, полагая
,
получаем, что
.
Теорема. Если
для элементов
кольца целостности
существуют
и
.
Тогда
а) 
;
б) 
,
.
Доказательство. Утверждение
а) вытекает непосредственно из определения
.
Для доказательства б) необходимо
убедиться, что элемент
,
определенный равенством
,
обладает свойствами 1., 2. НОД. Действительно,
из
,
следовательно
,
откуда после сокращения на
,
допустимого в любом кольце целостности
,
имеем
,
т.е.
.
Аналогично
,
т.е.
.
Этим доказано свойство 1. Для доказательства
свойства 2. Представим
.
Положим
.
Тогда
– общее кратное элементов
и
.
Согласно свойству
для некоторого
,
откуда
,
т.е.
и
,
что и требовалось доказать.
Определение. Элементы
кольца целостности
называются взаимно простыми, если они
не имеют общих делителей, отличных от
делителей единицы, т.е. если НОД
.
Пусть
– произвольный делитель единицы, и
– произвольный элемент кольца целостности
.
Тогда из условия
следует, что
.
Это означает, что все элементы
ассоциированные с элементом
,
и все делители единицы являются делителями
элемента
.
Их называюттривиальными
или несобственными
делителями элемента
.
Все делители отличные от
и
,
если такие существуют в
,
называютсянетривиальными,
или собственными
делителями элемента
.
Пример. В
кольце целых чисел
тривиальными делителями числа 10 являются
числа
и
,
а нетривиальными – числа
и
.
Определение. Элемент
кольца целостности
называется неразложимым, или простым,
если он не является делителем единицы
и не имеет нетривиальных делителей;
элемент
называется разложимым, или составным,
если он имеет нетривиальные делители.
Другими
словами, элемент
называется разложимым, если его можно
представить в виде произведения
двух нетривиальных делителей
;
элемент
– называется неразложимым, если его
нельзя представить в виде произведения
двух нетривиальных делителей.
Пример. В
кольце целых чисел
неразложимыми являются числа
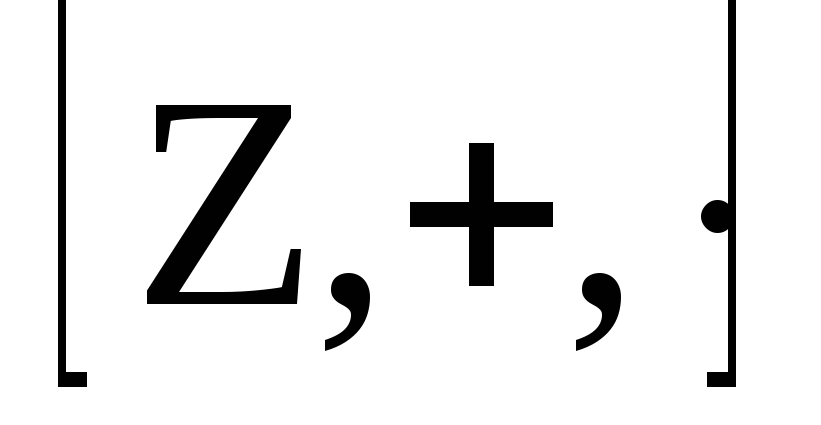
т.е. простые числа и противоположные
простым. Все остальные числа отличные
от
,
– разложимы.
Неразложимые
элементы обладают следующими свойствами:
Действительно,
первое свойство следует непосредственно
из свойства 7 делимости элементов кольца
целостности. Второе свойство докажем
следующим образом. Если НОД
,
то
как делитель неразложимого элемента
,
является либо некоторым делителем
единицы
,
либо элементом вида
.
В первом случае элементы
и
взаимно простые, во втором –
делится на
.
Определение. Кольцо
целостности
называется кольцом с однозначным
разложением на простые множители ( или
факториальным кольцом), если любой
элемент
из
можно представить в виде:
, (46)
где
обратный элемент, а
– простые элементы (не обязательно
попарно различные), причем из существования
другого такого разложения
следует,
что
и при надлежащей нумерации элементов
и
будет
,
,…,
,
где
– обратные элементы в
.
Допуская в разложении (46)
,
мы принимаем соглашение, что обратимые
элементы
в кольце целостности
также имеют разложение на простые
множители. Ясно, что если
– простой, а
обратный элемент в
,
то ассоциированный с
элемент
тоже простой.
Пример. В
кольце целых чисел
с обратимыми элементами
и
отношение порядка
дает возможность выделитьположительное
простое число
из двух возможных простых элементов
.
Теорема. Пусть
– произвольное кольцо целостности с
разложением на простые множители.
Однозначность разложения в
(факториальность
)
имеет место тогда и только тогда, когда
любой простой элемент
,
делящий произведение
,
делит по крайней мере один из сомножителей
или
.
Доказательство. Пусть
.
Если
разложения
на простые множители, а
– кольцо с однозначным разложением, то
из равенств
следует, что элемент
ассоциирован с одним из
или
,
т.е.
делит
или
.
Обратно,
установим однозначность разложения в
,
где
или
.
Рассуждая по индукции, допустим, что
разложение всех элементов из
с числом
простых множителей единственно (с
точностью до порядка сомножителей и их
ассоциированности).
Докажем
теперь это для любого элемента
,
который может быть разложен на
простых сомножителей. Именно, пусть
(47)
– два
разложения элемента
с
.
Условие
теоремы, примененное к
дает нам, что
должен делить один из элементов
.
Без ограничения общности (это вопрос
нумерации) будем считать, что
.
Но
– простой элемент, поэтому
,
где
– обратимый
элемент. Используя закон сокращения в
,
получаем из (41) равенство
. (48)
В
левой части равенства (42) стоит произведение
простых сомножителей. По предположению
индукции
и оба разложения отличаются лишь порядком
простых элементов, снабженных, возможно,
какими–то обратимыми сомножителями.
Замечание. В
произвольном кольце целостности
элемент
вообще не обязан допускать разложение
типа (40). Более интересным является тот
факт, что имеются кольца целостности,
в которых разложение на простые множители
хотя и возможно, но не является однозначным,
т.е. условия теоремы, кажущиеся тривиальными
не всегда выполняются.
Пример. Рассмотрим
кольцо целостности
,
где
.
Норма
каждого отличного от нуля элемента
– целое положительное число. Если
элемент
обратим в
,
то
,
откуда
.
Это возможно лишь при
.
Таким образом в
,
как и в 1
,
обратимыми элементами являются только
.
Если
,
то
.
Так как
,
то при заданном
число множителей
не может неограниченно расти. Следовательно,
разложение на простые множители в
возможно. Вместе с тем число 9 (да и не
только оно) допускает два существенно
различных разложения на простые
множители:
.
Неассоциированность
элементов 3 и
очевидна. Далее,
.
Поэтому из разложения
для
или
с необратимыми
следовало бы
,
т.е.
,
что невозможно, поскольку уравнение
с
неразрешимо. Этим доказана простота
элементов 3 и
.
Соседние файлы в папке ЛЕКЦИИ АиГ
- #
14.04.2015904.7 Кб67Копия ЛЕКЦИЯ 14.wbk
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обратный по модулю
❓Инструкция
Калькулятор онлайн для вычисления обратного элемента по модулю в кольце. Алгоритм поддерживает работу с большими числами с некоторыми ограничениями.
Использование:
Заполняются два поля — число a и модуль m. Число a — число к которому ищем обратный, m — модуль, по которому ищем.
Калькулятор выдает обратный элемент после нажатия на кнопку «Вычислить».
Если установлена галочка «подробнее», то калькулятор помимо обратного элемента по модулю выдает некоторые этапы вычисления.
Ограничения:
Калькулятор поддерживает работу с большими целыми числами (в том числе отрицательными числами для числа a, и только положительными для модулю m) длиной не более 10 000 символов.
📖 Теория
Что значит по модулю?
Синонимом к данному выражению является выражение «остаток от деления«. То есть выражение «5 по модулю 3» эквивалентно выражению «остаток от деления 5 на 3». И в том и в другом случае подразумевается в ответе число 2, так как остаток от деления 5 на 3 = 2.
Стоить отметить тот факт, что по модулю m мы имеем числа от 0 до m — 1. Действительно, остаток от деления на m никогда не превысит m — 1.
Что такое обратное?
Напомним, что число, умноженное на его обратное, равно 1. Из базовой арифметики мы знаем, что:
Число, обратное к числу A, равно 1 / A, поскольку A * (1 / A) = 1 (например, значение, обратное к 5, равно 1/5). Все действительные числа, кроме 0, имеют обратную Умножение числа на обратное к A эквивалентно делению на A (например, 10/5 соответствует 10 * 1/5)
Что такое обратное по модулю?
В модульной арифметике у нас нет операции деления. Тем не менее, у нас есть модульные инверсии.
Модульная инверсия a (mod m) есть a-1 (a * a-1) ≡ 1 (mod m) или эквивалентно (a * a-1) mod m = 1 Только числа, взаимно простые с модулем m, имеют модульное обратное.
Говоря проще, обратным элементом к a по модулю m является такое число b, что остаток от деления (a * b) на модуль m равно единице (a * a-1) mod m = 1
Как найти модульный обратный
Наивный метод нахождения модульного обратного a ( по модулю m) является:
Шаг 1. Рассчитать a * b mod m для значений b от 0 до m — 1
Шаг 2. Модульная инверсия a mod m — это значение b, при котором a * b mod m = 1
Обратите внимание, что термин b mod m может иметь только целочисленное значение от 0 до m — 1, поэтому тестирование больших значений чем (m-1) для b является излишним.
Вы наверно уже догадались, что наивный метод является очень медленным. Перебор всех чисел от 0 до m-1 для большого модуля довольно-таки трудоемкая задача. Существует гораздо более быстрый метод нахождения инверсии a (mod m). Таковым является расширенный алгоритм Евклида, который реализован в данном калькуляторе.
Расширенный алгоритм Евклида
Представим наибольший общий делитель числа a и модуля m в виде ax + my. То есть НОД(a, m) = ax + my. Помним, что обратный элемент существует только тогда, когда a и m взаимно просты, то есть их НОД(a, m) = 1. Отсюда: ax + my = 1 — линейное диофантово уравнение второго порядка. Необходимо решить данное уравнение в целых числах и найти x, y.
Найденный коэффициент x будет являться обратным элементом к a по модулю m. Это следует оттуда, что, если мы возьмём от обеих частей уравнения остаток по модулю m, то получим: ax = 1 (m).
Расширенный алгоритм Евклида, в отличие от классического, помимо наибольшего общего делителя позволяет найти также коэффициенты x, y.
Алгоритм:
Вход: a, m ≠ 0
Выход: d, x, y, такие что d = gcd(a, m) = ax + my
1. [Инициализация] (a0, a1) := (a, m); (x0, x1) := (1, 0); (y0; y1) := (0, 1).
2. [Основной цикл] Пока a1 ≠ 0 выполнять {q = QUO(a0, a1);
(a0, a1) := (a1, a0 — a1q); (x0, x1) := (x1, x0 — x1q); (y0, y1) := (y1, y0 — y1q);
QUO(a0, a1) — целая часть от деления a0 на a1
3. [Выход] Вернуть (d, x, y) = (a0, x0, y0)
Битовая сложность расширенного алгоритма Евклида равна O((log2(n))2) , где n = max (|a|, |m|)
Непонятен алгоритм? Ничего страшного, примеры ниже именно для этого и предназначены.
➕ Примеры
Пример для наивного метода.
Пусть a = 3, m = 7. То есть нам необходимо найти обратный элемент к 3 по модулю 7.
Шаг 1. Рассчитать a * b mod m для значений B от 0 до m-1. По очереди проверяем числа от 0 до 6.
3 * 0 ≡ 0 (mod 7) — не подходит
3 * 1 ≡ 3 (mod 7)
3 * 2 ≡ 6 (mod 7)
3 * 3 ≡ 9 ≡ 2 (mod 7)
3 * 4 ≡ 12 ≡ 5 (mod 7)
3 * 5 ≡ 15 (mod 7) ≡ 1 (mod 7) <—— Обратное найдено.
3 * 6 ≡ 18 (mod 7) ≡ 4 (mod 7)
при b = 5 выполнилось условие, что a * b ≡ 1 (m). Следовательно, b = 5 является обратным элементом к 3 по модулю 7.
Пример на расширенный алгоритм Евклида.
Пусть аналогично предыдущему примеру имеем a = 3, m = 7. Также, требуется найти обратный элемент к 3 по модулю 7. Согласно алгоритму начинаем заполнять таблицу на каждом этапе цикла.
| Итерация | q | a0 | a1 | x0 | x1 | y0 | y1 |
| 0 | — | 3 | 7 | 1 | 0 | 0 | 1 |
| 1 | 0 | 7 | 3 | 0 | 1 | 1 | 0 |
| 2 | 2 | 3 | 1 | 1 | -2 | 0 | 1 |
| 3 | 3 | 1 | 0 | -2 | 0 | 1 | -3 |
После 3-ей итерации получили a1 = 0, строго по алгоритму из раздела «Теория» заканчиваем работу алгоритма.
(d, x, y) = (a0, x0, y0)
(d, x, y) = (1, -2, 1), видим, что d = НОД(3, 7) = 1, следовательно числа 3 и 7 являются взаимно простыми, а значит обратный существует.
Делаем проверку:
3 * (-2) + 7 * 1 = 1
-6 + 7 = 1
1 = 1 — верно!
Обратным элементом к тройке по модулю 7 является x = -2. По модулю 7 число -2 равно 5. Получили, что x = 5 является обратным элементом к 3 по модулю 7.