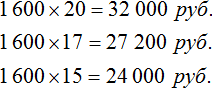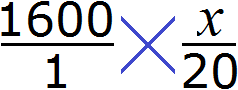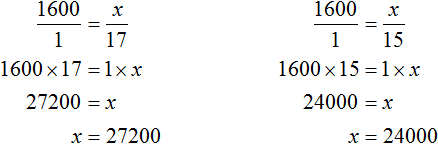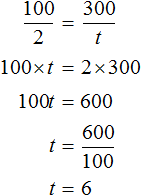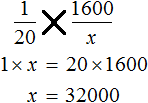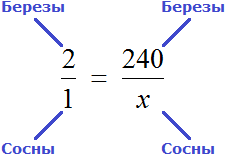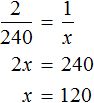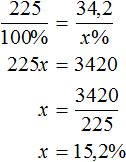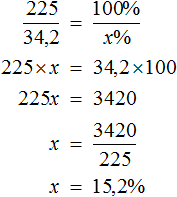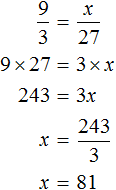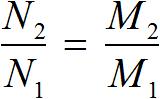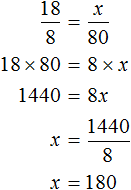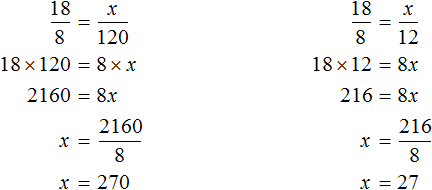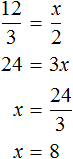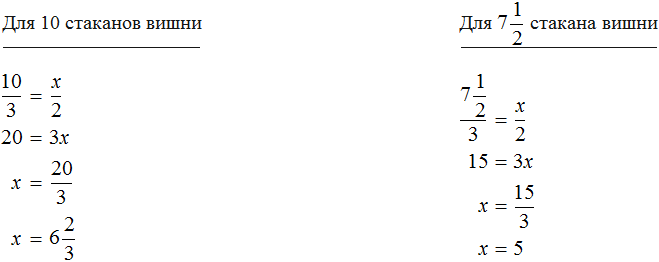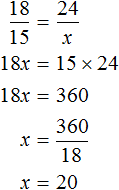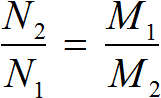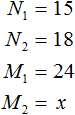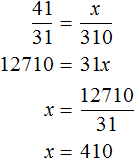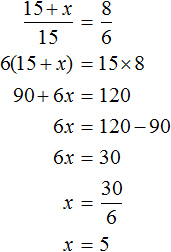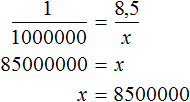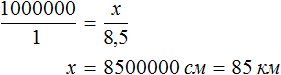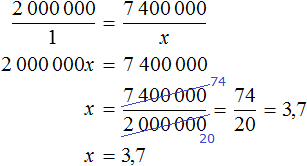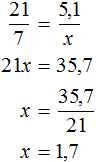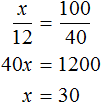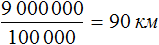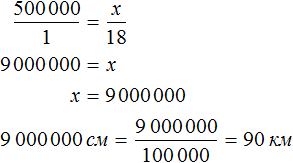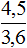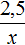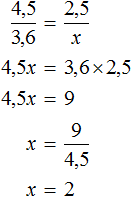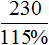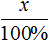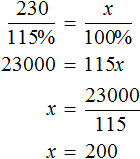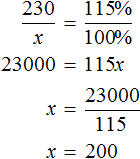Как найти обратно пропорциональную задачу - Исправление недочетов и поиск решений вместе с Examum.ru

Математика

6 класс

Урок № 7

Прямая и обратная пропорциональность. Решение задач

Перечень рассматриваемых вопросов:

Понятия прямой и обратной пропорциональной зависимости.
Краткая запись условия задачи.
Составление и решение пропорций по условию задачи.
Решение задач на прямую и обратную пропорциональную зависимость.

Тезаурус

Равенство двух отношений называют пропорцией.

Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.

Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.

Основная литература

Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

Дополнительная литература

Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

Прямая пропорциональность.

Обратная пропорциональность.

Для решения задач на пропорциональную зависимость, удобно составить таблицу или сделать краткую запись условия.

Столбцы таблицы соответствуют наименованиям зависимых величин.

Строки таблицы соответствуют значениям величин при первом и втором измерении.

Одинаково направленные стрелки показывают прямо пропорциональную зависимость, противоположно направленные – обратно пропорциональную.

Задача.

Поезд, скорость которого 55 км/ч, был в пути 5 часов. За сколько часов пройдёт этот же участок пути товарный поезд, скорость которого 45 км/ч?

Решение.

При постоянном пути скорость и время движения обратно пропорциональны.

Допустим, товарный поезд пройдёт этот же путь со скоростью 45 км/ч за x ч.

Сделаем краткую запись условия.

Задача.

Двигаясь с постоянной скоростью, велогонщик проезжает 40 метров за 3 с. Какой путь проедет велогонщик за 45 с?

Решение.

При постоянной скорости путь прямо пропорционален времени движения.

Пусть х м проедет велогонщик за 45 с.

Сделаем краткую запись условия.

Задача.

Усилие при восхождении на высоту 600 м равно усилию, требуемому для перехода 25 км по равнине. Турист поднялся в горы на 792 м. Какому расстоянию на равнине соответствует этот подъём?

Решение:

Решение.

Задача.

Четыре программиста могут написать игру за 12 месяцев. За сколько месяцев эту работу могут выполнить три программиста?

Решение.

Количество программистов и скорость написания игры – это обратно пропорциональная зависимость.

Разбор заданий тренировочного модуля

№ 1. Подстановка элементов в пропуски в тексте.

Подставьте нужные элементы в пропуски.

Пешеход шёл 3 часа со скоростью 8 км/ч. За сколько часов он пройдёт то же расстояние со скоростью 6 км/ч?

Решение:

При фиксированном расстоянии время в пути и скорость – ______ пропорциональны.

Пусть _____ часов – пешеход идёт со скоростью 6 км/ч.

Составим пропорцию:

_________

х=_______

х=_______(ч).

Правильный ответ.

Решение:

При фиксированном расстоянии время в пути и скорость – обратно пропорциональны.

Пусть х часов – пешеход идёт со скоростью 6 км/ч.

№ 2. Подстановка элементов в пропуски в таблице.

Заполните таблицу.

Поезд движется со скоростью 45 км/ч. Какое расстояние он пройдёт, если будет в пути 3 ч; 4 ч; 5 ч; 6 ч.

Варианты ответов:

135 км;

180 км;

225 км;

270 км.

Решение.

При постоянной скорости пройденный путь и время прямо пропорциональны. Скорость движения поезда 45 км/ч означает, что за 1 час поезд преодолевает расстояние в 45 км. Обозначим за x км – расстояние, которое поезд пройдёт за 3, 4, 5 и 6 часов.

Таким же способом находим расстояние, которое пройдёт поезд за 4, 5 и 6 часов, и подставляем соответствующие варианты в таблицу.

Ответ:

Источник

Сегодня мы рассмотрим, какие величины называются обратно пропорциональными, как выглядит график обратной пропорциональности и как все это может вам пригодится не только на уроках математики, но и вне школьных стен.

Такие разные пропорциональности

Пропорциональностью называют две величины, которые взаимно зависимы друг от друга.

Зависимость может быть прямой и обратной. Следовательно, отношения между величинами описывают прямая и обратная пропорциональность.

Прямая пропорциональность – это такая зависимость двух величин, при которой увеличение либо уменьшение одной из них ведет к увеличению либо уменьшению другой. Т.е. их отношение не изменяется.

Например, чем больше усилий вы прилагаете для подготовки к экзаменам, тем выше ваши оценки. Или чем больше вещей вы берете с собой в поход, тем тяжелее нести ваш рюкзак. Т.е. количество затраченных на подготовку к экзаменам усилий прямо пропорционально полученным оценкам. И количество запакованных в рюкзак вещей прямо пропорционально его весу.

Обратная пропорциональность – это функциональная зависимость, при которой уменьшение либо увеличение в несколько раз независимой величины (ее называют аргументом) вызывает пропорциональное (т.е. во столько же раз) увеличение либо уменьшение зависимой величины (ее называют функцией).

Проиллюстрируем простым примером. Вы хотите купить на рынке яблок. Яблоки на прилавке и количество денег в вашем кошельке находятся в обратной пропорциональности. Т.е. чем больше вы купите яблок, тем меньше денег у вас останется.

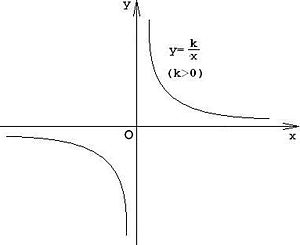
Функция и ее график

Функцию обратной пропорциональности можно описать как y = k/x. В котором x ≠ 0 и k ≠ 0.

Эта функция обладает следующими свойствами:

Областью ее определения является множество всех действительных чисел, кроме x = 0. D(y): (-∞; 0) U (0; +∞).
Областью значений являются все действительные числа, кроме y = 0. Е(у): (-∞; 0) U (0; +∞).
Не имеет наибольших и наименьших значений.
Является нечетной и ее график симметричен относительно начала координат.
Непериодическая.
Ее график не пересекает оси координат.
Не имеет нулей.
Если k > 0 (т.е. аргумент возрастает), функция пропорционально убывает на каждом из своих промежутков. Если k < 0 (т.е. аргумент убывает), функция пропорционально возрастает на каждом из своих промежутков.
При возрастании аргумента (k > 0) отрицательные значения функции находятся в промежутке (-∞; 0), а положительные – (0; +∞). При убывании аргумента (k < 0) отрицательные значения расположены на промежутке (0; +∞), положительные – (-∞; 0).

График функции обратной пропорциональности называется гиперболой. Изображается следующим образом:

Задачи на обратную пропорциональность

Чтобы стало понятнее, давайте разберем несколько задач. Они не слишком сложные, а их решение поможет вам наглядно представить, что такое обратная пропорциональность и как эти знания могут пригодиться в вашей обычной жизни.

Задача №1. Автомобиль движется со скоростью 60 км/ч. Чтобы доехать до места назначения, ему потребовалось 6 часов. Сколько времени ему потребуется, чтобы преодолеть такое же расстояние, если он будет двигаться со скоростью в 2 раза выше?

Можем начать с того, что запишем формулу, которая описывает отношения времени, расстояния и скорости: t = S/V. Согласитесь, она очень напоминает нам функцию обратной пропорциональности. И свидетельствует о том, что время, которое автомобиль проводит в пути, и скорость, с которой он движется, находятся в обратной пропорциональности.

Чтобы убедиться в этом, давайте найдем V₂, которая по условию выше в 2 раза: V₂ = 60 * 2 = 120 км/ч. Затем рассчитаем расстояние по формуле S = V * t = 60 * 6 = 360 км. Теперь совсем несложно узнать время t₂, которое требуется от нас по условию задачи: t₂ = 360/120 = 3 ч.

Как видите время в пути и скорость движения действительно обратно пропорциональны: со скоростью в 2 раза выше изначальной автомобиль потратит в 2 раза меньше времени на дорогу.

Решение этой задачи можно записать и в виде пропорции. Для чего сначала составим такую схему:

↓ 60 км/ч – 6 ч ↑

↓120 км/ч – х ч ↑

Стрелки обозначают обратно пропорциональную зависимость. А также подсказывают, что при составлении пропорции правую часть записи надо перевернуть: 60/120 = х/6. Откуда получаем х = 60 * 6/120 = 3 ч.

Задача №2. В мастерской трудятся 6 рабочих, которые с заданным объемом работы справляются за 4 часа. Если количество рабочих сократить в 2 раза, сколько времени потребуется оставшимся, чтобы выполнить тот же объем работы?

Запишем условия задачи в виде наглядной схемы:

↓ 6 рабочих – 4 ч ↑

↓ 3 рабочих – х ч ↑

Запишем это в виде пропорции: 6/3 = х/4. И получим х = 6 * 4/3 = 8 ч. Если рабочих станет в 2 раза меньше, оставшиеся затратят на выполнение всей работы в 2 раза больше времени.

Задача №3. В бассейн ведут две трубы. Через одну трубу вода поступает со скоростью 2 л/с и наполняет бассейн за 45 минут. Через другую трубу бассейн наполнится за 75 минут. С какой скоростью вода поступает в бассейн через эту трубу?

Для начала приведем все данные нам по условию задачи величины к одинаковым единицам измерения. Для этого выразим скорость наполнения бассейна в литрах в минуту: 2 л/с = 2 * 60 = 120 л/мин.

Поскольку из условия следует, что через вторую трубу бассейн заполняется медленнее, значит, и скорость поступления воды ниже. На лицо обратная пропорциональность. Неизвестную нам скорость выразим через х и составим такую схему:

↓ 120 л/мин – 45 мин ↑

↓ х л/мин – 75 мин ↑

А затем составим пропорцию: 120/х = 75/45, откуда х = 120 * 45/75 = 72 л/мин.

В задаче скорость наполнения бассейна выражена в литрах в секунду, приведем полученный нами ответ к такому же виду: 72/60 = 1,2 л/с.

Задача №4. В небольшой частной типографии печатают визитки. Сотрудник типографии работает со скоростью 42 визитки в час и трудится полный рабочий день – 8 часов. Если бы он работал быстрее и печатал 48 визиток за час, насколько раньше он смог бы уйти домой?

Идем проверенным путем и составляем по условию задачи схему, обозначив искомую величину как х:

↓ 42 визитки/ч – 8 ч ↑

↓ 48 визитки/ч – х ч ↑

Перед нами обратно пропорциональная зависимость: во сколько раз больше визиток в час напечатает сотрудник типографии, во столько же раз меньше времени ему потребуется на выполнение одной и той же работы. Зная это, составим пропорцию:

42/48 = х/8, х = 42 * 8/48 = 7ч.

Таким образом, справившись с работой за 7 часов, сотрудник типографии смогу бы уйти домой на час раньше.

Заключение

Нам кажется, что эти задачи на обратную пропорциональность действительно несложные. Надеемся, что теперь вы тоже считаете их такими. А главное, что знание об обратно пропорциональной зависимости величин действительно может оказаться для вас полезным еще не раз.

Не только на уроках математики и экзаменах. Но и тогда, когда вы соберетесь отправиться в путешествие, пойдете за покупками, решите немного подработать в каникулы и т.п.

Расскажите нам в комментариях, какие примеры обратной и прямой пропорциональной зависимости вы замечаете вокруг себя. Пускай это будет такая игра. Вот увидите, как это увлекательно. Не забудьте «расшарить» эту статью в социальных сетях, чтобы ваши друзья и одноклассники тоже смогли поиграть.

Источник

На этом уроке мы рассмотрим, что такое прямая и обратная пропорциональные зависимости, научимся оформлять и решать задачи с помощью пропорции, устанавливая пропорциональную зависимость между величинами в ней, рассмотрим примеры задач на прямую и обратную пропорциональную зависимость.

Эта информация доступна зарегистрированным пользователям

Давайте сначала разберемся, что такое пропорциональность.

Пропорциональность — это зависимость двух величин друг от друга таким образом, что значение отношения этих величин остается постоянным.

Зависимость величин друг от друга может быть прямой и обратной.

Отношение между величинами описываются прямой или обратной пропорциональностью.

Прямая пропорциональность выражается так: (mathbf{y = kx})

Обратная пропорциональность выражается так: (mathbf{y = frac{k}{x}})

где k — это число, которое называют коэффициентом пропорциональности.

x и y величины, зависящие друг от друга.

Пример

Площадь прямоугольника равна (mathbf{S = a cdot b}), где S— это площадь прямоугольника, а — длина прямоугольника, b — ширина прямоугольника.

Если один из множителей произведения — постоянная величина, то произведение прямо пропорционально второму множителю.

Если постоянно значение произведения, то множители зависят друг от друга обратно пропорционально.

По формуле видно, что площадь квадрата зависит от длины (ширины) его стороны, а длина стороны (ширина) зависит от его площади.

Какова эта зависимость, сейчас и рассмотрим.

(mathbf{S = a cdot b})

Зависимость площади прямоугольника от длины при постоянном значении ширины является прямо пропорциональной зависимостью этих величин.

Зависимость площади прямоугольника от ширины при постоянном значении длины является прямо пропорциональной зависимостью этих величин.

(mathbf{a = frac {S}{b}}) или (mathbf{b = frac {S}{a}})

Пусть одна клетка равна 1 см. Рассмотрим рисунок:

Эта информация доступна зарегистрированным пользователям

Ширина прямоугольника b постоянная величина

b = 4 см

a₁ = 6 см

Увеличим ширину прямоугольника — сторону a₁ на 1 см,получим

a₂ = 7 см

Эта информация доступна зарегистрированным пользователям

Найдем площади прямоугольников S₁ и S₂

(mathbf{S_{1} = a_{1} cdot b = 6 cdot 4 = 24}) см²

(mathbf{S_{2} = a_{2} cdot b = 7 cdot 4 = 28}) см²

Вывод: при увеличении стороны прямоугольника увеличилась площадь прямоугольника.

Рассмотрим другой вариант зависимости

Зависимость одной из сторон прямоугольника от второй стороны при постоянном значении площади прямоугольника является обратно пропорциональной зависимостью. Пусть одна клетка равна 1 см

Эта информация доступна зарегистрированным пользователям

Площадь прямоугольника S постоянная величина

S = 24 см²

b₁ = 4 см

(mathbf{a_{1} = frac{S}{b_{1}} = 6}) (см)

Увеличим высоту прямоугольника- сторону прямоугольника b₁ на 2 см_,получим

b₂ = 6 см

Найдем ширину прямоугольника- сторону a₂

(mathbf{a_{2} = frac{S}{b_{2}} = 4}) (см)

Эта информация доступна зарегистрированным пользователям

Вывод: при увеличении одной стороны прямоугольника и постоянном значении площади, вторая сторона уменьшается.

Таким образом, мы подошли к основным понятиям пропорциональной зависимости. Чтобы было легко разобраться в несложных схемах ниже, мы дадим пояснение символам:

Эта информация доступна зарегистрированным пользователям

Итак:

1) Две величины прямо пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, так же увеличивается (уменьшается) в n количество раз.

Эта информация доступна зарегистрированным пользователям

2) Две величины обратно пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, уменьшается (увеличивается) в n количество раз.

Эта информация доступна зарегистрированным пользователям

Примеров прямой и обратной пропорциональности множество.

Однако не все величины зависят друг от друга прямо пропорционально или обратно пропорционально, встречаются и более простые и более сложные зависимости величин.

Надо понимать, что даже если какие-нибудь две величины возрастают или убывают, то между ними не обязательно существует пропорциональная зависимость.

Например, с течением времени увеличивается возраст человека и его размер ноги, но эти величины не являются пропорциональными, так как при удвоении возраста размер ноги человека не удваивается

Эта информация доступна зарегистрированным пользователям

Алгоритм решения задач на пропорциональную зависимость состоит из нескольких основных пунктов:

Обозначить буквой значение неизвестной величины (чаще всего для этого выбирают латинскую букву Х)
Проанализировать задачу и кратко записать ее условия (краткую запись можно делать в виде таблицы или изображать в виде логической схемы)
Установить зависимость между величинами
В краткой записи задачи обозначить стрелками пропорциональную зависимость

— Стрелки, которые направлены в одну сторону, обозначают прямую пропорциональную зависимость величин

— Стрелки, которые направлены в разные стороны, обозначают обратную пропорциональную зависимость величин.

5. Записать пропорцию, учитывая характер пропорциональности величин

6. Составить уравнение

7. Найти неизвестный член уравнения (искомую величину)

8. Записать ответ задачи

Важно помнить, что при составлении краткой записи задачи величины с одинаковыми единицами измерения записывают друг под другом.

Если между величинами прямая пропорциональная зависимость, то пропорция составляется точно в соответствии с краткой записью задачи.

Если между величинами обратная пропорциональная зависимость, то при составлении пропорции одноименные величины меняются местами в одном любом из столбцов таблицы (логической схемы) краткой записи задачи.

Другими словами, при прямо пропорциональной зависимости отношение значений одной величины равно отношению соответствующих значений другой величины.

При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.

Эта информация доступна зарегистрированным пользователям

Рассмотрим некоторые варианты задач на пропорциональную зависимость, в которых величины зависят прямо пропорционально одна от другой.

Задача 1

Для приготовления из 3 кг черной смородины по рецепту требуется 3,3 кг сахара.

Сколько сахара потребуется для приготовления варенья из 5 кг черной смородины?

Эта информация доступна зарегистрированным пользователям

Решение:

Пусть х (кг) сахара потребуется для приготовления варенья из 5 кг ягод.

Составим краткую запись задачи в виде таблицы:

Эта информация доступна зарегистрированным пользователям

Определим, как зависят масса сахара и масса ягод.

Чем больше ягод, тем больше нужно сахара, следовательно, между величинами прямо пропорциональная зависимость.

В таблице вертикальными стрелками изображаем прямо пропорциональную зависимость величин.

Так как зависимость величин прямо пропорциональная, составим пропорцию в точном соответствии с таблицей.

Отношение значений одной величины равно отношению соответствующих значений другой величины.

Получим (mathbf{frac{3,3}{x} = frac{3}{5}})

Составим уравнение, используя основное свойство пропорции:

(mathbf{{3}cdot{x} = {5}cdot{3,3}})

(mathbf{ {x} = {(5}cdot{3,3)}div{3}})

(mathbf{ {x} = {5,5}}) (кг) сахара потребуется для приготовления варенья из 5 кг ягод.

Ответ: (mathbf{ {x} = {5,5}}) (кг)

Задача 2

Автомобиль, двигаясь с постоянной скоростью, проехал 400 км за 5 часов.

За какое время автомобиль проедет 600 км?

Эта информация доступна зарегистрированным пользователям

Решение:

Пусть х (ч) – время, за которое автомобиль проедет 600 км.

Составим краткую запись задачи в виде таблицы:

Эта информация доступна зарегистрированным пользователям

Определим, как зависят величины S от t, где S — это путь, а t — это время.

Так как движение происходит с постоянной скоростью, то (mathbf{ {S} = {V}cdot{t}}).

Чем больше расстояние, тем больше требуется времени для преодоления этого расстояния, значит, зависимость между величинами S и t прямо пропорциональная.

Изображаем в таблице краткой записи задачи вертикальными стрелками прямо пропорциональную зависимость величин.

Так как зависимость величин прямо пропорциональная, составим пропорцию в точном соответствии с таблицей.

Отношение значений одной величины равно отношению соответствующих значений другой величины.

Получим (mathbf{frac{5}{x} = frac{400}{600}})

Составим уравнение, используя основное свойство пропорции:

(mathbf{ {400}cdot{x} = {5}cdot{600}})

(mathbf{ {x} = {(5}cdot{600)}div{400}})

(mathbf{ {x} = {7,5}}) (ч) время, за которое автомобиль проедет 600 км

Ответ: (mathbf{ {x} = {7,5}}) (ч)

Примеры решения задач, в которых величины зависят обратно пропорционально одна от другой.

Задача 1

Для перевозки гравия потребовалось 42 машины грузоподъемностью 5 т.

Сколько нужно машин грузоподъемностью 7 т, чтобы перевезти тот же объем гравия?

Эта информация доступна зарегистрированным пользователям

Решение:

Пусть х (шт) — это количество машин грузоподъемностью 7 т, необходимых для перевозки груза.

Краткую запись задачи оформим в виде таблицы:

Эта информация доступна зарегистрированным пользователям

Определим, как зависят величины друг от друга.

Чем больше грузоподъемность машины, тем меньше машин потребуется для перевозки груза.

Получаем обратно пропорциональную зависимость.

Изображаем на краткой записи задачи вертикальными стрелками, направленными в разные стороны, обратно пропорциональную зависимость величин.

А это значит, что при составлении пропорции одно из отношений получится перевернутым.

Получим (mathbf{frac{42}{x} = frac{7}{5}})

Составим уравнение, используя основное свойство пропорции:

(mathbf{ {7}cdot{x} = {42}cdot{5}})

(mathbf{ {x} = {(42}cdot{5)}div{7}})

(mathbf{ {x} = {30}}) (шт.) машин грузоподъёмностью 7 т понадобится для перевозки гравия.

Ответ: (mathbf{ {x} = {30}}) (шт.)

Задача 2

Велосипедист проехал путь от дачи до дома за час со скоростью 10 км/ч. Сколько понадобится времени велосипедисту на преодоление этого пути со скоростью 20 км/ч?

Эта информация доступна зарегистрированным пользователям

Решение:

Пусть х (ч) время велосипедиста, если он будет двигаться со скоростью 20 км/ч. Составим краткую запись задачи в виде таблицы:

Эта информация доступна зарегистрированным пользователям

Определим, как зависят V и t, где V— скорость движения велосипедиста, t— время движения.

Чем больше скорость велосипедиста, тем меньше времени ему потребуется для преодоления пути.

Получаем обратно пропорциональную зависимость величин друг от друга.

А это значит, при составлении пропорции одно из отношений получаем перевернутым.

Получим (mathbf{frac{x}{1} = frac{10}{20}})

Составим уравнение, используя основное свойство пропорции:

(mathbf{ {20}cdot{x} = {10}cdot{1}})

(mathbf{ {x} = {(10}cdot{1)}div{20}})

(mathbf{ {x} = {0,5}}) (ч) время велосипедиста, если он будет двигаться со скоростью 20 км/ч.

Ответ: (mathbf{ {x} = {0,5}}) (ч)

Эта информация доступна зарегистрированным пользователям

Источник

Описание презентации по отдельным слайдам:

1 слайд

Решение задач
с помощью пропорции
2 слайд

Определение 2
Определение 1
Определение прямой и обратной пропорциональности
Две величины называют прямопропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая тоже увеличивается (уменьшается) во столько же раз.
Больш. 1 — Больш. 2
Меньш. 1 — Меньш.2
Меньш. 1 — Меньш. 2
Больш. 1 — Больш. 2

Две величины называют прямопропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.
Больш. 1 — Меньш. 2
Меньш. 1 — Больш. 2
3 слайд

Определение прямой и обратной пропорциональности
1) За 5 тетрадей в клетку заплатили 40 руб. Сколько заплатят за 12 таких же тетрадей?
3) На пошив 9 рубашек ушло 18 м ткани. Сколько рубашек получится из 14 метров?
Определи вид пропорциональности
2) 6 рабочих выполнят работу за 5 часов за какое время справятся с этой работой 3 рабочих?
4) У портного есть отрез материи. Если он сошьет из него платья, на каждое из которых уходит 2 метра, то получится 15 платьев. Сколько костюмов может выйти из этого же отреза, если на каждый костюм уходит по 3 метра ткани?
4 слайд

Определение прямой и обратной пропорциональности
Составить краткую запись и определить вид пропорциональности. (Одноименные величины записываются друг под другом)
Составить пропорцию.
Если прямая пропорциональность, то величины записываются в пропорцию без изменений.
Если обратная пропорциональность, то в одной из величин данные меняются местами (наоборот).
Находится неизвестный член пропорции.
Алгоритм решения задачи 1
За 5 тетрадей в клетку заплатили 40 руб. Сколько заплатят за 12 таких же тетрадей?
Кол-во Стоимость
5 тетрадей – 40 руб.
12 тетрадей – х руб.

Ответ: 96 рублей.
5 слайд

Определение прямой и обратной пропорциональности
Составить краткую запись и определить вид пропорциональности. (Одноименные величины записываются друг под другом)
Составить пропорцию.
Если прямая пропорциональность, то величины записываются в пропорцию без изменений.
Если обратная пропорциональность, то в одной из величин данные меняются местами (наоборот).
Находится неизвестный член пропорции.
Алгоритм решения задачи 2
6 рабочих выполнят работу за 5 часов за какое время справятся с этой работой 3 рабочих?
Кол-во Время
6 рабочих – 5 часов.
3 рабочих – х часов.

Ответ: 10 часов.
6 слайд

№ 3.
Рабочие бригады, состоящей из 8 человек, могут выложить бассейн плиткой за 6 дней. Сколько человек в другой бригаде, если они могут выполнить эту работу на 2 дня быстрее?
(Производительность бригад одинакова)

обратная
7 слайд

Решение:
1) 6 – 2 = 4 (дня) время работы второй бригады

2) 8 человек – 6 дней
х человек – 4 дня

Ответ: 12 человек
8 слайд

№ 4.
Вновь выстроенный бассейн необходимо заполнить морской водой.
За 4,8 ч заполняется 24% объема бассейна. За какое время будет заполнен весь бассейн?

прямая
9 слайд

Решение:

4,8 ч – 24%
х ч – 100%

Ответ: за 20 часов
10 слайд

Выполните самостоятельно:
11 слайд

Проверяем
прямая
9 рубашек = 18,9 м

12 рубашек = х м

9х = 18,9 * 12
Х = 18,9 * 12/9
х = 226,8/9
х = 25,2
Ответ: 25,2 м ткани пойдёт на пошив 12 рубашек.

Ответ: 21 рубашка.
обратная
6 труб = 24 мин

9 труб = х мин
Перевернуть отношение
6/9=х/24
9х=6*24
х = 6*24/9
Х = 16 (мин)
Ответ: понадобится 16 минут.
13 слайд

ЗАДАЧА

Сколько нужно сахара, чтобы сварить варенье из 10 кг клубники, если по рецепту на 4 кг ягод нужно 5 кг сахара?

Запишите решение с помощью пропорции:
14 слайд

4 кг ягод
5 кг сахара
10 кг ягод
x кг сахара
x=(10∙5):4
x=12,5
Ответ:12,5 кг
Проверяем
Запишем кратко условие задачи в виде таблицы.
Пусть х кг – нужно сахара на 10 кг ягод.

2)
3) Прямая пропорциональная зависимость.
4)
15 слайд

Задача. В школе 2 медсестры могут сделать вакцинацию за 3 дня. Сколько нужно времени, чтобы 3 медсестры выполнили ту же работу?

Решение
2 медсестры 3 дня
3 медсестры ? дней
Решение: Пусть х дней потребуется 3 медсестрам
Составим пропорцию:
3:2=3:х
3х=2∙3
Х=2
Ответ: за 2 дня
Содержание

Источник

Решение задачи с помощью пропорции сводится к тому, чтобы сделать неизвестное значение x членом этой пропорции. Затем используя основное свойство пропорции получить линейное уравнение и решить его.

Как решить задачу с помощью пропорции

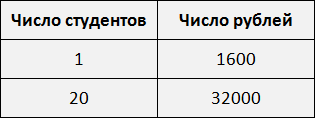
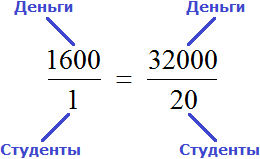
Рассмотрим простейший пример. Трем группам нужно выплатить стипендию по 1600 рублей каждому. В первой группе 20 студентов. Значит первой группе будет выплачено 1600 × 20, то есть 32 тыс. рублей.

Во второй группе 17 человек. Значит второй группе будет выплачено 1600 × 17, то есть 27,200 тыс. руб.

Ну и выплатим стипендию третьей группе. В ней 15 человек. На них нужно затратить 1600 × 15, то есть 24 тыс. руб.

В результате имеем следующее решение:

Для подобных задач решение можно записывать с помощью пропорции.

Пропорция по определению есть равенство двух отношений. К примеру, равенство является пропорцией. Эту пропорцию можно прочесть следующим образом:

a так относится к b, как c относится d

Аналогично можно соотнести стипендию и студентов, так чтобы каждому досталось по 1600 рублей.

Итак, запишем первое отношение, а именно отношение тысячи шестисот рублей на одного человека:

Мы выяснили, что для выплаты 20 студентам по 1600 рублей, нам потребуется 32 тыс. рублей. Значит второе отношение будет отношением тридцати двух тысяч к двадцати студентам:

Теперь соединим полученные отношения знаком равенства:

Мы получили пропорцию. Её можно прочесть следующим образом:

Тысяча шестьсот рублей так относятся к одному студенту, как тридцать две тысячи рублей относятся к двадцати студентам.

То есть по 1600 рублей каждому. Если выполнить деление в обеих частях равенства , то обнаружим, что одному студенту, как и двадцати студентам достанется по 1600 рублей.

Теперь представим, что сумма денег, необходимых для выплаты стипендии двадцати студентам, была бы неизвестной. Скажем, если бы вопрос стоял так: в группе 20 студентов и каждому нужно выплатить по 1600 рублей. Сколько всего рублей требуется для выплаты стипендии?

В таком случае пропорция приняла бы вид . То есть сумма денег, необходимая для выплаты стипендии, стала неизвестным членом пропорции. Эту пропорцию можно прочесть так:

Тысяча шестьсот рублей так относятся к одному студенту, как неизвестное число рублей относится к двадцати студентам

Теперь воспользуемся основным свойством пропорции. Оно гласит, что произведение крайних членов пропорции равно произведению средних:

Перемножив члены пропорции «крест-накрест», получим равенство 1600 × 20 = 1 × x. Вычислив обе части равенства, получим 32000 = x или x = 32000. Иными словами, мы найдём значение неизвестной величины, которое искали.

Аналогично можно было определить общую сумму и для остального количества студентов — для 17 и 15. Эти пропорции выглядели как и . Воспользовавшись основным свойством пропорции, можно найти значение x

Задача 2. Расстояние равное 100 км автобус проехал за 2 часа. Сколько времени потребуется автобусу, чтобы проехать 300 км, если будет ехать с той же скоростью?

Можно сначала определить расстояние, которое автобус проезжает за один час. Затем определить сколько раз это расстояние содержится в 300 километрах:

100 : 2 = 50 км на каждый час движения

300 км : 50 = 6 часов

Либо можно составить пропорцию «сто километров так относятся к двум часам, как триста километров к неизвестному числу часов»:

Отношение одноименных величин

Если крайние или средние члены пропорции поменять местами, то пропорция не нарушится.

Так, в пропорции можно поменять местами крайние члены. Тогда получится пропорция .

Пропорция также не нарушится, если её перевернуть, то есть использовать обратные отношения в обеих частях.

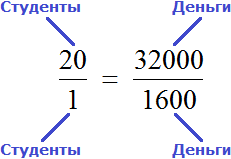
Перевернем пропорцию . Тогда получим пропорцию . Взаимосвязь при этом не нарушается. Отношение между студентами равно отношению между суммами денег, предназначенных для этих студентов. Такую пропорцию часто составляют в школе, когда для решения задачи составляются таблицы

Этот способ записи очень удобен, поскольку позволяет перевести условие задачи в более понятный вид. Решим задачу в которой требовалось определить сколько рублей нужно для выплаты стипендии двадцати студентам.

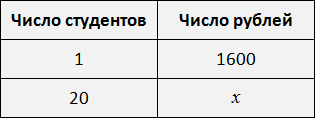
Условие задачи запишем следующим образом:

Составим таблицу на основе этого условия:

Составим пропорцию, используя данные таблицы:

Используя основное свойство пропорции, получим линейное уравнение и найдем его корень:

Изначально, мы имели дело с пропорцией , которая составлена из отношений величин разной природы. В числителях отношений располагались суммы денег, а в знаменателях количество студентов:

Поменяв местами крайние члены, мы получили пропорцию . Эта пропорция составлена из отношений величин одной природы. В первом отношении содержатся количества студентов, а во втором — суммы денег:

Если отношение составлено из величин одной природы, то мы будем называть его отношением одноименных величин. Например, отношения между фруктами, деньгами, физическими величинами, явлениями, действиями.

Отношение может быть составлено, как из одноименных величин, так и из величин разной природы. Примерами последних являются отношение расстояния ко времени, отношения стоимости товара к его количеству, отношение общей суммы стипендии к количеству студентов.

Пример 2. В школьном саду посажены сосны и березы, причём на каждую сосну приходится 2 березы. Сколько посадили сосен в саду, если берез посадили 240?

Определим сколько сосен было посажено в саду. Для этого составим пропорцию. В условии сказано, что на каждую сосну приходится 2 березы. Напишем отношение, показывающее что на одну сосну приходится две березы:

Теперь напишем второе отношение, показывающее что на x сосен приходится 240 берез

Соединим эти отношения знаком равенства, получим следующую пропорцию:

«2 березы так относятся к одной сосне,
как 240 берез относятся к x соснам»

Используя основное свойство пропорции, находим значение x

Либо пропорцию можно составить, предварительно записав условие, как в прошлом примере:

Получится та же пропорция, но в этот раз она будет составлена из отношений одноименных величин:

Значит в саду посадили 120 сосен.

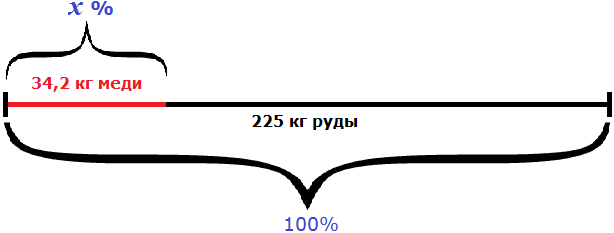
Пример 3. Из 225 кг руды получили 34,2 кг меди. Каково процентное содержание меди в руде?

Можно разделить 34,2 на 225 и полученный результат выразить в процентах:

Либо составить пропорцию 225 килограммам руды так приходятся на 100%, как 34,2 кг меди приходятся на неизвестное число процентов:

Либо составить пропорцию в которой отношения составлены из одноименных величин:

Задачи на прямую пропорциональность

Понимание отношений одноименных величин приводит к пониманию решения задач на прямую и обратную пропорциональность. Начнем с задач на прямую пропорциональность.

Для начала вспомним, что такое прямая пропорциональность. Это взаимосвязь между двумя величинами при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.

Если расстояние в 50 км автобус прошел за 1 час, то для прохождения расстояния в 100 км (при той же скорости) автобусу потребуется 2 часа. Во сколько раз увеличилось расстояние, во столько же раз увеличилось время движения. Как показать это с помощью пропорции?

Одно из предназначений отношения заключается в том, чтобы показать во сколько раз первая величина больше второй. А значит и мы c помощью пропорции можем показать, что расстояние и время увеличились в два раза. Для этого воспользуемся отношением одноименных величин.

Покажем, что расстояние увеличилось в два раза:

Аналогично покажем, что время увеличилось во столько же раз

Соединим эти отношения знаком равенства, получим пропорцию:

«100 километров так относятся к 50 километрам, как 2 часа относятся к 1 часу»

Если выполнить деление в обеих частях равенства , то обнаружим что расстояние и время были увеличены в одинаковое число раз.

2 = 2

Задача 2. За 3 ч на мельнице смололи 27 т пшеничной муки. Сколько тонн пшеничной муки можно смолоть за 9 ч, если темп работы не изменится?

Решение

Время работы мельницы и масса перемолотой муки — прямо пропорциональные величины. При увеличении времени работы в несколько раз, количество перемолотой муки увеличится во столько же раз. Покажем это с помощью пропорции.

В задаче дано 3 ч. Эти 3 ч увеличились до 9 ч. Запишем отношение 9 ч к 3 ч. Это отношение будет показывать во сколько раз увеличилось время работы мельницы:

Теперь запишем второе отношение. Это будет отношение x тонн пшеничной муки к 27 тоннам. Данное отношение будет показывать, что количество перемолотой муки увеличилось во столько же раз, сколько и время работы мельницы

Соединим эти отношения знаком равенства, получим пропорцию .

Воспользуемся основным свойством пропорции и найдем x

Значит за 9 ч можно смолоть 81 т пшеничной муки.

Вообще, если взять две прямо пропорциональные величины и увеличить их в одинаковое число раз, то отношение нового значения к старому значению первой величины будет равно отношению нового значения к старому значению второй величины.

Так и в предыдущей задаче старые значения были 3 ч и 27 т. Эти значения были увеличены в одинаковое число раз (в три раза). Новыми значениями стали 9 ч и 81 т. Тогда отношение нового значения времени работы мельницы к старому значению равно отношению нового значения массы перемолотой муки к старому значению

Если выполнить деление в обеих частях равенства, то обнаружим, что время работы мельницы и количество смолотой муки увеличилось в одинаковое число раз:

3 = 3

Пропорцию, которую составляют к задачам на прямую пропорциональность, можно описать с помощью выражения:

Применительно к нашей задаче значения переменных будут следующими:

Где впоследствии стало равно 81.

Задача 2. Для 8 коров в зимнее время доярка ежедневно заготовляет 80 кг сена, 96 кг корнеплодов, 120 кг силоса и 12 кг концентратов. Определить ежедневный расход этих кормов для 18 коров.

Решение

Количество коров и масса каждого из кормов — прямо пропорциональные величины. При увеличении количества коров в несколько раз, масса каждого из кормов увеличится во столько же раз.

Составим несколько пропорций, вычисляющих массу каждого из кормов для 18 коров.

Начнем с сена. Ежедневно для 8 коров его заготовляют 80 кг. Тогда для 18 коров будет заготовлено x кг сена.

Запишем отношение, показывающее во сколько раз увеличилось количество коров:

Теперь запишем отношение, показывающее во сколько раз увеличилась масса сена:

Соединим эти отношения знаком равенства, получим пропорцию:

Отсюда находим x

Значит для 18 коров нужно заготовить 180 кг сена. Аналогично определяем массу корнеплодов, силоса и концентратов.

Для 8 коров ежедневно заготовляют 96 кг корнеплодов. Тогда для 18 коров будет заготовлено x кг корнеплодов. Составим пропорцию из отношений и , затем вычислим значение x

Определим сколько силоса и концентратов нужно заготовить для 18 коров:

Значит для 18 коров ежедневно нужно заготавливать 180 кг сена, 216 кг корнеплодов, 270 кг силоса и 27 кг концентратов.

Задача 3. Хозяйка варит вишнёвое варенье, причём на 3 стакана вишни кладёт 2 стакана сахара. Сколько сахара нужно положить на 12 стаканов вишни? на 10 стаканов вишни? на стакана вишни?

Решение

Количество стаканов вишни и количество стаканов сахарного песка — прямо пропорциональные величины. При увеличении количества стаканов вишни в несколько раз, количество стаканов сахара увеличится во столько же раз.

Запишем отношение, показывающее во сколько раз увеличилось количество стаканов вишни:

Теперь запишем отношение, показывающее во сколько раз увеличилось количество стаканов сахара:

Соединим эти отношения знаком равенства, получим пропорцию и найдем значение x

Значит на 12 стаканов вишни нужно положить 8 стаканов сахара.

Определим количество стаканов сахара для 10 стаканов вишни и стакана вишни

Задачи на обратную пропорциональность

Для решения задач на обратную пропорциональность опять же можно использовать пропорцию, составленную из отношений одноименных величин.

В отличие от прямой пропорциональности, где величины увеличиваются или уменьшаются в одну и ту же сторону, в обратной пропорциональности величины изменяются обратно друг другу.

Если одна величина увеличивается в несколько раз, то другая уменьшается во столько же раз. И наоборот, если одна величина уменьшается в несколько раз, то другая увеличивается во столько же раз.

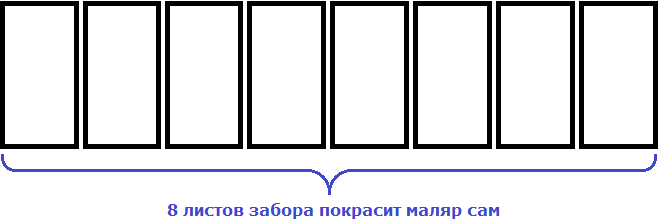
Допустим, что нужно покрасить забор, состоящий из 8 листов

Один маляр будет красить все 8 листов сам

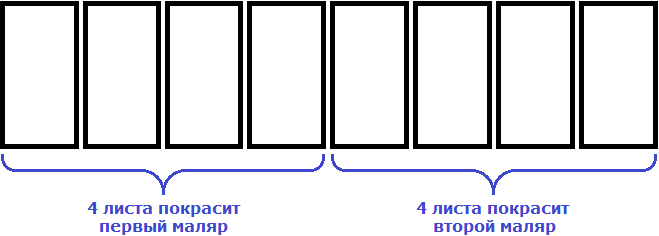
Если маляров будет 2, то каждый покрасит по 4 листа.

Это конечно же при условии, что маляры будут честными между собой и справедливо разделят эту работу поровну на двоих.

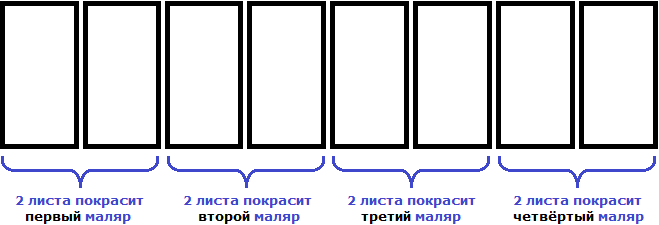
Если маляров будет 4, то каждый покрасит по 2 листа

Замечаем, что при увеличении количества маляров в несколько раз, количество листов которые приходятся на одного маляра уменьшаются во столько же раз.

Итак, мы увеличили количество маляров с 1 до 4. Другими словами, увеличили количество маляров в четыре раза. Запишем это с помощью отношения:

В результате количество листов забора, которые приходятся на одного маляра уменьшилось в четыре раза. Запишем это с помощью отношения:

Соединим эти отношения знаком равенства, получим пропорцию

«4 маляра так относятся к 1 маляру, как 8 листов относятся к 2 листам»

Задача 2. 15 рабочих закончили отделку квартир в новом доме за 24 дня. За сколько дней выполнили бы эту работу 18 рабочих?

Решение

Количество рабочих и количество дней, затраченных на работу — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней, необходимых для выполнения этой работы, уменьшится во столько же раз.

Запишем отношение 18 рабочих к 15 рабочим. Это отношение будет показывать во сколько раз увеличилось количество рабочих

Теперь запишем второе отношение, показывающее во сколько раз уменьшилось количество дней. Поскольку количество дней уменьшится с 24 дней до x дней, то второе отношение будет отношением старого количества дней (24 дня) к новому количеству дней (x дней)

Соединим полученные отношения знаком равенства, получим пропорцию:

Отсюда находим x

Значит 18 рабочих выполнят необходимую работу за 20 дней.

Вообще, если взять две обратно пропорциональные величины и увеличить одну из них в определенное число раз, то другая уменьшится во столько же раз. Тогда отношение нового значения к старому значению первой величины будет равно отношению старого значения к новому значению второй величины.

Так и в предыдущей задаче старые значения были 15 рабочих и 24 дня. Количество рабочих было увеличено с 15 до 18 (т.е. было увеличено в раза). В результате количество дней, необходимых для выполнения работы, уменьшилось во столько же раз. Новыми значениями стали 18 рабочих и 20 дней. Тогда отношение нового количества рабочих к старому количеству равно отношению старого количества дней к новому количеству

Для составления пропорции к задачам на обратную пропорциональность можно пользоваться формулой:

Применительно к нашей задаче значения переменных будут следующими:

Где впоследствии стало равно 20.

Задача 2. Скорость парохода относится к скорости течения реки, как 36 : 5. Пароход двигался вниз по течению 5 ч 10 мин. Сколько времени потребуется ему, чтобы вернуться обратно?

Решение

Собственная скорость парохода составляет 36 км/ч. Скорость течения реки реки 5 км/ч. Поскольку пароход двигался по течению руки, то скорость его движения составила 36 + 5 = 41 км/ч. Время пути составила 5 ч 10 мин. Для удобства выразим время в минутах:

5 ч 10 мин = 300 мин + 10 мин = 310 мин

Поскольку на обратном пути пароход двигался против течения реки, то его скорость составила 36 − 5 = 31 км/ч.

Скорость парохода и время его движения — обратно пропорциональные величины. При уменьшении скорости в несколько раз, время его движения увеличится во столько же раз.

Запишем отношение, показывающее во сколько раз уменьшилась скорость движения:

Теперь запишем второе отношение, показывающее во сколько раз увеличилось время движения. Поскольку новое время x будет больше старого времени, в числителе отношения запишем время x, а в знаменателе старое время, равное трёхсот десяти минутам

Соединим полученные отношения знаком равенства, получим пропорцию . Отсюда найдём значение x

410 минут это 6 часов и 50 минут. Значит пароходу потребуется 6 часов и 50 минут, чтобы вернуться обратно.

Задача 3. На ремонте дороги работало 15 человек, и они должны были закончить работу за 12 дней. На пятый день утром подошли еще несколько рабочих, и оставшаяся работа была выполнена за 6 дней. Сколько рабочих прибыло дополнительно?

Решение

Вычтем из 12 дней 4 отработанных дня. Так мы определим сколько ещё дней осталось работать пятнадцати рабочим

12 дней − 4 дня = 8 дней

На пятый день дополнительно прибыло x рабочих. Тогда всего рабочих стало 15 + x.

Количество рабочих и количество дней, необходимых для выполнения работы — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней уменьшится во столько же раз.

Запишем отношение, показывающее во сколько раз увеличилось количество рабочих:

Теперь запишем во сколько раз уменьшилось количество дней, необходимых для выполнения работы:

Соединим эти отношения знаком равенства, получим пропорцию . Отсюда можно вычислить значение x

Значит 5 рабочих прибыло дополнительно.

Масштаб

Масштабом называют отношение длины отрезка на изображении к длине соответствующего отрезка на местности.

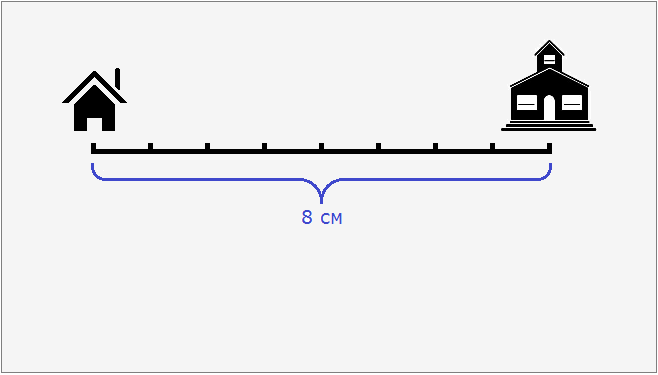
Допустим, что расстояние от дома до школы составляет 8 км. Попробуем нарисовать план местности, где будут указаны дом, школа и расстояние между ними. Но изобразить на бумаге расстояние, равное 8 км мы не можем, поскольку оно довольно велико. Но зато мы можем уменьшить это расстояние в несколько раз так, чтобы оно уместилось на бумаге.

Пусть километры на местности на нашем плане будут выражаться в сантиметрах. Переведем 8 километров в сантиметры, получим 800 000 сантиметров.

Уменьшим 800 000 см в сто тысяч раз:

800 000 см : 100 000 см = 8 см

8 см это расстояние от дома до школы, уменьшенное в сто тысяч раз. Теперь без труда можно нарисовать на бумаге дом и школу, расстояние между которыми будет 8 см.

Эти 8 см относятся к реальным 800 000 см. Так и запишем с помощью отношения:

8 : 800 000

Одно из свойств отношения гласит, что отношение не меняется если его члены умножить или разделить на одно и то же число.

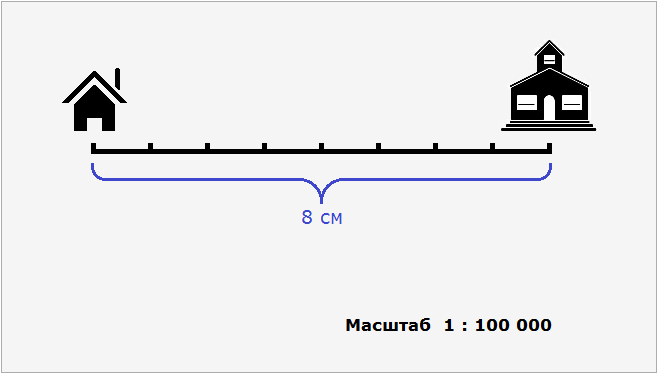
В целях упрощения отношения 8 : 800 000 оба его члена можно разделить на 8. Тогда получим отношение 1 : 100 000. Это отношение и назовём масштабом. Данное отношение показывает, что один сантиметр на плане относится (или соответствует) ста тысячам сантиметров на местности.

Поэтому на нашем рисунке необходимо указать, что план составлен в масштабе 1 : 100 000

Примеры:

1 см на плане относится к 100 000 см на местности;
2 см на плане относится к 200000 см на местности;
3 см на плане относится к 300000 на местности и т.д.

К любой карте или плану указывается в каком масштабе они сделаны. Этот масштаб позволяет определять реальное расстояние между объектами.

Так, наш план составлен в масштабе 1 : 100 000. На этом плане расстояние между домом и школой составляет 8 см. Чтобы вычислить реальное расстояние между домом и школой, нужно 8 см увеличить в 100 000 раз. Иными словами, умножить 8 см на 100 000

8 см × 100 000 = 800 000 см

Получаем 800 000 см или 8 км, если перевести сантиметры в километры.

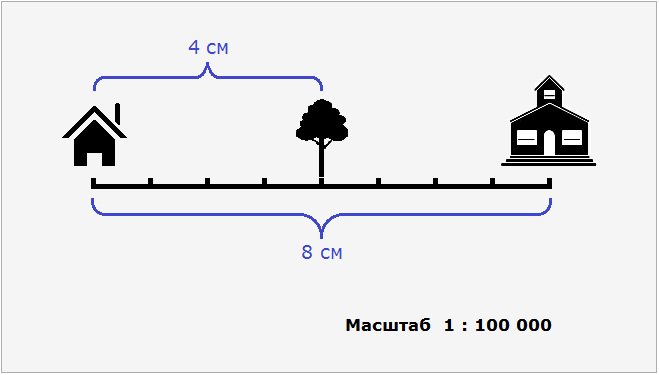
Допустим, что между домом и школой располагается дерево. На плане расстояние между школой и этим деревом составляет 4 см.

Тогда реальное расстояние между домом и деревом будет 4 см × 100 000 = 400 000 см или 4 км.

Расстояние на местности можно определять с помощью пропорции. В нашем примере расстояние между домом и школой будет вычисляться с помощью следующей пропорции:

Эту пропорцию можно прочитать так:

1 см на плане так относится к 100000 см на местности, как 8 см на плане относятся к x см на местности.

Из этой пропорции узнаём, что значение x равно 800000 см.

Пример 2. На карте расстояние между двумя городами составляет 8,5 см. Определить реальное расстояние между городами, если карта составлена в масштабе 1 : 1 000 000.

Решение

Масштаб 1 : 1 000 000 указывает, что 1 см на карте соответствует 1 000 000 см на местности. Тогда 8,5 см будут соответствовать x см на местности. Составим пропорцию 1 к 1000000 как 8,5 к x

В 1 км содержится 100000 см. Тогда в 8 500 000 см будет

Либо можно рассуждать так. Расстояние на карте и расстояние на местности — прямо пропорциональные величины. При увеличении расстояния на карте в несколько раз, расстояние на местности увеличится во столько же раз. Тогда пропорция примет следующий вид. Первое отношение будет показывать во сколько раз расстояние на местности больше расстояния на карте:

Второе отношение покажет, что расстояние на местности во столько же раз больше, чем 8,5 см на карте:

Отсюда x равен 8 500 000 см или 85 км.

Задача 3. Длина реки Невы 74 км. Чему равняется ее длина на карте, масштаб которой 1 : 2 000 000

Решение

Масштаб 1 : 2000000 говорит о том, что 1 см на карте соответствует 2 000 000 см на местности.

А 74 км на это 74 × 100 000 = 7 400 000 см на местности. Уменьшив 7 400 000 в 2 000 000, мы определим длину реки Невы на карте

7 400 000 : 2 000 000 = 3,7 см

Значит на карте, масштаб которой 1 : 2 000 000 длина реки Невы составляет 3,7 см.

Запишем решение с помощью пропорции. Первое отношение будет показывать сколько раз длина на карте меньше длины на местности:

Второе отношение будет показывать, что 74 км (7 400 000 см) уменьшились во столько же раз:

Отсюда находим x равный 3,7 см

Задачи для самостоятельного решения

Задача 1. Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?

Решение

Пусть x кг масла можно получить из 7 кг хлопкового семени. Масса хлопкового семени и масса получаемого масла — прямо пропорциональные величины. Тогда уменьшение хлопкового семени с 21 кг до 7 кг, приведет к уменьшению получаемого масла во столько же раз.

Ответ: из 7 кг хлопкового семени получится 1,7 кг масла.

Задача 2. На некотором участке железнодорожного пути старые рельсы длиной в 8 м заменили новыми длиной в 12 м. Сколько потребуется новых двенадцатиметровых рельсов, если сняли 360 старых рельсов?

Решение

Длина участка на котором производится замена рельсов равна 8 × 360 = 2880 м.

Пусть x двенадцатиметровых рельсов требуется для замены. Увеличение длины одного рельса с 8 м до 12 м приведет к уменьшению количества рельсов с 360 до x штук. Иными словами, длина рельса и их количество связаны обратно пропорциональной зависимостью

Ответ: для замены старых рельсов потребуется 240 новых.

Задача 3. 60% учеников класса пошли в кино, а остальные 12 человек – на выставку. Сколько учащихся в классе?

Решение

Если 60% учащихся пошли в кино, а остальные 12 человек на выставку, то на 40% учащихся и будут приходиться 12 человек, пошедших на выставку. Тогда можно составить пропорцию в которой 12 учащихся так относятся к 40%, как все x учащихся относятся к 100%

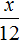
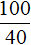
Либо можно составить пропорцию, состоящей из отношений одноименных величин. Количество учащихся и процентная доля изменяются прямо пропорционально. Тогда можно записать, что во сколько раз увеличилось количество участников во столько же раз увеличилась процентная доля (с 40% до 100%)

Ответ: в классе 30 учащихся.

Задача 4. Расстояние на карте между городами 18 см. Какое действительное расстояние между городами, если масштаб карты 1 : 500 000?

Решение

Масштаб 1 : 500000 говорит о том, что 1 см на карте соответствует 500 000 см на местности.

Тогда увеличив 18 см в 500 000, мы получим действительное расстояние между городами

18 см × 500 000 = 9 000 000 см

Переведем 9 000 000 см в километры. В одном километре 100 000 см. Тогда в 9 000 000 см будет

Запишем решение с помощью пропорции:

Ответ: расстояние между городами 90 км.

Задача 5. Пешеход затратил на путь 2,5 ч, двигаясь со скоростью 3,6 км/ч. Сколько времени затратит пешеход на тот же путь, если его скорость будет 4,5 км/ч

Решение

Скорость и время — обратно пропорциональные величины. При увеличении скорости в несколько раз, время движения уменьшится во столько же раз.

Запишем отношение, показывающее по сколько раз увеличилась скорость движения пешехода:

Запишем отношение, показывающее что время движения уменьшилось во столько же раз:

Соединим эти отношения знаком равенства, получим пропорцию и найдём значение x

Ответ: пешеход затратит 2 часа если будет двигаться со скорость 4,5 км/ч.

Задача 6. Перевыполнив план на 15%, завод выпустил за месяц 230 станков. Сколько станков должен был выпустить за месяц завод по плану?

Решение

Выражение «перевыполнили план на 15%» означает, что к имеющемуся 100% плану выполнили еще 15% того же плана. Итого выполнено 115% плана. На эти 115% приходятся 230 выпущенных станков

А по плану завод должен был выпустить x станков. Эти x станков приходятся на 100% изначального плана

Составим пропорцию из имеющихся отношений и найдём значение x

Либо можно воспользоваться отношениями одноименных величин. Количество выпущенных станков и процентная доля, на которые эти станки приходятся, связаны прямо пропорциональной зависимостью. При увеличении количества станков в несколько раз, процентная доля увеличивается во столько же раз. Тогда можно записать, что 230 станков во столько раз больше, чем x станков, во сколько раз больше 115%, чем 100%

Ответ: по плану завод должен был выпустить 200 станков.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник