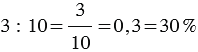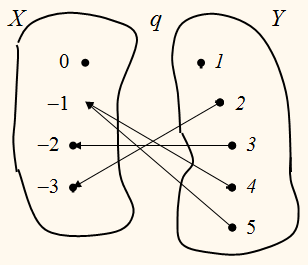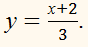1.Что такое отношение? 2.Что показывает отношение?
3.Как найти отношение?
4.Как найти обратное отношение
МАТЕМАТИКА СРОЧНО ЗА 30 МИНУТ
чтобы найти отношение, нужно оба числа разделить на одно и тоже число:
напр.: 12 : 3 = 4 : 1 (то есть оба числа — 12 и 3, разделили на 3 и получили 4 и 1),
Обратное отношение — это отношение, взятое в обратном порядке по отношению к данному.
Отношения
Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.
Где 



14 : 7 — отношение числа 14 к числу 7;
6 : 25 — отношение числа 6 к числу 25;
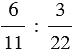
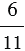
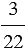
1,15 : 0,36 — отношение числа 1,15 к числу 0,36.
Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел 





Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел 



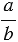
Основное свойство отношения:
Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Запишем отношение числа 3 к числу 10 и найдем его значение:
То есть отношение двух чисел можно выразить в процентах.
Процентное отношение двух чисел — это их отношение, выраженное в процентах.
Процентное отношение показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Пример:
Сколько процентов составляет число 5 от числа 10?
5 10 2 1 · 100 % = 1 2 · 100 % = 100 2 % = 50 % .
Ответ: 50% составляет число 5 от числа 10.
Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.
Например:
Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.
Отношение длины прямоугольника к его ширине равно 12 : 100 = 
Отношение ширины прямоугольника к его длине равно 100 : 12 = 
Дроби 

На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана).
Пусть на карте задан масштаб 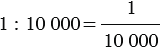
Найдем, какой длине на местности соответствует отрезок 5 см на карте.
Для решения обозначим через />длину отрезка на местности (в сантиметрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: 5 : />, данное отношение равно масштабу карты, поэтому получаем уравнение:
5 : 
Решаем данное уравнение:



50 000 см = 500 м = 0,5 км.
Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.
Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.
Для решения обозначим через />длину отрезка на карте (в километрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: />: 9,5, данное отношение равно масштабу карты, поэтому получаем уравнение:

Решаем данное уравнение:


0,00095 км = 0,95 м = 95 см.
Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.
математика — Как найти обратное отношение данному?
Если пара (x,y) принадлежит отношению R, то пара (y,x) принадлежит обратному отношению (и наоборот). Поэтому достаточно написать, что R^ <-1>состоит из всех пар вида (y,x), а дальше всё ровно то же самое.
Если по каким-то причинам хочется, чтобы первая переменная обозначалась x, а вторая y (хотя это ни к чему), то можно оставить (x,y), а после двоеточия написать всё с заменой x на y и наоборот.
Дел в том, что по заданию требуется записать отношение R^ <-1>аналитически и графически. А также найти для него область определения, область значений.
Сделайте рисунок. Уже говорилось, что R^ <-1>состоит из всех пар вида (x,y), где 2y-x>=2 на квадрате (обе переменные от -4 до 7). Рисуете квадрат, потом график прямой, и берёте то, что сверху от неё. А аналитически всё уже задано (поменяли местами x и y).
Надо иметь в виду, что в таких заданиях не бывает ничего нетривиального.
Спасибо большое! Еще вопрос, не подскажите, что такое $$overline$$ и как его найти?
@lisp: такие обозначения могут использоваться для чего угодно. Их надо сверять с «документацией», то есть с лекциями. Одно из возможных толкований такое: это дополнение отношения, заданного на множестве. Элемент x находится в отношении $%bar R$% с y тогда и только тогда, когда x не находится в отношении R с y. Если в Вашем случае отношение задано на отрезке [-4;7], то надо просто поменять знак $%ge$% на $%<$%, и получится аналитическая запись для $%bar$%. А геометрически это то, что не входит в R (в пределах квадрата).
Для решения задач этого типа достаточно двух-трёх определений.
Здравствуйте
Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Обратное отношение в математике — это отношение, взятое в обратном порядке по отношению к данному.
Определение
Пусть на множестве 


Свойства
- Если отношение
обладает одним из перечисленных свойств: рефлексивностью, нерефлексивностью, симметрией, антисимметрией, асимметрией, транзитивностью или полнотой, то и обратное отношение
также обладает им.
- Если
инъективно, сюръективно или функционально, то
, вообще говоря, не обязано обладать таким же свойством.
Примеры
|
п·о·р Бинарное отношение |
|---|
| между двумя множествами: инъективное · сюръективное · биективное · полное слева · полное справа · функциональное |
| на множестве: рефлексивное · нерефлексивное · симметричное · антисимметричное · асимметричное · транзитивное · полное · евклидово |
Отношение, обратное данному.
ПРИМЕР:
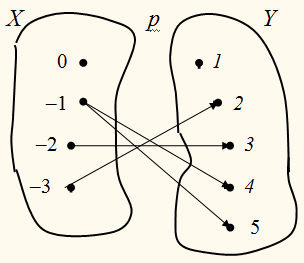
На рисунке отношение р между элементами множества Х и элементами множества Y задано с помощью стрелок.
Поменяем направление стрелок.
Получим другое отношение –
отношение q между элементами множества Y и элементами
множества Х.
Говорят, что q есть отношение,
обратное отношению р. В свою очередь отношение р является обратным отношению q.
Областью определения
отношения p является множество
{–3; –2; –1},
а областью значений –
множество
{2; 3; 4; 5}
Для отношения q,
обратного отношению р,
областью определения служит множество
{2; 3; 4; 5},
а областью значений –
множество
{–3; –2; –1}.
Таким образом, область определения и область значений взаимно-обратных
отношений меняются ролями.
Отношение p между элементами
множеств Х и Y определяется множеством пар:
{(–3; 2); (–2; 3); (–1; 4); (–1; 5)}
Поменяв в каждой паре местами
её элементы, получим множество пар, которым задаётся отношение q, обратное р:
{(2; –3); (3; –2); (4; –1); (5; –1)}
Если отношение
определяется некоторым множеством пар, то обратное ему отношение определяется множеством
пар, которое получено из первого перестановкой элементов в каждой паре.
ПРИМЕР:
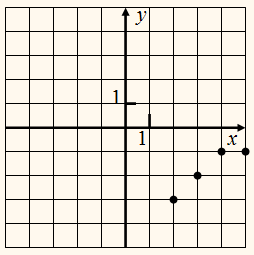
Вернёмся к рассмотренным выше
взаимно-обратным отношениям р и q.
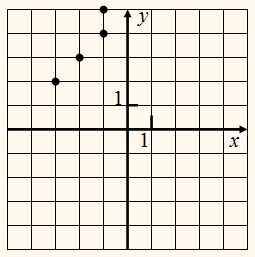
На рисунке построен график
отношения р.
На рисунке построен график
отношения q.
Построим теперь графики
отношений р и q в одной и той же системе координат.
Нетрудно заметить, что точки с координатами
(–3; 2) и (2; –3), (–1;
4) и (4; –1) и т. д.,
т. е. точки, у которых абсцисса первой является ординатой
второй и ордината первой является абсциссой второй, симметричны относительно
прямой
у = х.
Каждой точке графика отношения р
соответствует симметричная относительно прямой у = х
точка графика отношения q,
и наоборот, каждой точке графика отношения
q соответствует
симметричная относительно прямой у
= х точка графика
отношения р.
Поэтому графики отношений р и q симметричны относительно прямой у = х.
Вообще справедлива
следующая теорема:
Графики взаимно-обратных отношений между числами
симметричны относительно прямой у
= х.
Приведём примеры взаимно-обратных отношений
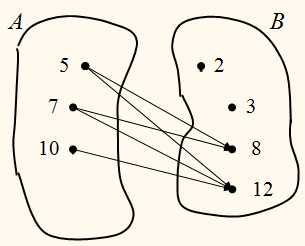
ПРИМЕР:
На рисунке с помощью стрелок
показано отношение <<меньше>> между элементами множества
А = {5; 7; 10}
В = {2; 3; 8; 12}
Обратное ему отношение является отношением <<больше>>
между элементами множества В и элементами множества А.
ПРИМЕР:
Отношение <<быть делителем>> и <<быть кратным>> между
натуральными числами – взаимно-обратные отношения.
Действительно, если а и b – некоторые натуральные числа и а делитель b,
то b кратно
а, и наоборот, если b кратно а,
то а делитель
b. Например, из того, что
<<2
делитель 6>>,
следует, что <<6 кратно 2>>; из того, что <<24
кратно 8>>,
следует, что <<8 делитель 24>>.
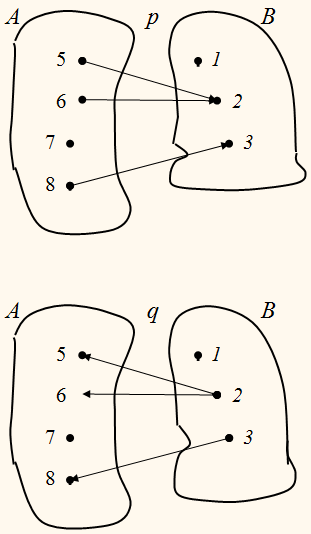
Понятие функции, обратной данной.
ПРИМЕР:
На рисунку с помощью стрелок
задано отношение р между элементами множеств А и В. Это
отношение – функция, так как каждому элементу множества А соответствует не более одного множества В.
Отношение q между элементами множества В и А,
обратное р,
не является функцией: в множестве
В существует
элемент (число 2), которому
соответствует более одного элемента из множества А (элементы 5 и 6).
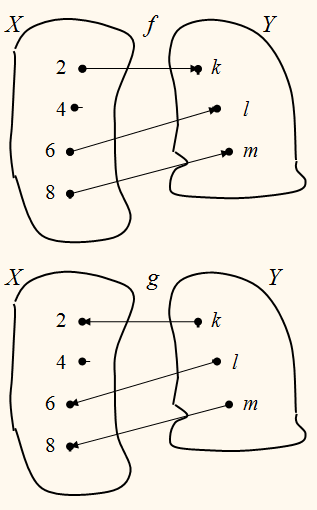
ПРИМЕР:
На рисунках с помощью стрелок
задано отношение f между элементами множеств X и Y и обратное ему отношение g между элементами
множеств Y и X.
Отношение f – функция, отношение
g, обратное f,
тоже функция.
Приведённые примеры показывают, что отношение, обратное функции, может быть
функцией, а может и не быть функцией.
Функция f называется обратимой, если обратное ей
отношение – функция.
В этом случае отношение, обратное функции
f,
называют функцией, обратной f.
Мы рассмотрели примеры функций p и f,
заданных с помощью стрелок. Обратимой оказалась функция в том случае, когда к
любому элементу области её значений было проведено не более одной стрелки, т.
е. когда каждое своё значение функции принимала только при одном значении
аргумента.
Функция
обратима тогда и только тогда, когда каждое своё значение она принимает лишь
при одном значении аргумента.
ПРИМЕР:
На рисунках изображены графики
функций g и h.
Функция g обратима, так как нет такого значения
функции, которое соответствовало бы различным значениям аргумента (любая прямая,
параллельная оси х,
пересекает график не более чем в одной точке).
Функция h необратима, так как существует такое значение
функции, например у
= 3, которое соответствует трём различным значениям
переменной х (прямая у = 3 пересекает график в трёх точках).
Всякая
возрастающая функция обратима.
Функция,
обратная возрастающей, является возрастающей.
Всякая убывающая
функция обратима.
Функция,
обратная убывающей, является убывающей.
Если некоторое
отношение f задано уравнением с двумя
переменными х и у,
то для задания уравнением отношения, обратного
f,
достаточно в данном уравнении поменять обозначения х на у и у на х.
ПРИМЕР:
Функция f,
заданная формулой
у = –2х + 3,
убывающая. Поэтому она
обратима. Обратная ей функция также убывающая.
Чтобы задать формулой функцию,
обратную f,
поменяем в уравнении
у = –2х + 3,
обозначения х на у и у на х. Получим
уравнение
х = –2у + 3,
Обычно при задании функции
уравнением с переменными х и у переменную
у выражают через
переменную х.
В данном случае имеем:
2у = –х + 3,
у = –0,5х + 1,5.
Мы получили формулу, которой
задаётся функция, обратная f.
ПРИМЕР:
Пусть дана функция:
у = 3х – 2.
Если определить х через у и в полученном равенстве вместо х написать
у, а вместо у написать
х, будем иметь:
Эта
функция, обратная данной. Данную функцию также можно назвать обратной по
отношению к полученной. Эти функции взаимно обратные.
ПРИМЕР:
Для функции, заданной равенством:
у = х2
На
]–∞; +∞
[,
обратной не существует. А для
функции:
у = х2
заданной на промежутке
[0; +∞ [,
обратная функция существует.
Графики двух взаимно обратных функций симметричны друг к другу относительно
биссектрисы первого и третьего координатных углов, то есть относительно прямой
у = х.
Задания к уроку 16
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
- Урок 1. Координатная плоскость
- Урок 2. Диаграммы
- Урок 3. Графики
- Урок 4. Множества
- Урок 5. Что такое функция ?
- Урок 6. Аналитический способ задания функции
- Урок 7. Табличный способ задания функции
- Урок 8. Графический способ задания функции
- Урок 9. Нахождение области определения и области значения функции аналитическим методом
- Урок 10. Нахождение области определения и области значения функции с помощью графика
- Урок 11. Нули функции
- Урок 12. Возрастание и убывание функции
- Урок 13. Экстремальные значения функции
- Урок 14. Симметричные функции
- Урок 15. Чётные и нечётные функции
- Урок 17. Линейная функция
- Урок 18. График линейной функции
- Урок 19. Прямая пропорциональность
- Урок 20. График прямой пропорциональности
- Урок 21. Взаимное расположение графиков линейных функций
- Урок 22. Обратно пропорциональная зависимость
- Урок 23. График обратно пропорциональной зависимости
- Урок 24. Квадратичная функция
- Урок 25. График функции у = aх2 + b
- Урок 26. График функции у = a(х — m)2 + n
- Урок 27. График функции у = aх2 + bx + c
- Урок 28. Функция y = √͞͞͞͞͞х и её график
- Урок 29. Функция y = хn и её график
- Урок 30. Построение графиков функций методом геометрических преобразований
Если мы хотим
определить такое понятие, как отношение,
мы должны, прежде всего, ввести такое
понятие, как упорядоченная
пара.
Различие между
неупорядоченной парой элементов {a,b}
и упорядоченной парой (a,b)
обычно поясняют на примере сравнения
двух пар элементов. Две неупорядоченные
пары {a,b}={c,d},
если a=b&c=da=c&b=d.
Для упорядоченных пар (a,b)=(c,d)
a=b&c=d.
То есть, в общем случае, для упорядоченных
пар (a,b)(b,a).
Иногда употребляют и такую запись:
R=(a,b)={a,{a,b}}.
Нетрудно догадаться, что существование
множества {a,b}
зависит от того, какое мы выберем a.
Если a,b
– числа, то мы можем описать множество
упорядоченных пар в виде графика,
откладывая по оси абсцисс значения a,
по оси ординат значения b,
для которых существует R=(a,b).

Упорядоченную
пару R
называют двухместным
или бинарным
отношением.
Упорядоченный набор из n
элементов (a1,
… , an)
называют n-местным
отношением или
кортежем.
Элементы для
формирования упорядоченных наборов
мы можем выбирать как из одного множества,
так и из разных. При построении графиков,
которые отображают бинарные отношения
между множествами действительных чисел
X
и Y,
мы используем так называемую декартову
систему координат.
Прямым (декартовым)
произведением двух множеств A
и B
называется множество упорядоченных
пар (a,b),
в которых aA
и bB:
AB={(a,b)|
aA
& bB}.
Степенью множества
A
называется его прямое произведение
само на себя: An=A…A
– всего n
раз.
Пользуясь введенным
понятием прямого произведения, можно
определить бинарное отношение как
подмножество
прямого произведения AB:
R=ab={(a,b)R|
RAB}.
Запись ab
обозначает
отношение между элементами a
и b
в общем виде, а запись (a,b)
обозначает конкретную упорядоченную
пару элементов, то есть один элемент
отношения.
Если у нас задан
некоторый универсум U,
то мы можем рассматривать понятия
принадлежности (),
включения (),
и равенства (=), как отношения на B(U)
– множестве всех подмножеств универсума
U.
Способы задания
отношений.
Если отношение содержит небольшое
количество пар (или наборов), его можно
задать, как и множество, перечислением.
Бинарные отношения, как уже говорилось,
могут быть заданы в виде графиков, если
A,B
– числовые множества. В общем случае
отношения могут быть заданы в виде
таблиц или графов. В реляционных базах
данных понятие «кортеж» соответствует
записи в таблице, а поля таблицы с
именами A,B,C,…,
из которых берутся элементы записи,
образуют прямое произведение множеств
ABC…
.
Основные понятия,
связанные с понятием бинарного отношения.
Пусть
R=ab={(a,b)R|
RAB}.
Тогда
существуют:
обратное отношение
R-1={(b,a)|(a,b)R};
дополнение
отношения R={(a,b)|(a,b)R}=(AB)R;
тождественное
отношение I={(a,a)|aA};
однородное
отношение:
UR={(a,b)|aA&bA}.
Композиция
отношений.
Пусть заданы два
бинарных отношения: R1AB
и R2BC
(говорят так: отношение из A
в B
и отношение из B
в C).
Композицией
отношений
R1
и R2
называется
отношение R
из A
в C:
R=
R1
o R2
={(a,c)|
aA
&
cC
&
bB
: (a,b)
R1
& (b,c)
R2}.
Пример.Пусть
A
— множество студентов ФПК, B
– множество специальностей, С –
множество учебных курсов, изучаемых
на этих специальностях. Нам нужно
определить, какие дисциплины будет
изучать каждый конкретный студент ФПК
(что будет включать его приложение к
диплому).
Здесь R1
AB
– «студент aA
получает специальность bB»,
R2
BC
– «на специальности bВ
изучается дисциплина cC».
Искомое отношение R
– «студент aA
изучает дисциплину cC»
есть композиция отношений R=
R1
R2.
То есть, чтобы студент aA
изучал дисциплину cC
нужно, чтобы он учился на специальности
bB,
что соответствует отношению ab,
и на этой специальности изучалась
данная дисциплина cC,
что соответствует отношению bc.
Значит, для решения задачи нам нужно
выяснить, для каких пар (a,b)
имеются пары (b,c),
и из этих пар составить новые пары
(a,c),
взяв первый элемент из пары (a,b),
а второй элемент – из пары (b,c).
Графически операцию
композиции можно проиллюстрировать
на следующей схеме.
В этой графической
схеме каждой упорядоченной паре
элементов (a,b)
и (b,c)
сопоставлены стрелки из множества А
в множество B
и из множества B
в множество C
соответственно. Искомым парам (a,c)
соответствуют возможные переходы по
стрелкам из множества A
в множество C.
Теперь составим
бинарные таблицы R1
и R2
для
представленных данной схемой отношений.
Элементы этих таблиц rij(1)
и rjk(2)
соответствуют
отношениям (ai,bj)
и (bj,ck).
Первая таблица будет содержать |A|
строк и |B|
столбцов, вторая — |B|
строк и |C|
столбцов. Для нашего примера таблицы
будут иметь вид:
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
R1
R2
Одновременное
существование отношений rij(1)
и rjk(2)
соответствует
логическому произведению (конъюнкции)
элементов таблицы rij(1)
rij(2),
и значение каждого элемента rik
итоговой таблицы R
будет зависеть от того, принимает ли
хотя бы одна из этих элементарных
конъюнкций значение «1», что соответствует
логическому сложению (дизъюнкции). Для
нашего примера r11=(r11(1)
r21(1)
r31(1)
r41(1)
)(
r11r12(2)
r13(2)
r14(2)
r15(2)
r16(2)),
и так далее. То есть при i=1,…,|A|,
j=1,…,|B|,
k=1,…,|C|
мы имеем: R=
R1
o
R2
= R1
R2
, где R1
R2
— логическое
перемножение матриц.
Степенью отношения
Rn
называется композиция отношения R
n
раз с самим собой.
Ядром отношения
RAB
называется композиция R*=
R
o
R-1.
Ядро отношения является отношением на
A.
9.Однородные
(универсальные) отношения. Примеры
универсальных отношений. Свойства
однородных отношений (рефлексивность,
симметричность, транзитивность).
Отношение эквивалентности и отношение
порядка.
однородным
отношением—
отношение R=
a
b={(a,b)|aA&bA}.
однородное отношение
– это отношение RA2.
Однородные
бинарные отношения
– важный тип отношений для многих
приложений информатики и других разделов
дискретной математики, для задач теории
графов. Ребра любого графа задают
однородное бинарное отношение на
множестве его вершин V.
Множество точек на плоскости с заданной
системой координат (X,Y)
– это тоже однородное бинарное отношение,
где A
– множество действительных чисел.
Свойства однородных
отношений.
1. Рефлексивность:
aA
имеет место отношение (a,a).
То есть отношение (a,b)
всегда существует при a=b.
Свойство рефлексивности означает,
что IR.
2.
Антирефлексивность:
aA
имеет место (a,a).
То есть отношение (a,
b)
не существует
ни при каких a=b.
Если для каких-то a=b
отношение существует, а для каких-то
нет, то следует говорить, что отношение
просто не
рефлексивно.
Примеры рефлексивных
отношений
на множестве точек плоскости XY:
1) R={(x,y)
| x=y};
2) R={(x,y)
| |y|<|x|+1};
3) R={(x,y)
| x+y=2k,
k=1,2,…,n}.
3.
Симметричность:
a,bA
(a,b)R
(b,a)R.
Свойство
симметричности означает, что R-1R.
Симметричными
отношениями на множестве точек плоскости
XY
являются отношения 1) и 3) из приведенных
выше.
4.
Антисимметричность:
a,bA
, ab,
(a,b)R
(b,a)R.
То есть
условие симметричности не
выполняется
ни при каких a,b.
Простейший пример антисимметричного
отношения на XY
– строгое неравенство x<y.
Если для каких-то
ab
симметричность выполняется, а для
каких-то нет, то следует говорить, что
отношение R
просто не
симметрично.
Примером такого отношения является
отношение 2).
5. Транзитивность.
a,b,cA
(a,b)R
& (b,c)R
(a,c)R.
Очень важное свойство отношений.
Свойство
транзитивности можно записать через
степень отношения (композицию отношения
с самим собой): R2
=R
R
R.
Антитранзитивность
обычно не рассматривают, хотя можно и
ее определить так же, как в первых двух
случаях.
Примеры транзитивных
отношений:
1) все три примера,
приведенных выше;
2) x<y
( в том числе и нестрогое неравенство);
3) отношение
вложенности на B(U):
пусть A,B,C
U.
Если A
B
& B
C
A
C.
6.
Полнота
(линейность):
a,bA
, ab
(a,b)R
(b,a)R
.
Полнота
отношения означает, что R
R-1
I
= UR.
Свойство полноты,
вообще говоря, довольно редкое. Пример
полного отношения — неравенство xy.
Отношения
эквивалентности и отношения порядка.
Определение 1.
Если однородное отношение RA2:
-
рефлексивно,
2)симметрично, 3) транзитивно
то оно называется
отношением
эквивалентности. Отношение
эквивалентности часто обозначается
«»,
как и операция эквивалентности в логике.
Множество элементов aA,
для которых выполняется отношение
эквивалентности R,
называется классом
эквивалентности.
Класс эквивалентности будем обозначать
[x]:
[x]
= {y
| yA
& yx}.
Из рассмотренных
выше примеров отношениями эквивалентности
являются примеры 1) и 3).
Примером отношения
эквивалентности на B(U)
может служить отношение равномощности
множеств: |A|=|B|.
То есть все подмножества из U
одинаковой мощности образуют класс
эквивалентности.
Определееие 2.
Если однородное отношение RA2:
-
антисимметрично,
2) транзитивно,
то
оно называется отношением
порядка.
Если отношение при этом еще и
антирефлексивно,
то это отношение
строгого порядка.
Отношение нестрогого порядка может
быть как рефлексивным, так и просто не
рефлексивным.Для обозначения отношения
порядка можно использовать обычный
знак неравенства.Если отношение порядка
не обладает свойством полноты
(линейности), то обычно говорят об
отношении частичного
порядка. В
задачах дискретной математики и
информатики чаще всего встречается
именно этот тип отношений.
Если на множестве
А определено отношение частичного
порядка, то оно называется частично
упорядоченным.
Множество, на котором определено
отношение полного порядка, называется
вполне
упорядоченным.
Например, числовые множества – это
вполне упорядоченные множества.
Теорема.
На всяком конечном, непустом, частично
упорядоченном множестве существует
минимальный
элемент y
|
xy
y<x.
Вполне упорядоченное
множество содержит только один
минимальный элемент, на частично
упорядоченном множестве их может быть
несколько. Булеан B(U),
— это вполне упорядоченное множество
относительно отношения вложенности
().
Минимальным элементом в этом случае
является пустое множество .
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.