Как найти обратное отношение множеств

Операции над соответствиями на множествах

Поскольку соответствия можно считать множествами, то все операции над множествами (пересечение, объединение, разность, дополнение и т.д.) можно применить и к соответствиям. Заметим, что, говоря о дополнении соответствия из в , мы имеем в виду дополнение до универсального соответствия из в , т.е. до декартова произведения . Естественно, что и равенство соответствий можно трактовать как равенство множеств.

В то же время на соответствия можно распространить операции, определяемые для отображений. Мы рассмотрим здесь две такие операции.

Композиция соответствии. Следуя аналогии с композицией отображнений, композицией (произведением) соответствий и называют соответствие

Поясним построение композиции двух соответствий. Обратимся сначала к отображениям (как частным случаям соответствий). Пусть заданы отображения (возможно, частичные): из в и из в . Композиция определяется как отображение из в , задаваемое формулой . Тем самым задается график отображения , т.е. множество упорядоченных пар , таких, что . При этом упорядоченная пара будет принадлежать графику отображения , если и только если найдется элемент , такой, что и . Таким образом, график композиции отображений и есть

Необходимо заметить, что запись означает , т.е. отображения в композиции пишутся в порядке, обратном тому, в каком они применяются. Мы же будем везде использовать запись , полагая, что и порядок записи отображений в композиции совпадает с порядком их применения. Это обусловлено тем, что композиция отображений определяется нами как частный случай композиции соответствий, при записи которой естественным оказывается именно такой порядок.

Легко видеть, что (1.4) есть частный случай (1.3). Отметим, что при построении композиции отображений обычно предполагают, что пересечение области значений отображения и области определения отображения не пусто , поскольку в противном случае композиция была бы пуста. Для отображений, не являющихся частичными, , так как . Поэтому в данном случае пересечение всегда не пусто.

Полезно отметить также, что если и — биекции, то и композиция их тоже будет биекцией.

Вернемся к рассмотрению композиции соответствий . Полагая, что область определения соответствия не пуста, возьмем произвольный элемент . Пусть сечение соответствия не пусто и найдется такой элемент , что сечение также не пусто. Тогда непустое множество будет подмножеством сечения соответствия в точке . Сечением соответствия в точке будет непустое в силу сделанных предположений множество всех таких упорядоченных пар , что , а для некоторого . Говоря неформально, нужно перебрать все элементы из сечения . Таким образом, различие в построении композиции соответствий и композиции отображений заключается в том, что «промежуточный» элемент z в общем случае не единственный и каждому такому элементу также ставится в соответствие не единственный элемент .

---

Пример 1.8. Соответствие возьмем из примера 1.3. Соответствие зададим как соответствие из множества программ в множество заказчиков программного обеспечения . Пусть

Рассмотрим процесс построения композиции соответствий и . Начнем с элемента . Имеем

Отсюда получаем сечение композиции по элементу

Рассуждая аналогично, получим и .

Построение графа композиции проиллюстрировано на рис. 1.3.

Отметим, что область определения композиции соответствий содержится в области определения первого соответствия, а область значений композиции соответствий — в области значений второго соответствия. Из приведенных рассуждений следует, что для того, чтобы композиция соответствий была отлична от пустого соответствия, необходимо и достаточно, чтобы пересечение области значений первого соответствия и области определения второго соответствия было не пусто.

К определению композиции соответствий можно подойти с более общих позиций. Пусть и . При этом на множества и априори не накладывается никаких органичений. Композиция соответствий и в этом случае также определяется соотношением (1.3). Чтобы такая композиция была отлична от пустого соответствия, необходимо и достаточно выполнение условия . В частности, всякий раз, когда .

---

Пример 1.9. Рассмотрим соответствие из множества в множество и соответствие из множества в множество . В данном случае , но , поскольку

Заметим, что композиция соответствий и не коммутативна, т.е. в общем случае , поскольку , а .

---

Композиция бинарного отношения на множестве

Бинарное отношение на множестве является частным случаем соответствия. Для двух бинарных отношении и , заданных на множестве , их композиция (1.3) как соответствий является бинарным отношением на том же множестве . В этом случае говорят о композиции бинарных отношений на множестве .

Композицию бинарного отношения на некотором множестве с самим собой называют квадратом бинарного отношения и обозначают .

Рассмотрим пример построения композиции бинарных отношений на множестве и покажем, что в общем случае для двух бинарных отношений и также имеет место неравенство , хотя обе композиции, в отличие от аналогичных композиций двух произвольных соответствий, заданы на одном и том же множестве.

---

Пример 1.10. а. Зададим на множестве бинарные отношения и найдем композицию , если

.

Имеем и . Следовательно, . Далее и . Так как , то в итоге получим . Построение композиции проиллюстрировано на рис. 1.4,а.

Найдем композицию . Поскольку , а , то . Аналогично , а , поэтому . Далее , поэтому , а и . Построение композиции проиллюстрировано на рис. 1.4,б.

Легко видеть, что .

б. Пусть отношение на множестве действительных чисел определено как функция . Найдем квадрат этого отношения (линейной функции от одного переменного).

Согласно (1.4), это будет функция , такая, что , то есть . Это тоже линейная функция, но с другими коэффициентами.

---

Свойства композиции соответствий

Приведем некоторые свойства композиции соответствий:

1) ;
2) для любого соответствия имеет место ;
3) ;
4) для любого бинарного отношения на множестве имеет место равенство .

Эти свойства нетрудно доказать методом двух включений. Рассмотрим в качестве примера доказательство свойства 3. Пусть некоторая упорядоченная пара принадлежит композиции . Тогда, согласно (1.3), найдется такой элемент , что и . Последнее означает, что или . Таким образом, для элемента имеем и или и . Первая альтернатива имеет место при , а вторая — при , что означает . Тем самым включение доказано.

Доказательство включения запишем коротко, используя логическую символику:

В данном случае доказательства двух включений не совсем симметричны: элементы и во второй части доказательства не обязаны совпадать.

Замечание 1.4. В тождестве, выражающем свойство 3, нельзя вместо объединения поставить пересечение, так как в этом случае тождество нарушатся. Можно доказать, что сохранится лишь включение

а обратное включение в общем случае не имеет места.

Анализ свойств 2 и 4 показывает, что роль пустого соответствия аналогична роли нуля при умножении чисел, а диагональ множества играет роль, аналогичную роли единицы, на множестве всех бинарных отношений на .

---

Обратное соответствие и его свойства

Соответствие, обратное к соответствию , есть соответствие из в , обозначаемое и равное, по определению, .

Для соответствия из примера 1.3

Обратное соответствие обладает следующими легко проверяемыми свойствами:

1) ;
2) .

Для бинарного отношения на множестве обратное соответствие есть бинарное отношение на том же множестве. В этом случае говорят о бинарном отношении на множестве , обратном к .

Заметим, что соответствия и в общем случае не совпадают. Даже для бинарного отношения на множестве

, а также и .

Например, для бинарного отношения на множестве графы самого отношения, обратного отношения , композиций и представлены на рис. 1.5.

Если — отображение, то оно является соответствием. Обратное к соответствие из в в общем случае не является отображением. Действительно, соответствие , обратное к , состоит из всех упорядоченных пар вида . Поскольку в общем случае могут найтись такие два различных элемента и , что , то соответствие в общем случае не будет функционально по второй компоненте и поэтому не будет отображением. Если отображение инъективно, то обратное соответствие есть частичное отображение из в . Если отображение биективно, то обратное соответствие является отображением из в , причем имеют место равенства

Отображение в этом случае называют отображением, обратным к .

---

Ограничение соответствия

Пусть — соответствие из в и . Ограничением соответствия на подмножества и (или -ограничением соответствия ) называется соответствие из в , обозначаемое , такое, что

Таким образом, -ограничение соответствия есть «то же самое» соответствие , но из последнего берутся только упорядоченные пары, первая компонента которых принадлежит подмножеству , а вторая — подмножеству . Можно записать

Так, «малый» арксинус, т.е. функция , есть ограничение «большого» арксинуса , который является соответствием на подмножества и .

Рассмотрим некоторые важные частные случаи ограничений соответствий (в частности, бинарных отношений и отображений).

Всякое -ограничение соответствия будем называть сужением соответствия на подмножество (коротко — C-сужением соответствия ), а всякое -ограничение соответствия — строгим сужением соответствия на подмножество (строгим C-сужением соответствия р). C-сужения соответствия будем обозначать , а строгое сужение — соответственно.

Полезно заметить, что для любого отображения строгое сужение есть сюръекция на . Если, сверх этого, является инъекцией, то есть биекция на . Допуская некоторую вольность речи, можно сказать, что любое отображение сюръективно отображает свою область определения на свою область значений, в частности, любая инъекция устанавливает взаимно однозначное соответствие между областью определения и областью значений. Так, функция сюръективно отображает множество всех действительных чисел на отрезок , а любая показательная функция биективно отображает на подмножество всех положительных действительных чисел.

Для бинарного отношения и любого подмножества (M,M)-ограничение бинарного отношения называют ограничением бинарного отношения на подмножество и обозначают . Можно записать .

Рассмотрим, например, отношение естественного порядка на множестве действительных чисел. Тогда отношение есть ограничение этого порядка на подмножество целых чисел. Но ни в коем случае нельзя путать это отношение с -сужением отношения ! Это последнее состоит из всех таких упорядоченных пар , что и , т.е. вторая компонента пары может быть произвольным действительным числом, не меньшим заданного целого .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Определение:

Композицией (произведением, суперпозицией) бинарных отношений (англ. composition of binary relations) и называется такое отношение , что: .

Примером такого отношения может служить отношение на некотором множестве населенных пунктов — отношение «можно доехать на поезде», а — отношение «можно доехать на автобусе». Тогда отношение — отношение «можно добраться из пункта А в пункт Б, сначала проехав на поезде, а потом на автобусе (только по одному разу)».

Степень отношений

Определение:

Степень отношения (англ. power of relation) , определяется следующим образом: ;

В связи с этим понятием, также вводятся обозначения:

— Транзитивное замыкание (англ. transitive closure) отношения ;

— Транзитивно-рефлексивное замыкание отношения

Обратное отношение

Определение:

Отношение называют обратным (англ. inverse relation) для отношения , если:

Определение:

Ядром отношения (англ. kernel of relation) называется отношение

Свойства

Композиция отношений обладает следующими свойствами:

• Ядро отношения симметрично:  

• Композиция отношений ассоциативна:  

• Обратное отношение для отношения, являющемуся обратным к есть само  

• Обратное отношение к композиции отношений и есть композиция отношений, обратных к и  

• Обратное отношение к объединению отношений и есть объединение отношений, обратных к и  

• Обратное отношение к пересечению отношений и есть пересечение отношений, обратных к и  

См. также

• Бинарное отношение
• Транзитивное замыкание

Источники информации

• Новиков Ф. А. — Дискретная математика для программистов: Учебник для вузов. 3-е изд. — СПБ.: Питер, 2009 — 52 с.
• Wikipedia — Composition of relations
• UNC Charlotte — Lectures in Discrete Mathematics: Composition of Relations and Directed Graphs.

Если мы хотим
определить такое понятие, как отношение,
мы должны, прежде всего, ввести такое
понятие, как упорядоченная
пара.

Различие между
неупорядоченной парой элементов {a,b}
и упорядоченной парой (a,b)
обычно поясняют на примере сравнения
двух пар элементов. Две неупорядоченные
пары {a,b}={c,d},
если a=b&c=da=c&b=d.
Для упорядоченных пар (a,b)=(c,d)

a=b&c=d.
То есть, в общем случае, для упорядоченных
пар (a,b)(b,a).
Иногда употребляют и такую запись:
R=(a,b)={a,{a,b}}.
Нетрудно догадаться, что существование
множества {a,b}
зависит от того, какое мы выберем a.
Если a,b
– числа, то мы можем описать множество
упорядоченных пар в виде графика,
откладывая по оси абсцисс значения a,
по оси ординат значения b,
для которых существует R=(a,b).

Упорядоченную
пару R
называют двухместным
или бинарным
отношением.
Упорядоченный набор из n
элементов (a₁,
… , a_n)
называют n-местным
отношением или
кортежем.

Элементы для
формирования упорядоченных наборов
мы можем выбирать как из одного множества,
так и из разных. При построении графиков,
которые отображают бинарные отношения
между множествами действительных чисел
X
и Y,
мы используем так называемую декартову
систему координат.

Прямым (декартовым)
произведением двух множеств A
и B
называется множество упорядоченных
пар (a,b),
в которых aA
и bB:
AB={(a,b)|
aA
& bB}.

Степенью множества
A
называется его прямое произведение
само на себя: Aⁿ=A…A
– всего n
раз.

Пользуясь введенным
понятием прямого произведения, можно
определить бинарное отношение как
подмножество
прямого произведения AB:
R=ab={(a,b)R|
RAB}.

Запись ab
обозначает
отношение между элементами a
и b
в общем виде, а запись (a,b)
обозначает конкретную упорядоченную
пару элементов, то есть один элемент
отношения.

Если у нас задан
некоторый универсум U,
то мы можем рассматривать понятия
принадлежности (),
включения (),
и равенства (=), как отношения на B(U)
– множестве всех подмножеств универсума
U.

Способы задания
отношений.
Если отношение содержит небольшое
количество пар (или наборов), его можно
задать, как и множество, перечислением.
Бинарные отношения, как уже говорилось,
могут быть заданы в виде графиков, если
A,B
– числовые множества. В общем случае
отношения могут быть заданы в виде
таблиц или графов. В реляционных базах
данных понятие «кортеж» соответствует
записи в таблице, а поля таблицы с
именами A,B,C,…,
из которых берутся элементы записи,
образуют прямое произведение множеств
ABC…
.

Основные понятия,
связанные с понятием бинарного отношения.

Пусть
R=ab={(a,b)R|
RAB}.
Тогда
существуют:

обратное отношение
R^-1={(b,a)|(a,b)R};

дополнение
отношения R={(a,b)|(a,b)R}=(AB)R;

тождественное
отношение I={(a,a)|aA};

однородное
отношение:
U_R={(a,b)|aA&bA}.

Композиция
отношений.

Пусть заданы два
бинарных отношения: R₁AB
и R₂BC
(говорят так: отношение из A
в B
и отношение из B
в C).

Композицией
отношений
R₁
и R₂
называется
отношение R
из A
в C:

R=
R₁
o R₂
={(a,c)|
aA
&
cC
&
bB
: (a,b)

R₁
& (b,c)

R₂}.

Пример.Пусть
A
— множество студентов ФПК, B
– множество специальностей, С –
множество учебных курсов, изучаемых
на этих специальностях. Нам нужно
определить, какие дисциплины будет
изучать каждый конкретный студент ФПК
(что будет включать его приложение к
диплому).

Здесь R₁
AB
– «студент aA
получает специальность bB»,
R₂
BC
– «на специальности bВ
изучается дисциплина cC».
Искомое отношение R
– «студент aA
изучает дисциплину cC»
есть композиция отношений R=
R₁
R₂.
То есть, чтобы студент aA
изучал дисциплину cC
нужно, чтобы он учился на специальности
bB,
что соответствует отношению ab,
и на этой специальности изучалась
данная дисциплина cC,
что соответствует отношению bc.
Значит, для решения задачи нам нужно
выяснить, для каких пар (a,b)
имеются пары (b,c),
и из этих пар составить новые пары
(a,c),
взяв первый элемент из пары (a,b),
а второй элемент – из пары (b,c).

Графически операцию
композиции можно проиллюстрировать
на следующей схеме.

В этой графической
схеме каждой упорядоченной паре
элементов (a,b)
и (b,c)
сопоставлены стрелки из множества А
в множество B
и из множества B
в множество C
соответственно. Искомым парам (a,c)
соответствуют возможные переходы по
стрелкам из множества A
в множество C.

Теперь составим
бинарные таблицы R₁
и R₂
для
представленных данной схемой отношений.
Элементы этих таблиц r_ij(1)
и r_jk(2)
соответствуют
отношениям (a_i,b_j)
и (b_j,c_k).
Первая таблица будет содержать |A|
строк и |B|
столбцов, вторая — |B|
строк и |C|
столбцов. Для нашего примера таблицы
будут иметь вид:

1	0	0
0	1	1
1	0	0
0	1	0

1	0	1	1	0	0
0	1	0	0	1	0
0	0	1	0	0	1

R₁

R₂

Одновременное
существование отношений r_ij(1)
и r_jk(2)
соответствует
логическому произведению (конъюнкции)
элементов таблицы r_ij(1)

r_ij(2),
и значение каждого элемента r_ik
итоговой таблицы R
будет зависеть от того, принимает ли
хотя бы одна из этих элементарных
конъюнкций значение «1», что соответствует
логическому сложению (дизъюнкции). Для
нашего примера r₁₁=(r₁₁₍₁₎
r₂₁₍₁₎
r₃₁₍₁₎
r₄₁₍₁₎
)(
r₁₁r₁₂₍₂₎
r₁₃₍₂₎
r₁₄₍₂₎
r₁₅₍₂₎
r₁₆₍₂₎),
и так далее. То есть при i=1,…,|A|,
j=1,…,|B|,
k=1,…,|C|
мы имеем: R=
R₁
o
R₂
= R₁
R₂
, где R₁
R₂
— логическое
перемножение матриц.

Степенью отношения
Rⁿ
называется композиция отношения R
n
раз с самим собой.

Ядром отношения
RAB
называется композиция R*=
R
o
R^-1.
Ядро отношения является отношением на
A.

9.Однородные
(универсальные) отношения. Примеры
универсальных отношений. Свойства
однородных отношений (рефлексивность,
симметричность, транзитивность).
Отношение эквивалентности и отношение
порядка.

однородным
отношением—
отношение R=
a

b={(a,b)|aA&bA}.

однородное отношение
– это отношение RA².
Однородные
бинарные отношения
– важный тип отношений для многих
приложений информатики и других разделов
дискретной математики, для задач теории
графов. Ребра любого графа задают
однородное бинарное отношение на
множестве его вершин V.
Множество точек на плоскости с заданной
системой координат (X,Y)
– это тоже однородное бинарное отношение,
где A
– множество действительных чисел.

Свойства однородных
отношений.

1. Рефлексивность:

aA
имеет место отношение (a,a).
То есть отношение (a,b)
всегда существует при a=b.
Свойство рефлексивности означает,
что IR.

2.
Антирефлексивность:

aA
имеет место (a,a).
То есть отношение (a,
b)
не существует
ни при каких a=b.
Если для каких-то a=b
отношение существует, а для каких-то
нет, то следует говорить, что отношение
просто не
рефлексивно.

Примеры рефлексивных
отношений
на множестве точек плоскости XY:

1) R={(x,y)
| x=y};

2) R={(x,y)
| |y|<|x|+1};

3) R={(x,y)
| x+y=2k,
k=1,2,…,n}.

3.
Симметричность:

a,bA
(a,b)R

(b,a)R.
Свойство
симметричности означает, что R^-1R.

Симметричными
отношениями на множестве точек плоскости
XY
являются отношения 1) и 3) из приведенных
выше.

4.
Антисимметричность:

a,bA
, ab,
(a,b)R


(b,a)R.
То есть
условие симметричности не
выполняется
ни при каких a,b.
Простейший пример антисимметричного
отношения на XY
– строгое неравенство x<y.

Если для каких-то
ab
симметричность выполняется, а для
каких-то нет, то следует говорить, что
отношение R
просто не
симметрично.
Примером такого отношения является
отношение 2).

5. Транзитивность.

a,b,cA
(a,b)R
& (b,c)R

(a,c)R.
Очень важное свойство отношений.

Свойство
транзитивности можно записать через
степень отношения (композицию отношения
с самим собой): R²
=R

R

R.

Антитранзитивность
обычно не рассматривают, хотя можно и
ее определить так же, как в первых двух
случаях.

Примеры транзитивных
отношений:

1) все три примера,
приведенных выше;

2) x<y
( в том числе и нестрогое неравенство);

3) отношение
вложенности на B(U):
пусть A,B,C

U.
Если A

B
& B

C

A

C.

6.
Полнота
(линейность):

a,bA
, ab


(a,b)R

(b,a)R
.
Полнота
отношения означает, что R

R^-1

I
= U_R.

Свойство полноты,
вообще говоря, довольно редкое. Пример
полного отношения — неравенство xy.

Отношения
эквивалентности и отношения порядка.

Определение 1.
Если однородное отношение RA²:

1. рефлексивно,
   2)симметрично, 3) транзитивно

то оно называется
отношением
эквивалентности. Отношение
эквивалентности часто обозначается
«»,
как и операция эквивалентности в логике.
Множество элементов aA,
для которых выполняется отношение
эквивалентности R,
называется классом
эквивалентности.
Класс эквивалентности будем обозначать
[x]_:

[x]_
= {y
| yA
& yx}.

Из рассмотренных
выше примеров отношениями эквивалентности
являются примеры 1) и 3).

Примером отношения
эквивалентности на B(U)
может служить отношение равномощности
множеств: |A|=|B|.
То есть все подмножества из U
одинаковой мощности образуют класс
эквивалентности.

Определееие 2.
Если однородное отношение RA²:

1. антисимметрично,
   2) транзитивно,

то
оно называется отношением
порядка.
Если отношение при этом еще и
антирефлексивно,
то это отношение
строгого порядка.
Отношение нестрогого порядка может
быть как рефлексивным, так и просто не
рефлексивным.Для обозначения отношения
порядка можно использовать обычный
знак неравенства.Если отношение порядка
не обладает свойством полноты
(линейности), то обычно говорят об
отношении частичного
порядка. В
задачах дискретной математики и
информатики чаще всего встречается
именно этот тип отношений.

Если на множестве
А определено отношение частичного
порядка, то оно называется частично
упорядоченным.
Множество, на котором определено
отношение полного порядка, называется
вполне
упорядоченным.
Например, числовые множества – это
вполне упорядоченные множества.

Теорема.
На всяком конечном, непустом, частично
упорядоченном множестве существует
минимальный
элемент y
| 
xy
y<x.

Вполне упорядоченное
множество содержит только один
минимальный элемент, на частично
упорядоченном множестве их может быть
несколько. Булеан B(U),
— это вполне упорядоченное множество
относительно отношения вложенности
().
Минимальным элементом в этом случае
является пустое множество .

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Обратное отношение в математике — это отношение, взятое в обратном порядке по отношению к данному.

Определение

Пусть на множестве задано бинарное отношение Тогда его обратным называется отношение построенное следующим образом:

Свойства

• Если отношение обладает одним из перечисленных свойств: рефлексивностью, нерефлексивностью, симметрией, антисимметрией, асимметрией, транзитивностью или полнотой, то и обратное отношение также обладает им.
• Если инъективно, сюръективно или функционально, то , вообще говоря, не обязано обладать таким же свойством.

Примеры

п·о·р Бинарное отношение
между двумя множествами: инъективное · сюръективное · биективное · полное слева · полное справа · функциональное
на множестве: рефлексивное · нерефлексивное · симметричное · антисимметричное · асимметричное · транзитивное · полное · евклидово

1.Что такое отношение? 2.Что показывает отношение?
3.Как найти отношение?
4.Как найти обратное отношение
МАТЕМАТИКА СРОЧНО ЗА 30 МИНУТ​

чтобы найти отношение, нужно оба числа разделить на одно и тоже число:

напр.: 12 : 3 = 4 : 1 (то есть оба числа — 12 и 3, разделили на 3 и получили 4 и 1),

Обратное отношение — это отношение, взятое в обратном порядке по отношению к данному.

Отношения

Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.

Где и — члены отношения; число — предыдущий член отношения; — последующий член отношения.

14 : 7 — отношение числа 14 к числу 7;

6 : 25 — отношение числа 6 к числу 25;

— отношение числа к числу ;

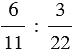
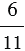
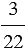
1,15 : 0,36 — отношение числа 1,15 к числу 0,36.

Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел и показывает, во сколько раз число больше числа или какую часть число составляет от числа .

Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел и можно записать двумя способами: : и .

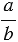
Основное свойство отношения:

Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.

Запишем отношение числа 3 к числу 10 и найдем его значение:

То есть отношение двух чисел можно выразить в процентах.

Процентное отношение двух чисел — это их отношение, выраженное в процентах.

Процентное отношение показывает, сколько процентов одно число составляет от другого.

Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.

Пример:

Сколько процентов составляет число 5 от числа 10?

5 10 2 1 · 100 % = 1 2 · 100 % = 100 2 % = 50 % .

Ответ: 50% составляет число 5 от числа 10.

Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.

Например:

Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.

Отношение длины прямоугольника к его ширине равно 12 : 100 = .

Отношение ширины прямоугольника к его длине равно 100 : 12 = .

Дроби и взаимно обратны, поэтому и отношения 12 к 100 и 100 к 12 называют взаимно обратными.

На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.

Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана).

Пусть на карте задан масштаб 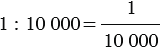, то есть карта сделана в масштабе одна десятитысячная.

Найдем, какой длине на местности соответствует отрезок 5 см на карте.

Для решения обозначим через />длину отрезка на местности (в сантиметрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: 5 : />, данное отношение равно масштабу карты, поэтому получаем уравнение:

5 : = 1 : 10 000;

Решаем данное уравнение:

= 510 000;

= 50 000;

50 000 см = 500 м = 0,5 км.

Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.

Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.

Для решения обозначим через />длину отрезка на карте (в километрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: />: 9,5, данное отношение равно масштабу карты, поэтому получаем уравнение:

: 9,5 = 1 : 10 000;

Решаем данное уравнение:

= 9,5 : 10 000;

= 0,00095;

0,00095 км = 0,95 м = 95 см.

Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.

математика — Как найти обратное отношение данному?

Если пара (x,y) принадлежит отношению R, то пара (y,x) принадлежит обратному отношению (и наоборот). Поэтому достаточно написать, что R^ <-1>состоит из всех пар вида (y,x), а дальше всё ровно то же самое.

Если по каким-то причинам хочется, чтобы первая переменная обозначалась x, а вторая y (хотя это ни к чему), то можно оставить (x,y), а после двоеточия написать всё с заменой x на y и наоборот.

Дел в том, что по заданию требуется записать отношение R^ <-1>аналитически и графически. А также найти для него область определения, область значений.

Сделайте рисунок. Уже говорилось, что R^ <-1>состоит из всех пар вида (x,y), где 2y-x>=2 на квадрате (обе переменные от -4 до 7). Рисуете квадрат, потом график прямой, и берёте то, что сверху от неё. А аналитически всё уже задано (поменяли местами x и y).

Надо иметь в виду, что в таких заданиях не бывает ничего нетривиального.

Спасибо большое! Еще вопрос, не подскажите, что такое $$overline$$ и как его найти?

@lisp: такие обозначения могут использоваться для чего угодно. Их надо сверять с «документацией», то есть с лекциями. Одно из возможных толкований такое: это дополнение отношения, заданного на множестве. Элемент x находится в отношении $%bar R$% с y тогда и только тогда, когда x не находится в отношении R с y. Если в Вашем случае отношение задано на отрезке [-4;7], то надо просто поменять знак $%ge$% на $%<$%, и получится аналитическая запись для $%bar$%. А геометрически это то, что не входит в R (в пределах квадрата).

Для решения задач этого типа достаточно двух-трёх определений.

Здравствуйте

Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.