Простыми словами о преобразовании Фурье
Уровень сложности
Средний
Время на прочтение
14 мин
Количество просмотров 989K
Я полагаю что все в общих чертах знают о существовании такого замечательного математического инструмента как преобразование Фурье. Однако в ВУЗах его почему-то преподают настолько плохо, что понимают как это преобразование работает и как им правильно следует пользоваться сравнительно немного людей. Между тем математика данного преобразования на удивление красива, проста и изящна. Я предлагаю всем желающим узнать немного больше о преобразовании Фурье и близкой ему теме того как аналоговые сигналы удается эффективно превращать для вычислительной обработки в цифровые.

Без использования сложных формул и матлаба я постараюсь ответить на следующие вопросы:
- FT, DTF, DTFT — в чем отличия и как совершенно разные казалось бы формулы дают столь концептуально похожие результаты?
- Как правильно интерпретировать результаты быстрого преобразования Фурье (FFT)
- Что делать если дан сигнал из 179 сэмплов а БПФ требует на вход последовательность по длине равную степени двойки
- Почему при попытке получить с помощью Фурье спектр синусоиды вместо ожидаемой одиночной “палки” на графике вылезает странная загогулина и что с этим можно сделать
- Зачем перед АЦП и после ЦАП ставят аналоговые фильтры
- Можно ли оцифровать АЦП сигнал с частотой выше половины частоты дискретизации (школьный ответ неверен, правильный ответ — можно)
- Как по цифровой последовательности восстанавливают исходный сигнал
Я буду исходить из предположения что читатель понимает что такое интеграл, комплексное число (а так же его модуль и аргумент), свертка функций, плюс хотя бы “на пальцах” представляет себе что такое дельта-функция Дирака. Не знаете — не беда, прочитайте вышеприведенные ссылки. Под “произведением функций” в данном тексте я везде буду понимать “поточечное умножение”
Начать надо, наверное, с того что обычное преобразование Фурье — это некая такая штука которая, как можно догадаться из названия, преобразует одни функции в другие, то есть ставит в соответствие каждой функции действительного переменного x(t) её спектр или фурье-образ y(w):
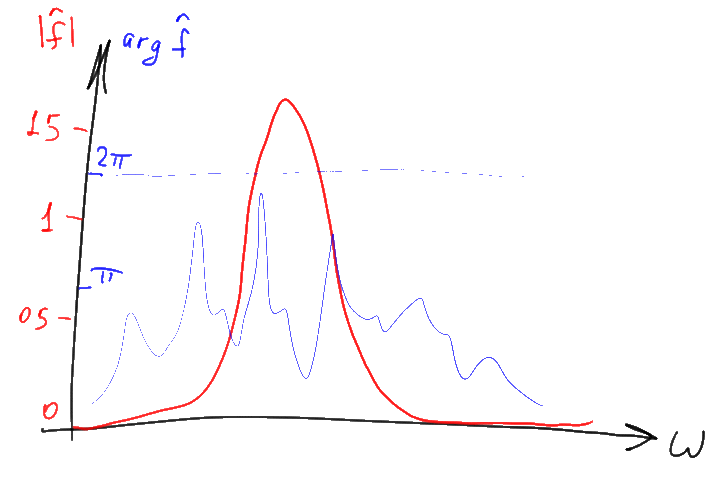
Если приводить аналогии, то примером аналогичного по смыслу преобразования может послужить например дифференцирование, превращающее функцию в её производную. То есть преобразование Фурье — такая же, по сути, операция как и взятие производной, и её часто обозначают схожим образом, рисуя треугольную “шапочку” над функцией. Только в отличие от дифференцирования которое можно определить и для действительных чисел, преобразование Фурье всегда “работает” с более общими комплексными числами. Из-за этого постоянно возникают проблемы с отображением результатов этого преобразования, поскольку комплексные числа определяются не одной, а двумя координатами на оперирующем действительными числами графике. Удобнее всего, как правило, оказывается представить комплексные числа в виде модуля и аргумента и нарисовать их по раздельности как два отдельных графика:
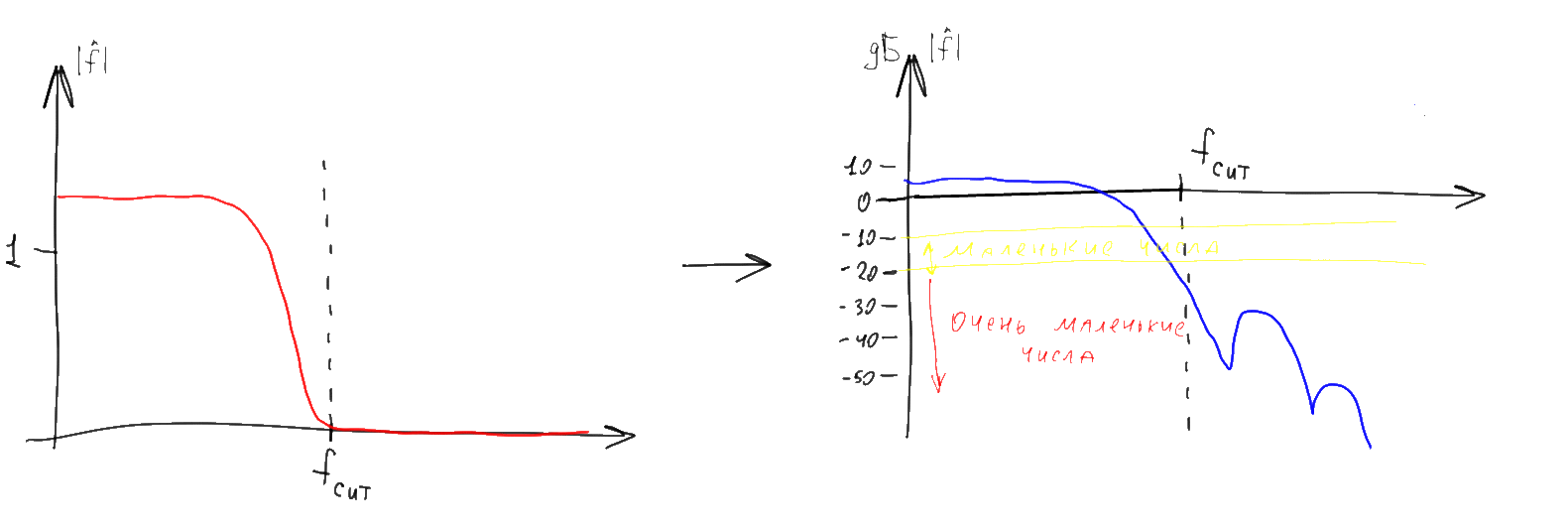
График аргумента комплексного значения часто называют в данном случае “фазовым спектром”, а график модуля — “амплитудным спектром”. Амплитудный спектр как правило представляет намного больший интерес, а потому “фазовую” часть спектра нередко пропускают. В этой статье мы тоже сосредоточимся на “амплитудных” вещах, но забывать про существование пропущенной фазовой части графика не следует. Кроме того, вместо обычного модуля комплексного значения часто рисуют его десятичный логарифм умноженный на 10. В результате получается логарифмический график, значения на котором отображаются в децибелах (дБ).
Обратите внимание что не очень сильно отрицательным числам логарифмического графика (-20 дБ и менее) при этом соответствуют практически нулевые числа на графике “обычном”. Поэтому длинные и широкие “хвосты” разнообразных спектров на таких графиках при отображении в “обычные” координаты как правило практически исчезают. Удобство подобного странного на первый взгляд представления возникает из того что фурье-образы различных функций часто необходимо перемножать между собой. При подобном поточечном умножении комплекснозначных фурье-образов их фазовые спектры складываются, а амплитудные — перемножаются. Первое выполняется легко, а второе — сравнительно сложно. Однако логарифмы амплитуды при перемножении амплитуд складываются, поэтому логарифмические графики амплитуды можно, как и графики фаз, просто поточечно складывать. Кроме того, в практических задачах часто удобнее оперировать не «амплитудой» сигнала, а его «мощностью» (квадратом амплитуды). На логарифмической шкале оба графика (и амплитуды и мощности) выглядят идентично и отличаются только коэффициентом — все значения на графике мощности ровно вдвое больше чем на шкале амплитуд. Соответственно для построения графика распределения мощности по частоте (в децибелах) можно не возводить ничего в квадрат, а посчитать десятичный логарифм и умножить его на 20.
Заскучали? Погодите, еще немного, с занудной частью статьи, объясняющей как интерпретировать графики, мы скоро покончим :). Но перед этим следует понять одну крайне важную вещь: хотя все вышеприведенные графики спектров были нарисованы для некоторых ограниченных диапазонов значений (в частности, положительных чисел), все эти графики на самом деле продолжаются в плюс и минус бесконечность. На графиках просто изображается некоторая “наиболее содержательная” часть графика, которая обычно зеркально отражается для отрицательных значений параметра и зачастую периодически повторяется с некоторым шагом, если рассматривать её в более крупном масштабе.
Определившись с тем, что же рисуется на графиках, давайте вернемся собственно к преобразованию Фурье и его свойствам. Существует несколько разных способов как определить это преобразование, отличающихся небольшими деталями (разными нормировками). Например в наших ВУЗах почему-то часто используют нормировку преобразования Фурье определяющую спектр в терминах угловой частоты (радианов в секунду). Я буду использовать более удобную западную формулировку, определяющую спектр в терминах обычной частоты (герцах). Прямое и обратное преобразование Фурье в этом случае определяются формулами слева, а некоторые свойства этого преобразования которые нам понадобятся — списком из семи пунктов справа:
Первое из этих свойств — линейность. Если мы берем какую-то линейную комбинацию функций, то преобразование Фурье этой комбинации будет такой же линейной комбинацией образов Фурье этих функций. Это свойство позволяет сводить сложные функции и их фурье-образы к более простым. Например, фурье-образ синусоидальной функции с частотой f и амплитудой a является комбинацией из двух дельта-функций расположенных в точках f и -f и с коэффициентом a/2:
Если взять функцию, состоящую из суммы множества синусоид с разными частотами, то согласно свойству линейности, фурье-образ этой функции будет состоять из соответствующего набора дельта-функций. Это позволяет дать наивную, но наглядную интерпретацию спектра по принципу “если в спектре функции частоте f соответствует амплитуда a, то исходную функцию можно представить как сумму синусоид, одной из которых будет синусоида с частотой f и амплитудой 2a”. Строго говоря, эта интерпретация неверна, поскольку дельта-функция и точка на графике — это совершенно разные вещи, но как мы увидим дальше, для дискретных преобразований Фурье она будет не так уж и далека от истины.
Второе свойство преобразования Фурье — это независимость амплитудного спектра от сдвига сигнала по времени. Если мы подвинем функцию влево или вправо по оси x, то поменяется лишь её фазовый спектр.
Третье свойство — растяжение (сжатие) исходной функции по оси времени (x) пропорционально сжимает (растягивает) её фурье-образ по шкале частот (w). В частности, спектр сигнала конечной длительности всегда бесконечно широк и наоборот, спектр конечной ширины всегда соответствует сигналу неограниченной длительности.
Четвертое и пятое свойства самые, пожалуй, полезные из всех. Они позволяют свести свертку функций к поточечному перемножению их фурье-образов и наоборот — поточечное перемножение функций к свертке их фурье-образов. Чуть дальше я покажу насколько это удобно.
Шестое свойство говорит о симметрии фурье-образов. В частности, из этого свойства следует что в фурье-образе действительнозначной функции (т.е. любого “реального” сигнала) амплитудный спектр всегда является четной функцией, а фазовый спектр (если его привести к диапазону -pi…pi) — нечетной. Именно по этой причине на графиках спектров практически никогда не рисуют отрицательную часть спектра — для действительнозначных сигналов она не дает никакой новой информации (но, повторюсь, и нулевой при этом не является).
Наконец последнее, седьмое свойство, говорит о том, что преобразование Фурье сохраняет “энергию” сигнала. Оно осмысленно только для сигналов конечной продолжительности, энергия которых конечна, и говорит о том, что спектр подобных сигналов на бесконечности быстро приближается к нулю. Именно в силу этого свойства на графиках спектров как правило изображают только “основную” часть сигнала, несущую в себе львиную долю энергии — остальная часть графика просто стремится к нулю (но, опять же, нулем не является).
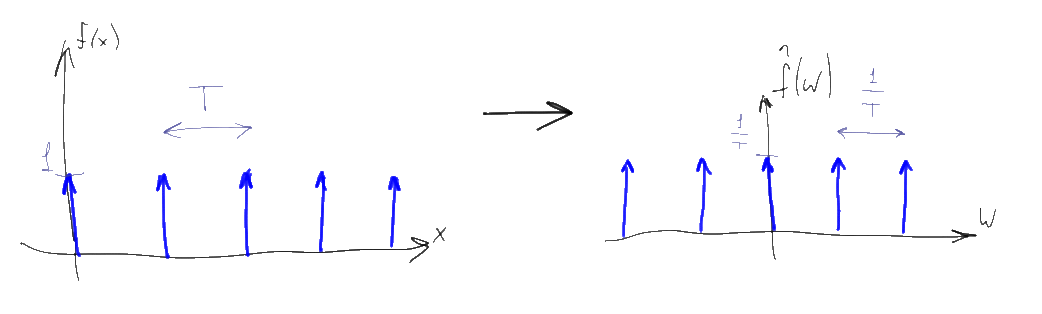
Вооружившись этими 7 свойствами, давайте посмотрим на математику “оцифровки” сигнала, позволяющую перевести непрерывный сигнал в последовательность цифр. Для этого нам понадобится взять функцию, известную как “гребенка Дирака”:
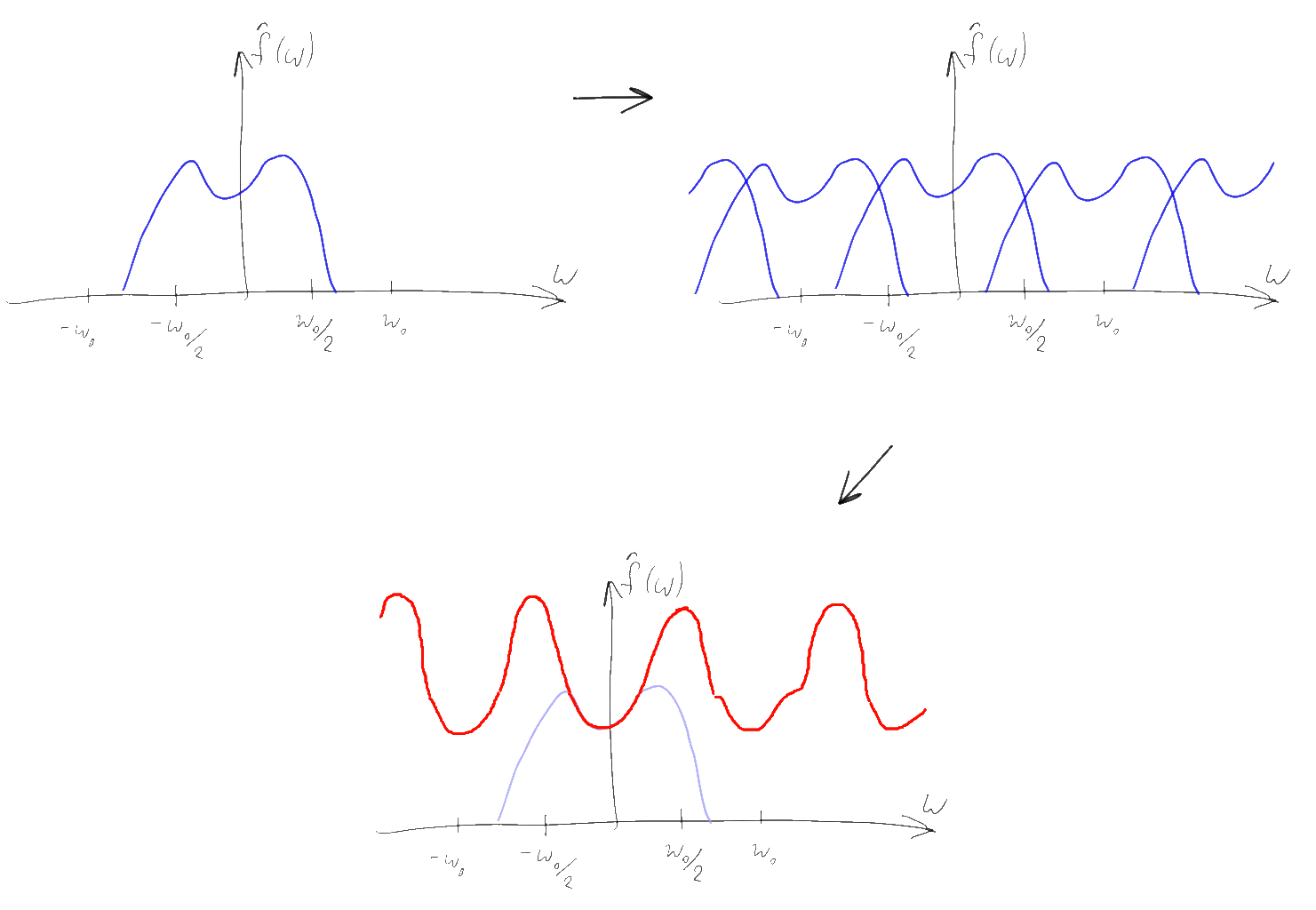
Гребенка Дирака — это просто периодическая последовательность дельта-функций с единичным коэффициентом, начинающаяся в нуле и идущая с шагом T. Для оцифровки сигналов, T выбирают по возможности малым числом, T<<1. Фурье-образ этой функции — тоже гребенка Дирака, только с гораздо большим шагом 1/T и несколько меньшим коэффициентом (1/T). С математической точки зрения, дискретизация сигнала по времени — это просто поточечное умножение исходного сигнала на гребенку Дирака. Значение 1/T при этом называют частотой дискретизации:
Вместо непрерывной функции после подобного перемножения получается последовательность дельта-импульсов определенной высоты. При этом согласно свойству 5 преобразования Фурье, спектр получившегося дискретного сигнала есть свертка исходного спектра с соответствующей гребенкой Дирака. Несложно понять, что исходя из свойств свертки, спектр исходного сигнала при этом как бы “копируется” бесконечное число раз вдоль оси частот с шагом 1/T, а затем суммируется.
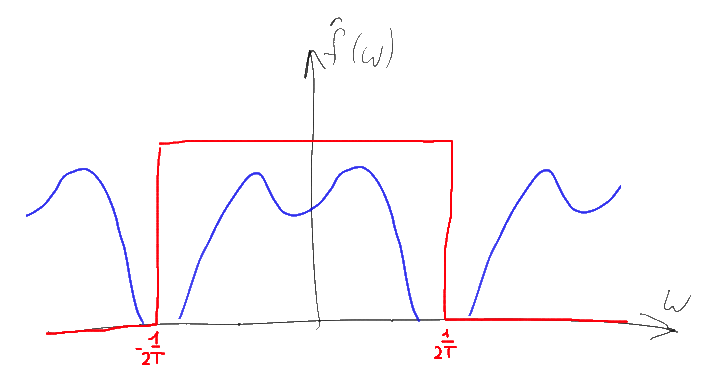
Заметим, что если исходный спектр имел конечную ширину и мы использовали достаточно большую частоту дискретизации, то копии исходного спектра не будут перекрываться, а следовательно и суммироваться друг с другом. Несложно понять что по подобному “свернутому” спектру будет легко восстановить исходный — достаточно будет просто взять компоненту спектра в районе нуля, “обрезав” лишние копии уходящие на бесконечность. Простейший способ это сделать — это домножить спектр на прямоугольную функцию, равную T в диапазоне -1/2T…1/2T и нулю — вне этого диапазона. Подобный Фурье-образ соответствует функции sinc(Tx) и согласно свойству 4, подобное умножение равнозначно свертке исходной последовательности дельта-функций с функцией sinc(Tx)
То есть с помощью преобразования Фурье мы получили способ легко восстановить исходный сигнал из дискретизированного по времени, работающий при условии что мы используем частоту дискретизации, по крайней мере вдвое (из-за наличия в спектре отрицательных частот) превышающую максимальную частоту присутствующую в исходном сигнале. Этот результат широко известен и называется “теорема Котельникова / Шеннона-Найквиста”. Однако, как несложно теперь (понимая доказательство) заметить, этот результат вопреки широко распространенному заблуждению определяет достаточное, но не необходимое условие для восстановления исходного сигнала. Все что нам требуется — это добиться того, чтобы интересующая нас часть спектра после дискретизации сигнала не накладывалась друг на друга и если сигнал достаточно узкополосный (имеет малую “ширину” ненулевой части спектра), то этого результата часто можно добиться и при частоте дискретизации намного ниже чем удвоенная максимальная частота сигнале. Подобная техника называется “undersampling” (субдискретизация, полосовая дискретизация) и довольно широко используется при обработке всевозможных радиосигналов. Например, если мы берем FM-радио действующее в полосе частот от 88 до 108 МГц, то для его оцифровки можно использовать АЦП с частотой всего 43.5 МГц вместо предполагающихся по теореме Котельникова 216 МГц. При этом, правда, понадобится качественный АЦП и хороший фильтр.
Замечу, что “дублирование” высоких частот частотами меньших порядков (алиасинг) — непосредственное свойство дискретизации сигнала, необратимо “портящее” результат. Поэтому если в сигнале в принципе могут присутствовать частоты высокого порядка (то есть практически всегда) перед АЦП ставят аналоговый фильтр, “отсекающий” все лишнее непосредственно в исходном сигнале (так как после дискретизации делать это уже будет поздно). Характеристики этих фильтров, как аналоговых устройств, неидеальны, поэтому некоторая “порча” сигнала при этом все равно происходит, и на практике из этого следует что наибольшие частоты в спектре, как правило, недостоверны. Чтобы уменьшить эту проблему, сигнал нередко сэмплируют с завышенной частотой дискретизации, ставя при этом входной аналоговый фильтр на меньшую полосу пропускания и используя только нижнюю часть теоретически доступного частотного диапазона АЦП.
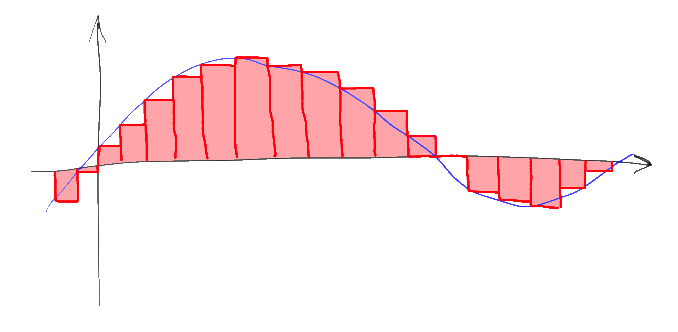
Еще одно распространенное заблуждение, кстати, — это когда сигнал на выходе ЦАП рисуют “ступеньками”. “Ступеньки” соответствуют свертке дискретизированной последовательности сигналов с прямоугольной функцией ширины T и высоты 1:
Спектр сигнала при таком преобразовании умножается на фурье-образ этой прямоугольной функции, а у подобной прямоугольной функции это снова sinc(w), “растянутый” тем сильнее, чем меньше ширина соответствующего прямоугольника. Спектр дискретизированного сигнала при подобном “ЦАП” поточечно умножается на этот спектр. При этом ненужные высокие частоты с “лишними копиями” спектра обрезаются не полностью, а верхняя часть “полезной” части спектра, напротив, ослабляется.
На практике так, естественно, никто не делает. Существует много разных подходов к построению ЦАП, но даже в наиболее близких по смыслу ЦАП взвешивающего типа прямоугольные импульсы в ЦАП напротив выбираются по возможности короткими (приближающимися к настоящей последовательности дельта-функций) чтобы избежать излишнего подавления полезной части спектра. “Лишние” частоты в получившемся широкополосном сигнале практически всегда гасят, пропуская сигнал через аналоговый фильтр низких частот, так что «цифровых ступенек» нет ни «внутри» преобразователя, ни, тем более, на его выходе.
Однако вернемся обратно к преобразованию Фурье. Описанное выше преобразование Фурье, примененное к заранее дискретизированной последовательности сигналов называется преобразованием Фурье дискретного времени (DTFT). Спектр получаемый подобным преобразованием всегда 1/T-периодичен, поэтому спектр DTFT полностью определяется её значениями на отрезке [0…1/T), поэтому часто этим отрезком спектр DTFT и ограничивают. При этом результат DTFT несмотря на то что это спектр дискретизированного сигнала — по-прежнему “аналоговая” функция. Кроме того, для “обычных” действительнозначных сигналов вторая половина этого спектра в силу свойства 6 зеркально повторяет левую половину, отраженную относительно частоты Найквиста 1/2T.
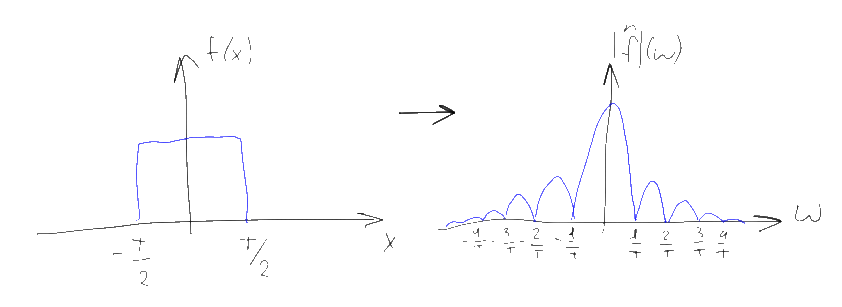
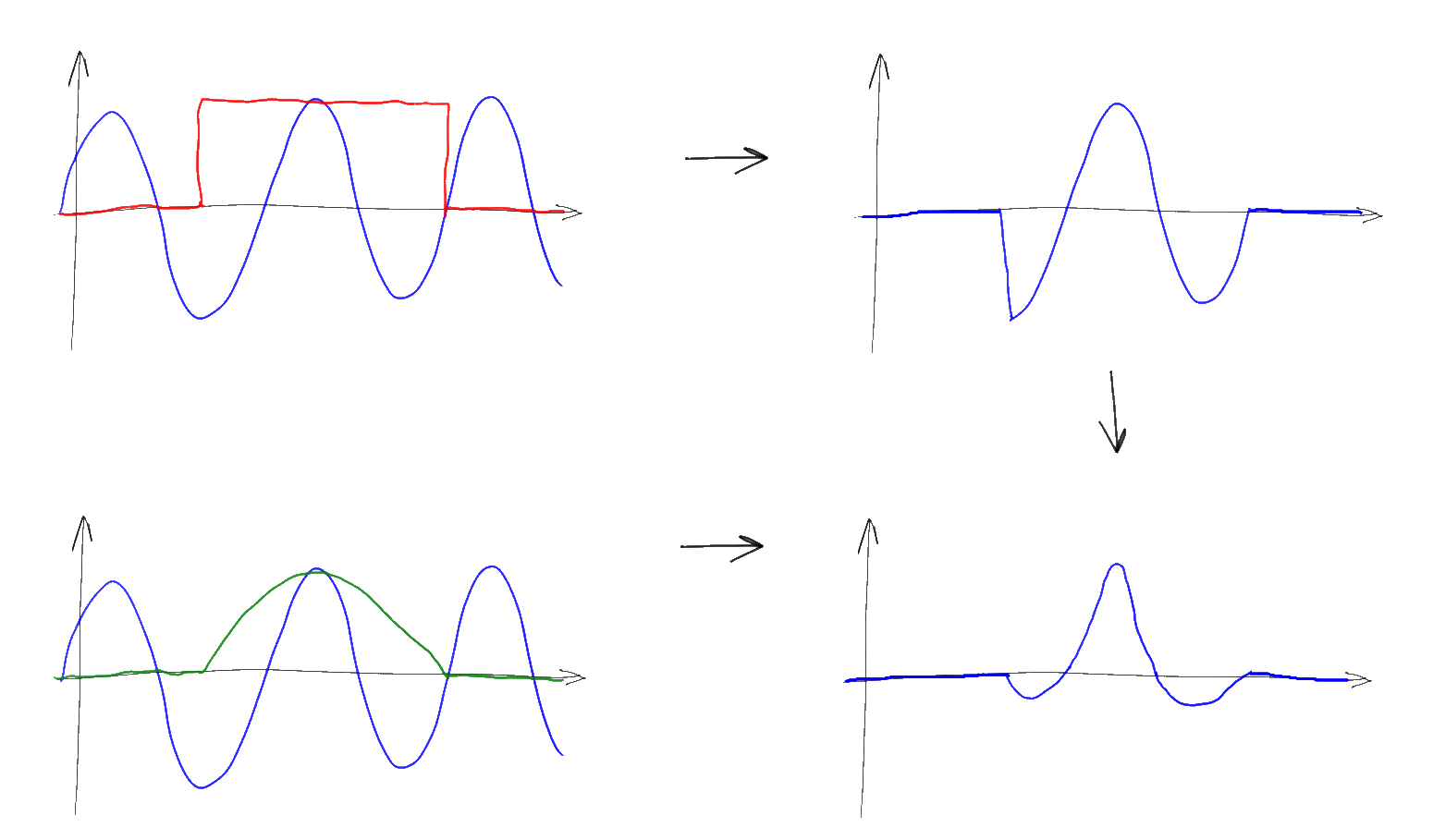
До сих пор мы предполагали что на вход наших преобразований поступает сигнал определенный от минус до плюс бесконечности. Однако реальные доступные нам сигналы всегда имеют конечную длину — что делать? Для решения этой проблемы в FT и DTFT конечный сигнал просто дополняют слева и справа на бесконечность нулями. Если исходный сигнал изначально был конечным (скажем, это отдельный импульс) и в преобразование Фурье он попал полностью, то этот подход напрямую дает желаемый результат. Однако часто «конечный» сигнал используемый для преобразования Фурье на самом деле является частью более длинного, возможно бесконечного сигнала, такого как, например, синусоида. В этом случае дополнение конечного отрезка нулями интерпретируют следующим образом: считают что исходный сигнал имеет бесконечно большую длину, но затем умножается на некоторую взвешивающую функцию — “окно”, обращающуюся в ноль вне доступного нам для измерения отрезка. В простейшем случае роль “окна” играет просто прямоугольная функция, соответствующая тому что мы просто дополняем конечный сигнал слева и справа бесконечным числом нулей. В более сложных — исходную последовательность умножают на весовые коэффициенты определяемые функцией “окна” и затем, опять же, дополняют нулями.
Пользуясь уже хорошо нам знакомым свойством 5, несложно сообразить, что при подобном умножении исходный сигнал прсто сворачивается со спектром функции окна. Например если мы пытаемся измерить спектр синусоиды (дельта-функцию), но ограничиваем интервал измерений прямоугольным окном, то в получившимся спектре на месте дельта-функции мы увидим спектр окна — т.е. Tsinc(T(x-f)):
В данном случае T — это длина интервала которым мы ограничили наш сигнал, так что чем длиннее будет входной сигнал — тем “уже” и ближе к истинной дельта-функции будет наблюдаемый нами спектр. Конечная “ширина” главного лепестка приводит к невозможности уверенно различать наличие в исходном сигнале синусоид близких друг к другу по частоте, а наличие “боковых лепестков” вносит небольшие искажения и в далеко расположенные частоты, мешая точному измерению амплитуды отдельных частот, особенно если нужно измерять спектр в областях небольшой амплитуды при наличии в спектре на порядок более мощных компонент. Этот эффект называют “спектральной утечкой” и полностью победить его для конечных сигналов невозможно, но чем длиннее интервал на котором измеряется сигнал — тем меньше влияние этой утечки. Выбором функции окна можно контролировать “ширину” этой утечки, либо концентрируя её вокруг главной частоты (сильно “размывая” спектр, но зато не мешая соседним частотам), либо размазывая её повсюду (размытие пиков уменьшается но сильно растет “шум” и как следствие — погрешность измерения амплитуды отдельных частот). Заметьте, что выбранная частота дискретизации в спектральной утечке почти не играет роли — короткий отрезок сигнала можно сэмплировать хоть на 10 ГГц, но это увеличит только количество поддающихся измерению частот, тогда как точность определения каждой отдельной частоты все равно останется низкой.
Интересным частным случаем является ситуация, в которой сигнал с набором дискретных частот nF дискретизируется на частоте mF, где m,n — целые числа. В этом случае нули “окна” и расположение дельта-функций в спектре в точности совпадают и хотя частоты все равно “размазываются”, но их амплитуда в точках mF совпадает с истинной — “шум” равен нулю. Это свойство позволяет доказать аналог теоремы Котельникова для дискретного преобразования Фурье, но на практике такие сигналы, к сожалению, фактически не встречаются.
Итак, со “входом” мы разобрались — из непрерывной функции бесконечной длины мы получили конечное число дискретных отсчетов, с которыми можем работать а взамен получили ограничения по ширине спектра и утечку частот. Однако “выход” DTFT по-прежнему является непрерывной функцией, работать с которой компьютеру проблематично. На практике эту проблему решают очень просто — полный отрезок [0,1/T) делят на k равных частей и считают DTFT в точках fi=i/kT, где i = 0,1,… k-1. Получившуюся конструкцию называют “дискретным преобразованием Фурье” (DFT).
Последнее преобразование удобно нормализовать, убрав из него T и вопросы связанные с выбором “окна”. Эту нормализованную запись часто используют в качестве определения DFT как преобразования последовательности из N комплексных чисел:
Прелесть преобразования Фурье записанного в такой форме — в том что сохраняя все достоинства DTFT, подобное DTF для “гладких” k (например, степеней двойки) можно вычислять чрезвычайно быстро, за время порядка k log(k). Соответствующие алгоритмы называют “быстрым преобразованием Фурье” (БПФ, FFT) и их, вообще говоря, существует несколько. С практической точки зрения, впрочем, их все можно рассматривать как “черные ящики”, получающие последовательность комплексных чисел на входе и выдающих последовательность комплексных чисел на выходе. Таким образом, работа с дискретизированным сигналом конечной длины сводится к тому, что этот сигнал вначале умножается на подходящую взвешивающую функцию, затем дополняется нужным числом нулей справа и передается в алгоритм БПФ.
Как интерпретировать получившийся результат? С учетом всего вышеизложенного,
- Получившиеся значения есть равномерная сетка отсчетов по спектру DTFT. Чем больше отсчетов — тем мельче сетка, тем подробнее виден спектр. Дописывая к известной последовательности нужное число нулей можно посчитать сколь угодно близкое приближение к непрерывному спектру
- Спектр DTFT задан на отрезке частот от 0 до 1/T (где 1/T — частота дискретизации) и периодически повторяется на бесконечность вне этого отрезка
- Этот спектр задан комплексными числами (парами действительных). Амплитуда определяется как модуль комплексного числа, фаза — как аргумент.
- Для действительнозначного входного сигнала, спектр в диапазоне 1/2T…1/T просто зеркально повторяет спектр 0…1/2T и не несет соответственно полезной нагрузки (для визуализации спектра его можно просто обрезать)
- Если исходный сигнал содержал частоты выше половины частоты дискретизации, то они будут отображены в более низкие частоты (возможно накладываясь поверх уже существующего сигнала этой частоты) — алиасинг
- В спектре всегда присутствует “спектральная утечка” определяющаяся выбранной взвешивающей “оконной функцией”. Чем длиннее исходный сигнал (до дополнения нулями!) — тем эта утечка меньше.
- Спектральная утечка ограничивает осмысленность расчета БПФ с большим дополнением нулями. Однако дополнение все же часто бывает полезным, поскольку, например, позволяет точнее определить максимум узкополосного синусоидального сигнала, если он не попадает точно в одну из частот вида k/T.
- Синусоиде амплитуды A в амплитудном спектре (при выбранной мной нормировке преобразования Фурье) соответствует значение A*N/2, за исключением нулевой частоты, которая не раскладывается на “плюс” и “минус” частоту и потому имеет амплитуду A*N, а также частоты Найквиста 1/2T в которой касаются в предельном случае друг друга отдельные копии спектра (там тоже будет A*N, но, в отличие от нуля в выход БПФ это значение не попадает да и достоверным в реальных схемах все равно никогда не является). Здесь N = T1/T0, где T1 — это длина исходного сигнала (она определяет коэффициент перед спектром «окна»), а T0 — длина одного периода дискретизации (она определяет коэффициент у гребенки Дирака) и по смыслу это, как несложно видеть, попросту число отсчетов в исходном сигнале (до его дополнения нулями)
Ну вот, в общем, и всё. Надеюсь преобразование Фурье и алгоритмы БПФ будут теперь для Вас простыми, понятными и приятными в обращении инструментами.
-
Понятие преобразования Фурье и обратного преобразования Фурье.
Начать изучение
-
Свойства преобразования Фурье абсолютно интегрируемых на R функций.
Начать изучение
-
Преобразование Фурье производной.
Начать изучение
-
Дифференцирование преобразования Фурье.
Начать изучение
Понятие преобразования Фурье и обратного преобразования Фурье.
Определение 1.
Пусть (f(x)) есть комплекснозначная функция действительного переменного. Тогда преобразование Фурье функции (f(x)) (оно обозначается через (F[f]) или (widehat{f})) определяется формулой
$$
widehat{f}(y) = F[f] = mbox{v.p.} intlimits_{-infty}^{+infty} f(x) e^{-iyx} dx.label{ref1}
$$
Здесь (displaystylembox{v.p.}intlimits_{-infty}^{+infty} f(x) dx) означает интеграл в смысле главного значения.
Определение 2.
Обратное преобразование Фурье (обозначается через (F^{-1}[f]) или (tilde{f})) определяется формулой
$$
tilde{f}(y) = F^{-1}[f] = mbox{v.p.} frac{1}{2pi} intlimits_{-infty}^{+infty} f(x) e^{iyx} dx.label{ref2}
$$
Предполагается, что интегралы eqref{ref1} и eqref{ref2} существуют. Если функция (f(x)) абсолютно интегрируема, то несобственные интегралы (displaystyleintlimits_{-infty}^{+infty} f(x) e^{-iyx} dx) и (displaystyleintlimits_{-infty}^{+infty} f(x) e^{iyx} dx) существуют и совпадают с соответствующими интегралами в смысле главного значения. Поэтому для абсолютно интегрируемых функций преобразование Фурье и обратное преобразование Фурье определяются как следующие несобственные интегралы:
$$
F[f] = intlimits_{-infty}^{+infty} f(x) e^{-iyx} dx.label{ref3}
$$
$$
F^{-1}[f] = frac{1}{2pi} intlimits_{-infty}^{+infty} f(x) e^{iyx} dx.label{ref4}
$$
Свойства преобразования Фурье абсолютно интегрируемых на R функций.
Лемма 1.
Преобразование Фурье абсолютно интегрируемой на (boldsymbol{R}) функции есть ограниченная и непрерывная на (boldsymbol{R}) функция.
Доказательство.
(circ) Так как функция (f(x)) абсолютно интегрируема на (boldsymbol{R}), то
$$
|widehat{f}(y)| = left|intlimits_{-infty}^{+infty} f(x) e^{-iyx} dxright| leq intlimits_{-infty}^{+infty} |f(x)| dx = C_{0}.
$$
и, следовательно, (widehat{f}(y)) есть ограниченная функция на (boldsymbol{R}).
Для доказательства непрерывности функции (widehat{f}(y)) запишем ее в виде
$$
widehat{f}(y) = intlimits_{-infty}^{+infty} f(x) cos yx dx-i intlimits_{-infty}^{+infty} f(x) sin yx dx = a(y)-ib(y)
$$
и заметим, что, в силу леммы 4 отсюда функции (a(y)) и (b(y)) непрерывны на (boldsymbol{R}). (bullet)
Теорема 1.
Если функция (f(x)) абсолютно интегрируема на (boldsymbol{R}) и имеет в каждой точке конечную производную (f'(x)), то справедливы формулы обращения
$$
F^{-1}[F[f]] = f,quad F[F^{-1}[f]] = f.label{ref5}
$$
Доказательство.
(circ) Так как выполнены условия теоремы 3 для интеграла Фурье, то справедливы равенства для этой теоремы, которые, применяя обозначения eqref{ref1} и eqref{ref2}, можно записать в виде eqref{ref5}. (bullet)
Преобразование Фурье производной.
Теорема 2.
Если непрерывная и абсолютно интегрируемая на (boldsymbol{R}) функция (f(x)) является кусочно гладкой на любом отрезке ([a, b] subset boldsymbol{R}), а функция (f'(x)) абсолютно интегрируема на (boldsymbol{R}), то
$$
F[f’] = iyF[f].label{ref6}
$$
Доказательство.
(circ) Для функции (f(x)) справедлива формула Ньютона-Лейбница
$$
f(x) = f(0)+intlimits_{0}^{x} f'(t) dt.nonumber
$$
Так как производная (f'(x)) абсолютно интегрируемая функция, то существует
$$
lim_{substack{x rightarrow +infty}} f(x) = f(0)+intlimits_{0}^{+infty} f'(x) dx = A.nonumber
$$
Покажем, что (A = 0). Если, например, (A > 0), то существует такое число (a in boldsymbol{R}), что при (x > a) выполнено неравенство (f(x) > displaystylefrac{1}{2}A), откуда по признаку сравнения следует, что интеграл (displaystyleintlimits_{a}^{+infty} f(x) dx) является расходящимся, что противоречит условию теоремы. Итак, (displaystylelim_{substack{x rightarrow +infty}} f(x) = 0).
Аналогично доказывается, что (displaystylelim_{substack{x rightarrow -infty}} f(x) = 0).
Применяя интегрирование по частям, получаем равенство
$$
F[f’] = intlimits_{-infty}^{+infty} f'(x) e^{-ixy} dx = left.f(x) e^{-ixy}right|_{-infty}^{+infty}+iy intlimits_{-infty}^{+infty} f(x) e^{-ixy} dx.nonumber
$$
Так как (|e^{-ixy}| = 1), то внеинтегральный член в правой части этого равенства обращается в нуль и, следовательно, справедливо равенство eqref{ref6}. (bullet)
Следствие.
Если функции (f(x), f'(x), ldots, f^{(k)}(x)) непрерывны и абсолютно интегрируемы на (boldsymbol{R}), то
$$
F[f^{(k)}] = (iy)^{k}F[f].label{ref7}
$$
(circ) Формула eqref{ref7} доказывается по индукции с использованием формулы eqref{ref6}. (bullet)
Дифференцирование преобразования Фурье.
Теорема 3.
Если функция (f(x)) непрерывна на (boldsymbol{R}), а функции (f(x)) и (xf(x)) абсолютно интегрируемы на (boldsymbol{R}), то функция (widehat{f}(y) = F[f]) имеет на (boldsymbol{R}) непрерывную производную, причем
$$
widehat{f}'(y) = frac{d}{dy} (F[f]) = F[(-ix)f(x)].label{ref8}
$$
Доказательство.
(circ) Дифференцируя интеграл eqref{ref3} по параметру (y), получаем равенство
$$
frac{d}{dy} (F[f]) = frac{d}{dy} intlimits_{-infty}^{+infty} f(x) e^{-ixy} dx = intlimits_{-infty}^{+infty} (-ix)f(x) e^{-ixy} dx.label{ref9}
$$
Обоснование законности дифференцирования под знаком интеграла сводится к проверке условий теоремы о дифференцировании несобственного интеграла по параметру. Интеграл (displaystyleintlimits_{-infty}^{+infty} (-ix)f(x) e^{-ixy} dx) сходится равномерно по параметру (y) на (boldsymbol{R}) по признаку Вейерштрасса, так как (|(-ix)f(x)e^{-ixy}| = |xf(x)|), а интеграл (displaystyleintlimits_{-infty}^{+infty} |xf(x)| dx) сходится. (bullet)
Следствие.
Если (f(x)) есть непрерывная на (boldsymbol{R}) функция, а функции (f(x), x f(x), ldots, x^{n}f(x)) абсолютно интегрируемы на (boldsymbol{R}), то
$$
frac{d^{k}}{dy^{k}} (F[f]) = F[(-ix)^{k}f(x)], k = overline{1, n}.nonumber
$$
Иногда функцию (f(x)) называют оригиналом, а функцию (widehat{f}(y) = F[f]) ее изображением по Фурье. Из теорем 2 и 3 следует, что операции дифференцирования оригинала соответствует операция умножения изображения на независимую переменную (iy), а операции умножения оригинала на независимую переменную (-ix) соответствует операция дифференцирования изображения. Эти свойства преобразования Фурье являются основой операционных методов решения дифференциальных уравнений.
Пример 1.
Найти изображение по Фурье функции (e^{-x^{2}/2}).
Решение.
(vartriangle) Пусть
$$
I(y) = F[e^{-x^{2}/2}] = intlimits_{-infty}^{+infty} f(x) e^{-(x^{2}/2)-ixy} dx.label{ref10}
$$
Дифференцируя интеграл eqref{ref10} по параметру (y), получаем
$$
I'(y) = -i intlimits_{-infty}^{+infty} xe^{-(x^{2}/2)-ixy} dx = i intlimits_{-infty}^{+infty} (-iy-x+iy) e^{-(x^{2}/2)-ixy} dx =\= i intlimits_{-infty}^{+infty} left(frac{d}{dx} e^{-(x^{2}/2)-ixy}right) dx-y intlimits_{-infty}^{+infty} e^{-(x^{2}/2)-ixy} dx =\= i e^{-(x^{2}/2)-ixy}|_{-infty}^{+infty}-yI(y) = -yI(y),nonumber
$$
откуда
$$
frac{I'(y)}{I(y)} = -y, frac{d}{dy}(ln I(y)) = -y, ln I(y) = -frac{y^{2}}{2}+ln c, I(y) = ce^{-y^{2}/2},nonumber
$$
$$
c = I(0) = intlimits_{-infty}^{+infty} e^{-x^{2}/2} dx = sqrt{2} intlimits_{-infty}^{+infty} e^{-t^{2}} dt = 2sqrt{2} intlimits_{-infty}^{+infty} e^{-t^{2}} dt =\=2sqrt{2} frac{sqrt{pi}}{2} = sqrt{2pi}, I(y) = sqrt{2pi}e^{-y^{2}/2}.nonumber
$$
Здесь было использовано выражение для интеграла Эйлера Пуасcона (displaystyleintlimits_{-infty}^{+infty} e^{-t^{2}} dt = frac{1}{2}sqrt{pi}).
Таким образом,
$$
F[e^{-x^{2}/2}] = sqrt{2pi} e^{-y^{2}/2}. blacktrianglelabel{ref11}
$$
Пример 2.
Доказать, что для любого (t > 0) справедлива формула
$$
Fleft[frac{1}{2sqrt{pi t}} e^{-x^{2}/(4t)}right] = e^{-y^{2}t}.nonumber
$$
Решение.
(vartriangle) Используя результат примера 1, получаем
$$
Fleft[frac{1}{2sqrt{pi t}} e^{-x^{2}/(4t)}right] = frac{1}{2sqrt{pi t}} intlimits_{-infty}^{+infty} e^{-(x^{2}/(4t))-ixy} dx =\=frac{1}{sqrt{2pi}} intlimits_{-infty}^{+infty} e^{-(xi^{2}/2)-ixi(sqrt{2t}y)} dxi = frac{1}{sqrt{2pi}} I(y sqrt{2t}) = e^{-y^{2}t}. blacktrianglenonumber
$$
Преобразование Фурье – одно из базовых понятий в обработке сигналов и анализе данных. Но что оно означает? Геометрическая интерпретация.
Возьмём классическую задачу – работу со звуком. Теперь добавим конкретики.
Ваш друг приносит запись своего живого выступления. И это очень удачное выступление. Но! Хотя запись делали на хороший микрофон, в ней всё равно присутствует шум. Друг просит помочь убрать его или хотя бы уменьшить.
Здесь и пригодится знание преобразования Фурье.
Что такое звук в математическом смысле?
Отдельная нота – это гармонический сигнал с определённой частотой и амплитудой.
Как правило, мелодию, речь или иной звуковой сигнал можно представить как сумму гармонических сигналов. Шумом в таком случае мы называем слагаемые, соответствующие любым нежелательным звукам.
Преобразование Фурье позволяет разложить исходный сигнал на гармонические составляющие, что потребуется для выделения шумов.
Запишем определение:
Здесь g(t) – это исходный сигнал (в нашем случае запись друга). В контексте преобразования Фурье его называют оригиналом. G(f) – изображение по Фурье, а параметром f выступает частота.
Возможно, вам уже знакомо это определение. Но знаете ли вы, как происходит это преобразование? Если бы увидели его впервые, поняли бы, как с его помощью анализировать исходный сигнал?
Геометрическая интерпретация преобразования Фурье
Грант Сандерсон предлагает геометрический аналог преобразования Фурье. За несколько графических переходов от исходного сигнала к изображению каждая из компонент определения обретает смысл, а само преобразование получает новое геометрическое прочтение.
В дальнейшем обсуждении предполагается, что вы знакомы с векторами, интегрированием и понятием комплексного числа. Если каких-то знаний вам всё-таки не хватает, ознакомьтесь с материалами из нашей подборки по вузовской математике.
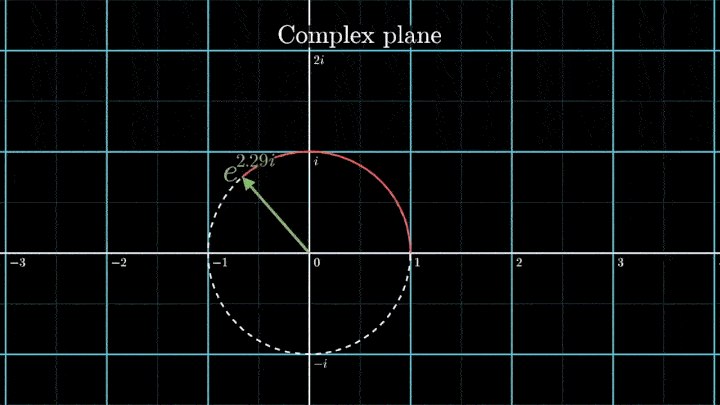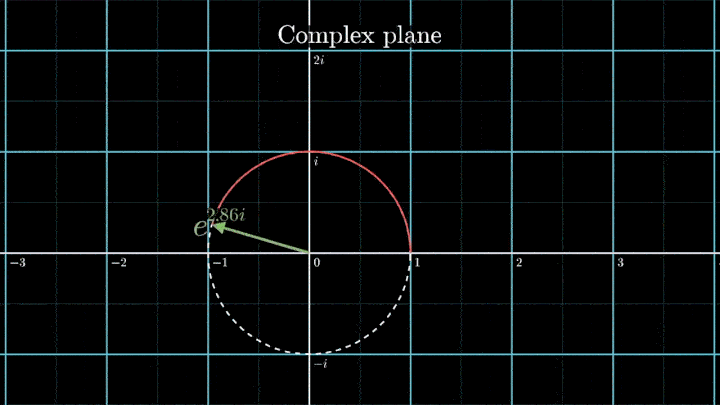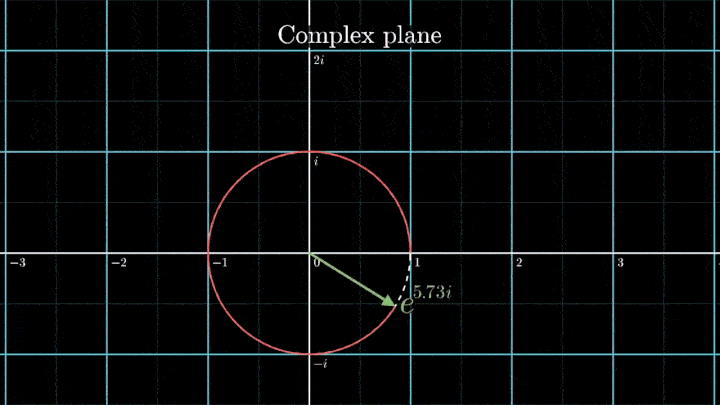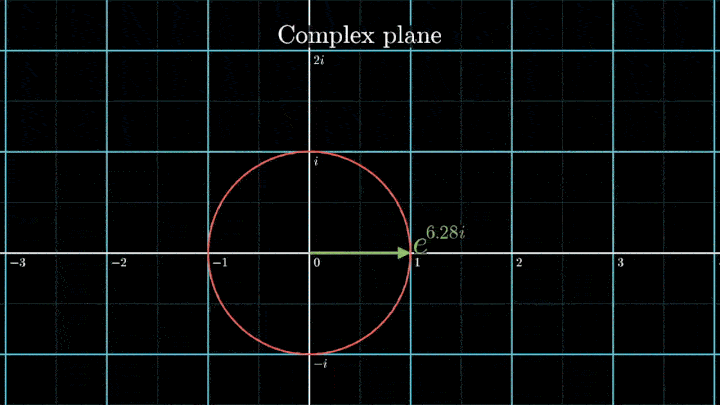
1. Наматываем сигнал
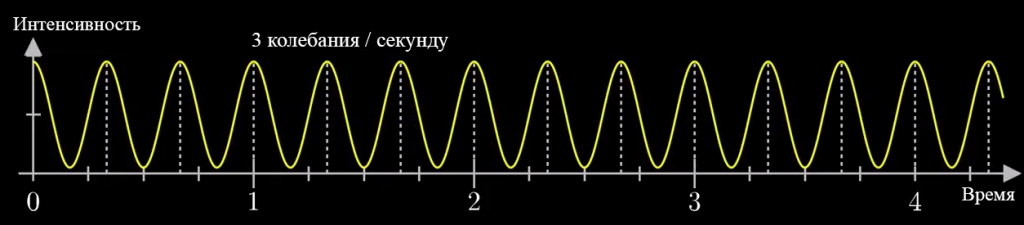
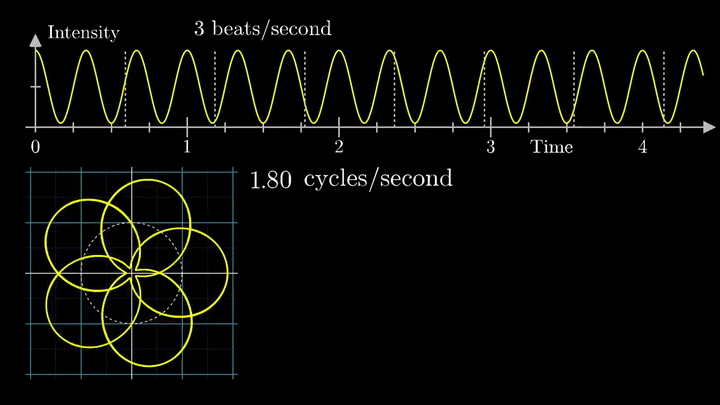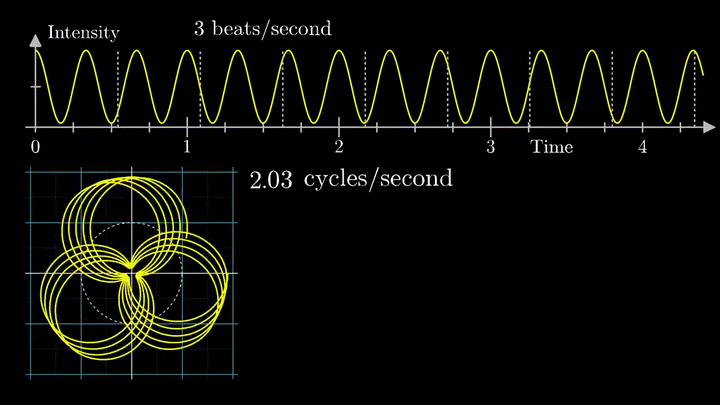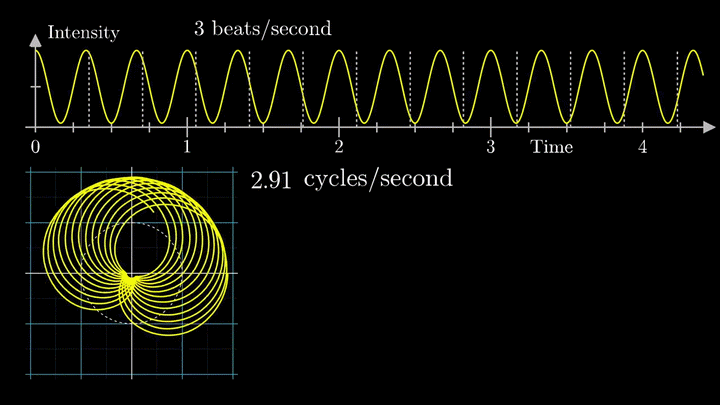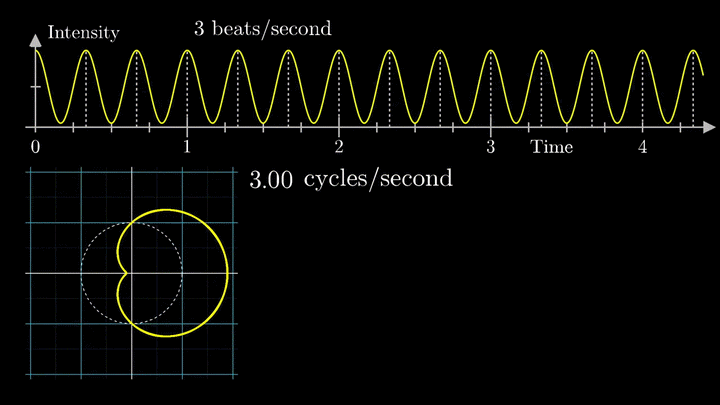
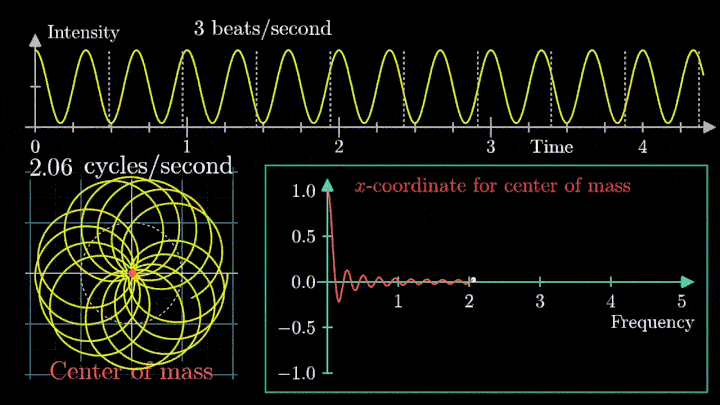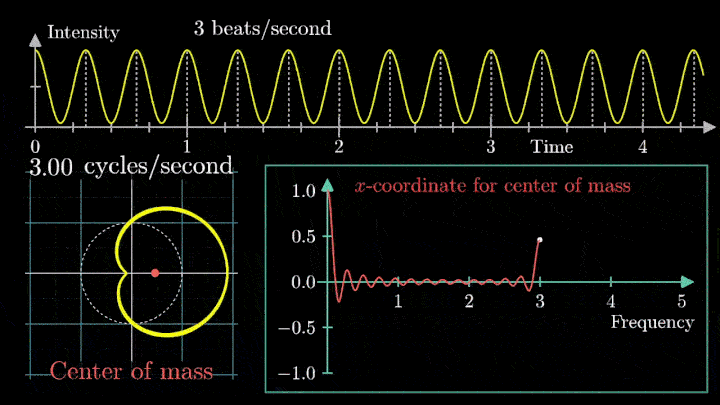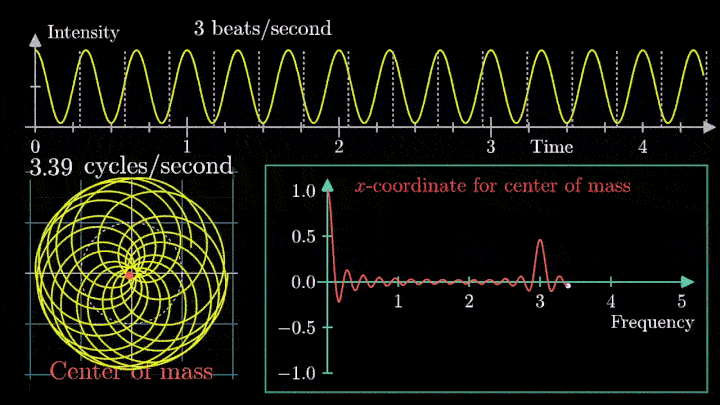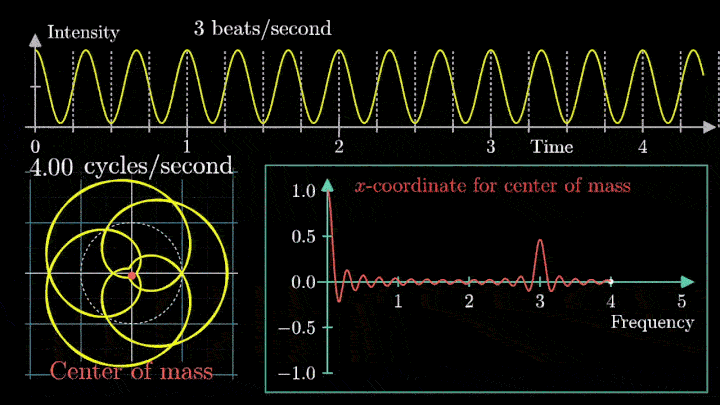
Давайте начнём с самого простого случая. Рассмотрим гармонический сигнал, совершающий 3 колебания в секунду (f0 = 3с-1):
g(t) = 1 + cos (6πt).
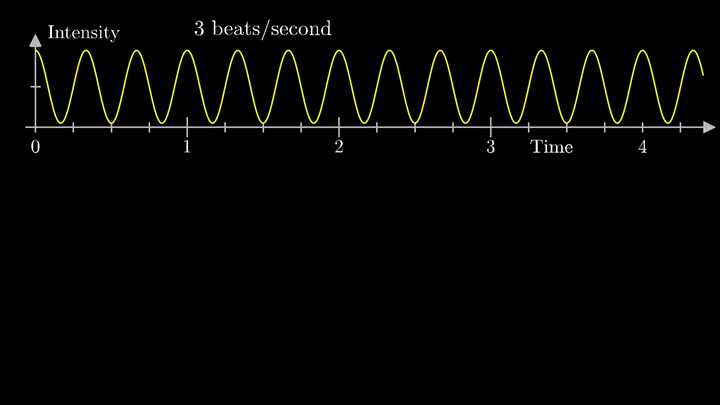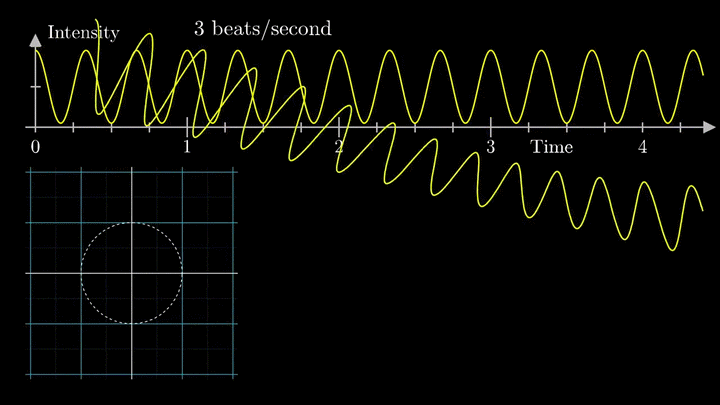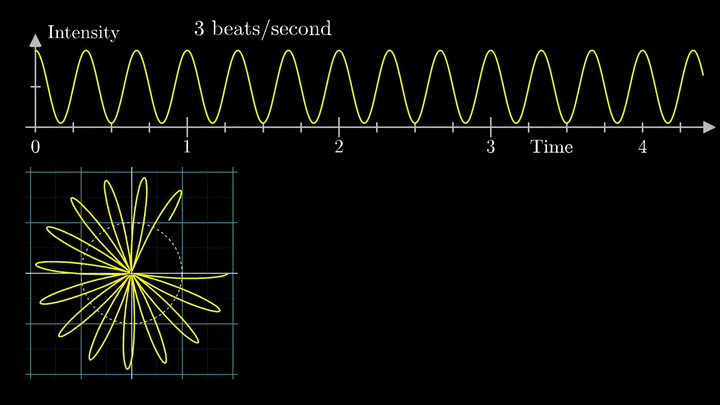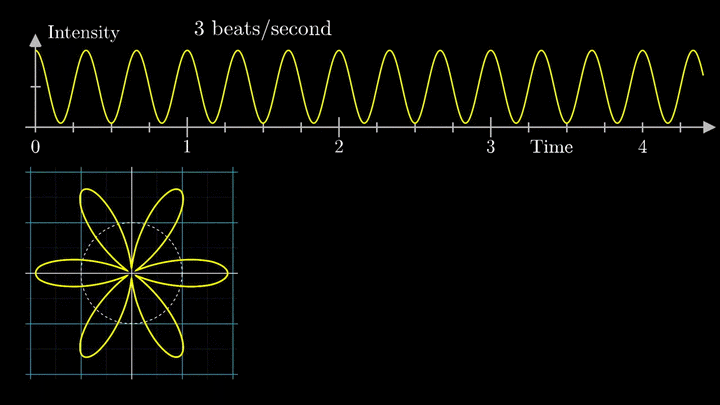
Отобразим g(t) на комплексную плоскость. Для этого введём радиус-вектор, который равномерно вращается по часовой стрелке. Его длина в каждый момент времени равна модулю значения сигнала, а частота вращения выбирается произвольным образом.
Теперь построим траекторию движения конца вектора, совершающего полный оборот за две секунды, или, другими словами, с частотой вращения fВ = 0.5 об/с.
Выглядит, будто мы намотали исходный сигнал на начало координат. В минимумах сигнала полученная «намотка» сливается с началом координат, а при приближении к максимумам – отклоняется.
Пока выглядит не особо информативно, не так ли?
А теперь увеличим частоты намотки.
Сначала график распределяется довольно симметрично относительно начала координат до частоты вращения fВ = 3 об/с. Затем максимумы резко смещаются в правую полуплоскость, а намотка перестаёт напоминать узор спирографа.
2. Ищем центр масс
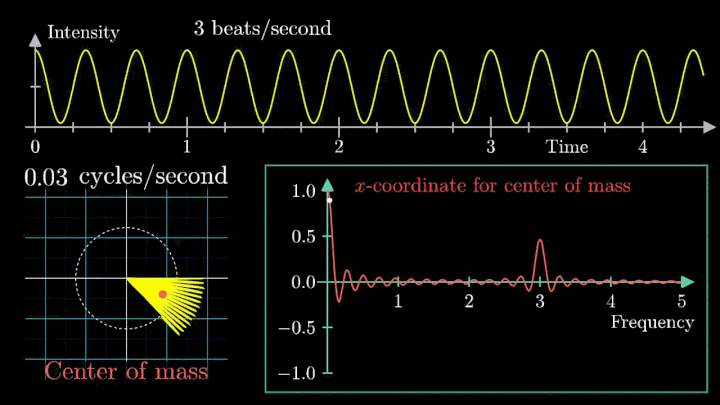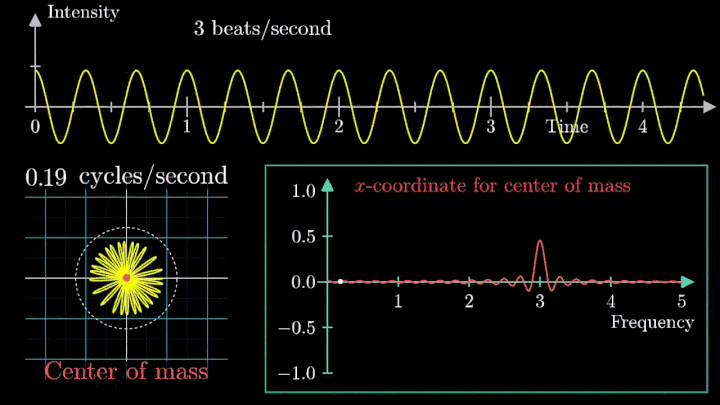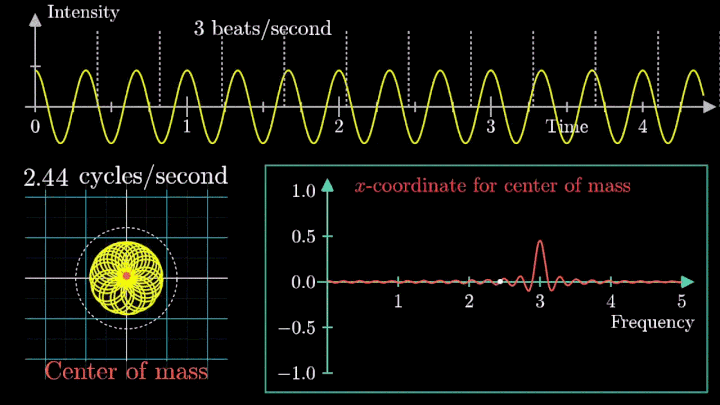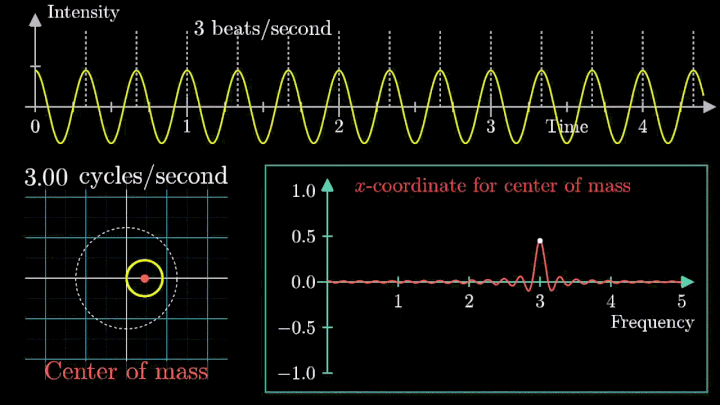
Посмотрим внимательнее, что происходит. В качестве характеристики намотки возьмём усреднённое значение всех её точек – центр масс (отметим его оранжевым цветом).
Строим зависимость положения центра масс от частоты намотки. Сейчас нам достаточно рассмотреть х-кординату, но в дальнейшем для определения преобразования Фурье потребуются обе координаты.
Мы видим два пика: в точках fВ = 0 об/с и fВ = 3 об/с. На основании такого поведения центра масс уже можно судить о частоте исходного сигнала (он колеблется с f = 3с-1).
Тогда что означает всплеск на низких частотах?
3. Анализируем влияние смещения
Возможно, вы обратили внимание, что рассматриваемый нами сигнал смещён на единицу. Сдвиг был введён для наглядности, но именно он приводит к усложнению поведения центра масс.
При нулевой частоте всё отображение сигнала на комплексной плоскости располагается на оси абсцисс. На малых частотах намотка по-прежнему группируется в правой полуплоскости.
Как только мы убираем сдвиг, т. е. берём сигнал вида g(t) = cos (6πt), намотка при низких частотах сдвигается влево по оси абсцисс.
Построение радиус-вектора остаётся аналогичным. Его длина равна модулю значения сигнала, направление вращения – положительное. Но при смене знака g(t) направление вектора меняется на противоположное.
Сейчас вы увидите, как меняется намотка и х-координата центра масс несмещённого сигнала.
Таким образом, на графике остался только один резкий скачок.
Это важный момент при использовании преобразования Фурье: линейный тренд и смещение проявляются на низких частотах, потому их исключают из исходного сигнала.
4. Выделяем частоты полигармонического сигнала
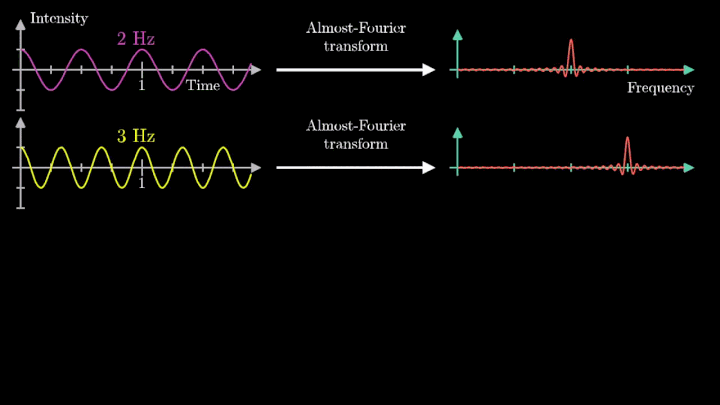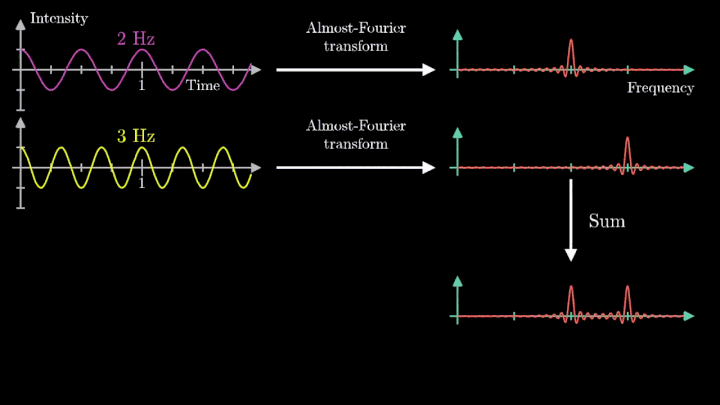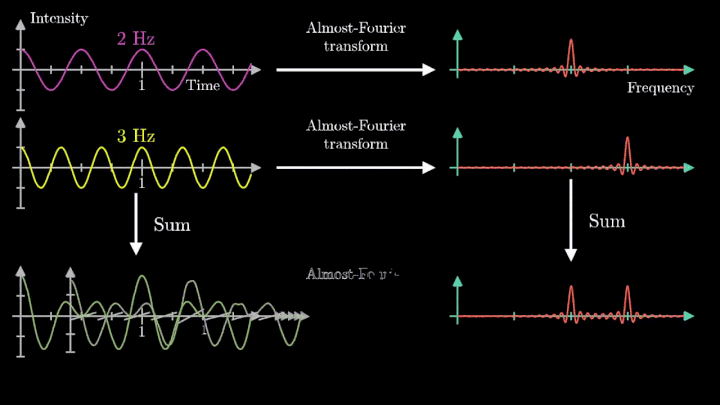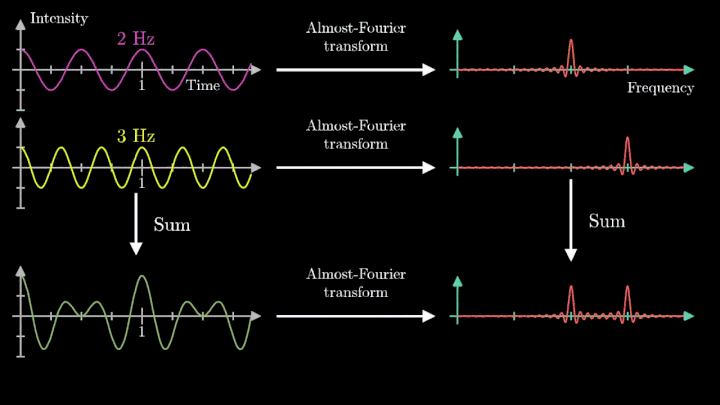
Теперь рассмотрим сумму двух гармонических сигналов с частотой колебаний f1 = 2 с-1 и f2 = 3 с-1. Проделаем с ней те же операции – «намотаем» возле начала координат, и, меняя частоту вращения, построим график х-координаты центра масс.
Мы наблюдаем два пика в точках fВ = 2 об/с и fВ = 3 об/с, что соответствует частотному составу исходной суммы.
Отметим ещё один интересный факт, верный как для х-координаты, так и для преобразования Фурье. Преобразование для суммы сигналов и сумма преобразований сигналов имеют один и тот же вид. Т. е. преобразование Фурье линейно.
Таким образом, этот подход позволяет определить частоту колебаний как моно-, так и полигармонического сигнала. Осталось математически описать процедуру вычисления центра масс намотки.
Вывод преобразования Фурье
В самом начале рассмотрения мы отобразили исходный сигнал на комплексную плоскость. Такой выбор не случаен – это позволяет рассматривать точки на плоскости как комплексные числа и использовать формулу Эйлера для описания намотки:
eiφ=cos(φ)+i·sin(φ).
Геометрически это соотношение означает, что при любом φ точка eiφ на комплексной плоскости лежит на единичной окружности.
Построим радиус-вектор eiφ при разных значениях φ.
При изменении φ на 2π вектор проходит полный оборот против часовой стрелки, так как 2π – длина единичной окружности. Чтобы задать скорость вращения вектора, показатель степени домножаем на ft, а для смены направления вращения – на -1.
Тогда намотка сигнала g(t) описывается как g(t)e-2πift.
Теперь вычисляем центр масс. Для этого отметим N произвольных точек на графике намотки и вычислим среднее:
Если мы будем увеличивать количество рассматриваемых точек, придём к предельному случаю:
где t1 и t2 – границы интервала, на котором рассматривается сигнал.
Выражение перед интегралом представляет собой масштабирующий коэффициент, но не отражает поведение центра масс. Потому его можно отбросить.
Полученное выражение и будет являться преобразованием Фурье с той разницей, что в общем виде интегрирование задаётся на интервале от -∞ до +∞.
Такой переход к бесконечному интервалу означает, что мы не накладываем никаких ограничений на длительность рассматриваемого сигнала.
Применение преобразования Фурье для фильтрации
Теперь, говоря о преобразовании Фурье, вы можете представлять его геометрическую интерпретацию – намотку сигнала на комплексную плоскость и вычисление центр масс.
При этом частота намотки f становится входным параметром для изображения по Фурье. Центр масс выступает оценкой, насколько хорошо соотносится (коррелирует) параметр f с присутствующими в сигнале частотами.
После того, как вы найдёте в принесённой другом записи все частотные компоненты, вам останется только вычесть их из изображения и применить обратное преобразование Фурье.
Мы что-то упустили? Напишите об этом в комментариях 
From Wikipedia, the free encyclopedia
In mathematics, the Fourier inversion theorem says that for many types of functions it is possible to recover a function from its Fourier transform. Intuitively it may be viewed as the statement that if we know all frequency and phase information about a wave then we may reconstruct the original wave precisely.
The theorem says that if we have a function 
then
In other words, the theorem says that
This last equation is called the Fourier integral theorem.
Another way to state the theorem is that if 

The theorem holds if both 


Statement[edit]
In this section we assume that 
Furthermore, we assume that the Fourier transform is also integrable.
Inverse Fourier transform as an integral[edit]
The most common statement of the Fourier inversion theorem is to state the inverse transform as an integral. For any integrable function 

Then for all 
Fourier integral theorem[edit]
The theorem can be restated as
If f is real valued then by taking the real part of each side of the above we obtain
Inverse transform in terms of flip operator[edit]
For any function 

Then we may instead define
It is immediate from the definition of the Fourier transform and the flip operator that both 



Since 

Two-sided inverse[edit]
The form of the Fourier inversion theorem stated above, as is common, is that
In other words, 
Since 


Alternatively, this can be seen from the relation between 
Conditions on the function[edit]
When used in physics and engineering, the Fourier inversion theorem is often used under the assumption that everything «behaves nicely». In mathematics such heuristic arguments are not permitted, and the Fourier inversion theorem includes an explicit specification of what class of functions is being allowed. However, there is no «best» class of functions to consider so several variants of the Fourier inversion theorem exist, albeit with compatible conclusions.
Schwartz functions[edit]
The Fourier inversion theorem holds for all Schwartz functions (roughly speaking, smooth functions that decay quickly and whose derivatives all decay quickly). This condition has the benefit that it is an elementary direct statement about the function (as opposed to imposing a condition on its Fourier transform), and the integral that defines the Fourier transform and its inverse are absolutely integrable. This version of the theorem is used in the proof of the Fourier inversion theorem for tempered distributions (see below).
Integrable functions with integrable Fourier transform[edit]
The Fourier inversion theorem holds for all continuous functions that are absolutely integrable (i.e. 
A slight variant is to drop the condition that the function 



Integrable functions in one dimension[edit]
- Piecewise smooth; one dimension
If the function is absolutely integrable in one dimension (i.e. 
Then for all 
i.e. 




A higher-dimensional analogue of this form of the theorem also holds, but according to Folland (1992) is «rather delicate and not terribly useful».
- Piecewise continuous; one dimension
If the function is absolutely integrable in one dimension (i.e. 
The conclusion of the theorem is then the same as for the piecewise smooth case discussed above.
- Continuous; any number of dimensions
If 

The conclusion is now simply that for all 
- No regularity condition; any number of dimensions
If we drop all assumptions about the (piecewise) continuity of 
for almost every 
Square integrable functions[edit]
In this case the Fourier transform cannot be defined directly as an integral since it may not be absolutely convergent, so it is instead defined by a density argument (see the Fourier transform article). For example, putting
we can set 

in the mean squared norm. In one dimension (and one dimension only), it can also be shown that it converges for almost every x∈ℝ— this is Carleson’s theorem, but is much harder to prove than convergence in the mean squared norm.
Tempered distributions[edit]
The Fourier transform may be defined on the space of tempered distributions 


where 


Relation to Fourier series[edit]
When considering the Fourier series of a function it is conventional to rescale it so that it acts on ![[0,2pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/348d40bf3f8b7e1c00c4346440d7e2e4f0cc9b91)


![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
The Fourier inversion theorem is analogous to the convergence of Fourier series. In the Fourier transform case we have
In the Fourier series case we instead have
In particular, in one dimension 


Applications[edit]
Some problems, such as certain differential equations, become easier to solve when the Fourier transform is applied. In that case the solution to the original problem is recovered using the inverse Fourier transform.
In applications of the Fourier transform the Fourier inversion theorem often plays a critical role. In many situations the basic strategy is to apply the Fourier transform, perform some operation or simplification, and then apply the inverse Fourier transform.
More abstractly, the Fourier inversion theorem is a statement about the Fourier transform as an operator (see Fourier transform on function spaces). For example, the Fourier inversion theorem on 

Properties of inverse transform[edit]
The inverse Fourier transform is extremely similar to the original Fourier transform: as discussed above, it differs only in the application of a flip operator. For this reason the properties of the Fourier transform hold for the inverse Fourier transform, such as the Convolution theorem and the Riemann–Lebesgue lemma.
Tables of Fourier transforms may easily be used for the inverse Fourier transform by composing the looked-up function with the flip operator. For example, looking up the Fourier transform of the rect function we see that
so the corresponding fact for the inverse transform is
Proof[edit]
The proof uses a few facts, given 

- If
and
, then
.
- If
and
, then
.
- For
, Fubini’s theorem implies that
.
- Define
; then
.
- Define
. Then with
denoting convolution,
is an approximation to the identity: for any continuous
and point
,
(where the convergence is pointwise).
Since, by assumption, 
Define 
Using fact 3 on 


the convolution of 

Putting together the above we have shown that
Notes[edit]
- ^ An operator is a transformation that maps functions to functions. The flip operator, the Fourier transform, the inverse Fourier transform and the identity transform are all examples of operators.
References[edit]
- Folland, G. B. (1992). Fourier Analysis and its Applications. Belmont, CA, USA: Wadsworth. ISBN 0-534-17094-3.
- Folland, G. B. (1995). Introduction to Partial Differential Equations (2nd ed.). Princeton, USA: Princeton Univ. Press. ISBN 978-0-691-04361-6.
- ^ «DMat0101, Notes 3: The Fourier transform on L^1». I Woke Up In A Strange Place. 2011-03-10. Retrieved 2018-02-12.


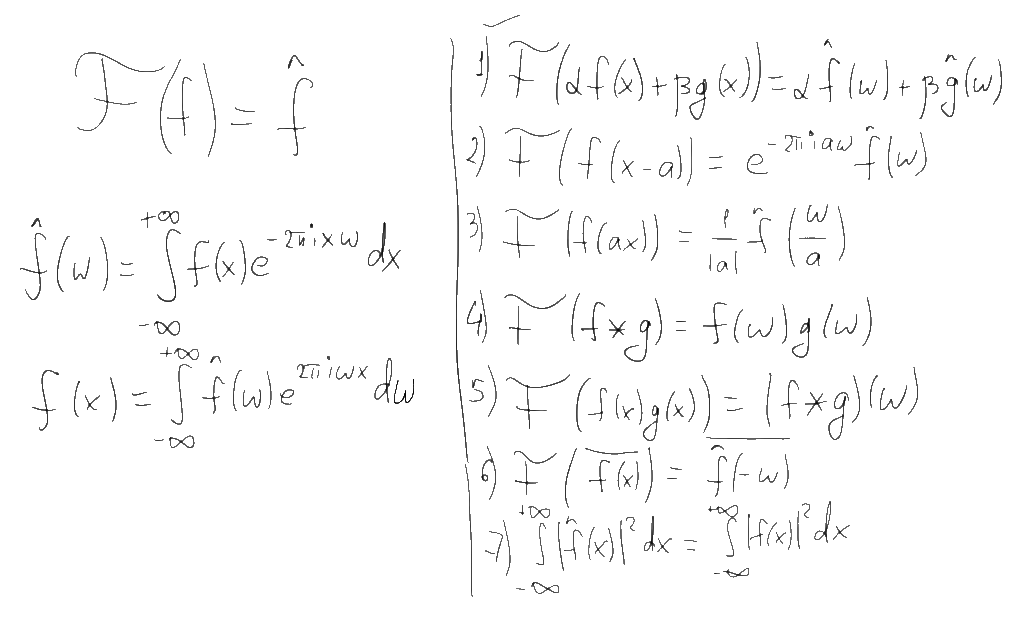






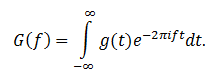
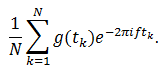
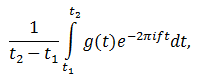














![{displaystyle {begin{aligned}f&={mathcal {F}}^{-1}({mathcal {F}}f)(x)\[6pt]&=int _{mathbb {R} ^{n}}int _{mathbb {R} ^{n}}e^{2pi ixcdot xi },e^{-2pi iycdot xi },f(y),dy,dxi \[6pt]&=int _{mathbb {R} ^{n}}int _{mathbb {R} ^{n}}e^{-2pi ixcdot zeta },e^{2pi iycdot zeta },f(y),dy,dzeta \[6pt]&={mathcal {F}}({mathcal {F}}^{-1}f)(x).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7658a684b311374b97442cd907857473ebd4f71)












![fcolon[0,1]^ntomathbb{C},quadhat fcolonmathbb{Z}^ntomathbb{C},](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd3860e1a4e6bdcd7e705f6ab489c86638d4a851)
![hat f(k):=int_{[0,1]^n} e^{-2pi iycdot k} , f(y),dy,](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbacfb859d551e558f0358273ca1598d6c7e064)





















