Как найти обратную функцию для квадратичной функции - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Обратные функции помогают решить многие математические задачи. Умение найти обратную функцию очень полезно. Однако в случае квадратичных функций эта процедура может оказаться довольно сложной. Во-первых, следует точно записать уравнение и установить область определения и область значений функции. Затем необходимо выбрать один из трех методов нахождения обратной функции. Выбор метода зависит в основном от ваших предпочтений.

1
2

Объедините одинаковые члены, чтобы упростить уравнение. Начальное уравнение может содержать несколько схожих слагаемых со знаком «плюс» или «минус». Прежде всего следует объединить их, чтобы упростить уравнение и записать его в стандартном виде ${displaystyle y=ax^{2}+c}$ .
3

Определите область определения и область значений упрощенной функции. Область определения функции включает в себя те значения независимой переменной x, при которых имеются действительные решения. Этим величинам переменной x соответствует область значений функции, в которой она принимает значения y. Чтобы найти область определения функции, посмотрите, при каких значениях x невозможно получить конкретную величину. Все другие значения переменной x соответствуют области определения данной функции. Чтобы определить область значений функции, проверьте, как она ведет себя в граничных точках.^[1]
4

Поменяйте местами x и y. Запишите то же самое уравнение таким образом, чтобы вместо x стоял y, и наоборот. В результате вы получите обратную функцию.^[3]
5

Выразите обратную функцию через y. С помощью алгебраических действий выделите переменную y — при этом внимательно выполняйте одни и те же операции по обе стороны знака равенства. В случае нашего примера ${displaystyle x=2y^{2}+2}$ получится следующее:^[4]
6
Найдите область определения и область значений обратной функции. Как вы делали раньше с прямой функцией, установите область определения и область значений обратной функции. Из двух возможных решений следует выбрать то, для которого область определения и область значений соответствуют области значений и области определения исходной функции.^[5]
- Рассмотрим наш пример с решениями ± ${displaystyle {sqrt {frac {x-2}{2}}}=y}$ . Поскольку квадратный корень не определен для отрицательных чисел, дробь ${displaystyle {frac {x-2}{2}}}$ должна быть положительной. Таким образом, для допустимых значений x (области определения) должно выполняться условие x≥2. Исходя из этого, y (область значений) должен удовлетворять условию y≥0 для положительных значений квадратного корня, либо y≤0 для отрицательных значений. Чтобы определить обратную функцию, вспомним, что первоначально для области определения мы установили x≥0. Таким образом, правильным решением являются положительные значения квадратного корня.
- Сравните область определения и область значений обратной функции с аналогичными областями прямой функции. Для первоначальной функции ${displaystyle y=2x^{2}+2}$ для области определения выполняется условие x≥0, а для области значений — y≥2. В случае обратной функции эти условия меняются местами, то есть области определения соответствуют x≥2, а для области значений выполняется условие y≥0.
7

Проверьте, правильно ли вы нашли обратную функцию. Чтобы убедиться, что вы все сделали правильно, выберите любое значение переменной x, подставьте его в начальное уравнение и найдите y. После этого подставьте найденную величину y вместо x в обратную функцию и посмотрите, получится ли первоначальное значение. Если вы получите выбранное значение, обратная функция найдена правильно.^[6]

Реклама

1
Запишите квадратичную функцию в подходящей форме. Чтобы найти обратную функцию, для начала следует записать уравнение в виде $f(x)=ax^{2}+bx+c$ . При необходимости можно объединить подобные члены, чтобы получить выражение в данном виде. После этого вы сможете получить больше информации о функции.^[7]
- Первым делом следует обратить внимание на коэффициент a. Если a>0, уравнение соответствует параболе, ветви которой направлены вверх. Если a<0, функция определяет параболу, ветви которой направлены вниз. Проверьте, чтобы a≠0. Если коэффициент a равен нулю, вы имеете дело с линейной, а не квадратичной функцией.
2
Запишите квадратичную функцию в стандартном виде. Прежде чем приступить к нахождению обратной функции, необходимо переписать уравнение в стандартной форме. Стандартная форма любой квадратичной функции выглядит следующим образом: $f(x)=a(x-h)^{2}+k$ . Значения a, h и k определяются в результате процедуры, известной как «выделение квадрата».^[8]
- Обратите внимание, что данный стандартный формат содержит квадратный член ${displaystyle (x-h)^{2}}$ , а также два коэффициента a и k. Чтобы получить эту квадратную форму, необходимо определенным образом преобразовать квадратную функцию.
3
4

Убедитесь, что коэффициент при $x^{2}$ равен 1. Вспомните каноничный вид квадратичной функции $ax^{2}+bx+c$ . Если коэффициент при первом слагаемом отличается от 1, следует поделить на него все члены, чтобы получилось a=1.^[10]
5

Поделите средний коэффициент на 2 и возведите полученный результат в квадрат. У вас уже есть два первых члена каноничной квадратичной формы. Это $x^{2}$ и коэффициент перед x. Каким бы ни был этот коэффициент, вы прибавите или отнимете необходимое число, чтобы привести квадратную функцию к каноничному виду. Как вы помните, чтобы найти третий член квадратичной формы, следует поделить этот второй коэффициент на два, а затем возвести полученное значение в квадрат.^[11]
6

Одновременно прибавьте И вычтите необходимый третий член. Это довольно хитрый прием, но он работает. Если прибавить к функции и вычесть из нее одно и то же число, ее значение не изменится. В то же время это позволит вам придать функции нужный вид.^[12]
7
8
Найдите область определения и область значений функции. Область определения представляет собой значения переменной x, для которых задана функция. Область значений — это величины y, которые принимает данная функция. Вспомним, что парабола не имеет однозначно определенной обратной функции, так как нет однозначного соответствия между значениями x и y из-за того, что у нее две симметричные ветви. Чтобы преодолеть данное затруднение, необходимо взять в качестве области определения все значения x, которые больше h, то есть лежат по одну сторону от вершины параболы.^[14]
- Продолжим рассматривать функцию ${displaystyle f(x)=(x-2)^{2}+5}$ . Поскольку она записана в каноническом виде, можно сразу определить координаты вершины параболы: x=2, y=5. Чтобы избежать неоднозначности, рассмотрим лишь правую половину параболы и в качестве области определения возьмем все значения x≥2. Подставим значение x=2 в функцию и получим y=5. Видно, что значения y увеличиваются с ростом x. Таким образом, области значений данной функции соответствуют y≥5.
9

Поменяйте местами переменные x и y. На этом шаге вы приступите к нахождению обратной функции. Оставьте все как есть, просто поменяйте местами переменные.^[15]
10

Перепишите обратную функцию относительно y. Необходимо выделить переменную y с помощью одних и тех же алгебраических действий с обеих сторон знака равенства. Для нашей функции ${displaystyle x=(y-2)^{2}+5}$ это будет выглядеть следующим образом:^[16]
11
Найдите область определения и область значений обратной функции. Как вы уже делали в начале, установите область определения и область значений обратной функции. Из двух возможных решений выберите то, область определения и область значений которого являются обратными по отношению к аналогичным областям исходной функции.^[17]
- Рассмотрим полученное решение ±. Поскольку квадратный корень не определен для отрицательных чисел, член должен быть положительным. Таким образом, допустимые значения x (область определения) должны удовлетворять условию x≥5. Для данной области определения получаются такие величины y (область значений), которые либо y≥2, если взять положительное значение квадратного корня, либо y≤2 для отрицательных значений. Вспомним, что ранее мы установили область определения x≥2, чтобы найти обратную функцию. Следовательно, правильным ответом для обратной функции будут положительные значения.
- Сравните область определения и область значений обратной функции с этими же областями исходной функции. Вспомним, что для первоначальной функции в качестве области определения мы взяли x≥2, а область значений удовлетворяла условию y≥5. В случае обратной функции эти области поменяются местами: области определения соответствуют x≥5, а области значений — y≥2.
12

Проверьте, правильно ли вы нашли обратную функцию. Для этого возьмите какое-либо значение x, подставьте его в первоначальную функцию и найдите y. Затем подставьте найденное значение y в обратную функцию вместо x и посмотрите, получится ли у вас то значение, которое вы выбрали в начале. Если да, обратная функция правильна.^[18]

Реклама

1
Вспомните квадратичную формулу для решения квадратных уравнений. Один из методов решения квадратных уравнений заключается в том, чтобы попытаться разложить их на множители. Если это не удается, используют квадратичную формулу, которая позволяет найти действительные корни любого квадратного уравнения. С помощью квадратичной формулы можно найти и обратную функцию.^[19]
- Квадратичная формула записывается следующим образом: x=[-b±√(b^2-4ac)]/2a.
- Учтите, что квадратичная формула даст два возможных решения, положительное и отрицательное. Необходимо выбрать подходящее решение, исходя из области определения и области значений функции.
2
Запишите квадратное уравнение, чтобы найти обратную функцию. Оно должно иметь следующий вид: $f(x)=ax^{2}+bx+c$ . Проделайте необходимые алгебраические операции, чтобы привести функцию к этому виду.^[20]
- В данном разделе в качестве примера рассмотрим функцию ${displaystyle f(x)=x^{2}+2x-3}$ .
3

Постройте график функции, чтобы найти область определения и область значений. Используйте для этого графический калькулятор или просто отложите несколько точек, чтобы обозначить параболу. В результате у вас получится парабола с вершиной в точке (-1,-4). Таким образом, чтобы найти обратную функцию, можно взять в качестве области определения x≤-1. Область значений при этом будет удовлетворять условию y≥-4.^[21]
4

Поменяйте местами переменные x и y. Чтобы приступить к нахождению обратной функции, переставьте переменные x и y. При этом оставьте все остальное неизменным. На данном этапе вы замените x на f(x).^[22]
5
Получите в левой части 0. Чтобы использовать квадратичную формулу, необходимо приравнять функцию 0, а затем найти входящие в формулу коэффициенты. Этот метод следует использовать и при нахождении обратной функции: приравняйте функцию нулю.
- В нашем примере нужно вычесть x с обеих сторон, в результате слева у вас получится 0. Должно получиться следующее уравнение: ${displaystyle 0=y^{2}+2y-3-x}$ .
6

Переопределите переменные, чтобы они соответствовали квадратичной формуле. Это довольно хитрый прием. Квадратичная формула служит для того, чтобы найти решение x квадратного уравнения ${displaystyle 0=ax^{2}+bx+c}$ . Чтобы текущее уравнение ${displaystyle 0=y^{2}+2y-3-x}$ соответствовало этому виду, необходимо переопределить переменные следующим образом:^[23]
7
Используйте квадратичную формулу после того, как переопределите переменные. Обычно в квадратичную формулу подставляют коэффициенты a, b и c, чтобы найти x. Однако выше мы поменяли местами переменные x и y, чтобы найти обратную функцию. Таким образом, если вы используете квадратичную формулу, чтобы найти x, то на самом деле решите уравнение относительно y, то есть f(x). Используйте квадратичную формулу следующим образом:^[24]
- x=[-b±√(b^2-4ac)]/2a
- x=(-2)±√((-2)^2-4(1)(-3-x)) / 2(1)
- x=((-2)±√(4+12+4x))/2
- x=(-2±√(16+4x))/2
- x=(-2±√(4)(4+x))/2
- x=-2±2√(4+x))/2
- x=-1±√(4+x)
- f-обратная = -1±√(4+x) (этот последний шаг возможен благодаря тому, что ранее вы подставили вместо f(x) x).
8

Запишите два возможных решения. Учтите, что квадратичная формула дает два возможных решения, что обозначается знаком ±. Запишите оба решения, чтобы вам легче было найти область определения и область значений и выбрать правильный ответ. В нашем примере эти решения выглядят следующим образом:^[25]
9

Установите область определения и область значений обратной функции. Обратите внимание, что для существования квадратного корня область определения должна удовлетворять условию x≥-4. Вспомним, что область определения первоначальной функции была x≤-1, а область значений задавалась условием y≥-4. Чтобы выбрать соответствующую обратную функцию, ее следует взять в виде второго решения ${displaystyle f^{-1}=-1-{sqrt {4+x}}}$ .^[26]
10

Проверьте, правильно ли вы нашли обратную функцию. Для этого возьмите какое-либо значение x, подставьте его в первоначальную функцию и найдите y. Затем подставьте найденное значение y в обратную функцию вместо x и посмотрите, получится ли у вас то значение, которое вы выбрали в начале. Если да, обратная функция найдена правильно.^[27]

Реклама

Об этой статье

Эту страницу просматривали 32 597 раз.

Была ли эта статья полезной?

Источник

Download Article

Inverse functions can be very useful in solving numerous mathematical problems. Being able to take a function and find its inverse function is a powerful tool. With quadratic equations, however, this can be quite a complicated process. First, you must define the equation carefully, be setting an appropriate domain and range. You then have a choice of three methods to calculate the inverse function. The choice of method is mostly up to your personal preference.

1
2

Simplify by combining like terms. The initial equation may have multiple terms in a combination of addition and subtraction. Your first step is to combine like terms to simplify the equation and rewrite it in the standard format of $y=ax^{2}+c$ .

Advertisement
3
Determine the domain and range of the simplified function. Recall that the domain of a function consists of the possible values of x that can be applied to provide a real solution. The range of a function consists of the values of y that will result. To determine the domain of the function, look for values that create a mathematically impossible result. You will then report the domain as all other values of x. To find the range, consider the values of y at any boundary points and look at the behavior of the function.^[1]
- Consider the sample equation $y=2x^{2}+2$ . There is no limitation on allowable values of x for this equation. However, you should recognize that this is the equation of a parabola, centered at x=0, and a parabola is not a function because it does not consist of a one-to-one mapping of x and y values. To limit this equation and make it a function, for which we can find an inverse, we must define the domain as x≥0.
- The range is similarly limited. Notice that the first term, $2x^{2}$ , will always be positive or 0, for any value of x. When the equation then adds +2, the range will be any values y≥2.
- Defining the domain and range at this early stage is necessary. You will use these definitions later in defining the domain and range of the inverse function. In fact, the domain of the original function will become the range of the inverse function, and the range of the original will become the domain of the inverse.
4

Switch the roles of the x and y terms. Without changing the equation in any other way, you need to replace all appearance of y with an x, and all appearances of x with a y. This is the step that actually “inverts” the equation.
5

Rewrite the inverted equation in terms of y. Using a combination of algebraic steps, and taking care to perform the same operation evenly on both sides of the equation, you will need to isolate the y variable. For the working equation $x=2y^{2}+2$ , this revision will look like the following:^[2]
6
Determine the domain and range of the inverse function. As you did at the beginning, examine the inverted equation to define its domain and range. With two possible solutions, you will select the one that has a domain and range that are inverses of the original domain and range.^[3]
- Examine the sample equation solution of ± ${sqrt {{frac {x-2}{2}}}}=y$ . Because the square root function is not defined for any negative values, the term ${frac {x-2}{2}}$ must always be positive. Therefore, allowable values of x (the domain) must be x≥2. Using that as the domain, the resulting values of y (the range) are either all values y≥0, if you take the positive solution of the square root, or y≤0, if you select the negative solution of the square root. Recall that you originally defined the domain as x≥0, in order to be able to find the inverse function. Therefore, the correct solution for the inverse function is the positive option.
- Compare the domain and range of the inverse to the domain and range of the original. Recall that for the original function, $y=2x^{2}+2$ , the domain was defined as all values of x≥0, and the range was defined as all values y≥2. For the inverse function, now, these values switch, and the domain is all values x≥2, and the range is all values of y≥0.
7

Check that your inverse function works. To make sure that your work is correct and your inverse is the right equation, select any value for x and place it into the original equation to find y. Then, put that value of y in the place of x in your inverse equation, and see if you generate the number that you started with. If so, your inverse function is correct.^[4]

1
Set up the quadratic equation in the proper form. In order to begin finding the inverse, you must begin with the equation in the format $f(x)=ax^{2}+bx+c$ . If necessary, you may need to combine similar terms to get the equation into this format. With the equation written this way, you can begin to tell some information about it.^[5]
- The first thing to notice is the value of the coefficient a. If a>0, then the equation defines a parabola whose ends point upward. If a<0, the equation defines a parabola whose ends point downward. Notice that a≠0. If it did, then this would be a linear function and not quadratic.
2
Recognize the standard format of the quadratic. Before you can find the inverse function, you will need to rewrite your equation into the standard format. The standard format for any quadratic function is $f(x)=a(x-h)^{2}+k$ . The numerical terms a, h and k will be developed as you transform the equation through a process known as completing the square.^[6]
- Notice that this standard format consists of a perfect square term, $(x-h)^{2}$ , which is then adjusted by the other two elements a and k. To get to this perfect square form, you will need to create certain conditions in your quadratic equation.
3
4

Make sure the coefficient on $x^{2}$ is 1. Recall the original form of the quadratic function $ax^{2}+bx+c$ . If the first coefficient is anything other than 1, then you must divide all terms by that value, to set a=1.^[8]
5

Find one-half of the middle coefficient and square it. You already have the first two terms of the perfect square quadratic. These are the $x^{2}$ term and whatever coefficient appears in front of the x-term. By taking that coefficient to be whatever value it is, you will add or subtract whatever number is necessary to create a perfect square quadratic. Recall from above that the required third term of the quadratic is this second coefficient, divided by two, and then squared.^[9]
6

Add AND subtract the needed third term, at the same time. This is a tricky concept but it works. By both adding and subtracting the same number in different locations of your function, you are really making no change to the value of the function. However, doing this will allow you to get your function into the proper format.^[10]
7
Factor the perfect square quadratic. The polynomial inside the parentheses should be a perfect square quadratic, which you can rewrite in the form $(x+b)^{2}$ . In the example from the prior step, $f(x)=(x^{2}-4x+4)+5$ , the quadratic factors into $(x-2)^{2}$ . Carry along the rest of the equation, so your solution will be $f(x)=(x-2)^{2}+5$ . This is the same function as your original quadratic, $f(x)=x^{2}-4x+9$ , simply revised into standard $f(x)=a(x-h)^{2}+k$ form.^[11]
- Notice that for this function, a=1, h=2, and k=5. The value of writing the equation in this form is that a, being positive, tells you that the parabola points upward. The values of (h,k) tell you the apex point at the bottom of the parabola, if you wanted to graph it.
8
Define the domain and range of the function. The domain is the set of x-values that can be used as input into the function. The range is the set of y-values that can be the outcome. Recall that a parabola is not a function with a definable inverse, because there is not a one-to-one mapping of x-values to y-values, as a result of the symmetry of the parabola. To resolve this problem, you need to define the domain as all values of x that are greater than x=h, the apex point of the parabola.
- Continue working with the sample function $f(x)=(x-2)^{2}+5$ . Because this is in standard format, you can identify the apex point as x=2, y=5. Thus, to avoid the symmetry, you will only work with the right-side of the graph, and set the domain as all values x≥2. Inserting the value x=2 into the function gives the result of y=5. You can see that the values of y will increase as x increases. Therefore the range of this equation is y≥5.
9

Switch the x and y values. This is the step where you begin to find the inverted form of the equation. Leave the equation in its entirety, except for switching these variables.
10

Rewrite the inverted equation in terms of y. Using a combination of algebraic steps, and taking care to perform the same operation evenly on both sides of the equation, you will need to isolate the y variable. For the working equation $x=(y-2)^{2}+5$ , this revision will look like the following:^[12]
11
Determine the domain and range of the inverse function. As you did at the beginning, examine the inverted equation to define its domain and range. With two possible solutions, you will select the one that has a domain and range that are inverses of the original domain and range.
- Examine the sample equation solution of ±. Because the square root function is not defined for any negative values, the term must always be positive. Therefore, allowable values of x (the domain) must be x≥5. Using that as the domain, the resulting values of y (the range) are either all values y≥2, if you take the positive solution of the square root, or y≤2 if you select the negative solution of the square root. Recall that you originally defined the domain as x≥2, in order to be able to find the inverse function. Therefore, the correct solution for the inverse function is the positive option.
- Compare the domain and range of the inverse to the domain and range of the original. Recall that for the original function the domain was defined as all values of x≥2, and the range was defined as all values y≥5. For the inverse function, now, these values switch, and the domain is all values x≥5, and the range is all values of y≥2.
12

Check that your inverse function works. To make sure that your work is correct and your inverse is the right equation, select any value for x and place it into the original equation to find y. Then, put that value of y in the place of x in your inverse equation, and see if you generate the number that you started with. If so, your inverse function is correct.^[13]

1
Remember the Quadratic Formula for solving x. Recall that, when solving quadratic equations, one method was to factor them, if possible. If factoring did not work, then you could resort to the Quadratic Formula, which would yield the real solutions for any quadratic formula. You can use the Quadratic Formula as another method to find inverse functions.^[14]
- The Quadratic Formula is x=[-b±√(b^2-4ac)]/2a.
- Notice that the Quadratic Formula will result in two possible solutions, one positive and one negative. You will make this selection based on defining the domain and range of the function.
2
Begin with a quadratic equation to find the inverse. Your quadratic equation must begin in the format $f(x)=ax^{2}+bx+c$ . Take whatever algebraic steps you must in order to get your equation into that form.
- For this section of this article, use the sample equation $f(x)=x^{2}+2x-3$ .
3

Graph the equation to define the domain and range. Determine the graph of the function, either by using a graphing calculator or just plotting various points until the parabola appears. You will find that this equation defines a parabola with its apex at (-1,-4). Thus, to define this as a function that will have an inverse, define the domain as all values of x≤-1. The range will then be all y≥-4.
4

Interchange the variables x and y. To begin finding the inverse, switch the variables x and y. Leave the equation unchanged, except for reversing the variables. At this stage, you will replace x for f(x).^[15]
5
Set the left side of the equation equal to 0. Recall that to use the Quadratic Formula, you must set your equation equal to 0, and then use the coefficients in the formula. Similarly, this method of finding an inverse function begins by setting the equation equal to 0.
- For the sample equation, to get the left side equal to 0, you must subtract x from both sides of the equation. This will give the result $0=y^{2}+2y-3-x$ .
6

Redefine the variables to fit the Quadratic Formula. This step is a bit tricky. Recall that the Quadratic Formula solves for x, in the equation $0=ax^{2}+bx+c$ . So, to get the equation you currently have, $0=y^{2}+2y-3-x$ , to match that format, you need to redefine terms as follows:^[16]
7
Solve the Quadratic Formula using those redefined values. Normally, you would place the values of a, b and c into the Quadratic Formula to solve for x. However, recall that you previously switched x and y for finding the inverse function. Therefore, when you use the Quadratic Formula to solve for x, you are really solving for y, or the f-inverse. The steps of solving the Quadratic Formula will work like this:
- x=[-b±√(b^2-4ac)]/2a
- x=(-2)±√((-2)^2-4(1)(-3-x)) / 2(1)
- x=((-2)±√(4+12+4x))/2
- x=(-2±√(16+4x))/2
- x=(-2±√(4)(4+x))/2
- x=-2±2√(4+x))/2
- x=-1±√(4+x)
- f-inverse = -1±√(4+x) (This final step is possible because you earlier put x in place of the f(x) variable.)
8

Write out the two possible solutions. Notice that the Quadratic Formula gives two possible results, using the ± symbol. Write out the two separate solutions to make it easier to define the domain and range and make the correct final solution. These two solutions are:
9

Define the domain and range of the inverse function. Notice that, for the square root to be defined, the domain must be x≥-4. Recall that the domain of the original function was x≤-1 and the range was y≥-4. To choose the inverse function that matches, you will need to choose the second solution, $f^{{-1}}=-1-{sqrt {4+x}}$ as the correct inverse function.^[17]
10

Check that your inverse function works. To make sure that your work is correct and your inverse is the right equation, select any value for x and place it into the original equation to find y. Then, put that value of y in the place of x in your inverse equation, and see if you generate the number that you started with. If so, your inverse function is correct.

Add New Question

Question

Find the inverse of (1 — 2x)^3

First, let me point out that this question is beyond the scope of this particular article. The article is about quadratic equations, which implies that the highest exponent is 2. Your question presents a cubic equation (exponent =3). Nevertheless, basic algebra allows you to find the inverse of this particular type of equation, because it is already in the «perfect cube» form. First, set the expression you have given equal to y, so the equation is y=(1-2x)^3. Then invert it by switching x and y, to give x=(1-2y)^3. Now perform a series of inverse algebraic steps to solve for y. These steps are: (1) take the cube root of both sides to get cbrt(x)=1-2y [NOTE: I am making up the notation “cbrt(x) to mean “cube root of x” since I can’t show it any other way here]; (2) Subtract 1 from both sides to get cbrt(x)-1=-2y; (3) Divide both sides by -2 to get (cbrt(x)-1)/-2=y; (4) simplify the negative sign on the left to get (1-cbrt(x))/2=y. The final equation should be (1-cbrt(x))/2=y. This is your inverse function.
Question

Where can I find more examples so that I know how to set up and solve my homework problems?

The Internet is filled with examples of problems of this nature. Google «find the inverse of a quadratic function» to find them.
Question

How do I find the inverse of f(x)=1/(sqrt(x^2-1)?

Begin by switching the x and y terms (let f(x)=y), to get x=1/(sqrt(y^2-1). Then perform basic algebraic steps to each side to isolate y. Without getting too lengthy here, the steps are (1) square both sides to get x^2=1/(y^2-1); (2) transpose numerators and denominators to get y^2-1=1/x^2; (3) add 1 to both sides to get y^2=(1/x^2)+1; (4) square root both sides to get y=sqrt((1/x^2)+1).

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Thanks for submitting a tip for review!

About This Article

Article SummaryX

To find the inverse of a quadratic function, start by simplifying the function by combining like terms. Then, determine the domain and range of the simplified function. Once you have the domain and range, switch the roles of the x and y terms in the function and rewrite the inverted equation in terms of y. Finally, determine the domain and range of the inverse function. To learn how to find the inverse of a quadratic function by completing the square, scroll down!

Did this summary help you?

Thanks to all authors for creating a page that has been read 345,400 times.

Did this article help you?

Источник

Как найти функцию, обратную квадратичной функции

Найти функцию, обратную линейной функции, легко: надо просто сделать «х» зависимой переменной, а затем заменить «х» на «у». Этот процесс значительно усложняется в случае квадратичной функции.

Шаги

Выполняйте любые алгебраические операции с обеих сторон функции, чтобы не изменить ее.
Перепишите функцию в виде y=a(x-h)+k. Это не только упростит нахождение обратной функции, но и позволит определить, имеет ли исходная функция обратную. Вы можете сделать это двумя способами:
- Дополнение до полного квадрата.
  1. Вынесите коэффициент «а» (коэффициент при х) за скобку, а члены функции разделите на коэффициент «а».
  2. Теперь коэффициент при «х» равен b/а. Разделите его на 2 и получите b/2a, а затем возведите в квадрат: (b/2a). Полученное значение одновременно прибавьте и вычтите из функции (чтобы не поменять ее значение). Теперь три первых члены в скобках записываются в виде a+2ab+b, где а = х, b = b/2a (эти величины имеют числовые значения). Эти три первых члена являются полным квадратом.
  3. Первые три члена можно записать в виде (a-b) или (a+b) (знак зависит от знака коэффициента при «х» в исходной функции).
  4. Оставшийся член вынесите за скобки и получите: y=a(x-h)+k.
- Сравнение коэффициентов.
  1. Слева запишите исходную функцию, а справа – ее желаемый вид (в нашем случае a(x-h)+k). Это позволит вам найти значения a, h, k, верные при любом значении «х».
  2. Раскройте скобки с правой стороны уравнения (левую часть вообще не трогайте).
  3. Определите коэффициенты при х и «х».
  4. Сравните коэффициенты при х и «х» на правой и левой сторонах уравнения – они должны быть равны друг другу. Это приводит к функции вида a(x-h)+k), в которой вместо «а» подставьте найденное значение. Коэффициент при x (или 1) на левой стороне уравнения должен быть равен коэффициенту на правой стороне. Сравнивая их, получите уравнение, которое поможет найти значение k.
  5. Используя найденные значения а, h, k, вы можете написать функцию в нужном виде.
Убедитесь, что значение h лежит либо на границе области определения, либо вне ее. Значение h – это координата «х» экстремума функции. Если h лежит внутри области определения, то исходная функция не имеет обратной функции. Обратите внимание на знак в скобках: (x—h)+k. Таким образом, если дано (х + 3), то h = -3 (отрицательное значение).
Сделайте (x-h) зависимым выражением. Для этого вычтите k из обеих сторон уравнения, а затем разделите обе стороны уравнения на «а».
Извлеките корень из обеих сторон уравнения. Вы избавитесь от степени. Не забудьте поставить знак +/- на другой стороне уравнения.
Определите правильный знак (вы не можете оставить оба знака). Для этого рассмотрите область определения. Если х < определенного значения, то выберите «-». Если х > определенного значения, выберите «+». Теперь сделайте «х» зависимой переменной.
Вместо «у» подставьте «х», а вместо «х» подставьте f(x). Вы нашли обратную функцию.

Советы

Проверьте ответ, вычислив f(х) для некоторого значения «х», а затем подставьте найденное значение в обратную функцию, чтобы найти исходное значение «х». Например, если при х = 3, f(х) = 4, то, подставив 4 в обратную функцию, вы должны получить 3.
Если возможно, проверьте ответ, построив график обратной функции. Он должен иметь вид графика исходной функции, но симметричный относительно прямой у = х.

Теги:

Информация

Посетители, находящиеся в группе Guests, не могут оставлять комментарии к данной публикации.

Источник

Многие приложения в алгебре и исчислении зависят от знания того, как найти обратную функцию, и это тема данного руководства.

Прежде всего, вам нужно понять, что перед тем, как найти инверсию функции, вы должны убедиться, что такая инверсия существует.

Преимущество метода поиска обратного, который мы будем использовать, заключается в том, что мы найдем обратное и выясним, существует ли оно одновременно.

Готовый?? Тогда пристегнитесь.

Как узнать, есть ли у функции инверсия?

Технически функция имеет инверсию, когда она взаимно однозначна (инъективна) и сюръективна.

Однако решающим условием является то, что она должна быть взаимно однозначной, потому что функцию можно сделать сюръективной, ограничив ее диапазон своим собственным изображением.

Как узнать, что функция взаимно однозначна?

Что ж, есть как минимум пара способов. Один из них — алгебраический, а другой — графический (держу пари, я знаю, какой из них вы предпочитаете, да?)

Алгебраический путь

Для алгебраического подхода, чтобы функция (f) была взаимно однозначной, нам нужно доказать, что каждый раз, когда это (f(x) = f(y)), нам нужно иметь это (x = y).

Другими словами, нам нужно доказать, что

[f(x) = f(y) ,,Rightarrow ,, x = y]

Графический способ

Для графического способа нам нужно использовать

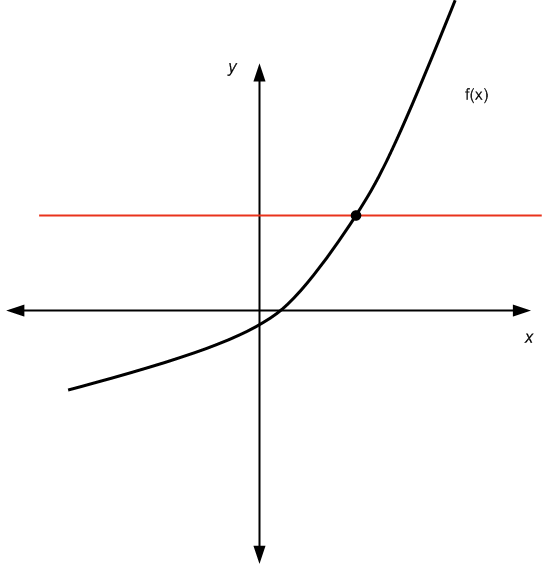
проверка горизонтальной линии

: Для любой горизонтальной линии, которую мы рисуем, график функции не более одного раза пересекает эту горизонтальную линию.

Графически:

Проходит тест горизонтальной линии

Не проходит тест горизонтальной линии

В поисках обратного

Чтобы найти обратную функцию для заданной функции (f(x)), необходимо решить уравнение.

Действительно, у вас есть уравнение (f(x) = y), вы берете (y) как заданное число, и вам нужно решить его для (x), и вам нужно убедиться, что решение УНИКАЛЬНО.

Это все. Легко, правда ??

Теперь о практических шагах:

Шаг 1:

Для заданного (y) задайте уравнение:

[f(x) = y]

и решите его для (x).

Шаг 2:

Обязательно обратите внимание на то, для какого (y) существует действительно уникальное решение.

Шаг 3:

Как только вы решите (x) в терминах (y), это выражение, которое зависит от (y), будет вашим (f^{-1}(y)).

Шаг 4:

Измените имя переменной с (y) на (x), и у вас будет обратная функция (f^{-1}(x)).

ПРИМЕР 1

Найдите обратную функцию (f(x) = sqrt x)

ОТВЕЧАТЬ:

Итак, мы берем (y) как данное, и нам нужно решить (f(x) = y), что в данном случае соответствует решению

[sqrt x = y]

Обратите внимание, что квадратный корень всегда неотрицателен, поэтому для решения нам понадобится (yge 0).

Применяя квадрат к обеим сторонам, получаем, что

[Rightarrow ,, (sqrt x)^2 = y^2]

[Rightarrow ,, x = y^2]

Итак, (f^{-1}(y) = y^2), переключая имя переменной, мы получаем обратную функцию:

[f^{-1}(x) = x^2]

для (xge 0).

ПРИМЕР 2

Найдите обратную функцию (f(x) = displaystyle frac{x}{x+1}) для (x > -1)

ОТВЕЧАТЬ:

Опять же, мы берем (y) как дано, и теперь нам нужно решить для (x) уравнение (f(x) = y). Итак, у нас есть

[displaystyle frac{x}{x+1} = y]

[Rightarrow ,, x = y(x+1)]

[Rightarrow ,, x = yx + y]

[Rightarrow ,, x — yx = y]

[Rightarrow ,, x(1 — y) = y]

[Rightarrow displaystyle ,, x = frac{y}{1-y}]

Итак, (f^{-1}(y) = displaystyle frac{y}{1-y}), переключая имя переменной, мы получаем обратную функцию:

[f^{-1}(x) = displaystyle frac{x}{1-x}]

Подробнее о поиске обратной функции

Одним из важнейших свойств обратной функции (f^{-1}(x)) является то, что (f(f^{-1}(x)) = x).

Подумайте, о чем это говорит. Что-то вроде: «Функция, вычисленная в обратном порядке, дает вам идентичность».

Или, другими словами, вычисление инверсии через функцию похоже на бездействие с аргументом.

Или, как некоторые любят говорить: функция может каким-то образом отменить обратное.

Вы выбираете свою версию.

Как найти обратную квадратичную функцию? Ты можешь?

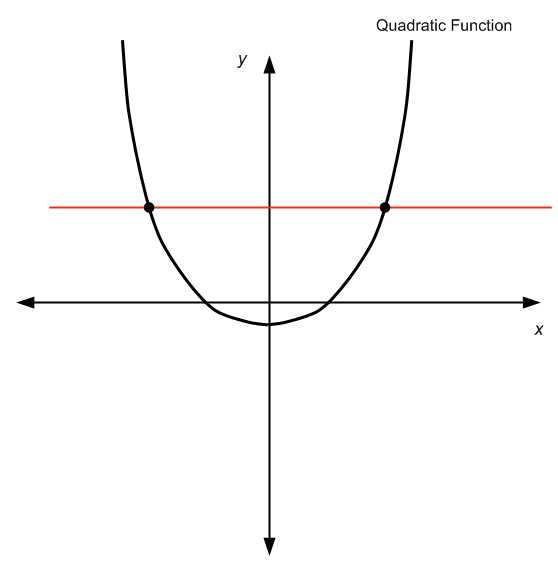
Собственно, ответ таков: это зависит от обстоятельств. Это потому, что если мы рассмотрим квадратичную функцию

по всей реальной линии

, то это не один к одному, поскольку он не проходит тест горизонтальной линии, как вы можете видеть на диаграмме ниже:

Не пройдя тест горизонтальной линии, мы можем увидеть, что для данного (y) существует более одного значения (x), так что (f(x) = y), поэтому мы не можем «решить» для (x), поскольку существует более одного (x).

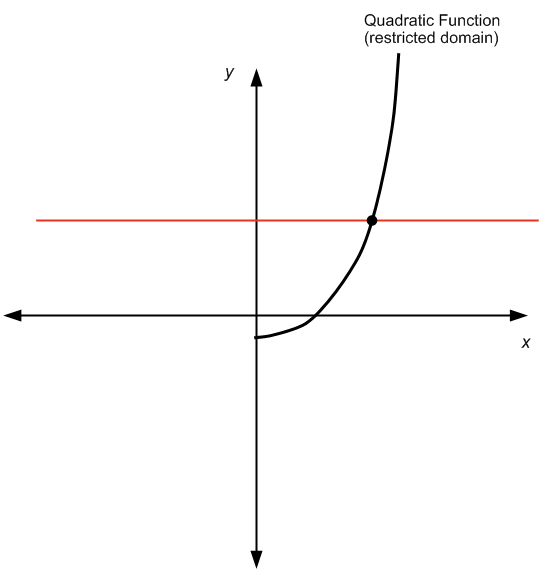
НО, если вы ограничите домен и рассмотрите, скажем, только положительные числа, мы получим следующее:

который проходит проверку горизонтальной линии, и, следовательно, квадратичная функция обратима.

НРАВСТВЕННОСТЬ ИСТОРИИ: Чтобы проверить, является ли что-то обратимым, речь идет НЕ только о функции. Речь идет о функции И ее

домен и диапазон

Как быстро построить график обратных функций

Всегда существует требование оценки, является ли функция (f(x)) обратимой или нет (проверяя, является ли она взаимно однозначной). Но если предположить, что вы знаете, что это обратимо, есть простой способ найти график обратимости.

Сначала изобразите график данной функции (f(x)).

Затем нарисуйте линию под углом 45 градусов (y = x).

Чтобы построить график (f^{-1}(x)), все, что вам нужно сделать, это отразить график (f(x)) через линию (y = x) под углом 45 градусов, как зеркало.

См. Пример ниже с функциями (f(x) = sin x) и (f^{-1}(x) = arcsin x).

Другой способ увидеть это — использовать оригинал

график

и измените значение (x) на значение (y).

Есть ли способ сделать функцию обратной?

Да, это действительно возможно, но это происходит только для функции идентификации, то есть с (f(x) = x).

Источник