Функция
принимает каждое свое значение только
при одном
значении
аргумента, поскольку линейное
уравнение
только один корень (рис.6). Значит, эта
функция имеет обратную функцию

которая определена на

так как

множеством значений функции
(рис.7). Обратная функция
произвольному числу
ставит в соответствие число

которое определяется условием
(рис.7). Выразив из этого равенства
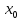
получаем
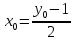
Значит, для каждого
имеем

то есть
.
Обозначив
аргумент обратной функции буквой х, а
зависимую переменную буквой

то есть, поменяв переменные местами,
получим

Итак, обратной функцией к линейной
функции
будет функция
, которая также является линейной.
Замечание.
При решении задач можно обозначать
произвольное значение аргумента обратной
функции буквой

а не

как это для ясности сделано в разобранных
примерах.
-
Пусть
обратимая функция, заданная формулой.
На основании определения обратной
функции можно сформулировать порядок
действий для нахождения функции,
обратной к функции
.
-
Теорема.
Если функция
является возрастающей (или убывающей),
то она обратима.
Пусть
для определенности функция
является возрастающей. Возьмем два
различных значения аргумента, меньшее
обозначим через

большее — через

то есть

Из этого неравенства в силу определения
возрастающей функции следует, что

а значит
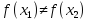
Поэтому разным значениям аргумента
соответствуют разные значения функции
и, следовательно, функция
обратима. Для убывающей функции
доказательство аналогично.
Отметим,
что любая линейная функция
обратима, если
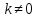
поскольку является либо возрастающей,
либо убывающей функцией, в зависимости
от знака коэффициента

Обратима также возрастающая функция

Если
функция задана формулой и нам неизвестен
ее график, то определить, будет
ли функция обратимой можно только путем
исследования количества корней уравнения

Если при некотором значении
их два или более, то функция не является
обратимой.
-
Если известен график обратимой функции, то график обратной функции можно построить путем преобразования графика функции . Следующая теорема определяет вид этого преобразования.
Теорема.
График функции
и график обратной к ней функции
симметричны
относительно прямой

Пусть
точка
с координатами
принадлежит графику функции

то есть

Тогда, по определению обратной функции

Это означает, что точка
с координатами
принадлежит графику обратной функции
(рис. 11).
Докажем,
что точки
и
симметричны относительно прямой

Для определенности рассмотрим случай,
когда точка
лежит в первом координатном угле и

Проведем через точки
и
прямые, перпендикулярные осям координат
(рис.8). Прямоугольник
является квадратом, так как имеет равные
смежные стороны:
Вершины квадрата

точки
и

имеют координаты
и
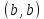
соответственно, и, значит, принадлежат
прямой
(рис.9). Поскольку диагонали квадрата
перпендикулярны и делятся точкой
пересечения пополам, то точки
и
симметричны относительно диагонали

а, следовательно, и относительно прямой

Таким
образом, мы доказали, что точка плоскости,
симметричная точке графика функции
относительно прямой

принадлежат графику обратной функции

Аналогично доказывается, что верно и
обратное утверждение: точка, симметричная
точке графика обратной функции
относительно прямой

принадлежат графику функции
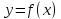
Значит, графики этих функций симметричны.
Теорема доказана.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Загрузить PDF
Загрузить PDF
Одной из важнейших составляющих алгебры является понятие обратной функции. Обратная функции обозначается как f^-1(х) и графически представляется как отражение графика исходной функции относительно прямой у=х. В этой статье мы расскажем вам, как найти обратную функцию.
Шаги
-
1
Убедитесь, что данная функция биективна. Только биективные функции имеют обратные функции.
- Функция биективна, если она проходит тест вертикальной и горизонтальной прямыми. Проведите вертикальную прямую через график функции и подсчитайте количество раз, которое прямая пересекает график функции. Потом проведите горизонтальную прямую через график функции и подсчитайте количество раз, которое прямая пересекает график функции. Если каждая прямая пересекает график функции только один раз, то функция биективна.
- Если график не проходит тест вертикальной прямой, то он не задан функцией.
- Для алгебраического определения биективности функции подставьте f(а) и f(b) в данную функцию и определите, выполняется ли равенство a=b. В качестве примера рассмотрим функцию f(x) = 3x+5.
- f(a) = 3a + 5; f(b) = 3b + 5
- 3a + 5 = 3b + 5
- 3a = 3b
- a = b
- Таким образом, данная функция биективна.
- Функция биективна, если она проходит тест вертикальной и горизонтальной прямыми. Проведите вертикальную прямую через график функции и подсчитайте количество раз, которое прямая пересекает график функции. Потом проведите горизонтальную прямую через график функции и подсчитайте количество раз, которое прямая пересекает график функции. Если каждая прямая пересекает график функции только один раз, то функция биективна.
-
2
В данной функции поменяйте местами «х» и «у». Помните, что f(х) — другое написание «у».
- «f(x)» или «y» представляет собой функцию, а «х» — переменную. Чтобы найти обратную функцию, нужно поменять местами функцию и переменную.
- Пример: рассмотрим функцию f(x) = (4x+3)/(2x+5), которая является биективной. Поменяв местами «х» и «у», получите x = (4y + 3)/(2y + 5).
-
3
Найдите «у». Решите новое уравнение и найдите «у».
- Возможно, чтобы найти значение выражения и упростить его, вам понадобятся алгебраические приемы вроде умножения дробей или разложения на множители.
- Решение нашего примера:
- х = (4y + 3)/(2y + 5)
- х(2y + 5) = 4y + 3 — избавьтесь от дроби. Для этого умножьте обе части уравнения на знаменатель дроби (2у + 5).
- 2xy + 5x = 4y + 3 — раскройте скобки.
- 2xy — 4y = 3 — 5x — перенесите все члены с переменной (в данном случае это «у») на одну сторону уравнения.
- у (2x — 4) = 3 — 5x — вынесите «у» за скобку.
- у = (3 — 5x)/(2x — 4) — разделите обе части уравнения на (2х-4), чтобы получить окончательный ответ.
-
4
Замените «у» на f^-1(х). Это есть обратная функция для исходной функции.
- Окончательный ответ: f^-1(x) = (3 — 5x)/(2x — 4). Это обратная функция для f(х) = (4x + 3)/(2x + 5) .
Реклама
Об этой статье
Эту страницу просматривали 213 121 раз.
Была ли эта статья полезной?
Обратная функция
Что такое обратная функция? Как найти функцию, обратную данной?
Определение.
Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо:
1) В формулу функции вместо y подставить x, вместо x — y:
x=f(y).
2) Из полученного равенства выразить y через x:
y=g(x).
Пример.
Найти функцию, обратную функции y=2x-6.
1) x=2y-6
2) -2y=-x-6
y=0,5x+3.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).
y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.

Теорема (необходимое и достаточное условие обратимости функции)
Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.
Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.
Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.
Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.
Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).
1) x=y².
2)
Так как y≥0, то
то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:
В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.
Инструкции:
Найдите обратную функцию заданной вами линейной функции. Пожалуйста, введите допустимое линейное уравнение в поле ниже, чтобы найти его обратное.
Как использовать этот калькулятор обратной линейной функции
Идея нахождения обратной функции — очень важное понятие в алгебре. Существует формальное определение обратной функции, которая принимает различные формы.
Один из распространенных способов определения функции, обратной заданной функции (y = f(x) ), заключается в том, что (f^{-1}(x)) является обратной, если (f(f^{-1}(x)) = f^{-1}(f(x)) = x), для всех (x) в соответствующем наборе.
Теперь вычисление обратной функции в целом не обязательно является простым алгебраическим упражнением, поскольку оно обычно включает в себя
Решение для х
начиная с исходной функции (y = f(x) ), что может быть алгебраически сложно или невозможно.
Но, когда вы имеете дело с
линейная функция
формы (y = ax + b), то становится немного проще
Решите для х
и, наконец, найти обратное.
Как найти обратную линейную функцию?
Во-первых, вы начинаете с допустимой линейной функции формы (y = ax + b). Ваша первая задача состоит в том, чтобы
Решите для х
:
[ax = y-b]
[Rightarrow x = frac{y-b}{a}]
Теперь вы сделаете острое наблюдение: «Что произойдет, если (a = 0)», и вы будете правы в этом. Существует проблема, когда (a = 0), и в этом случае вы не можете решить для (x) и нет обратного.
Действительно, когда (a = 0) оказывается, что исходной функцией на самом деле была (f(x) = b), которая является константой, которая не является инъективной, поэтому невозможно однозначно связать изображения и прообразы.
Но мы все в деле, если (a ne 0). Теперь вы замените (x) на (f^{-1}(x)) и (y) на (x), и у вас получится фактическая обратная функция:
[Rightarrow f^{-1}(x) = frac{x-b}{a}]
Как пользоваться этим калькулятором
Чтобы найти обратную линейную функцию с шагами, просто поместите допустимую линейную функцию формы (y = ax + b).
Если вы укажете правильную линейную функцию, калькулятор покажет вам все шаги, необходимые для получения обратной функции, а также вы получите
график исходной функции
и его обратное, если обратное существует.
Обратите внимание, что этот калькулятор работает только для линейных функций. Вычисление обратной функции, которая не является линейной, может быть более сложным, и это не всегда возможно.
Пример
Найдите обратную функцию следующей линейной функции (y = 3x — 2).
Отвечать:
Чтобы найти функцию, обратную заданной линейной функции, необходимо выполнить следующие шаги.
Шаг 1 — Решение для x
: Первым шагом в поиске обратного уравнения линейного уравнения является решение (x):
Нам было предложено следующее уравнение:
[displaystyle y=3x-2]
Помещая (x) в левую часть и (y) и константу в правую часть, мы получаем
[displaystyle 3x = y + 2]
Теперь, находя (x), получаем следующее
[displaystyle x=frac{1}{3}y+frac{2}{3}]
и упрощая все термины, которые нуждаются в упрощении, окончательно получаем следующее
[displaystyle x=frac{1}{3}y+frac{2}{3}]
Следовательно, на основе представленного уравнения мы заключаем, что результатом решения для (x) из данного уравнения является (displaystyle x=frac{1}{3}y+frac{2}{3}).
Шаг 2 — Переключение ролей переменных
: Теперь, чтобы найти обратную функцию, мы просто меняем значение (y) на (x) и значение (x) на (f^{-1}(x)) в предыдущем уравнении, что приводит к:
[displaystyle f^{-1}(x)=frac{1}{3}x+frac{2}{3}]
Вывод
: На основе представленного уравнения найдено, что обратная исходная линейная функция (y=3x-2), которая была передана, равна (displaystyle f^{-1}(x)=frac{1}{3}x+frac{2}{3}).
Функция — это действие над переменной. Но что будет, если сделать действие — и обратное действие? Открыть дверь и закрыть дверь. Включить свет и выключить свет. Будет то же, что и было раньше, верно? Так и с функциями.
Функции f(x) и g(x) называются взаимно-обратными, если f(g(x)) = x.
Например, при
Сделали действие (возвели в квадрат). Сделали обратное действие (извлекли квадратный корень). И получили то, что и было раньше, то есть переменную
.
А вот . Подумайте, почему это так.
Другой пример взаимно-обратных функций: показательная и логарифмическая. Помните основное логарифмическое тождество: для
. Для положительных х функции
и
являются взаимно-обратными.
Еще один пример взаимно-обратных функций:
и
при
Вспомним определение функции. Числовая функция y = f(x) — это такое соответствие между двумя числовыми множествами A и B, при котором каждому числу x ∈ A отвечает одно-единственное число y ∈ B. Множество A называется при этом областью определения функции, множество B — областью значений.
Пусть соответствие f является взаимно-однозначным:
Тогда существует функция g, которая действует в обратную сторону: каждому числу y ∈ B она ставит в соответствие одно-единственное число x ∈ A, такое, что f(x) = y:
Функция g называется обратной к функции f. Точно так же и функция f будет обратной к функции g.
Если мы возьмём какое-либо число x ∈ A и подействуем на него функцией f, то получим число y = f(x) ∈ B. Теперь на полученное число y подействуем функцией g. Куда попадём? Правильно, вернёмся к исходному числу x. Это можно записать так:
 |
(1) |
Последовательное применение двух взаимно-обратных действий возвращает нас в исходную точку. Как и в жизни: сначала открыли дверь, а потом совершили обратное действие — закрыли дверь; в итоге вернулись к начальной ситуации.
Так, если возвести число 3 в степень x, а затем совершить обратное действие — взять от полученного числа 3x логарифм по основанию 3 — мы вернёмся к исходному числу x:
Графики взаимно-обратных функций симметричны относительно прямой у = x.
То, что для функции является областью определения, для обратной функции будет областью значений.
Как вывести формулу обратной функции?
Если вы учитесь в математическом классе или на первом курсе вуза, вам может встретиться такое задание.
Например, у вас есть линейная функция Какая же функция будет к ней обратной?
Действуем следующим образом:
1) Выражаем из формулы функции x через у.
Получаем:
2) В формуле меняем x и у местами. Получаем формулу обратной функции:
Другой пример. Найдем обратную функцию для функции .
1) Выражаем из формулы функции x через у. Получаем:
2) В формуле меняем x и у местами. Получаем формулу обратной функции:
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Обратная функция» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023





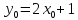
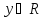





 .
.



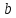
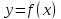

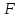


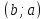







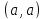







![Rendered by QuickLaTeX.com [begin{array}{l} y = 2x - 6\ begin{array}{*{20}{c}} x&vline& 0&vline& 3\ hline y&vline& { - 6}&vline& 0 end{array} end{array}]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-d7fa80623853e96d4e8f32fe255e4c99_l3.png)
![Rendered by QuickLaTeX.com [begin{array}{l} y = 0,5x + 3\ begin{array}{*{20}{c}} x&vline& 0&vline& { - 6}\ hline y&vline& 3&vline& 0 end{array} end{array}]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-c9a8b5feb781d3c105f0903d50e2b586_l3.png)





