Как найти обратную функцию на промежутке - Исправление недочетов и поиск решений вместе с Examum.ru

Обратная функция

Что такое обратная функция? Как найти функцию, обратную данной?

Определение.

Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.

Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.

Чтобы найти функцию, обратную данной функции y=f(x), надо:

1) В формулу функции вместо y подставить x, вместо x — y:

x=f(y).

2) Из полученного равенства выразить y через x:

y=g(x).

Пример.

Найти функцию, обратную функции y=2x-6.

1) x=2y-6

2) -2y=-x-6

y=0,5x+3.

Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.

Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).

y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.

$[begin{array}{l} y = 2x - 6\ begin{array}{*{20}{c}} x&vline& 0&vline& 3\ hline y&vline& { - 6}&vline& 0 end{array} end{array}]$

$[begin{array}{l} y = 0,5x + 3\ begin{array}{*{20}{c}} x&vline& 0&vline& { - 6}\ hline y&vline& 3&vline& 0 end{array} end{array}]$

Однозначно выразить y через x можно в том случае, когда уравнение x=f(y) имеет единственное решение. Это можно сделать в том случае, если каждое своё значение функция y=f(x) принимает в единственной точке её области определения (такая функция называется обратимой).

Теорема (необходимое и достаточное условие обратимости функции)

Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.

Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.

Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.

Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.

Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).

1) x=y².

$[{y^2} = x, Rightarrow y = pm sqrt x .]$

Так как y≥0, то

то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:

В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.

Источник

Нахождение формулы для функции, обратной данной

Пользуясь формулой (y = f(x)), следует выразить (x) через (y), а в полученной формуле (x = g(y)) заменить (x) на (y), а (y) на (x).

Пример:

найти функцию, обратную для функции

y=x2,x∈0;+∞)

Функция

y=x2

возрастает на промежутке

0;+∞)

. Делаем вывод, что обратная функция существует. Если значения (x) принадлежат промежутку

0;+∞)

, то

x=y

. Заменим (x) на (y), а (y) на (x), получим обратную функцию

y=x,x∈0;+∞)

. Обратная функция определена на промежутке

0;+∞)

и её график симметричен графику функции

y=x2,x∈0;+∞)

относительно прямой (y=x).

Источник

Загрузить PDF

Математические функции, обычно обозначаемые как f(x) или g(x), можно представить как порядок выполнения математических операций, которые позволяют прийти от «x» к «y». Обратная функция f(x) записывается как f^-1(x).^[1] В случае простых функций найти обратную функцию несложно.

Шаги

1
Полностью перепишите функцию, заменив f(x) на y. При этом «у» должна находиться на одной стороне функции, а «x» — на другой. Если вам дана функция вида 2 + y = 3x², вам необходимо изолировать «у» на одной стороне, а «x» — на другой.
- Пример. Перепишем данную функцию f(x) = 5x — 2 как y = 5x — 2. f(x) и «y» взаимозаменяемы.
- f(x) — это стандартная запись функции, но если вы имеете дело с несколькими функциями, то каждой из них нужно будет присвоить свою букву, чтобы их было легче отличать друг от друга. Например, часто функции обозначают как g(x) и h(x).
2
Найдите «x». Другими словами, выполните математические операции, необходимые для изолирования «x» по одну сторону от знака равенства. Основные алгебраические принципы: если «x» имеет числовой коэффициент, то разделите обе стороны функции на этот коэффициент; если к члену с «x» прибавляется некоторый свободный член, вычтите его с обеих сторон функции (и так далее).
- Помните, что вы можете применять любую операцию по отношению к одной из сторон уравнения только в том случае, если вы применяете ту же операцию по отношению ко всем членам по обе стороны от знака равенства.^[2]
- В нашем примере добавьте 2 к обеим частям уравнения. Вы получите y + 2 = 5x. Затем разделите обе части уравнения на 5 и получите (y + 2)/5 = x. И, наконец, перепишите уравнение с «x» в левой части: x = (y + 2)/5.
3
Поменяйте переменные, заменив «x» на «y» и наоборот. Результатом будет функция, обратная исходной. Другими словами, если мы подставим значение «x» в исходное уравнение и найдем значение «у», то, подставив это значение «у» в обратную функцию, мы получим значение «x».
- В нашем примере получим y = (x + 2)/5.
4
Замените «у» на f^-1(x). Обратные функции обычно записывают в виде f^-1(x) = (члены с «x»). Следует отметить, что в данном случае -1 — это не показатель степени; это просто обозначение обратной функции.
- Так как «x» в -1 степени равно 1/x, то f^-1(x) — это форма записи 1/f(x), что также обозначает функцию, обратную f(x).
5
Проверьте работу, вместо «x» подставив постоянное значение в исходную функцию. Если вы правильно нашли обратную функцию, подставив в нее значение «у», вы найдете подставленное значение «x».
- Например, подставьте x = 4. Вы получите f(x) = 5(4) — 2 или f(x) = 18.
- Теперь подставьте 18 в обратную функцию и получите y = (18 + 2)/5 = 20/5 = 4. То есть у = 4. Это подставленное значение «x», поэтому вы правильно нашли обратную функцию.
Реклама

Советы

Когда вы выполняете алгебраические операции над функциями, вы можете свободно заменять f(x) = y и f^(-1)(x) = y в обоих направлениях. Но прямая запись обратной функции может привести к путанице, поэтому придерживайтесь записи f(x) или f^(-1)(x), которая поможет вам отличить их друг от друга.
Обратите внимание, что обратная функция обычно (но не всегда) является функциональной зависимостью.^[3]

Об этой статье

Эту страницу просматривали 63 637 раз.

Была ли эта статья полезной?

Источник

Обратная функция — функция y=g(x), которая получается из данной функции y=f(x), если из отношения x=f(y) выразить y через x.

Чтобы для данной функции y=f(x) найти обратную, надо:

1.В соотношении y=f(x) заменить x на y, а y — на x: x=f(y) .

2.В полученном выражении x=f(y) выразить y через x.

Функции f(x) и g(x) — взаимно обратны.

Примеры нахождения обратных функций:

1) y=3x-8

1. x=3y-8

2. 3y=x+8

y=(x+8)/3.

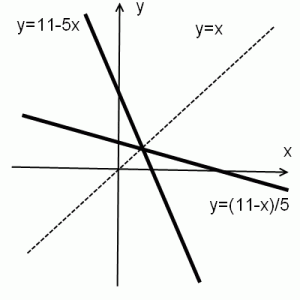
2) y=11-5x

1. x=11-5y

2. 5y=11-x

y=(11-x)/5.

Область определения и область значений функций f и g меняются местами: область определения f является областью значений g, а область значений f — областью определения g.

Не для всякой функции можно указать обратную. Условие обратимости функции — ее монотонность, то есть функция должна только возрастать или только убывать. Если функция не монотонна на всей области определения, но монотонная на некотором промежутке, тогда можно задать обратную ей функцию только на этом промежутке.

Пример обратных функций, заданных на промежутке.

y=x².

Это — квадратичная функция. Она убывает на промежутке (-∞;0), и

возрастает на промежутке (0;∞). Возьмем промежуток [0;∞). На этом промежутке функция монотонна, поэтому обратима. Ищем обратную функцию.

1. x=y²

2. y=√x.

y=x² и y=√x на [0;∞) — взаимно обратные функции.

Графики взаимно-обратных функций симметричны относительно прямой y=x.

Источник

Функцию y=f(x)называютобратимойна промежутке|a,b|,
если любое свое значение она принимает
не более чем в одной точке этого
промежутка; иными словами, если различным
значениям аргумента соответствуют
различные значения функции.

Пусть обратимая функция y=f(x)задана на промежутке|a,b|и пустьE(y)=|A,B|.
Каждомуy|A,B|поставим в соответствие то единственное
значениеx[a,b],
для которогоf(x)=y.
Тем самым на|A,B|будет определена функция,
которую называютобратнойпо
отношению к функцииy=f(x).

Отметим, что если
обратная дляy=f(x),
то и функцияy=f(x)является обратной для.
Поэтому, эти две функции часто называютвзаимнообратными. Такие функции
обладают очевидными свойствами:

Графики взаимно обратных функций
совпадают. Можно, однако, потребовать,
чтобы и аргумент обратной функции
обозначался буквой x,
т.е. вместорассматривать функцию.
Графики такой пары функцийy=f
(x)исимметричны относительно прямойy=x.

Можно доказать, что всякая строго
монотонная функция имеет обратную,
причем с тем же направлением монотонности.

Алгоритм нахождения обратной функции
для функции y=f(x)следующий:

1) убедиться, что y=f(x)обратима (например, монотонная);

2) решить уравнение y=f(x)относительноx;

3) в полученном равенстве поменять
местами xиy.

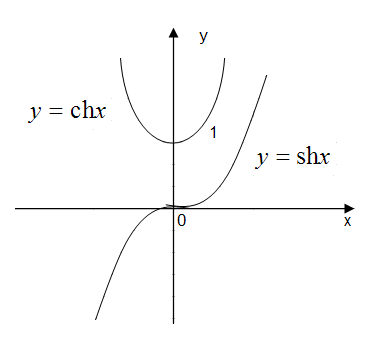
Пример. Найдем обратную
функцию для функции(т.н. синус гиперболический).

а) Проверим монотонность. Пусть x₁>x₂.
Тогда.

Функция y=e^x– возрастающая, поэтому разность в
первой скобке положительна, аy=e^^x– убывающая, поэтому вторая разность
– отрицательна. Значит,
т.е,
т.е.y=
shx– возрастающая функция, следовательно,
обратимая.

б) Решим уравнение y=shx
относительноx:

– не подходит, ибо

Итак,
,
т.е..

в) Поменяв местами xиy,
получим искомую обратную функцию:

§2. Элементарные функции

I Основные элементарные функции

Косновным элементарным функциям относят
константы, степенные, показательные,
логарифмические, тригонометрические
и обратные тригонометрические.

1) Константыy
= Const.

D(y)
= R,
E(y)={c}.

не существует, четная.

График – прямая, параллельная оси
абсцисс.

2)Степенные
.

D(y)
иE(y)
зависят от,
но
(0,
+)
D(y).

Четность-нечетность зависит от .

Обратная для
есть.

Для <0
оси координат – асимптоты.

Показательные
(0<a1).

D(y)
= R,
E(y)
= (0,
+).

Функция общего вида.

Ось абсцисс – асимптота.

Обратная для функции
есть логарифмическая функция.

Логарифмическая(0<a1).

D(y)
= (0,
+),
E(y)
= R.

Функция общего вида.

Ось ординат – асимптота.

Обратная для логарифмической –
показательная функция.

В математическом анализе в основном
используют натуральные логарифмы lnx,
т.е. логарифмы с основанием
a=e=2,7…

5) Тригонометрические

а)
.

D(y)
= R,
E(y)
= [1,
1].

Нечетная.

Периодическая,
.

б)
.

D(y)
= R,
E(y)
= [1,
1].

Четная.

Периодическая,
.

в).

D(y)
= R
{,
kz},

E(y)
= R.

Нечетная.

Периодическая,
.

Прямые
асимптоты.

г)
.

D(y)
= R
{k,
kz},
E(y)
= R

Нечетная.

Периодическая,
.

Прямые x
= kасимптоты.

6) Обратные тригонометрические

При определении этих функций выбираются
следующие участки монотонности: для
синуса ,
для косинуса[0,
],
для тангенса,
для котангенса(0,
).

Определение, например, арксинуса:

arcsina
– это угол
такой, что
sin=a.
Остальные
функции
определяются аналогично.

а)
.

D(y)
= [1,
1], E(y)
= .

Нечетная.

б).

D(y)
= [1,
1], E(y)
= [0, ].

arccos(x)
= 

arccosx.

arcsinx
+ arccosx
=
.

в)
.

D(y)
= R,
E(y)
= .

Нечетная.

Прямые
асимптоты.

г).

D(y)
= R,
E(y)
= (0, ).

arcctg(x)
= 

arcctgx.

Прямые y
= 0иy
= асимптоты.

Замечание. Иногда к основным
элементарным функциям относят еще и
т.н. гиперболические функции и обратные
к ним. Все эти функции достаточно просто
выражаются через показательную и
логарифмическую функции.

а) синус гиперболический
:D(y)
= R,
E(y)
= R,
нечетная; обратная функция имеет видy
= Arshx
=.