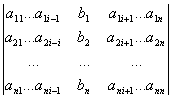Как найти обратную матрицу для неквадратной матрицы

Содержание

Вычисление обратной матрицы

Напомним, что обратной для квадратной матрицы $A$ порядка $n$ называется такая матрица, обычно ее обозначают $A^{-1}$, которая удовлетворяет условиям:

$Acdot A^{-1}=E$ и $A^{-1}cdot A=E$.

Существует по крайней мере два «хороших»1) алгоритма нахождения обратной матрицы.

Метод алгебраических дополнений

Задача 1. Найти обратную матрицу для

$A=begin{pmatrix}1 & 2\2 & 5end{pmatrix}$.

Решение. Матрица квадратная — по крайней мере в этом подвоха нет. Запомните, что для неквадратной матрицы обратную вычислить нельзя!!!

Шаг 1. Вычислить определитель. Вычисляем по формуле из примера 1.2)

$begin{vmatrix}1 & 2\2 & 5end{vmatrix} = 1cdot 5 - 2cdot 2 = 1$.

Определитель не равен нулю, поэтому обратная матрица существует. Переходим на следующий шаг.

Шаг 2. Вычислить алгебраические дополнения для каждого элемента.

Алгебраическое дополнение для левого верхнего элемента ( для 1 ).
Он стоит в первой строке и первом столбце. Мысленно вычеркнем их. Останется 5. Поэтому алгебраическое дополнение

$A^{1}_{1}=(-1)^{1+1}cdot 5=5$.

Алгебраическое дополнение для 2 ( 1-я строка, 2-й столбец ):

$A^{1}_{2}=(-1)^{1+2}cdot 2=-2$.

Алгебраическое дополнение для 2 ( 2-я строка, 1-й столбец ):

$A^{2}_{1}=(-1)^{2+1}cdot 2=-2$.

Алгебраическое дополнение для 5 ( 2-я строка, 2-й столбец ):

$A^{2}_{2}=(-1)^{2+2}cdot 1=1$.

Шаг 3. Составить матрицу из алгебраических дополнений.

$widetilde{A}=begin{pmatrix}A^{1}_{1} & A^{1}_{2}\A^{2}_{1} & A^{2}_{2}end{pmatrix}= begin{pmatrix}5 & -2\-2 & 1end{pmatrix}$.

Шаг 4. Транспонировать матрицу $widetilde{A}$ из шага 3.

$A^*=begin{pmatrix}5 & -2\-2 & 1end{pmatrix}$.

Совершенно случайно у нас получилось то же самое. Так бывает. Иногда.

Шаг 5. ( Последний! ) Умножить матрицу $A^*$ на число, обратное определителю.
Определитель у нас был равен 1.

$A^{-1}=dfrac{1}{1}cdot begin{pmatrix}5 & -2\-2 & 1end{pmatrix}= begin{pmatrix}5 & -2\-2 & 1end{pmatrix}$.

Это и есть обратная матрица.

Сделаем проверку. Если не помните, как умножать матрицы, загляните сначала сюда.

$begin{pmatrix}5 & -2\-2 & 1end{pmatrix}cdot begin{pmatrix}1 & 2\2 & 5end{pmatrix}=begin{pmatrix}5cdot 1-2cdot 2 & 5cdot 2-2cdot 5\ -2cdot 1+1cdot 2 & -2cdot 2+1cdot 5end{pmatrix}=begin{pmatrix}1 & 0\0 & 1end{pmatrix}$.

Получили единичную матрицу, значит, обратную матрицу $A^{-1}$ нашли правильно.

Вообще нужно делать проверку и для

$begin{pmatrix}1 & 2\2 & 5end{pmatrix}cdot begin{pmatrix}5 & -2\-2 & 1end{pmatrix}$.

Но мы этого делать не будем, потому что знаем из теории, что если $A^{-1}cdot A=E$ выполнено, то и $Acdot A^{-1}=E$ также будет выполнено. ( Проверьте! )

Метод элементарных преобразований

Задача 3. Найти обратную матрицу для

$A=begin{pmatrix}1 & 2\2 & 5end{pmatrix}$.

Решение. Это матрица из задачи 1. Найдем обратную к ней другим способом.

1. Припишем справа от матрицы единичную матрицу. Получим

$begin{pmatrix}1 & 2 & 1 & 0\2 & 5 & 0 & 1end{pmatrix}$

2. Теперь методом элементарных преобразований только над строками матрицы приведем ее к виду

$begin{pmatrix}1 & 0 & * & *\0 & 1 & * & *end{pmatrix}$

.

Вычтем из второй строки первую, умноженную на 2:

$begin{pmatrix}1 & 2 & 1 & 0\0 & 1 & -2 & 1end{pmatrix}$

Вычтем из первой строки вторую, умноженную на 2:

$begin{pmatrix}1 & 0 & 5 & -2\0 & 1 & -2 & 1end{pmatrix}$

Матрица справа будет обратной:

$begin{pmatrix}5 & -2\-2 & 1end{pmatrix}$.

Решение совпадает с решением задачи 1.

Наверх

Источник

Обра́тная
ма́трица — такая матрица A−1, при
умножении на которую, исходная матрица
A даёт в результате единичную матрицу
E:

Квадратная
матрица обратима тогда и только тогда,
когда она невырожденная, то есть её
определитель не равен нулю. Для
неквадратных матриц и вырожденных
матриц обратных матриц не существует.

Свойства
обратной матрицы

,
гдеобозначает определитель.

для любых двух обратимых матрици.

гдеобозначает транспонированную матрицу.

для любого коэффициента.

Если необходимо
решить систему линейных уравнений
,
(b — ненулевой вектор) где— искомый вектор, и еслисуществует, то.
В противном случае либо размерность
пространства решений больше нуля, либо
их нет вовсе.

Нахождение
с помощью матрицы алгебраических
дополнений

— транспонированная матрица алгебраических
дополнений;

Полученная
матрица A−1и будет обратной.
Сложность алгоритма зависит от сложности
алгоритма расчета определителя Odet и
равна O(n²)·Odet.

Иначе говоря,
обратная матрица равна единице, делённой
на определитель исходной матрицы и
умноженной на транспонированную матрицу
алгебраических дополнений элементов
исходной матрицы.

5)Теорема о существовании и единственности обратной матрицы.

Теорема
(единственности существования обратной
матрицы): Если у матрицы
существует обратная матрица,
то она единственна.

Доказательство.

Пусть существует
матрица
,
для которойи матрица,
для которой.

Тогда
,
то есть.
Умножим обе части равенства на матрицу,
получим,
гдеи.

Значит,
,
что и требовалось доказать.

6) Теорема Кронекера – Капели

Система линейных
алгебраических уравнений совместна
тогда и только тогда, когда ранг её
основной матрицы равен рангу её
расширенной матрицы, причём система
имеет единственное решение, если ранг
равен числу неизвестных, и бесконечное
множество решений, если ранг меньше
числа неизвестных.

Необходимость

Пусть система
совместна. Тогда существуют числа
такие, что.
Следовательно, столбецявляется линейной комбинацией столбцовматрицы.
Из того, что ранг матрицы не изменится,
если из системы его строк (столбцов)
вычеркнуть или приписать строку
(столбец), которая является линейной
комбинацией других строк (столбцов)
следует, что.

Достаточность

Пусть
.
Возьмем в матрицекакой-нибудь базисный минор. Так как,
то он же и будет базисным минором и
матрицы.
Тогда согласно теореме о базисном миноре
последний столбец матрицыбудет линейной комбинацией базисных
столбцов, то есть столбцов матрицы.
Следовательно, столбец свободных членов
системы является линейной комбинацией
столбцов матрицы.

7) Метод крамера (вывод) решения систем линейных уравнений.

Метод (Крамера).

Если матрица
квадратной системы невырожденная, то
система определенная.

В этом случае
решение системы может быть найдено по
формулам
,

где
—
определитель системы;—
определитель матрицы, получаемой из
основной матрицы системы заменой её-го
столбца столбцом свободных членов.

Теорема.
(Правило Крамера):

Теорема.
Система из n уравнений с n неизвестными

в случае, если
определитель матрицы системы не равен
нулю, имеет единственное решение и это
решение находится по формулам:

xi= Di/D,
где

D = det A, а Di– определитель матрицы, получаемой из
матрицы системы заменой столбца i
столбцом свободных членов bi.

Di=

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #

    29.05.20154.35 Mб56начерталка.rar.pdf

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Обра́тная ма́трица — такая матрица A-1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

{displaystyle AA^{-1}=A^{-1}A=E}

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, т.е. её определитель не равен нулю. Для неквадратных матриц и сингулярных матриц обратных матриц не существует.

Свойства обратной матрицы

Способы нахождения обратной матрицы

Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:

Точные (прямые) методы

Метод Гаусса

Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A-1.

При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц {displaystyle Lambda _{i}} (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):

{displaystyle Lambda _{1}cdot dots cdot Lambda _{n}cdot A=Lambda A=ERightarrow Lambda =A^{-1}}.
{displaystyle Lambda _{m}={begin{bmatrix}1&dots &0&-a_{1m}/a_{mm}&0&dots &0\&&&dots &&&\0&dots &1&-a_{m-1m}/a_{mm}&0&dots &0\0&dots &0&1/a_{mm}&0&dots &0\0&dots &0&-a_{m+1m}/a_{mm}&1&dots &0\&&&dots &&&\0&dots &0&-a_{nm}/a_{mm}&0&dots &1end{bmatrix}}}.

Вторая матрица после применения всех операций станет равна {displaystyle Lambda }, то есть будет искомой. Сложность алгоритма — {displaystyle O(n^{3})}.

С помощью союзной матрицы

{displaystyle A^{-1}={frac {1}{det A}}cdot (C^{*})^{T}}

{displaystyle C^{*}} — союзная матрица;

{displaystyle (C^{*})^{T}} — матрица, полученная в результате транспонирования союзной матрицы;

Полученная матрица A-1 и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n2)Odet.

Использование LU/LUP-разложения

Если матрица A невырождена то для нее можно расчитать LUP-разложение {displaystyle PA=LU}. Пусть {displaystyle PA=B}, {displaystyle B^{-1}=D}. Тогда из свойств обратной матрицы можно записать: {displaystyle D=U^{-1}L^{-1}}. Если умножить это равенство на U и L то можно получить два равенства вида {displaystyle UD=L^{-1}} и {displaystyle DL=U^{-1}}. Первое из этих равенств представляет собой систему из n2 линейных уравнений для {displaystyle {frac {n(n+1)}{2}}} из которых известны правые части (из свойств треугольных матриц). Второе представляет также систему из n2 линейных уравнений для {displaystyle {frac {n(n-1)}{2}}} из которых известны правые части (также из свойств треугольных матриц). Вместе они престаляют собой систему из n2 равенств. С помощью этих равенств можно реккурентно определить все n2 элементов матрицы D. Тогда из равенства (PA)-1 = A-1P-1 = B-1 = D. получаем равенство A-1 = DP.

Ниже представлен псевдокод на языке C++ алгоритма обращения матрицы с помощью LUP-разложения. 

Matrix Inverse(const Matrix &A) {
    //n - размерность квадратной матрицы A
    const int n=A.Rows();
    //при инициализации задается размерность nxn
    Matrix X(n, n);
    Matrix P(n, n);
    Matrix C(n, n);
    //предполагается что в результате следующего вызова матрица C = L + U - E
    LUP(A, C, P);
    for(int k = n-1; k >= 0; k--) {
        X[ k ][ k ] = 1;
        for( int j = n-1; j > k; j--) X[ k ][ k ] -= C[ k ][ j ]*X[ j ][ k ];
        X[ k ][ k ] /= C[ k ][ k ];
        for( int i = k-1; i >= 0; i-- ) {
            for( int j = n-1; j > i; j-- ) {
                X[ i ][ k ] -= C[ i ][ j ]*X[ j ][ k ];
                X[ k ][ i ] -= C[ j ][ i ]*X[ k ][ j ];
            }
            X[ i ][ k ] /= C[ i ][ i ];
        }
    }
    X = X*P
    return( X );
}

В случае использования вектора перестановок (см. LUP-разложение) вместо финального умножения потребуется следующий код: 

int temp;
for( int i = 0; i < n; i++ ) {
    temp = i;
    while( p[ temp ] != i ) temp++;
    X.SwapColumns(i, temp);
    p[ temp ] = p[ i ];
}

В случае использования LU-разложения не требуется перестановки столбцов матрицы D но решение может разойтись даже если матрица A невырождена.

Сложность алгоритма — O(n3).

Итерационные методы

Методы Шульца

{displaystyle {begin{cases}Psi _{k}=E-AU_{k},\U_{k+1}=U_{k}sum _{i=0}^{n}Psi _{k}^{i}end{cases}}}

Зейделева модификация метода

Оценка погрешности

Выбор начального приближения

Вообще, проблема выбора начального приближения {displaystyle U_{0}~} в рассматриваемых здесь процессах итерационного обращения матриц не позволяет относиться к ним как к самостоятельным универсальным методам, конкурирующими с прямыми методами обращения, основанными, например, на LU-разложении матриц. Имеются некоторые рекомендации по выбору {displaystyle U_{0}~}, обеспечивающие выполнение условия {displaystyle rho (Psi _{0})<1~} (спектральный радиус матрицы меньше единицы), являющегося необходимым и достаточным для сходимости процесса. Однако при этом, во-первых, требуется знать сверху оценку спектра обращаемой матрицы A либо матрицы {displaystyle AA^{T}~} (а именно, если A – симметричная положительно определенная матрица и {displaystyle rho (A)leq beta ~}, то можно взять {displaystyle U_{0}={alpha }E~}, где {displaystyle alpha in left(0,{frac {2}{beta }}right)~}; если же A – произвольная невырожденная матрица и {displaystyle rho (AA^{T})leq beta ~}, то полагают {displaystyle U_{0}={alpha }A^{T}~}, где также {displaystyle alpha in left(0,{frac {2}{beta }}right)~}; можно конечно упростить ситуацию и, воспользовавшись тем, что {displaystyle rho (AA^{T})leq {mathcal {k}}AA^{T}{mathcal {k}}~}, положить {displaystyle U_{0}={frac {A^{T}}{AA^{T}}}~}). Во-вторых, при таком задании начальной матрицы нет гарантии, что {displaystyle {mathcal {k}}Psi _{0}{mathcal {k}}~} будет малой (возможно, даже окажется {displaystyle {mathcal {k}}Psi _{0}{mathcal {k}}>1~}), и высокий порядок скорости сходимости обнаружится далеко не сразу.

См. также

  • Псевдообратные матрицы

Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Обратная матрица. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

Источник

Заказать задачи по любым предметам можно здесь от 10 минут

Как найти обратную матрицу

  1. Быстрый способ для матриц $2 times 2$
    1. Пример 1
    2. Пример 2
  2. Нахождение с помощью метода Гаусса
    1. Пример 3
    2. Пример 4
  3. Метод союзной матрицы(алгебраические дополнения)
    1. Пример 5

Обратная матрица обозначается $ A^{-1} $ и существует только для матриц, у которых определитель не равен нулю $ det A neq 0 $.

Быстрый способ для матриц $2 times 2$

Пусть задана матрица $A = begin{pmatrix} a&b\c&d end{pmatrix}$. Для быстрого способа нахождения обратной матрицы необходимо поменять местами элементы стоящие на главной диагонали, а для оставшихся элементов поменять знак на противоположный. Затем каждый элемент разделить матрицы разделить на определитель исходной матрицы. Математическая формула выглядит следующим образом $$A^{-1} = frac{1}{det A} begin{pmatrix} d&-b \ -c&a end{pmatrix} = frac{1}{ad-bc} begin{pmatrix} d&-b \ -c&a end{pmatrix}.$$ 

Пример 1
Найти обратную матрицу для $A = begin{pmatrix} 3&4 \ 5&9 end{pmatrix}$.
Решение

Первым делом вычисляем определитель и убеждаемся, что он не равен нулю $$det A = begin{vmatrix} 3&4 \ 5&9 end{vmatrix} = 3cdot9 — 4cdot5 = 27 — 20 = 7.$$

Итак, определитель не равен нулю, значит, обратная матрица существует. Продолжаем наш алгоритм. Меняем элементы на главной диагонали местами, а у оставшихся элементов меняем знак на противоположный. $$A^{-1} = frac{1}{7} begin{pmatrix} 9&-4 \ -5&3 end{pmatrix} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}.$$
Ответ
$$A^{-1} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}$$
Пример 2
Вычислить обратную матрицу для $A = begin{pmatrix} 2&-1 \ 4&-6 end{pmatrix}$.
Решение

Находим определитель $$det A = begin{vmatrix} 2&-1 \ 4&-6 end{vmatrix} = 2cdot(-6) — 4cdot(-1) = -12 + 4 = -8.$$

Меняем местами элементы главной диагонали, а остальным меняем знак на противоположный. Не забываем затем каждый элемент разделить на определитель. $$A^{-1} = frac{1}{-8} begin{pmatrix} -6&1 \ -4&2 end{pmatrix} = begin{pmatrix} frac{-6}{-8}&frac{1}{-8} \ frac{-4}{-8}&frac{2}{-8} end{pmatrix} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$
Ответ
$$A^{-1} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$

Нахождение с помощью метода Гаусса

На практике чаще всего метод Гаусса используется как способ нахождения обратной матрицы. Суть метода в том, что к основной матрице добавляется дополнительная единичная матрица с такой же размерностью.

$$ Bigg (begin{matrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{matrix} Bigg | begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg ) $$

Далее нужно путем простейших элементарных преобразований привести левую матрицу к единичной, а одновременно с ней справа получится обратная матрица:

$$ Bigg (begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg | begin{matrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{matrix} Bigg ) $$

$$A^{-1} = begin{pmatrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{pmatrix}$$

Пример 3
Найти обратную матрицу элементарными преобразованиями $$A = begin{pmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{pmatrix}.$$
Решение

Вычисляем определитель матрицы, чтобы убедиться что он не равен нулю $$det A = begin{vmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{vmatrix} = 4-1+0-0-2-0=1 neq 0.$$

Выписываем основную матрицу и добавляем справа единичную матрицу. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ -1&-1&1 &|& 0&0&1 end{pmatrix}$$

Проводим элементарные преобразования над строками матриц таким образом, чтобы слева получилась единичная матрица. В то же время как справа получим обратную матрицу.

Умножаем третью строку на 2 и прибавляем первую. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&-3&2 &|& 1&0&2 end{pmatrix}$$

Умножаем третью строку на 2 и прибавляем к ней вторую строку, умноженную на 3. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$

Теперь запускаем обратный ход преобразований снизу вверх. Ко второй строке прибавляем третью. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$

Умножаем первую строку на 2 и прибавляем к ней вторую строчку матрицы. $$begin{pmatrix} 4&0&0 &|& 4&4&4 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$

Теперь, чтобы слева получилась единичная матрица нужно первую строку разделить на 4, вторую на 2. $$begin{pmatrix} 1&0&0 &|& 1&1&1 \ 0&1&0 &|& 1&2&2 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$

Справа как видим получилась обратная матрица $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}.$$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Ответ
$$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}$$
Пример 4
Дана матрица, найти обратную $$A = begin{pmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{pmatrix}.$$
Решение

Первым делом вычисляем определитель, чтобы убедиться в существовании обратной матрицы $$det A = begin{vmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{vmatrix} = 0+16+1-0-6-6=5.$$

Теперь справа от матрицы дописываем единичную матрицу $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 1&0&2 &|& 0&1&0 \ 4&1&3 &|& 0&0&1 end{pmatrix}.$$

Теперь с помощью элементарных преобразований делаем так, чтобы слева стояла единичная матрица. А справа получим одновременно обратную матрицу.

Умножаем вторую строку на 3 и вычитаем из неё первую. Умножаем третью строчку на 3 и вычитаем первую, умноженную на 4. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&-5&5 &|& -4&0&3 end{pmatrix}$$

Умножаем третью строку на 2 и вычитаем вторую, умноженную на 5. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-15 &|& -3&-15&6 end{pmatrix}$$

Третью строку можно разделить на 3, чтобы уменьшить числа для дальнейшего удобства. Сделаем это. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$

Начинаем проводить преобразования над строками теперь снизу вверх. Умножаем первую строку на 5 и прибавляем к ней третью. Ко второй строке просто прибавляем третью. $$begin{pmatrix} 15&10&0 &|& 4&-5&2 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$

К первой строке прибавляем вторую, умноженную на 5. $$begin{pmatrix} 15&0&0 &|& -6&-15&12 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$

Осталось разделить первую строку на 15, вторую на (-2), а третью на (-5). $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$
Ответ
$$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$

Метод союзной матрицы(алгебраические дополнения)

Формула нахождения обратной матрицы через алгебраические дополнения выглядит следующим образом

$$A^{-1} = frac{1}{|A|} (A^*)^T. $$

Матрица $A^*$ называется союзной (присоединенной) матрицей и представляет собой набор алгебраических дополнений матрицы $ A $:

$$ A^* = begin{pmatrix} A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_{31}&A_{22}&A_{33} end{pmatrix}, text{ где } A_{ij}=(-1)^{i+j} M_{ij} $$

$M_{ij} $ называется минором матрицы, который получается путем вычеркивания $ i $-ой строки и $ j $-того столбца из матрицы.

Пример 5
Найти обратную матрицу методом алгебраических дополнений $$ A = begin{pmatrix} 3&1&2\-1&3&-2\0&-1&4 end{pmatrix} $$
Решение

Итак, пользуемся формулой $ A^{-1} = frac{1}{|A|} (A^*)^T $

Первым делом вычисляем определитель матрицы $ A $, так как необходимым условием существование обратной матрицы является неравенство его к нулю:

$$ |A| = begin{vmatrix} 3&1&2\-1&3&-2\0&-1&4 end{vmatrix} = 36 + 0 + 2 — 0 — 6 + 4 = 36 neq 0 $$

Находим алгебраические дополнения матрицы $ A $. Для этого удаляем все элементы стоящие в i-ой строке и в j-ом столбце. Оставшиеся элементы матрицы переписываем в определитель и проводим его вычисление.

Вычеркиваем первую строку и первый столбец:

$$ A_{11} = (-1)^{1+1} cdot begin{vmatrix} 3&-2\-1&4 end{vmatrix} = 12 — 2 = 10 $$

Убираем первую строку и второй столбец:

$$ A_{12} = (-1)^{1+2} cdot begin{vmatrix} -1&-2\0&4 end{vmatrix} = -(-4 — 0) = 4 $$

Оставшиеся алгебраические дополнения находим по аналогии с предыдущими двумя.

$$ A_{13} = (-1)^{1+3} cdot begin{vmatrix} -1&3\0&-1 end{vmatrix} = 1 — 0 = 1 $$

$$ A_{21} = (-1)^{2+1} cdot begin{vmatrix} 1&2\-1&4 end{vmatrix} = -(4 + 2) = -6 $$

$$ A_{22} = (-1)^{2+2} cdot begin{vmatrix} 3&2\0&4 end{vmatrix} = 12 — 0 = 12 $$

$$ A_{23} = (-1)^{2+3} cdot begin{vmatrix} 3&1\0&-1 end{vmatrix} = -(-3 — 0) = 3 $$

$$ A_{31} = (-1)^{3+1} cdot begin{vmatrix} 1&2\3&-2 end{vmatrix} = -2 — 6 = -8 $$

$$ A_{32} = (-1)^{3+2} cdot begin{vmatrix} 3&2\-1&-2 end{vmatrix} = -(-6 + 2) = 4 $$

$$ A_{33} = (-1)^{3+3} cdot begin{vmatrix} 3&1\-1&3 end{vmatrix} = 9+1 = 10 $$

Составляем союзную (присоединенную) матрицу $ A^* $ из алгебраических дополнений:

$$ A^* = begin{pmatrix} 10&4&1\-6&12&3\-8&4&10 end{pmatrix}. $$

Транспонируем её и обозначаем $ (A^*)^T $:

$$ (A^*)^T = begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$

В итоге находим обратную матрицу $ A^{-1} $:

$$ A^{-1} = frac{1}{36} begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$

Делим каждый элемент матрицы на 36 и получаем следующее: $$begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}.$$
Ответ
$$A^{-1} =begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}$$
Источник

Матрица BB является обратной матрицей к квадратной матрице AA, если AB=BA=EAB = BA = E.
Из определения можно понять, что обратная матрица BB будет квадратной матрицей аналогичного порядка, какой имеет матрица AA (иначе какое-либо из произведений ABAB или BABA будет не определено).
Обратная матрица для исходной матрицы AA определяется так: A−1A^{-1}. Можно утверждать, что если A−1A^{-1} существует, то AA−1=A−1A=EAA^{-1} = A^{-1} A= E.
Также легко видеть, что (A−1)−1=A(A^{-1})^{-1} = A.

Если детерминант матрицы является нулем, то обратную к ней матрицу нельзя получить.

Онлайн-калькулятор

Квадратную матрицу AA можно назвать вырожденной матрицей тогда, когда определитель матрицы AA равен нулю, и невырожденной, если определитель не равен нулю.

Важно

В том случае, если обратная матрица может существовать, то она будет единственной.

Формула для вычисления обратной матрицы

Обратную матрицу A−1A^{-1} к матрице AA можно найти по формуле:

A−1=1det⁡A⋅A∗A^{-1}=frac{1}{det A}cdot A^*

det⁡Adet A — определитель матрицы A,A,

A∗A^* — транспонированая матрица алгебраических дополнений к матрице A.A.

Задача 1

Нужно найти обратную матрицу для следующей матрицы:

A=(1−20 342 −131)A = begin{pmatrix}
1& -2 & 0\
3 & 4 & 2\
-1& 3& 1 \
end{pmatrix}

Решение

Вычислим детерминант:

det⁡A=∣1−20342−131∣=1∣4231∣−(−2)∣32−11∣+0∣34−13∣=8det A = begin{vmatrix}
1 & -2 & 0 \
3 & 4 & 2 \
-1 & 3 & 1 \
end{vmatrix} = 1 begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} — (-2) begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} +0 begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 8

Так как det⁡A≠0det A neq 0, то матрица – невырожденная, и обратная для нее существует.

Посчитаем алгебраические дополнение:

A11=(−1)1+1∣4231∣=−2,A_{11} = (-1)^{1+1} begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} = -2,

A12=(−1)1+2∣32−11∣=−5,A_{12} = (-1)^{1+2} begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} = -5,

A13=(−1)1+3∣34−13∣=13A_{13} = (-1)^{1+3} begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 13,

A21=(−1)2+1∣−2031∣=2A_{21} = (-1)^{2+1} begin{vmatrix}
-2 & 0 \
3 & 1 \
end{vmatrix} = 2,

A22=(−1)2+2∣10−11∣=1A_{22} = (-1)^{2+2} begin{vmatrix}
1 & 0 \
-1 & 1 \
end{vmatrix} = 1,

A23=(−1)2+3∣1−2−13∣=−1A_{23} = (-1)^{2+3} begin{vmatrix}
1 & -2 \
-1 & 3 \
end{vmatrix} = -1,

A31=(−1)3+1∣−2042∣=−4A_{31} = (-1)^{3+1} begin{vmatrix}
-2 & 0 \
4 & 2 \
end{vmatrix} = -4,

A32=(−1)3+2∣1032∣=−2A_{32} = (-1)^{3+2} begin{vmatrix}
1 & 0 \
3 & 2 \
end{vmatrix} = -2,

A33=(−1)3+3∣1−234∣=10.A_{33} = (-1)^{3+3} begin{vmatrix}
1 & -2 \
3 & 4 \
end{vmatrix} = 10.

Обратная матрица:

A−1=18(−22−4−51−213−110)A^{-1} = frac{1}{8} begin{pmatrix}
-2 & 2 & -4 \
-5 & 1 & -2 \
13 & -1 & 10 \
end{pmatrix}

Важно

Чтобы избежать ошибок, необходимо сделать проверку: для этого нужно посчитать произведение первоначальной матрицы на конечную. Если в результате получится единичная матрица, то вы нашли обратную матрицу безошибочно.

Задача 2

Найдите обратную матрицу для матрицы:

A=(13−25)A = begin{pmatrix}
1 & 3\
-2 & 5 \
end{pmatrix}

Решение

det⁡A=11≠0→A−1det A= 11 neq 0 rightarrow A^{-1} – существует.

A11=(−1)1+1⋅5=5A_{11} = (-1)^ {1+1} cdot 5 = 5,

A12=(−1)1+2⋅(−2)=2A_{12} = (-1)^ {1+2} cdot (-2) = 2,

A21=(−1)2+1⋅3=−3A_{21} = (-1)^ {2+1} cdot 3 = -3,

A22=(−1)2+2⋅1=1.A_{22} = (-1)^ {2+2} cdot 1 = 1.

Ответ:

A−1=111(5−321)A^{-1} = frac{1}{11} begin{pmatrix}
5 & -3 \
2 & 1 \
end{pmatrix}

Нами был рассмотрен способ нахождения матрицы с помощью алгебраических дополнений. Существует еще один способ, который называется методом элементарных преобразований.

Метод элементарных преобразований

Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:

  1. перестановка местами любых двух рядов (строк или столбцов) матрицы;
  2. умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
  3. прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.

Рассмотрим алгоритм нахождения обратной матрицы данным методом.

Алгоритм нахождения обратной матрицы методом элементарных преобразований

  1. Из исходной матрицы AA и единичной матрицы EE того же порядка составить расширенную матрицу, т.е. матрицу вида (A∣E)begin{pmatrix}A|Eend{pmatrix}.
  2. С помощью элементарных преобразований над строками расширенной матрицы получить единичную матрицу слева от черты: (E∣A−1)begin{pmatrix}E|A^{-1}end{pmatrix}.
  3. Выписать обратную матрицу, которая находится справа от черты.
Задача 1

Найти матрицу K−1K^{-1}, если K=(1301)K=begin{pmatrix}1&3\0&1end{pmatrix}.

Из матрицы KK второго порядка и единичной матрицы второго порядка составим расширенную матрицу:

(1301∣1001)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.

Произведем элементарные преобразования расширенной матрицы.

Прибавим к строке №1 строку №3, умноженную на -3:

(1301∣1001)∼(1001∣1−301)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}1&-3\0&1end{matrix}end{pmatrix}.

Слева получили единичную матрицу.

Выпишем обратную матрицу:

K−1=(1−301)K^{-1}=begin{pmatrix}1&-3\0&1end{pmatrix}.

Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.

K⋅K−1=(1301)⋅(1−301)=(1⋅1+3⋅01⋅(−3)+3⋅10⋅1+1⋅00⋅(−3)+1⋅1)=(1001)Kcdot K^{-1}=begin{pmatrix}1&3\0&1end{pmatrix}cdotbegin{pmatrix}1&-3\0&1end{pmatrix}=begin{pmatrix}1cdot1+3cdot0&1cdot(-3)+3cdot1\0cdot1+1cdot0&0cdot(-3)+1cdot1end{pmatrix}=begin{pmatrix}1&0\0&1end{pmatrix}.

Значит, обратная матрица найдена правильно.

Задача 2

Найти матрицу F−1F^{-1}, если F=(110010033)F=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}.

Из матрицы FF третьего порядка и единичной матрицы третьего порядка составим расширенную матрицу:

(110010033∣100010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}.

Произведем элементарные преобразования расширенной матрицы.

Прибавим к строке №1 строку №2, умноженную на -1:

(110010033∣100010001)∼(100010033∣1−10010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}.

Прибавим к строке №3 строку №2, умноженную на -3:

(100010033∣1−10010001)∼(100010003∣1−100100−31)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}.

Умножим строку №3 на 13frac{1}{3}:

(100010003∣1−100100−31)∼(100010001∣1−100100−113)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{matrix}end{pmatrix}.

Слева получили единичную матрицу.

Выпишем обратную матрицу:

F−1=(1−100100−113)F^{-1}=begin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}.

Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.

F⋅F−1=(110010033)⋅(1−100100−113)=(100010001)Fcdot F^{-1}=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}cdotbegin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}=begin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}.

Значит, обратная матрица найдена правильно.

Выполнение контрольных работ на заказ недорого от профильных авторов на бирже Студворк!

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти крутящий момент через угловую скорость
  • Как найти период волны формулы
  • Советы как найти автомобиль
  • Как найти фотофиксацию нарушения пдд
  • Как найти тематический чат в телеграмме