Как найти обратные подстановки

Определение 3.3.
Перестановками
из
элементов без повторенийназывают
размещения без повторений из
по.

Число всех
перестановок без повторений из
элементов обозначают символом.
Из определения 3.3 и формул (3.7) и (3.8)
получаем формулу вычисления:

(3.9)

Замечание.

Согласно определению
3.2, размещения без повторений есть
инъективные функциональные соответствия
на множестве
.
В случае перестановок.
Следовательно, перестановки являются
взаимно однозначными соответствиями
на множестве.
Переформулируем определение 3.3, используя
это замечание.

Определение 3.4.
Перестановками
из
элементов без повторений
называют взаимно однозначные соответствия
на множестве
_,
где
,.

Полезным в
приложениях является также следующая
формулировка определения перестановок

Определение
3.4^*.
Перестановками
из
элементов без повторенийназывают
последовательности, составленные из
элементов множества
,
(),
причем, никакие два элемента в любой
из таких последовательностей не равны
между собой.

Примеры.

1. Сколькими способами можно рассадить
10 гостей за прямоугольным столом?
Сколькими способами можно рассадить
гостей так, чтобы двое из них сидели
рядом?

На
рисунке указаны номера мест, на которые
рассаживаются гости. Место №1 – это
место «во главе стола», все остальные
места отсчитываются от него.

Рассадить гостей за таким столом – это
значит установить взаимно однозначное
соответствие между множеством
и множеством,
где— это список гостей. Число таких
соответствий есть число перестановок
без повторений из 10 элементов.
Следовательно, число способов рассадить
гостей равно.

Если два гостя хотят сидеть рядом, то
число распределяемых мест уменьшается,
можно считать в данной ситуации, что
два этих гостя занимают одно место,
являясь при распределении мест «одним
гостем». Число мест и гостей становится
меньше на единицу. Число способов,
которыми можно рассадить девять гостей
по девяти местам, равно числу перестановок
из девяти элементов:.

2. Требуется ответить на вопросы примера
1, но при условии, что стол круглый. (См.
рисунок).

Если стол круглый, то нет места «во
главе стола». Куда бы ни сел первый
гость, его место и будет началом отсчета
остальных мест. Иначе говоря, после того
как сел первый гость остается распределить
девять мест между девятью гостями.

Число способов сделать это равно числу
перестановок из девяти элементов:
.

Если при этом двоих гостей надо посадить
рядом (см. рисунок), то останется лишь
восемь мест для распределения. Число
способов сделать это равно числу
перестановок из восьми элементов:
.

Определение 3.5.
Подстановкой
множества

называют взаимно однозначное соответствие
на множестве
.

Не теряя общности
множество

в подстановке можно считать отрезком
числового ряда
.
Число всех подстановок такого множества
равно числу перестановок

Пусть Ρ_n=
– множество
всех таких подстановок. Определим на
множестве Ρ_n
бинарную операцию – умножение подстановок.

Определение 3.6.
Произведением
подстановок

(Ρ_n)
называют композицию этих подстановок.

Пример.

Рассмотрим
все подстановки множества,
представляя их матрицами и графами.

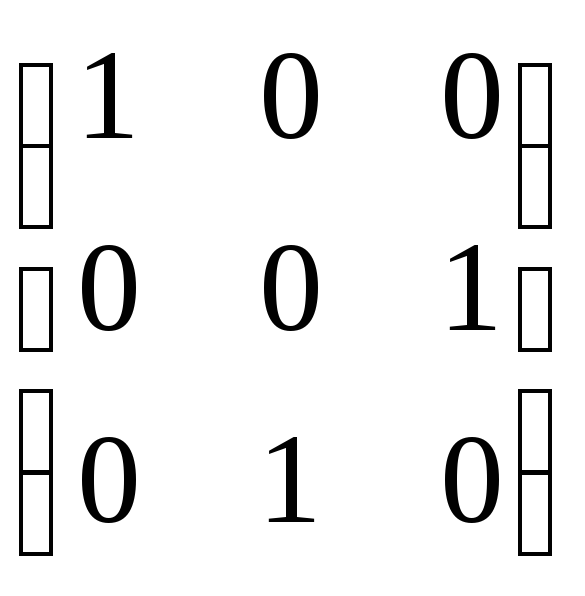
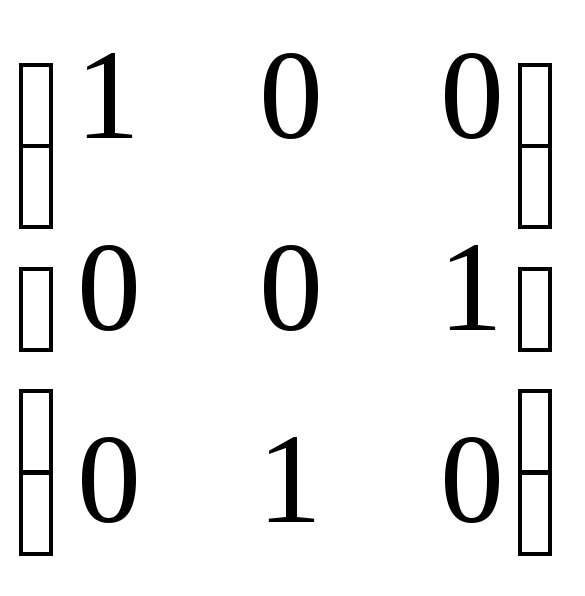
Подстановка
,
переводящая каждый элемент множествав себя, называют тождественной
подстановкой. Чтобы перемножить две
подстановки, надо перемножить их матрицы.
Например,

=;

==;

==.

Композиции подстановок можно находить
с помощью двустрочных матриц:

=;

=;

=.

Поскольку умножение матриц не является
коммутативным, умножение подстановок
также некоммутативно, например,
.

Тождественная подстановка имеет
единичную матрицу, поэтому умножение
любой подстановки
на тождественную не меняет,
т.е.играет в умножении подстановок роль
единицы.

Если
,
тоиназываютвзаимно обратными
подстановками, аналогично тому,
как числа, дающие при умножении друг на
друга единицу, называют взаимно обратными
числами. Подстановку, обратнуюобозначают.
Например,,
т.е.является обратной самой себе.

Покажем, как можно найти обратную
подстановку. Найдем, к примеру,
.
Пусть двустрочная матрица искомой
подстановки имеет вид:.
По определению обратной подстановки:,
следовательно, имеем:

.

.

Выполним проверку, перемножив матрицы
прямого и обратного соответствий:

==.

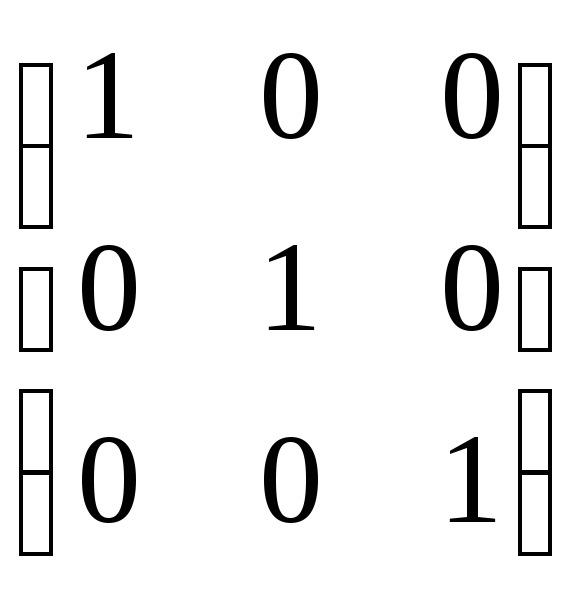
Найдем
.

=

Выполним проверку:

==.

Сделаем выводы,
обобщив результаты примера.

1. Множество всех
подстановок Ρ_n
содержит
элементов.

2. Произведение
любых двух подстановок из Ρ_n
есть подстановка из Ρ_n.

3. Во множестве Ρ_n
имеется тождественная подстановка
,
для которой выполняется равенство:Ρ_n).

4. Для каждой
подстановки
найдется обратная ей подстановка,
для которой выполняются равенства:.

5. Для
умножение подстановок не является
коммутативным.

Множество Ρ_n
с определенной в нем операцией умножения
называется симметрической
группой.

В перестановках
и подстановках элементы в последовательностях
не повторяются. Однако во многих задачах
требуется уметь находить число
последовательностей, отличающихся друг
от друга только порядком расположения
элементов, как в перестановках, но
содержащих определенное число одинаковых
элементов. Такие последовательности
называют перестановками
с повторениями.

Задача о вычислении
числа перестановок с повторениями
ставится следующим образом.

Пусть множество
,
из элементов которого образуются
последовательности, разбито на
непересекающиеся классыпо какому-либо отношению эквивалентности.
Напомним, что отношение эквивалентности
– это отношение сходства, «одинаковости»
элементов по какому-то признаку (см.
глава 2). Будем считать элементы одного
классанеразличимыми,
равными.

Таким образом,
,
причем, если,
то.
Элементы одного класса будем обозначать
одним символом:.
Пусть.

Определение 3.7.
Перестановками
с повторениями
называют последовательности, составленные
из всех элементов множества
,
(),
разбитого на классы эквивалентности,,
причем элементы, принадлежащие одному
классу равны друг другу.

–число всех
перестановок, в которых элемент
множестваповторяетсяраз,–раз, и т. д.,–раз,.

Найдем число таких
перестановок.

Возьмем какую-либо
последовательность
элементов множества.
Последовательность эта содержитэлементов из класса,– из класса,…,– из класса.
Переставляя между собой элементы классав последовательности, будем получать
неотличимые друг от друга последовательности,
поскольку неразличимы переставляемые
элементы. Всего таких одинаковых
последовательностей можно составить!,
так как именно столько существует
перестановок изэлементов. Далее в каждой полученной
последовательности выполним перестановки
элементов из класса.
При этом каждая имеющаяся перестановка
распадется на!
перестановок. Всего получитсянеотличимых друг от друга перестановок.
Продолжая этот процесс, получим класс
неотличимых друг от друга перестановок,
содержащийодинаковых последовательностей. Назовем
этот класс.

Теперь возьмем
последовательность
,
не вошедшую в класс,
и вновь переставляя неразличимые
элементы, получим классравных друг другу последовательностей
и также содержащийперестановок.

Будем продолжать
этот процесс, пока не исчерпаем всех
перестановок, которые можно образовать
из элементов множества
.
Посколькуэлементы множестваможно переставитьспособами.

Итак, имеем
последовательностей разбитых на классы,,…,равных друг другу последовательностей,
причем в каждый класс входитперестановок. Различных перестановок
столько, сколько образовано классов,
т.е..
Именно столько перестановок с повторениями
и можно получить из элементов множества.

Учитывая равенство
.
Получаем формулу (3.10).

(3.10)

Примеры.

1. Имеем множество
,
разбитое на два классаи,
причем,.
Составим из элементов множествавсе возможные перестановки.

Различные перестановки представлены
шестью классами
,,,,,по 4 перестановки в каждом классе. Внутри
классов перестановки неразличимы. Это
согласуется с формулой
.

Итак, из элементов множества
,
где,,
можно составить 6 различных перестановок.

2. Сколько различных семизначных кодов
можно составить из знаков «│» и
«|», если первый знак повторяется
3 раза, а второй – 4 раза?

Каждый код представляет собой
последовательность и 7 элементов, причем
элементы повторяются. В каждой
последовательности 3 элемента одного
вида и четыре элемента другого вида.
Следовательно каждый код есть перестановка
с повторениями. Число таких перестановок
.

Ответ: можно сделать 35 различных кодов,
удовлетворяющих заданным условиям.

Соседние файлы в папке учебник

• #
• #
• #
• #
• #
• #
• #
• #

Умножение перестановок

Определение:

Умножением (англ. multiplication) или композицией (англ. composition) перестановок, представленных в виде целочисленных функций , где позиция элемента, а — его номер, называется перестановка, получаемая по следующему правилу:

Утверждение:

Умножение перестановок ассоциативно:

Доказывается простым раскрытием скобок.

Перед прочтением примера перемножения перестановок рекомендуем познакомиться с циклами в данной статье: Действие перестановки на набор из элементов, представление в виде циклов

Пример

или

Обратная перестановка

Определение:

Обратной перестановкой (англ. inverse permutation) к перестановке называется такая перестановка, что:

Утверждение:

Для каждой перестановки существует перестановка, обратная ей.

Пусть дана перестановка , построим обратную ей перестановку : если , то . Очевидно, что данная перестановка является обратной к .

Также обратная перестановка единственна. Это следует из того, что для каждой -ой позиций в исходной перестановке однозначно определяется -ая позиций в обратной перестановке, значение которой есть

Определение:

Перестановка, равная своей обратной, называется инволюцией (англ. involution): , то есть её представление в виде циклов не содержит цикла, размер которого больше двух.

Утверждение:

Количество инволюционных перестановок длины может быть получено по формуле: , где

Докажем формулу по индукции. Базой являются . Предположим, что для всех , где , , формула верна. Рассмотрим перестановку длины и попробуем найти количество инволюций этой длины. Существует инволюций, при (у которых последний элемент представляет собой цикл длины ), а число инволюций длины , содержащих в своём представлении в виде циклов цикл , где , (так как при фиксированных и имеем перестановок оставшихся элементов, которые не нарушают свойств инволюции). Таким образом,

Определение:

Перестановка, содержащая чётное количество инверсий, называется чётной (англ. even permutation), в противном случае нечётной (англ. odd permutation).

Определение:

Перестановка, меняющая местами только два элемента, называется транспозицией (англ. transposition).

Лемма:

Если в перестановке, длина которой больше , поменять местами элемента, то её четность изменится.

Доказательство:

Для элементов, стоящих рядом, истинность утверждения очевидна: их взаимное расположение относительно других элементов не изменилось, а транспозиция этих чисел изменяет количество инверсий на единицу. Пусть теперь между перемещаемыми элементами и находятся элементов, то есть перестановка имеет вид: , . Сначала поменяем последовательно с числами , а затем число с рядом стоящими . В итоге мы выполним транспозиций рядом стоящих элементов, то есть чётность перестановки изменится.

Получение обратной перестановки

Пусть в массиве содержится перестановка, длины , тогда после выполнения алгоритма в массиве будет содержаться перестановка, обратная ей.

fun reversePerm(p : int[], rep : int[])
  for i = 1 to n
      rep[p[i]] = i;

Группа перестановок

Определение:

Группой (англ. group) называется множество с заданной на нём бинарной операцией , удовлетворяющей следующим свойствам: — ассоциативность соответствующей бинарной операции. Существование нейтрального элемента относительно операции , такого, что для любого Для любого существует называемый обратным элементом, такой, что

Утверждение:

Множество перестановок с элементами с операцией умножения является группой (часто группу перестановок называют симметрической (англ. symmetric group), и обозначают ).

Свойства и (ассоциативность умножения и существование обратной перестановки для любой из перестановок) доказаны выше, а в качестве нейтрального элемента выступает тождественная перестановка ().

Мощность симметрической группы:

Теорема Кэли утверждает, что любая конечная группа изоморфна подгруппе некоторой группе перестановок.

Группа чётных перестановок

Определение:

Группа чётных перестановок (англ. alternating group) является подгруппой симметричной группы перестановок, образованной всеми чётными перестановками. Композиция не выводит из группы, так как если представить каждую перестановку группы в виде чётного числа транспозиций и перемножить их, чётность не изменится.

Утверждение:

Количество чётных перестановок длины равно количеству нечётных и равно

Пусть число число чётных перестановок , а нечётных . Сделаем транспозицию для всех чётных перестановок. Получим нечётных различных перестановок, то есть . Проделаем то же самое с нечётными перестановками. Получим, что , то есть и .

Группа подстановок

Определение:

Подстановкой (англ. substitution) называется всякое взаимно однозначное отображение множества первых натуральных чисел на себя.

Всякая подстановка может быть записана при помощи двух перестановок, подписанных одна под другой:

Где через обозначается то число, в которое при подстановке переходит число .

Определение:

Группой подстановок (англ. group of substitutions) называется некоторая совокупность подстановок, замкнутая относительно композиции отображений, определяющей бинарную операцию для подстановок на одном и том же множестве.

См. также

• Теорема Кэли
• Действие перестановки на набор из элементов, представление в виде циклов

Источники информации

• Wikipedia — Involution

В чем разница между перестановкой и обратной перестановкой

Из любой таблицы инверсий d₁,d₂,…d_n можно однозначно восстановить перестановку, которая порождает данную таблицу, путем последовательного определения относительного расположения элементов n, n-1,….,1 (в этом порядке). Например перестановку, соответствующую таблице инверсий (2,3,6,4,0,2,2,1,0) = (d₁,d₂,d₃,d₄,d₅,d₆,d₇,d₈,d₉), можно построить следующим образом: выпишем число 9, так как d₈=1, то 8 стоит правее 9. Поскольку d₇=2, то 7 стоит правее 8 и 9. Так как d₆=2, то 6 стоит правее двух уже выписанных чисел, таким образом получается расположение чисел 9,8,6,7. Припишем теперь 5 слева, потому что d5=0, помещаем 4 вслед за четырьмя уже выписных числами, 3 после 6 выписанных чисел (т.е. в правый конец) и получаем 5,9,8,6,4,7,3. Вставив аналогичным образом 2 и 1, придем к перестановке (5,9,1,8,2,6,4,7,3).

Обратные перестановки

Не следует путать «инверсии» перестановок с обратными перестановками. Пусть a₁,a₂,….a_n — различные шары, индексы которых свяжем с номерами шаров. Тогда исходное расположение шаров однозначно определяется тождественной перестановкой (e=1,2,…n)

Обратной к перестановке называется перестановка которая получается, если в исходной перестановке поменять местами строки, а затем упорядочить столбцы в возрастающем порядке по верхним элементам, т.е. Ясно, что последовательное изменение порядка шаров согласно перестановкам и обратной приводит к исходному их расположению, т.е. к тождественной перестановке.

So, you have that $sigma_1$ is the cycle such that,

$$begin{align} 1 mapsto 2 \ 2 mapsto 3 \ 3 mapsto 1end{align}$$

It’s inverse, $sigma_1^{-1}$ is a cycle such that composition, $ sigma_1 circ sigma_1^{-1}=sigma_1^{-1} circ sigma_1$ is identity. So, the inverse cycle should look like :

$$begin{align} 2 mapsto 1 \ 3 mapsto 2 \ 1 mapsto 3end{align}$$

What is this in cycle notation?

$sigma_1^{-1} equiv(213)$

I’ll let you try the other one.

---

A particularly easy way of doing this, once you understand what the inverses do is: just to write the cycle backwards!

Note that for $(123)$, this is just $(321)$. Now, recall, that set of all permutations form a group. In a group, inverses are unique. So, can you tell me why $(321)$ and $(213)$ are the same?