Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Обратный элемент по модулю
Часто в задачах требуется посчитать что-то по простому модулю (чаще всего (10^9 + 7)). Это делают для того, чтобы участникам не приходилось использовать длинную арифметику, и они могли сосредоточиться на самой задаче.
Обычные арифметические операции выполняются не сильно сложнее — просто нужно брать модули и заботиться о переполнении. Например:
c = (a + b) % mod;
c = (mod + a - b) % mod;
c = a * b % mod;Но вот с делением возникают проблемы — мы не можем просто взять и поделить. Пример: (frac{8}{2} = 4), но (frac{8 % 5 = 3}{2 % 5 = 2} neq 4).
Нужно найти некоторый элемент, который будет себя вести как (frac{1}{a} = a^{-1}), и вместо «деления» домножать на него. Назовем такой элемент обратным.
Способ 1: бинарное возведение в степень
Если модуль (p) простой, то решением будет (a^{-1} equiv a^{p-2}). Это следует из малой теоремы Ферма:
Теорема. (a^p equiv a pmod p) для всех (a), не делящихся на (p).
Доказательство. (для понимания несущественно, можно пропустить)
[
begin{aligned}
a^p &= (underbrace{1+1+ldots+1+1}_text{$a$ раз})^p
\ &= sum_{x_1+x_2+ldots+x_a = p} P(x_1, x_2, ldots, x_a) & text{(раскладываем по определению)}
\ &= sum_{x_1+x_2+ldots+x_a = p} frac{p!}{x_1! x_2! ldots x_a!} & text{(какие слагаемые не делятся на $p$?)}
\ &equiv P(p, 0, ldots, 0) + ldots + P(0, 0, ldots, p) & text{(все остальные не убьют $p$ в знаменателе)}
\ &= a
end{aligned}
]
Здесь (P(x_1, x_2, ldots, x_n) = frac{k}{prod (x_i!)}) это мультиномиальный коеффициент — количество раз, которое элемент (a_1^{x_1} a_2^{x_2} ldots a_n^{x_n}) появится при раскрытии скобки ((a_1 + a_2 + ldots + a_n)^k).
Теперь два раза «поделим» наш результат на (a).
[ a^p equiv a implies a^{p-1} equiv 1 implies a^{p-2} equiv a^{-1} ]
Получается, что (a^{p-2}) ведет себя как (a^{-1}), что нам по сути и нужно. Посчитать (a^{p-2}) можно за (O(log p)) бинарным возведением в степень.
Приведем код, который позволяет считает (C_n^k).
int t[maxn]; // факториалы, можно предподситать простым циклом
// бинарное возведение в степень
int bp (int a, int n) {
int res = 1;
while (n) {
if (n & 1) res = res * a % mod;
a = a * a % mod;
n >>= 1;
}
return res;
}
// находит обратный элемент как a^(p-2)
int inv (int x) {
return bp(x, mod-2);
}
int c (int n, int k) {
return t[n] * inv(t[k]) % mod * inv(t[n-k]) % mod;
}Способ 2: диофантово уравнение
Диофантовыми уравнениями называют такие штуки:
[ ax + by = 1 ]
Требуется решить их в целых числах, то есть (a) и (b) известны, и нужно найти такие целые (возможно, отрицательные) (x) и (y), чтобы равенство выполнялось. Решают такие вещи расширенным алгоритмом Евклида. TODO: описать, как он работает.
Подставим в качестве (a) и (b) соответственно (a) и (m)
[ ax + my = 1 ]
Одним из решений уравнения и будет (a^{-1}), потому что если взять уравнение по модулю (m), то получим
[ ax + by = 1 iff ax equiv 1 iff x equiv a^{-1} pmod m ]
Преимущества этого метода над возведением в степень:
- Если обратное существует, то оно найдется даже если модуль не простой. Способ с бинарным возведением тоже можно заставить работать с произвольным модулем, но это будет намного труднее.
- Алгоритм проще выполнять руками.
Сам автор почти всегда использует возведение в степень.
Почему (10^9+7)?
- Это выражение довольно легко вбивать (
1e9+7). - Простое число.
- Достаточно большое.
intне переполняется при сложении.long longне переполняется при умножении.
Кстати, (10^9 + 9) обладает теми же свойствами. Иногда используют и его.
Предподсчёт обратных факториалов за линейное время
Пусть нам нужно зачем-то посчитать все те же (C_n^k), но для больших (n) и (k), поэтому асимптотика (O(n log m)) нас не устроит. Оказывается, мы можем сразу предподсчитать все обратные ко всем факториалам.
Если у нас уже написан inv, то нам не жалко потратить (O(log m)) операций, посчитав (m!^{-1}).
После этого мы будем считать ((m-1)!^{-1}) как (m!^{-1} m = frac{1}{1 cdot 2 cdot ldots cdot (m-1)}).
int f[maxn];
f[0] = 1;
for (int i = 1; i < maxn; i++)
f[i] = i*f[i-1] % mod;
int r[maxn];
r[maxn-1] = inv(f[maxn-1])
for (int i = maxn-1; i >= 1; i--)
r[i-1] = r[i]*i % mod;TODO: техника с сайта емакса.
Written on 23 Мая 2007.
Для начала заметим, что элемент a кольца Zn обратим тогда и только тогда, когда НОД(a,n)=1. То есть ответ есть не всегда. Из определения обратного элемента прямо следует алгоритм.
Псевдокод
НА ВХОДЕ: а из Zn.
НА ВЫХОДЕ: обратный к а в кольце, если он существует.1. Использовать расширенный алгоритм Евклида для нахождения
x и y, таких что ax + ny = d, где d=НОД(a,n).
2. Если d > 1, то обратного элемента не существует.
Иначе возвращаем x.
Исходник на Си
/* Author: Pate Williams (c) 1997 */#include <stdio.h>
void extended_euclid(long a, long b, long *x, long *y, long *d)
/* вычисление a * *x + b * *y = gcd(a, b) = *d */
{
long q, r, x1, x2, y1, y2;
if (b == 0) {
*d = a, *x = 1, *y = 0;
return;
}x2 = 1, x1 = 0, y2 = 0, y1 = 1;
while (b > 0) {
q = a / b, r = a - q * b;
*x = x2 - q * x1, *y = y2 - q * y1;
a = b, b = r;
x2 = x1, x1 = *x, y2 = y1, y1 = *y;
}*d = a, *x = x2, *y = y2;
}long inverse(long a, long n)
/* вычисление инверсии модуля n */
{
long d, x, y;
extended_euclid(a, n, &x, &y, &d);
if (d == 1) return x;
return 0;
}// главная фукнция
инверсия %ld modulo %2ld is %ldn", a, n, inverse(a, n));
int main(void)
{
long a = 5, n = 7;
printf("инверсия %ld modulo %2ld is %ldn", a, n, inverse(a, n));
a = 2, n = 12;
printf("
return 0;
}
Помогаю со студенческими работами здесь

Добрый день. Нужно решить несколько заданий с помощью расширенного алгоритма Евклида:
17-1mod32…
Обратный элемент в кольце по модулю
Привет , пытаюсь написать программу которая будет вычислять обратное число по модулю . Первый код -…
Обратный элемент в кольце по модулю(инверсия в криптографии)
Доброго времени суток. Имеется функция ,которая реализует обобщенные алгоритм Евклида. т.е. находит…
Найти обратный элемент для числа a по модулю m
Найти обратный элемент для числа a по модулю m.
a=64, m=743
Задачи: Математическая индукция, остаток от деления, обратный элемент по модулю, системы уравнений
Задания во вложении.
Правила форума :rtfm:
5.16. Запрещено создавать темы с множеством вопросов…
Заменить минимальный по модулю положительный элемент нулём. Заменить элементы с К1 по K3 на обратный. Из элементоа массива A сформировать массив D тог
Заменить минимальный по модулю положительный элемент нулём. Заменить элементы с К1 по K3 на…
Искать еще темы с ответами
Или воспользуйтесь поиском по форуму:
Нахождение обратного элемента по модулю
Материал из Модулярная арифметики
Перейти к: навигация,
поиск
Нахождение обратного элемента по модулю 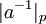

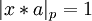
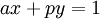

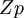
Псевдокод
- Использовать расширенный алгоритм Евклида для нахождения x и y, таких что ax + ny = d.
- Если d > 1, то обратного элемента не существует. Иначе возвращаем x.
Код на Си
#include <stdio.h>
/* calculates a * *x + b * *y = gcd(a, b) = *d */
void extended_euclid(long a, long b, long *x, long *y, long *d) {
long q, r, x1, x2, y1, y2;
if (b == 0) {
*d = a, *x = 1, *y = 0;
return;
}
x2 = 1, x1 = 0, y2 = 0, y1 = 1;
while (b > 0) {
q = a / b, r = a - q * b;
*x = x2 - q * x1, *y = y2 - q * y1;
a = b, b = r;
x2 = x1, x1 = *x, y2 = y1, y1 = *y;
}
*d = a, *x = x2, *y = y2;
}
/* computes the inverse of a modulo n */
long inverse(long a, long n) {
long d, x, y;
extended_euclid(a, n, &x, &y, &d);
if (d == 1) return x;
return 0;
}
int main(void) {
long a = 5, n = 7;
printf("Inverse of %ld modulo %2ld is %ldn", a, n, inverse(a, n));
return 0;
}
Программа он-лайн
- Найти обратный элемент по модулю
Пытаюсь реализовать генерацию параметров для алгоритма RSA, но при вычислении параметра d, где d = e^-1 mod f получаю неверный ответ. Это происходит непостоянно и иногда, при новом запуске программы я получаю верное значение d. Все параметры и результаты вычисления программы я проверял с помощью онлайн — калькуляторов. В чем может быть проблема?
#include <stdio.h>
#include <stdlib.h>
#define uint64 unsigned long long
uint64 gcd(uint64 a, uint64 b);
uint64 exgcd(uint64 a, uint64 b, uint64* x, uint64* y);
uint64 modInv(uint64 a, uint64 m);
int main()
{
// Инициализация p
uint64 p = 1009;
printf("p: %llunn", p);
// Инициализация q
uint64 q = 1013;
printf("q: %llunn", q);
// Вычисление n
// n = p * q
uint64 n = p * q;
printf("N: %llunn", n);
// Вычисление f
// f = (p - 1) * (q - 1);
uint64 f = (p - 1) * (q - 1);
printf("f: %llunn", f);
// Вычисление e
// e < f and gcd(e,f) == 1
uint64 e;
do
{
srand(time(NULL));
e = 1 + (rand() % ((f - 1) - 1));
sleep(1);
}while (gcd(e, f) != 1);
printf("e: %llunn", e);
// Вычисление d
// d = e^-1 mod f
uint64 d = modInv(e, f);
printf("d: %llun", d);
return 0;
}
// Алгоритм Евклида
uint64 gcd(uint64 a, uint64 b)
{
while (b)
{
a %= b;
uint64 tempVar = a;
a = b;
b = tempVar;
}
return a;
}
// Расширенный алгоритм Евклида
uint64 exgcd(uint64 a, uint64 b, uint64* x, uint64* y)
{
if (a == 0)
{
*x = 0;
*y = 1;
return b;
}
uint64 x1;
uint64 y1;
uint64 gcd = exgcd(b % a, a, &x1, &y1);
*x = y1 - (b / a) * x1;
*y = x1;
return gcd;
}
// Инверсия числа а по модулю m
uint64 modInv(uint64 a, uint64 m)
{
uint64 x, y;
uint64 g = exgcd(a, m, &x, &y);
if (g != 1)
{
printf("nNO SOLUTIONn");
return 0;
}
else
{
uint64 res = (x % m + m) % m;
return res;
}
}
UPD
Проблема была в использовании беззнакового типа данных у переменных в функциях exgcd() и modInv(). Изменение типа данных на знаковый long long решает проблему
