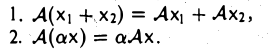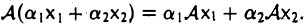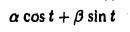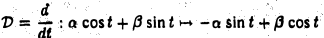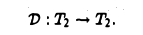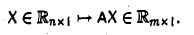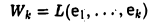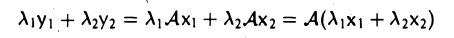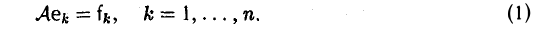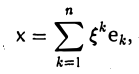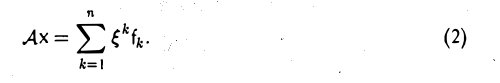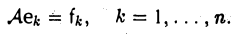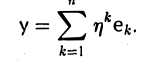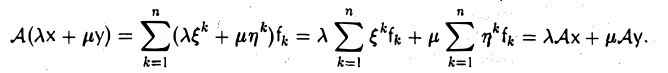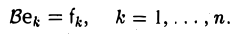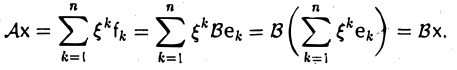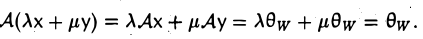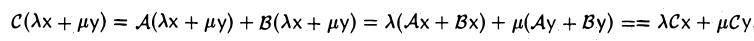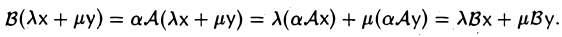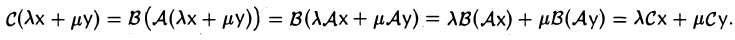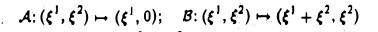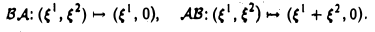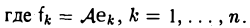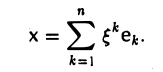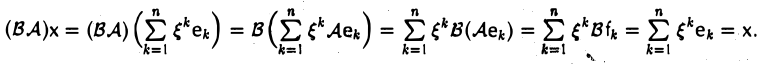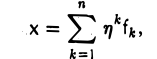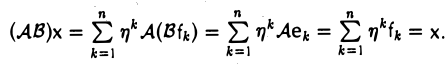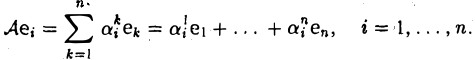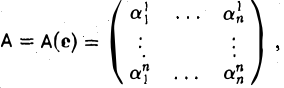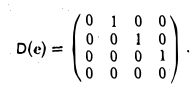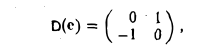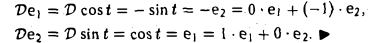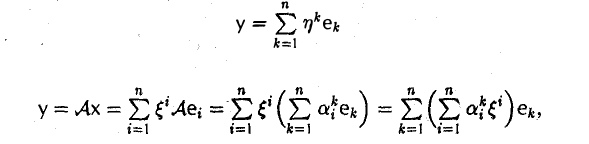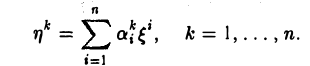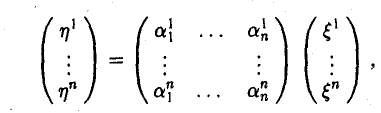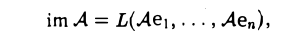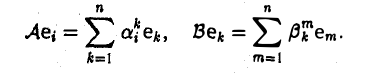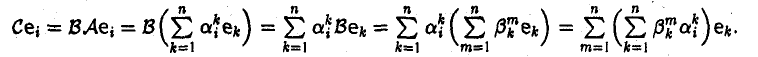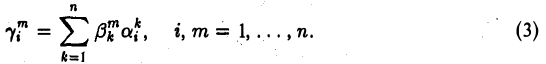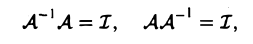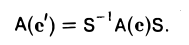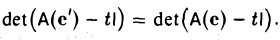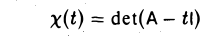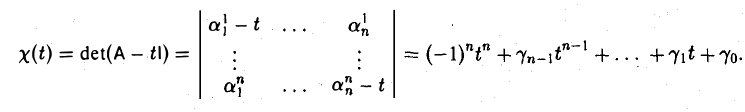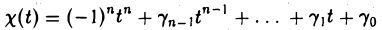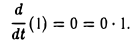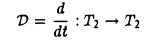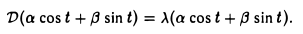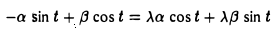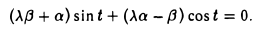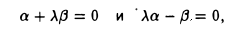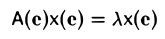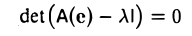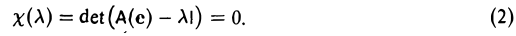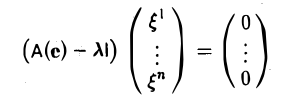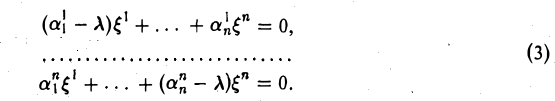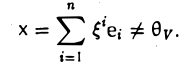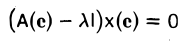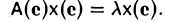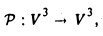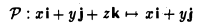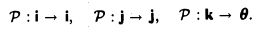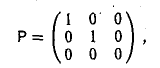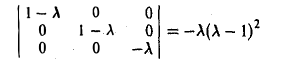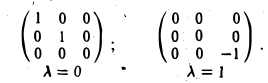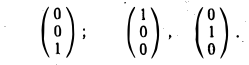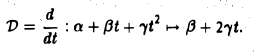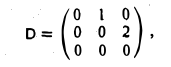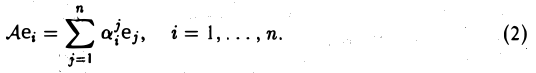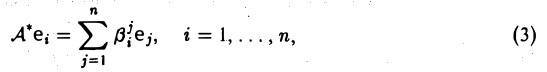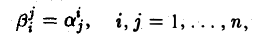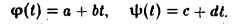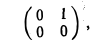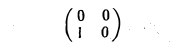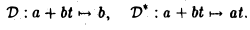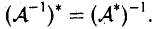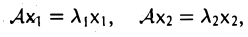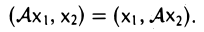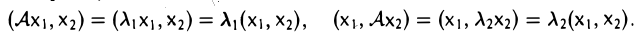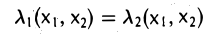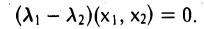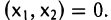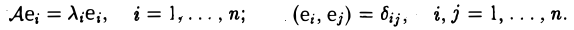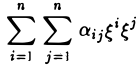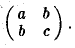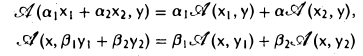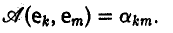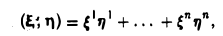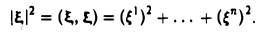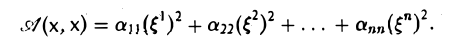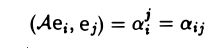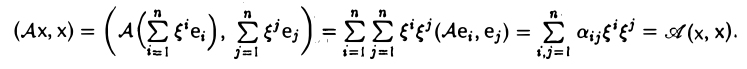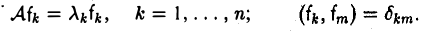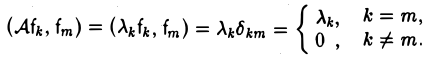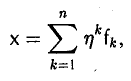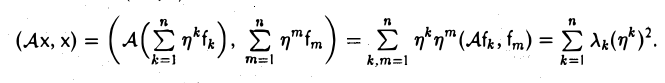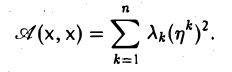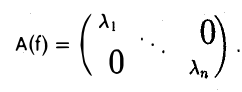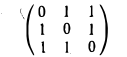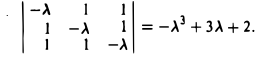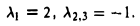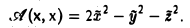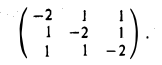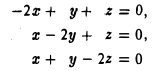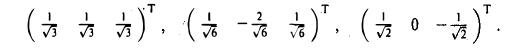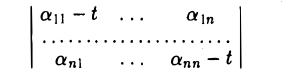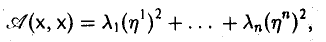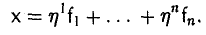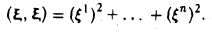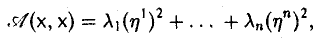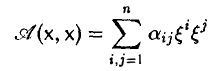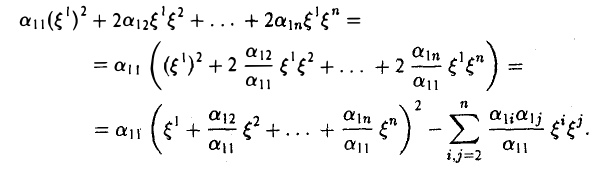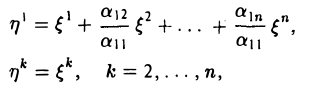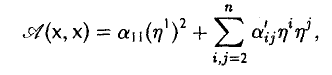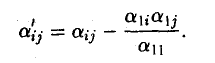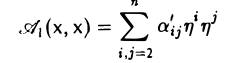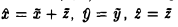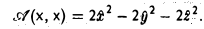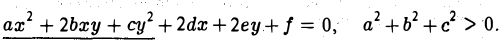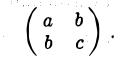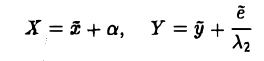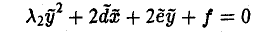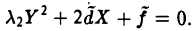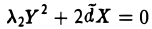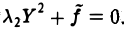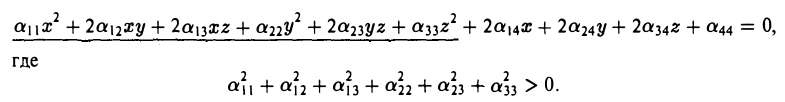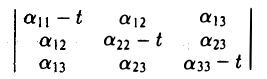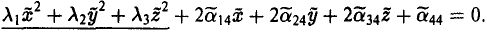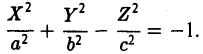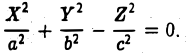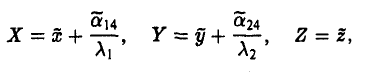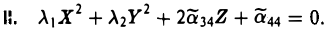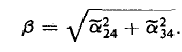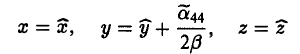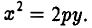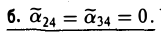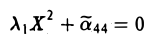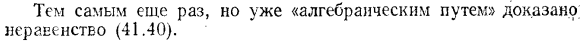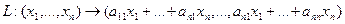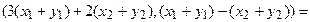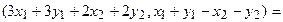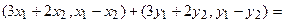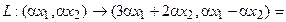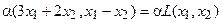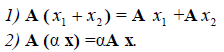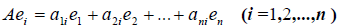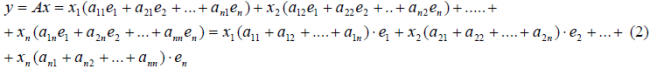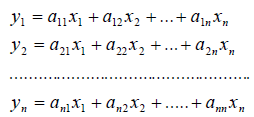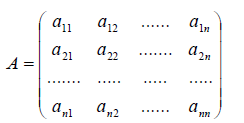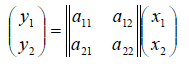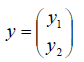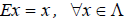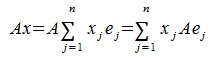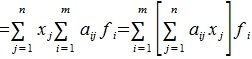Как найти образ элемента

Функции играют центральную роль в
математике, где они используются для
описания любых процессов, при которых
элементы одного множества каким-то
образом переходят в элементы другого.

Определение
4.1. Отношение f
на AB
называется отображением
(функцией)
из A в B,
если для каждого xA
существует один и только один yB.

f: AB
или y=f(x)

Множество A называется
областью определения.

Множество B – областью
значений.

Если y=f(x),
то x называют аргументом,
а y – значением
функции.

Пусть f: AB,
тогда

множество
определения функции:
;

множество
значений функции:
.

Множество определения функции является
подмножеством области определения,
т.е. D_f
 A,
а множество значений функции является
подмножеством области значений функции,
т.е. R_f
 B.

Если D_f
= A, то функция называется
тотальной, а если D_f
≠ A 
частичной функцией.

Диаграмма Венна служит удобной
иллюстрацией функции, определенной на
множестве A со значениями
в множестве B.

Определение 4.2. Если MA,
то множество f(M)=y
f(x)=y
для некоторого x из
M
называется образом множества
M.

Если KB,
то множество
(K)=x
f(x)K
называется прообразом множества
K.

Пример ..
Дано отображение f:
QZ,
где f(x)=x³5
для всех xQ
(Q – рациональные числа,
Z – целые числа)
.

Найти: 1) образ элемента 1;

2) f ^-1(3); f
^-1(5).

Решение.

1) Сначала надо убедиться, что 1Q.
Это так.

Чтобы найти образ элемента, достаточно
в отображение подставить вместо x
число 1. Получаем, f(1)=1³5=
 4. 
4Z.
Значит, элемент 1 имеет образ, и он равен
 4.

2) Сначала убедимся, что 3Z.
Это так.

Чтобы найти прообраз, вместо f(x)
подставляем 3, и решаем уравнение: x³-5=3.
Получаем, x=2. Причем
2Q.
Значит, f ^-1(3)=2.

По аналогии находим прообраз 5. Решаем
уравнение x³-5=5,
и получаем
.
Но
Q.
Значит, f ^-1(5)=.

Ответ: 1) -4; 2) 2; .

Определение 4.3. Функция

называется функцией n
аргументов, или n—местной
функцией. Такая функция отображает
кортеж

в элемент bB,

.

Свойства отображений (функций).

1) Отображение f: AB
называется инъективным, если
оно различные элементы из A
отображает в различные элементы из B:
.

2) Отображение f: AB
называется сюръективным или
отображением на все множество B,
если в каждый элемент множества B
отображается хотя бы один элемент из
A:
.

3) Отображение f:
AB,
которое одновременно инъективно и
сюръективно, называется биективным
или взаимно однозначным отображением
множества A на множество
B.

Вопрос: на какой из предыдущих диаграмм
представлена биективная функция?

Пример ..
Пусть дано отображение f:
RR,
которое определено таким образом, что
.
Выяснить, какими свойствами обладает
это отображение.

Решение. Даная функция инъективна,
т.к. если f (x₁)
= f (x₂),
тогда

и, следовательно, x₁=x₂.

Функция f является
также сюръекцией. Для любого действительного
числа y требуется
найти такое x, что f
(x)=y=3x+5.
Решая это уравнение относительно x,
находим, что если
,
тогда f (x)=y.

Поэтому f представляет
собой взаимно однозначное соответствие.
А, значит, является биекцией.

Пример ..
Пусть дано отображение f:
RR,
которое определено таким образом, что
.
Выяснить, какими свойствами обладает
это отображение.

Решение. Функция f
не является инъективной, т.к. f
(2)=f (2),
но 2
2.

Функция f не является
также и сюръективной, поскольку не
существует такого действительного
числа x, для которого
f (x)=
1.

Определение 4.4. Пусть f
 биективное
отображение множества A
в множество B. Если
поставить в соответствие каждому
элементу из B связанный
с ним элемент из A, то
такое соответствие является отображением
B в A.
Это отображение обозначается

и называется отображением, обратным
отображению f.

Теорема
4.1. (свойства обратного отображения)

Если f: AB
– биекция, то

1)
для
любого y из B;

2)
для
любого x из A.

Доказательство.

1) Пусть yB.
Т.к. биекция сюрьективна, то .
Такой x единственен
и f(x)=y.
Имеем:
.

2) Аналогично доказывается, что

для любого x из A.

Определение 4.5. Композицией
(суперпозицией, произведением) отображений
f: AB
и g: BC
называется отображение h:
,
которое записывается h=
g 
.f

Следует отметить, что

Пример
..
Рассмотрим две функции

и

.

Найти:
.

Решение.
Все четыре новые функции определены
на R со значениями в
R.

;

;

;

.

Соседние файлы в папке Лекции_2

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Соответствия и бинарные отношения на множествах

Отображение из множества в множество считается заданным, если каждому элементу сопоставлен единственный элемент . Отображение из множества в множество обозначают записью или . Элемент , который отображением сопоставляется элементу , называют образом элемента при отображении и обозначают .

Каждое отображение однозначно определяет множество упорядоченных пар , являющееся подмножеством декартова произведения множества на множество и называемое графиком отображения .

Наоборот, пусть в декартовом произведении задано такое подмножество , что:

1) для любого существует , для которого ;
2) для любых двух пар и множества из равенства следует равенство .

Тогда множество единственным образом определяет некоторое отображение из в . Это отображение, обозначаемое также , элементу сопоставляет элемент , удовлетворяющий условию . Таким образом, мы можем отождествить отображения с их графиками и считать, что отображение есть подмножество декартова произведения.

Отображение множества в себя называют тождественным, если при всех из .

В общем случае для отображения может существовать несколько различных элементов множества , образы которых совпадают. Множество всех элементов , для которых , называют прообразом элемента при отображении .

Так, прообраз числа при отображении есть множество всех решений уравнения , т.е. множество

Прообраз элемента может быть пустым множеством. Это имеет место, например, для числа при отображении .

Множество всех , таких, что найдется , для которого , называют областью значений отображения . Область значений отображения будем обозначать .

Отображение называют инъективным (инъекцией), если каждый элемент из области его значений имеет единственный прообраз, т.е. из следует .

Отображение называют сюръективным (сюръекцией), если его область значений совпадает со всем множеством . Сюръективное отображение из в называют также отображением множества на множество .

Отображение называют биективным (биекцией), если оно одновременно инъективно и сюръективно.

Таким образом, если отображение биективно, то каждому элементу множества отвечает единственный элемент множества и наоборот. Тогда говорят, что множества и находятся между собой во взаимно однозначном соответствии.

Биекцию множества на себя называют автоморфизмом множества . Используют также термин «подстановка множества».

---

Пример 1.2. а. Отображение, заданное равенством , есть, как нетрудно показать, биекция множества натуральных чисел на его подмножество .

б. Отображение есть биекция множества всех натуральных чисел на множество всех четных натуральных чисел.

в. Любая показательная функция , есть биекция множества всех действительных чисел на множество всех положительных действительных чисел.

г. Функция есть биекция множества на интервал .

д. Поворот окружности на заданный угол , т.е. отображение, сопоставляющее каждой точке окружности точку, в которую она перейдет при повороте всей окружности вокруг ее центра на угол , есть автоморфизм множества точек окружности.

---

Образ и прообраз множества

Пусть задано отображение и — некоторое множество. Множество элементов , таких, что , называют образом множества при отображении . Например, при отображении отрезок является образом множества (отрезка) , равно как и любого объединения отрезков вида (для произвольного целого ). При это можно записать следующим образом: .

Заметим, что для любого отображения образ всего множества есть область значений данного отображения.

Для произвольного множества множество всех элементов , таких, что , называют прообразом множества при отображении .

Например, для любого действительного числа множество, которое является объединением всех отрезков вида

есть прообраз отрезка при отображении .

Прообраз области значений произвольного отображения совпадает со всем множеством .

Множество всех отображений из в будем обозначать как .

---

Частичное отображение и его область определения

Понятие отображения можно обобщить. Обобщение может проходить по двум позициям. Во-первых, можно отказаться от полной определенности отображения, полагая, что образ определен не для каждого элемента множества , а для некоторых элементов этого множества. Тогда придем к понятию частичного отображения. При этом подмножество всех элементов , для которых определен образ, называют областью определения данного частичного отображения.

Многие элементарные функции являются частичными отображениями множества всех действительных чисел в себя. Например, функция есть частичное отображение с областью определения

Во-вторых, можно отказаться от однозначности отображения, полагая, что данному сопоставлен не один, а несколько образов (множество образов) в множестве . В этом случае говорят, что задано соответствие из множества в множество .

Примером могут служить обратные тригонометрические функции: скажем, «большой» арксинус, сопоставляющий каждому множество всех таких чисел , что , т.е. множество, являющееся прообразом элемента при отображении, определяемом графиком функции .

Если задано соответствие из в , будем использовать обозначение по аналогии с обозначением для отображений, понимая при этом, что есть уже не элемент множества , а его подмножество.

Аналогично графику отображения можно определить график соответствия из множества в множество как множество упорядоченных пар , таких, что и элементы связаны соответствием , то есть . Указанное множество упорядоченных пар есть подмножество декартова произведения .

Обратно, фиксируя на декартовом произведении какое-либо подмножество , мы тем самым однозначно определяем некоторое соответствие из в , а именно

Нетрудно заметить, что графиком соответствия будет как раз множество , а соответствием, отвечающим графику , будет . Поэтому можно отождествить соответствие с его графиком и считать, что соответствие из множества в множество есть некоторое подмножество декартова произведения , то есть . В частности, при получаем пустое соответствие, а при , совпадающем со всем указанным декартовым произведением, — универсальное соответствие.

При этом будем писать для упорядоченных пар, связанных соответствием .

Используют также термины «частичное мультиотображение» и «частичная многозначная функция».

---

Пример 1.3. Рассмотрим множество программистов и множество программ . Зададим соответствие из в , связывающее программистов и разрабатываемые ими программы:

Область определения соответствия из множества в множество — это множество всех первых компонент упорядоченных пар из

Область значения соответствия — это множество всех вторых компонент упорядоченных пар из

Из определения вытекает, что . Соответствие из в называют всюду определенным, если его область определения совпадает с множеством .

Сечением соответствия для фиксированного элемента будем называть множество . Можно сказать, что сечение соответствия есть множество всех «образов» элемента при данном соответствии.

Сечением соответствия по множеству будем называть множество

Пример 1.4. Область определения соответствия т из примера 1.3 есть все множество , а область значения — все множество . Сечением соответствия по элементу будет множество .

---

Бинарные отношения на множествах

Соответствие из множества в себя, т.е. подмножество множества , называют бинарным отношением на множестве .

Пример 1.5. Простейшим примером бинарного отношения является отношение нестрогого неравенства на множестве действительных чисел . Здесь каждому поставлены в соответствие такие , для которых справедливо .

Для произвольного бинарного отношения на некотором множестве часто используют запись вместо , говоря при этом об элементах, связанных бинарным отношением . Это согласуется с традиционной формой записи некоторых часто используемых бинарных отношений. Так, пишут , а не . Для таких бинарных отношений употребляют устоявшиеся словосочетания. Например, запись читается так: « не больше «.

Бинарное отношение на множестве , состоящее из всех пар , т.е. пар с совпадающими компонентами, называют диагональю множества и обозначают . Нетрудно понять, что диагональ есть тождественное отображение на себя.

Иногда говорят о диагонали в множестве , хотя правильнее было бы называть это отношение диагональю декартова квадрата множества .

Для наглядного изображения соответствий из в (бинарных отношений, в частности) будем использовать два способа. Первый из этих способов состоит в интерпретации соответствия как подмножества декартова произведения, которое можно изображать примерно так же, как на плоскости можно изображать подмножества декартова квадрата числовых множеств. Второй способ, применяемый для конечных множеств в , — построение так называемого графа соответствия. В этом случае элементы множеств в изображаются на плоскости кружочками. Если и только если пара принадлежит соответствию , то в графе соответствия из кружочка, обозначающего элемент , проводим стрелку к кружочку, обозначающему элемент . Для бинарного отношения на конечном множестве часто удобнее использовать граф другого вида. Элементы множества изображаются кружочками только один раз, а стрелки проводятся по тем же правилам, что и в графе соответствия. Заметим, что при таком построении возможно соединение кружочка стрелкой с самим собой (петля).

---

Пример 1.6. а. На рис. 1.1, а изображены график и граф бинарного соответствия из примера 1.3.

б. Пусть . Бинарное отношение на определим как множество всех упорядоченных пар , таких, что . Тогда

Область определения отношения , область значений . График и два варианта графа отношения изображены на рис. 1.1, б.

в. Множество точек окружности есть график бинарного отношения на множестве действительных чисел, состоящего из всех таких упорядоченных пар , что , или, что равносильно, компоненты пары удовлетворяют уравнению . Область определения бинарного отношения есть отрезок , область значения — также отрезок .

---

Функциональное соответствие

Соответствие называют функциональным по второй (первой) компоненте, если для любых двух упорядоченных пар и из равенства следует (и из следует ). Функциональность соответствия по второй компоненте означает, что, фиксируя в любой упорядоченной паре, принадлежащей данному соответствию, первую компоненту, мы однозначно определяем и вторую компоненту. Таким образом, мы можем сказать, что соответствие, функциональное по второй компоненте, есть отображение (возможно, частичное).

Поэтому соответствие является отображением из в , если и только если оно всюду определено (т.е. ) и функционально по второй компоненте. Отметим также, что отображение из в является инъекцией тогда и только тогда, когда оно функционально по первой компоненте.

---

Отношения произвольной арности

В заключение обобщим понятие соответствия, определив отношения произвольной арности.

Определение 1.4. Произвольное подмножество декартова произведения называют (п-арным или п-местным) отношением на множествах .

В случае если все множества совпадают, т.е. , говорят об n-арном отношении на множестве .

Если — n-арное отношение на множествах и , то говорят об элементах , связанных отношением .

Замечание 1.3. При получаем бинарное отношение на множествах . Это не что иное, как соответствие из в , где множества и , вообще говоря, различны.

При получаем введенное ранее бинарное отношение на множестве, т.е. подмножество декартова квадрата .

Таким образом, в общем случае (при произвольном ) следует, строго говоря, различать термины «n-арное отношение» и «n-арное отношение на множестве».

Связь между введенными понятиями отношения, соответствия и отображения проиллюстрирована на рис. 1.2.

Пусть n-арное отношение удовлетворяет условию: для любых двух кортежей

и

из выполнения равенств для любого следует, что и . Тогда отношение называют функциональным по i-й компоненте .

Другими словами, функциональность n-местного отношения по i-й компоненте равносильна условию, что, фиксируя все компоненты, кроме i-й, мы однозначно определяем и i-ю компоненту.

---

Пример 1.7. а. Представим строку учебного расписания как кортеж вида

(преподаватель, группа, дисциплина, аудитория, день, час).

Тогда расписание можно рассматривать как секстарное (шестиместное) отношение на соответствующих множествах. Оно будет функционально по первой компоненте, если, конечно, предположить, что два преподавателя или более не проводят одно и то же занятие одновременно в одном и том же месте (хотя, например, на лабораторных работах это возможно). Оно также функционально по третьей компоненте (один преподаватель не может вести одновременно занятия по разным дисциплинам), по четвертой (преподаватель со своей группой не могут находиться в разных аудиториях) и не будет, вообще говоря, функционально по второй, пятой и шестой компонентам.

б. Рассмотрим на множестве геометрических векторов в пространстве тернарное (трехместное) отношение , состоящее из всех упорядоченных троек компланарных векторов. Это отношение не является функциональным ни по одной компоненте, так как любым двум векторам соответствует бесконечно много векторов, образующих с ними компланарную тройку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

ЛЕКЦИЯ 12 Образ и прообраз множества при данном соответствии 21. 11. 2012 г.

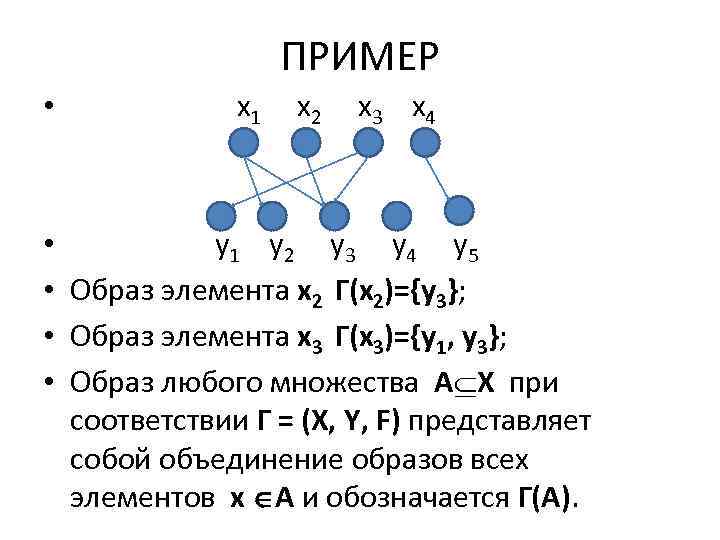
• Пусть дано соответствие Г = (X, Y, F). • Образом элемента х Х при соответствии Г называется и через Г(х) обозначается множество элементов y Y, для которых пара F. Иначе, Г(х)={y Y| F}. Т. е. , образ элемента х Х – это множество тех элементов y Y, которые соответствуют элементу x. • На графе образ элемента x можно представить как множество тех вершин y, в которые входят дуги, выходящие из вершины x.

ПРИМЕР • x 1 x 2 x 3 x 4 • y 1 y 2 y 3 y 4 y 5 • Образ элемента x 2 Г(x 2)={y 3}; • Образ элемента x 3 Г(x 3)={y 1, y 3}; • Образ любого множества A X при соответствии Г = (X, Y, F) представляет собой объединение образов всех элементов x A и обозначается Г(А).

• В общем случае справедливо: • Г(А) = Г(х) • х А • Для рассмотренного примера если А={x 2, x 3}, то Г(А)=Г(х2) Г(х3)={y 3} {y 1, y 3}={y 1, y 3}. • Пусть дано соответствие Г = (X, Y, F). • Прообразом элемента y Y при соответствии Г называется и через Г-1(y) обозначается множество элементов x X, для которых пара F.

5 • Таким образом, Г-1(y)={x X| F } – это множество тех элементов из Х, которым соответствует элемент y. • На графе прообраз элемента y можно представить множеством тех вершин х, из которых выходят дуги, заходящие в вершину y. Для рассмотренного примера • Г-1(y 3)={x 1, x 2, x 3}, Г(y 4)= .

6 • Прообразом произвольного множества B Y при соответствии Г = (X, Y, F) называется объединение прообразов всех элементов y B и обозначается Г-1(В), т. е. • Г-1(В) = Г-1(y) • y B • Если В={y 3, y 4, y 5}, то при соответствии Г для рассмотренного примера прообраз запишется • Г-1(В)={x 1, x 2, x 3, x 4}.

7 • Пусть Г = (X, Y, F) – произвольное соответствие и А – произвольное подмножество множества Х. • Сужением соответствия Г на множество А называется и через ГА обозначается соответствие, график которого FA определяется выражением: • FA = (A Y) F, т. е. ГА = (X, Y, FA). • Соответствие ГА Г. Соответствие Г в этом случае называют продолжением соответствия ГА на множество Х.

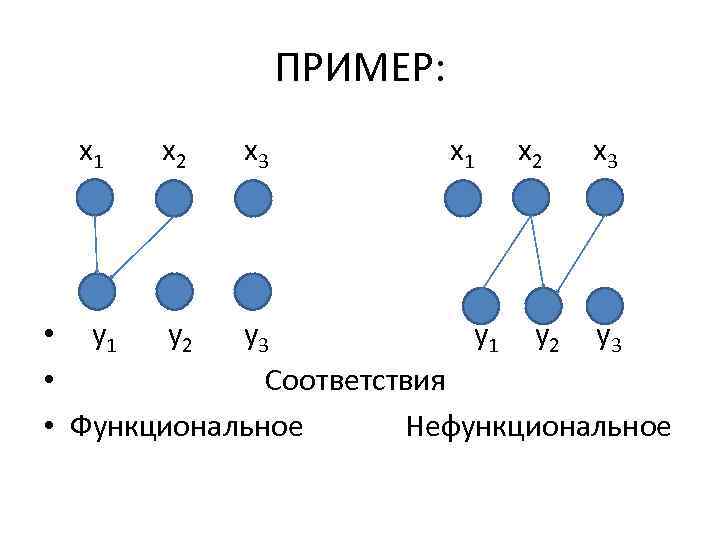
Основные свойства соответствий • 1. ФУНКЦИОНАЛЬНОСТЬ: • Соответствие Г = (X, Y, F) называется функциональным, если для любого х Х образ Г(х) содержит не более одного элемента y Y, в противном случае соответствие называется нефункциональным.

ПРИМЕР: x 1 x 2 x 3 • y 1 y 2 y 3 • Соответствия • Функциональное Нефункциональное

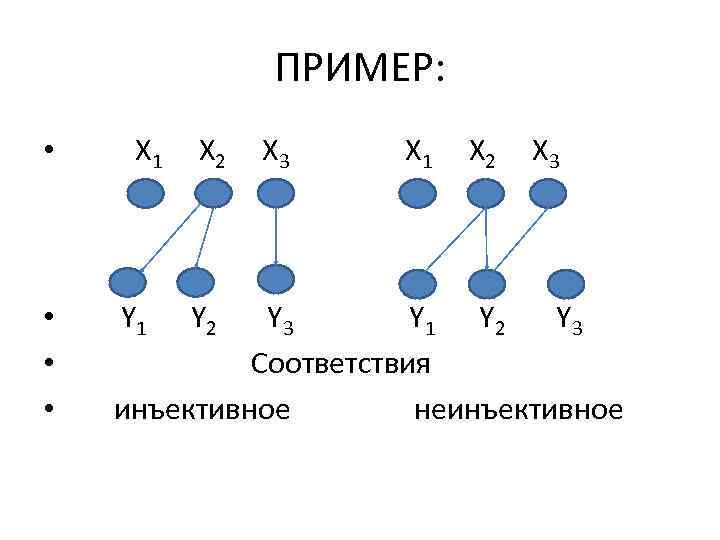
10 • 2. ИНЪЕКТИВНОСТЬ: • Соответствие Г = (X, Y, F) называется инъективным, если для любого y Y прообраз Г-1(y) содержит не более одного элемента х Х, в противном случае соответствие называется неинъективным.

ПРИМЕР: • • X 1 Y 1 X 2 Y 2 X 3 X 1 X 2 X 3 Y 1 Y 2 Y 3 Соответствия инъективное неинъективное

12 • 3. ОПРЕДЕЛЕННОСТЬ: • Соответствие Г = (X, Y, F) называется всюду определенным, если для каждого х Х образ Г(х) , в противном случае соответствие не всюду определено. • В графе всюду определенного соответствия из каждой вершины х Х выходит хотя бы одна дуга.

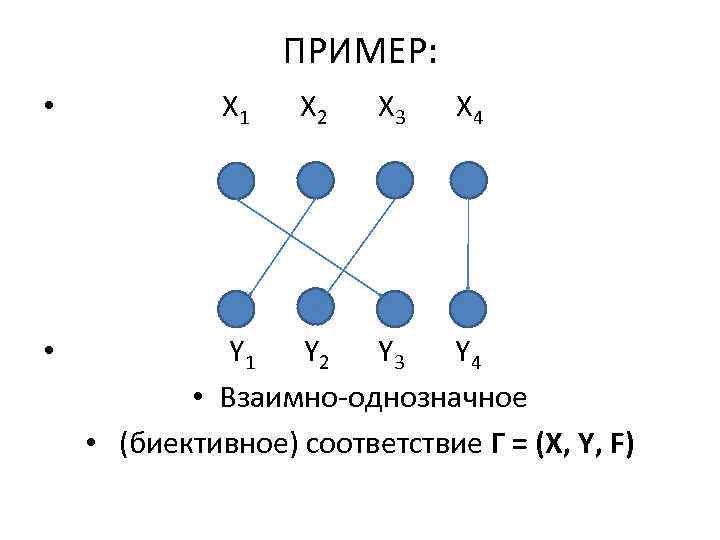
13 • 4. СЮРЪЕКТИВНОСТЬ: • Соответствие Г = (X, Y, F) называется сюръективным, если для любого элемента y Y прообраз Г-1(y) , в противном случае соответствие несюръективно. • В графе сюръективного соответствия в каждую вершину, соответствующую y Y, входит хотя бы одно ребро (дуга, стрелка). • Если соответствие одновременно функциональное, инъективное, всюду определенное и сюръективное, то оно называется взаимно-однозначным или биективным.

ПРИМЕР: • • X 1 X 2 X 3 X 4 Y 1 Y 2 Y 3 Y 4 • Взаимно-однозначное • (биективное) соответствие Г = (X, Y, F)

14 • Биекция — это отображение, которое является одновременно и сюръективным, и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением (соответствием), одно-однозначным отображением. • Если между двумя множествами можно установить взаимно-однозначное соответствие (биекция), то такие множества называются равномощными. С точки зрения теории множеств, равномощные множества неразличимы. • Взаимно-однозначное отображение конечного множества в себя называется перестановкой (элементов этого множества). (википедия)

Общее понятие функции • Пусть Х – некоторое числовое множество. • Говорят, что на Х задана функция, если любому элементу из множества Х поставлено в соответствие определенное число y Y. • Если теперь перейти от числовых множеств к множествам произвольной природы, то приходим к самому общему понятию ФУНКЦИИ.

17 • Пусть X и Y – множества произвольной природы, и пусть между ними задано соответствие. • Если соответствие функционально, то оно называется функцией и обозначается • f = (X, Y, F). • Из определения следует, что функция может быть определена не на всех элементах множества Х.

18 • Если же функция определена на всех элементах множества Х, т. е. введенное соответствие не только функциональное, но и всюду определенное, то такая функция называется ОТОБРАЖЕНИЕМ. • Различают отображение X на Y и отображение X в Y. • X на Y, если f(X) = Y, • X в Y, если f(X) Y. • ФУНКЦИЯ – частный вид СООТВЕТСТВИЯ.

Линейное отображение с примерами решения и образцами выполнения

Линейное отображение — обобщение линейной числовой функции, а точнее, функции на случай более общего множества аргументов и значений. Линейные отображения, в отличие от нелинейных, достаточно хорошо исследованы, что позволяет успешно применять результаты общей теории, так как их свойства не зависят от природы величин.

Определение линейного отображения. Образ и ядро линейного отображения

Пусть V и W — линейные пространства (либо оба вещественные, либо оба комплексные). Линейным отображением линейного пространства V в линейное пространство W называется правило А, согласно которому каждому элементу х из пространства V ставится в соответствие (единственный) элемент у = Ах из пространства W так, что

Эти два требования можно объединить в одно:

Обозначение: A:V → W.

Примеры линейных отображений

1. Пусть V = W = Мп, где Мп — пространство многочленов, степень которых не выше п. Правило

согласно которому каждому многочлену из Мп ставится в соответствие его производная, является линейным отображением (производная суммы равна сумме производных, постоянный сомножитель можно выносить из-под знака производной).

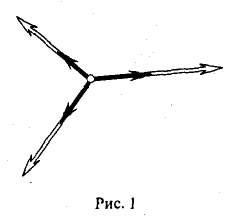
2. Правило, по которому каждому элементу х из V ставится в соответствие элемент λх из V ( λ ≠ 0 и фиксировано), — преобразование подобия — является линейным отображением (рис. 1).

3. Пусть у = (еi…, еn) — базис пространства V. Поставим произвольному элементу

в соответствие элемент

(здесь k

4. Cовокупность Т2 тригонометрических многочленов вида

образует линейное пространство. Правило

является линейным отображением

5. Пусть 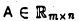— фиксированная матрица, X — произвольный столбец высоты п. Умножение столбца X на матрицу А слева является линейным отображением пространства столбцов высоты п в пространство столбцов высоты m,

Образом линейного отображения А: V → W называется множество im А всех элементов из пространства W, обладающих следующим свойством элемент у лежит в im А, если в пространстве V найдется элемент х, такой, что Ах = у. Примеры.

1′. Образом операции дифференцирования V : Мn — Мп является совокупность многочленов, степень которых не выше п — 1,

2′. Образ отображения подобия совпадает со всем пространством V.

3′. Образ отображения проектирования V : V → V является подпространством

4′. Образ операции дифференцирования V : T2 → Т2 совпадает со всем пространством Т2

Теорема:

Образ im А линейного отображения А: V → W является линейным подпространством пространства W.

Пусть у1 и у2 — элементы из im А. Это означает, что в пространстве V найдутся элементы x1 и х2, такие, что -Ax1 = y1 и Ах2 = у2. Из формулы

вытекает, что произвольная линейная комбинация элементов y1 и у2 также лежит в im А.

Размерность образа линейного отображения называется рангом этого линейного отображения.

Обозначение: rang А.

Определение:

Линейные отображения А: V → W и В: V W называются равными, если для любого элемента х из пространства V выполняется равенство Ах = Вх.

Обозначение: А = В.

Теорема:

Построение линейного отображения. Пусть V и W — линейные пространства, e = (e1… , еn) — базис пространства V, a f1. . ., fn — произвольные элементы из пространства W. Тогда существует и притом ровно одно линейное отображение

A :V → W,

А. Существование. Разложим произвольный элемент х из пространства V по базису с этого пространства,

и построим отображение А: V → W по следующему правилу:

В линейности отображения А убедимся непосредственно. Пусть

Тогда согласно правилу (2)

Б. Единственность. Покажем, что требованием (1) линейное отображение А определяется однозначно.

Пусть В: V → W — линейное отображение и

Вычисляя действия А и В на произвольный элемент х из V, убеждаемся в том, что в обоих случаях результат один и тот же —

Значит, отображения A и В совпадают.

Таким образом, линейное отображение можно задать его действием только на элементы базиса.

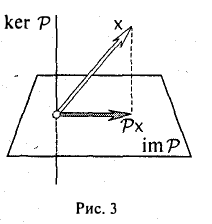
Ядром линейного отображения А: V → W называется множество ker А всех элементов из пространства V, каждый из которых отображение А переводит в нулевой элемент θ_w пространства W.

Примеры:

1″. Многочлены нулевой степени образуют ядро операции дифференцирования V: Мп -> Мп.

2″. Ядро отображения подобия состоит из нулевого элемента θ_v пространства V.

3″. Ядром отображения проектирования P: V→V является линейное подпространство L(ek+1,…, еn) (рис. 3).

4″. Ядро операции дифференцирования D:T2→Т2 состоит из нуля.

5″. Ядром отображения

является множество решений однородной линейной системы

АХ = 0.

Теорема:

Ядро линейного отображения А: V
→W является линейным подпространством пространства V.

Из равенств Ах = θ_w и Ay = θ_w вытекает, что

Размерность ядра линейного отображения называется дефектом этого отображения.

Обозначение: defect . Операции над линейными отображениям

Пусть V и W — линейные пространства и A:V W, B:V→W — линейные отображения. Суммой линейных отображений А и В называется отображение С: V→W, определяемое п о следующему правилу:

Сх = Ах + Вх

для любого элемента х из V. Нетрудно убедиться в том, что отображение С является линейным. В самом деле,

Обозначение: С = А + В.

Произведением линейного отображения A:V→W на число а называется отображение В: V —> W, определяемое по правилу:

Вх = аАх

для любого элемента х из V. Отображение В линейно:

Обозначение: В = а А.

В дальнейшем мы ограничимся рассмотрением линейных операторов — линейных отображений, действующих из пространства V в это же пространство V. Среди рассмотренных выше примеров отображений линейными операторами являются дифференцирование, подобие и проектирование; умножение столбца на квадратную матрицу также является линейным оператором.

Оператор I: V —> V, задаваемый правилом Ix = х для любого элемента х из V, называется тождественным.

Введем операцию умножения линейных операторов. Пусть А: V → V и В: V→V — линейные операторы. Произведением оператора А на оператор В называется отображение С: V → V, определяемое по правилу

Сх = В(Ах),

где х — произвольный элемент из V. Покажем, что С — линейный оператор:

Обозначение: С = В А.

Замечание:

Порядок сомножителей в произведении линейных операторов является существенным, как показывает следующий пример.

Пример:

Пусть V = R 2 . Отображения

— линейные операторы, действующие из R 2 в R 2 (рис. 4). Тогда

Пусть A: V → V — линейный оператор. Линейный оператор В: V → V называется обратным оператору А, если выполнены следующие равенства

ВА = АВ= I,

где I: V —> V — тождественный оператор.

Теорема:

Для того, чтобы у линейного оператора А: V → V был обратный, необходимо и достаточно, чтобы образ оператора А совпадал со всем пространством,

im А = V.

Предположим сначала, что обратный оператор В у заданного оператора А существует и покажем, что произвольно взятый элемент у из пространства V непременно лежит в im А. Подействовав оператором А на элемент х = В у, согласно определению (1), получим

Ах = А(Ву) = (АВ)у = Iу — у.

Значит, элемент у является образом элемента х = By и, следовательно, лежит в im А. Тем самым imA = V.

Пусть теперь образ оператора А совпадает со всем пространством V:

imA = V.

rang А = dim V.

Поэтому оператор А переводит базис пространства V снова в базис:

Построим линейный оператор В по следующему правилу

Согласно теореме 1, условием (2) оператор В определяется однозначно.

Пусть х — произвольный элемент пространства V. Вычислим (ВA)х и (АВ)х. Разложим х по базису с. Имеем

Подействовав на него оператором В А, с учетом формул (2) получаем, что

Аналогично, раскладывая элемент х по базису f,

и действуя на него оператором АВ, имеем

ВAх = х, АВх = х

для любого элемента х из V и, значит,

В А = АВ = I.

Замечание:

В ходе доказательства этой теоремы мы установили также, что обратный к А оператор В определен однозначно.

Для оператора, обратного к А, принято следующее обозначение: А -1 .

Следствие:

Линейный оператор А: V → V обратим (имеет обратный) тогда и только тогда, когда его ядро тривиально,

ker А= < θ _v>.

Справедливость этого утверждения вытекает из теоремы 3 и формулы.

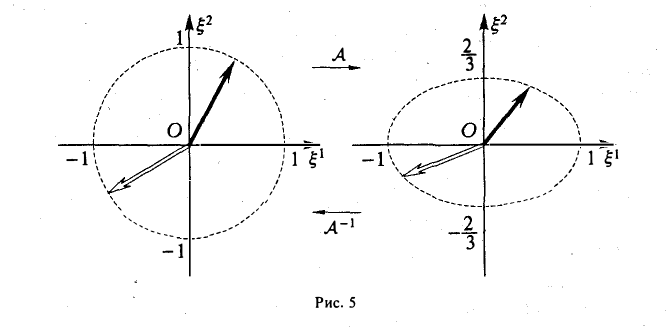
Пример:

осуществляет равномерное сжатие плоскости к оси ξ 1 (с коэффициентом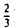); обратный оператор

— равномерное растяжение (с коэффициентом 3/2) (рис. 5).

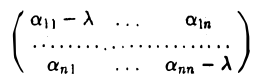
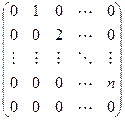
Матрица линейного оператора

Пусть линейный оператор А: V —> V преобразует элементы базиса e = (e1,…, еn) пространства V по следующему правилу

столбцами которой являются координаты образов базисных элементов, называется матрицей линейного оператора А в базисе e.

Пример:

Матрица D(с) оператора дифференцирования V: Мз → Mз в базисе ео = l. e1 = t, 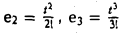имеет вид

Пример:

Матрица D(e) оператора дифференцирования V: T2 → T2 в базисе e1 = cos t, е2 = sin t имеет вид

У = Ax.

Разложим элементы x и у no базису e:

элементов х и у в базисе с связаны соотношением

у(e) = A(e)х(e). (1)

в силу единственности разложения элемента у по базису e получаем

Записывая полученные п равенств в матричной форме

получаем требуемое равенство (1).

Теорема:

Ранг матрицы А(с) линейного оператора А: V —> V не зависит от выбора базиса с и равен рангу rang А оператора А.

то rang A равен максимальному числу линейно независимых элементов в системе Ае1,…, Аеn. В силу теоремы 4 главы V, последнее совпадает с максимальным числом линейно независимых столбцов матрицы А(e), т. е. с ее рангом. Таким образом,

rang А(с) = rang A.

Легко убедиться в том, что при сложении линейных операторов их матрицы (вычисленные в одном базисе) складываются, а при умножении линейного оператора на число его матрица умножается на это число.
Матрица произведения С = ВА операторов А и B равна произведению матриц этих операторов (относительно одного и того же базиса e):

С(e) = В(e)А(e). (2)

Вследствие того, что 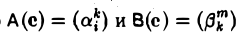из формул (3) и (4) получаем

С (e) = В(e)А(e).

Отсюда, в частности, вытекает, что

матрица оператора A -1 , обратного к A, является обратной к его матрице А.

В самом деле, из соотношений

определяющих обратный оператор, получаем, что его матрица В удовлетворяет равенствам

ВА = I, АВ = I,

и, значит, является обратной к А:

В = A -1 .

Теорема:

Матрицы А = А(е) и А’ = А(е’) линейного оператора А: V → V относительно базисов с и с’ пространства V связаны равенством

где S — матрица перехода от базиса е к базису е’.

Пусть у = Ах. Координатные столбцы элементов х и у относительно базисов с и с’ связаны равенствами

у(е) = Ах (е), у(е’) = А’х(е’) (6)

соответственно. Согласно свойству 2 матрицы перехода имеем

х(е) = Sx(c’), у(е) = Sy(е’). (7)

Заменяя в первом из равенств (6) столбцы х(е) и у(е) их выражениями (7), получаем

Sy(е’) = ASx(е’).

Пользуясь вторым равенством (6), имеем

SA’x(е’) = ASx(е’).

Отсюда в силу произвольности столбца х(е’) получаем, что

SA’ = AS.

Так как матрица перехода S невырождена и, значит, обратима, то умножая обе части последнего равенства на матрицу S -1 слева приходим к требуемой формуле (5).

Следствие:

Определитель матрицы линейного оператора не зависит от выбора базиса.

Вычислим определитель матрицы

Последнее равенство выполняется в силу того, что

Таким же свойством обладает и определитель матрицы линейного оператора

А — tI,

где I — тождественный оператор, a t — произвольное число. * Рассмотрим матрицы этого оператора в базисах e и e’ соответственно:

Воспользовавшись равенством (5)

и доказанным выше следствием, получаем, что

Пусть 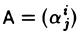— матрица линейного оператора A в каком-нибудь базисе. Функция

является многочленом от t и, согласно только что доказанному, не зависит от выбора базиса. Расписав определитель матрицы А — t1 подробнее, получаем, что

называется характеристическим многочленом линейного оператора А (матрицы А). Его корни называются характеристическими, или собственными, числами линейного оператора А (матрицы А).

Собственные значения и собственные элементы

Ненулевой элемент х ∈ V называется собственным элементом линейного оператора А: V —> V, если найдется такое число λ — собственное значение линейного оператора А, что

Ах = λх.

Пример:

Всякий многочлен нулевой степени является собственным элементом оператора дифференцирования

соответствующее собственное значение равно нулю:

Пример:

Оператор дифференцирования собственных элементов не имеет.

Пусть некоторый тригонометрический многочлен a cos t + β sin t после дифференцирования переходит в пропорциональный:

Это означает, что

Последнее равенство выполняется в том и только в том случае, если

откуда вытекает, что а = β = 0 и, значит, многочлен может быть только нулевым.

Теорема:

Вещественное число λ является собственным значением линейного оператора А в том и только в том случае, когда это число — корень его характеристического многочлена: х( λ ) = 0.
Необходимость, Пусть λ — собственное значение оператора А. Тогда найдется ненулевой элемент х, для которого Ах = λх.

Пусть е = (е1 …, еп) — базис пространства. Тогда последнее равенство можно переписать в эквивалентном матричном виде

Из того, что х — собственный элемент, вытекает, что его координатный столбец х(е) ненулевой. Это означает, что линейная система (1) имеет ненулевое решение. Последнее возможно лишь при условии, что

x (λ) = у.

Достаточность. Способ построения собственного элемента

Пусть λ — корень многочлена т- е-

Рассмотрим однородную линейную систему с матрицей А(е) — λ1:

В силу условия (2) эта система имеет ненулевое решение .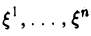

Построим элемент х по правилу

Координатный столбец х(е) этого элемента удовлетворяет условию

Последнее эквивалентно тому, что

Ах = λх.

Следовательно, х — собственный элемент линейного оператора λ, а А — соответствующее ему собственное значение.

Замечание:

Для нахождения всех собственных элементов, отвечающих заданному собственному значению λ, необходимо построить ФСР системы (3).

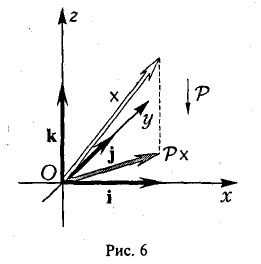
Пример:

Найти собственные векторы линейного оператора

действующего по правилу

(оператор проектирования) (рис.6).

Рассмотрим действия линейного оператора Р на базисные векторы. Имеем

Запишем матрицу оператора:

построим характеристический многочлен

и найдем его корни. Имеем λ1 = λ2,з = 1. Построим однородные линейные системы с матрицами:

Найдем фундаментальные системы решений для каждой из этих систем. Имеем

Таким образом, собственными векторами этого оператора проектирования являются: вектор к с собственным значением 0 и любой вектор 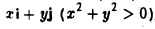с собственным значением 1.

Пример:

Найти собственные элементы линейного оператора дифференцирования D, действующего в пространстве M3 многочленов степени не выше двух:

Матрица D заданного оператора в базисе I, t, t 2 имеет вид

характеристический многочлен — λ 3 имеет ровно один корень λ = 0. Решением системы

является набор 1,0,0, которому соответствует многочлен нулевой степени.

Сопряженный оператор

В евклидовом пространстве над линейными операторами можно ввести еще одно действие — операцию сопряжения.

Пусть V — n-мерное евклидово пространство. С каждым линейным оператором

A: V → V,

действующим в этом пространстве; естественно связан другой линейный оператор, сопряженный данному.

Определение:

Л*: V → V

(читается: «а со звездой») называется сопряженным линейному оператору А: V → , если для любых элементов х и у из пространства V выполняется равенство

(Ах, у) = (х, A*у). (1)

Линейный оператор А*, сопряженный данному оператору А, всегда существует.

Пусть e = (e1…..еn) — ортобазис пространства V и А = А(e) = 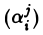— матрица линейного оператора А в этом базисе, т. е.

Непосредственными вычислениями можно убедиться в том, что для линейного оператора А*: V —> V, определяемого по правилу

равенство (1) выполнено при любых х и у. Напомним. что согласно теореме 1, для того, чтобы построить линейный оператор, достаточно задать его действие на базисные элементы.

Пример:

Введем в линейном пространстве М многочленов с вещественными коэффициентами степени не выше первой операцию скалярного умножения по следующему правилу. Пусть

Тем самым, М1 — двумерное евклидово пространство.

Пусть D: М1 — М1 — оператор дифференцирования-. D(a + bt) = b. Построим сопряженный оператор D*: М1 → М1.

Многочлены l и t образуют ортобазис пространства Af (, так как согласно правилу (*) (1. 1) = (t, t) = 1. (l, t) = 0. Матрица оператора D в этом базисе имеет вид

т.к. D(1) = 0, D(t) = 1. Тогда

— матрица сопряженного оператора D* действующего по правилу:

D*(l)=l, D*(t)=0.

Для произвольного многочлена φ(t) = а +bt получаем

Свойства операции сопряжения

1. У каждого линейного оператора существует ровно один сопряженный ему оператор.

Пусть В и С — операторы, сопряженные заданному оператору A. Это означает, что для любых элементов х и у из пространства V выполняются равенства

(Ах, у) = (х, By), (Ах, у) = (х, Су).

Отсюда вытекает, что

(х, Ву)=(х, Су)

(х, By — Су) = 0.

В силу произвольности выбора элемента х заключаем, что элемент Ву-Су ортогонален любому элементу пространства V и, в частности, себе самому. Последнее возможно лишь в случае, когда By — Су = θ и, значит, By = Су. Вследствие того, что у — произвольный элемент, получаем В = С.

2. (аA)* = аA*, где а — произвольное вещественное число.

Пусть A: V —> V н B: V → V — линейные операторы. Тогда

Свойства 2-5 легко вытекают из единственности сопряженного оператора.

6. Пусть e — ортобазис пространства V. Для того, чтобы операторы А: V —> V и В: V —> V были взаимносопряженными, т.е. выполнялись равенства В = А, А= В, необходимо и достаточно, чтобы их матрицы А = А(e) и В = В(e) получались одна из другой транспонированием.

Замечание:

Подчеркнем, что свойство 6 справедливо только для матриц, построенных в ортонормиро-ванном базисе. Для произвольного базиса оно неверно.

7. Если линейный оператор А невырожден, то сопряженный ему оператор А* также невырожден и выполняется равенство

Симметричный оператор

Линейный оператор А называется самосопряженным (или симметричным), если он совпадает с сопряженным ему оператором А*, т. е.

А* = А.

В силу свойства 6 из предыдущего параграфа матрица самосопряженного оператора в ортобазисе симметрична, т. е. не изменяется при транспонировании. Поэтому самосопряженный оператор называют также симметричным оператором.

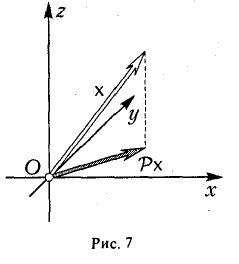
Пример:

Рассмотрим оператор Р ортогонального проектирования трехмерного евклидова пространства Oxyz на координатную плоскость Оху (рис. 7). В ортобазисе i,j,k матрица этого оператора имеет следующий вид

(так как Рi = i, Рj = j, Pk = θ, т. е. является симметричной. Значит, оператор проектирования P симметричен.
Симметричный оператор обладает рядом замечательных свойств.

Свойства симметричного оператора

Первые два вытекают из его определения.

1. Для того, чтобы линейный оператор А: V → V был симметричным, необходимо и достаточно, чтобы для любых элементов х и у из пространства V выполнялось равенство
   (Ах, У) = (х, Aу). (6)
2. Для того, чтобы линейный оператор был симметричен, необходимо и достаточно, чтобы его матрица в (каком-нибудь) ортонормированном базисе была симметрична.
3. Характеристический многочлен симметричного оператора (и симметричной матрицы) имеет только вещественные корни.

Напомним, что вещественный корень λ характеристического многочлена линейного оператора А является его собственным значением, т.е. существует ненулевой элемент х (собственный вектор оператора А), который оператор А преобразует так: Ах = λх.

4. Собственные элементы симметричного оператора, отвечающие различным собственным значениям, ортогональны.

Пусть x1 и х2 — собственные элементы оператора А,

И 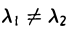. В силу симметричности оператора имеем

С другой стороны,

Из вытекающего отсюда равенства

Отсюда в силу неравенства 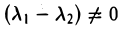имеем

5. Пусть А: V —> V — симметричный оператор. Тогда в пространстве V существует ортонормированный базис е = (е1,… ,еп), состоящий из собственных элементов оператора А:

В приведенном выше примере таким базисом является тройка i, j, к: векторы i и j — собственные векторы оператора проектирования Р с собственными значениями, равными единице, а к — его собственный вектор с нулевым собственным значением.

6. Пусть А: V —» V — невырожденный симметричный оператор. Тогда обратный ему оператор А -1 : V —> V также является симметричным.

Замечание:

Все собственные значения невырожденного оператора отличны от нуля. Если λ ≠ 0 — собственное значение оператора А, то 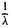— собственное значение обратного оператора А -1 .

Симметричный оператор называется положительным, если для любого ненулевого элемента х из пространства V выполняется неравенство (Ах, х) > 0.

Свойства положительного оператора

1. Симметричный оператор А: V —» V является положительным в том и только в том случае, когда все его собственные значения λ1…, λп положительны.
2. Положительный оператор невырожден (обратим).
3. Оператор, обратный положительному, также положителен.

Квадратичные формы

Пусть А = (aij) — симметричная матрица порядка п, ajj = Выражение
(1)

называется квадратичной формой переменных 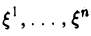. Матрица А называется матрицей этой квадратичной формы.

Примером квадратичной формы двух переменных х и у может служить выражение ах2 + 2bху + су2, где а, b и с — некоторые действительные числа; ее матрица

Набор чисел 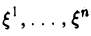можно рассматривать как координаты элемента п-мерного евклидова пространства V в некотором фиксированном ортобазисе e = (e1,…, еn) этого пространства,

Тогда выражение (1) будет представлять собой числовую функцию аргумента х, заданную на всем пространстве V. Эту функцию принято обозначать так: A(х, х). О такой квадратичной форме
(2)

говорят, что она задана в n-мерном евклидовом пространстве

Со всякой квадратичной формой A(x, x) естественно связана симметричная билинейная форма
(3)

где — координаты элемента у в ортобазисе e:

Замечание:

Форма (3) называется билинейной, так как она линейна по каждому аргументу — и по х, и по у :

(здесь a1, a2, β1, β2 — произвольные числа).

Билинейная форма (3) называется симметричной вследствие того, что ее значение не зависит от порядка аргументов,

Вычисляя значения билинейной формы A (x, у) на базисных элементах, т. е. полагая х = еk, у = ет, получаем, что (4)

Это означает, что элементы матрицы А квадратичной формы (2) суть значения билинейной формы на элементах базиса с.

Примером билинейной формы может служить скалярное произведение векторов n-мерного координатного пространства Rn

где 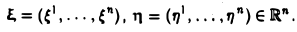Соответствующая квадратичная форма

определяет квадрат длины вектора ξ.

При переходе к другому базису координаты элемента х изменяются. Меняется и матрица А = А(e) квадратичной формы.

В приложениях часто возникает необходимость приведения квадратичной формы к наиболее простому виду. Таким видом является диагональный, или нормальный вид. Будем говорить, что квадратичная форма в базисе с имеет нормальный вид, если все коэффициенты при произведениях различных координат равны нулю, т.е. аij = 0 при i ≠ j. Тогда

Матрица квадратичной формы в этом базисе имеет диагональный вид:

Теорема:

Для каждой квадратичной формы, заданной в евклидовом пространстве, можно указать (ортонормированный) базис, в котором ее матрица имеет диагональный вид.
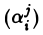
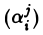
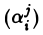
Чтобы убедиться в справедливости этого утверждения, воспользуемся свойствами симметричного оператора. Построим линейный оператор А: V → V так, чтобы его матрица в базисе е совпадала с матрицей (aij) квадратичной формы в этом же базисе е, т.е. положим = aij. В силу симметричности матрицы оператор А симметричен.’

Вычислим (Aх, х). Замечая, что

вследствие ортонормированности базиса e, получаем

Тем самым, м ы установили важную связь

A(х, х) = (Aх, х) (5)

между квадратичной формой, заданной в евклидовом пространстве V, и действующим в нем симметричным оператором.

В силу симметричности построенного оператора А в евклидовом пространстве V существует ортонормированный базис f = (f1,… ,fn) состоящий из собственных элементов оператора А:

Разложим элемент х по базису f,

и вновь вычислим (Aх, х). Имеем

Отсюда в силу равенства (5) получаем, что

Тем самым, матрица A(f) исходной квадратичной формы в базисе f является диагональной:

Сам диагональный вид квадратичной формы можно (с точностью до порядка слагаемых) записать и не вычисляя элементов базиса f. Достаточно найти собственные значения линейного оператора А или, что тоже самое, собственные значения матрицы А = (aij) и выписать их с учетом кратности.

Пример:

Привести квадратичную форму

A(х, х) = 2ху + 2yz + 2xz

к диагональному виду.
Запишем матрицу квадратичной формы

и построим ее характеристический многочлен:

Приравняв полученное выражение к нулю, найдем его корни:

Построение соответствующего ортобазиxа сложнее.

Собственные векторы симметричного оператора А суть собственные векторы матрицы квадратичной формы. Найдем их.

Пусть λ = 2. Рассмотрим однородную линейную систему с матрицей

Все решения системы

пропорциональны набору (1 1 1 ) т.

Пусть λ = — I. Однородная линейная система с матрицей

сводится к одному уравнению

х + y + z = 0

и имеет два линейно независимых решения. Выберем их так, чтобы они были ортогональны: (1 -2 1 )Т, (1 0 — 1 )Т. Легко убедиться в том, что векторы с найденными координатными столбцами попарно ортогональны. Пронормируем их:

Искомый базис построен:

Замечание:

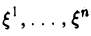
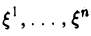
В качестве пространства V можно взять любое п-мерное евклидово пространство. Однако в задачах наиболее часто встречается координатное пространство Rn, элементами которого являются всевозможные упорядоченные наборы действительных чисел — ξ = (), стандартный базис состоит из наборов (1,0,…, 0,0), (0,1…..0,0),… , (0,0,….,), 0), (0,0…..0, I), а скалярное произведение наборов ξ = () и η = () определяется формулой

Опишем алгоритм, посредством которого для произвольной квадратичной формы, заданной в n-мерном координатном пространстве, строится базис, в котором эта квадратичная форма имеет диагональный вид.

— заданная квадратичная форма.

1. Выпишем матрицу квадратичной формы

2. Построим характеристический многочлен

и найдем его корни (в силу симметричности матрицы все корни вещественны). Запишем их с учетом кратности:

3. Пусть λ — один из этих корней, кратности k. Однородная линейная система с матрицей

имеет ровно к линейно независимых решений (образующих фундаментальную систему решений). Ортонормировав ее, получим к попарно ортогональных решений единичной длины.

4. Поступая так с каждым корнем характеристического многочлена, получаем набор ровной попарно ортогональных элементов единичной длины, т. с. ортобазис f1 …, fn пространства Rn.

В построенном ортобазисе f = (f1,…,fn) заданная квадратичная форма имеет диагональный вид:

Определение:

называется положительно определенной или знакоположительной, если для любого ненулевого элемента х (или, что то же, для любого ненулевого набора 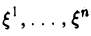, выполняется неравенство

A(х, х) > 0.

Примером знакоположительной квадратичной формы может служить скалярный квадрат произвольного вектора ξ = (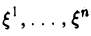) координатного пространства:

После приведения знакоположительной квадратичной формы к диагональному виду получаем

где λ1 > 0, …, λn > 0

Критерий Сильвестра (знакоположительное квадратичной формы)

Для того, чтобы квадратичная форма (6) была знакоположительной, необходимо и достаточно, чтобы все миноры ее матрицы, расположенные в левом верхнем углу, были положительны, т. е.

Метод Лагранжа

Существует еще один (простой) метод приведения квадратичной формы к диагональному виду, удобный, например, при получении ответа на вопрос, является ли квадратичная форма знакоопределенной или нет. Этот метод Лагранжа, или метод выделения полного квадрата, заключается в следующем. Пусть

— заданная квадратичная форма и a11 ≠ 0. Выпишем сначала все слагаемые, содержащие переменную ξ 1 и преобразуем их так:

Замечая, что выражение

также является квадратичной формой, но уже зависящей от меньшего числа переменных, вновь выделяем полный квадрат и т.д.

Если a11 = 0, но отлично от нуля аii(2

В результате проведенного преобразования координат, в частности, получим

И, тем самым, придем к общему случаю.

Пример:

Методом Лагранжа привести к диагональному виду квадратичную форму

A(x, х) = 2ху + 2yz + 2zx.

Введем новые координаты

Замечание:

Недостаток метола Лагранжа состоит в том, что при указанных преобразованиях координат новые координатные оси уже не являются попарно ортогональными.

Существуют и другие способы приведения квадратичной формы к диагональному виду.

Сравнивая результаты описанных выше двух способов приведения квадратичной формы 2ху + 2yz + 2zx к диагональному виду (речь идет о последних двух разобранных примерах), можно заметить, что в них соответственно одинаковы: число отрицательных коэффициентов и число положительных коэффициентов. Это совпадение не случайно, а является важным свойством квадратичных форм, называемым законом инерции:

число положительных, число отрицательных и число нулевых коэффициентов при квадратах неизвестных в диагональном виде квадратичной формы всегда одни и те же и не зависят от способа приведения квадратичной формы к этому виду.

Классификация кривых и поверхностей второго порядка

Применим описанный выше алгоритм приведения квадратичной формы к диагональному виду для классификации кривых и поверхностей второго порядка.

Кривые

Рассмотрим общее уравнение кривой второго порядка на плоскости Оху :

Построим матрицу квадратичной части ах2 + 2bху+су2:

Найдем корни λ1 и λ2 характеристического многочлена и соответствующие им собственные векторы i и j (единичные и взаимноортогональные).. Возьмем эти векторы за орты новых осей Ох и Оу (рис. 8).

Переходя к новым координатам 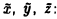, получим

Возможны два случая: 1) λ1 • λ2 ≠ 0, 2) λ1 (или λ2 ) равно нулю.

В первом случае сдвигом точки начала отсчета

добиваемся исчезновения линейных членов

Далее, как это и делалось, рассматриваем всевозможные сочетания знаков у коэффициентов λ1, λ2 и f. В результате получаем: эллипс, гиперболу, пару пересекающихся прямых, точку, пустое множество.

Во втором случае (положим для определенности λ1 = 0, λ2 ≠ 0) сдвигом начала отсчета

приходим к уравнению

Если же d= 0,то взяв а = 0, имеем

В зависимости от знака 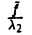получаем: пару параллельных прямых, пару совпадающих прямых, пустое множество.

Замечание:

Операция отыскания корней характеристического многочлена квадратичной части уравнения кривой и взаимноортогональных единичных собственных векторов, описанная здесь, заменяет уничтожение произведения разноименных координат путем поворота на подходящий угол. В случае поверхностей второго порядка дело обстоит сложнее (и для того, чтобы разобраться с классификацией до конца, нужны и внимание и терпение).

Поверхности

Общее уравнение поверхности второго порядка имеет следующий вид

Упростим вид квадратичной части этого уравнения (подчеркнута), пользуясь описанным выше алгоритмом. Построим матрицу

найдем корни λ1, λ2, λз характеристического многочлена

и соответствующие им собственные векторы i, J, k так, чтобы они образовывали ортонормированную тройку (это всегда возможно). Возьмем векторы i, J и k за орты новых координатных осей Ox, Ox, Oz. Производя замену координат, получим (*)

Возможны три случая:

(I) Все три корня λ1, λ2, λ3 отличны от нуля. Путем сдвига начала

уравнение (*) поверхности приводится к следующему виду

имеют один и тот же знак, противоположный знаку .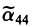

получаем уравнение эллипсоида

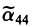
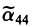
β ) Знаки λ1 и λ2 противоположны знаку , а знаки A3 и совпадают. Полагая

получаем уравнение однополостного гиперболоида

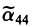
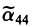
γ ) Знаки λ1 и λ2 совпадают со знаком , а знаки λ3 и противоположны. Полагая

получаем уравнение двуполостного гиперболоида

б. 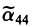= 0.

а) Если λ1, λ2 и λз имеют один и тот же знак, то получаем точку (0, 0, 0).

β) Если одно из λ, имеет знак, противоположный знаку двух других, то получаем уравнение конуса второго порядка

(II) Ровно один корень равен нулю (для определенности λз = 0). Полагая

Тогда сдвигом точки начала отсчета

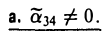
получаем уравнение вида

а) Если λ1 и λ2 — одного знака, то, полагая

(можно считать, что знак 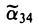противоположен знаку λ1 и λ2; этого всегда можно добиться, поменяв в случае необходимости ориентацию оси z на противоположную), получаем уравнение эллиптического параболоида

β) Если λ1 и λ2 имеют противоположные знаки, то, положив

получим уравнение гиперболического параболоида

б. 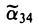=0. Тогда уравнение поверхности имеет следующий вид

Классификация поверхностей с уравнениями такого типа приводится в таблице.

Замечание:

Отсутствие третьей координаты (точнее, ее неявное присутствие) приводит к цилиндрическим поверхностям, направляющими которых являются кривые второго порядка, лежащие в плоскости Z = 0 и имеющие уравнения вила

(III) Ровно два корня равны нулю (для определенности λ2 = λ3 = 0). Преобразованием координат

приходим к уравнению

Покажем, что этот случай всегда можно свести к такому: , = 0. Преобразованием координат

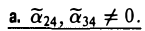
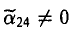
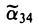
уравнение поверхности приводится к следующему виду

Замечание:

Преобразование координат, упрощающее вид уравнения, выбирается так, чтобы новая координатная система вновь была прямоугольной декартовой.

Сдвигом начала координат

получаем уравнение параболического цилиндра

описывает либо пару параллельных плоскостей ( λ1 • 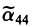0).

Дополнение к линейным отображениям

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Ядро и образ линейного отображения

Ядром линейного отображения называется множество таких векторов , что , т.е. множество векторов из , которые отображаются в нулевой вектор пространства . Ядро отображения обозначается:

Образом линейного отображения называется множество образов всех векторов из . Образ отображения обозначается или

Заметим, что символ следует отличать от — мнимой части комплексного числа.

Примеры ядер и образов линейных отображений

1. Ядром нулевого отображения является все пространство , а образом служит один нулевой вектор, т.е.

2. Рассмотрим отображение , которое ставит в соответствие каждому вектору n-мерного линейного пространства его координатный столбец относительно заданного базиса . Ядром этого отображения является нулевой вектор пространства , поскольку только этот вектор имеет нулевой координатный столбец . Образ преобразования совпадает со всем пространством , так как это преобразование сюръективно (любой столбец из является координатным столбцом некоторого вектора пространства ).

3. Рассмотрим отображение , которое каждому вектору n-мерного евклидова пространства ставит в соответствие алгебраическое значение его проекции на направление, задаваемое единичным вектором . Ядром этого преобразования является ортогональное дополнение — множество векторов, ортогональных . Образом является все множество действительных чисел .

4. Рассмотрим отображение , которое каждому многочлену степени не выше ставит в соответствие его производную. Ядром этого отображения является множество многочленов нулевой степени, а образом — все пространство .

Свойства ядра и образа линейного отображения

1. Ядро любого линейного отображения является подпространством: .

В соответствии с определением требуется доказать, что множество является непустым и замкнутым относительно операций сложения векторов и умножения вектора на число. В самом деле, из однородности отображения следует, что

т.е. нулевой вектор отображается в нулевой вектор . Следовательно, ядро любого линейного отображения не является пустым и содержит, по крайней мере, нулевой элемент: . Покажем, что множество замкнуто по отношению к операциям сложения векторов и умножения вектора на число. Действительно:

Следовательно, множество является линейным подпространством пространства .

2. Образ любого линейного отображения является подпространством: .

В самом деле, докажем, например, замкнутость множества по отношению к операции умножения вектора на число. Если , то существует вектор такой, что . Тогда , то есть .

Поскольку ядро и образ линейного отображения являются линейными подпространствами (свойства 1 и 2), можно говорить об их размерностях.

Дефектом линейного отображения называется размерность его ядра: , а рангом линейного отображения — размерность его образа: .

3. Ранг линейного отображения равен рангу его матрицы (определенной относительно любых базисов).

В самом деле, если любой базис пространства , то . Поэтому максимальное число линейно независимых векторов системы (ранг системы векторов) равно максимальному числу линейно независимых столбцов матрицы отображения, т.е. рангу матрицы: .

4. Линейное отображение инъективно тогда и только тогда, когда , другими словами, когда дефект отображения равен нулю: .

Действительно, образом нулевого вектора служит нулевой вектор . Поэтому, если отображение инъективно, то ядро содержит только нулевой вектор , иначе два разных вектора имели бы один и тот же образ . Обратно, при условии разные векторы не могут иметь одинаковые образы , так как в этом случае из равенств , следует, что ненулевой вектор (приходим к противоречию).

5. Линейное отображение сюръективно тогда и только тогда, когда , другими словами, когда ранг отображения равен размерности пространства образов: .

6. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда и одновременно.

Теорема (9.1) о размерностях ядра и образа. Сумма размерностей ядра и образа любого линейного отображения равна размерности пространства прообразов:

Действительно, пусть . Выберем в подпространстве базис и дополним его векторами до базиса всего пространства . Покажем, что векторы образуют базис подпространства .

Во-первых, , так как образ любого вектора линейно выражается через векторы

Во-вторых, образующие линейно независимы. Если их линейная комбинация равна нулевому вектору:

то вектор принадлежит ядру (его образ — нулевой вектор). Однако, по построению этот вектор принадлежит алгебраическому дополнению . Учитывая, что , заключаем: . Получили разложение нулевого вектора по линейно независимой системе векторов, значит, все коэффициенты . Поэтому равенство справедливо только для тривиальной линейной комбинации, т.е. система векторов линейно независимая.

Таким образом, векторы образуют базис подпространства , а его размерность определяется количеством базисных векторов, т.е. , что равносильно (9.3).

Следствие. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда обратима его матрица (определенная относительно любых базисов).

Действительно, для обратимости преобразования (см. свойство 6) его матрица (размеров ) должна удовлетворять условиям (см. свойства 3,4,5):

Тогда по теореме 9.1 заключаем, что , т.е. матрица — квадратная n-го порядка и невырожденная , что и требовалось доказать.

Обратимые линейные отображения называются также невырожденными (имея в виду невырожденность их матрицы).

Матрица линейного оператора примеры

Построение матрицы по заданной формуле отображения.

Пусть отображение задано с помощью формулы:

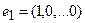
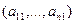
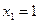
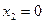
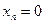
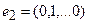
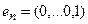
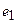
то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор , найдём его образ, это будет вектор . Для этого в формуле, задающей образ вектора, полагаем , ,…, . Аналогично находим образы для ,…, . Из координат образа вектора составляем 1-й столбец матрицы линейного оператора, аналогично из координат последующих векторов – остальные столбцы. Рассмотрим на примере.

Пример 1. Пусть оператор задан с помощью формулы:

.

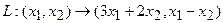
Прежде всего, докажем, что это отображение – действительно линейный оператор.

Отобразим сумму векторов:

Теперь каждую координату получившегося вектора можем преобразовать:

.

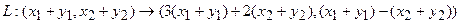
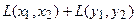
Аналогично для умножения на константу:

Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x₁ = 1, x₂ = 0, а затем x₁ = 0, x₂ = 1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1).

Поэтому матрица линейного оператора будет иметь вид:

.

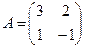
Аналогичным способом решается задача и для 3 и большего количества переменных.

Пример 2. .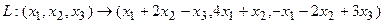

Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3).

Матрица линейного оператора:

.

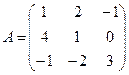
2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается.

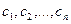
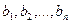
Если задана система из n векторов, образующих базис, и какая-нибудь произвольная система n векторов (возможно, линейно-зависимая), то однозначно определён линейный оператор, отображающий каждый вектор первой системы в соответствующий вектор второй системы.

Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.

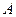
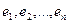
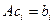
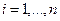
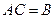
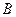
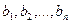
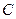
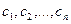
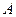
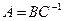
Пусть – матрица оператора в базисе . По условию, для всех индексов . Данные n равенств можно записать в виде одного матричного равенства: , при этом столбцы матрицы – это векторы , а столбцы матрицы – векторы . Тогда матрица может быть найдена в виде .

Пример. Найти матрицу линейного оператора, отображающего базис

в систему векторов .

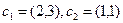
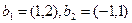
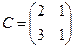
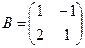
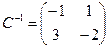
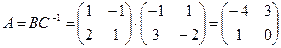
Здесь , , , и получаем:

.

Проверка осуществляется умножением получившейся матрицы на каждый вектор: .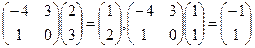

Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач.

2.3. Прочие способы нахождения матрицы оператора.

Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2.

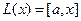
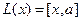
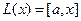
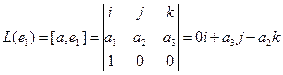
Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида и . Построим матрицу одного из этих операторов, . Для этого найдём образы всех трёх базисных векторов линейного пространства.

.

Аналогично, ,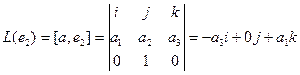

.

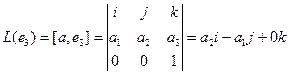
Координаты полученных векторов запишем в виде столбцов матрицы оператора.

Матрица оператора: .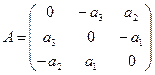

Аналогично можно построить матрицу линейного оператора :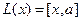

.

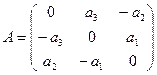
Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n + 1. Возьмём в качестве базиса элементы , , ,…, .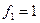

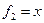
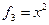
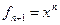
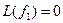
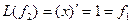
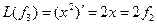
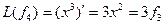
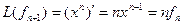
, , , аналогично получим ,…, .

Матрица этого линейного оператора:

Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10219 – | 7588 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Матрица линейного оператора

Определение 1. Если задан закон, который каждому вектору x?? ставит в соот ветствие вектор y . то говорят, что в линейном пространстве ? задан оператор A , при этом пишут:

Определение 2. Оператор A называется линейным, если для любых x 1 ?? и x 2 ?? и произвольного числа ? выполняются условия:

Рассмотрим теперь в евклидовом пространстве E n базис e 1 ,e 2 . e n и пусть в этом пространстве определён линейный оператор A : y = A x .

Разложим векторы x и y по базису e 1 ,e 2 . e n :

В силу линейности оператора A можно написать

Заметим, что каждый вектор , следовательно, его также можно разложить по базису e 1 ,e 2 . e n , т.е.

В силу единственности разложения по данному базису мы можем при равнять коэффициенты при базисных векторах в правых частях формул (1) и (2); тогда получим:

Получили, что линейному оператору A в данном базисе соответствует квадратная матрица

которая называется матрицей линейного оператора A , i -й столбец которой состоит из координат вектора Ae i (i = 1,2. n ) относительно данного базиса. Отметим, что матрица A оператора A зависит от выбора базиса e 1 ,e 2 . e n .

Итак, мы показали, что всякому линейному оператору A в евклидовом пространстве E n соответствует матрица A ; можно доказать и обратное утверждение: всякую квадратную матрицу A можно рассматривать как матрицу некоторого линейного оператора A в данном базисе e 1 ,e 2 . e n .

Представляют интерес невырожденные линейные операторы, т.е. такие операторы, матрицы которых имеют обратную A -1 , т.е. также являются невырожденными. В этом случае каждому вектору y (образу), определённому соотношением, отвечает единственный вектор x (прообраз) и при этом имеет место матричное равенство: X = A -1 ? Y .

Примеры линейных операторов

1. В пространстве 2-мерных векторов линейным оператором является правило

связывающее вектор-прообраз 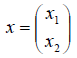с вектором-образом

2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого простран ства его производную функцию.

3. В пространстве многочленов P n (t) линейным оператором является операция умножения многочлена на независимую переменную t .

Пример: Известны образы базисных векторов E 3 под действием оператора A :

Найти матрицу этого оператора в исходном базисе.

Решение: По определению y = A x, значит в матричном виде можно записать, что A = X -1 Y . Для нашего примера получаем

Действия над операторами

Сложение линейных операторов. Пусть x?E n , A и B – два линейных оператора в этом пространстве.

Определение 1. Суммой линейных операторов A и B в E n называется оператор C, определяемый равенством Cx = A x + Bx , где x – любой вектор из E n .

Сумма линейных операторов является линейным оператором, причём его матрица C = A + B, где A и B – матрицы линейных операторов A и B .

Умножение линейного оператора на число. Пусть x?E n , линейный оператор A определён в E n , ? – некоторое число.

Определение 2. Произведением линейного оператора A на число ? называется оператор ?A , определяемый равенством .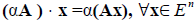

?A является линейным оператором, а матрица этого линейного оператора получается из матрицы A умножением её на число ? , т.е. она равна ? ? A.

Умножение линейных операторов. Пусть x? E n , y ? E n , z ? E n и кроме того в E n определены линейные операторы A и B таким образом, что y = Bx, z = A y .

Определение 3. Произведением A ? B линейных операторов A и B называется оператор C, определяемый соотношением Cx = A (Bx) .

Таким образом, перемножение линейных операторов состоит в последовательном их применении по отношению к вектору x .

Рассмотрим матрицы – столбцы:

и обозначим через A, B и C – соответственно матрицы линейных операторов A, B и C. Тогда Z = A ? (B ? X) = (A ? B) ? X = C ? X , таким образом, C = A ? B, т.е. матрица произведения линей ных операторов также является линейным оператором.

a) (A ? B)(x + y) = A (B(x + y)) = A (Bx + By) = A (Bx) + A (By) = = (A ? B) ? x + (A ? B) ? y

б) (A ? B)(? x) = A (B(? x)) = A (?Bx) =?A (Bx) =? (A ? B)x

Свойства умножения линейных операторов вытекают из свойств умножения матриц.

Определение 4. Линейные операторы A и В называются равными, если 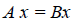. Равенство операторов обозначается как A = B .

Определение 5. Оператор E называется единичным (или тождественным) оператором, если каждому элементу x линейного пространства он ставит в соответствие тот же самый элемент, то есть

1. Понятие линейного оператора

Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 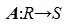, сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.

Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x₁ и x₂ пространства R и любого λ из числового поля K выполняются соотношения

Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.

Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы и соответственно. Пусть задано отображение

где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:

Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов и в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.

Пусть x − произвольный элемент в R. Тогда

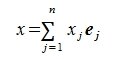(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

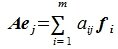(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

Сделаем следующее обозначение:

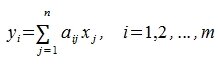(6)

Тогда равенство (5) примет следующий вид:

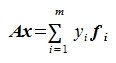(7)

Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты y_i, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента x_j, j=1,2. n с коэффициентами a_ij i=1,2. m; j=1,2. n.

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.

Применим оператор C к базисному вектору e_j, тогда:

Cej= Aej+ Bej=	n	(aij+bij) ej
∑
j= 1

Следовательно оператору C отвечает матрица 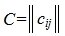,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.

Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:

Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.

Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:

Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.

Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.

8. Образ линейного оператора

Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).

Образ функции — это множество всех значений, которые даёт функция.

В более общем виде, вычисление значения заданной функции [math]displaystyle{ f }[/math] для каждого элемента заданного подмножества [math]displaystyle{ A }[/math] области определения функции даёт множество, называемое «образом [math]displaystyle{ A }[/math] для функции [math]displaystyle{ f }[/math]». Аналогично, обратный образ (или прообраз) заданного подмножества [math]displaystyle{ B }[/math] кодомена функции [math]displaystyle{ f }[/math] — это множество всех элементов области определения, которые отображаются в элементы множества [math]displaystyle{ B }[/math].

Образ и обратный образ могут также быть определены для общих бинарных отношений, а не только функций.

Определение

Слово «образ» используется тремя связанными способами. В этих определениях [math]displaystyle{ fcolon X to Y }[/math] — это функция из множества [math]displaystyle{ X }[/math] в множество [math]displaystyle{ Y }[/math].

Образ элемента

Если [math]displaystyle{ x }[/math] является элементом множества [math]displaystyle{ X }[/math], то образ элемента [math]displaystyle{ x }[/math] для функции [math]displaystyle{ f }[/math], обозначаемый [math]displaystyle{ f(x) }[/math]^[1], — это значение функции [math]displaystyle{ f }[/math] для аргумента [math]displaystyle{ x }[/math].

Образ подмножества

Образ подмножества [math]displaystyle{ A subseteq X }[/math] для функции [math]displaystyle{ f }[/math], обозначаемый [math]displaystyle{ f[A] }[/math], является подмножеством множества [math]displaystyle{ Y }[/math], которое может быть определено с помощью следующей формы записи^[2]:

[math]displaystyle{ f[A] = { f(x) mid x in A } }[/math]

Если нет риска путаницы, [math]displaystyle{ f[A] }[/math] записывается просто как [math]displaystyle{ f(A) }[/math]. Это соглашение является общепринятым. Предполагаемый смысл должен быть определён из контекста. Это делает f[.] функцией, областью определения которой является степень множества X (множество всех подмножеств множества X), а кодоменом является степень множества Y. См. раздел § Обозначения.

Образ функции

Образ функции — это образ всей области определения, известный также как область значений функции^[3].

Обобщение к бинарным отношениям

Если [math]displaystyle{ R }[/math] является произвольным бинарным отношением на X[math]displaystyle{ times }[/math]Y, то множество [math]displaystyle{ { y in Y | xRy, x in X } }[/math] называется образом отношения [math]displaystyle{ R }[/math]. Множество [math]displaystyle{ { xin X | xRy, y in Y} }[/math] называется областью определения отношения [math]displaystyle{ R }[/math].

Обратный образ

Пусть [math]displaystyle{ f }[/math] будет функцией из [math]displaystyle{ X }[/math] в [math]displaystyle{ Y }[/math]. Прообраз или обратный образ множества [math]displaystyle{ B subseteq Y }[/math] для функции [math]displaystyle{ f }[/math], обозначаемый [math]displaystyle{ f^{-1}[B] }[/math], — это подмножество [math]displaystyle{ X }[/math] определённое как:

[math]displaystyle{ f^{-1}[ B ] = { x in X , | , f(x) in B }. }[/math]

Возможны и другие обозначения, как, например: [math]displaystyle{ f^{-1}(B) }[/math]^[4] и [math]displaystyle{ f^-(B) }[/math].^[5]

Обратный образ синглтона, обозначаемый [math]displaystyle{ f^{-1}[{y}] }[/math] или [math]displaystyle{ f^{-1}[y] }[/math], называется также слоем для [math]displaystyle{ y }[/math] или множеством уровня элемента [math]displaystyle{ y }[/math]. Множество всех слоёв для элементов [math]displaystyle{ Y }[/math] — это семейство подмножеств, индексированных элементами [math]displaystyle{ Y }[/math].

Например, для функции [math]displaystyle{ f(x) = x^2 }[/math] обратным образом [math]displaystyle{ {4} }[/math] будет [math]displaystyle{ {-2, 2} }[/math]. Снова, если нет риска путаницы, [math]displaystyle{ f^{-1}[B] }[/math] может обозначаться как [math]displaystyle{ f^{-1}(B) }[/math], а [math]displaystyle{ f^{-1} }[/math] можно рассматривать как функцию из множества всех подмножеств (булеана) множества [math]displaystyle{ Y }[/math] в булеан множества [math]displaystyle{ X }[/math]. Обозначение [math]displaystyle{ f^{-1} }[/math] не следует путать с обратной функцией, хотя оно и согласуется с обычной обратной функцией для биекций в том, что обратный образ [math]displaystyle{ B }[/math] для [math]displaystyle{ f }[/math] является образом [math]displaystyle{ B }[/math] для [math]displaystyle{ f^{-1} }[/math].

Обозначения для образа и обратного образа

Традиционные обозначения, использованные в предыдущих разделах, могут вызвать сложности в понимании. Альтернативой^[6] является задание явных имён для образа и прообраза функций между булеанами:

Стрелочные обозначения

• [math]displaystyle{ f^to:mathcal{P}(X)tomathcal{P}(Y) }[/math] для [math]displaystyle{ f^to(A) = { f(a);|; a in A} }[/math]
• [math]displaystyle{ f^leftarrow:mathcal{P}(Y)tomathcal{P}(X) }[/math] для [math]displaystyle{ f^leftarrow(B) = { a in X ;|; f(a) in B} }[/math]

Обозначения со звёздочками

• [math]displaystyle{ f_star:mathcal{P}(X)tomathcal{P}(Y) }[/math] вместо [math]displaystyle{ f^to }[/math]
• [math]displaystyle{ f^star:mathcal{P}(Y)tomathcal{P}(X) }[/math] вместо [math]displaystyle{ f^leftarrow }[/math]

Другая терминология

• Альтернативные обозначения [math]displaystyle{ f[A] }[/math], используемые в математической логике и теории множеств, это [math]displaystyle{ f^{primeprime}A }[/math]^[7][8].
• Некоторые книги называют образ [math]displaystyle{ f }[/math] областью значений [math]displaystyle{ f }[/math], но этого следует избегать, поскольку термин «область значений» используется широко также для обозначения кодомена функции [math]displaystyle{ f }[/math].

Примеры

1. [math]displaystyle{ fcolon {1, 2, 3} to {a, b, c, d} }[/math] определена как [math]displaystyle{
   f(x) = left{begin{matrix}
   a, & mbox{ если } x=1 \
   a, & mbox{ если } x=2 \
   c, & mbox{ если } x=3.
   end{matrix}right.
   }[/math] Образом множества {2, 3} для функции [math]displaystyle{ f }[/math] является [math]displaystyle{ f({2, 3}) = {a, c} }[/math]. Образ функции [math]displaystyle{ f }[/math] — это [math]displaystyle{ {a, c} }[/math]. Прообразом [math]displaystyle{ a }[/math] является [math]displaystyle{ f^{-1}({a}) = {1, 2} }[/math]. Прообразом множества [math]displaystyle{ {a, b} }[/math] также является [math]displaystyle{ {1, 2} }[/math]. Прообразом множества [math]displaystyle{ {b, d} }[/math] является пустое множество [math]displaystyle{ {} }[/math].
2. [math]displaystyle{ fcolon mathbf{R} to mathbf{R} }[/math] определена как [math]displaystyle{ f(x) = x^2 }[/math]. Образ [math]displaystyle{ {-2, 3} }[/math] для функции [math]displaystyle{ f }[/math] — это [math]displaystyle{ f({-2, 3}) = {4, 9} }[/math], а образ функции [math]displaystyle{ f }[/math] — это [math]displaystyle{ mathbf{R}^+ }[/math]. Прообраз [math]displaystyle{ {4, 9} }[/math] для [math]displaystyle{ f }[/math] — это [math]displaystyle{ f^{-1}({4, 9}) = {-3, -2, 2, 3} }[/math]. Прообраз множества [math]displaystyle{ N = {n in mathbf{R} | n lt 0} }[/math] для [math]displaystyle{ f }[/math] — это пустое множество, поскольку отрицательные числа не имеют квадратных корней в множестве вещественных чисел.
3. [math]displaystyle{ fcolon mathbf{R}^2 to mathbf{R} }[/math] определена как [math]displaystyle{ f(x, y) = x^2 + y^2 }[/math]. Слои [math]displaystyle{ f^{-1}({a}) }[/math] являются концентричными окружностями вокруг начала координат, единственная точка начала координат или пустого множества в зависимости от того, [math]displaystyle{ a gt 0 }[/math], [math]displaystyle{ a = 0 }[/math] или [math]displaystyle{ a lt 0 }[/math] соответственно.
4. Если [math]displaystyle{ M }[/math] — это многообразие, а [math]displaystyle{ pi: TM to M }[/math] — это каноническая проекция из касательного расслоения [math]displaystyle{ TM }[/math] в [math]displaystyle{ M }[/math], то слоями отображения [math]displaystyle{ pi }[/math] являются касательные пространства [math]displaystyle{ T_x(M) }[/math] для [math]displaystyle{ x in M }[/math]. Это также пример расслоённого пространства.
5. Факторгруппа — это гомоморфный образ.

Свойства

Контрпримеры

Контрпримеры на основе [math]displaystyle{ fcolonmathbb{R} rightarrow mathbb{R}, x mapsto x^2 }[/math], показывающие, что это равенство обычно не выполняется для некоторых законов:
[math]displaystyle{ f(A_1cap A_2) varsubsetneq f(A_1) cap f(A_2) }[/math]
[math]displaystyle{ f(f^{-1}(B_3))subseteq B_3 }[/math]
[math]displaystyle{ f^{-1}(f(A_4))supseteq A_4 }[/math]

Общий случай

Для любой функции [math]displaystyle{ f colon X to Y }[/math] и всех подмножеств [math]displaystyle{ A subseteq X }[/math] и [math]displaystyle{ B subseteq Y }[/math] выполняются следующие свойства:

Образ	Прообраз
[math]displaystyle{ f(X) subseteq Y }[/math]	[math]displaystyle{ f^{-1}(Y) = X }[/math]
[math]displaystyle{ f(f^{-1}(Y)) = f(X) }[/math]	[math]displaystyle{ f^{-1}(f(X)) = X }[/math]
[math]displaystyle{ f(f^{-1}(B)) subseteq B }[/math] (равны, если [math]displaystyle{ B subseteq f(X) }[/math], т.е. [math]displaystyle{ f }[/math] сюръектвна)[9][10]	[math]displaystyle{ f^{-1}(f(A)) supseteq A }[/math] (равны, если [math]displaystyle{ f }[/math] инъективна) [9][10]
[math]displaystyle{ f(f^{-1}(B)) = B cap f(X) }[/math]	[math]displaystyle{ (f vert_A)^{-1}(B) = A cap f^{-1}(B) }[/math]
[math]displaystyle{ f(f^{-1}(f(A))) = f(A) }[/math]	[math]displaystyle{ f^{-1}(f(f^{-1}(B))) = f^{-1}(B) }[/math]
[math]displaystyle{ f(A) = varnothing Leftrightarrow A = varnothing }[/math]	[math]displaystyle{ f^{-1}(B) = varnothing Leftrightarrow B subseteq Y setminus f(X) }[/math]
[math]displaystyle{ f(A) supseteq B Leftrightarrow exists C subseteq A : f(C) = B }[/math]	[math]displaystyle{ f^{-1}(B) supseteq A Leftrightarrow f(A) subseteq B }[/math]
[math]displaystyle{ f(A) supseteq f(X setminus A) Leftrightarrow f(A) = f(X) }[/math]	[math]displaystyle{ f^{-1}(B) supseteq f^{-1}(Y setminus B) Leftrightarrow f^{-1}(B) = X }[/math]
[math]displaystyle{ f(X setminus A) supseteq f(X) setminus f(A) }[/math]	[math]displaystyle{ f^{-1}(Y setminus B) = X setminus f^{-1}(B) }[/math][9]
[math]displaystyle{ f(A cup f^{-1}(B)) subseteq f(A) cup B }[/math][11]	[math]displaystyle{ f^{-1}(f(A) cup B) supseteq A cup f^{-1}(B) }[/math][11]
[math]displaystyle{ f(A cap f^{-1}(B)) = f(A) cap B }[/math][11]	[math]displaystyle{ f^{-1}(f(A) cap B) supseteq A cap f^{-1}(B) }[/math][11]

Также:

• [math]displaystyle{ f(A) cap B = varnothing Leftrightarrow A cap f^{-1}(B) = varnothing }[/math]

Для нескольких функций

Для функций [math]displaystyle{ fcolon X to Y }[/math] и [math]displaystyle{ gcolon Y to Z }[/math] с подмножествами [math]displaystyle{ A subseteq X }[/math] и [math]displaystyle{ C subseteq Z }[/math] выполняются следующие свойства:

• [math]displaystyle{ (g circ f)(A) = g(f(A)) }[/math]
• [math]displaystyle{ (g circ f)^{-1}(C) = f^{-1}(g^{-1}(C)) }[/math]

Несколько подмножеств домена или кодомена

Для функции [math]displaystyle{ fcolon X to Y }[/math] и подмножеств [math]displaystyle{ A_1,A_2 subseteq X }[/math] и [math]displaystyle{ B_1,B_2 subseteq Y }[/math] выполняются следующие свойства:

Образ	Прообраз
[math]displaystyle{ A_1 subseteq A_2 Rightarrow f(A_1) subseteq f(A_2) }[/math]	[math]displaystyle{ B_1 subseteq B_2 Rightarrow f^{-1}(B_1) subseteq f^{-1}(B_2) }[/math]
[math]displaystyle{ f(A_1 cup A_2) = f(A_1) cup f(A_2) }[/math][11][12]	[math]displaystyle{ f^{-1}(B_1 cup B_2) = f^{-1}(B_1) cup f^{-1}(B_2) }[/math]
[math]displaystyle{ f(A_1 cap A_2) subseteq f(A_1) cap f(A_2) }[/math][11][12] (равны, если [math]displaystyle{ f }[/math] инъективны[13])	[math]displaystyle{ f^{-1}(B_1 cap B_2) = f^{-1}(B_1) cap f^{-1}(B_2) }[/math]
[math]displaystyle{ f(A_1 setminus A_2) supseteq f(A_1) setminus f(A_2) }[/math][11] (равны, если [math]displaystyle{ f }[/math] инъективна[13])	[math]displaystyle{ f^{-1}(B_1 setminus B_2) = f^{-1}(B_1) setminus f^{-1}(B_2) }[/math][11]
[math]displaystyle{ f(A_1 triangle A_2) supseteq f(A_1) triangle f(A_2) }[/math] (равны , если [math]displaystyle{ f }[/math] инъективна)	[math]displaystyle{ f^{-1}(B_1 triangle B_2) = f^{-1}(B_1) triangle f^{-1}(B_2) }[/math]

Результаты для образов и прообразов (булевой) алгебры пересечений и объединений работает для любой коллекции подмножеств, не только для пар подмножеств:

• [math]displaystyle{ fleft(bigcup_{sin S}A_sright) = bigcup_{sin S} f(A_s) }[/math]
• [math]displaystyle{ fleft(bigcap_{sin S}A_sright) subseteq bigcap_{sin S} f(A_s) }[/math]
• [math]displaystyle{ f^{-1}left(bigcup_{sin S}B_sright) = bigcup_{sin S} f^{-1}(B_s) }[/math]
• [math]displaystyle{ f^{-1}left(bigcap_{sin S}B_sright) = bigcap_{sin S} f^{-1}(B_s) }[/math]

(Здесь [math]displaystyle{ S }[/math] может быть бесконечным множеством, даже несчётным.)

Что касается описанной выше алгебры подмножеств, обратная отображающая функция — это гомоморфизм решётки, в то время как отображающая функция — это лишь гомоморфизм полурешёток (т.е., она не всегда сохраняет пересечения).

См. также

• Биекция, инъекция и сюръекция^[en]
• Образ (теория категорий)^[en]
• Ядро (теория множеств)^[en]

Примечания

Литература