Как найти образ гомоморфизма - Исправление недочетов и поиск решений вместе с Examum.ru

From Wikipedia, the free encyclopedia

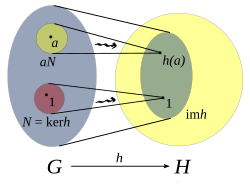
Depiction of a group homomorphism (h) from G (left) to H (right). The oval inside H is the image of h. N is the kernel of h and aN is a coset of N.

In mathematics, given two groups, (G, ∗) and (H, ·), a group homomorphism from (G, ∗) to (H, ·) is a function h : G → H such that for all u and v in G it holds that

where the group operation on the left side of the equation is that of G and on the right side that of H.

From this property, one can deduce that h maps the identity element e_G of G to the identity element e_H of H,

${displaystyle h(e_{G})=e_{H}}$

and it also maps inverses to inverses in the sense that

$hleft(u^{-1}right)=h(u)^{-1}.,$

Hence one can say that h «is compatible with the group structure».

Older notations for the homomorphism h(x) may be x^h or x_h,^{[citation needed]} though this may be confused as an index or a general subscript. In automata theory, sometimes homomorphisms are written to the right of their arguments without parentheses, so that h(x) becomes simply .^{[citation needed]}

In areas of mathematics where one considers groups endowed with additional structure, a homomorphism sometimes means a map which respects not only the group structure (as above) but also the extra structure. For example, a homomorphism of topological groups is often required to be continuous.

Intuition[edit]

The purpose of defining a group homomorphism is to create functions that preserve the algebraic structure. An equivalent definition of group homomorphism is: The function h : G → H is a group homomorphism if whenever

a ∗ b = c we have h(a) ⋅ h(b) = h(c).

In other words, the group H in some sense has a similar algebraic structure as G and the homomorphism h preserves that.

Types[edit]

Monomorphism: A group homomorphism that is injective (or, one-to-one); i.e., preserves distinctness.
Epimorphism: A group homomorphism that is surjective (or, onto); i.e., reaches every point in the codomain.
Isomorphism: A group homomorphism that is bijective; i.e., injective and surjective. Its inverse is also a group homomorphism. In this case, the groups G and H are called isomorphic; they differ only in the notation of their elements and are identical for all practical purposes.
Endomorphism: A group homomorphism, h: G → G; the domain and codomain are the same. Also called an endomorphism of G.
Automorphism: A group endomorphism that is bijective, and hence an isomorphism. The set of all automorphisms of a group G, with functional composition as operation, itself forms a group, the automorphism group of G. It is denoted by Aut(G). As an example, the automorphism group of (Z, +) contains only two elements, the identity transformation and multiplication with −1; it is isomorphic to (Z/2Z, +).

Image and kernel[edit]

We define the kernel of h to be the set of elements in G which are mapped to the identity in H

${displaystyle operatorname {ker} (h):=left{uin Gcolon h(u)=e_{H}right}.}$

and the image of h to be

{displaystyle operatorname {im} (h):=h(G)equiv left{h(u)colon uin Gright}.}

The kernel and image of a homomorphism can be interpreted as measuring how close it is to being an isomorphism. The first isomorphism theorem states that the image of a group homomorphism, h(G) is isomorphic to the quotient group G/ker h.

The kernel of h is a normal subgroup of G and the image of h is a subgroup of H:

${begin{aligned}hleft(g^{-1}circ ucirc gright)&=h(g)^{-1}cdot h(u)cdot h(g)\&=h(g)^{-1}cdot e_{H}cdot h(g)\&=h(g)^{-1}cdot h(g)=e_{H}.end{aligned}}$

If and only if ker(h) = {e_G}, the homomorphism, h, is a group monomorphism; i.e., h is injective (one-to-one). Injection directly gives that there is a unique element in the kernel, and, conversely, a unique element in the kernel gives injection:

${begin{aligned}&&h(g_{1})&=h(g_{2})\Leftrightarrow &&h(g_{1})cdot h(g_{2})^{-1}&=e_{H}\Leftrightarrow &&hleft(g_{1}circ g_{2}^{-1}right)&=e_{H}, operatorname {ker} (h)={e_{G}}\Rightarrow &&g_{1}circ g_{2}^{-1}&=e_{G}\Leftrightarrow &&g_{1}&=g_{2}end{aligned}}$

Examples[edit]

Consider the cyclic group Z₃ = (Z/3Z, +) = ({0, 1, 2}, +) and the group of integers (Z, +). The map h : Z → Z/3Z with h(u) = u mod 3 is a group homomorphism. It is surjective and its kernel consists of all integers which are divisible by 3.

The exponential map yields a group homomorphism from the group of real numbers R with addition to the group of non-zero real numbers R* with multiplication. The kernel is {0} and the image consists of the positive real numbers.
The exponential map also yields a group homomorphism from the group of complex numbers C with addition to the group of non-zero complex numbers C* with multiplication. This map is surjective and has the kernel {2πki : k ∈ Z}, as can be seen from Euler’s formula. Fields like R and C that have homomorphisms from their additive group to their multiplicative group are thus called exponential fields.

Category of groups[edit]

If h : G → H and k : H → K are group homomorphisms, then so is k ∘ h : G → K. This shows that the class of all groups, together with group homomorphisms as morphisms, forms a category.

Homomorphisms of abelian groups[edit]

If G and H are abelian (i.e., commutative) groups, then the set Hom(G, H) of all group homomorphisms from G to H is itself an abelian group: the sum h + k of two homomorphisms is defined by

(h + k)(u) = h(u) + k(u) for all u in G.

The commutativity of H is needed to prove that h + k is again a group homomorphism.

The addition of homomorphisms is compatible with the composition of homomorphisms in the following sense: if f is in Hom(K, G), h, k are elements of Hom(G, H), and g is in Hom(H, L), then

(h + k) ∘ f = (h ∘ f) + (k ∘ f) and g ∘ (h + k) = (g ∘ h) + (g ∘ k).

Since the composition is associative, this shows that the set End(G) of all endomorphisms of an abelian group forms a ring, the endomorphism ring of G. For example, the endomorphism ring of the abelian group consisting of the direct sum of m copies of Z/nZ is isomorphic to the ring of m-by-m matrices with entries in Z/nZ. The above compatibility also shows that the category of all abelian groups with group homomorphisms forms a preadditive category; the existence of direct sums and well-behaved kernels makes this category the prototypical example of an abelian category.

References[edit]

Dummit, D. S.; Foote, R. (2004). Abstract Algebra (3rd ed.). Wiley. pp. 71–72. ISBN 978-0-471-43334-7.
Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, vol. 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556, Zbl 0984.00001

External links[edit]

Rowland, Todd & Weisstein, Eric W. «Group Homomorphism». MathWorld.

Источник

Материал из Викиконспекты

Перейти к: навигация, поиск

Определение:

Отображение группы в группу называется гомоморфизмом, если оно сохраняет групповую структуру:

Обозначения:
единица в -ой группе.

Определение:

— ядро гомоморфизма .

Определение:

— образ гомоморфизма .

Примеры

Возьмём отображение , определённое следующим образом: , — а в качестве бинарной операции возьмём сложение. Ядром такого гомоморфизма будут числа, кратные трём.

Свойства гомоморфизмов групп

Утверждение:

Гомоморфизм переводит нейтральный элемент в нейтральный ( в ).

По определению гомоморфизма имеем:

Умножая с обеих сторон на обратный к элемент, получим:

, что и требовалось доказать.

Заметим, что доказательство опирается на существование обратного элемента, для моноидов аналогичное утверждение неверно.

Утверждение:

Гомоморфизм переводит обратный элемент в обратный:

что вместе с единственностью обратного к элемента означает .

См. также

Циклическая группа

Ссылки

Wikipedia — Group homomorphism
Homomorphism examples

Источник

Содержание

Гомоморфизм групп

Определение гомоморфизма

Пусть даны произвольные группы и с единицами $e_G$ и $e_H$ соответственно.

Определение 1. Отображение называется гомоморфизмом групп¹⁾, если:

для

Пример 1. Пусть $G$ — группа. Отображение называется тождественным и обозначается символом $textrm{id}_G$ . Очевидно, что $textrm{id}_G$ является автоморфизмом группы $G$ .

Пример 2. Рассмотрим группу $G$ , записываемую мультипликативно, и . Отображение $varphicolon Grightarrow G:xmapsto underbrace{xcdotldotscdot x}_n=x^n$ , является гомоморфизмом групп и называется возведением в $n$ -ю степень.

Определение 2. Гомоморфизм групп называется мономорфизмом групп²⁾, если отображение инъективно.

Определение 3. Гомоморфизм групп называется эпиморфизмом групп³⁾, если отображение сюръективно.

Пример 3. Пусть $N$ — нормальная подгруппа группы $G$ . Тогда отображение группы $G$ на факторгруппу $G/N$ такое, что , является эпиморфизмом групп и называется канонической проекцией.

Определение 4. Гомоморфизм групп называется изоморфизмом групп⁴⁾, если он является мономорфизмом и эпиморфизмом одновременно.

Определение 5. Ядро гомоморфизма⁵⁾ — это множество $textrm{ker}varphi={xin Gvertvarphi(x)=e_H}$ .

Определение 6. Образ гомоморфизма⁶⁾ — это множество .

Гомоморфизм групп является морфизмом в категории групп. В частности, понятия мономорфизма, эпиморфизма и изоморфизма можно переформулировать:

Предложение 1. Гомоморфизм является мономорфизмом тогда и только тогда, когда .

Предложение 2. Гомоморфизм является эпиморфизмом тогда и только тогда, когда .

Предложение 3. Гомоморфизм является изоморфизмом тогда и только тогда, когда существует гомоморфизм $varphi^{-1}:Hrightarrow G$ такой, что $varphi^{-1}circvarphi=textrm{id}_G$ и $varphicircvarphi^{-1}=textrm{id}_H$ .

Определение 7. Автоморфизмом группы⁷⁾ $ G $ называется изоморфизм .

Свойства гомоморфизма групп

Предложение 4. Пусть — гомоморфизм групп. Тогда

$varphi(x^{-1})=varphi(x)^{-1}$ для всех

Предложение 5. Ядро гомоморфизма групп является нормальной подгруппой группы $ G $ .

Предложение 6. Образ гомоморфизма групп является подгруппой группы $ H $ .

Теоремы о гомоморфизмах

Основная теорема о гомоморфизме. Пусть — гомоморфизм групп с ядром . Через обозначим каноническую проекцию. Тогда существует единственный гомоморфизм групп , инъективный и такой, что , то есть делающий коммутативной диаграмму

$begin{diagram}node{G}arrow{se,b}{pi}arrow[2]{e,t}{varphi}node[2]{H}\node[2]{G/N}arrow{ne,b}{varphi_*}end{diagram}$ .

Если сюръективно, то — изоморфизм. Гомоморфизм левому смежному классу $gN$ ставит в соответствие .

Первая теорема об изоморфизме. Пусть $H$ и $K$ — подгруппы в $G$ , и $H$ нормальна в $G$ . Тогда

— подгруппа в , содержащая , причем нормальна в ;
подгруппа нормальна в ;
отображение является изоморфизмом групп .

Теорема о соответствии. Пусть — эпиморфизм групп с ядром . Тогда существует биекция между множеством подгрупп в $G$ , содержащих $N$ , и множеством всех подгрупп в $H$ . При этом нормальным делителям группы $G$ соответствуют нормальные делители группы $H$ .

Теорема о сокращении. Пусть $ H $ и $ K $ — нормальные подгруппы в группе $ G $ , причем . Тогда факторгруппа $H/K$ является нормальной подгруппой в $G/K$ и имеет место изоморфизм: .

Пример 4. Идеалы и нормальны в , откуда получаем: , или, что то же самое, $mathbb{Z}_4/mathbb{Z}_2congmathbb{Z}_2$ .

Литература

Наверх

Источник

Гомоморфизмы групп и нормальные делители

Пусть заданы группы $mathcal{G}_1=(G_1,cdot,bold{1})$ и $mathcal{G}_2= (G_2,cdot,bold{1})$ . Отображение fcolon G_1to G_2 называют гомоморфизмом группы $mathcal{G}_1$ в группу $mathcal{G}_2$ (гомоморфизмом групп), если для любых x,yin G_1 выполняется равенство f(xcdot y)=f(x)cdot f(y) , т.е. образ произведения любых двух элементов группы $mathcal{G}_1$ при отображении равен произведению их образов в группе $mathcal{G}_2$ .

Если отображение сюръективно (биективно), то его называют эпиморфизмом (изоморфизмом) групп. В этом случае говорят также об эпиморфизме (изоморфизме) группы $mathcal{G}_1$ на группу $mathcal{G}_2$ .

Замечание 2.5. Мы обозначили операции групп $mathcal{G}_1$ и $mathcal{G}_2$ одинаково, как это обычно и делается для однотипных алгебр, хотя, конечно, это разные операции разных групп.

Пример 2.21. Пусть $mathcal{G}_1=(mathbb{Z},+,0)$ — аддитивная группа целых чисел, а $mathcal{G}_2=mathbb{Z}_{k}^{+}$ — аддитивная группа вычетов по модулю .

Зададим отображение так: для всякого целого га образ f(m) равен остатку от деления на . Можно проверить, что для любых целых и имеет место равенство $f(m+n)= f(m)oplus_{m}f(n)$ , т.е. для целых чисел остаток от деления суммы на равен сумме по модулю остатков от деления на каждого слагаемого.

Следовательно, данное отображение есть гомоморфизм группы $mathcal{G}_1$ в группу $mathcal{G}_2$ . Далее, поскольку любое целое число от 0 до k-1 есть остаток от деления на какого-то числа, то отображение является и эпиморфизмом группы $mathcal{G}_1$ на группу $mathcal{G}_2$ .

Теорема 2.14. Пусть $mathcal{G}_1,mathcal{G}_2$ — произвольные группы. Если $fcolonmathcal{G}_1to mathcal{G}_2$ — гомоморфизм, то:

1) образом единицы (нейтрального элемента) группы $mathcal{G}_1$ при отображении является единица группы $mathcal{G}_2$ , то есть f(bold{1})= bold{1} ;

2) для всякого элемента группы $mathcal{G}_1$ образом элемента $x^{-1}$ является элемент $[f(x)]^{-1}$ , обратный элементу f(x) , то есть $f(x^{-1})= [f(x)]^{-1}$ .

Согласно определению гомоморфизма, для произвольного xin G_1 имеем f(x)cdot f(bold{1})= f(xcdotbold{1}) . Далее, f(xcdotbold{1})=f(x) , то есть f(x)cdot f(bold{1})=f(x) . Следовательно, $f(bold{1})= (f(x))^{-1}cdot f(x)= bold{1}$ , то есть f(bold{1})=bold{1} .

Докажем второе утверждение теоремы. Используя определение гомоморфизма и уже доказанное первое утверждение теоремы, получаем

$f(x^{-1})cdot f(x)= f(x^{-1}cdot x)= f(bold{1})= bold{1}$ , то есть $f(x^{-1})= [f(x)]^{-1}$ .

Множество f(G_1) — образ носителя группы $mathcal{G}_1$ при гомоморфизме — замкнуто относительно умножения группы $mathcal{G}_2$ . Действительно, если $g_2,g'_2in f(mathcal{G}_1)$ , то существуют такие $g_1,g'_1in mathcal{G}_1$ , что f(g_1)=g_2 и f(g'_1)=g'_2 . Тогда

$g_2g'_2= f(g_1)f(g'_1)= f(g_1g'_1)in f(mathcal{G}_1).$

Из теоремы 2.14 следует, что $f(mathcal{G}_1)$ содержит единицу этой группы и вместе с каждым элементом обратный к нему элемент. Это значит, что можно определить подгруппу группы $mathcal{G}_2$ носителем которой будет множество $f(mathcal{G}_1)$ . Эту группу называют гомоморфным образом группы $mathcal{G}_1$ при гомоморфизме .

Группу mathcal{K} называют просто гомоморфным образом группы mathcal{G} , если существует гомоморфизм группы на группу . Так, группа $mathbb{Z}_{k}^{ast}$ при любом k>1 является гомоморфным образом аддитивной группы целых чисел (см. пример 2.21).

Пример 2.22. Рассмотрим мультипликативную группу (mathbb{C}setminus{0}, cdot,1) комплексных чисел с обычной операцией умножения комплексных чисел. Легко понять, что эта группа не что иное, как мультипликативная группа поля комплексных чисел.

Рассмотрим также группу $mathcal{M}_2$ невырожденных квадратных матриц второго порядка с операцией умножения матриц (см. пример 2.9.е).

Определим отображение множества mathbb{C} комплексных чисел в множество квадратных матриц второго порядка, положив для произвольного ненулевого комплексного числа a+bi , что

$f(a+bi)= begin{pmatrix}a&b\-b&aend{pmatrix}!.$

Покажем, что — гомоморфизм групп. С одной стороны,

$fbigl[(a+bi)cdot (c+di)bigr]= fbigl[(ac-bd)+i(ad+bc)bigr]= begin{pmatrix}ac-bd& ad+bc\ -ad-bc& ac-bd end{pmatrix}!.$

С другой стороны,

$f(a+bi)cdot f(c+di)= begin{pmatrix}a&b\ -b&aend{pmatrix}!cdot! begin{pmatrix} c&d\ -d&c end{pmatrix}= begin{pmatrix}ac-bd& ad+bc\ -ad-bc& ac-bd end{pmatrix}!.$

Следовательно,

fbigl[(a+bi)cdot (c+di)bigr]= f(a+bi)cdot f(c+di).

Таким образом, отображение — гомоморфизм групп, а гомоморфный образ мультипликативной группы комплексных чисел при — это подгруппа mathcal{K} группы матриц $mathcal{M}_2$ , состоящая из матриц вида $begin{pmatrix}a&b\ -b&aend{pmatrix}$ . Здесь мы учли, что любая матрица вида $begin{pmatrix}a&b\ -b&aend{pmatrix}$ является образом некоторого комплексного числа (а именно a+bi ) при отображении . Группа mathcal{K} — собственная подгруппа группы $mathcal{M}_2$ .

Важное свойство гомоморфизмов групп

Сформулируем без доказательства одно важное свойство гомоморфизмов групп.

Теорема 2.15. Если — гомоморфизм группы mathcal{G} в группу mathcal{K} , а — гомоморфизм группы в группу mathcal{L} , то композиция отображений fcirc g есть гомоморфизм группы в группу .

Рассмотрим некоторые свойства изоморфизмов групп.

Теорема 2.16. Если $fcolonmathcal{G}_1to mathcal{G}_2$ — изоморфизм группы $mathcal{G}_1$ на группу $mathcal{G}_2$ , то отображение $f^{-1}$ , обратное к отображению , есть изоморфизм группы $mathcal{G}_2$ на группу $mathcal{G}_1$ .

Пусть и — произвольные элементы группы $mathcal{G}_2$ , пусть также x=f(u) , а y=f(v) , где и {v} — элементы группы $mathcal{G}_1$ . Тогда

$f^{-1}(xy)= f^{-1}bigl(f(u)f(v)bigr)= f^{-1}(f(uv))= uv= f^{-1}(x)f^{-1}(y),$

т.е. отображение $f^{-1}$ — гомоморфизм второй группы в первую. Но так как отображение, обратное к биекции, есть биекция, то $f^{-1}$ — изоморфизм группы $mathcal{G}_2$ на группу $mathcal{G}_1$ .

Группы mathcal{G} и mathcal{K} называют изоморфными, если существует изоморфизм одной из них на другую. При этом используют обозначение mathcal{G}cong mathcal{K} .

Изоморфные группы с точки зрения их алгебраических свойств совершенно одинаковы, хотя их элементы могут иметь различную природу. Вернемся в этой связи к примеру 2.22. Легко убедиться в том, что определенное там отображение множества комплексных чисел на множество квадратных матриц специального вида является биекцией. Следовательно, мультипликативная группа комплексных чисел и группа матриц указанного вида с операцией умножения матриц изоморфны, хотя элементы этих групп на первый взгляд не имеют между собой ничего общего.

Определение 2.8. Ядром гомоморфизма группы mathcal{G} в группу mathcal{K} называют прообраз ker f единицы группы при гомоморфизме

$ker f=f^{-1}(bold{1})subset G,.$

Пример 2.23. Ядром гомоморфизма, рассмотренного в примере 2.21, служит множество всех целых чисел, делящихся на .

Теорема 2.17. Ядро ker f гомоморфизма fcolonmathcal{G}to mathcal{K} есть подгруппа группы .

Нужно убедиться в том, что множество ker f замкнуто относительно умножения группы mathcal{G} , содержит единицу этой группы и вместе с каждым элементом содержит обратный к нему элемент.

Если a,binker f , то есть f(a)=f(b)=bold{1} , то f(ab)= f(a)f(b)= bold{1} и abinker f . Ясно, что bold{1}inker f , так как f(bold{1})=bold{1} (см. теорему 2.14). Если ainker f , то

$f(a^{-1})= [f(a)]^{-1}= bold{1}^{-1}= bold{1}$ , то есть $a^{-1}inker f$ .

Ядро гомоморфизма, приведенного в примере 2.21, представляет собой подгруппу аддитивной группы целых чисел, состоящую из всех чисел, кратных .

Подгруппа mathcal{H} группы mathcal{G} называется нормальной подгруппой (нормальным делителем) группы , если aH=Ha для любого ain G .

В коммутативной группе, как было отмечено выше, aH=Ha . Следовательно, в этом случае любая подгруппа является нормальным делителем.

Пусть mathcal{H}=(H,cdot,bold{1}) — подгруппа группы mathcal{G}= (G,cdot, bold{1}) . Для фиксированных элементов a,bin G через aHb обозначим множество всех произведений вида ahb , где hin H . В силу ассоциативности групповой операции это обозначение корректно.

Теорема 2.18. Подгруппа mathcal{H}=(H,cdot,bold{1}) является нормальным делителем группы mathcal{G}=(G,cdot,bold{1}) тогда и только тогда, когда $aHa^{-1}subseteq H$ для любого ain G .

Если mathcal{H} — нормальный делитель, то для любого ain G имеем aH=Ha , т.е. для любого hin H найдется такое h_1in H , что ah=h_1a . Пусть элемент $xin aHa^{-1}$ , то есть $x=aha^{-1}$ для некоторого hin H . Так как ah=h_1a , то $x=h_1aa^{-1}=h_1in H$ и поэтому $aHa^{-1}subseteq H$ .

Обратно, если $aHa^{-1}subseteq H$ , то любой элемент $x=aha^{-1}$ , где hin H , принадлежит и множеству , то есть $aha^{-1}= h_1$ для некоторого h_1in H . Отсюда, умножая последнее равенство на справа, получим ah=h_1a , т.е. элемент из левого смежного класса принадлежит и правому смежному классу . Итак, aHsubseteq Ha .

Теперь возьмем для произвольного ain G обратный к элемент $a^{-1}$ и для него запишем включение $a^{-1}Hasubseteq H$ (напомним, что ( $(a^{-1})^{-1}=a$ ). Рассуждая как и выше, получим, что для некоторых h,h_1in H имеет место равенство $a^{-1}h=h_1a^{-1}$ , то есть ha=ah_1 и Ha subseteq aH . Итак, aH=Ha и mathcal{H} — нормальный делитель.

Связь между понятием нормального делителя и понятием гомоморфизма

Оказывается, существует связь между понятием нормального делителя и понятием гомоморфизма, которая продолжает и углубляет на новом уровне уже известную нам из первых лекций связь между понятиями отображения и класса эквивалентности.

Теорема 2.19. Ядро гомоморфизма группы mathcal{G} в группу mathcal{K} является нормальным делителем группы .

Для любого yinker f и любого ain G имеем

$f(aya^{-1})= f(a)f(y)f(a^{-1})= f(a)cdotbold{0}cdot f(a^{-1})= f(a) f(a^{-1})= bold{1},.$

Это значит, что для любого ain G выполняется соотношение $a(ker f)a^{-1}subseteqker f$ , а, согласно теореме 2.18, ker f — нормальный делитель.

Пусть mathcal{H}=(H,cdot,bold{1}) — нормальный делитель группы mathcal{G}= (G,cdot,bold{1}) . Рассмотрим множество всех левых смежных классов {aHcolon,ain G} . Это будет не что иное, как фактор-множество множества по определенному выше (см. теорему 2.11) отношению эквивалентности $sim_{H}$ .

Введем операцию умножения на множестве всех левых смежных классов следующим образом: произведением aHcdot bH классов и назовем класс abH .

Это определение корректно, так как множество aHcdot bH , т.е. множество всех произведений вида ahbh_1 для различных h,h_1in H , в силу того что Hb=bH для всякого bin G , совпадает с левым смежным классом abH . Действительно, поскольку hb=bh' для некоторого h'in H , то ahbh_1=abh'h_1in abH .

Теперь рассмотрим некоторый ain abH , т.е. x=abh для некоторого hin H_1 . Поскольку bh=h'b для некоторого h'in H , то x=ah'b= ah'bbold{1}in aHbH . Следовательно, aHcdot bH=abH .

Можно далее легко показать, что для каждого ain G имеют место

aHcdot H=Hcdot aH=aH и $aHcdot a^{-1}H= a^{-1}Hcdot aH=H$ .

Тем самым определена группа, носителем которой является фактор-множество $G/sim_{H}$ множества по отношению эквивалентности $sim_{H}$ с операцией умножения левых смежных классов, причем нейтральным элементом относительно этой операции служит носитель подгруппы mathcal{H} , а обратным к левому смежному классу будет левый смежный класс $a^{-1}H$ . Эту группу называют фактор-группой группы mathcal{G} по нормальному делителю и обозначают mathcal{G}/ mathcal{H} . Можно указать естественный гомоморфизм группы в фактор-группу mathcal{G}/mathcal{H} , который вводится согласно правилу: (forall cin G)(f(x)=xH) . Так как xHcdot yH= xyH , то для любых x,yin G имеем

f(xcdot y)= xyH= xHcdot yH= f(x)cdot f(y)

и — действительно гомоморфизм. Его называют каноническим гомоморфизмом группы mathcal{G} в фактор-группу mathcal{G}/mathcal{H} .

Пример 2.24. а. Рассмотрим аддитивную группу mathbb{R}= (mathbb{R},+,0) действительных чисел. Эта группа коммутативна. Напомним, что в коммутативной группе любая подгруппа будет нормальным делителем. Поэтому для нее нормальным делителем является подгруппа целых чисел mathbb{Z}= (mathbb{Z},+,0) (аддитивная группа целых чисел). (Для этих групп мы приняли такие же обозначения, как и для их носителей: mathbb{R} и соответственно.)

Выясним смысл отношения эквивалентности $sim_{mathbb{Z}}$ , определяемого через равенство левых смежных классов, по подгруппе в этом случае.

Равенство левых смежных классов a+mathbb{Z}= b+mathbb{Z} означает, что для любого целого найдется такое целое , что a+m=b+n , то есть a-b=n-min mathbb{Z} . Обратно, если разность a-b есть целое число, т.е. a-b=nin mathbb{Z} , то a+mathbb{Z}= (b+n)+mathbb{Z}= b+mathbb{Z} . Итак, $asim_{mathbb{Z}}b$ тогда и только тогда, когда a-bin mathbb{Z} , или, иначе говоря, действительные числа и эквивалентны по $sim_{mathbb{Z}}$ тогда и только тогда, когда их дробные части равны.

Аддитивная группа смежных классов, т.е. фактор-группа mathbb{R}/mathbb{Z} группы по нормальному делителю строится так: сумма классов a+mathbb{Z} и b+mathbb{Z} равна классу (a+b)+mathbb{Z} . Вводя обозначение a+mathbb{Z}=[a] , получаем [a]+[ b ]=[a+b] . При этом [0]=mathbb{Z} (т.е. единица фактор-группы — это смежный класс нуля — множество всех целых чисел), причем -[a]=[-a]=(-a)+mathbb{Z} . Обратим внимание на то, что смежный класс числа однозначно определяется его дробной частью <x> (см. пример 1.14.6), то есть [x]=[<x>] . Канонический гомоморфизм в данном случае задается так: xmapsto[x] .

б. Рассмотрим теперь аддитивную группу действительных чисел по модулю 1, т.е. группу $mathbf{S}^1=([0;1),oplus_{1},0)$ , заданную на полуинтервале [0;1) , сложение в которой определяется так: $xoplus_{1}y=<x+y>$ (дробная часть суммы x+y ). Другими словами,

$xoplus_{1}y= begin{cases}x+y,& text{if}quad x+y leqslant 1;\ x+y-1,& text{if}quad x+y geqslant 1.end{cases}$

Докажем, что группа $mathbf{S}^1$ изоморфна фактор-группе mathbb{R}/ mathbb{Z} , то есть $mathbb{R}/mathbb{Z}congmathbf{S}^1$ .

Зададим отображение varphi множества {[a]colon, ain mathbb{R}} смежных классов в полуинтервал [0;1) так, что varphi([x])=<x> . Поскольку [x]=[<x>] , то varphi — биекция и, кроме того,

$varphibigl([x]+[y]bigr)= varphibigl([x+y]bigr)= <x+y>= <<x>+<y>>= <x>oplus_{1}<y>= varphi([x])oplus_{1}varphi([y]).$

Это значит, что varphi — изоморфизм mathbb{R}/ mathbb{Z} на $mathbf{S}^1$ .

Группу $mathbf{S}^1$ можно воспринимать как «наглядный образ» фактор-группы mathbb{R}/ mathbb{Z} . Довольно абстрактная идея фактор-группы кристаллизуется в виде группы с носителем [0;1) и операцией сложения неотрицательных действительных чисел, строго меньших единицы, с отбрасыванием в результате целой части. Здесь хорошо видна «польза» понятия изоморфизма. То, что само по себе не очень наглядно, становится наглядным через свой изоморфный образ.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Определение.
Пусть

и

– группы. Отображение

называется гомоморфизмом, если для
любых

Определение.
Изоморфизмом
групп

называется гомоморфизм, который является
взаимно однозначным отображением. Если
группы

и

изоморфны,
то принято обозначать

.

При гомоморфизме
единица группы всегда переходит в
единицу. Действительно, если

– единицы групп

соответственно,
то

.
Умножив это равенство на

,
получим

.

Далее, при
гомоморфизме обратный к элементу

элемент переходит в обратный к

.
Действительно,

.
Аналогично,

Это и означает, что

Определение.
Пусть G
– группа с единицей e
и элемент

Наименьшее натуральное n,
для которого

называется
порядком элемента g
и обозначается o(g).
Если такого n
не существует, то считается, что

Если

–
гомоморфизм
групп, то порядки элементов
g
и f(g)
связаны, а
именно, если

то
n
делится на
m.
Действительно,

,
поэтому элемент f(g)
имеет конечный
порядок. Допустим, что n
не делится на m.
Тогда

,
где

В этом случае

что противоречит тому, что m
– наименьшая степень такая, что

Задача 1.4.1.
Определите
порядки всех элементов в следующих
группах а)

б)

в)

а)

В
группе

единицей
является элемент

Групповая операция – это сложение по
модулю 12. Порядок элемента x
это наименьшее натуральное n
такое, что

Например,

Поэтому порядок элемента

обзначаемый

равен
2. Порядки элементов

равны 3. Элементы

имеют четвертый порядок,

– шестой. Наконец, элементы

имеют двенадцатый порядок. Сам элемент

как и единица любой группы, имеет первый
порядок.

б), в) Решите
самостоятельно.

Пример 1. Покажем,
что

Каждому преобразованию группы

можно сопоставить перестановку –
перестановку вершин треугольника ABC.
Действительно,
занумеруем вершины: A
– 1, B
– 2, C
– 3. Тогда отображение

при котором

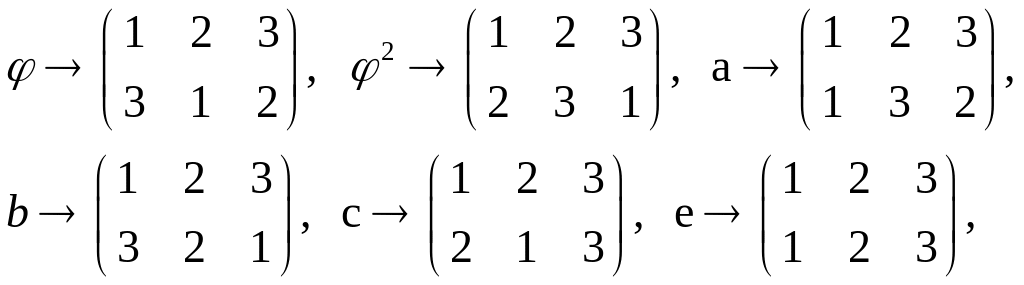
является изоморфизмом.

Пример 2.
Отображение

при котором каждому целому

ставится в соответствие его остаток

при делении на n
, является
гомоморфизмом групп, но не изоморфизмом.
Например, если

то

т.к.

Пример 3. Пусть

– группа всех действительных чисел
отличных от нуля с обычной операцией
умножения. Отображение

сопоставляет
каждой матрице ее определитель. Тогда
f
– гомоморфизм групп, т.к. определитель
произведения матриц равен произведению
определителей. Гомоморфизм f
не является
изоморфизмом, т.к. разные матрицы могут
иметь одинаковые определители.