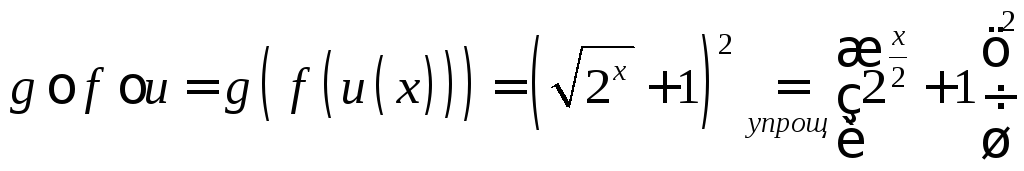Как найти образ множества функции - Исправление недочетов и поиск решений вместе с Examum.ru

Образы и прообразы множеств при отображениях

Пусть
задана функция
и задано множество.

Образом
множества А при отображении f
называется множество всех,
являющихся значениями функцииfв точках.

Обозначается
.

В
частности,
,
то есть образом множества задания
функции является множество ее значений.

Если
множество,
то множество всех значений аргументах, для которых,
называетсяпрообразом
множества В при отображении f.

Записать кратко определение прообраза
можно так:
.

Пример
4 (образы
и прообразы множеств при различных
отображениях)

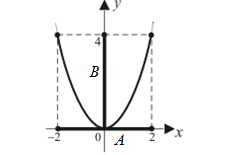
1) Множество является образом
множествапри отображении
функцией

Дирихле; множество
является прообразом
множествапри отображении
той же функцией;

В
— это образ множестваА
при отображении функцией,

A
— это прообраз множества B
при этом отображении функцией
;

2) найдем образ
множества
при отображении функцией:

то есть

—это образ
множествапри отображении
функцией ;

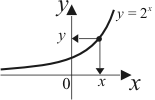
3) найдем образ
множества
при отображении функцией.

или— это образ множестваАпри отображении функцией;

4) найдем прообраз
множества
при отображении функцией:

— это прообраз множестваВпри отображении функцией.

Понятие многозначного отображения

Отображениеназываетсямногозначным
отображением, еслитакие, что им соответствуют более одного
элемента(рис. 32).

Рис. 32

Многозначные функции рассматривать
будем пока только в исключительных
случаях, поэтому по умолчанию любая
функция
считается задающей однозначное
отображение.

Обратное отображение

Пусть
,
причем,
где(рис. 33).

Рис.
33

Функцияназываетсяобратным
отображением по отношению к отображению,
или— этообратная
функция по отношению к функции.

Обратная функция
является, вообще говоря, многозначной.

Если
отображение
является взаимно однозначным, т.е.
биективным, то отображениеявляется также взаимно однозначным
отображением множестваYна множествоX (рис.
34).

Рис.
34

если
— биекция,
то— тоже биекция.

В этом случае функцияявляется обратной по отношению к функции,
а обе эти функцииfиназываютсявзаимно
обратными функциями.

Пример
5
(взаимно обратные функции)

и
;

и
.

Подробнее
о взаимно обратных функциях изложено
в §8 данного конспекта.

Суперпозиция отображений (сложная функция)

Если заданы два отображенияи,
то отображение,
ставящее в соответствие любому элементуединственный элемент,
называетсясуперпозицией
отображений f и g (другие
названия:композиция
отображений,сложное
отображение).

Обозначение
суперпозиции отображений:
или.

Иллюстрация
к сложному отображению приведена на
рис. 35.

Рис.
35

Пример
6 (сложные
отображения)

;

Запись
сложных отображений как сложных функций:

Сложное отображение
(сложная функция) может получаться
суперпозицией любого количества
отображений.

Пример
7 (составление
сложных функций)

1) — сложная функция

;

Упражнения для самостоятельной работы

1. Найдите
образ
множествапри отображении функцией:
1),; 2),;
3),; 4),;

5) , ; 6)

;

2. Найдите
прообраз множества
при отображении функцией:
1),; 2),;
3),; 4),;
5),. 6)

3. Составьте
суперпозиции
идля заданныхии укажите множество задания и множество
значений каждого из составленных
отображений:
1),;
2),.

4. Запишите
суперпозиции
,,,
если,,;
укажите отображения множеств, которые
они задают.

Ответы
к упражнениям для самостоятельной
работы

1. 1) ; 2);

3) ; 4);

5) ; 6).

2. 1)
,; 2);
3); 4);
5); 6).

3. 1) ;;
2); .

4.fsdfsfsdfsdfsdfsdfsdfsdfsdfsdfsdfs

Источник

ЛЕКЦИЯ 12 Образ и прообраз множества при данном соответствии 21. 11. 2012 г.

• Пусть дано соответствие Г = (X, Y, F). • Образом элемента х Х при соответствии Г называется и через Г(х) обозначается множество элементов y Y, для которых пара F. Иначе, Г(х)={y Y| F}. Т. е. , образ элемента х Х – это множество тех элементов y Y, которые соответствуют элементу x. • На графе образ элемента x можно представить как множество тех вершин y, в которые входят дуги, выходящие из вершины x.

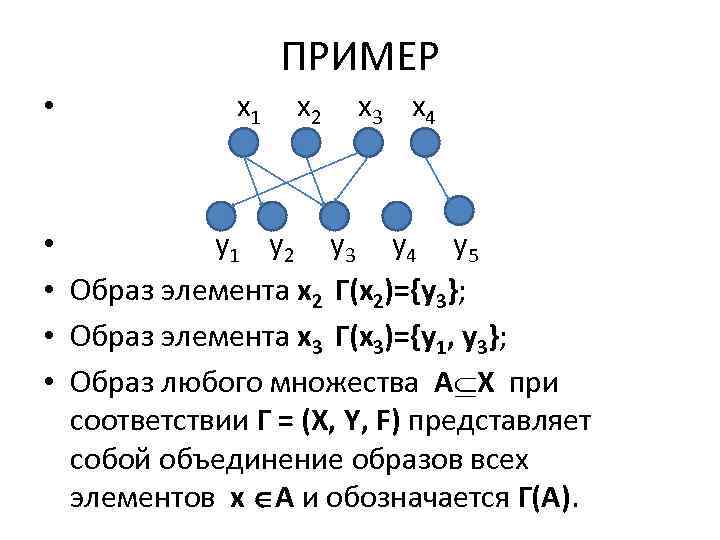
ПРИМЕР • x 1 x 2 x 3 x 4 • y 1 y 2 y 3 y 4 y 5 • Образ элемента x 2 Г(x 2)={y 3}; • Образ элемента x 3 Г(x 3)={y 1, y 3}; • Образ любого множества A X при соответствии Г = (X, Y, F) представляет собой объединение образов всех элементов x A и обозначается Г(А).

• В общем случае справедливо: • Г(А) = Г(х) • х А • Для рассмотренного примера если А={x 2, x 3}, то Г(А)=Г(х2) Г(х3)={y 3} {y 1, y 3}={y 1, y 3}. • Пусть дано соответствие Г = (X, Y, F). • Прообразом элемента y Y при соответствии Г называется и через Г-1(y) обозначается множество элементов x X, для которых пара F.

5 • Таким образом, Г-1(y)={x X| F } – это множество тех элементов из Х, которым соответствует элемент y. • На графе прообраз элемента y можно представить множеством тех вершин х, из которых выходят дуги, заходящие в вершину y. Для рассмотренного примера • Г-1(y 3)={x 1, x 2, x 3}, Г(y 4)= .

6 • Прообразом произвольного множества B Y при соответствии Г = (X, Y, F) называется объединение прообразов всех элементов y B и обозначается Г-1(В), т. е. • Г-1(В) = Г-1(y) • y B • Если В={y 3, y 4, y 5}, то при соответствии Г для рассмотренного примера прообраз запишется • Г-1(В)={x 1, x 2, x 3, x 4}.

7 • Пусть Г = (X, Y, F) – произвольное соответствие и А – произвольное подмножество множества Х. • Сужением соответствия Г на множество А называется и через ГА обозначается соответствие, график которого FA определяется выражением: • FA = (A Y) F, т. е. ГА = (X, Y, FA). • Соответствие ГА Г. Соответствие Г в этом случае называют продолжением соответствия ГА на множество Х.

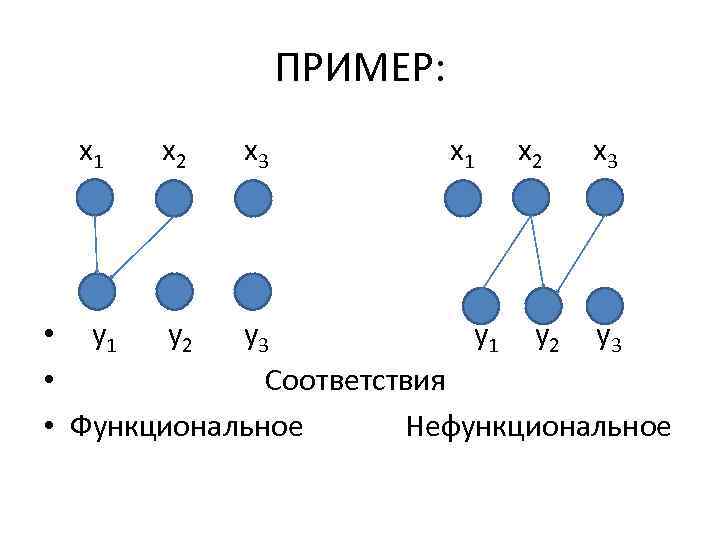
Основные свойства соответствий • 1. ФУНКЦИОНАЛЬНОСТЬ: • Соответствие Г = (X, Y, F) называется функциональным, если для любого х Х образ Г(х) содержит не более одного элемента y Y, в противном случае соответствие называется нефункциональным.

ПРИМЕР: x 1 x 2 x 3 • y 1 y 2 y 3 • Соответствия • Функциональное Нефункциональное

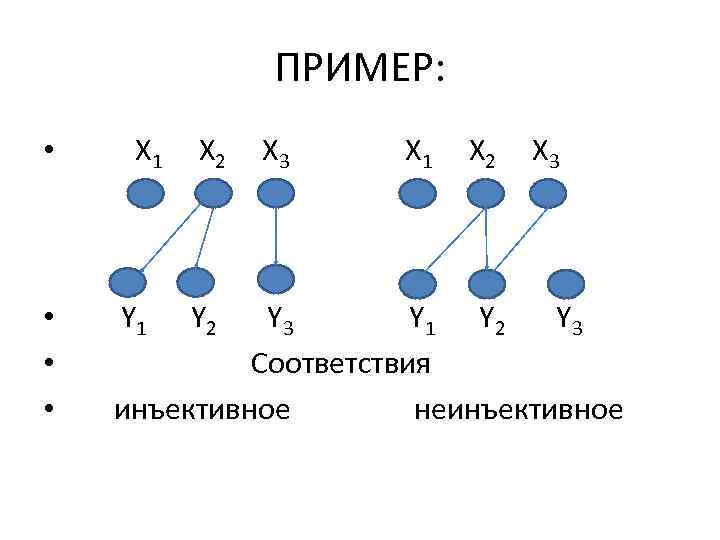
10 • 2. ИНЪЕКТИВНОСТЬ: • Соответствие Г = (X, Y, F) называется инъективным, если для любого y Y прообраз Г-1(y) содержит не более одного элемента х Х, в противном случае соответствие называется неинъективным.

ПРИМЕР: • • X 1 Y 1 X 2 Y 2 X 3 X 1 X 2 X 3 Y 1 Y 2 Y 3 Соответствия инъективное неинъективное

12 • 3. ОПРЕДЕЛЕННОСТЬ: • Соответствие Г = (X, Y, F) называется всюду определенным, если для каждого х Х образ Г(х) , в противном случае соответствие не всюду определено. • В графе всюду определенного соответствия из каждой вершины х Х выходит хотя бы одна дуга.

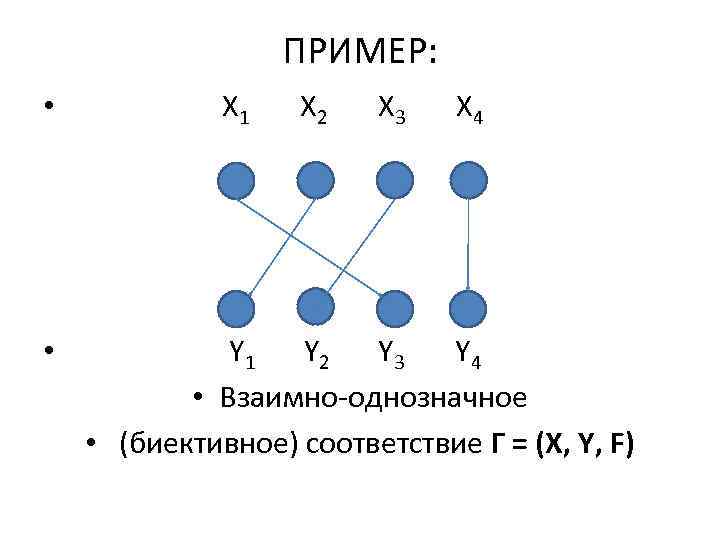
13 • 4. СЮРЪЕКТИВНОСТЬ: • Соответствие Г = (X, Y, F) называется сюръективным, если для любого элемента y Y прообраз Г-1(y) , в противном случае соответствие несюръективно. • В графе сюръективного соответствия в каждую вершину, соответствующую y Y, входит хотя бы одно ребро (дуга, стрелка). • Если соответствие одновременно функциональное, инъективное, всюду определенное и сюръективное, то оно называется взаимно-однозначным или биективным.

ПРИМЕР: • • X 1 X 2 X 3 X 4 Y 1 Y 2 Y 3 Y 4 • Взаимно-однозначное • (биективное) соответствие Г = (X, Y, F)

14 • Биекция — это отображение, которое является одновременно и сюръективным, и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением (соответствием), одно-однозначным отображением. • Если между двумя множествами можно установить взаимно-однозначное соответствие (биекция), то такие множества называются равномощными. С точки зрения теории множеств, равномощные множества неразличимы. • Взаимно-однозначное отображение конечного множества в себя называется перестановкой (элементов этого множества). (википедия)

Общее понятие функции • Пусть Х – некоторое числовое множество. • Говорят, что на Х задана функция, если любому элементу из множества Х поставлено в соответствие определенное число y Y. • Если теперь перейти от числовых множеств к множествам произвольной природы, то приходим к самому общему понятию ФУНКЦИИ.

17 • Пусть X и Y – множества произвольной природы, и пусть между ними задано соответствие. • Если соответствие функционально, то оно называется функцией и обозначается • f = (X, Y, F). • Из определения следует, что функция может быть определена не на всех элементах множества Х.

18 • Если же функция определена на всех элементах множества Х, т. е. введенное соответствие не только функциональное, но и всюду определенное, то такая функция называется ОТОБРАЖЕНИЕМ. • Различают отображение X на Y и отображение X в Y. • X на Y, если f(X) = Y, • X в Y, если f(X) Y. • ФУНКЦИЯ – частный вид СООТВЕТСТВИЯ.

Источник

Соответствия и бинарные отношения на множествах

Отображение из множества в множество считается заданным, если каждому элементу xin A сопоставлен единственный элемент yin B . Отображение из множества в множество обозначают записью fcolon Ato B или Aoverset{f}{longrightarrow}B . Элемент yin B , который отображением сопоставляется элементу xin A , называют образом элемента при отображении и обозначают f(x) .

Каждое отображение однозначно определяет множество упорядоченных пар {(x,y)colon, xin A,~ y=f(x)} , являющееся подмножеством декартова произведения Atimes B множества на множество и называемое графиком отображения .

Наоборот, пусть в декартовом произведении Atimes B задано такое подмножество , что:

1) для любого xin A существует yin B , для которого (x,y)in f ;
2) для любых двух пар (x,y) и (x',y') множества из равенства x=x' следует равенство y=y' .

Тогда множество единственным образом определяет некоторое отображение из в . Это отображение, обозначаемое также , элементу xin A сопоставляет элемент yin B , удовлетворяющий условию (x,y)in f . Таким образом, мы можем отождествить отображения с их графиками и считать, что отображение есть подмножество декартова произведения.

Отображение множества в себя называют тождественным, если f(x)=x при всех из .

В общем случае для отображения fcolon Ato B может существовать несколько различных элементов множества , образы которых совпадают. Множество всех элементов xin A , для которых f(x)=y_0 , называют прообразом элемента y_0in B при отображении .

Так, прообраз числа a~(|a|leqslant 1) при отображении y=sin{x} есть множество всех решений уравнения sin{x}=a , т.е. множество

bigl{xcolon, x=arcsin{a}+2pi n,~ nin mathbb{Z}bigr}cup bigl{ xcolon, x=pi-arcsin{a}+2pi n,~ nin mathbb{Z}bigr}.

Прообраз элемента y_0in B может быть пустым множеством. Это имеет место, например, для числа a=2 при отображении y=sin{x} .

Множество всех yin B , таких, что найдется xin A , для которого y=f(x) , называют областью значений отображения . Область значений отображения будем обозначать R(f) .

Отображение fcolon Ato B называют инъективным (инъекцией), если каждый элемент из области его значений имеет единственный прообраз, т.е. из f(x_1)=f(x_2) следует x_1=x_2 .

Отображение fcolon Ato B называют сюръективным (сюръекцией), если его область значений совпадает со всем множеством . Сюръективное отображение из в называют также отображением множества на множество .

Отображение fcolon Ato B называют биективным (биекцией), если оно одновременно инъективно и сюръективно.

Таким образом, если отображение fcolon Ato B биективно, то каждому элементу множества отвечает единственный элемент множества и наоборот. Тогда говорят, что множества и находятся между собой во взаимно однозначном соответствии.

Биекцию множества на себя называют автоморфизмом множества . Используют также термин «подстановка множества».

Пример 1.2. а. Отображение, заданное равенством nu(n)=n+1 , есть, как нетрудно показать, биекция множества натуральных чисел mathbb{N} на его подмножество mathbb{N}setminus{1} .

б. Отображение nucolon nmapsto2n есть биекция множества всех натуральных чисел на множество всех четных натуральных чисел.

в. Любая показательная функция y=a^x,~ a>0 , есть биекция множества mathbb{R} всех действительных чисел на множество $mathbb{R}^{+}$ всех положительных действительных чисел.

г. Функция y=operatorname{arctg}x есть биекция множества mathbb{R} на интервал $left(-tfrac{pi}{2};,tfrac{pi}{2}right)$ .

д. Поворот окружности на заданный угол alpha , т.е. отображение, сопоставляющее каждой точке окружности точку, в которую она перейдет при повороте всей окружности вокруг ее центра на угол alpha , есть автоморфизм множества точек окружности.

Образ и прообраз множества

Пусть задано отображение fcolon Ato B и C subseteq A — некоторое множество. Множество f(C) элементов yin B , таких, что y=f(C),~ xin C , называют образом множества при отображении . Например, при отображении y=sin{x} отрезок [0;1] является образом множества (отрезка) [0;pi] , равно как и любого объединения отрезков вида [2pi k; (2k+1)pi] (для произвольного целого ). При k=0 это можно записать следующим образом: sin([0;pi])=[0;1] .

Заметим, что для любого отображения fcolon Ato B образ f(A) всего множества есть область значений данного отображения.

Для произвольного множества D subseteq B множество всех элементов xin A , таких, что f(x)in D , называют прообразом множества при отображении .

Например, для любого действительного числа ain[0;1) множество, которое является объединением всех отрезков вида

bigl[arcsin{a}+2pi k,, pi-arcsin{a}+2pi kbigr],quad kinmathbb{Z},,

есть прообраз отрезка [a,1] при отображении y=sin{x} .

Прообраз области значений произвольного отображения fcolon Ato B совпадает со всем множеством .

Множество всех отображений из в будем обозначать как B^A .

Частичное отображение и его область определения

Понятие отображения можно обобщить. Обобщение может проходить по двум позициям. Во-первых, можно отказаться от полной определенности отображения, полагая, что образ определен не для каждого элемента множества , а для некоторых элементов этого множества. Тогда придем к понятию частичного отображения. При этом подмножество всех элементов , для которых определен образ, называют областью определения данного частичного отображения.

Многие элементарные функции являются частичными отображениями множества mathbb{R} всех действительных чисел в себя. Например, функция y=operatorname{tg}x есть частичное отображение с областью определения

$mathbb{R} setminusleft{xcolon, x=frac{pi}{2}+pi k,~ kinmathbb{Z} right}.$

Во-вторых, можно отказаться от однозначности отображения, полагая, что данному xin A сопоставлен не один, а несколько образов (множество образов) в множестве . В этом случае говорят, что задано соответствие из множества в множество .

Примером могут служить обратные тригонометрические функции: скажем, «большой» арксинус, сопоставляющий каждому xin mathbb{R} множество всех таких чисел , что sin{y}=x , т.е. множество, являющееся прообразом элемента при отображении, определяемом графиком функции y=sin{x} .

Если задано соответствие rho из в , будем использовать обозначение rho(x) по аналогии с обозначением f(x) для отображений, понимая при этом, что rho(x) есть уже не элемент множества , а его подмножество.

Аналогично графику отображения можно определить график соответствия rho из множества в множество как множество $C_{rho}$ упорядоченных пар (x,y) , таких, что xin A,,yin B и элементы x,y связаны соответствием rho , то есть yinrho(x) . Указанное множество $C_{rho}$ упорядоченных пар есть подмножество декартова произведения Atimes B .

Обратно, фиксируя на декартовом произведении Atimes B какое-либо подмножество , мы тем самым однозначно определяем некоторое соответствие rho_C из в , а именно

$rho_C(x)= bigl{ycolon, yin Bland (x,y)in Cbigr}.$

Нетрудно заметить, что графиком соответствия rho_C будет как раз множество , а соответствием, отвечающим графику Crho , будет rho . Поэтому можно отождествить соответствие с его графиком и считать, что соответствие из множества в множество есть некоторое подмножество rho декартова произведения Atimes B , то есть rhosubseteq Atimes B . В частности, при rho=varnothing получаем пустое соответствие, а при rho , совпадающем со всем указанным декартовым произведением, — универсальное соответствие.

При этом будем писать (x,y)inrho для упорядоченных пар, связанных соответствием rho .

Используют также термины «частичное мультиотображение» и «частичная многозначная функция».

Пример 1.3. Рассмотрим множество программистов A={I,P,S} и множество программ $B={n_1,n_2,n_3,n_4,n_5}$ . Зададим соответствие tau из в , связывающее программистов и разрабатываемые ими программы:

$tau= bigl{(I,n_1),, (I,n_3),, (I,n_5),, (P,n_2),, (P,n_4),, (S,n_2),, (S,n_5)bigr} subseteq Atimes B,.$

Область определения соответствия rho subseteq Btimes B из множества в множество — это множество всех первых компонент упорядоченных пар из rho:

D(rho)= bigl{xcolon, (exists yin B)(x,y)inrhobigr}.

Область значения соответствия rho — это множество всех вторых компонент упорядоченных пар из rho:

R(rho)= bigl{ycolon, (exists xin A)(x,y)inrhobigr}.

Из определения вытекает, что D(rho)subseteq A,~ R(rho)subseteq B . Соответствие из в называют всюду определенным, если его область определения совпадает с множеством Acolon,D(rho)=A .

Сечением соответствия rho subseteq Atimes B для фиксированного элемента xin A будем называть множество rho(x)= {ycolon, (x,y)inrho} . Можно сказать, что сечение соответствия rho(x) есть множество всех «образов» элемента при данном соответствии.

Сечением соответствия rho по множеству Csubseteq A будем называть множество

rho(C)= bigl{ycolon, (x,y)inrho,~ xin Cbigr}.

Пример 1.4. Область определения соответствия т из примера 1.3 есть все множество , а область значения — все множество . Сечением соответствия tau по элементу будет множество $tau(Pi)={n_2,n_4}$ .

Бинарные отношения на множествах

Соответствие rho subseteq Atimes A из множества в себя, т.е. подмножество множества A^2 , называют бинарным отношением на множестве .

Пример 1.5. Простейшим примером бинарного отношения является отношение нестрогого неравенства на множестве действительных чисел mathbb{R} . Здесь каждому xinmathbb{R} поставлены в соответствие такие yin mathbb{R} , для которых справедливо x leqslant y .

Для произвольного бинарного отношения на некотором множестве часто используют запись xrho y вместо (x,y)inrho , говоря при этом об элементах, связанных бинарным отношением rho . Это согласуется с традиционной формой записи некоторых часто используемых бинарных отношений. Так, пишут xleqslant y , а не (x,y)in leqslant . Для таких бинарных отношений употребляют устоявшиеся словосочетания. Например, запись читается так: « не больше «.

Бинарное отношение на множестве , состоящее из всех пар (x,y) , т.е. пар с совпадающими компонентами, называют диагональю множества и обозначают operatorname{id}A . Нетрудно понять, что диагональ есть тождественное отображение на себя.

Иногда говорят о диагонали в множестве , хотя правильнее было бы называть это отношение диагональю декартова квадрата множества .

Для наглядного изображения соответствий из в (бинарных отношений, в частности) будем использовать два способа. Первый из этих способов состоит в интерпретации соответствия как подмножества декартова произведения, которое можно изображать примерно так же, как на плоскости можно изображать подмножества декартова квадрата числовых множеств. Второй способ, применяемый для конечных множеств в , — построение так называемого графа соответствия. В этом случае элементы множеств в изображаются на плоскости кружочками. Если и только если пара (u,v) принадлежит соответствию rho , то в графе соответствия из кружочка, обозначающего элемент uin A , проводим стрелку к кружочку, обозначающему элемент vin B . Для бинарного отношения на конечном множестве часто удобнее использовать граф другого вида. Элементы множества изображаются кружочками только один раз, а стрелки проводятся по тем же правилам, что и в графе соответствия. Заметим, что при таком построении возможно соединение кружочка стрелкой с самим собой (петля).

Пример 1.6. а. На рис. 1.1, а изображены график и граф бинарного соответствия из примера 1.3.

б. Пусть A={1;2;3;4} . Бинарное отношение rho на определим как множество всех упорядоченных пар (x,y) , таких, что x geqslant y . Тогда

rho=bigl{(1;1),, (2;1),, (2;2),, (3;1),, (3;2),, (3;3),, (4;1),, (4;2),, (4;3),, (4;4)bigr}

Область определения отношения D(rho)={1;2;3;4} , область значений R(rho)= {1;2;3;4} . График и два варианта графа отношения rho изображены на рис. 1.1, б.

в. Множество точек окружности x^2+y^2=1 есть график бинарного отношения на множестве действительных чисел, состоящего из всех таких упорядоченных пар (x,y) , что $y=pmsqrt{1-x^2}$ , или, что равносильно, компоненты пары удовлетворяют уравнению x^2+y^2=1 . Область определения бинарного отношения есть отрезок [-1;1] , область значения — также отрезок [-1;1] .

Графики и графы бинарных соответствий

Функциональное соответствие

Соответствие rho subseteq Atimes B называют функциональным по второй (первой) компоненте, если для любых двух упорядоченных пар (x,y)inrho и (x'y')inrho из равенства x=x' следует y=y' (и из y=y' следует x=x' ). Функциональность соответствия по второй компоненте означает, что, фиксируя в любой упорядоченной паре, принадлежащей данному соответствию, первую компоненту, мы однозначно определяем и вторую компоненту. Таким образом, мы можем сказать, что соответствие, функциональное по второй компоненте, есть отображение (возможно, частичное).

Поэтому соответствие f subseteq Atimes B является отображением из в , если и только если оно всюду определено (т.е. D(f)=A ) и функционально по второй компоненте. Отметим также, что отображение из в является инъекцией тогда и только тогда, когда оно функционально по первой компоненте.

Отношения произвольной арности

Связь между понятиями отношения, соответствия и отображения

В заключение обобщим понятие соответствия, определив отношения произвольной арности.

Определение 1.4. Произвольное подмножество rho декартова произведения A_1times A_n называют (п-арным или п-местным) отношением на множествах A_1,ldots,A_n .

В случае если все множества A_1,ldots,A_n совпадают, т.е. A_1=ldots= A_n=A , говорят об n-арном отношении на множестве .

Если rho — n-арное отношение на множествах A_1,ldots,A_n и (a_1,ldots,a_n)inrho , то говорят об элементах , связанных отношением rho .

Замечание 1.3. При n=2 получаем бинарное отношение на множествах A_1,A_2 . Это не что иное, как соответствие из A_1 в A_2 , где множества A_1 и A_2 , вообще говоря, различны.

При A_1=A_2=A получаем введенное ранее бинарное отношение на множестве, т.е. подмножество декартова квадрата .

Таким образом, в общем случае (при произвольном ngeqslant 2 ) следует, строго говоря, различать термины «n-арное отношение» и «n-арное отношение на множестве».

Связь между введенными понятиями отношения, соответствия и отображения проиллюстрирована на рис. 1.2.

Пусть n-арное отношение rho subseteq A_1timesldotstimes A_n удовлетворяет условию: для любых двух кортежей

(x_1, ldots, x_i,ldots, x_n)inrho и (y_1,ldots, y_i,ldots, y_n)inrho

из выполнения равенств x_k=y_k для любого kne i~(0 leqslant k leqslant n) следует, что и x_i=y_i . Тогда отношение rho называют функциональным по i-й компоненте (1 leqslant i leqslant n) .

Другими словами, функциональность n-местного отношения по i-й (ileqslant n) компоненте равносильна условию, что, фиксируя все компоненты, кроме i-й, мы однозначно определяем и i-ю компоненту.

Пример 1.7. а. Представим строку учебного расписания как кортеж вида

(преподаватель, группа, дисциплина, аудитория, день, час).

Тогда расписание можно рассматривать как секстарное (шестиместное) отношение на соответствующих множествах. Оно будет функционально по первой компоненте, если, конечно, предположить, что два преподавателя или более не проводят одно и то же занятие одновременно в одном и том же месте (хотя, например, на лабораторных работах это возможно). Оно также функционально по третьей компоненте (один преподаватель не может вести одновременно занятия по разным дисциплинам), по четвертой (преподаватель со своей группой не могут находиться в разных аудиториях) и не будет, вообще говоря, функционально по второй, пятой и шестой компонентам.

б. Рассмотрим на множестве V_3 геометрических векторов в пространстве тернарное (трехместное) отношение rho , состоящее из всех упорядоченных троек (boldsymbol{x},boldsymbol{y},boldsymbol{z}) компланарных векторов. Это отношение не является функциональным ни по одной компоненте, так как любым двум векторам соответствует бесконечно много векторов, образующих с ними компланарную тройку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Образы и прообразы множеств при отображениях

Понятие многозначного отображения

Обратное отображение

Суперпозиция отображений (сложная функция)

Упражнения для самостоятельной работы

Соответствия и бинарные отношения на множествах

Образ и прообраз множества

Частичное отображение и его область определения

Бинарные отношения на множествах

Функциональное соответствие

Отношения произвольной арности