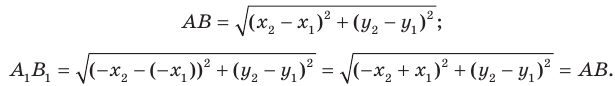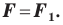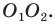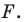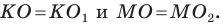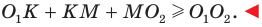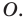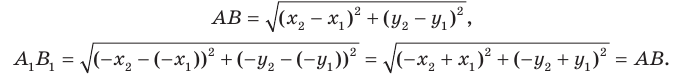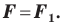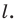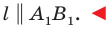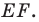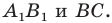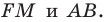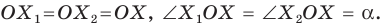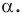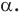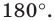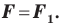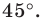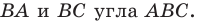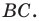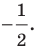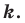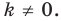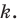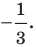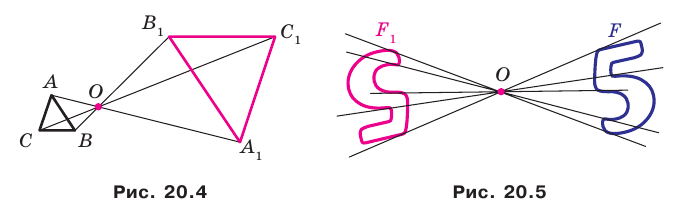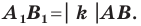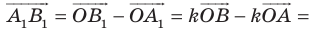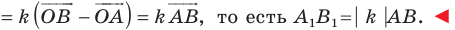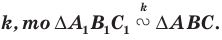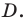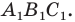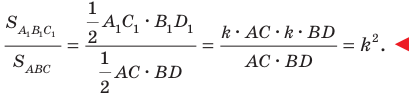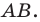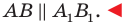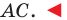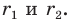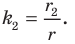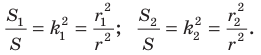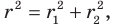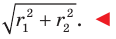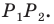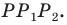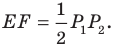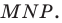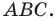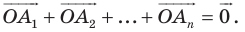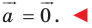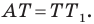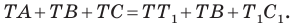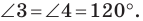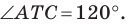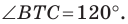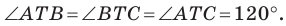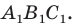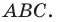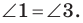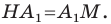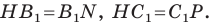Содержание:
Геометрические преобразования:
В этой лекции вы узнаете, что такое преобразование фигуры. Ознакомитесь с такими видами преобразований, как параллельный перенос, центральная симметрия, осевая симметрия, поворот, гомотетия, подобие.
Вы научитесь применять свойства преобразований при решении задач и доказательстве теорем.
Движение (перемещение) фигуры. Параллельный перенос
Пример:
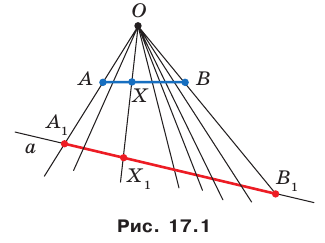
На рисунке 17.1 изображены отрезок
Мы указали правило, с помощью которого каждой точке 
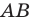
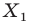
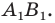
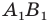
Пример:
На рисунке 17.2 изображены полуокружность 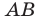
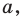
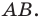
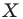
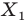
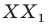
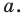
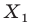
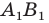
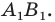
Пример:
Пусть даны некоторая фигура 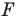
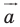
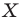
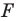
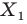
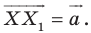
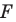
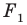
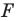
Обобщим приведенные примеры.
Пусть задана некоторая фигура 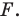
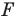
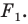
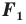
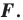
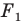
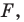
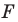
Так, в примере 1 отрезок 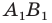
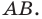
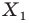
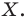
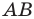
Обратим внимание на то, что в примере 3 фигура 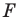
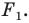
Какими же свойствами должно обладать преобразование, чтобы образ и прообраз были равными фигурами? Оказывается, что достаточно лишь одного свойства: преобразование должно сохранять расстояние между точками, то есть если 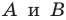
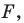
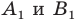
Что такое преобразование фигур
Определение. Преобразование фигуры 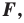
Если каждой точке 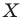
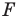
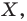
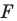
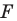
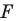
Мы давно используем понятие «равенство фигур», хотя не давали ему строгого определения.
На то, что движение связано с равенством фигур, указывают следующие свойства движения.
Если преобразование является движением, то:
- образом прямой является прямая,
- образом отрезка является отрезок, равный данному;
- образом угла является угол, равный данному,
- образом треугольника является треугольник, равный данному.
Доказательство этих свойств выходит за рамки рассматриваемого курса геометрии.
Свойства движения подсказывают следующее определение.
Определение. Две фигуры называют равными, если существует движение, при котором одна из данных фигур является образом другой.
Запись 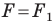
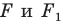
Если существует движение, при котором фигура 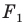
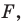
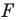
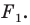
Замечание. Ранее равными фигурами мы называли такие фигуры, которые совпадали при наложении. Термин «наложение» интуитивно понятен, и в нашем представлении он связывается с наложением реальных тел. Но геометрические фигуры нельзя наложить в буквальном смысле этого слова. Теперь наложение фигуры 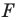
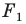
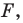
Термин «движение» также ассоциируется с определенным физическим действием: изменением положения тела без деформации.
Именно с этим связано появление этого термина в математике. Однако в геометрии предметом исследования является не процесс, происходящий во времени, а лишь свойства фигуры и ее образа.
То, что изображенные на рисунке 17.3 фигуры 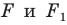
Теорема 17.1 (свойство параллельного переноса). Параллельный перенос является движением.
Доказательство: Пусть 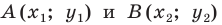
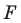
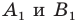
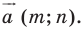
Имеем: 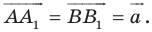
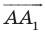
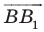
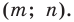
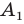
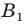
Найдем расстояние между точками
Найдем расстояние между точками
Следовательно, мы показали, что 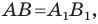
Следствие. Если фигура 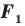
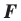
Это свойство используется при создании рисунков на тканях, обоях, покрытиях для пола и т. п. (рис. 17.5).
Если фигура 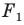
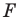
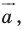
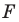
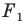
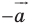
Параллельные переносы на векторы 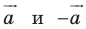
Пример №1
Каждой точке 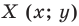
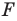
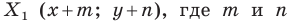
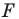
Решение:
Рассмотрим вектор 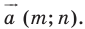
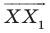
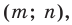
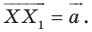
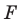
Пример №2
Точка 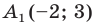
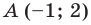
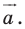
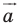
Решение:
Из условия следует, что 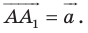
Пусть 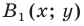
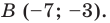
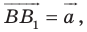
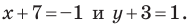
Ответ:
Пример №3
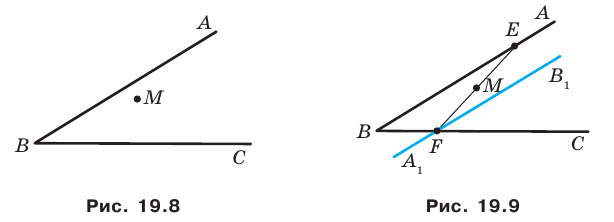
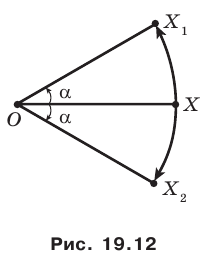
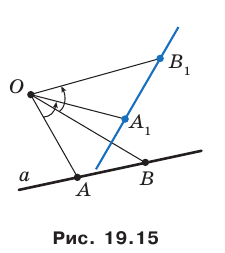
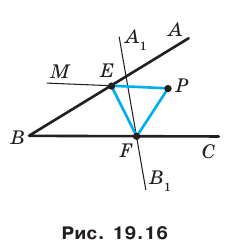
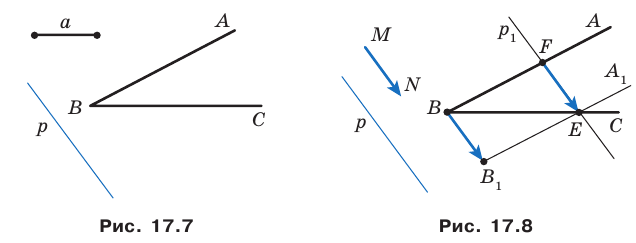
Даны угол 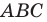
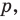
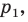
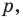
Решение:
Рассмотрим вектор 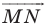

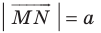
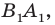
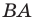
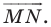
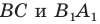
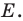
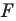
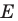
Приведенные рассуждения подсказывают следующий алгоритм построения:
- найти образ луча
при параллельном переносе на вектор
- отметить точку пересечения луча
с построенным образом;
- через найденную точку провести прямую
параллельную прямой
Прямая
будет искомой.
Осевая симметрия
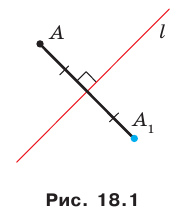
Определение. Точки 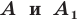
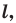
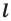
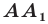
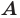
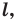
Например, точки 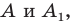
Рассмотрим фигуру 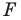
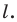
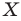
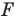
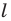
В результате такого преобразования фигуры 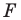
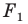
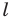
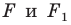
Теорема 18.1 (свойство осевой симметрии). Осевая симметрия является движением.
Доказательство: Выберем систему координат так, чтобы ось симметрии совпала с осью ординат. Пусть 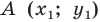
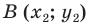
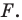
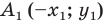
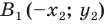
Мы получили, что 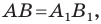
Следствие. Если фигуры 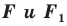
Определение. Фигуру называют симметричной относительно прямой 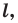
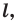
Прямую 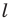
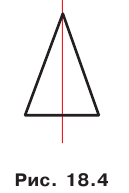
Приведем примеры фигур, имеющих ось симметрии. На рисунке 18.4 изображен равнобедренный треугольник. Прямая, содержащая его высоту, проведенную к основанию, является осью симметрии треугольника.
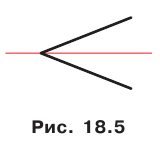
Любой угол имеет ось симметрии — это пря-Рис. 18.5 мая, содержащая его биссектрису (рис. 18.5).
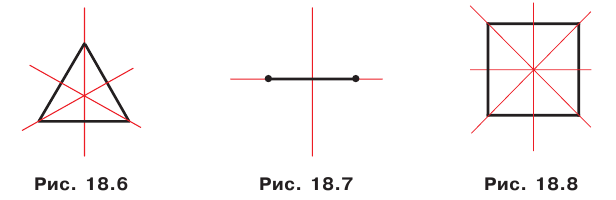
Равносторонний треугольник имеет три оси симметрии (рис. 18.6). Две оси симметрии имеет отрезок: это его серединный перпендикуляр и прямая, содержащая этот отрезок (рис. 18.7).
Квадрат имеет четыре оси симметрии (рис. 18.8).
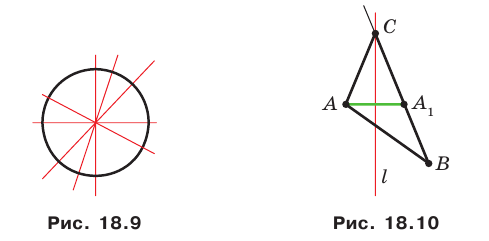
Существуют фигуры, имеющие бесконечно много осей симметрии, например окружность. Любая прямая, проходящая через центр окружности, является ее осью симметрии (рис. 18.9).
Бесконечно много осей симметрии имеет и прямая: сама прямая и любая прямая, ей перпендикулярная, являются ее осями симметрии.
Пример №4
Начертили неравнобедренный треугольник 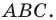
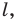
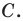
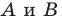
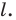
Решение:
Поскольку прямая 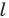
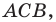
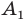
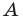
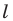
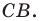
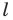
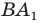
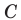
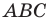
Эти соображения подсказывают, как построить искомый треугольник: строим точку 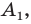
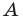
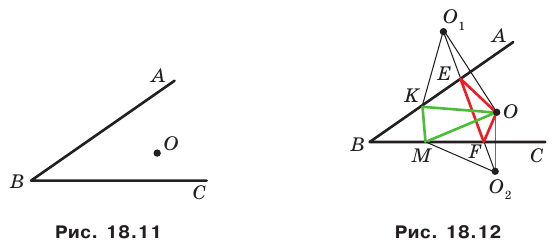
Пример №5
Точка 
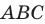
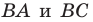
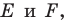
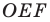
Решение:
Пусть точки 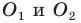
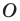
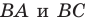
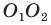
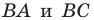
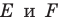
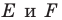
Заметим, что отрезки 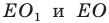
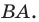
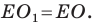
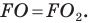
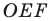
Покажем, что построенный треугольник имеет наименьший периметр из возможных.
Рассмотрим треугольник 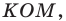
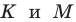
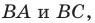
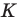
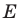
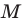
Понятно, что
Тогда периметр треугольника 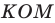
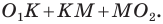
Центральная симметрия. Поворот
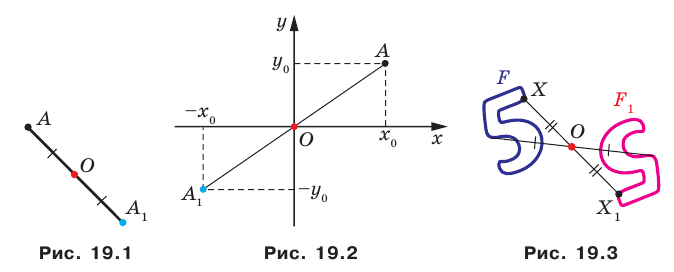
Определение. Точки 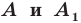
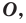
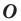
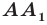
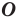
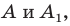
Рассмотрим фигуру 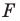
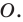
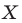
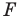
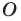
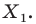
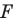
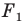
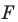
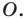
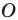
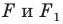
Теорема 19.1 (свойство центральной симметрии). Центральная симметрия является движением.
Доказательство: Выберем систему координат так, чтобы центр симметрии совпал с началом координат. Пусть 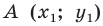
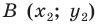
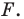
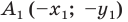
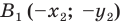
Мы получили, что 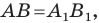
Следствие. Если фигуры 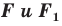
Определение. Фигуру называют симметричной относительно точки 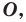
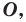
Точку 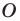
Приведем примеры фигур, имеющих центр симметрии.
Центром симметрии отрезка является его середина (рис. 19.4).
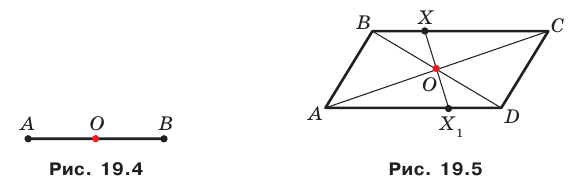
Точка пересечения диагоналей параллелограмма является его центром симметрии (рис. 19.5).
Существуют фигуры, имеющие бесконечно много центров симметрии. Например, каждая точка прямой является ее центром симметрии.
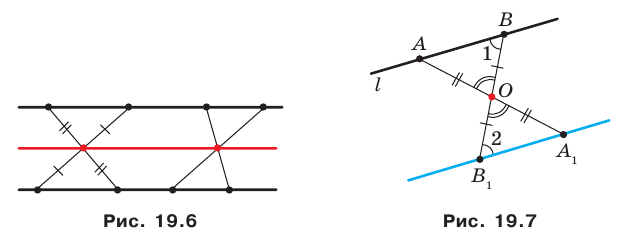
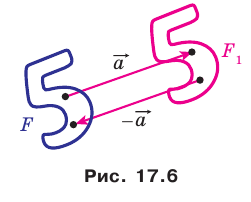
Также бесконечно много центров симметрии имеет фигура, состоящая из двух параллельных прямых. Любая точка прямой, равноудаленной от двух данных, является центром симметрии рассматриваемой фигуры (рис. 19.6).
Пример №6
Докажите, что образом данной прямой 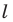
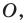
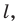
Решение:
Поскольку центральная симметрия — это движение, то образом прямой 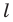
Выберем на прямой 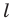
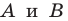
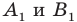
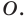
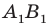
Поскольку 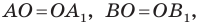
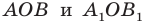
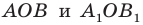
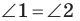
Пример №7
Точка 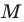
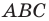
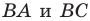
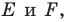
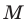
Решение:
Пусть прямая 
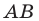
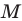
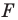
Найдем прообраз точки 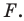
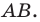
Обозначим эту точку буквой 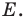
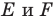
Изучая окружающий мир, мы часто видим примеры проявления симметрии в природе (рис. 19.10). Объекты, имеющие ось или центр симметрии, легко воспринимаются и радуют взгляд. Недаром в Древней Греции слово «симметрия» служило синонимом слов «гармония», «красота».
Идея симметрии широко используется в изобразительном искусстве, архитектуре и технике (рис. 19.11).
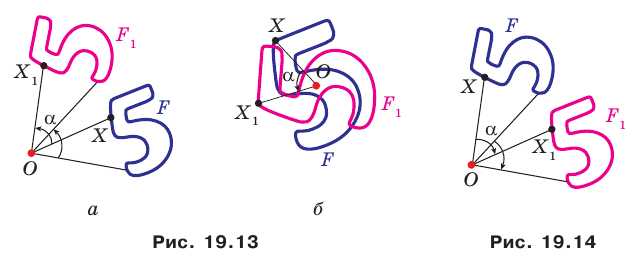
На рисунке 19.12 изображены точки 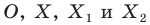
Говорят, что точка 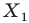
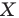
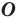
Так же говорят, что точка 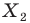
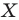
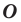
Точку 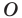
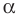
Рассмотрим фигуру 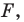
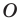
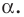
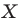
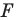
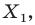
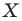
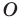
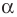
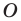
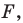
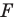
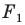
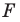
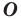
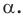
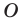
Аналогично определяют преобразование поворота фигуры 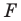
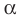
Заметим, что центральная симметрия является поворотом вокруг центра симметрии на угол
Теорема 19.2 (свойство поворота). Поворот является движением.
Докажите эту теорему самостоятельно.
Следствие. Если фигура 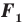
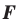
Пример №8
Даны прямая 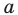
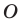
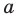
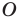
Решение:
Поскольку поворот — это движение, то образом прямой 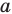
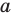
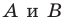
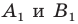
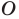
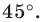
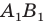
Пример №9
Точка 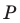
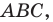
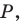
Решение:
Пусть прямая 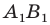
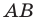
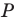
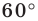
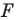
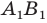
Пусть точка 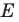
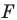
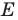
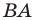
Эти соображения подсказывают, как построить искомый треугольник.
Строим прямую 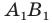
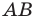
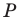
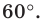
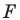
Строим угол 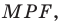
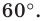
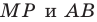
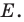
Имеем: 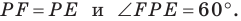
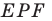
Подобие фигур
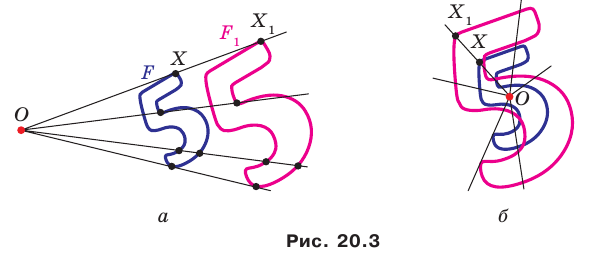
На рисунке 20.1 изображены точки 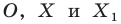
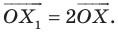
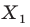
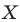
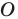
На рисунке 20.2 изображены точки 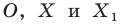
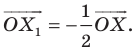
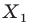
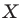
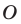
Вообще, если точки 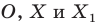
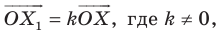
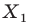
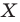
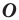
Точку 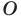
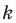
Рассмотрим фигуру 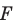
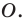
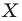
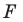
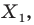
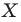
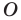
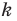
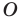
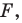
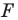
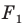
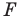
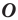
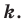
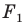
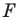
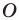
Например, на рисунке 20.4 треугольник 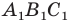
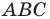
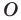
можно сказать, что треугольник 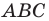
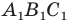
Отметим, что при 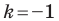
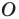
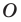
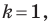
Очевидно, что при 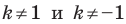
Теорема 20.1. При гомотетии фигуры 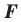
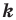
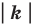
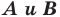
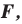
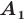
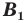
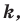
Доказательство: Пусть точка 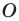
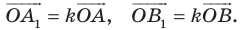
Следствие. Если треугольник 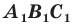
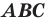
Для доказательства этого утверждения достаточно воспользоваться теоремой 20.1 и третьим признаком подобия треугольников.
Гомотетия обладает целым рядом других свойств.
При гомотетии:
Эти свойства вы можете доказать на занятиях математического кружка.
Перечисленные свойства гомотетии указывают на то, что это преобразование может изменить размеры фигуры, но не меняет ее форму, то есть при гомотетии образ и прообраз являются подобными фигурами. Заметим, что в курсе геометрии 8 класса, говоря о подобии фигур, мы давали определение только подобных треугольников. Сейчас определим понятие подобия для произвольных фигур.
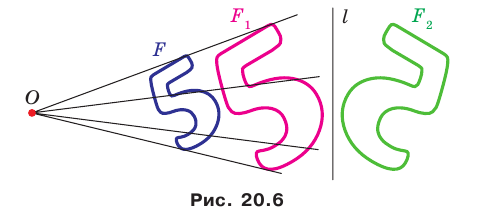
На рисунке 20.6 фигура 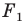
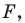
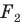
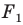
Говорят, что фигура 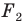
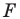
Поскольку 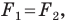
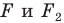
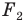
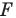
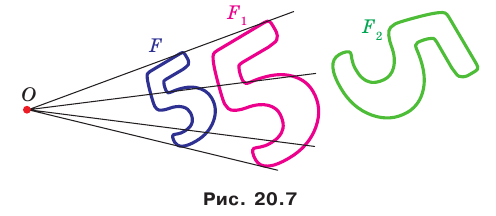
На рисунке 20.7 фигура 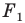
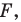
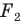
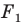
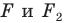
Из сказанного следует, что целесообразно принять такое определение.
Определение. Две фигуры называют подобными, если одну из них можно получить из другой в результате композиции двух преобразований: гомотетии и движения.
Это определение иллюстрирует схема, изображенная на рисунке 20.8.
Запись 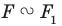
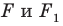
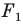
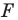
Из приведенного определения следует, что при преобразовании подобия фигуры 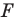
Так как тождественное преобразование является движением, то из схемы, изображенной на рисунке 20.8, следует, что гомотетия — частный случай преобразования подобия.
Пусть 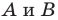
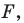
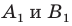
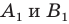
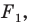
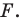
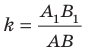
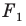
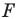
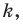
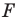
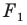
Заметим, что преобразование подобия с коэффициентом 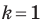
С преобразованием подобия мы часто встречаемся в повседневной жизни (рис. 20.9). Например, в результате изменения масштаба карты получаем карту, подобную данной. Фотография — это преобразование негатива в подобное изображение на фотобумаге. Перенося в свою тетрадь рисунок, сделанный учителем на доске, вы также выполняете преобразование подобия. 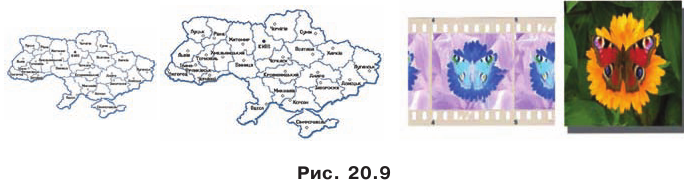
Доказательство этой теоремы выходит за рамки рассматриваемого курса геометрии. Мы докажем ее для частного случая, рассмотрев подобные треугольники.
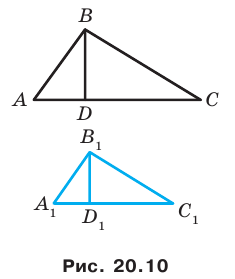
Доказательство: Пусть треугольник 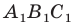
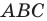
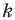
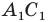
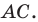
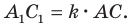
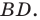
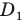
Поскольку при преобразовании подобия сохраняются углы, то отрезок 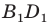
Тогда 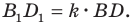
Пример №10
Докажите, что образом прямой 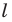
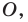
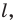
Решение:
Из свойств гомотетии следует, что образом прямой 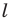
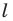
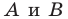
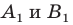
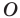
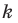
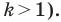
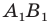
При доказательстве теоремы 20.1 мы показали, что 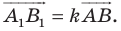
Пример №11
В остроугольный треугольник 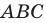
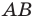
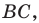
Решение:
Из произвольной точки 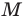
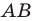
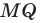
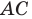
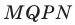
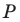
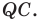
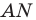
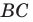
Рассмотрим гомотетию с центром 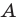
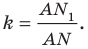
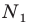
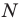
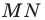
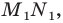
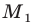
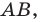
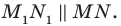
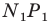
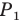
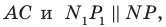
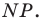
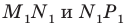
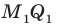
Пример №12
Отрезок 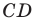
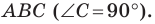
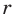

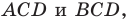
Решение:
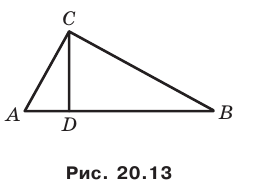
Поскольку угол 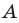
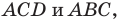
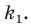
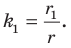
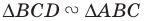
Обозначим площади треугольников 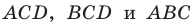
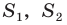
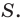
Отсюда 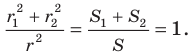
Ответ:
Применение преобразований фигур при решении задач
Преобразование фигур — эффективный метод решения целого ряда геометрических задач. Проиллюстрируем это на примерах.
Пример №13
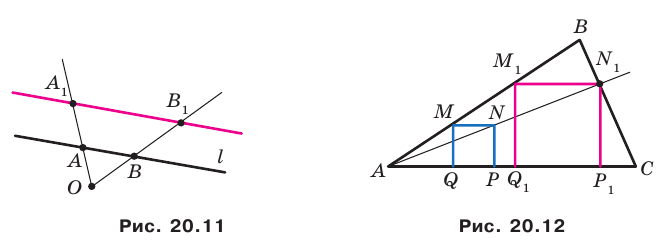
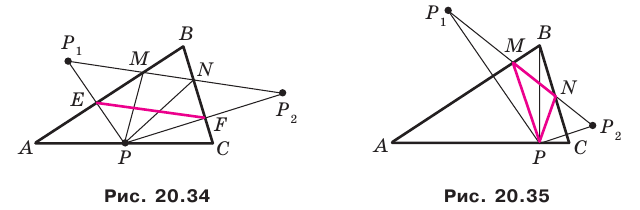
На сторонах 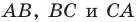
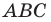
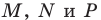
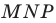
Решение:
Пусть 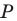
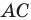
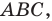
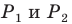
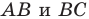
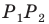
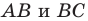
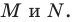
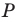
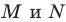
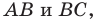
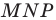
Заметим, что отрезок 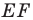
Тогда
Поскольку 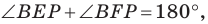
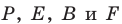
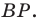
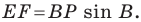
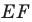
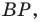
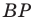
На рисунке 20.35 отрезок 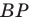
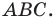
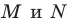
Из построения следует, что периметр любого другого треугольника, вершины которого лежат на сторонах треугольника 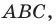
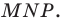
Можно показать (сделайте это самостоятельно), что точки 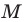
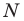
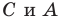
Следовательно, вершины искомого треугольника — это основания высот данного треугольника 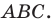
Пример №14
Точка 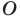
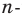
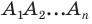
Решение:
Пусть 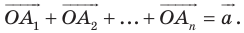
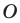
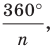
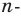
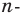
Пример №15
Внутри треугольника 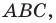
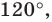
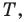
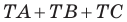
Решение:
Пусть 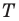
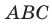
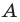
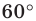
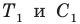
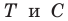
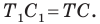
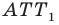
Имеем:
Понятно, что сумма 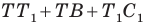
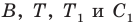
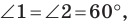
Так как угол 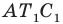
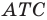
Итак, точки 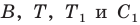
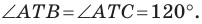
Таким образом, сумма 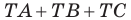
Найти точку 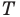
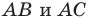
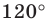
Понятно, что если один из углов треугольника 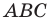
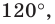
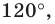
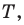
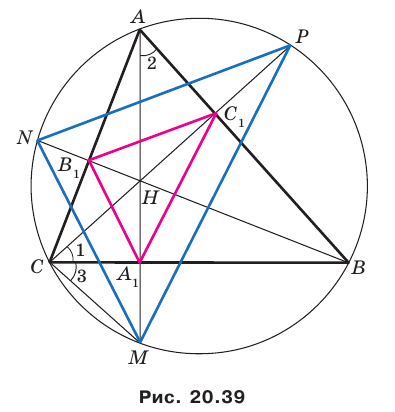
Пример №16
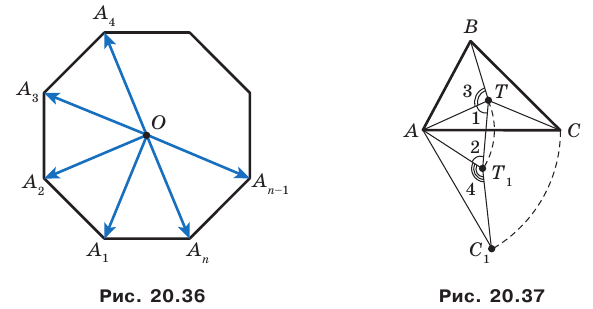
Отрезки 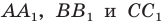
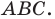
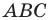
Решение:
Пусть прямые 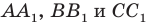
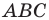
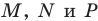
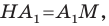
Имеем:
Углы 2 и 3 равны как вписанные, опирающиеся на дугу 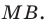
Тогда в треугольнике 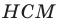
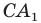
Аналогично можно доказать, что
Теперь понятно, что треугольник 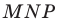
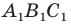
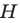
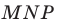
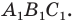
- Планиметрия — формулы, определение и вычисление
- Стереометрия — формулы, определение и вычисление
- Возникновение геометрии
- Призма в геометрии
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
Если при параллельном переносе одна точка переходит в другую точку, какую информацию можно получить из этих данных, если координаты обеих точек известны?
Параллельный перенос, при котором точка A (x;y) переходит в точку
A1 (x1; y1), задаётся формулами:
1) При параллельном переносе точка A (-2;7) переходит в точку B (4;-3). Найти формулы параллельного переноса.
Решение:
Чтобы найти числа a и b в формулах параллельного переноса, подставим в них координаты точек A и B:
x=-2, y=7; x1=4, y1=-3:
Отсюда a=6, b= -4. Следовательно, формулы параллельного переноса
2) При параллельном переносе точка A (-9; 4) переходит в точку B (2; -2). В какую точку при этом параллельном переносе переходит точка C (0; 7)?
Решение:
Сначала найдём формулы параллельного переноса, который переводит точку A в точку B. Для этого в формулы подставим координаты точек A и B:
Отсюда a=11, b=-6. Значит, данный параллельный перенос задаётся формулами
Чтобы найти, в какую точку переходит C, подставим её координаты x=0, y=7 в формулы параллельного переноса и найдём x1и y1:
Таким образом, точка C переходит в точку (11; 1).
Ответ: (11; 1).
3) Найти координаты точки, являющейся образом точки A (-8; 5) при параллельном переносе на вектор
Решение:
x=-8; y=5; a1=3; a2=4:
Ответ: (5;9).
Сегодня на уроке мы вспомним, какое отображение
плоскости на себя мы называли параллельным переносом, введём понятие
параллельного переноса в пространстве. Проверим, будет ли параллельный перенос
движением пространства.
Вернёмся в планиметрию и вспомним, что параллельным
переносом мы называли преобразование, при котором каждая точка фигуры
перемещается в одном и том же направлении и на одно и то же расстояние. Мы
говорили, что для того, чтобы задать перенос достаточно задать вектор.
Другими словами, параллельным переносом на
вектор называется
отображение плоскости на себя, при котором каждая точка отображается
в такую точку ,
что вектор равен
вектору .
То, что параллельный перенос является примером
движения плоскости, мы уже доказывали. Давайте вспомним это доказательство.
Пусть при параллельном переносе на вектор точки
и
отображаются
в точки и
.
Так как векторы и
,
то значит, эти векторы равны между собой .
То есть они параллельны и
их длины равны, поэтому четырёхугольник –
параллелограмм. Следовательно, ,
то есть расстояние между точками и
равно
расстоянию между точками и
.
Случай, когда точки и
лежат
на прямой параллельной вектору ,
вы можете рассмотреть самостоятельно. Но и в этом случае расстояние между
точками и
будет
равно расстоянию между точками и
.
Таким образом, параллельный перенос сохраняет
расстояние между точками и поэтому представляет собой движение. Это
движение можно представить себе как сдвиг всей плоскости в направлении данного
вектора на
его длину.
В планиметрии мы говорили, что параллельный перенос
обладает некоторыми свойствами.
Свойства параллельного переноса:
·
При
параллельном переносе отрезок переходит в равный ему отрезок.
·
Угол
переходит в равный ему угол.
·
Окружность
переходит в равную ей окружность.
·
Любой
многоугольник переходит в равный ему многоугольник.
·
Параллельные
прямые переходят в параллельные прямые.
·
Перпендикулярные
прямые переходят в перпендикулярные прямые.
Теперь давайте определим, что мы будем понимать под
параллельным переносом в пространстве.
Определение:
Параллельным переносом на вектор называется
такое отображение пространства на себя, при котором любая точка переходит
в такую точку что
.
Проверим, будет ли параллельный перенос в
пространстве примером движения пространства.
При параллельном переносе точки пространства и
переходят
в такие точки и
,
что вектора и
.
Сложим по правилу треугольника векторы
Поскольку левые части равенств равны, значит, равны
и правые части равенств.
Значит, можно записать, что .
Заменим вектора и
на
вектор .
Получим, что .
Отсюда получаем, что вектор .
Поскольку векторы равны, значит, равны и их длины, то есть .
То есть расстояние между точками при параллельном переносе в пространстве
сохраняется, значит, параллельный перенос в пространстве также является
движением, но уже не плоскости, а пространства.
Сформулируем свойства параллельного переноса.
Свойства параллельного переноса:
·
Параллельный
перенос является примером движения пространства.
·
При
параллельном переносе точки смещаются по параллельным или совпадающим прямым на
одно и то же расстояние.
·
При
параллельном переносе прямая переходит в параллельную прямую (или сама в себя).
·
Каковы
бы не были две точки и
,
существует, и притом единственный, параллельный перенос, при котором точка переходит
в точку .
·
При
параллельном переносе в пространстве каждая плоскость переходит либо в себя,
либо в параллельную ей плоскость.
Движение в пространстве обладает теми же свойствами,
что и движение плоскости.
Свойства движения пространства:
·
Движение
сохраняет расстояние между точками.
·
При
любом движении пространства отрезок отображается на отрезок, прямая – в прямую,
плоскость – в плоскость.
Решим несколько задач.
Задача:
начертить отрезок и
вектор .
Построить отрезок ,
который получится из отрезка параллельным
переносом на вектор .
Решение:
для того, чтобы построить отрезок ,
отобразим точку в
точку ,
точку в
точку с
помощью параллельного переноса. Тогда соединив точки ,
мы
получим отрезок .
Задача:
начертить треугольник и
вектор .
Построить треугольник ,
который получится из треугольникa
параллельным
переносом на вектор .
Решение:
отобразим с помощью параллельного переноса точки ,
,
в
точки ,
,
.
Соединив полученные точки, мы получим искомый треугольник .
Задача:
начертить пятиугольник и
вектор .
Построить пятиугольник ,
который получится из пятиугольника параллельным
переносом на вектор .
Решение:
решать эту задачу будем аналогично тому, как мы решали предыдущую задачу.
Отобразим каждую вершину пятиугольника с помощью параллельного переноса на
вектор .
Соединим получившиеся точки и получим искомый пятиугольник .
Итоги:
Сегодня на уроке мы вспомнили, что мы понимали под
параллельным переносом в планиметрии. Ввели понятие параллельного переноса в пространстве.
Сформулировали основные свойства параллельного переноса, движения пространства.
Образ точки на векторе
Пусть 




Можно доказать, что точка M имеет при данном отображении единственный образ — точку М ′ , а для точки М ′ существует единственный прообраз — точка М .
Таким образом, получаем биективное отображение пространства на себя, т. е. преобразование пространства, которое называют параллельным переносом на вектор 
Определение. Параллельным переносом на вектор 


Иногда параллельный перенос называют коротко переносом. При этом вектор 



Из определения следует, что параллельный перенос задаётся либо вектором, либо парой соответствующих точек ( М, М ′ ) .
Если при переносе на вектор 







Перенос на нулевой вектор 

5.2. Параллельный перенос в координатах
Пусть в прямоугольной системе координат Охyz задан вектор 

Так как M ′ = 







Соотношения (1) называются формулами параллельного переноса пространства на вектор 
Докажем, что параллельный перенос пространства есть движение . Пусть: A ( x 1 ; y 1 ; z 1 ) и C ( x 2 ; y 2 ; z 2 ) — данные точки; A ′ ( 












Расстояние между точками А и C равно

Найдём расстояние между точками А ′ и C ′ .
Учитывая (2), получаем
| A ′ C ′ | = 
= 
Таким образом, при параллельном переносе расстояние между точками сохраняется. Значит, параллельный перенос есть движение.
5.3. Свойства параллельного переноса
Можно доказать, что параллельный перенос отображает :
— прямую на параллельную ей прямую либо на себя;
— луч на сонаправленный с ним луч;
— вектор 

— плоскость на параллельную ей плоскость либо на себя.
Докажем, например, что параллельный перенос отображает плоскость на параллельную ей плоскость или на себя.
Действительно, параллельный перенос — движение, поэтому он отображает плоскость α на некоторую плоскость α′ . Докажем, что α′ || α или α′ совпадает с α .
На плоскости α выберем две пересекающиеся прямые a и b ; a ∩ b = O.
Пусть 

Так как любое преобразование отображает пересечение фигур на пересечение их образов и прямые a и b пересекаются в точке O, то пересекаются и прямые a ′ и b ′ в такой точке O ′ , что O ′ = 
Рассмотрим вопрос о неподвижных точках, неподвижных прямых и неподвижных плоскостях при параллельном переносе.
Неподвижных точек параллельный перенос на ненулевой вектор не имеет.
Неподвижной прямой при параллельном переносе на ненулевой вектор 


Неподвижной плоскостью при параллельном переносе на ненулевой вектор 


Параллельный перенос, отображая любой вектор на себя, не меняет ориентацию пространства, следовательно, является движением первого рода.
Рассмотрим композицию двух переносов, заданных векторами 





Пусть М — любая точка пространства. Перенос на вектор 














Таким образом, композиция переносов на векторы 



Так как 







5 .4. Скользящая симметрия
Среди преобразований пространства важное место занимает «скользящая симметрия», представляющая собой композицию симметрии S α относительно плоскости α и параллельного переноса на вектор 
Отметим ряд характерных свойств скользящей симметрии:
— скользящая симметрия является движением (как композиция двух движений);
— скользящая симметрия не имеет неподвижных точек;
— любая прямая плоскости α , параллельная вектору переноса, является неподвижной прямой скользящей симметрии; на каждой из них индуцируется параллельный перенос;
— неподвижной плоскостью скользящей симметрии является не только плоскость симметрии α (на ней индуцируется параллельный перенос на вектор 


— скользящая симметрия меняет ориентацию тетраэдра (значит, и ориентацию пространства), т. е. является движением второго рода;
— преобразованием, обратным скользящей симметрии, заданной плоскостью α и вектором 


Попробуйте доказать самостоятельно, что композиция двух центральных симметрий есть параллельный перенос, причём Z B ∘ Z A = 2 
Параллельный перенос
Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.
Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.
1) Введём на плоскости декартовы координаты x, y.
Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.
Формулы параллельного переноса
Если при параллельном переносе точка A(x;y) переходит в точку A1(x1;y1)
то параллельный перенос задаётся формулами:
Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.
2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:
Свойства параллельного переноса
1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).
2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).
4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.
В алгебре параллельный перенос широко используется для построения графиков функций.
Геометрия для новичков. Часть 1: координаты и векторы — теория
Внимание! Этот документ ещё не опубликован.
О чем данная статья
В данной статье дается теоретическое описание векторов, координат векторов и операций над ними.
На кого рассчитана статья
Прежде чем читать эту статью, нужно знать:
- что такое прямоугольная система координат и координаты точки на плоскости
- что такое теорема Пифагора
Введение
Зачем нужны координаты точек в играх
В любой игре положение игрового объекта задается координатами какой-либо точки, привязанной к этому объекту, т.е. эта точка перемещается вместе с объектом. Например, мы можем задать координаты объектов в «Супер Марио» следующим образом:
На этом рисунке крупные черные точки — это точки, привязанные к игровым объектам. Координаты этих точек мы и будем считать координатами игровых объектов.
Итак, на этом рисунке:
- координаты Марио равны (-0.5, -2)
- координаты улитки равны (3, -2)
- координаты кубика равны (4, 1)
Пример координат вектора
Я намеренно не написал конкретные значения для координат точек – пусть они будут произвольными.
Зададим себе вопрос «Как нужно изменить начальные координаты Марио, что получить конечные?» Чтобы ответить на этот вопрос, нам нужно найти пару чисел (x, y), таких, чтобы:
Ax + x = Bx
Ay + y = By
Решая эти 2 уравнения, получаем:
x = Bx — Ax
y = By — Ay
Пара (x, y) в нашей задаче является координатами вектора перемещения Марио. Но это — лишь конкретный пример координат вектора. Что такое вектор и что такое его координаты в общем случае? Сейчас узнаем.
Векторы
Что такое направленный отрезок
Стрелка показывает, что А – начало отрезка, а B – конец.
Что такое вектор
Что у этих отрезков общего? Хм, пожалуй 2 вещи:
- Направление
- Длина
Так вот, вектор – это как раз и есть совокупность направления и длины.
Направленный отрезок – не вектор, который мы изучаем в геометрии. Направленный отрезок задает, или как еще говорят, представляет вектор. Но это — не вектор.
В нашем примере направленный отрезок 

Примечание: о тонкостях приведенного мной определения — в конце статьи.
Равенство векторов
Если задуматься, все направленные отрезки одинаковой длины, которые лежат на параллельных прямых и указывают в одну сторону, имеют одинаковое направление и длину. Следовательно, все эти направленные отрезки представляют один и тот же вектор. Из этого следует определение равенства 2 векторов:
Два вектора 



Из данного определения следует, что при параллельном переносе произвольный направленный отрезок продолжает представлять тот же вектор, что он представлял до переноса. Это свойство активно используется для операций над векторами.
Длина вектора
Коллинеарные векторы
На рисунке любая пара из векторов 


Если отрезки, представляющие коллинеарные векторы, имеют одинаковое направления, то векторы называют сонаправленными:
Пишут:
Если отрезки, представляющие коллинеарные векторы, имеют противоположное направления, то векторы, представленные данными отрезками, называют противоположно направленными:
Пишут:
Нулевой вектор
Единичные векторы

Обратный вектор
Арифметические операции над векторами
- Вектор можно умножать на число. Вектор
, умноженный на число, записывается как k*
. Вектор будет сонаправлен (противоположно направлен) с вектором
, если k — положительное (отрицательное) число. Вектор k*
будет иметь длину |k|*|
|:
|k*

k* 

k* 

|k * 
Т.е. в результате нормализации мы получаем единичный вектор, сонаправленный с исходным вектором 
Важно: нулевой вектор НЕЛЬЗЯ нормализовать, так как для любого числа k:
|k*

Итак, как же найти это число k?
Распишем |k * 
|k * 


Здесь мы убрали с k знак модуля, так как по определению k > 0.
Итак:
k * |
Из этого следует, что:
k = 1 / |
Т.е. чтобы нормализовать произвольный ненулевой вектор, нам нужно разделить вектор на его длину.
Координаты вектора
Вроде бы из примера, приведенного в начале статьи, все понятно: координаты вектора — разность координат конца и начала направленного отрезка, представляющего вектор.
Но это не так. Действительно, значения координат вектора численно равны этой разности. Но определение координат вектора в корне отличается от определения координат точки.
Разложение вектора по 2 неколлинеарным векторам
В геометрии доказывается следующий факт.
Ecли мы возьмем 2 неколлинеарных вектора 

то для каждого вектора 


Теперь возьмем в качестве таких неколлинеарных векторов 

Векторы 

Определение координат вектора


то пара чисел (x, y) будет называться координатами вектора 
Часто пишут:

Эта запись означает, что вектор 
Арифметические операции над координатами векторов
— 
Координаты вектора, умноженного на число, равны координатам исходного вектора, умноженными на это число:
k* 
Пусть у нас есть 2 произвольных вектора 

- кoординаты суммы 2 векторов равны сумме x- и y-координат векторов:
+
= (ax + bx, ay + by)
- как следствие из предыдущих свойств, координаты разности 2 векторов равны разности координат этих векторов:
—
= (ax — bx, ay — by)
Т.е. арифметика для координат векторов – такая же, как и для обычных чисел, только все считается покоординатно.
Радиус-вектор
Можно доказать, что численные значения координат точки совпадают со значения координат ее радиус-вектора. Здесь примем это как факт: 
где (Ax, Ay) — координаты точки A
Связь между координатами вектора и координатами концов отрезка
если 


(x, y) = (Bx — Ax, By — Ay)
где (Ax, Ay), (Bx, By) — координаты точек А и B соответственно.
Докажем это.
Мы можем записать простое равенство для произвольного вектора 


Заметим, что 

Из равенства значений координат точки и радиус-вектора и предыдущей формулы следует, что:
(x, y) = (Bx — Ax, By — Ay)
Нахождение длины вектора по его координатам
Пусть у нас есть вектор 


Чтобы найти длину вектора 


По теореме Пифагора:
AC = |
СB = |
то в итоге получаем равенство:
Заключение
Применению векторов в реальных задачах игровой разработки будет посвящена следующая моя статья. В ней практически не будет математики и будет много программирования.
Здесь же я описал то, что будет необходимо для понимания практических приемов использования векторов.
Если не иметь представления, как связаны координаты точек и координаты векторов, очень сложно понять, как работают алгоритмы определения расстояний от точки до геометрической фигуры, алгоритмы обнаружения столкновений и т.д.
Так что не жалейте, если вы (о ужас!) кое-что запомнили из «всей этой математики». Все это вам пригодится очень скоро, обещаю.
Литература
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. «Геометрия», 7-9 классы»
Главы: «Векторы», «Метод координат».
PS: корректность определения вектора в статье
Вся хитрость в том, что существует несколько определений вектора даже в рамках геометрии.
Направленный отрезок – тоже вектор, так называемый фиксированный вектор. Но нужно учитывать один важный факт – 2 фиксированных вектора равны тогда и только тогда, когда их концы и начала совпадают. А это не то определение равенства 2 векторов, что дает учебник геометрии.
Определение вектора, данное в этой статье – определение так называемого свободного вектора.
Каждый свободный вектор – это множество фиксированных векторов, которые имеют равную длину и одинаковое направление.
Именно это определение учебник геометрии и пытается дать в неявном виде, когда вводит понятие равенства векторов. Но здесь возникает нестыковка – учебник объясняет, как работать со свободными векторами, изначально дав определение фиксированного вектора.
Надеюсь, вышесказанное объясняет, почему я привел в данной статье «свое» определение вектора.
http://gamedev.ru/code/articles/geometry_for_beginners_1
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Движения
- Параллельный перенос
Если нам дан вектор 

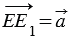
Доказательство:
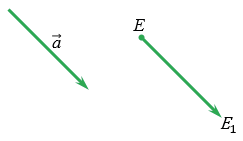
Дано: точки Е и К отображаются в точки Е1 и К1 при параллельном переносе на 
Доказать: параллельный перенос — движение.
Доказательство:
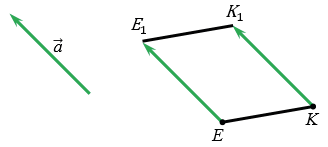
1 случай
Точки Е и К не лежат на одной прямой параллельной вектору 
По условию точки Е и К отображаются в точки Е1 и К1 соответственно при параллельном переносе на вектор 
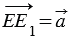
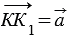

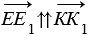
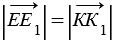
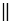

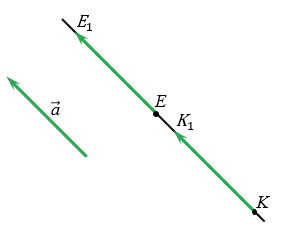
2 случай
Точки Е и К лежат на одной прямой параллельной вектору 
По условию точки Е и К отображаются в точки Е1 и К1 соответственно при параллельном переносе на вектор 
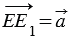
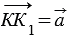

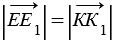
ЕК = КК1 + ЕК1, Е1К1 = ЕЕ1 + ЕК1, тогда, учитывая (1), получим: ЕК = Е1К1, т.е. расстояние между точками Е и К равно расстоянию между точками Е1 и К1. Получаем, что параллельный перенос сохраняет расстояния между точками, значит, является частным случаем движения.
Пример
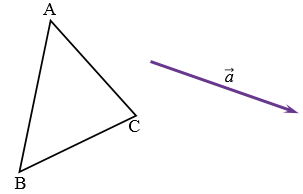
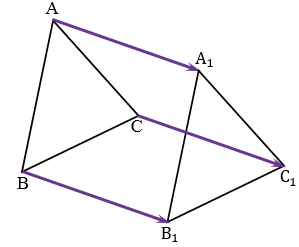
Построить 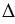
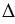

Дано: 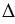

Построить: 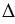

Решение:
Построим точки А1, В1, С1, которые получаются из точек А, В, С соответственно, параллельным переносом на вектор 

Советуем посмотреть:
Отображение плоскости на себя
Понятие движения
Наложения и движения
Поворот
Движения
Правило встречается в следующих упражнениях:
7 класс
Задание 1162,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1163,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1164,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1165,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 14,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1178,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1179,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1182,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1301,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

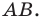
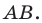
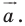
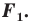
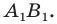
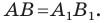
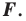
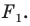
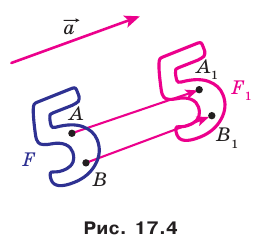
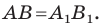
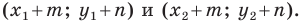
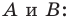
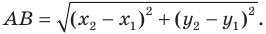
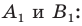
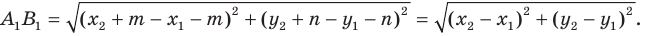

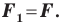

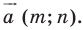

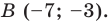
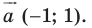
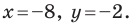
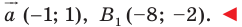
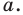
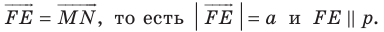
 при параллельном переносе на вектор
при параллельном переносе на вектор 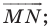
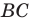 с построенным образом;
с построенным образом;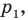 параллельную прямой
параллельную прямой 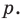 Прямая
Прямая 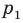 будет искомой.
будет искомой.