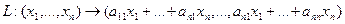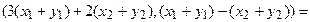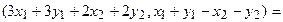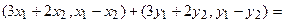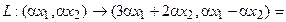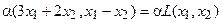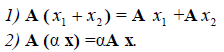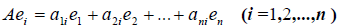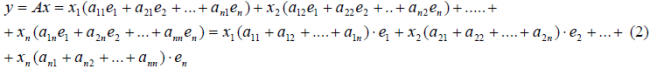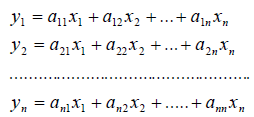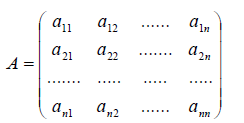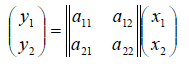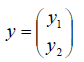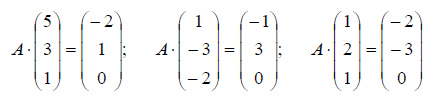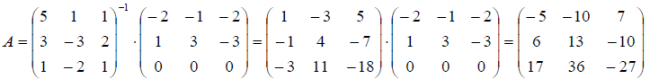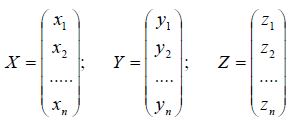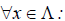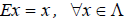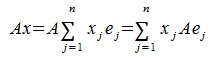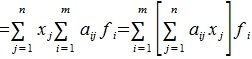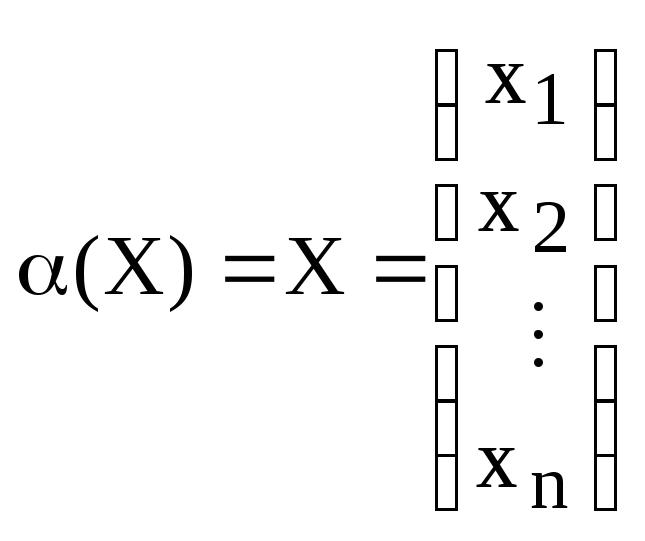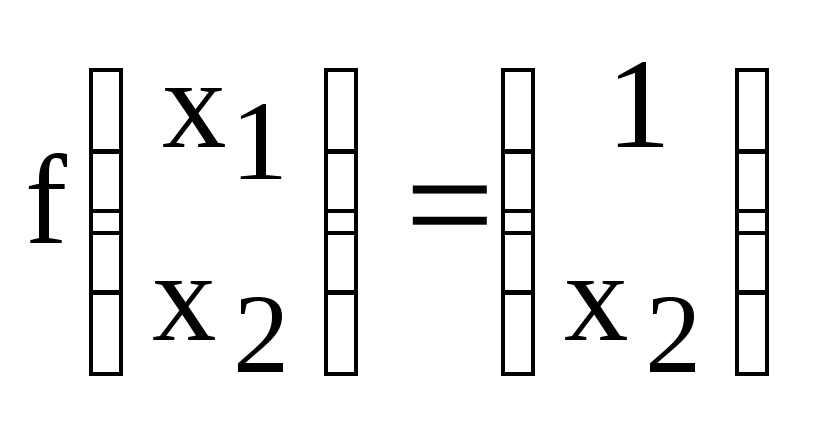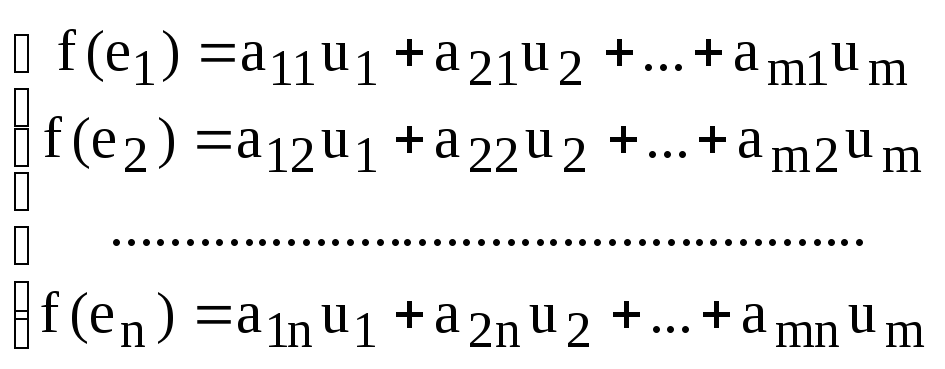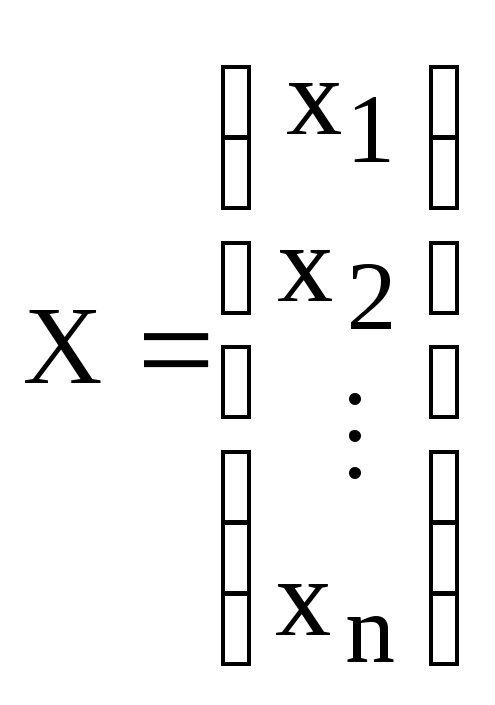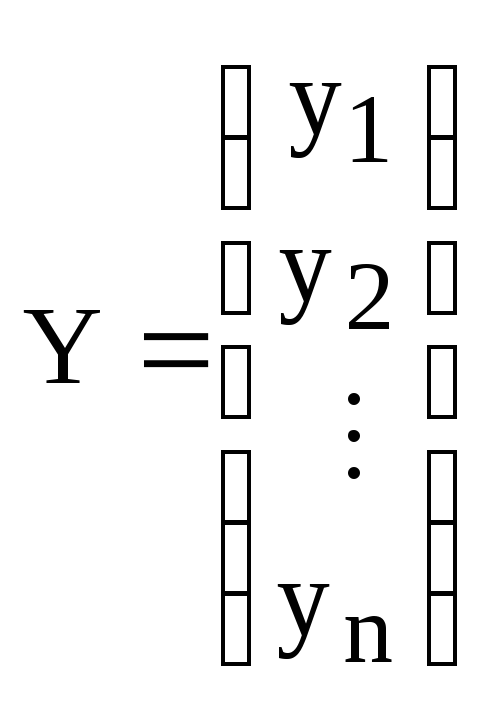Как найти образ в алгебре

Ядро и образ линейного отображения

Ядром линейного отображения называется множество таких векторов , что , т.е. множество векторов из , которые отображаются в нулевой вектор пространства . Ядро отображения обозначается:

Образом линейного отображения называется множество образов всех векторов из . Образ отображения обозначается или

Заметим, что символ следует отличать от — мнимой части комплексного числа.

---

Примеры ядер и образов линейных отображений

1. Ядром нулевого отображения является все пространство , а образом служит один нулевой вектор, т.е.

2. Рассмотрим отображение , которое ставит в соответствие каждому вектору n-мерного линейного пространства его координатный столбец относительно заданного базиса . Ядром этого отображения является нулевой вектор пространства , поскольку только этот вектор имеет нулевой координатный столбец . Образ преобразования совпадает со всем пространством , так как это преобразование сюръективно (любой столбец из является координатным столбцом некоторого вектора пространства ).

3. Рассмотрим отображение , которое каждому вектору n-мерного евклидова пространства ставит в соответствие алгебраическое значение его проекции на направление, задаваемое единичным вектором . Ядром этого преобразования является ортогональное дополнение — множество векторов, ортогональных . Образом является все множество действительных чисел .

4. Рассмотрим отображение , которое каждому многочлену степени не выше ставит в соответствие его производную. Ядром этого отображения является множество многочленов нулевой степени, а образом — все пространство .

---

Свойства ядра и образа линейного отображения

1. Ядро любого линейного отображения является подпространством: .

В соответствии с определением требуется доказать, что множество является непустым и замкнутым относительно операций сложения векторов и умножения вектора на число. В самом деле, из однородности отображения следует, что

т.е. нулевой вектор отображается в нулевой вектор . Следовательно, ядро любого линейного отображения не является пустым и содержит, по крайней мере, нулевой элемент: . Покажем, что множество замкнуто по отношению к операциям сложения векторов и умножения вектора на число. Действительно:

Следовательно, множество является линейным подпространством пространства .

2. Образ любого линейного отображения является подпространством: .

В самом деле, докажем, например, замкнутость множества по отношению к операции умножения вектора на число. Если , то существует вектор такой, что . Тогда , то есть .

Поскольку ядро и образ линейного отображения являются линейными подпространствами (свойства 1 и 2), можно говорить об их размерностях.

Дефектом линейного отображения называется размерность его ядра: , а рангом линейного отображения — размерность его образа: .

3. Ранг линейного отображения равен рангу его матрицы (определенной относительно любых базисов).

В самом деле, если любой базис пространства , то . Поэтому максимальное число линейно независимых векторов системы (ранг системы векторов) равно максимальному числу линейно независимых столбцов матрицы отображения, т.е. рангу матрицы: .

4. Линейное отображение инъективно тогда и только тогда, когда , другими словами, когда дефект отображения равен нулю: .

Действительно, образом нулевого вектора служит нулевой вектор . Поэтому, если отображение инъективно, то ядро содержит только нулевой вектор , иначе два разных вектора имели бы один и тот же образ . Обратно, при условии разные векторы не могут иметь одинаковые образы , так как в этом случае из равенств , следует, что ненулевой вектор (приходим к противоречию).

5. Линейное отображение сюръективно тогда и только тогда, когда , другими словами, когда ранг отображения равен размерности пространства образов: .

6. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда и одновременно.

---

Теорема (9.1) о размерностях ядра и образа. Сумма размерностей ядра и образа любого линейного отображения равна размерности пространства прообразов:

Действительно, пусть . Выберем в подпространстве базис и дополним его векторами до базиса всего пространства . Покажем, что векторы образуют базис подпространства .

Во-первых, , так как образ любого вектора линейно выражается через векторы

Во-вторых, образующие линейно независимы. Если их линейная комбинация равна нулевому вектору:

то вектор принадлежит ядру (его образ — нулевой вектор). Однако, по построению этот вектор принадлежит алгебраическому дополнению . Учитывая, что , заключаем: . Получили разложение нулевого вектора по линейно независимой системе векторов, значит, все коэффициенты . Поэтому равенство справедливо только для тривиальной линейной комбинации, т.е. система векторов линейно независимая.

Таким образом, векторы образуют базис подпространства , а его размерность определяется количеством базисных векторов, т.е. , что равносильно (9.3).

Следствие. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда обратима его матрица (определенная относительно любых базисов).

Действительно, для обратимости преобразования (см. свойство 6) его матрица (размеров ) должна удовлетворять условиям (см. свойства 3,4,5):

Тогда по теореме 9.1 заключаем, что , т.е. матрица — квадратная n-го порядка и невырожденная , что и требовалось доказать.

Обратимые линейные отображения называются также невырожденными (имея в виду невырожденность их матрицы).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Определение:

Пусть — линейный оператор. Ядром линейного оператора называется множество

Определение:

Пусть — линейный оператор. Образом линейного оператора называется множество (множество значений)

Лемма:

Ядро и образ линейного оператора являются подпространствами линейных пространств и соответственно.

Теорема (O ядре и базисе):

Доказательство:

— подпространство Шаг 1. Пусть — базис Дополним до базиса , получим базис , где Шаг 2. Докажем, что — линейная оболочка Рассмотрим Шаг 3. Осталось доказать следующее: Л.О. Докажем от противного. Пусть — линейно зависимы существует нетривиальная линейная комбинация, что Пусть Рассмотрим в соответствии с Получаем, что , что противоречит выбору Значит,

Функции от линейного оператора

Пусть

(n раз)

Если , то переходим к квазиполиномам:

Источники

• Анин конспект. Гы

Матрица линейного оператора примеры

Построение матрицы по заданной формуле отображения.

Пусть отображение задано с помощью формулы:

то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор , найдём его образ, это будет вектор . Для этого в формуле, задающей образ вектора, полагаем , ,…, . Аналогично находим образы для ,…, . Из координат образа вектора составляем 1-й столбец матрицы линейного оператора, аналогично из координат последующих векторов – остальные столбцы. Рассмотрим на примере.

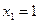
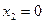
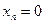
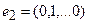
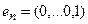
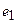
Пример 1. Пусть оператор задан с помощью формулы:

.

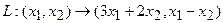
Прежде всего, докажем, что это отображение – действительно линейный оператор.

Отобразим сумму векторов:

Теперь каждую координату получившегося вектора можем преобразовать:

.

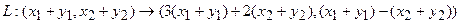
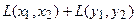
Аналогично для умножения на константу:

Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x₁ = 1, x₂ = 0, а затем x₁ = 0, x₂ = 1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1).

Поэтому матрица линейного оператора будет иметь вид:

.

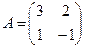
Аналогичным способом решается задача и для 3 и большего количества переменных.

Пример 2. .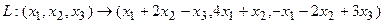

Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3).

Матрица линейного оператора:

.

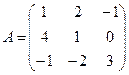
2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается.

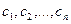
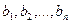
Если задана система из n векторов, образующих базис, и какая-нибудь произвольная система n векторов (возможно, линейно-зависимая), то однозначно определён линейный оператор, отображающий каждый вектор первой системы в соответствующий вектор второй системы.

Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.

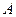
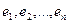
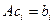
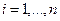
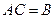
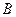
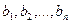
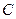
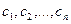
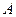
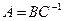
Пусть – матрица оператора в базисе . По условию, для всех индексов . Данные n равенств можно записать в виде одного матричного равенства: , при этом столбцы матрицы – это векторы , а столбцы матрицы – векторы . Тогда матрица может быть найдена в виде .

Пример. Найти матрицу линейного оператора, отображающего базис

в систему векторов .

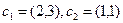
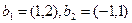
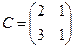
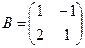
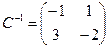
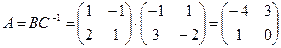
Здесь , , , и получаем:

.

Проверка осуществляется умножением получившейся матрицы на каждый вектор: .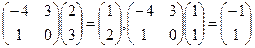

Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач.

2.3. Прочие способы нахождения матрицы оператора.

Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2.

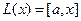
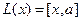
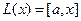
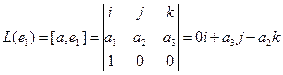
Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида и . Построим матрицу одного из этих операторов, . Для этого найдём образы всех трёх базисных векторов линейного пространства.

.

Аналогично, ,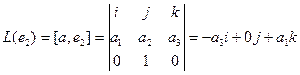

.

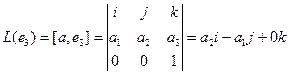
Координаты полученных векторов запишем в виде столбцов матрицы оператора.

Матрица оператора: .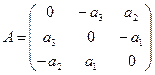

Аналогично можно построить матрицу линейного оператора :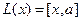

.

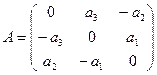
Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n + 1. Возьмём в качестве базиса элементы , , ,…, .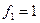

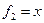
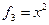
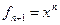
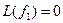
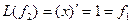
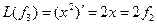
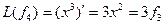
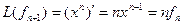
, , , аналогично получим ,…, .

Матрица этого линейного оператора:

Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10219 – | 7588 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Матрица линейного оператора

Определение 1. Если задан закон, который каждому вектору x?? ставит в соот ветствие вектор y . то говорят, что в линейном пространстве ? задан оператор A , при этом пишут:

Определение 2. Оператор A называется линейным, если для любых x 1 ?? и x 2 ?? и произвольного числа ? выполняются условия:

Рассмотрим теперь в евклидовом пространстве E n базис e 1 ,e 2 . e n и пусть в этом пространстве определён линейный оператор A : y = A x .

Разложим векторы x и y по базису e 1 ,e 2 . e n :

В силу линейности оператора A можно написать

Заметим, что каждый вектор 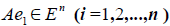, следовательно, его также можно разложить по базису e 1 ,e 2 . e n , т.е.

В силу единственности разложения по данному базису мы можем при равнять коэффициенты при базисных векторах в правых частях формул (1) и (2); тогда получим:

Получили, что линейному оператору A в данном базисе соответствует квадратная матрица

которая называется матрицей линейного оператора A , i -й столбец которой состоит из координат вектора Ae i (i = 1,2. n ) относительно данного базиса. Отметим, что матрица A оператора A зависит от выбора базиса e 1 ,e 2 . e n .

Итак, мы показали, что всякому линейному оператору A в евклидовом пространстве E n соответствует матрица A ; можно доказать и обратное утверждение: всякую квадратную матрицу A можно рассматривать как матрицу некоторого линейного оператора A в данном базисе e 1 ,e 2 . e n .

Представляют интерес невырожденные линейные операторы, т.е. такие операторы, матрицы которых имеют обратную A -1 , т.е. также являются невырожденными. В этом случае каждому вектору y (образу), определённому соотношением, отвечает единственный вектор x (прообраз) и при этом имеет место матричное равенство: X = A -1 ? Y .

Примеры линейных операторов

1. В пространстве 2-мерных векторов линейным оператором является правило

связывающее вектор-прообраз 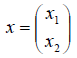с вектором-образом

2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого простран ства его производную функцию.

3. В пространстве многочленов P n (t) линейным оператором является операция умножения многочлена на независимую переменную t .

Пример: Известны образы базисных векторов E 3 под действием оператора A :

Найти матрицу этого оператора в исходном базисе.

Решение: По определению y = A x, значит в матричном виде можно записать, что A = X -1 Y . Для нашего примера получаем

Действия над операторами

Сложение линейных операторов. Пусть x?E n , A и B – два линейных оператора в этом пространстве.

Определение 1. Суммой линейных операторов A и B в E n называется оператор C, определяемый равенством Cx = A x + Bx , где x – любой вектор из E n .

Сумма линейных операторов является линейным оператором, причём его матрица C = A + B, где A и B – матрицы линейных операторов A и B .

Умножение линейного оператора на число. Пусть x?E n , линейный оператор A определён в E n , ? – некоторое число.

Определение 2. Произведением линейного оператора A на число ? называется оператор ?A , определяемый равенством .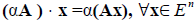

?A является линейным оператором, а матрица этого линейного оператора получается из матрицы A умножением её на число ? , т.е. она равна ? ? A.

Умножение линейных операторов. Пусть x? E n , y ? E n , z ? E n и кроме того в E n определены линейные операторы A и B таким образом, что y = Bx, z = A y .

Определение 3. Произведением A ? B линейных операторов A и B называется оператор C, определяемый соотношением Cx = A (Bx) .

Таким образом, перемножение линейных операторов состоит в последовательном их применении по отношению к вектору x .

Рассмотрим матрицы – столбцы:

и обозначим через A, B и C – соответственно матрицы линейных операторов A, B и C. Тогда Z = A ? (B ? X) = (A ? B) ? X = C ? X , таким образом, C = A ? B, т.е. матрица произведения линей ных операторов также является линейным оператором.

a) (A ? B)(x + y) = A (B(x + y)) = A (Bx + By) = A (Bx) + A (By) = = (A ? B) ? x + (A ? B) ? y

б) (A ? B)(? x) = A (B(? x)) = A (?Bx) =?A (Bx) =? (A ? B)x

Свойства умножения линейных операторов вытекают из свойств умножения матриц.

Определение 4. Линейные операторы A и В называются равными, если 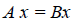. Равенство операторов обозначается как A = B .

Определение 5. Оператор E называется единичным (или тождественным) оператором, если каждому элементу x линейного пространства 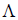он ставит в соответствие тот же самый элемент, то есть

1. Понятие линейного оператора

Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 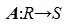, сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.

Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x₁ и x₂ пространства R и любого λ из числового поля K выполняются соотношения

Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.

Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы и соответственно. Пусть задано отображение

где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:

Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов и в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.

Пусть x − произвольный элемент в R. Тогда

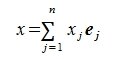(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

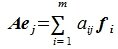(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

Сделаем следующее обозначение:

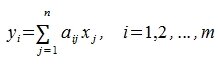(6)

Тогда равенство (5) примет следующий вид:

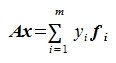(7)

Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты y_i, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента x_j, j=1,2. n с коэффициентами a_ij i=1,2. m; j=1,2. n.

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.

Применим оператор C к базисному вектору e_j, тогда:

Cej= Aej+ Bej=	n	(aij+bij) ej
∑
j= 1

Следовательно оператору C отвечает матрица 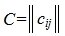,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.

Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:

Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.

Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:

Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.

Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.

8. Образ линейного оператора

Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).

Ядро и образ линейного отображения

Ядром линейного отображения называется множество таких векторов , что , т.е. множество векторов из , которые отображаются в нулевой вектор пространства . Ядро отображения обозначается:

Образом линейного отображения называется множество образов всех векторов из . Образ отображения обозначается или

Заметим, что символ следует отличать от — мнимой части комплексного числа.

Примеры ядер и образов линейных отображений

1. Ядром нулевого отображения является все пространство , а образом служит один нулевой вектор, т.е.

2. Рассмотрим отображение , которое ставит в соответствие каждому вектору n-мерного линейного пространства его координатный столбец относительно заданного базиса . Ядром этого отображения является нулевой вектор пространства , поскольку только этот вектор имеет нулевой координатный столбец . Образ преобразования совпадает со всем пространством , так как это преобразование сюръективно (любой столбец из является координатным столбцом некоторого вектора пространства ).

3. Рассмотрим отображение , которое каждому вектору n-мерного евклидова пространства ставит в соответствие алгебраическое значение его проекции на направление, задаваемое единичным вектором . Ядром этого преобразования является ортогональное дополнение — множество векторов, ортогональных . Образом является все множество действительных чисел .

4. Рассмотрим отображение , которое каждому многочлену степени не выше ставит в соответствие его производную. Ядром этого отображения является множество многочленов нулевой степени, а образом — все пространство .

Свойства ядра и образа линейного отображения

1. Ядро любого линейного отображения является подпространством: .

В соответствии с определением требуется доказать, что множество является непустым и замкнутым относительно операций сложения векторов и умножения вектора на число. В самом деле, из однородности отображения следует, что

т.е. нулевой вектор отображается в нулевой вектор . Следовательно, ядро любого линейного отображения не является пустым и содержит, по крайней мере, нулевой элемент: . Покажем, что множество замкнуто по отношению к операциям сложения векторов и умножения вектора на число. Действительно:

Следовательно, множество является линейным подпространством пространства .

2. Образ любого линейного отображения является подпространством: .

В самом деле, докажем, например, замкнутость множества по отношению к операции умножения вектора на число. Если , то существует вектор такой, что . Тогда , то есть .

Поскольку ядро и образ линейного отображения являются линейными подпространствами (свойства 1 и 2), можно говорить об их размерностях.

Дефектом линейного отображения называется размерность его ядра: , а рангом линейного отображения — размерность его образа: .

3. Ранг линейного отображения равен рангу его матрицы (определенной относительно любых базисов).

В самом деле, если любой базис пространства , то . Поэтому максимальное число линейно независимых векторов системы (ранг системы векторов) равно максимальному числу линейно независимых столбцов матрицы отображения, т.е. рангу матрицы: .

4. Линейное отображение инъективно тогда и только тогда, когда , другими словами, когда дефект отображения равен нулю: .

Действительно, образом нулевого вектора служит нулевой вектор . Поэтому, если отображение инъективно, то ядро содержит только нулевой вектор , иначе два разных вектора имели бы один и тот же образ . Обратно, при условии разные векторы не могут иметь одинаковые образы , так как в этом случае из равенств , следует, что ненулевой вектор (приходим к противоречию).

5. Линейное отображение сюръективно тогда и только тогда, когда , другими словами, когда ранг отображения равен размерности пространства образов: .

6. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда и одновременно.

Теорема (9.1) о размерностях ядра и образа. Сумма размерностей ядра и образа любого линейного отображения равна размерности пространства прообразов:

Действительно, пусть . Выберем в подпространстве базис и дополним его векторами до базиса всего пространства . Покажем, что векторы образуют базис подпространства .

Во-первых, , так как образ любого вектора линейно выражается через векторы

Во-вторых, образующие линейно независимы. Если их линейная комбинация равна нулевому вектору:

то вектор принадлежит ядру (его образ — нулевой вектор). Однако, по построению этот вектор принадлежит алгебраическому дополнению . Учитывая, что , заключаем: . Получили разложение нулевого вектора по линейно независимой системе векторов, значит, все коэффициенты . Поэтому равенство справедливо только для тривиальной линейной комбинации, т.е. система векторов линейно независимая.

Таким образом, векторы образуют базис подпространства , а его размерность определяется количеством базисных векторов, т.е. , что равносильно (9.3).

Следствие. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда обратима его матрица (определенная относительно любых базисов).

Действительно, для обратимости преобразования (см. свойство 6) его матрица (размеров ) должна удовлетворять условиям (см. свойства 3,4,5):

Тогда по теореме 9.1 заключаем, что , т.е. матрица — квадратная n-го порядка и невырожденная , что и требовалось доказать.

Обратимые линейные отображения называются также невырожденными (имея в виду невырожденность их матрицы).

Линейные операторы

1. Понятие линейного оператора

Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 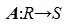, сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.

Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x₁ и x₂ пространства R и любого λ из числового поля K выполняются соотношения

Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.

Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы и соответственно. Пусть задано отображение

где A — m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:

Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов и в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.

Пусть x − произвольный элемент в R. Тогда

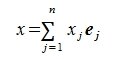(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

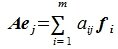(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

Сделаем следующее обозначение:

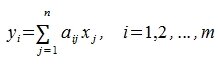(6)

Тогда равенство (5) примет следующий вид:

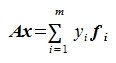(7)

Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты y_i, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента x_j, j=1,2. n с коэффициентами a_ij i=1,2. m; j=1,2. n.

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Пусть A и B два линейных оператора действующих из R в S и пусть A и B — mxn − матрицы соответствующие этим операторам.

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.

Применим оператор C к базисному вектору e_j, тогда:

Cej= Aej+ Bej=	n	(aij+bij) ej
∑
j= 1

Следовательно оператору C отвечает матрица 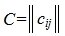,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.

Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:

Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.

Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:

Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.

Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.

8. Образ линейного оператора

Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).

Головизин
В.В. Лекции по алгебре и геометрии.
Лекция 26. 6

Лекции
по алгебре и геометрии. Семестр 2.

Лекция
26. Линейные отображения векторных
пространств.

Краткое содержание: определение линейного
отображения (гомоморфизма) векторных
пространств, примеры и их простейшие
свойства, ядро и образ линейного
отображения, теорема о размерности ядра
и образа, матрица линейного отображения
и ее изменение при изменении базиса,
векторное пространство гомоморфизмов,
линейный оператор (эндоморфизм) и его
матрица, кольцо эндоморфизмов, матрица
как форма задания линейного отображения.

п.1.
Линейное отображение векторных
пространств.

Определение.
Пусть V и W
– произвольные векторные пространства
над полем K. Отображение

называется линейным отображением или
гомоморфизмом векторного пространства
V в векторное пространство
W, если оно обладает
свойствами:

1)
свойство аддитивности:
,
;

2)
свойство однородности:
,
.

Если, кроме этого,
гомоморфизм f является
биекцией, то он называется изоморфизмом
векторных пространств V
и W.

Определение.
Если существует изоморфизм
,
то векторные пространства V
и W называются изоморфными.

Обозначение
изоморфных векторных пространств:

.

Теорема.
Отношение изоморфизма на множестве
всех векторных пространств над полем
K является отношением
эквивалентности.

Доказательство
оставляется читателю.

Обозначение.

Пусть V
и W – произвольные
фиксированные векторные пространства
над полем K.

Множество
всех линейных отображений (гомоморфизмов)
из пространства V в
пространство W обозначается

или просто
.

Определение.
Линейное отображение из векторного
пространства V в себя:

называется линейным оператором или
эндоморфизмом векторного пространства
V. Биективный эндоморфизм
называется автоморфизмом векторного
пространства V.

Обозначение.

Множество всех
линейных операторов (эндоморфизмов)
векторного пространства V
над полем K обозначается

или
.
Множество всех автоморфизмов векторного
пространства V обозначается
.

Говорят также, что
линейный оператор действует на векторном
пространстве V.

п.2.
Примеры линейных отображений.

Пример
1. Пусть V и W
– произвольные векторные пространства
над полем K. Зададим
отображение

с
помощью правила:

положим
.

Это
отображение называется нулевым
отображением.

Очевидно, что
нулевое отображение векторного
пространства V в векторное
пространство W является
линейным, поэтому оно называется нулевым
гомоморфизмом.

Пример
2. Зададим отображение

с
помощью правила:

положим
.

Это
отображение называется тождественным
отображением (тождественным оператором)
векторного пространства V
в себя.

Легко проверить,
что тождественное отображение векторного
пространства V в себя
является линейным.

Действительно,
,

.

Отсюда,

и
.

Тождественный
оператор называется также тождественным
или единичным эндоморфизмом и часто
обозначается буквой Е.

Пример
3. Пусть А – матрица размера

над полем K,

и

– арифметические векторные пространства
столбцов высоты

и

соответственно над полем K.
Устроим отображение

с
помощью правила:

положим
.

Проверим, что
данное отображение является линейным.
Пусть
.
Тогда

.

Здесь мы
воспользовались свойствами действий
с матрицами, а именно законом
дистрибутивности умножения матриц
относительно их сложения.

Далее,
,

.

Таким образом,
умножение матрицы на столбец соответствующей
высоты обладает свойствами аддитивности
и однородности и, следовательно, является
линейным отображением (линейным
оператором, если
).

Пример
4. Пусть V – произвольное
векторное пространство над полем K
размерности n и

–пространство столбцов высоты n.
Зафиксируем в пространстве V
какой-нибудь базис. Отображение

,

которое
каждому вектору

ставит в соответствие упорядоченный
набор

его
координат относительно данного базиса
является биективным линейным отображением
или изоморфизмом векторных пространств.
(См. лекцию 24.)

Пример
5. Пусть
–
множество векторов на плоскости, как
направленных отрезков. Устроим отображение

по
правилу:

каждому
вектору

поставим в соответствие вектор
,
который получается из вектора

поворотом вокруг своего начала на угол

против часовой стрелки.

В
наших обозначениях:

.

Легко
видеть, что это отображение является
линейным:
,
,

и
.

(Чтобы
увидеть это, сложите два вектора по
правилу параллелограмма и поверните
полученный параллелограмм на заданный
угол против часовой стрелки. Аналогично
проверяется свойство однородности.)

Таким образом,
данное отображение является линейным
оператором, который называют оператором
поворота на заданный угол в пространстве
векторов на плоскости.

п.3.
Простейшие свойства линейных отображений.

Теорема.
Пусть

линейное отображение векторного
пространства V в векторное
пространство W над полем
K. Тогда справедливы
следующие утверждения:

1)
;

2)
,
;

3)
,
,

.

Доказательство
оставляется читателю.

Замечание. При
проверке линейности отображения, полезно
проверять свойство (1):
,
т.к. оно легко проверяется и если оно не
выполняется, то данное отображение не
является линейным. Например, отображение
из пространства столбцов высоты 2 в себя
по правилу:

не
является линейным, т.к.

.

п.4.
Ядро и образ линейного отображения.

Определение.
Пусть

линейное отображение векторных
пространств. Ядром линейного отображения
f называется множество:

.

Образом
линейного отображения f
называют множество:

.

Другими словами,
ядро линейного отображения состоит из
векторов пространства V,
которые отображаются в нулевой вектор
пространства W, а образ
линейного отображения это просто
множество значений функции f.

Если
f – линейный оператор, то
говорят об ядре и образе линейного
оператора.

Найдем ядро и образ
линейных отображений, рассмотренных в
примерах пункта 2.

Пример
1. Так как нулевое отображение

все векторы пространства

отображает в нулевой вектор пространства
,
то из определения ядра и образа линейного
отображения сразу же следует, что

и
.

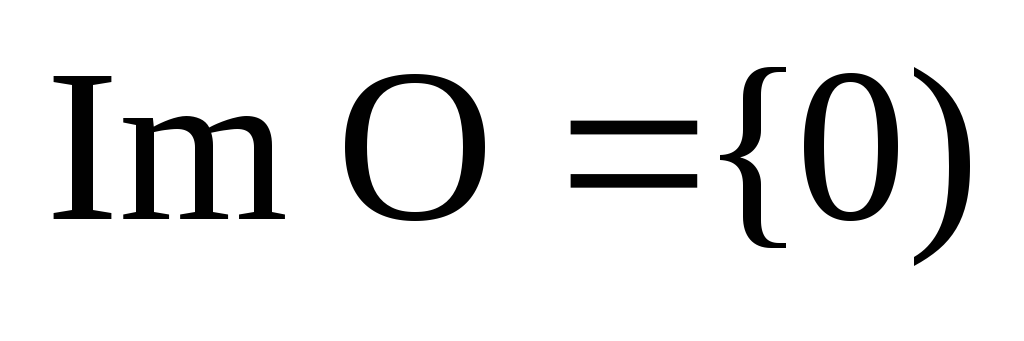
Пример
2. Пусть
:
,
.
Тогда, очевидно,
.

Пример
3. Пусть
:
,
,
где А – матрица размера

над полем
.
Тогда,

–
множество решений
однородной системы из

линейных уравнений с

неизвестными, где А – матрица коэффициентов
системы;

.

Изучим это множество
подробнее. Обозначим через
–
столбцы матрицы А,

– столбец неизвестных. Тогда произведение
матрицы А на столбец Х можно представить
в виде:
–
линейная оболочка, натянутая на столбцы
матрицы А.

Следовательно,
образ этого линейного отображения есть
линейная оболочка, натянутая на столбцы
матрицы А:

.

Замечание. Обычно
линейное отображение

обозначают не буквой
,
а той же буквой, что и матрицу, с помощью
которой определяется это отображение:

,
где
,

т.е.
это отображение, которое каждому столбцу

ставит в соответствие столбец
,
так что

.

Обычно столбец

обозначают буквой
,
т.е.
.
И вместо того, чтобы говорить о ядре и
образе линейного отображения
,
говорят: ядро матрицы А, образ матрицы
А, молчаливо подразумевая под этим ядро
и образ соответствующего линейного
отображения.

(Заметим, в скобках,
что вот такие «молчаливые подразумения»,
о которых не пишут, и, даже не говорят,
полагая их очевидными, составляют одну
из трудностей при изучении математики.
Сами же математики признают, что, бывает,
две пропущенные подряд «очевидности»
составляют почти непреодолимую
трудность.)

Пример
4. Пусть

– отображение, которое каждому вектору
пространства V ставит в
соответствие столбец его координат,
относительно некоторого фиксированного
базиса пространства V.
Очевидно, что ядро этого отображения
нулевое, т.е. состоит из одного нулевого
вектора, а образ этого отображения
совпадает с пространством столбцов
:

.

Пример
5. Легко видеть, что
,
.

Теорема.
Пусть

линейное отображение векторных
пространств. Тогда ядро линейного
отображения

является векторным подпространством
пространства
,
а образ

– векторным подпространством пространства
.

Доказательство.
1) Пусть
,
.
Тогда
.
Но f – гомоморфизм,
поэтому,

,

.

2)
.
Так как f – гомоморфизм,
то

,

,
.

Теорема
доказана.

Теорема
(О размерности ядра и образа линейного
отображения.) Пусть

линейное отображение векторных
пространств. Тогда

.

Доказательство.
Пусть

и

– базис ядра. Так как

– подпространство пространства V,
то дополним базис ядра до базиса
пространства V. Пусть

– базис пространства V и

.

Докажем, что

– базис
,
откуда сразу же будет следовать теорема.

Докажем, что

является порождающей системой
подпространства
.
Пусть

– произвольный вектор подпространства
.
Тогда
.
Разложим вектор х по базису

пространства V:

,

где
.
Отсюда,

,
ч.т.д.

Здесь, мы
воспользовались свойством линейности
гомоморфизма f и тем, что
,
откуда

.

Докажем, что

является линейно независимой системой.
Пусть

.

По
свойствам линейности,

.

Разложим
вектор v по базису ядра:
,
откуда получаем равенство:

.

Так
как

– базис пространства V,
то все коэффициенты в этой линейной
комбинации равны нулю, т.е. система

может представлять нулевой вектор
только тривиально и она является линейно
независимой, ч.т.д.

Теорема
доказана.

п.5.
Матрица линейного отображения.

Пусть

– линейное отображение векторного
пространства V в векторное
пространство W над полем
K,
–
базис пространства V,

–
базис пространства
W,

– произвольный вектор,

– его образ в пространстве W.

Поставим задачу
нахождения вектора f(x)
для заданного вектора х.

Разложим вектор
х по данному базису:

.

Здесь

– координаты вектора х относительно
базиса

пространства V. Так как f
– линейное отображение, то

.
(1)

Из
этого равенства мы видим, что если мы
знаем образы базисных векторов
,
то тем самым мы найдем образ f(x)
любого вектора х из пространства V.

Разложим образы
базисных векторов
,

по базису

пространства W:

(2)

Определение.
Матрица

,

взятая
из равенств (2), называется матрицей
линейного отображения

относительно базисов

и

пространств V и W
соответственно.

Замечание.
Равенства (2) удобно записывать в матричной
форме:

(3)

Здесь,
при умножении строки

на матрицу А по правилам умножения
матриц, получаем строку длины n,
так что равенство (3) есть равенство двух
строк одинаковой длины, которое мы
рассматриваем как равенство матриц.
Две строки равной длины равны, если
равны ее соответствующие компоненты.
Приравнивая соответствующие компоненты,
получаем равенства (2).

Обозначение.
Удобно снабжать матрицу линейного
отображения двумя нижними индексами:
.

Теперь
равенство (3) можно записать в виде:

.
(4)

Равенство (1) тоже
можно записать в матричной форме:

(5)

Теперь,
подставим равенства (2) в равенство (1).
Но выполним эту подстановку в матричной
форме, т.е. подставим равенство (4) в
равенство (5). Получаем:

(6)

Обозначим
.
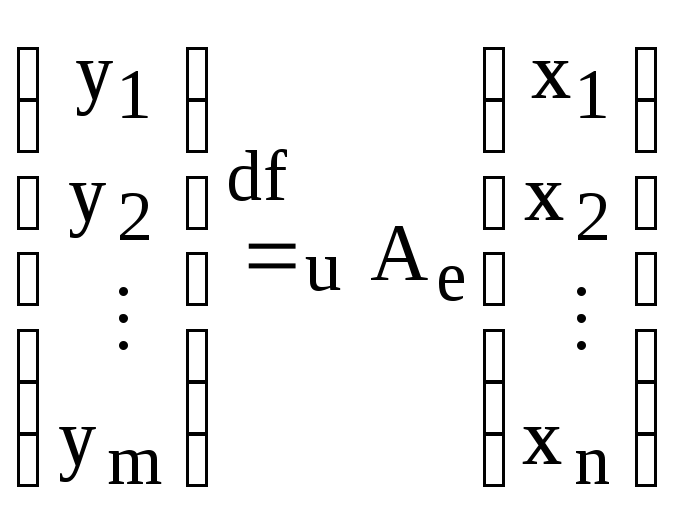
Тогда,

,

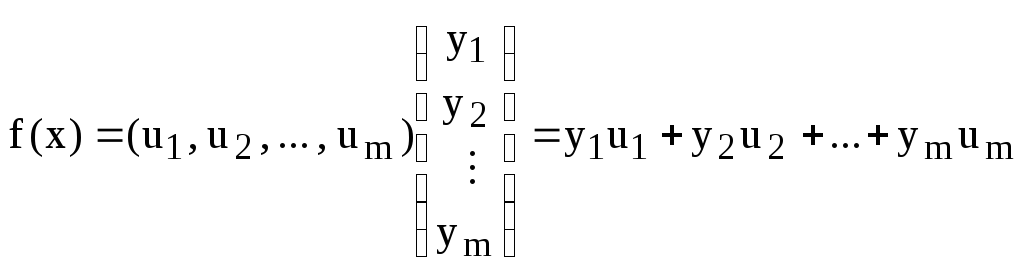
где
–
координаты вектора

относительно базиса
.

Таким образом, мы
выполнили поставленную задачу нахождения
координат вектора

и тем самым доказали следующую теорему.

Теорема.
Пусть

– линейное отображение векторных
пространств,

и

– базисы

и

соответственно.

Пусть

– координаты вектора
,

– координаты вектора
.
Тогда

,
(7)

где
А – матрица данного линейного отображения.

п.6.
Матрица линейного оператора.

Определение.
Пусть

– линейный оператор (эндоморфизм),
действующий на пространстве V
над полем K. Пусть
–
базис пространства V,

– произвольный вектор,

– его образ в пространстве V.
Разложим вектор х по данному базису:

,

где

– координаты вектора х относительно
базиса

пространства V. Так как f
– линейное отображение, то

.

Разложим образы
базисных векторов
,
,
по базису

пространства V :

.
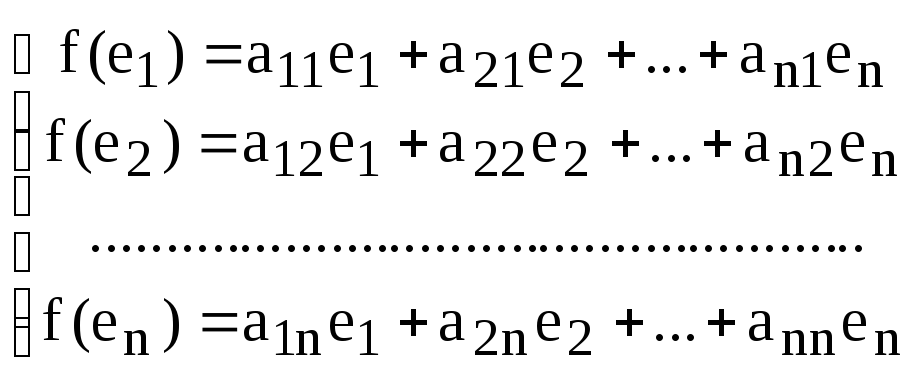
(8)

Определение.
Матрица

,

называется
матрицей линейного оператора

относительно базиса

пространства V.

Равенства (8) в
матричной форме:

.
(9)

Аналогично
предыдущей доказывается теорема.

Теорема.
Пусть

– линейный оператор,

– базис V.

Пусть

– координаты вектора
,

– координаты вектора
.
Тогда

,
(10)

где
А – матрица данного линейного оператора.

п.7.
Изменение матрицы линейного отображения
и линейного оператора при изменении
базиса.

Теорема.
Пусть V, W –
векторные пространства над полем K,
,

– два базиса пространства
,
,

– два базиса пространства
.
Пусть С – матрица перехода от базиса

к базису
,
–
матрица перехода от базиса

к базису
.
Пусть А – матрица линейного отображения
,
относительно базисов

и
,

– матрица этого же линейного отображения

относительно базисов

и
.

Пусть — линейный оператор действующий в линейном пространстве V (комплексном или вещественном)

Определение: Совокупность всевозможных векторов вида называется образом оператора A и обозначается ImA. Таким образом .

Определение: Совокупность всевозможных векторов для которых называется ядром оператора A и обозначается KerA. Таким образом .

Утверждение: образ и ядро линейного оператора А являются подпространствами линейного пространства V.

Доказательство: В самом деле в силу линейности оператора А имеем:

1) тогда и т. к то

и т. к. , то является подпространством пространства V.

2) отсюда .

является подпространством пространства V. #

Пример:

Пусть V – n мерное комплексное или вещественное линейное пространство.

1) Тождественный оператор , при этом Ax = Ix = X, тогда ImA=ImI=V, KerA=KerI={θ}

/ ядро состоит из единственного нулевого элемента /

2) Нулевой оператор, тогда

3) Рассмотрим оператор дифференцирования на пространстве многочленов степени не выше N, тогда отсюда. Видно, что во всех приведенных примерах справедливо:

, что не является случайным.

Теорема (о сумме размерностей образа и ядра линейного оператора) :

Пусть A — линейный оператор, действующий в линейном пространстве V. Тогда сумма размерностей образа и ядра оператора равна размерности данного линейного пространства, т. е.

Доказательство:

Пусть , причем

Выберем в пространстве V произвольный базис . Поскольку по определению , то можно записать, что линейная оболочка, порождаемая совокупностью образов базисных векторов , причем , где R – максимальное число л. н.з. векторов в системе. Но координаты именно этих векторов стоят в столбцах матрицы линейного оператора А в базисе, поэтому .

Рассмотрим ядро оператора А: .

В выбранном базисе равенству соответствует однородная СЛАУ:, которая, как известно, имеет (N—R) л. н.з. решений, образующих ФСР. Поскольку неизвестными данной системы являются координаты векторов, составляющих KerA, то отсюда заключаем, что dim(KerA)=N—R. В результате получаем, что

Определение: Размерность образа оператора называется рангом оператора, размерность ядра оператора называется дефектом оператора.

Определение: Линейный оператор называется невырожденным, если в произвольном базисе (E) данного линейного пространства V Оператор А имеет невырожденную матрицу .

Следствие: Если А – невырожденный линейный оператор, то его образ совпадает со всем пространством, в котором этот оператор действует.

Доказательство: Если , то по предыдущей теореме запишем . По Свойству 40 невырожденных операторов (докажем позже в параграфе 12 главе 7) равенство возможно только при отсюда откуда . Т. к. , то отсюда следует, что .

Определение: Подпространство L пространства V называется инвариантным относительно линейного оператора А, если .

Теорема (об инвариантности образа и ядра линейного оператора):

Образ и ядро линейного оператора А являются подпространствами инвариантными относительно оператора А.

Доказательство:

1) Пусть , т. к. то и поэтому , т. е. подпространство ImA является инвариантным относительно оператора А.

2) Пусть . Тогда, т. у. а значит подпространство KerA инвариантно относительно оператора А.

Следующая >