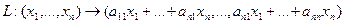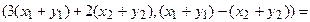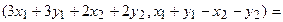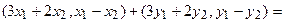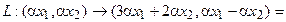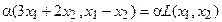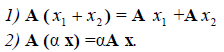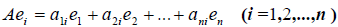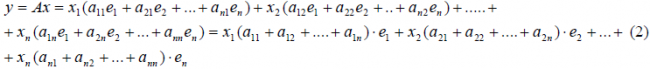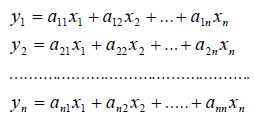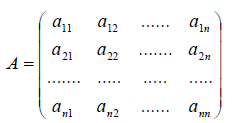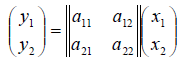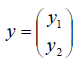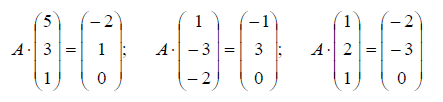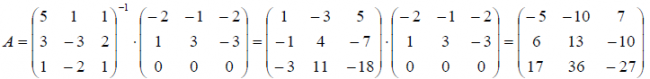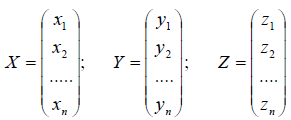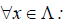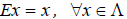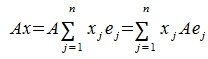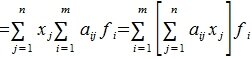Как найти образ вектора при линейном операторе - Исправление недочетов и поиск решений вместе с Examum.ru

Линейный
оператор ,
действующий из пространства
в пространство ,
ставит в соответствие каждому вектору

определенный вектор
из .
При этом вектор
называется образом
вектора
,
а вектор
— прообразом
вектора

при отображении .

Пусть

и
— некоторые базисы линейных пространств

и
соответственно. Тогда ,

и координаты вектора — образа
связаны с координатами вектора — прообраза

соотношением

(7.2.1)

в
котором
— матрица линейного оператора
в паре базисов
и .

В
случае, когда пространства
и
совпадают, базисы
и
также совпадают, и формула (7.2.1) принимает
вид

(7.2.2)

Образом
(областью
значений)
линейного
оператора

называется
множество всех элементов
вида .
Образ линейного оператора является
подпространством пространства
и обозначается .
Размерность образа называется рангом
оператора
и обозначается .

Ядром
линейного оператора

называется
множество всех векторов пространства
,
которые переводятся оператором
в нулевой вектор пространства .
Ядро линейного оператора является
подпространством пространства
и обозначается .
Размерность ядра называется дефектом
оператора
и обозначается .

Сумма
ранга и дефекта оператора

равна размерности пространства
.

Ранг
линейного оператора равен рангу матрицы
этого оператора.

Базис
системы векторов — столбцов матрицы
линейного оператора
образует систему координатных столбцов
базиса образа .
Базис подпространства решений однородной
системы линейных алгебраических
уравнений с матрицей оператора
образует базис ядра .

Пример
1.
Из пространства
с базисом
в пространство
с базисом
действует линейный оператор ,
имеющий в данной паре базисов матрицу
.
Найдите столбец координат в базисе
образа вектора
и столбец координат в базисе
прообраза вектора .

Решение.
Столбец координат образа вектора
в базисе находим
непосредственно по формуле (7.2.1):

Для
определения прообраза вектора
по той же формуле (7.2.1) имеем

или,
что то же самое,

Отсюда
находим все прообразы
вектора ,
где
— свободная переменная, принимающая
произвольные значения.

Пример
2.
В пространстве с
базисом линейный
оператор
переводит векторы ,
в
векторы ,

соответственно. Найдите матрицу оператора
в
базисе .

Решение.
Пусть —
матрица оператора в
базисе .
Тогда из условий ,

по формуле (7.2.2) имеем ,

или,
в подробной записи,

Отсюда
получаем
Следовательно,
.

Пример
3.
Найдите базис ядра и базис образа
линейного оператора пространства ,
если этот оператор задан матрицей .

Решение.
При помощи элементарных преобразований
над строками матрицы
приведём её к ступенчатому виду:

Отсюда
следует, что .
Базис составляют,
например, векторы
и .

Дефект
оператора найдём по формуле

т.е.
фундаментальная система решений
однородной системы линейных алгебраических
уравнений с матрицей
будет состоять из одного вектора. Общее
решение однородной системы можно
записать в виде .
Полагая
получаем базисный вектор .

7.2.1.
Линейный оператор переводит
вектор
в вектор.
Найдите образ вектора
и прообраз вектора ,
если

,
;

,
.

7.2.2.
Линейный оператор в
паре базисов и

имеет матрицу .
Найдите прообраз вектора ,
если

,
;

б)
,
;

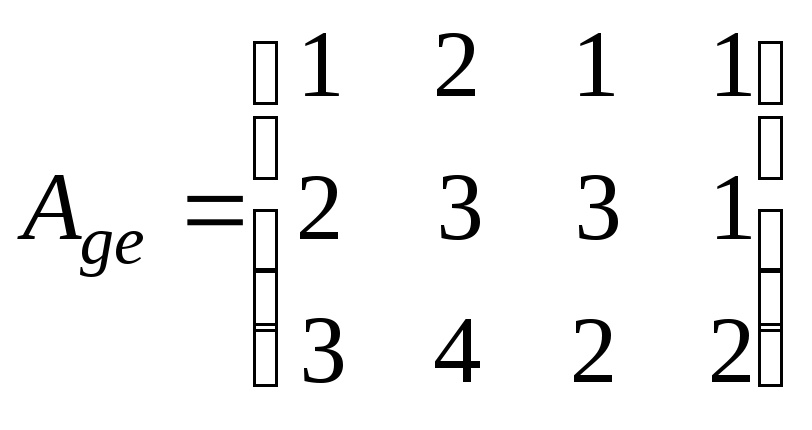
в)
,
.

7.2.3.
Выясните, существует ли линейный оператор
двумерного пространства, переводящий
векторы ,

соответственно в векторы ,
,
и найдите матрицу этого оператора в
базисе ,
:

а)

б)

в)

7.2.4.
Выясните, существует ли линейный оператор
трехмерного пространства, переводящий
векторы ,
,

соответственно в векторы ,
,
,
и найдите матрицу этого оператора в том
же базисе, в котором даны координаты
всех векторов:

а)

б)

7.2.5.
Для указанных линейных операторов
пространства
найдите дефект и ранг, а также постройте
базисы ядра и образа. Каждый оператор
описывается своим действием на
произвольный вектор :

а)

б)

в)

7.2.6.
Найдите образ и ядро оператора
дифференцирования в пространстве .

7.2.7.
В пространстве
рассмотрите разностный
оператор

где

— фиксированное
число, отличное от нуля. Найдите его
образ и ядро.

7.2.8.
Найдите образ и ядро оператора
проектирования (см. задачу 7.1.2) на
параллельно
и оператора отражения (см. задачу 7.1.3) в

параллельно .

7.2.9.
Найдите базис ядра и базис образа
линейного
оператора из ,
заданного в некотором базисе матрицей
:

а)
;
б)
;
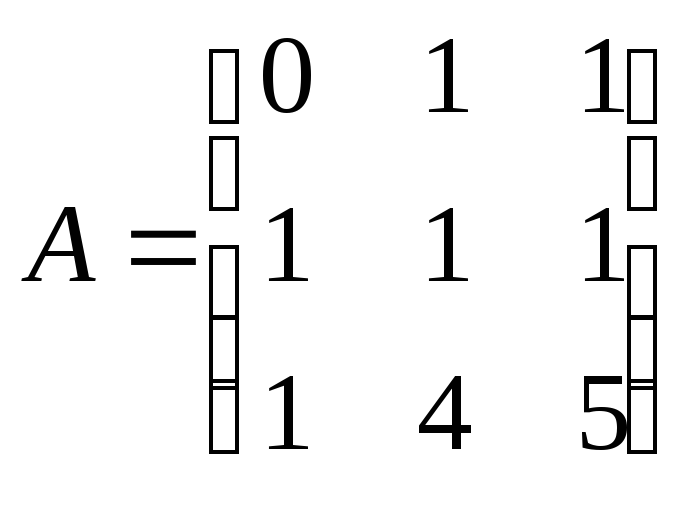
в)
.

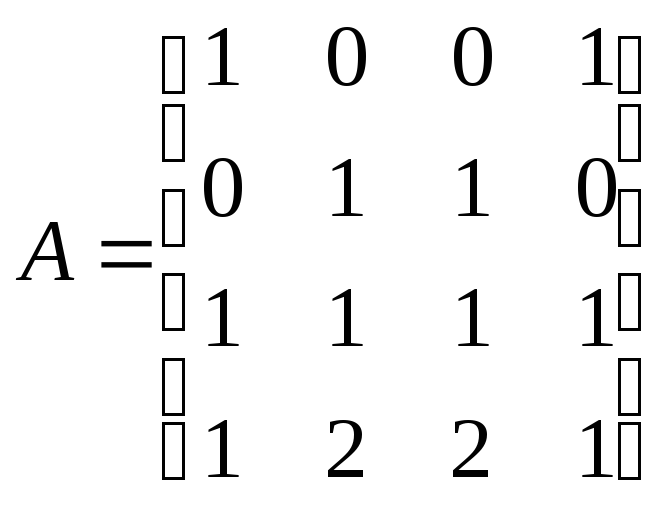
7.2.10.
Найдите размерность линейного пространства

всех линейных операторов, действующих
в
— мерном линейном пространстве
и постройте базис пространства .

Соседние файлы в папке Задачник-2

Источник

Матрица линейного оператора примеры

Построение матрицы по заданной формуле отображения.

Пусть отображение задано с помощью формулы:

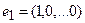
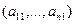
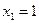
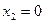
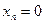
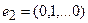
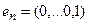
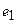
то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор , найдём его образ, это будет вектор . Для этого в формуле, задающей образ вектора, полагаем , ,…, . Аналогично находим образы для ,…, . Из координат образа вектора составляем 1-й столбец матрицы линейного оператора, аналогично из координат последующих векторов – остальные столбцы. Рассмотрим на примере.

Пример 1. Пусть оператор задан с помощью формулы:

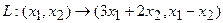
Прежде всего, докажем, что это отображение – действительно линейный оператор.

Отобразим сумму векторов:

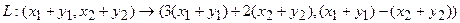
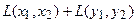
Теперь каждую координату получившегося вектора можем преобразовать:

Аналогично для умножения на константу:

Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x₁ = 1, x₂ = 0, а затем x₁ = 0, x₂ = 1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1).

Поэтому матрица линейного оператора будет иметь вид:

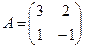
Аналогичным способом решается задача и для 3 и большего количества переменных.

Пример 2. .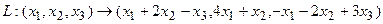

Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3).

Матрица линейного оператора:

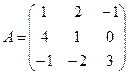
2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается.

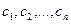
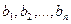
Если задана система из n векторов, образующих базис, и какая-нибудь произвольная система n векторов (возможно, линейно-зависимая), то однозначно определён линейный оператор, отображающий каждый вектор первой системы в соответствующий вектор второй системы.

Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.

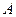
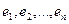
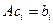
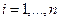
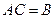
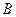
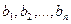
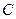
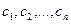
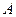
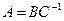
Пусть – матрица оператора в базисе . По условию, для всех индексов . Данные n равенств можно записать в виде одного матричного равенства: , при этом столбцы матрицы – это векторы , а столбцы матрицы – векторы . Тогда матрица может быть найдена в виде .

Пример. Найти матрицу линейного оператора, отображающего базис

в систему векторов .

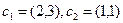
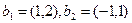
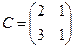
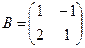
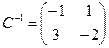
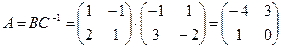
Здесь , , , и получаем:

Проверка осуществляется умножением получившейся матрицы на каждый вектор: .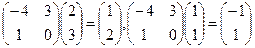

Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач.

2.3. Прочие способы нахождения матрицы оператора.

Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2.

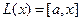
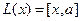
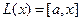
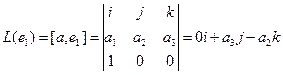
Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида и . Построим матрицу одного из этих операторов, . Для этого найдём образы всех трёх базисных векторов линейного пространства.

Аналогично, ,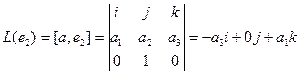

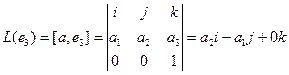
Координаты полученных векторов запишем в виде столбцов матрицы оператора.

Матрица оператора: .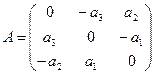

Аналогично можно построить матрицу линейного оператора :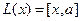

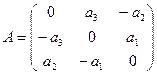
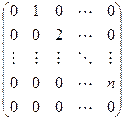
Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n + 1. Возьмём в качестве базиса элементы , , ,…, .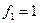

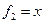
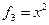
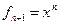
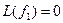
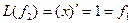
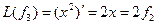
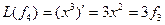
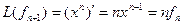
, , , аналогично получим ,…, .

Матрица этого линейного оператора:

Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10219 – | 7588 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Матрица линейного оператора

Определение 1. Если задан закон, который каждому вектору x?? ставит в соот ветствие вектор y . то говорят, что в линейном пространстве ? задан оператор A , при этом пишут:

Определение 2. Оператор A называется линейным, если для любых x 1 ?? и x 2 ?? и произвольного числа ? выполняются условия:

Рассмотрим теперь в евклидовом пространстве E n базис e 1 ,e 2 . e n и пусть в этом пространстве определён линейный оператор A : y = A x .

Разложим векторы x и y по базису e 1 ,e 2 . e n :

В силу линейности оператора A можно написать

Заметим, что каждый вектор 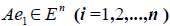, следовательно, его также можно разложить по базису e 1 ,e 2 . e n , т.е.

В силу единственности разложения по данному базису мы можем при равнять коэффициенты при базисных векторах в правых частях формул (1) и (2); тогда получим:

Получили, что линейному оператору A в данном базисе соответствует квадратная матрица

которая называется матрицей линейного оператора A , i -й столбец которой состоит из координат вектора Ae i (i = 1,2. n ) относительно данного базиса. Отметим, что матрица A оператора A зависит от выбора базиса e 1 ,e 2 . e n .

Итак, мы показали, что всякому линейному оператору A в евклидовом пространстве E n соответствует матрица A ; можно доказать и обратное утверждение: всякую квадратную матрицу A можно рассматривать как матрицу некоторого линейного оператора A в данном базисе e 1 ,e 2 . e n .

Представляют интерес невырожденные линейные операторы, т.е. такие операторы, матрицы которых имеют обратную A -1 , т.е. также являются невырожденными. В этом случае каждому вектору y (образу), определённому соотношением, отвечает единственный вектор x (прообраз) и при этом имеет место матричное равенство: X = A -1 ? Y .

Примеры линейных операторов

1. В пространстве 2-мерных векторов линейным оператором является правило

связывающее вектор-прообраз 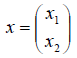с вектором-образом

2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого простран ства его производную функцию.

3. В пространстве многочленов P n (t) линейным оператором является операция умножения многочлена на независимую переменную t .

Пример: Известны образы базисных векторов E 3 под действием оператора A :

Найти матрицу этого оператора в исходном базисе.

Решение: По определению y = A x, значит в матричном виде можно записать, что A = X -1 Y . Для нашего примера получаем

Действия над операторами

Сложение линейных операторов. Пусть x?E n , A и B – два линейных оператора в этом пространстве.

Определение 1. Суммой линейных операторов A и B в E n называется оператор C, определяемый равенством Cx = A x + Bx , где x – любой вектор из E n .

Сумма линейных операторов является линейным оператором, причём его матрица C = A + B, где A и B – матрицы линейных операторов A и B .

Умножение линейного оператора на число. Пусть x?E n , линейный оператор A определён в E n , ? – некоторое число.

Определение 2. Произведением линейного оператора A на число ? называется оператор ?A , определяемый равенством .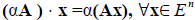

?A является линейным оператором, а матрица этого линейного оператора получается из матрицы A умножением её на число ? , т.е. она равна ? ? A.

Умножение линейных операторов. Пусть x? E n , y ? E n , z ? E n и кроме того в E n определены линейные операторы A и B таким образом, что y = Bx, z = A y .

Определение 3. Произведением A ? B линейных операторов A и B называется оператор C, определяемый соотношением Cx = A (Bx) .

Таким образом, перемножение линейных операторов состоит в последовательном их применении по отношению к вектору x .

Рассмотрим матрицы – столбцы:

и обозначим через A, B и C – соответственно матрицы линейных операторов A, B и C. Тогда Z = A ? (B ? X) = (A ? B) ? X = C ? X , таким образом, C = A ? B, т.е. матрица произведения линей ных операторов также является линейным оператором.

a) (A ? B)(x + y) = A (B(x + y)) = A (Bx + By) = A (Bx) + A (By) = = (A ? B) ? x + (A ? B) ? y

б) (A ? B)(? x) = A (B(? x)) = A (?Bx) =?A (Bx) =? (A ? B)x

Свойства умножения линейных операторов вытекают из свойств умножения матриц.

Определение 4. Линейные операторы A и В называются равными, если 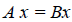. Равенство операторов обозначается как A = B .

Определение 5. Оператор E называется единичным (или тождественным) оператором, если каждому элементу x линейного пространства 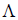он ставит в соответствие тот же самый элемент, то есть

1. Понятие линейного оператора

Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида , сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.

Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x₁ и x₂ пространства R и любого λ из числового поля K выполняются соотношения

Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.

Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы и соответственно. Пусть задано отображение

где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:

Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов и в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.

Пусть x − произвольный элемент в R. Тогда

(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

Сделаем следующее обозначение:

(6)

Тогда равенство (5) примет следующий вид:

(7)

Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты y_i, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента x_j, j=1,2. n с коэффициентами a_ij i=1,2. m; j=1,2. n.

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.

Применим оператор C к базисному вектору e_j, тогда:

Ce_j= Ae_j+ Be_j=	n	(a_ij+b_ij) e_j
∑
j= 1

Следовательно оператору C отвечает матрица ,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.

Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:

Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.

Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:

Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.

Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.

8. Образ линейного оператора

Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).

Ядро и образ линейного отображения

Ядром линейного отображения называется множество таких векторов , что , т.е. множество векторов из , которые отображаются в нулевой вектор пространства . Ядро отображения обозначается:

Образом линейного отображения называется множество образов всех векторов из . Образ отображения обозначается или

Заметим, что символ следует отличать от — мнимой части комплексного числа.

Примеры ядер и образов линейных отображений

1. Ядром нулевого отображения является все пространство , а образом служит один нулевой вектор, т.е.

2. Рассмотрим отображение , которое ставит в соответствие каждому вектору n-мерного линейного пространства его координатный столбец относительно заданного базиса . Ядром этого отображения является нулевой вектор пространства , поскольку только этот вектор имеет нулевой координатный столбец . Образ преобразования совпадает со всем пространством , так как это преобразование сюръективно (любой столбец из является координатным столбцом некоторого вектора пространства ).

3. Рассмотрим отображение , которое каждому вектору n-мерного евклидова пространства ставит в соответствие алгебраическое значение его проекции на направление, задаваемое единичным вектором . Ядром этого преобразования является ортогональное дополнение — множество векторов, ортогональных . Образом является все множество действительных чисел .

4. Рассмотрим отображение , которое каждому многочлену степени не выше ставит в соответствие его производную. Ядром этого отображения является множество многочленов нулевой степени, а образом — все пространство .

Свойства ядра и образа линейного отображения

1. Ядро любого линейного отображения является подпространством: .

В соответствии с определением требуется доказать, что множество является непустым и замкнутым относительно операций сложения векторов и умножения вектора на число. В самом деле, из однородности отображения следует, что

т.е. нулевой вектор отображается в нулевой вектор . Следовательно, ядро любого линейного отображения не является пустым и содержит, по крайней мере, нулевой элемент: . Покажем, что множество замкнуто по отношению к операциям сложения векторов и умножения вектора на число. Действительно:

Следовательно, множество является линейным подпространством пространства .

2. Образ любого линейного отображения является подпространством: .

В самом деле, докажем, например, замкнутость множества по отношению к операции умножения вектора на число. Если , то существует вектор такой, что . Тогда , то есть .

Поскольку ядро и образ линейного отображения являются линейными подпространствами (свойства 1 и 2), можно говорить об их размерностях.

Дефектом линейного отображения называется размерность его ядра: , а рангом линейного отображения — размерность его образа: .

3. Ранг линейного отображения равен рангу его матрицы (определенной относительно любых базисов).

В самом деле, если любой базис пространства , то . Поэтому максимальное число линейно независимых векторов системы (ранг системы векторов) равно максимальному числу линейно независимых столбцов матрицы отображения, т.е. рангу матрицы: .

4. Линейное отображение инъективно тогда и только тогда, когда , другими словами, когда дефект отображения равен нулю: .

Действительно, образом нулевого вектора служит нулевой вектор . Поэтому, если отображение инъективно, то ядро содержит только нулевой вектор , иначе два разных вектора имели бы один и тот же образ . Обратно, при условии разные векторы не могут иметь одинаковые образы , так как в этом случае из равенств , следует, что ненулевой вектор (приходим к противоречию).

5. Линейное отображение сюръективно тогда и только тогда, когда , другими словами, когда ранг отображения равен размерности пространства образов: .

6. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда и одновременно.

Теорема (9.1) о размерностях ядра и образа. Сумма размерностей ядра и образа любого линейного отображения равна размерности пространства прообразов:

Действительно, пусть . Выберем в подпространстве базис и дополним его векторами до базиса всего пространства . Покажем, что векторы образуют базис подпространства .

Во-первых, , так как образ любого вектора линейно выражается через векторы

Во-вторых, образующие линейно независимы. Если их линейная комбинация равна нулевому вектору:

то вектор принадлежит ядру (его образ — нулевой вектор). Однако, по построению этот вектор принадлежит алгебраическому дополнению . Учитывая, что , заключаем: . Получили разложение нулевого вектора по линейно независимой системе векторов, значит, все коэффициенты . Поэтому равенство справедливо только для тривиальной линейной комбинации, т.е. система векторов линейно независимая.

Таким образом, векторы образуют базис подпространства , а его размерность определяется количеством базисных векторов, т.е. , что равносильно (9.3).

Следствие. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда обратима его матрица (определенная относительно любых базисов).

Действительно, для обратимости преобразования (см. свойство 6) его матрица (размеров ) должна удовлетворять условиям (см. свойства 3,4,5):

Тогда по теореме 9.1 заключаем, что , т.е. матрица — квадратная n-го порядка и невырожденная , что и требовалось доказать.

Обратимые линейные отображения называются также невырожденными (имея в виду невырожденность их матрицы).

Линейные операторы

1. Понятие линейного оператора

где A — m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:

Пусть x − произвольный элемент в R. Тогда

(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

Сделаем следующее обозначение:

(6)

Тогда равенство (5) примет следующий вид:

(7)

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Пусть A и B два линейных оператора действующих из R в S и пусть A и B — mxn − матрицы соответствующие этим операторам.

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Применим оператор C к базисному вектору e_j, тогда:

Ce_j= Ae_j+ Be_j=	n	(a_ij+b_ij) e_j
∑
j= 1

Следовательно оператору C отвечает матрица ,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

8. Образ линейного оператора

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

источники:

http://mathhelpplanet.com/static.php?p=yadro-i-obraz-linyeinogo-otobrazheniya

http://matworld.ru/linear-algebra/linear-operator.php

Источник

Линейные операторы

1. Понятие линейного оператора

A(x₁+x₂)=Ax₁+Ax₂.
A(λx)=λAx.

Пусть x − произвольный элемент в R. Тогда

(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

(5)

Сделаем следующее обозначение:

(6)

Тогда равенство (5) примет следующий вид:

(7)

Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты y_i, i=1,2,…,m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента x_j, j=1,2,…n с коэффициентами a_ij i=1,2,…,m; j=1,2,…,n.

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.

Применим оператор C к базисному вектору e_j, тогда:

Ce_j=Ae_j+Be_j=	n	(a_ij+b_ij)e_j
∑
j=1

Следовательно оператору C отвечает матрица ,где i=1,2,…m, j=1,2,…n, т.е.

3. Умножение линейных операторов

Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

8. Образ линейного оператора

Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

Источник

§ 1. Понятие отображения

Пусть Х и Y – множества элементов произвольной природы. Говорят, что задано Отображение (читается: отображение f множества X во множество Y), если задан закон, по которому каждому элементу ставится в соответствие вполне определенный элемент (рис. 1).

Рис. 1.

Если , то называется Образом элемента , – Прообразом элемента при отображении F.

Примерами отображений являются функции, которые изучаются в школе и в математическом анализе, например, функция – это отображение . Классный журнал является примером отображения множества учеников в классе во множество всех фамилий.

Отображение называется Тождественным, если оно любой элемент оставляет на месте. Тождественное отображение множества X на себя будем обозначать . Таким образом, .

Отображение называется Взаимно однозначным (или биективным, или биекцией), если оно удовлетворяет двум условиям:

1. такой, что.

Или одному, эквивалентному им, третьему условию:

3.Такой, что

Хороший пример взаимно однозначного отображения: в театре дают билет, каждому билету соответствует некоторое кресло, причем только одно.

Отображения и называются Равными, если .

Пусть заданы отображения и . Произведением (или композицией) отображений F и G называется отображение , такое, что (рис. 2)

Рис. 2.

Замечание. В произведении отображений сначала действует внутреннее, а затем внешнее отображение.

Примером произведения отображений является сложная функция.

Лемма. Произведение отображений ассоциативно, т. е., если заданы отображения , и , то

UДля доказательства равенства отображений и нужно показать, что .

Итак, выберем произвольное . Тогда

; (1)

(2)

Сравнивая (1) и (2), видим, что и, поэтому, .t

Отображение называется Обратным к отображению , если и (рис. 3).

Рис. 3.

Упражнение. Докажите следующие утверждения:

1. Для того чтобы отображение F имело обратное необходимо и достаточно, чтобы F было взаимно однозначным.

2. Если отображение имеет обратное, то это обратное определяется однозначно.

§2. Определение линейного оператора и его простейшие свойства

Определение. Пусть и – линейные пространства над одним и тем же полем . Отображение называется Линейным оператором, если оно удовлетворяет следующим условиям:

1*.

2*.

Следствие. При линейном операторе образ линейной комбинации векторов равен такой же линейной комбинации их образов, т. е. если – линейный оператор, то

(1)

UДоказательство проведем методом математической индукции по количеству векторов.

А) N=1: [2*] – истинно.

Б) Предполагая, что утверждение верно для (N-1)-го вектора, доказываем его для N векторов.

= [1*] =

[2* и предположение индукции] =

Примеры линейных операторов

1. Нулевой оператор : . Очевидно, этот оператор удовлетворяет условиям 1* и 2*, значит, является линейным.

2. Тождественный оператор также, очевидно, является линейным.

3. Оператор дифференцирования , который каждой дифференцируемой функции ставит в соответствие ее производную, является линейным, т. к. производная суммы функций равна сумме их производных, а при умножении функции на число её производная умножается на это число.

4. Пусть – пространство свободных векторов, .

Покажем, что оператор проектирования на ось также является линейным.

►В аналитической геометрии доказывалось, что . Тогда

====;

===

Таким образом, условия 1* и 2* выполняются, а значит, оператор проектирования вектора на ось является линейным.◄

5. В пространстве Векторов плоскости, закрепленных в начале координат О, рассмотрим оператор поворота вектора на угол против часовой стрелки и докажем его линейность.

►1*. Пусть – произвольные векторы, ,

(рис. 1). Построим и по правилу параллелограмма. Так как плоскость поворачивается

Рис.1. как жесткое целое, методами элементарной геометрии нетрудно показать, что при этом повороте диагональ переходит в диагональ . Значит, .

2* . Пусть α>0, , , , (рис.2). Очевидно, вектор получен из поворотом на угол, следовательно, , а значит,. Аналогично это свойство проверяется

И при , а при оно очевидно.◄

Теорема. Пусть и – линейные пространства над одним и тем же полем P и пусть в пространстве задан базис

, (2)

А в пространстве – произвольная система векторов

. (3)

Тогда существует единственный линейный оператор , переводящий базис (2) в систему (3), то есть такой, что

. (4)

►Построение. Выберем произвольный вектор и разложим его по базису (2): . Положим по определению

Линейность. Если — произвольные векторы, то , , . Тогда

= [определение F ] = ;

Выполнение (4). Заметим, что все координаты вектора В базисе (2) равны нулю, за исключением K-й, которая равна 1. Таким образом, I-я координата вектора равна , то есть . Тогда

Значит, условие (4) выполнено.

Единственность. Предположим, что существует еще один линейный оператор , , переводящий (2) в (3), то есть такой, что . Тогда – противоречие.◄

Простейшие свойства линейного оператора

1º. Линейный оператор переводит нейтральный элемент пространства в нейтральный элемент пространства .

►Пусть – линейный оператор. Тогда .◄

2º. При линейном операторе линейно зависимые векторы пространства переходят в линейно зависимые векторы пространства .

►Пусть — линейно зависимые векторы. Это значит, что существуют числа , не все равные нулю, такие, что

. (5)

Подействуем линейным оператором на обе части равенства (5). Тогда

(5) [(1) и 1º]

. (6)

Так как среди чисел есть отличные от нуля, то система {} линейно зависима.◄

Упражнение. Верно ли утверждение: при линейном операторе линейно независимые векторы переходят в линейно независимые?

§ 3. Матрица линейного оператора

Определение матрицы линейного оператора

Пусть в линейном пространстве над полем задан базис

(1)

И пусть – линейный оператор (читается так: в себя). Построим систему векторов

(). (2)

Каждый из векторов системы (2) можно разложить по базису (1):

(3)

Сокращенно система (3) записывается одним равенством:

. (4)

Расположим числа в матрицу А по нашей договоренности: верхний индекс обозначает номер строки, а нижний – номер столбца:

Заметим, что столбцы полученной матрицы А являются координатными столбцами образов векторов базиса (1) в том же базисе. Обозначим

[]=.

Равенство (4) можно переписать и так: , откуда, руководствуясь правилом цепочки, (4) записываем в матричном виде:

. (5)

Матрицей линейного оператора в некотором базисе называется матрица А, столбцами которой являются координатные столбцы образов базисных векторов в том же базисе. Это матрица , элементы которой удовлетворяют системе равенств (3) или (4), а сама матрица удовлетворяет матричному равенству (5).

Примеры

1. Матрицей нулевого оператора в любом базисе является нулевая матрица; матрицей тождественного оператора также в любом базисе является матрица единичная.

2. Пусть . Составим матрицу оператора проектирования на ось OX в базисе . Для этого находим образы базисных векторов и разлагаем их по базису:

3. Составим матрицу оператора поворота плоскости на угол (см.§2) в базисе . Из рисунков 1 и 2 видно, что

Тогда

Рис. 1. Рис. 2.

Итак, если в пространстве задан какой-либо базис, то каждому линейному оператору можно поставить в соответствие его матрицу в этом базисе, то есть квадратную матрицу A n-Ого порядка, причем эта матрица определяется однозначно.

Пусть теперь задана квадратная матрица А с элементами из поля P . Обозначим вектор, координатный столбец которого в базисе (1) совпадает с I-м столбцом матрицы А. Получим упорядоченную систему векторов

() (6)

Согласно теореме § 2 существует единственный линейный оператор такой, что . По определению, матрица этого оператора в базисе (1) совпадает с А.

Обозначим — множество всех линейных операторов линейного пространства над полем Р в себя. Из вышесказанного вытекает: если в задан базис, то определяется отображение

Которое ставит в соответствие каждому линейному оператору его матрицу в этом базисе, причем это отображение взаимно однозначно. Это дает возможность в конечномерных линейных пространствах линейные операторы изучать с помощью их матриц.

Связь координат вектора с координатами его образа

Пусть в линейном пространстве задан базис (1), и пусть –матрица линейного оператора В этом базисе. Выберем произвольный вектор и положим . Обозначим и – координатные столбцы векторов и соответственно в базисе (1). Тогда

[(1) § 2] = [(4)] = ,

И, т. о.,

. (7)

Равенство (7) есть не что иное, как разложение вектора по базису (1), а коэффициенты разложения – это координаты вектора в этом базисе. В силу единственности координат вектора в данном базисе, получаем:

(8)

Записав (8) по правилу цепочки (), получаем

. (9)

Формула (8) и задает связь координат вектора и координат его образа при линейном операторе, а (9) – это её матричная запись.

Изменение матрицы линейного оператора при изменении базиса

Теорема. Пусть в линейном пространстве заданы два базиса:

(10)

, (11)

И пусть A= и – матрицы линейного оператора в базисах (10) и (11) соответственно. Тогда

, (12)

Где Т – матрица перехода от (10) к (11).

►Для того чтобы найти матрицу , следует образы векторов базиса (11) разложить опять же по этому базису. Имеем:

= [определение матрицы перехода] = = [(1) § 2] = = =[(4)]= = [свойство 6º §9 гл. 3] = .

Итак,

= . (13)

Равенство (13) есть не что иное, как разложение вектора по базису (11). С другой стороны, по определению матрицы линейного оператора,

. (14)

В силу единственности координат вектора в данном базисе, из (13) и (14) получаем равенство

, (15)

Которое и дает нам связь элементов матриц линейного оператора в различных базисах. Запишем (15) по правилу цепочки:

. (16)

Так как (см. замечание в § 9 гл. 3), то из (16) получаем (12). ◄

Определение. Квадратные матрицы А и В называются Подобными, если существует невырожденная матрица Т такая, что .

Таким образом, мы видим, что матрицы линейного оператора в различных базисах подобны.

Лемма. Подобные матрицы имеют одинаковые определители. ►.◄

Определение. Определителем линейного оператора называется определитель его матрицы в некотором, а значит, и в любом базисе пространства .

§4. Геометрический смысл определителя матрицы линейного

Оператора

Пусть – линейный оператор, — его матрица в некотором ортонормированном базисе , и пусть – некомпланарные векторы, а — их образы. Обозначим и координатные столбцы в выбранном базисе векторов и соответственно, , – объем параллелепипеда, построенного на векторах , а – объем параллелепипеда, построенного на векторах . Тогда, учитывая (9) §3, получаем:

[(9) § 3] [§ 5 главы 1] =

[§ 6 главы 1] . (1)

Рассмотрим теперь пространство . Выберем в нем точку и линейно независимых векторов , . Параллелепипедом в (-мерным параллелепипедом) будем называть множество точек в

. (2)

Обозначим координатный столбец вектора в каноническом базисе. По аналогии с трехмерным пространством, Объемом — мерного параллелепипеда (2) будем называть число

Можно доказать, что при переходе от одного ортонормированного базиса к другому ортонормированному это число не меняется, т. е. определение объема параллелепипеда является корректным.

Точно так же, как и для трехмерного пространства, для пространства доказывается равенство (1).

Вывод: из формулы (1) на основании леммы §3 вытекает, что коэффициент изменения объема параллелепипеда при линейном операторе равен модулю определителя этого оператора.

§ 5. Операции над линейными операторами

Определения. Пусть и — линейные пространства над одним и тем же полем .

Суммой линейных операторов и называется отображение такое, что .

Произведением линейного оператора на число называется отображение , такое что .

Произведением линейных операторов и называется отображение такое, что (т. е. произведение линейных операторов – это просто произведение или композиция отображений).

Теорема. Сумма линейных операторов, произведение линейного оператора на число, а также произведение линейных операторов также являются линейными операторами. При этом, если , А и В – матрицы линейных операторов F и G соответственно в некотором базисе пространства , то матрицы операторов , и Gf в том же базисе совпадают соответственно с матрицами А+В, αА и ВА.

►Доказательство проведем для произведения линейных операторов.

Пусть и — линейные операторы. Тогда

= [линейность F ] = =

=[ линейность G ] = = ;

Таким образом, Gf – линейный оператор.

Пусть — матрицы линейных операторов и соответственно в базисе пространства , и пусть — матрица оператора Gf В том же базисе. Тогда, по определению матрицы линейного оператора

. (1)

С другой стороны,

[линейность G] = (2)

Сравнивая (1) и (2), на основании единственности координат вектора в данном базисе, делаем вывод: , откуда и получаем матричную запись: С=ВА.◄

Упражнение. Докажите, что множество

— линейный}

Всех линейных операторов пространства в пространство есть линейное пространство над тем же полем, что и пространства и Относительно введенных операций сложения линейных операторов и умножения их на число. Найдите размерность .

§ 6. Невырожденные линейные операторы

Определение. Линейный оператор называется невырожденным, если он любой ненулевой вектор переводит в ненулевой

Теорема 1. Для того чтобы линейный оператор был невырожденным необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом базисе пространства была невырожденной

►Пусть А – матрица линейного оператора в некотором базисе, Х, как обычно, координатный столбец вектора в том же базисе. Тогда

{F – невырожденный}

{однородная система линейных уравнений AX = O имеет единственное тривиальное решение} {}.

Так как определители подобных матриц совпадают, то утверждение справедливо и для любого базиса. ◄

Теорема 2. Для того чтобы линейный оператор был невырожденным необходимо и достаточно, чтобы он был взаимно однозначным.

►Пусть — линейный оператор, А— его матрица в некотором базисе, X и Y – координатные столбцы в том же базисе векторов и соответственно. Тогда

{ невырожденный} {Система имеет единственное решение} { единственный , что }

{ единственный , что } {F – взаимно однозначный}.◄

Теорема 3. Произведение невырожденных линейных операторов – невырожденный линейный оператор.

►Пусть и — невырожденные линейные операторы. Тогда

{} {} {}.

Tаким образом, Gf – невырожденный линейный оператор.◄

§ 7. Обратный линейный оператор

Теорема. Для любого невырожденного линейного оператора существует единственный обратный оператор , который также является линейным. При этом, если А – матрица оператора в некотором базисе, то матрица оператора в том же базисе совпадает с матрицей .

►Единственность. Пусть некоторый оператор имеет два разных обратных: И . Тогда

—

Противоречие.

Существование. Пусть А — матрица оператора в некотором базисе. Тогда, по теореме 1 § 6, , значит, существует . Обозначим — тот линейный оператор, матрица которого в выбранном базисе совпадает с .

Так как , и т. к. произведению матриц соответствует произведение операторов, то , и, таким образом, .◄

Замечание. МОжно доказать, что любой взаимно однозначный линейный оператор имеет единственный обратный, который тоже является линейным.

§ 8. Изоморфизм линейных пространств

Определение. Изоморфизмом Линейных пространств называется взаимно однозначный линейный оператор. Если существует изоморфизм , то линейные пространства и называются изоморфными. Изоморфизм обозначается так: .

Так как изоморфизм – взаимно однозначное отображение, то изоморфные объекты содержат одинаковое количество элементов. Кроме того, в силу линейности, действия, производимые над элементами пространства , одновременно производятся и над элементами пространства . Поэтому в математике изоморфные объекты не различаются.

Свойства изоморфизма

1. — рефлективность (изоморфизм осуществляет тождественное отображение).

2. — симметричность (если первый изоморфизм осуществляет с помощью отображения F, то второй — с помощью ).

3. {, } — транзитивность (если первый изоморфизм осуществляется с помощью отображения , второй — , то третий изоморфизм осуществляется с помощью отображения ).

Строгого доказательства этих свойств мы не приводим.

Теорема 1. Изоморфные линейные пространства имеют одинаковые размерности.

►Пусть и пусть — изоморфизм. Выберем в какой-либо базис

(1)

И покажем, что система

— (2)

Базис пространства . Действительно, в силу взаимной однозначности F, единственный такой, что . Тогда, если , то . Значит, (2) – система образующих в .

Докажем теперь линейную независимость (2).

[линейность F]

[взаимная однозначность F ] [линейная независимость (1)] {(2) — линейно независима}.

Таким образом, (2) – базис в , а значит, . ◄

Теорема 2. Все N — мерные линейные пространства над полем Р изоморфны между собой, т. е. существует единственное с точностью до изоморфизма N-Мерное линейное пространство над полем Р.

►а) Докажем, что .

Выберем в какой-либо базис . Тогда . Обозначим . Очевидно, отображение — взаимно однозначное. Кроме того, ,

Поэтому F — линейный оператор, а значит, и изоморфизм. Итак, .

Б) Пусть теперь и — N-Мерные линейные пространства над одним и тем же полем Р. Тогда

{ и } [симметричность] { и } [транзитивность] {}.◄

Таким образом, мы показали, что с точки зрения математики единственным N-Мерным линейным пространством над полем Р является .

§ 9. Образ и ядро линейного оператора

Определения. Образом Линейного оператора называется подмножество линейного пространства

Ядром линейного оператора называется подмножество линейного пространства

Теорема 1. Образ линейного оператора является подпространством пространства , а его ядро – подпространством пространства .

Упражнение. Докажите теорему 1.

Размерность подпространства называется Рангом оператора и обозначается , а размерность подпространства называется Дефектом и обозначается .

Теорема 2. Если — — мерное линейное пространство, — линейный оператор, то

. (1)

►Обозначим . Так как — подпространство пространства , то . Рассмотрим сначала случай, когда . Выберем в какой-либо базис

. (2)

По теореме 2 § 4 гл. 3 систему (1) можно дополнить до базиса

(3)

Пространства . Обозначим . Очевидно,

— (4)

Базис пространства . Докажем, что . Действительно,

Где , а . Таким образом, . Покажем, что сумма прямая. Пусть . Тогда можно разложить как по базису (2), так и по базису (4): и . Получаем

Откуда, в силу линейной независимости (3), вытекает, что . Поэтому , а значит, сумма действительно прямая.

Покажем теперь, что . Построим отображение

Очевидно, — линейный оператор. Кроме того, такой, что . Так как , то где , . Тогда. . Таким образом, такой, что . Предположим, что таких векторов два, т. е., что , но . Имеем: . Отсюда вытекает, что . Но , следовательно, , и поэтому . Итак, мы показали, что — взаимно однозначное отображение, следовательно, и изоморфизм. Так как изоморфные линейные пространства имеют одинаковые размерности, то , откуда и вытекает доказываемое утверждение.