Конус – это геометрическая фигура, полученная вращением прямоугольного треугольника вокруг одного из катетов. У каждого конуса есть основание и боковая поверхность.
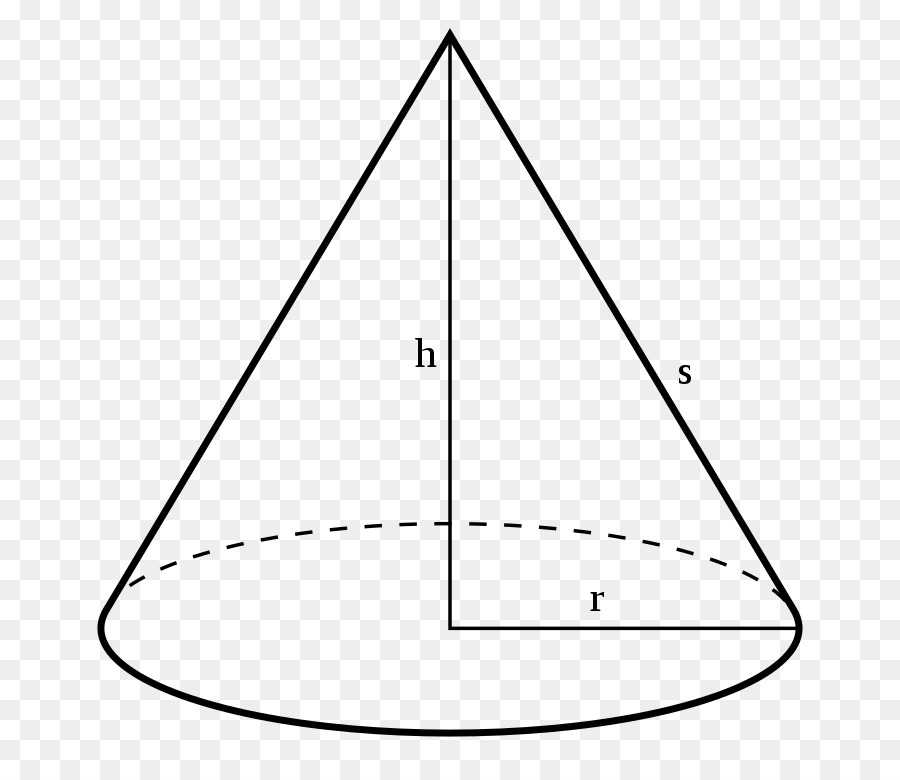
Любой конус характеризуется высотой h (осевой линией), радиусом r и образующей l (см. рисунок). Именно эти характеристики используются в формулах конуса при вычислении объема, площади поверхности и площади боковой поверхности.
Высота конуса (осевая линия) – это перпендикуляр, проведенный из вершины конуса к основанию.
Радиус конуса – это радиус его основания.
Образующая конуса – это отрезок, который соединяет вершину конуса с любой точкой, лежащей на линии окружности основания.
Формула образующей конуса
Образующую конуса можно найти, зная ее высоту H и радиус R:
L = √H2 + R2
Формула площади боковой поверхности конуса
Площадь боковой поверхности конуса можно получить, зная его радиус R и образующую L:
Sбок.пов = πRL
Формула площади основания конуса
Площадь основания конуса можно вычислить по его радиусу R:
Sосн = πR2
Формула площади конуса
Площадь поверхности конуса можно получить, сложив площадь боковой поверхности и площадь основания конуса:
S = Sбок.пов + Sосн = πRL + πR2
Формула объема конуса
Объем конуса можно вычислить, зная его высоту H и площадь основания:
V = 1/3 ⋅ Sосн ⋅ H = 1/3πR2H
Конус — тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета.
Треугольник (POA) вращается вокруг стороны (PO).
(PO) — ось конуса и высота конуса.
(P) — вершина конуса.
(PA) — образующая конуса.
Круг с центром (O) — основание конуса.
(AO) — радиус основания конуса.
Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось (PO) конуса.
Осевое сечение конуса — это равнобедренный треугольник.
(APB) — осевое сечение конуса.
— углы между образующими и основанием конуса.
Для конуса построим развёртку боковой поверхности. Это круговой сектор.

Сектор имеет длину дуги, равную длине окружности в основании конуса
2πR
, угол развёртки боковой поверхности
α
.
В конусе нельзя обозначить угол развёртки.
На развёртке конуса нельзя обозначить высоту и радиус конуса.
Образующая конуса (l) является радиусом сектора.
Таким образом, боковая поверхность конуса является частью полного круга с радиусом (l):
Длина дуги также является частью длины полной окружности с радиусом (l), но в то же время длина дуги — это длина окружности основания конуса с радиусом (R).
Сравним выражения длины дуги и выразим
α
через (R):
2πl⋅α360°=2πR;α=2πR⋅360°2πl=R⋅360°l.
Получаем ещё одну формулу боковой поверхности конуса; не используется угол развёртки боковой поверхности:
.
Если провести сечение конуса плоскостью, перпендикулярной оси конуса, то эта плоскость разбивает конус на две части, одна из которых — конус, а другую часть называют усечённым конусом.
Также усечённый конус можно рассматривать как тело вращения, которое образовалось в результате вращения прямоугольной трапеции вокруг боковой стороны (которая перпендикулярна к основанию трапеции) или в результате вращения равнобедренной трапеции вокруг высоты, проведённой через серединные точки оснований трапеции.
— ось конуса и высота конуса.
Круги с центрами (O) и
O1
— основания усечённого конуса.
(AO) и
A1O1
— радиусы оснований конуса.
Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось
OO1
конуса.
Осевое сечение конуса — это равнобедренная трапеция.
— осевое сечение конуса.
Боковая поверхность определяется как разность боковой поверхности данного конуса и отсечённого конуса:
Sбок.=πR⋅PA−πr⋅PA1=πR⋅PA1+AA1−πr⋅PA1==πR⋅PA1+πR⋅AA1−πr⋅PA1==πR⋅l+πR−πr⋅PA1.
Так как
ΔPAO∼ΔPA1O1
, то стороны их пропорциональны:
PAPA1=Rr;l+PA1PA1=Rr;r⋅l+PA1=R⋅PA1;rl=R⋅PA1−r⋅PA1;PA1⋅R−r=rl;PA1=rlR−r.
Таким образом получаем формулу боковой поверхности усечённого конуса, которая содержит радиусы оснований и образующую усечённого конуса:
Sбок.=πRl+π⋅PA1⋅R−r=πRl+π⋅rlR−r⋅R−r;Sбок.=πRl+πrl=πl⋅R+r.
Пространственные фигуры подробно рассматриваются в старших классах общеобразовательных школ в курсе стереометрии. Данная статья содержит ответ на вопрос о том, как найти образующую конуса круглого прямого и образующую соответствующей усеченной фигуры.
Фигура конус
Чтобы понять, как найти образующую конуса, следует дать представление об этой фигуре. Круглым прямым конусом называют фигуру вращения прямоугольного треугольника вокруг одного из его катетов. Рисунок ниже демонстрирует процесс вращения.
Полученная пространственная фигура имеет следующие характеристики:
- Сторона AB треугольника является высотой h конуса. Она лежит на оси вращения фигуры.
- Сторона AC треугольника — это радиус r конуса. Круг, который описывает этот радиус, называется основанием фигуры.
- Сторона CB треугольника для конуса является его образующей, или генератрисой. Это название она получила за то, что в процессе вращения она описывает коническую поверхность.
- Вершина B треугольника — это вершина конуса.
Заметим, что высота фигуры пересекает круглое основание в его центре. Это является достаточным условием, чтобы считать конус прямым.
Образующая конуса
Теперь можно переходить к ответу на вопрос о том, как найти образующую конуса круглого прямого. Выше было сказано, что она представляет собой отрезок, который лежит на конической поверхности и соединяет вершину с точкой окружности основания. В прямоугольном треугольнике, из которого был конус получен, образующая является гипотенузой. Это наблюдение позволяет записать известную теорему Пифагора, связав образующую g с радиусом r и высотой h фигуры. Формула, как найти образующую конуса, имеет вид:
g = √(r2 + h2)
Помимо этой формулы, на практике вместо высоты или радиуса фигуры может быть известен угол φ между образующей и основанием. В этом случае генератрису g можно рассчитать с помощью следующих выражений:
g = h/sin(φ);
g = r/cos(φ)
Эти формулы следуют из свойств тригонометрических функций синуса и косинуса.
Таким образом, вычисление образующей конуса возможно, если знать любые два параметра фигуры.
Фигура конус усеченный
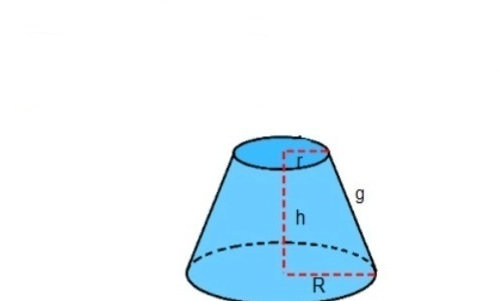
Он также является фигурой вращения, только вместо прямоугольного треугольника следует вращать прямоугольную трапецию. На рисунке ниже показан усеченный конус.
Здесь синие стрелки показывают прямоугольную трапецию. Длина вертикальной стрелки является высотой h фигуры, длины двух других синих стрелок — это радиусы оснований конуса. В отличие от цилиндра, основания усеченного конуса имеют разную площадь. Обозначим их радиусы r1 и r2. Четвертая наклонная к основанию сторона трапеции является образующей или генератрисой. Как и для обычного конуса, для усеченного все генератрисы равны друг другу и образуют боковую поверхность фигуры.
Заметим, что усеченный конус получил такое название потому, что его можно получить не только вращением трапеции, но и с помощью отсечения плоскостью верхней части круглого прямого конуса.
Генератриса усеченной фигуры
Итак, мы познакомились с усеченным конусом, а также с понятием о его образующей. Как находить образующую конуса усеченного? Для того чтобы получить нужную формулу, заметим, если высоту h перенести параллельно самой себе к боковой поверхности конуса так, чтобы она касалась одним концом образующей фигуры, то получится прямоугольный треугольник. Его сторонами будут высота h (катет), генератриса g (гипотенуза) и r1-r2 (катет). Тогда можно записать формулу для определения g:
g = √((r1 — r2)2 + h2)
Соответственно, если дан острый угол φ1 между большим основанием и генератрисой, тогда последнюю можно определить так:
g = h/sin(φ1);
g = (r1 — r2)/cos(φ1)
Если же известен тупой угол φ2 между малым основанием и генератрисой, тогда для ее вычисления необходимо применять такие выражения:
g = h/sin(φ2);
g = (r2 — r1)/cos(φ2)
Здесь первая формула является точно такой же, как для угла φ1, а во второй формуле радиусы в числителе поменялись местами.
Таким образом, найти образующую конуса усеченного можно, если знать любые три его параметра.
Просмотры: 24
Формула длины образующей конуса по радиусу и высоте, расчет в см
Введите радиус основания конуса в см
Введите длину образующей конуса в см:
Расчет приведен для прямого кругового конуса (подробное описание внизу страницы)
Длина образующей конуса равна:
0.00см
0.00м
Как рассчитать длину образующей прямого кругового конуса по радиусу основания и высоте?
Прямой круговой конус — конус в основании которого лежит круг и центр симметрии совпадает с центром этого круга (то есть это обычный, в простом понимании, конус).
Длина образующей прямого кругового конуса вычисляется по формуле:
l = √(r2 + h2), где
h — высота конуса;
r — радиус основания конуса.
l — образующая конуса;
Квадрат длины образующей конуса равен сумме квадрата радиуса основания конуса и квадрата высоты конуса (теорема Пифагора)
Если радиус и высота конуса измерены в см (сантиметрах), то длина образующей равна:
lсм = √(r2см+ h2см)
lм = (√(r2см+ h2см))/100
Цилиндр и конус являются фигурами вращения, которые получаются в результате перемещения образующей вдоль направляющей линии. В данной статье раскроем вопрос, что это — образующая конуса, а также покажем, как рассчитывать ее длину в случае обычного конуса и его усеченного варианта.
Фигура конус общего типа
Речь идет о геометрической объемной фигуре, которая получается следующим образом: представим, что имеется некоторая кривая на плоскости, например, эллипс. Выберем в пространстве совершенно любую точку, которая не лежит в плоскости эллипса. Теперь с помощью прямого отрезка соединим точку и эллипс, а затем будем перемещать этот отрезок вдоль эллиптической кривой. Результатом такого перемещения будет коническая поверхность. Она показана ниже на рисунке.
Здесь лежащая в начале координат точка называется вершиной конуса. Эллиптическая кривая — это направляющая или директриса фигуры. Образующая конуса — это отрезок, который соединяет его вершину с любой точкой направляющей кривой. Образующая также называется генератрисой. Из рисунка понятно, что длина образующей изменяется при ее движении вдоль эллипса.
Конус круглый
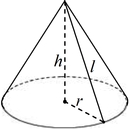
Круглым называется любой конус, направляющая кривая которого является окружностью. Если перпендикуляр, который проведен из вершины этого конуса, пересекает круглое основание в центре, то такая фигура будет называться прямой. Круглый прямой конус приведен на рисунке.
Рисунок ясно показывает, что для этой фигуры высота h, любой радиус r и образующая s составляют прямоугольный треугольник. Используя абстрактное воображение, можно представить, что если этот треугольник вращать вокруг h, то получится круглый конус.
Образующая конуса — это гипотенуза описанного прямоугольного треугольника. Этот факт позволяет записать равенство, которое можно использовать при вычислении длины образующей s:
s = √(r2+h2)
Отметим, что в отличие от конуса общего типа, все длины образующих для круглой фигуры равны между собой и составляют с основанием определенный угол. Если обозначить этот угол буквой φ, то можно записать еще две формулы для определения длины s:
s = r/cos(φ);
s = h/sin(φ).
Конус круглый усеченный
Предположим, что у нас имеется трапеция с двумя прямыми углами. Если вращать ее вокруг стороны, прилегающей к этим углам, то получится усеченный конус.
Рисунок показывает штриховыми линиями трапецию. Здесь r и R — радиусы малого и большого оснований, h — высота, g — это образующая конуса усеченного. Из рисунка видно, что все образующие для этой фигуры являются одинаковыми. Для определения длины g можно записать следующие три формулы:
g = √((R-r)2 + h2);
g = h/sin(φ);
g = (R-r)/cos(φ).
Здесь угол φ соответствует углу между образующей и большим основанием.
Заметим, что усеченный конус можно получить из обычного конуса, если отсечь плоскостью, которая параллельна его основанию, верхнюю часть фигуры.
Задача на определение генератрисы конуса усеченного
Решим интересную геометрическую задачу. Предположим, что имеется круглый конус усеченный. Известно, что высота этой фигуры равна 14 см, а угол между его образующей и малым основанием составляет 135o. Необходимо найти длину образующей конуса.
Если бы был дан угол между образующей и большим основанием, то мы сразу могли применить соответствующую формулу для вычисления g. Тем не менее, этот угол φ определить несложно.
Обратимся к предыдущему рисунку. Известен угол между r и g. Если переместить высоту h вдоль радиуса r к его концу, тогда стороны h, R-r и g образуют прямоугольный треугольник. Поскольку между h и r угол равен 90o, то между h и g он составит:
α = 135o — 90o = 45o.
Это означает, что угол φ будет также равен 45o, поскольку он является углом прямоугольного треугольника, упомянутого выше.
Для определения длины образующей g следует подставить известные данные в формулу. Получаем:
g = h/sin(φ) = 14/sin(45o) ≈ 19,8 см.
Для любого конуса длина его образующей больше высоты.