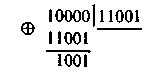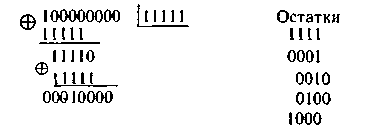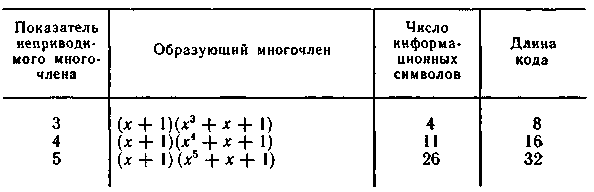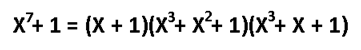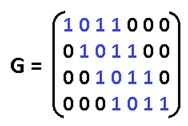Как найти образующий многочлен для ко

По
заданному объему кода однозначно
определяется число информационных
разрядов k.
Далее
необходимо найти наименьшее n,
обеспечивающее обнаружение или
исправление ошибок заданной кратности.
В случае циклического кода эта проблема
сводится к нахождению нужного многочлена
g(x).

Начнем рассмотрение
с простейшего циклического кода,
обнаруживающего все одиночные ошибки.

Обнаружение
одиночных ошибок.
Любая принятая по каналу связи кодовая
комбинация h(x),
возможно
содержащая ошибку, может быть представлена
в виде суммы по модулю два неискаженной
комбинации кода f(x)
и вектора
ошибки ξ(x)
:

При
делении h(x)
на образующий
многочлен g(x)
остаток,
указывающий на наличие ошибки,
обнаруживается только в том случае,
если многочлен, соответствующий вектору
ошибки, не делится на g(x):
f(x) — неискаженная
комбинация кода и, следовательно, на
g(x)
делится
без остатка.

Вектор
одиночной ошибки имеет единицу в
искаженном разряде и нули во всех
остальных разрядах. Ему соответствует
многочлен ξ(x)
= хⁱ·
Последний не должен делиться на g(x).
Среди
неприводимых многочленов, входящих в
разложении хⁿ⁺¹,
многочленом наименьшей степени,
удовлетворяющим указанному условию,
является x+1.
Остаток
от деления любого многочлена на x+1
представляет
собой многочлен нулевой степени и может
принимать только два значения: 0 или 1.
Все кольцо в данном случае состоит из
идеала, содержащего многочлены с четным
числом членов, и одного класса вычетов,
соответствующего единственному остатку,
равному 1. Таким образом, при любом числе
информационных разрядов необходим
только один проверочный разряд. Значение
символа этого разряда как раз и
обеспечивает четность числа единиц в
любой разрешенной кодовой комбинации,
а следовательно, и делимость ее на х+1.

Полученный
циклический код с проверкой на четность
способен обнаруживать не только одиночные
ошибки в отдельных разрядах, но и ошибки
в любом нечетном числе разрядов.

Исправление
одиночных или обнаружение двойных
ошибок.
Прежде чем исправить одиночную ошибку
в принятой комбинации из n
разрядов, необходимо определить, какой
из разрядов был искажен. Это можно
сделать только в том случае, если каждой
одиночной ошибке в определенном разряде
соответствуют свой класс вычетов и свой
опознаватель. Так как в циклическом
коде опознавателями ошибок являются
остатки от деления многочленов ошибок
на образующий многочлен кода g(x),
то g(x)
должно
обеспечить требуемое число различных
остатков при делении векторов ошибок
с единицей в искаженном разряде. Как
отмечалось, наибольшее число остатков
дает неприводимый многочлен. При степени
многочлена m
= n — k он
может дать 2^n—k-1
ненулевых остатков (нулевой остаток
является опознавателем безошибочной
передачи).

Следовательно,
необходимым условием исправления любой
одиночной ошибки является выполнение
неравенства

где
С_n
— общее число разновидностей одиночных
ошибок в кодовой комбинации из n
символов; отсюда находим степень
образующего многочлена кода

и
общее число символов в кодовой комбинации.
Наибольшие значения k
и n
для различных m
можно найти, пользуясь табл. 6.11.

Как
указывалось, образующий многочлен g(x)
должен
быть делителем двучлена хⁿ⁺¹.
Доказано [20], что любой двучлен типаможет
быть представлен произведением всех
неприводимых многочленов, степени
которых являются делителями числаm
(от 1 до m
включительно). Следовательно, для любого
m
существует по крайней мере один
неприводимый многочлен степени m,
входящий сомножителем в разложение
двучлена хⁿ⁺¹.

Таблица 6.11

Пользуясь этим
свойством, а также имеющимися в ряде
книг [20] таблицами многочленов, неприводимых
при двоичных коэффициентах, выбрать
образующий многочлен при известных nиmнесложно. Определив
образующий многочлен, необходимо
убедиться в том, что он обеспечивает
заданное число остатков.

Пример
6.13.
Выберем образующий многочлен для случая
n
= 15 и m
= 4.

Двучлен
x¹⁵+1
можно записать в виде произведения всех
неприводимых многочленов, степени
которых являются делителями числа 4.
Последнее делится на 1, 2, 4.

В
таблице неприводимых многочленов
находим один многочлен первой степени,
а именно х+1, один многочлен второй
степени х²
+ х+1 и три многочлена четвертой степени:
х⁴
+ x
+ 1, х⁴
+ х³+1,
х⁴
+ х³+х
+ 1. Перемножив все многочлены, убедимся
в справедливости соотношения (х+1)(х²
+ х + 1)(х⁴
+ х+1)(х⁴
+ х³+
l)(x⁴
+ x³
+ +x²+x+1)
= x¹²+1.

Один
из сомножителей четвертой степени может
быть принят за образующий многочлен
кода. Возьмем, например, многочлен х⁴
+ х³
+ 1, или в виде двоичной последовательности
11001.

Чтобы убедиться,
что каждому вектору ошибки соответствует
отличный от других остаток, необходимо
поделить каждый из этих векторов на
11001.

Векторы ошибок т
младших разрядов имеют вид:

00…0001, 00…0010,
00…0100, 00…1000.

Степени
соответствующих им многочленов меньше
степени образующего многочлена g(x).
Поэтому
они сами являются остатками при нулевой
целой части. Остаток, соответствующий
вектору ошибки в следующем старшем
разряде, получаем при делении 00…10000 на
11001, т.е.

Аналогично
могут быть найдены и остальные остатки.
Однако их можно получить проще, деля на
g(x)
комбинацию
в виде единицы с рядом нулей и выписывая
все промежуточные остатки:

При последующем делении остатки
повторяются.

Таким
образом, мы убедились в том, что число
различных остатков при выбранном g(x)
равно n
= 15, и, следовательно, код, образованный
таким g(x),
способен
исправить любую одиночную ошибку С тем
же успехом за образующий многочлен кода
мог быть принят и многочлен х⁴+x+1.
При этом был бы получен код, эквивалентный
выбранному.

Однако
использовать для тех же целей многочлен
x⁴
+ х³
+ х²
+ x
+ 1 нельзя. При проверке числа различных
остатков обнаруживается, что их у него
не 15, а только 5 Действительно,

Это
объясняется тем, что многочлен x⁴
+ х³
+ х²
+ x
+ 1 входит в разложение не только двучлена
x¹⁵
+ 1, но и двучлена х⁵
+ 1.

Из
приведенного примера следует, что в
качестве образующего следует выбирать
такой неприводимый многочлен g(x)
(или
произведение таких многочленов), который,
являясь делителем двучлена хⁿ⁺¹,
не входит в разложение ни одного двучлена
типа x^
λ+1, степень
которого λ
меньше n.
В этом случае говорят, что многочлен
q(x)
принадлежит показателю степени n.

В табл. 6.12 приведены
основные характеристики некоторых
кодов, способных исправлять одиночные
ошибки или обнаруживать все одиночные
и двойные ошибки.

Таблица 6.12

Это циклические
коды Хэмминга для исправления одной
ошибки, в которых в отличие от групповых
кодов Хэмминга все проверочные разряды
размещаются в конце кодовой комбинации.

Эти
коды могут быть использованы для
обнаружения любых двойных ошибок.
Многочлен, соответствующий вектору
двойной ошибки, имеет вид ξ(χ)
= xⁱ
+ xⁱ,
или ξ(x)
= xⁱ(x^j—i
+ 1) при j>i.
Так как j-i<n
а g(x)
не кратен
x
и принадлежит показателю степени n,
то ξ(x)
не делится на g(x),
что и
позволяет обнаружить двойные ошибки.

Обнаружение
ошибок кратности три и ниже.
Образующие многочлены кодов, способных
обнаруживать одиночные, двойные и
тройные ошибки, можно определить,
базируясь на следующем указании Хэмминга.
Если известен образующий многочлен
p(x^m)
кода длины n,
позволяющего обнаруживать ошибки
некоторой кратности z
то образующий многочлен g(x)
кода,
способного обнаруживать ошибки следующей
кратности (z+1),
может быть получен умножением многочлена
р(х^m)
на многочлен x+1,
что соответствует введению дополнительной
проверки на четность. При этом число
символов в комбинациях кода за счет
добавления еще одного проверочного
символа увеличивается до n
+ 1.

В
табл. 6.13 приведены основные характеристики
некоторых кодов, способных обнаруживать
ошибки кратности три и менее.

Таблица 6.13

Обнаружение
и исправление независимых ошибок
произвольной кратности. Важнейшим
классом кодов, используемых в каналах,
где ошибки в последовательностях
символов возникают независимо, являются
коды Боуза — Чоудхури — Хоквингема.
Доказано, что для любых целых положительных
чисел m
и s<n/2
существует
двоичный код этого класса длины n
= 2^m—1
с числом проверочных символов не более
ms,
который
способен обнаруживать ошибки кратности
2s
или
исправлять ошибки кратности s.
Для понимания
теоретических аспектов этих кодов
необходимо ознакомиться с рядом новых
понятий высшей алгебры. Вопросы их
построения и технической реализации
рассмотрены в § 6.9. — Обнаружение и
исправление пачек ошибок. Для произвольного
линейного блокового (n,
k)-кода,
рассчитанного на исправление пакетов
ошибок длины b
или менее,
основным соотношением, устанавливающим
связь корректирующей способности с
числом избыточных символов, является
граница Рейджера:

При
исправлении линейным кодом пакетов
длины b
или менее
с одновременным обнаружением пакетов
длины l>=b
или менее требуется по крайней мере b
+ l проверочных
символов.

Из циклических
кодов, предназначенных для исправления
пакетов ошибок, широко известны коды
Бартона, Файра и Рида — Соломона.

Первые две
разновидности кодов служат для исправления
одного пакета ошибок в блоке. Коды Рида
— Соломона способны исправлять несколько
пачек ошибок.

Особенности
декодирования циклических кодов,
исправляющих пакеты ошибок, рассмотрены
далее на примере кодов Файра.

Методы
образования циклического кода.
Существует несколько различных способов
кодирования. Принципиально наиболее
просто комбинации циклического кода
можно получить, умножая многочлены
а(х), соответствующие комбинациям
безызбыточного кода (информационным
символам), на образующий многочлен кода
g(x).
Такой
способ легко реализуется. Однако он
имеет тот существенный недостаток, что
получающиеся в результате умножения
комбинации кода не содержат информационные
символы в явном виде. После исправления
ошибок такие комбинации для выделения
информационных символов приходится
делить на образующий многочлен кода.

Применительно
к циклическим кодам принято (хотя это
и не обязательно) отводить под
информационные k
символов,
соответствующих старшим степеням
многочлена кода, а под проверочные n
— k
символов
низших разрядов.

Чтобы
получить такой систематический код,
применяется следующая процедура
кодирования.

Многочлен
а(х), соответствующий k-разрядной
комбинации безызбыточного кода, умножаем
на х^m,
где m
= n
— k.
Степень
каждого одночлена, входящего в а(х),
увеличивается, что по отношению к
комбинации кода означает необходимость
приписать со стороны младших разрядов
m
нулей.
Произведение а(х)х^m
делим на образующий многочлен g(x).
В общем
случае при этом получаем некоторое
частное q(x)
той же
степени, что и а(х) и остаток r(х).
Последний прибавляем к а(х)х^m.
В результате получаем многочлен

Поскольку
степень g(x)
выбираем
равной m,
степень остатка r(х)
не превышает m
— 1. В комбинации, соответствующей
многочлену а(х)х^m,
m
младших разрядов нулевые, и, следовательно,
указанная операция сложения равносильна
приписыванию r(х)
к а(х) со стороны младших разрядов.

Покажем,
что f(x)
делится
на g(x)
без остатка,
т. е. является многочленом, соответствующим
комбинации кода. Действительно, запишем
многочлен а(х)х^m
в виде

Так как операции
сложения и вычитания по модулю два
идентичны, r(х) можно
перенести влево, тогда

что и требовалось
доказать.

Таким образом,
циклический код можно строить, приписывая
к каждой комбинации безызбыточного
кода остаток от деления соответствующего
этой комбинации многочлена на образующий
многочлен кода. Для кодов, число
информационных символов в которых
больше числа проверочных, рассмотренный
способ реализуется наиболее просто.

Следует указать
еще на один способ кодирования. Так как
циклический код является разновидностью
группового кода, то его проверочные
символы должны выражаться через суммы
по модулю два определенных информационных
символов.

Равенства
для определения проверочных символов
могут быть получены путем решения
рекуррентных соотношений:

где
h
— двоичные коэффициенты так называемого
генераторного многочлена h(x),
определяемого
так

Соотношение
(6.40) позволяет по заданной последовательности
информационных сигналов a₀,
a₁,
…, a_k-1,
вычислить n
— k
проверочных
символов a_k,
a_k+1,
… ,а_n-1.
Проверочные символы, как и ранее,
размещаются на местах младших разрядов.
При одних и тех же информационных
символах комбинации кода, получающиеся
таким путем, полностью совпадают с
комбинациями, получающимися при
использовании предыдущего способа
кодирования. Применение данного способа
целесообразно для кодов с числом
проверочных символов, превышающим число
информационных, например, для кодов
Боуза — Чоудхури — Хоквингема.

Матричная
запись циклического кода.
Полная образующая матрица циклического
кода Mn,k
составляется
из двух матриц: единичной I_k
(соответствующей k
информационным
разрядам) и дополнительной C_k,n—k
(соответствующей
проверочным разрядам):

Построение
матрицы I_kтрудностей не представляет.

Если
образование циклического кода производится
на основе решения рекуррентных
соотношений, то его дополнительную
матрицу можно определить, воспользовавшись
правилами, указанными ранее. Однако
обычно строки дополнительной матрицы
циклического кода C_k,n—k
определяются
путем вычисления многочленов r(х).
Для каждой строки матрицы Ik
соответствующий r(х)
находят делением информационного
многочлена а(х)х^m
этой строки на образующий многочлен
кода g(x).

Дополнительную
матрицу можно определить и не строя I_k.
Для этого достаточно делить на g(x)
комбинацию
в виде единицы с рядом нулей и получающиеся
остатки записывать в качестве строк
дополнительной матрицы. При этом если
степень какого-либо r(х)
оказывается меньше n
— k—
1, то
следующие за этим остатком строки
матрицы получают путем циклического
сдвига предыдущей строки влево до тех
пор, пока степень r(х)
не станет равной n
— k—1.
Деление производится до получения k
строк
дополнительной матрицы.

Пример
6.14. Запишем
образующую матрицу для циклического
кода (15,11) с порождающим многочленом
g(x)
= x⁴
+ x³
+ 1 ·

Воспользовавшись
результатами ранее проведенного деления,
получим

Существует
другой способ построения образующей
матрицы, базирующийся на основной
особенности циклического (n,k)-кода (см § 6.6). Он проще
описанного, но получающаяся матрица
менее удобна.

Матричная запись
кодов достаточно широко распространена.

Укороченные
циклические коды.
Корректирующие возможности циклических
кодов определяются степенью m
образующего многочлена. В то время как
необходимое число информационных
символов может быть любым целым числом,
возможности в выборе разрядности кода
весьма ограничены.

Если,
например, необходимо исправить единичные
ошибки при k
= 5, то нельзя
взять образующий многочлен третьей
степени, поскольку он даст только семь
остатков, а общее число разрядов получится
равным 8.

Следовательно,
необходимо брать многочлен четвертой
степени и тогда n=
15. Такой код рассчитан на 11 информационных
разрядов.

Однако
можно построить код минимальной
разрядности, заменив в (n,
k)
-коде j
первых информационных символов нулями
и исключив их из кодовых комбинаций.
Код уже не будет циклическим, поскольку
циклический сдвиг одной разрешенной
кодовой комбинации не всегда приводит
к другой разрешенной комбинации того
же кода. Получаемый таким путем линейный
(n
— j,
k —
j)-код
называют укороченным циклическим кодом.
Минимальное расстояние этого кода не
менее, чем минимальное кодовое расстояние
(n,
k)-кода,
из которого он получен. Матрица
укороченного кода получается из
образующей матрицы (n,
k)-кода
исключением j
строк и столбцов, соответствующих
старшим разрядам. Например, образующая
матрица кода (9,5), полученная из матрицы
кода (15,11), имеет вид

Циклические
коды позволяют обнаруживать и исправлять
групповые ошибки. В циклических кодах
широко используется операция циклической
перестановки (самый старший разряд
переставляется в конец кодовой комбинации,
а остальные сдвигаются влево или,
наоборот, младший разряд переставляется
в начало, остальные сдвигаются вправо).

При
формировании циклических кодов происходит
деление на образующий полином.

Представление
кодовой комбинации в виде полинома.

Q(x)=111111=x⁵+x⁴+x³+x²+x¹+x⁰

x_i
– двоичный разряд. x¹=x,
x⁰=1

Если
какой-либо разряд x_i
= 0 в составе полинома, то его опускают.

Q(x)=1100110=x⁶+x⁵+x²+x

Образующий
полином
– это полином,
который является простым числом: (11)₁₀,
(13)₁₀,
(17)₁₀,
(19)₁₀
и т.д. Он выбирается заранее как делитель,
позволяющий выполнять обнаружение и
исправление ошибки.

P(x)=(11)₁₀=(1011)₂=x³+x+1
Степень образующего полинома – к.
(к=3)

Операция
деления полинома на полином.

Деление
сходно с алгебраическим, но есть отличие:

• операция
  вычитания заменяется суммированием
  по модулю 2;

• деление
  заканчивается, если наивысшая степень
  у остатка меньшей таковой у делителя;

• интерес
  представляет не частное от деления, а
  остаток.

Рассмотрим
пример деления.

Пусть
Q (x) = x ⁵
+ x ³
+ x — делимое

P
(x) = x ³
+ x + 1 — делитель

x 5 + x 3 + x	x 3 + x + 1
x 5 + x 3 + x 2	x 2
x 2 + x

Остаток:
R
(x)
= x
²
+ x
= 110

Формирование
циклического кода.

Правило:
нужно исходную кодовую комбинацию (КК)
— Q(x)
разделить на образующий полином Р(х) и
дописать справа остаток от деления к
исходной КК. Обозначим F(x)
– комбинация циклического кода.

F(x)
= Q(x)
*x
^k
R(x)
, где k
– степень образующего полинома.

Величина
k
показывает количество сдвигов влево,
которое Q(x)
должно претерпеть.

Пример:
Q(x)
= x
⁵
+ x
³
+ x
= 101010 – исходная КК,

Р(х)
= x
³
+ x
+ 1 = 1011 — образующий полином

R(x)
= x
²
+ x
= 110 — полученный остаток от деления,

F(x)
= 101010 110 — комбинация циклического кода,

где:
101010 — информационная часть,

110
– контрольная часть

Остаток
R(x)
называется синдромом..

Пусть
Q(x)
= 1110. Если k
=3, то Q(x)
X
^k
= 1110 000

Проверка
правильности циклического кода.

Правильность
циклического кода проверяется с помощью
операции деления на образующий полином.
Если в результате деления остаток равен
нулю (R(x)=0),
то считается ,что комбинация циклического
кода ошибки не содержит. Если же при
делении получился остаток, то комбинация
содержит ошибку, которую можно исправить.
Процедура отыскания места ошибки
сводится к циклическим сдвигам КК F(х)
и деление ее на образующий полином.

W
— вес остатка (количество единиц в нем).

S
— кратность ошибки (количество ошибочных
разрядов в кодовой комбинации).

В
алгоритме используются циклические
сдвиги влево и вправо, количество которых
подсчитывается во время выполнения.

C_n
— счетчик
циклических сдвигов.

Соседние файлы в папке Метрология и ТМ

• #
• #
• #

Время на прочтение
6 мин

Количество просмотров 60K

Код Хэмминга – не цель этой статьи. Я лишь хочу на его примере познакомить вас с самими принципами кодирования. Но здесь не будет строгих определений, математических формулировок и т.д. Эта просто неплохой трамплин для понимания более сложных блочных кодов.

Самый, пожалуй, известный код Хэмминга (7,4). Что значат эти цифры? Вторая – число бит информационного слова — то, что мы хотим передать в целости и сохранности. А первое – размер кодового слова: информация удобренная избыточностью. Кстати термины «информационное слово» и «кодовое слово», употребляются во всех 7-ми книгах по теории помехоустойчивого кодирования, которые мне довелось бегло пролистать.

Такой код исправляет 1 ошибку. И не важно где она возникла. Избыточность несёт в себе 3 бита информации, этого достаточно, чтобы указать на одно из 7 положений ошибки или показать, что её нет. То есть ровно 8 вариантов ответов мы ждём. А 8 = 2^3, вот как всё совпало.

Чтобы получить кодовое слово, нужно информационное слово представить в виде полинома и умножить его на порождающий полином g(x). Любое число, переведя в двоичный вид, можно представить в виде полинома. Это может показаться странным и у не подготовленного читателя сразу встаёт только один вопрос «да зачем же так усложнять?». Уверяю вас, он отпадёт сам собой, когда мы получим первые результаты.

К примеру информационное слово 1010, значение каждого его разряда это коэффициент в полиноме:

Во многих книгах пишут наоборот x+x^3. Не поддавайтесь на провокацию, это вносит только путаницу, ведь в записи числа 2-ичного, 16-ричного, младшие разряды идут справа, и сдвиги мы делаем влево/вправо ориентируясь на это. А теперь давайте умножим этот полином на порождающий полином. Порождающий полином специально для Хэмминга (7,4), встречайте: g(x)=x^3+x+1. Откуда он взялся? Ну пока считайте что он дан человечеству свыше, богами (объясню позже).

Если нужно складывать коэффициенты, то делаем по модулю 2: операция сложения заменяется на логическое исключающее или (XOR), то есть x^4+x^4=0. И в конечном итоге результат перемножения как видите из 4х членов. В двоичном виде это 1001110. Итак, получили кодовое слово, которое будем передавать на сторону по зашумлённому каналу. Замете, что перемножив информационное слово (1010) на порождающий полином (1011) как обычные числа – получим другой результат 1101110. Этого нам не надо, требуется именно «полиномиальное» перемножение. Программная реализация такого умножения очень простая. Нам потребуется 2 операции XOR и 2 сдвига влево (1й из которых на один разряд, второй на два, в соответствии с g(x)=1011):

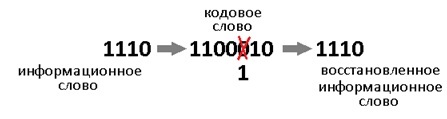
Давайте теперь специально внесём ошибку в полученное кодовое слово. Например в 3-й разряд. Получиться повреждённое слово: 1000110.

Как расшифровать сообщение и исправить ошибку? Разумеется надо «полиномиально» разделить кодовое слово на g(x). Тут я уже не буду писать иксы. Помните что вычитание по модулю 2 — это то же самое что сложение, что в свою очередь, тоже самое что исключающее или. Поехали:

В программной реализации опять же ничего сверх сложного. Делитель (1011) сдвигаем влево до самого конца на 3 разряда. И начинаем удалять (не без помощи XOR) самые левые единицы в делимом (100110), на его младшие разряды даже не смотрим. Делимое поэтапно уменьшается 100110 -> 0011110 -> 0001000 -> 0000011, когда в 4м и левее разрядах не остаётся единиц, мы останавливаемся.

Нацело разделить не получилось, значит у нас есть ошибка (ну конечно же). Результат деления в таком случае нам без надобности. Остаток от деления является синдром, его размер равен размеру избыточности, поэтому мы дописали там ноль. В данном случае содержание синдрома нам никак не помогает найти местоположение повреждения. А жаль. Но если мы возьмём любое другое информационное слово, к примеру 1100. Точно так же перемножим его на g(x), получим 1110100, внесём ошибку в тот же самый разряд 1111100. Разделим на g(x) и получим в остатке тот же самый синдром 011. И я гарантирую вам, что к такому синдрому мы придём в обще для всех кодовых слов с ошибкой в 3-м разряде. Вывод напрашивается сам собой: можно составить таблицу синдромов для всех 7 ошибок, делая каждую из них специально и считая синдром.

В результате собираем список синдромов, и то на какую болезнь он указывает:

Теперь у нас всё есть. Нашли синдром, исправили ошибку, ещё раз поделили в данном случае 1001110 на 1011 и получили в частном наше долгожданное информационное слово 1010. В остатке после исправления уже будет 000. Таблица синдромов имеет право на жизнь в случае маленьких кодов. Но для кодов, исправляющих несколько ошибок – там список синдромов разрастается как чума. Поэтому рассмотрим метод «вылавливания ошибок» не имея на руках таблицы.

Внимательный читатель заметит, что первые 3 синдрома вполне однозначно указывают на положение ошибки. Это касается только тех синдромов, где одна единица. Кол-во единиц в синдроме называют его «весом». Опять вернёмся к злосчастной ошибке в 3м разряде. Там, как вы помните был синдром 011, его вес 2, нам не повезло. Сделаем финт ушами — циклический сдвиг кодового слова вправо. Остаток от деления 0100011 / 1011 будет равен 100, это «хороший синдром», указывает что ошибка во втором разряде. Но поскольку мы сделали один сдвиг, значит и ошибка сдвинулась на 1. Вот собственно и вся хитрость. Даже в случае жуткого невезения, когда ошибка в 6м разряде, вы, обливаясь потом, после 3 мучительных делений, но всё таки находите ошибку – это победа, лишь потому, что вы не использовали таблицу синдромов.

А как насчёт других кодов Хэмминга? Я бы сказал кодов Хэмминга бесконечное множество: (7,4), (15,11), (31,26),… (2^m-1, 2^m-1-m). Размер избыточности – m. Все они исправляют 1 ошибку, с ростом информационного слова растёт избыточность. Помехоустойчивость слабеет, но в случае слабых помех код весьма экономный. Ну ладно, а как мне найти порождающую функцию например для (15,11)? Резонный вопрос. Есть теорема, гласящая: порождающий многочлен циклического кода g(x) делит (x^n+1) без остатка. Где n – нашем случае размер кодового слова. Кроме того порождающий полином должен быть простым (делиться только на 1 и на самого себя без остатка), а его степень равна размеру избыточности. Можно показать, что для Хэмминга (7,4):

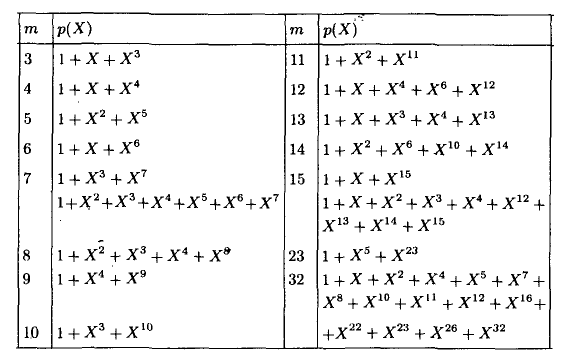
Этот код имеет целых 2 порождающих полинома. Не будет ошибкой использовать любой из них. Для остальных «хэммингов» используйте вот эту таблицу примитивных полиномов:

Соответственно для (15,11) порождающий многочлен g(x)=x^4+x+1. Ну а теперь переходим к десерту – к матрицам. С этого обычно начинают, но мы этим закончим. Для начала преобразую g(x) в матрицу, на которую можно умножить информационное слово, получив кодовое слово. Если g = 1011, то:

Называют её «порождающей матрицей». Дадим обозначение информационному слову d = 1010, а кодовое обозначим k, тогда:

Это довольно изящная формулировка. По быстродействию ещё быстрее, чем перемножение полиномов. Там нужно было делать сдвиги, а тут уже всё сдвинуто. Вектор d указывает нам: какие строки брать в расчёт. Самая нижняя строка матрицы – нулевая, строки нумеруются снизу вверх. Да, да, всё потому что младшие разряды располагаются справа и от этого никуда не деться. Так как d=1010, то я беру 1ю и 3ю строки, произвожу над ними операцию XOR и вуаля. Но это ещё не всё, приготовьтесь удивляться, существует ещё проверочная матрица H. Теперь перемножением вектора на матрицу мы можем получить синдром и никаких делений полиномов делать не надо.

Посмотрите на проверочную матрицу и на список синдромов, который получили выше. Это ответ на вопрос откуда берётся эта матрица. Здесь я как обычно подпортил кодовое слово в 3м разряде, и получил тот самый синдром. Поскольку сама матрица – это и есть список синдромов, то мы тут же находим положение ошибки. Но в кодах, исправляющие несколько ошибок, такой метод не прокатит. Придётся вылавливать ошибки по методу, описанному выше.

Чтобы лучше понять саму природу исправления ошибок, сгенерируем в обще все 16 кодовых слов, ведь информационное слово состоит всего из 4х бит:

Посмотрите внимательно на кодовые слова, все они, отличаются друг от друга хотя бы на 3 бита. К примеру возьмёте слово 1011000, измените в нём любой бит, скажем первый, получиться 1011010. Вы не найдёте более на него похожего слова, чем 1011000. Как видите для формирования кодового слова не обязательно производить вычисления, достаточно иметь эту таблицу в памяти, если она мала. Показанное различие в 3 бита — называется минимальное «хэммингово расстояние», оно является характеристикой блокового кода, по нему судят сколько ошибок можно исправить, а именно (d-1)/2. В более общем виде код Хэмминга можно записать так (7,4,3). Отмечу только, что Хэммингово расстояние не является разностью между размерами кодового и информационного слов. Код Голея (23,12,7) исправляет 3 ошибки. Код (48, 36, 5) использовался в сотовой связи с временным разделением каналов (стандарт IS-54). Для кодов Рида-Соломона применима та же запись, но это уже недвоичные коды.

Список используемой литературы:

1. М. Вернер. Основы кодирования (Мир программирования) — 2004
2. Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования (Мир связи) — 2006
3. Р. Блейхут. Теория и практика кодов, контролирующих ошибки — 1986