Как найти образующую конуса без высоты

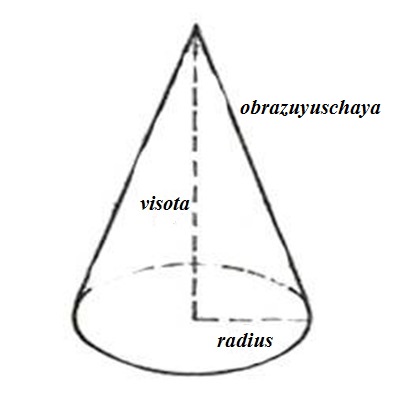
Через образующую и высоту конуса можно найти радиус, построив прямоугольный треугольник, в котором образующая является гипотенузой, а высота и радиус – катетами. Из этого же треугольника становится возможным вычислить угол между образующей и основанием, а для того чтобы найти угол раствора конуса, необходимо вернуться к равнобедренному треугольнику из двух образующих и диаметра, в котором угол раствора будет равен разности двух углов при основании от 180 градусов. (рис.40.1, 40.2)
r=√(l^2-h^2 )
sin⁡β=h/l
α=180°-2β

Теперь, зная радиус конуса, можно найти диаметр, периметр и площадь основания круга, подставив в стандартные формулы квадратный корень, полученный по теореме Пифагора.
d=2r=2√(l^2-h^2 )
P=2πr=2π√(l^2-h^2 )
S_(осн.)=πr^2=π(l^2-h^2)

Площадь боковой поверхности конуса и площадь полной поверхности конуса, выраженные через высоту и образующую, также содержат в формулах вместо радиуса квадратный корень из разности квадратов образующей и высоты.
S_(б.п.)=πrl=πl√(l^2-h^2 )
S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=π(lr+r^2 )=π(l√(l^2-h^2 )+l^2-h^2)

Чтобы вычислить объем конуса через высоту и образующую, необходимо умножить треть числа π на высоту и разность квадратов образующей и высоты вместо квадрата радиуса.
V=1/3 S_(осн.) h=(πr^2 h)/3=(πh(l^2-h^2))/3

Радиус сферы, которая может быть вписана в конус, напрямую зависит не только от высоты и образующей, но и от радиуса, поэтому его формула существенно услояжняется наличием радикала, полученного через теорему Пифагора для радиуса конуса. В то же время радиус описанной вокруг конуса сферы зависит только от образующей и высоты, представляя собой отношение квадрата образующей к удвоенной высоте. (рис.40.3, 40.4)
r_1=hr/(l+r)=(h√(l^2-h^2 ))/(l+√(l^2-h^2 ))
R=l^2/2h

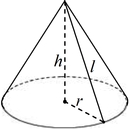
Конус – это геометрическая фигура, полученная вращением прямоугольного треугольника вокруг одного из катетов. У каждого конуса есть основание и боковая поверхность.

Любой конус характеризуется высотой h (осевой линией), радиусом r и образующей l (см. рисунок). Именно эти характеристики используются в формулах конуса при вычислении объема, площади поверхности и площади боковой поверхности.

Высота конуса (осевая линия) – это перпендикуляр, проведенный из вершины конуса к основанию.

Радиус конуса – это радиус его основания.

Образующая конуса – это отрезок, который соединяет вершину конуса с любой точкой, лежащей на линии окружности основания.

Формула образующей конуса

Образующую конуса можно найти, зная ее высоту H и радиус R:

L = √H² + R²

Формула площади боковой поверхности конуса

Площадь боковой поверхности конуса можно получить, зная его радиус R и образующую L:

S_{бок.пов} = πRL

Формула площади основания конуса

Площадь основания конуса можно вычислить по его радиусу R:

S_осн = πR²

Формула площади конуса

Площадь поверхности конуса можно получить, сложив площадь боковой поверхности и площадь основания конуса:

S = S_{бок.пов} + S_осн = πRL + πR²

Формула объема конуса

Объем конуса можно вычислить, зная его высоту H и площадь основания:

V = 1/3 ⋅ S_осн ⋅ H = 1/3πR²H

Как найти образующую усеченного конуса

Усеченным конусом называется геометрическое тело, которое получилось в результате сечения полного конуса плоскостью, параллельной его основанию. Согласно другому определению, усеченный конус образован вращением прямоугольной трапеции вокруг той ее боковой стороны, которая перпендикулярна основаниям. Вторая боковая сторона при этом является образующей. Вычислять ее необходимо так же, как и боковую сторону прямоугольной трапеции.

Вам понадобится

• — усеченный конус с заданными параметрами;
• — линейка;
• — карандаш;
• — калькулятор;
• — теорема Пифагора;
• — теоремы синусов и косинусов.

Инструкция

Сделайте чертеж. Обозначьте на нем заданные размеры усеченного конуса. Его можно построить по нескольким параметрам. Вам должны быть известны радиусы основания и высота. Могут быть и другие наборы данных — например, радиусы обоих оснований и угол наклона образующей к одному из них. Могут быть заданы высота, угол наклона и один из радиусов. Если вы пока еще не знаете нужных для построения точного чертежа параметров, начертите конус приблизительно и обозначьте имеющиеся условия.

Постройте осевое сечение. Оно представляет собой равнобедренную трапецию ABCD, параллельные стороны которой являются диаметрами основания, а боковые — образующими. Обозначьте точки пересечения оси с основаниями усеченного конуса как O’ и O». Ось О’О» одновременно является и высотой прямого усеченного конуса. Обозначьте радиус нижнего основания как R, а верхнего — как r. Образующую CD обозначьте как L.

Выполните дополнительное построение. Начертите из точки C высоту к радиусу нижнего основания. Она будет параллельная и равна оси O’O». Точку пересечения ее с плоскостью нижнего основания обозначьте как N, а саму высоту — h. У вас получился прямоугольный треугольник CND.

Посмотрите, какие данные для вычисления гипотенузы этого треугольника у вас имеются и найдите недостающие. При условии, что даны оба радиуса, найдите сторону DN. Она равна разности радиусов R и r. То есть, согласно теореме Пифагора, сторона L в данном случае равна квадратному корню из суммы квадратов высоты и разности радиусов или L = √h2+(R-r)2.

Если даны высота h и угол наклона образующей к основанию, найдите образующую L по теореме синусов. Она равна дроби, в числителе которой будет известный катет h, а в знаменателе — синус противолежащего ей угла СDN.

При условии, что даны радиус верхней окружности, высота и угол BCD, вычислите сначала нужный вам угол наклона образующей к нижнему основанию. Вспомните, чему равна сумма углов выпуклого четырехугольника. Она равна 360°. У прямоугольной трапеции O’O»CD вам известны три угла. Найдите по ним четвертый и по его синусу — образующую.

Видео по теме

Источники:

• образующая усеченного конуса

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Задание.
Как найти образующую конуса, если диаметр его основания равен 12 см, а высота равна 8 см.

Решение.
Изобразим схематически конус, на котором обозначим его высоту, радиус основания и образующую. Образующая конуса соединяет его вершину с одной из точек на окружности основания конуса. Радиус также соединяет центр окружности с любой из точек на этой окружности. Поэтому можем изобразить радиус и высоту на рисунке так, как нам будет удобно использовать их для решения задачи. Пусть концы радиуса и образующей совпадают.

Из рисунка хорошо видно, что из высоты, радиуса и образующей получается прямоугольный треугольник, к которому можно применить теорему Пифагора. Запишем уравнение для данного треугольника:

   

Значение высоты известно из условия, радиус можно найти через диаметр. Таким образом, вычислим значение образующей.
Итак, найдем длину радиуса, зная, что диаметр равен 12 см:
(см).
Теперь подставим известные значения в теорему Пифагора:

   

   

   

   

(см).

Ответ. 10 см.

Площадь поверхности конуса. Для вас очередная статья с конусами. Рекомендую посмотреть статью. Здесь в некоторых заданиях используется тот же подход к решению.

В представленных заданиях речь идет о площади боковой поверхности конуса. Необходимо знать формулу, по которой она вычисляется:

где l – длина окружности основания

L – образующая

*Образующая конуса – это отрезок, соединяющий вершину конуса

и точку, лежащую на окружности основания.

Мы знаем, что длина окружности вычисляется по формуле:

Поэтому можем записать:

где R – радиус основания конуса

L – длина образующей

*Стоит отметить некоторую некорректность в условиях (не только в представленных задачах), а именно — не даны единицы измерения (метры, сантиметры, …), а только числовое выражение линейных характеристик.

Поэтому при нахождении площади следовало бы записывать ответ в задачах следующим образом:

10 кв.ед. или 49 кв.ед. (квадратные единицы)

Но мы с вами закроем на это глаза. Итак, р ассмотрим задачи:

27135. Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.

Подставляем данные:

Ответ: 3

75697. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 36 раз, а радиус основания останется прежним?

Площадь боковой поверхности конуса:

Образующая увеличивается в 36 раз. Радиус остался прежним, значит длина окружности основания не изменилась.

Значит площадь боковой поверхности изменённого конуса будет иметь вид:

Таким образом, она увеличится в 36 раз.

*Зависимость прямолинейная, поэтому эту задачу без труда можно решить устно.

Ответ: 36

27137. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 1,5 раза?

Площадь боковой поверхности конуса равна:

Радиус уменьшается в 1,5 раза, то есть:

Получили, что площадь боковой поверхности уменьшилась в 1,5 раза.

Ответ: 1,5

27159. Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на Пи.

Полная поверхность конуса:

Необходимо найти радиус.

Известна высота и образующая, по теореме Пифагора вычислим радиус:

Таким образом:

Полученный результат разделим на Пи и запишем ответ.

Ответ: 144

76299. Площадь полной поверхности конуса равна 108. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

Формула полной поверхности конуса:

Сечение проходит через середину высоты параллельно основанию. Значит радиус основания и образующая отсеченного конуса будут в 2 раза меньше радиуса и образующей исходного конуса. Запишем чему равна площадь поверхности отсечённого конуса:

Получили, что она будет в 4 раза меньше площади поверхности исходного, то есть 108:4 = 27.

Ответ: 27

*Так как исходный и отсечённый конус являются подобными телами, то можно было воспользоваться свойством подобия:

27167. Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на Пи.

Пусть α — плоскость, точка S — точка, не лежащая в этой плоскости. Возьмем на плоскости произвольный круг с радиусом R . Соединим произвольную точку A этого круга с точкой S отрезком AS . Если точка А будет описывать круг с радиусом R , то отрезки AS будут заполнять некоторое тело. Это тело называют круговым конусом .

Границей конуса является круг радиуса R и боковая поверхность конуса.
Боковую поверхность описывает отрезок AS , когда точка A описывает круг.
Точка S является вершиной конуса. Множество отрезков AS , соединяющих вершину с окружностью основания являются направляющими конуса.Если перпендикуляр, опущенный из точки S , совпадает с центром основания, то конус называется прямым.Очень часто говорят, что прямой конус образуется в результате вращения прямоугольного треугольника вокруг оси, содержащий его катет.
На данном рисунке прямой конус получился в результате вращения прямоугольного треугольника AOS вокруг катета SO . Тогда говорят, что

• Катет SO –это высота конуса;
• Гипотенуза AS –образующая конуса;
• Катет AO – радиус конуса.

Площадь боковой поверхности конуса через его радиус и направляющую

Пусть дан конус с радиусом R и образующей L
AS=L, AO=R

Разрежем конус по образующей L и развернем его боковую поверхность.
В результате получим криволинейный треугольник ASA` , где AS=L, A`S=L.
Дуга AA` -это вытянутая окружность основания конуса с радиусом R . Следовательно, длина дуги AA` будет равна 2πR
Площадь боковой поверхности будет равна площади сектора круга с радиусом R .
Если угол α — радиальная мера угла, то:
где α=∠{ASA`}
Чтобы найти угол ∠{ASA`} воспользуемся формулой длины дуги, которая стягивает данный угол:
Но с другой стороны:
Приравняем правые части равенств. Имеем:
Выразим α:
Подставим полученное выражение в формулу площади сектора:
Следовательно, боковая поверхность конуса равна произведению числа π на радиус конуса и его образующую.
Формула боковой поверхности конуса будет иметь следующий вид:

Пример расчета площади боковой поверхности конуса, если известны его радиус и направляющая
Найти площадь боковой поверхности конуса с радиусом равным 3 см, образованным направляющей равной 7 см
По условию задачи L = 5см, R =3см
Формула боковой поверхности конуса:

Подставив в формулу значения из условия задачи, имеем:

Площадь боковой поверхности конуса через его радиус и высоту

Очень часто в задачах на вычисление площади боковой поверхности конуса известна высота конуса вместо его направляющей.
Так как конус прямой, то треугольник AOS — прямоугольный, где AO и OS – катеты, а AS –гипотенуза. Воспользовавшись теоремой Пифагора, получаем:
Отсюда:
Но
Тогда:
Подставим данное выражение в формулу площади боковой поверхности конуса:
Боковая поверхность конуса равна произведению числа на радиус конуса и корень квадратный из суммы квадратов радиуса и высоты конуса

Конусом (прямым круговым конусом) называется тело, состоящее из круга (основания конуса), точки, не лежащей в плоскости этого круга (вершины конуса), и всех отрезков, соединяющих вершину конуса с точками основания.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса .

Конус – тело, которое ограничено конической поверхностью и плоскостью, на которой лежат концы образующих конической поверхности.

Коническая поверхность – поверхность, которая образуется движением отрезка, один из концов которого неподвижен, а другой перемещается на плоскости вдоль некоторой кривой. Отрезки называют образующими конической поверхности, а кривую – направляющей . Неподвижная точка – вершина конической поверхности.

Боковая поверхность конуса – часть конической поверхности, ограниченная плоскостью.

Основание конуса – часть плоскости, отсекаемая боковой поверхностью конуса.

Конус называется прямым , если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания (См.Рис.1 ). В противном случае, конус называется наклонным . В школьном курсе изучается .

Круговой конус – конус, у которого в основании круг.

Прямой круговой конус (просто конус) – круговой конус, у которого прямая, соединяющая вершину конуса с центром круга, лежащего в основании, перпендикулярна плоскости основания.

Ось конуса – прямая, проходящая через вершину конуса и центр основания конуса.

Высота конуса – отрезок оси конуса, соединяющий вершину конуса с центром основания.

Конус можно рассматривать как тело, полученное вращением прямоугольного треугольника вокруг прямой, содержащей его катет.

Образующие конуса совпадают с образующими конической поверхности.

Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением . Плоскость, проходящая через образующую конуса и перпендикулярная осевому сечению, проведенному через эту образующую, называется . См.Рис.2 .

Развёртка боковой поверхности конуса – круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса.

Площадь боковой поверхности (круглого) конуса равна произведению половины длины окружности основания (C ) на образующую (l ): $$S_{бок}=frac{1}{2}cdot Cl=picdot rl$$ , где r – радиус основания, l – длина образующей.

Площадь полной поверхности конуса – сумма площадей основания конуса и его боковой поверхности, которая записывается формулой: $$S_{полн}=picdot r(l+r)$$ , где r – радиус основания, l – длина образующей.

Объем всякого конуса равен трети произведения площади основания (S ) на высоту (h ): $$V=frac{1}{3}cdot Sh$$ Объем круглого конуса : $$V=frac{1}{3}cdot Sh=frac{1}{3}cdotpi r^2 cdot h$$

Усеченный конус – это часть конуса, ограниченная его основанием и сечением, параллельным плоскости основания. См.Рис.3

Мы знаем, что такое конус, попробуем найти площадь его поверхности. Зачем нужно решать такую задачу? Например, нужно понять, сколько теста пойдет на изготовление вафельного рожка? Или сколько кирпичей понадобится, чтобы сложить кирпичную крышу замка?

Измерить площадь боковой поверхности конуса просто так не получится. Но представим себе все тот же рожок, обмотанный тканью. Чтобы найти площадь куска ткани, нужно разрезать и разложить ее на столе. Получится плоская фигура, ее площадь мы сможем найти.

Рис. 1. Разрез конуса по образующей

Сделаем так же с конусом. «Разрежем» его боковую поверхность вдоль любой образующей, например, (см. рис. 1).

Теперь «размотаем» боковую поверхность на плоскость. Получаем сектор. Центр этого сектора – вершина конуса, радиус сектора равен образующей конуса, а длина его дуги совпадает с длиной окружности основания конуса. Такой сектор называется разверткой боковой поверхности конуса (см. рис. 2).

Рис. 2. Развертка боковой поверхности

Рис. 3. Измерение угла в радианах

Попробуем найти площадь сектора по имеющимся данным. Сперва введем обозначение: пусть угол при вершине сектора в радианах (см. рис. 3).

С углом при вершине развертки нам придется часто сталкиваться в задачах. Пока же попробуем ответить на вопрос: а не может ли этот угол получиться больше 360 градусов? То есть не получится ли так, что развертка наложится сама на себя? Конечно же, нет. Докажем это математически. Пусть развертка «наложилась» сама на себя. Это означает, что длина дуги развертки больше длины окружности радиуса . Но, как уже было сказано, длина дуги развертки есть длина окружности радиуса . А радиус основания конуса, разумеется, меньше образующей, например, потому, что катет прямоугольного треугольника меньше гипотенузы

Тогда вспомним две формулы из курса планиметрии: длина дуги . Площадь сектора: .

В нашем случае роль играет образующая , а длина дуги равна длине окружности основания конуса, то есть . Имеем:

Окончательно получаем: .

Наряду с площадью боковой поверхности можно найти и площадь полной поверхности. Для этого к площади боковой поверхности надо прибавить площадь основания. Но основание – это круг радиуса , чья площадь по формуле равна .

Окончательно имеем: , где – радиус основания цилиндра, – образующая.