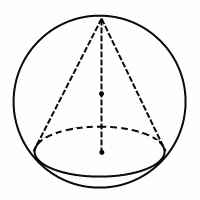
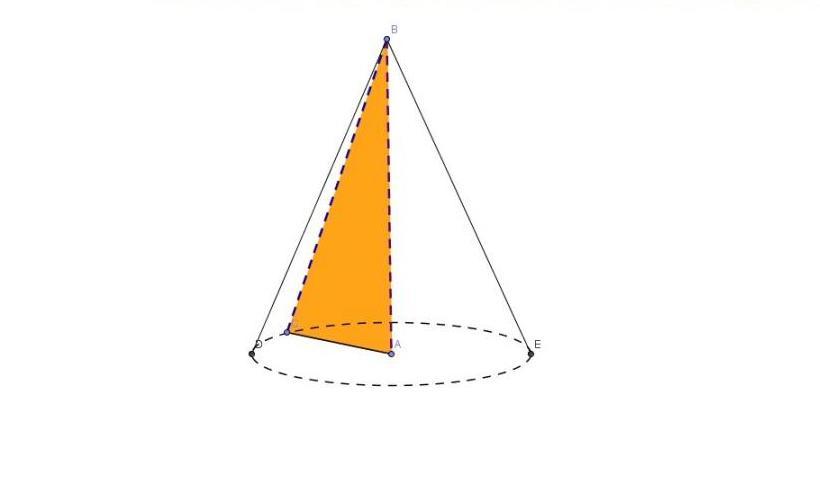
Решение задач на конус, вписанный в шар (конус, вписанный в сферу) сводится к рассмотрению одного или нескольких треугольников.
Конус вписан в шар, если его вершина и окружность основания лежат на поверхности шара, то есть на сфере. Центр шара лежит на оси конуса.
При решении задач на конус, вписанный в шар, удобно рассматривать сечение комбинации тел плоскостью, проходящей через ось конуса и центр шара. Сечение представляет собой большой круг шара (то есть круг, радиус которого равен радиусу шара) с вписанным в него равнобедренным треугольником — осевым сечением конуса. Боковые стороны этого треугольника — образующие конуса, основание — диаметр конуса.
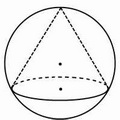
Если угол между образующими острый, центр описанного круга лежит внутри треугольника (соответственно, центр описанного около конуса шара — внутри конуса).
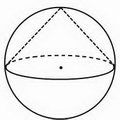
Если угол между образующими прямой, центр круга лежит на середине основания треугольника (центр шара совпадает с центром основания конуса).
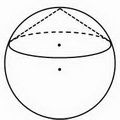
Если угол между образующими тупой, центр круга лежит вне треугольника (центр описанного шара — вне конуса).
Если в условии задачи не сказано, где именно лежит центр описанного шара, желательно рассмотреть, как могут повлиять на решение различные варианты его расположения.
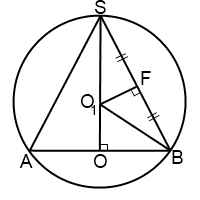
Треугольник SO1B — равнобедренный с основанием SB (так как SO1=O1B=R). Значит, у него углы при основании равны: ∠OSB=∠O1BS=α, и O1F — медиана, высота и биссектриса. Отсюда SF=l/2.
При решении задач на конус, вписанный в шар, можно рассмотреть прямоугольные треугольники SFO1 и SOB. Они подобны (по острому углу S). Из подобия треугольников
В прямоугольном треугольнике SOB ∠OBS=90º — ∠OSB=90º-α. По теореме Пифагора
В прямоугольном треугольнике O1OB ∠OBO1=90º — ∠O1BS=90º — α — α=90º — 2α.
и уже полученное соотношение
Радиус и образующая конуса
Свойства
Поскольку радиус конуса характеризует размер его основания, то зная его, можно найти диаметр, длину окружности и площадь круга, лежащего в основании. Диаметр представляет собой удвоенный радиус, длина окружности – удвоенный радиус, умноженный на число π, а площадь круга – квадрат радиуса, умноженный на число π. d=2r P=2πr S_(осн.)=πr^2
Зная радиус и образующую конуса, можно уже найти его высоту, угол между образующей и основанием, угол раствора конуса. Высота конуса через радиус и образующую ищется по теореме Пифагора в прямоугольном треугольнике, оттуда же можно вычислить и угол β через тригонометрические отношения сторон. Угол α можно найти из равнобедренного треугольника, образованного двумя образующими и диаметром, отняв из 180 градусов два угла β. (рис.40.1, 40.2) h=√(l^2-r^2 ) cosβ=r/l α=180°-2β
Площадь боковой поверхности конуса равна произведению полупериметра основания на образующую или произведению числа π на радиус и образующую. Чтобы найти площадь полной поверхности, зная радиус и образующую конуса, необходимо прибавить к площади боковой поверхности произведение числа π на квадрат радиуса, что является площадью основания конуса. S_(б.п.)=πrl S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)
Объем конуса, также как и объем пирамиды рассчитывается как одна треть основания, умноженная на высоту. V=1/3 S_(осн.) h=(πr^2 h)/3
Радиус сферы, вписанной в конус, вычисляется как произведение высоты на радиус конуса, деленное на сумму радиуса и образующей. Радиус сферы, описанной вокруг конуса, представляет собой отношение квадрата образующей к удвоенной высоте. (рис.40.3, 40.4) r_1=hr/(l+r)=(r√(l^2-r^2 ))/(l+r) R=l^2/2h
Как найти образующую конуса обычного и усеченного. Формулы
Пространственные фигуры подробно рассматриваются в старших классах общеобразовательных школ в курсе стереометрии. Данная статья содержит ответ на вопрос о том, как найти образующую конуса круглого прямого и образующую соответствующей усеченной фигуры.
Фигура конус
Чтобы понять, как найти образующую конуса, следует дать представление об этой фигуре. Круглым прямым конусом называют фигуру вращения прямоугольного треугольника вокруг одного из его катетов. Рисунок ниже демонстрирует процесс вращения.

Полученная пространственная фигура имеет следующие характеристики:
Заметим, что высота фигуры пересекает круглое основание в его центре. Это является достаточным условием, чтобы считать конус прямым.
Образующая конуса
Теперь можно переходить к ответу на вопрос о том, как найти образующую конуса круглого прямого. Выше было сказано, что она представляет собой отрезок, который лежит на конической поверхности и соединяет вершину с точкой окружности основания. В прямоугольном треугольнике, из которого был конус получен, образующая является гипотенузой. Это наблюдение позволяет записать известную теорему Пифагора, связав образующую g с радиусом r и высотой h фигуры. Формула, как найти образующую конуса, имеет вид:
Помимо этой формулы, на практике вместо высоты или радиуса фигуры может быть известен угол φ между образующей и основанием. В этом случае генератрису g можно рассчитать с помощью следующих выражений:
Эти формулы следуют из свойств тригонометрических функций синуса и косинуса.
Таким образом, вычисление образующей конуса возможно, если знать любые два параметра фигуры.
Фигура конус усеченный
Он также является фигурой вращения, только вместо прямоугольного треугольника следует вращать прямоугольную трапецию. На рисунке ниже показан усеченный конус.
Здесь синие стрелки показывают прямоугольную трапецию. Длина вертикальной стрелки является высотой h фигуры, длины двух других синих стрелок — это радиусы оснований конуса. В отличие от цилиндра, основания усеченного конуса имеют разную площадь. Обозначим их радиусы r1 и r2. Четвертая наклонная к основанию сторона трапеции является образующей или генератрисой. Как и для обычного конуса, для усеченного все генератрисы равны друг другу и образуют боковую поверхность фигуры.
Заметим, что усеченный конус получил такое название потому, что его можно получить не только вращением трапеции, но и с помощью отсечения плоскостью верхней части круглого прямого конуса.
Генератриса усеченной фигуры
Итак, мы познакомились с усеченным конусом, а также с понятием о его образующей. Как находить образующую конуса усеченного? Для того чтобы получить нужную формулу, заметим, если высоту h перенести параллельно самой себе к боковой поверхности конуса так, чтобы она касалась одним концом образующей фигуры, то получится прямоугольный треугольник. Его сторонами будут высота h (катет), генератриса g (гипотенуза) и r1-r2 (катет). Тогда можно записать формулу для определения g:
Соответственно, если дан острый угол φ1 между большим основанием и генератрисой, тогда последнюю можно определить так:
Если же известен тупой угол φ2 между малым основанием и генератрисой, тогда для ее вычисления необходимо применять такие выражения:
Здесь первая формула является точно такой же, как для угла φ1, а во второй формуле радиусы в числителе поменялись местами.
Таким образом, найти образующую конуса усеченного можно, если знать любые три его параметра.
Узнать ещё
Знание — сила. Познавательная информация
Конус, вписанный в шар
Решение задач на конус, вписанный в шар (конус, вписанный в сферу) сводится к рассмотрению одного или нескольких треугольников.
Конус вписан в шар, если его вершина и окружность основания лежат на поверхности шара, то есть на сфере. Центр шара лежит на оси конуса.
При решении задач на конус, вписанный в шар, удобно рассматривать сечение комбинации тел плоскостью, проходящей через ось конуса и центр шара. Сечение представляет собой большой круг шара (то есть круг, радиус которого равен радиусу шара) с вписанным в него равнобедренным треугольником — осевым сечением конуса. Боковые стороны этого треугольника — образующие конуса, основание — диаметр конуса.
Если угол между образующими острый, центр описанного круга лежит внутри треугольника (соответственно, центр описанного около конуса шара — внутри конуса).
Если угол между образующими прямой, центр круга лежит на середине основания треугольника (центр шара совпадает с центром основания конуса).
Если угол между образующими тупой, центр круга лежит вне треугольника (центр описанного шара — вне конуса).
Если в условии задачи не сказано, где именно лежит центр описанного шара, желательно рассмотреть, как могут повлиять на решение различные варианты его расположения.
Рассмотрим конуса и описанного около него шара плоскостью, проходящей через ось конуса и центр шара. Здесь SO=H — высота конуса, SB=l — образующая конуса,SO1=O1B=R — радиус шара, OB=r — радиус основания конуса, ∠OSB=α — угол между высотой и образующей конуса.
Треугольник SO1B — равнобедренный с основанием SB (так как SO1=O1B=R). Значит, у него углы при основании равны: ∠OSB=∠O1BS=α, и O1F — медиана, высота и биссектриса. Отсюда SF=l/2.
При решении задач на конус, вписанный в шар, можно рассмотреть прямоугольные треугольники SFO1 и SOB. Они подобны (по острому углу S). Из подобия треугольников
В прямоугольном треугольнике SOB ∠OBS=90º — ∠OSB=90º-α. По теореме Пифагора
В прямоугольном треугольнике O1OB ∠OBO1=90º — ∠O1BS=90º — α — α=90º — 2α.
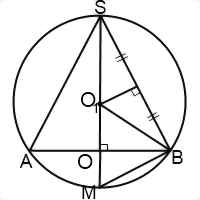
Если продлить SO до пересечения с окружностью, получим прямоугольный треугольник SBM (∠SBM=90º как вписанный угол, опирающийся на диаметр SM). В нем BO- высота, проведенная к гипотенузе. По свойствам прямоугольного треугольника
http://1ku.ru/obrazovanie/45666-kak-najti-obrazujushhuju-konusa-obychnogo-i-usechennogo-formuly/
Введение
Как всегда, речь пойдет исключительно о прямых круговых конусах и усеченных конусах (см. Рис. 1).
Рис.1 Прямой круговой и усеченный
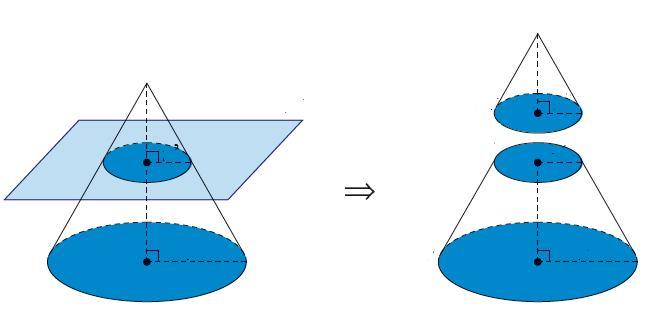
Шар, описанный около конуса
Шар называют описанным около конуса, если вершина конуса и окружность основания конуса принадлежат поверхности шара. Конус в этом случае называют вписанным в шар (см. Рис. 2). Аналогично с усеченным: его можно вписать в шар, если окружности обоих его оснований лежат на поверхн
Рис.2 Шар, описанный около конуса
Всегда ли конус можно вписать в шар? Оказывается, что всегда.
Доказательство. Пусть – вершина конуса,
– диаметр его основания,
– высота конуса (
).
Рис.3 Иллюстрация условия
Тогда рассмотрим осевое сечение , около которого можно описать окружность (свойство треугольника) (см. Рис. 4).
Рис.4 Окружность, описанная около треугольника
Отметим точку – центр описанной окружности около треугольника
. Она лежит на перпендикуляре
, но не обязательно строго на отрезке
– она может лежать и вне его, вне конуса, например под точкой
(см. Рис.5).
Рис.5 Возможные расположения точки
Но это неважно. Важно доказать, что если точка равноудалена от точек
,
и
(см. Рис. 6), то она является центром описанного шара.
Рис.6 равноотдалена от точек
,
и
Для этого необходимо доказать, что точка и все точки основания лежат на поверхности шара. Рассмотрим шар с центром в точке
и радиусом
(см. Рис. 7).
Рис. 7 Шар с центром в точке и радиусом
По построению , значит, точки
и
также лежат на поверхности шара (они удалены на радиус
). С другой стороны, если рассмотреть любую точку
, которая лежит на основании конуса, то
(по двум катетам:
– общий катет,
– как радиусы основания) (см. Рис. 8).
Рис.8
Тогда гипотенузы тоже равны , значит,
, откуда следует, что точка
также лежит на поверхности шара.
Либо проще. – перпендикуляр, ось конуса. Любая точка на оси равноудалена от точек окружности основания. Тогда, раз точка
равноудалена от точек
,
и
, значит, она и является центром искомого шара (см. Рис. 9). Что и требовалось доказать.
Рис. 9 – центр искомого шара
Доказательство.
Докажем, что конус всегда можно вписать в шар. По сути, нужно найти точку, которая равноудалена от вершины конуса и всех вершин окружности его основания. Заметим, что ГМТ (ГМТ — геометрическое место точек) равноудаленных от окружности основания, – это перпендикуляр, проведенный к плоскости основания из центра этой окружности (см. Рис. 1).
Рис.1 ГМТ, равноудаленных от окружности основания
С другой стороны, ГМТ равноудаленных от точек и
– это плоскость, проходящая через середину отрезка
, перпендикулярная ему. Очевидно, эта плоскость не параллельна высоте конуса, а значит, пересекает ее (см. Рис. 2).
Рис.2 ГМТ равноудаленных от точек и
Точка пересечения и будет искомым центром шара, т. к. она равноудалена от точек основания конуса и от его вершины (см. Рис. 3). Отметим, что эта точка может быть как внутри конуса, так и вне его.
Рис.3 Точка пересечения плоскости и высоты конуса
Пример 1
Дан конус, образующая , высота
. Найти радиус описанного шара
.(см. Рис. 10).
Рис.10 Иллюстрация к примеру
Решение. Как известно, центр шара совпадает с центром окружности, описанной около треугольника, являющимся осевым сечением конуса. Соответственно, радиус описанного шара равен радиусу этой окружности. Тогда найдем радиус окружности, описанной около треугольника . Рассмотрим осевое сечение
(см. Рис. 11).
Рис. 11 Осевое сечение
Видно, что и
– египетские, значит,
. (см. Рис. 12).
Рис. 12 Египетские треугольники в осевом сечении
По следствию из теоремы синусов (см. Рис. 13).
 |
Рис.13 Иллюстрация к теореме синусов
Ответ: .
Можно было найти радиус и по формуле .
Шар, описанный около усеченного конуса
Шар называют описанным около усеченного конуса, если оба основания усеченного конуса лежат на поверхности шара (см. Рис. 14).
Рис.14 Шар, описанный около усеченного конуса
Всегда ли усеченный конус можно вписать в шар? Рассмотрим осевое сечение, на этот раз им будет трапеция (см. Рис. 15).
Рис. 15 Трапеция – осевое сечение
Нужно, чтобы около осевого сечения можно было описать окружность (см. Рис. 16).
Рис. 16 Вписанная в окружность трапеция
Это можно сделать только в том случае, когда трапеция равнобедренная. С другой стороны, образующие всегда равны, значит, трапеция будет равнобедренной. То есть около любого усеченного конуса можно описать шар, и центр этого шара будет совпадать с центром окружности, описанной около осевого сечения. Аналогично с радиусом – радиус шара мы будем искать как радиус описанной около трапеции окружности (см. Рис. 17).
Рис. 17 Центр и радиус описанного шара
Рассмотрим теорию на примере.
Пример 2
Дан усеченный конус, радиусы оснований ,
, а высота
. Найти радиус шара, описанного около данного усеченного конуса
(см. Рис. 18).
Рис.18 Иллюстрация к примеру
Решение. Необходимо найти радиус окружности, описанной около трапеции . Рассмотрим осевое сечение – равнобедренную трапецию
(
как образующие). Ее основания
,
(диаметры оснований усеченного конуса), высота
(см. Рис. 19).
Рис. 19 Выносной рисунок трапеции
Найдем радиус описанной окружности двумя способами.
Способ 1. Пусть – центр искомой описанной окружности. Опустим перпендикуляр
– он разделит отрезки
и
пополам. Пусть
,
и
(как радиусы описанной окружности) (см. Рис. 20).
Рис.20 Способ 1
Рассмотрим и
. По теореме Пифагора:
Раскрывая скобки и вычитая из верхнего нижнее, находим .
Получили, что длина отрезка отрицательная. На самом деле, противоречия нет, просто мы неверно отметили точку . То, что
отрицателен, означает, что на самом деле точка
лежит ниже
. В этом случае
, а не
(см. Рис. 21).
Рис. 21 Верное положение точки
Тогда получаем, что ;
.
Способ 2. Можно найти радиус описанной окружности как радиус окружности, описанной около треугольника, вершины которого являются также вершинами трапеции, например (см. Рис. 22).
Рис.22 Радиус искомой окружности совпадает с радиусом окружности, описанной около треугольника
Найдем радиус по формуле .
Проведем и
– высоты трапеции.
Далее, .
Тогда ,
(см. Рис. 23).
Рис.23 Вычисление элементов
Значит .
Ответ:.
Шар, вписанный в конус (усеченный конус)
Шар вписан в конус, если поверхность шара касается основания конуса и его боковой поверхности (см. Рис. 24).
Рис.24 Шар, вписанный в конус
Что значит «шар касается основания и боковой поверхности»? Касание шара с основанием – это касание шара плоскости основания (см. Рис. 25).
Рис.25 Касание шара с плоскостью основания
Под фразой «шар касается боковой поверхности конуса» подразумевается, что шар «не выходит» за границы конуса, однако соприкасается с ним, то есть у них есть общая окружность на боковой поверхности (см. Рис. 26).
Рис.26 Общая окружность при касании шара с боковой поверхностью
Радиус такого шара ищется через радиус окружности, вписанной в осевое сечение (см. Рис. 27).
Рис.27 Окружность, вписанная в осевое сечение
Возникает вопрос: всегда ли шар можно вписать в конус? Всегда, т. к. в треугольник всегда можно вписать окружность.
Шар вписан в усеченный конус, если он касается оснований усеченного конуса и его боковой поверхности (см. Рис. 28).
Рис.28 Шар, вписанный в усеченный конус
Радиус такого шара можно найти через радиус окружности, вписанной в осевое сечение – трапецию (см. Рис. 29).
Шар вписать в усеченный конус можно не всегда, ведь в трапецию можно вписать окружность тогда и только тогда, когда сумма оснований равна сумме боковых сторон (см. Рис. 30).
Рис.30 Суммы противоположных сторон
Иначе говоря, сумма радиусов усеченного конуса должна быть равна образующей (см. Рис. 31) – это необходимое и достаточное условие для существования вписанного в усеченный конус шара.
Рис. 31 Сумма радиусов равна
Пример 3
Дан конус, ,
. Найти радиус вписанного в него шара
(см. Рис. 32).
Рис.32 Иллюстрация к задаче
Решение. Достаточно найти радиус окружности, вписанной в треугольник – осевое сечение. Рассмотрим осевое сечение .
(образующие конуса),
,
, тогда
. По теореме Пифагора из
(прямоугольный)
Получаем
, тогда
(см. Рис. 33).
Тогда по формуле
.
Рис.33 Выносной рисунок осевого сечения
Ответ:
.
Рис.34 Иллюстрация к условию задачи
Задача
Дан усеченный конус, в который вписан шар. Основания конуса и
. Найти радиус вписанного шара
(см. Рис. 34).
Решение. Рассмотрим осевое сечение – это равнобедренная трапеция. Так как в нее можно вписать окружность, то образующая равна сумме радиусов, то есть 15.
Рис.35 Равнобедренная трапеция в сечении
Проведем две высоты. Получаем, что отрезки, на которые они разделили основание, равны 9-6-9 (см. Рис. 36).
Рис.36 Проведенные высоты
Значит, по теореме Пифагора (см. Рис. 37).
Тогда
.
Ответ:.
Рис. 37. Прямоугольный
Заключение
Сегодня речь шла о таких конструкциях, как шар – конус и шар – усеченный конус. Мы выяснили, когда шар можно описать около конуса и усеченного конуса и как искать радиус такого шара (радиус описанного шара – это радиус окружности, описанной около осевого сечения конуса (усеченного конуса)). Кроме того, мы выяснили, когда шар можно вписать в конус (усеченный конус) и как искать радиус такого шара (радиус вписанного шара – это радиус окружности, вписанной в осевое сечение конуса (усеченного конуса)).
Список литературы
Атанасян Л.С. и др. 18-е изд. Геометрия. Учебник для 10–11 классов. – М.: Просвещение, 2009. – 255 с. А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002. Рабочая тетрадь по геометрии 11 класс, В.Ф. Бутузов, Ю.А. Глазков
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-сайт hot.ee (Источник)
- Интернет-сайт hot.ee (Источник)
- Интернет-сайт schools.keldysh.ru (Источник)
Домашнее задание
Равносторонний конус (осевое сечение – равносторонний треугольник) вписан в шар. Найдите радиус шара, если образующая конуса равна 6 см. В шар вписан конус так, что центр основания конуса совпадает с центром шара. Найдите объем шара, если объем конуса равен 12. Около сферы радиуса описан конус, высота которого равна
. Найдите площадь полной поверхности конуса.
В данной статье рассмотрим четыре задачи по стереометрии. Дана комбинация тел – конус и шар. Во всех заданиях речь идёт о конусе, который вписан в шар. Отмечу, что в условии взаимное расположение данных тел озвучено может быть по разному, например: «Конус вписан в шар» или «Около конуса описана сфера».
Суть одна – если сказать простым (нематематическим) языком, то конус находится «внутри» сферы, она содержит окружность его основания и вершину. Посмотрите на эскиз:
При решении необходимо знать формулы объёмов шара и конуса.
Объём шара:
Объём конуса:
*Эти формулы необходимо знать!
Площадь основания конуса является кругом, она равна:
Рассмотрим частный случай! Если высота конуса будет равна радиусу его основания, то формула объёма конуса будет иметь вид:
Эскиз:
Понятно, что центральным сечением такого конуса будет являться прямоугольный равнобедренный треугольник, причём высота проведённая из прямого угла разбивает его также на два прямоугольных равнобедренных треугольника:
Вспомним понятие образующей, оно часто используется в задачах с конусами, будет и в заданиях ниже.
Образующая конуса – это отрезок, соединяющий вершину конуса с точкой его основания. На предыдущем эскизе она обозначена буквой l.
Напрашивается простой вывод: образующих у конуса имеется бесконечное количество и все они равны.
На блоге, кстати, уже есть пара статей с шарами, можете посмотреть их «Задачи с шарами. Это просто!» и «Цилиндр описан около шара. Три задачи».
Теперь рассмотрим задачи:
245351. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
Так как сказано, что радиус основания конуса равен радиусу шара, то становится понятно, что основание конуса совпадает с плоскостью центрального сечения шара.
Построим эскиз данной комбинации для наглядности (это осевое сечение):
Сказано, что высота конуса равна радиусу его основания (и, разумеется, радиусу шара). Запишем формулы объёмов шара и конуса:
Так как объём шара известен (он равен 28), можем вычислить радиус. Вернее, нам понадобится не сам радиус, а его куб:
Таким образом, объём конуса будет равен:
*Можно было обойтись без вычислений. Посмотрите, если сопоставить две формулы:
то видно, что объём шара в 4 раза больше объёма конуса.
Значит объём конуса будет равен 28/4 = 7.
То есть, задача решается практически устно.
Ответ: 7
245352. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
Задача обратная предыдущей, рисунок тот же.
Формулы:
Из формул понятно, что объём шара в 4 раза больше объёма конуса:
Таким образом, искомый объём равен 24.
Ответ: 24
316555. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна 
Здесь условие звучит по-другому, но тела расположены относительно друг друга абсолютно также, как и в предыдущих задачах – конус вписан в сферу, основание конуса совпадает с центральным сечением сферы.
Эскиз тот же, отметим радиус, высоту равную радиусу и образующую:
Задача сводится к использованию одной формулы. Рассмотрим прямоугольный треугольник (выделен жёлтым). По теореме Пифагора:
Радиус сферы равен семи.
Ответ: 7
316556. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен 
Эта задача обратная предыдущей, эскиз:
Рассмотрим прямоугольный треугольник (выделен жёлтым), х – это образующая. По теореме Пифагора:
Образующая конуса равна 56.
Ответ: 56
На этом всё. Успеха Вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.