Как найти образуют ли вектора базис

Базисом
в
-мерном пространстве называется упорядоченная система из

линейно-независимых векторов.

Введём также некоторые дополнительные понятия, необходимые для дальнейшего изложения.

Выражение вида:

, где
−
некоторые числа и

называется
линейной комбинацией
векторов
.

Если существуют такие числа

из которых хотя бы одно не равно нулю (например
) и при этом выполняется равенство:

, то система векторов
−
является
линейно-зависимой.

Если же указанное равенство выполняется лишь при условии, что все числа
,
тогда система векторов
−
является
линейно-независимой.

Базис
может образовывать только
линейно-независимая
система векторов. Понятие линейной зависимости/независимости системы векторов, тесно связано с понятием
ранга матрицы.

Наш онлайн калькулятор позволяет проверить образует ли система векторов
базис.
При этом калькулятор выдаёт подробное решение на русском языке.

Как доказать, что вектора образуют базис

Базисом в n-мерном пространстве называется такая система из n векторов, когда все остальные векторы пространства можно представить в виде комбинации векторов, входящих в базис. В трехмерном пространстве в любой базис входят три вектора. Но не любые три образуют базис, поэтому и существует задача проверки системы векторов на возможность построения из них базиса.

Вам понадобится

• — умение вычислять определитель матрицы

Инструкция

Пусть в линейном n-мерном пространстве существует система векторов e1, е2, е3, … , еn. Их координаты: e1 = (e11; e21; e31; … ; en1), е2 = (е12; е22; е32; … ; еn2), … , еn = (e1n; e2n; e3n; … ; enn). Чтобы узнать, образуют ли они базис в этом пространстве, составьте матрицу со столбцами e1, е2, е3, … , еn. Найдите ее определитель и сравните его с нулем. Если определитель матрицы из этих векторов не равен нулю, то такие векторы образуют базис в данном n-мерном линейном пространстве.

Например, пусть даны три вектора в трехмерном пространстве a1, a2 и a3. Их координаты: а1 = (3; 1; 4), а2 = (-4; 2; 3) и а3 = (2; -1; -2). Надо выяснить, образуют ли эти вектора базис в трехмерном пространстве. Составьте матрицу из векторов, как показано на рисунке.

Вычислите определитель получившейся матрицы. На рисунке показан простой способ вычисления определителя матрицы 3 на 3. Элементы, соединенные линией, следует перемножить. При этом произведения, обозначенные красной линией входят в общую сумму со знаком «+», а соединенные синей линией — со знаком «-«. det A = 3*2*(-2) + 1*2*3 + 4*(-4)*(-1) — 2*2*4 — 1*(-4)*(-2) — 3*3*(-1) = -12 + 6 + 16 — 16 — 8 + 9 = -5 -5≠0, следовательно, а1, а2 и а3 образуют базис.

Видео по теме

Источники:

• Базис и размерность линейного пространства

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

© 2011-2023 Довжик Михаил
Копирование материалов запрещено.

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com

10. Определение линейной зависимости и независимости векторов. Введем важные понятия, играющие большую роль в линейных уравнениях, например, – понятия линейной зависимости и независимости векторов

Определение 1. Линейной
комбинацией векторовназывается сумма произведений этих
векторов на скаляры:

.
(2.8)

Определение 2. Система
векторовназывается линейно зависимой системой,
если линейная комбинация их (2.8) обращается
в нуль:

=0,
(2.9)

причем среди чиселсуществует хотя бы одно, отличное от
нуля.

Определение 3. Векторыназываются линейно независимыми, если
их линейная комбинация (2.8) обращается
в нуль лишь в случае, когда все числа.

Из этих определений можно
получить следующие следствия.

Следствие 1. В линейно
зависимой системе векторов хотя бы один
вектор может быть выражен как линейная
комбинация остальных.

Доказательство. Пусть
выполнено (2.9) и пусть для определенности,
коэффициент.
Имеем тогда:.
Заметим, что справедливо и обратное
утверждение.

Следствие 2. Если система
векторовсодержит нулевой вектор, то эта система
(обязательно) линейно зависима –
доказательство очевидно.

Следствие 3. Если средиnвекторовкакие либоk()
векторов линейно зависимы, то и всеnвекторов линейно зависимы (опустим
доказательство).

2⁰. Линейные
комбинации двух, трех и четырех векторов.
Рассмотрим вопросы линейной зависимости
и независимости векторов на прямой,
плоскости и в пространстве. Приведем
соответствующие теоремы.

Теорема 1. Для того чтобы
два вектора были линейно зависимы,
необходимо и достаточно, чтобы они были
коллинеарны.

Необходимость. Пусть векторыилинейно зависимы. Это означает, что их
линейная комбинация=0
и (ради определенности).
Отсюда следует равенство,
и (по определению умножения вектора на
число) векторыиколлинеарны.

Достаточность. Пусть векторыиколлинеарны (║)
(предполагаем, что они отличны от нулевого
вектора; иначе их линейная зависимость
очевидна).

По теореме (2.7)
(см. §2.1,п.2⁰) тогдатакое, что,
или– линейная комбинация равна нулю, причем
коэффициент приравен 1 – векторыилинейно зависимы.

Из этой теоремы вытекает
следующее следствие.

Следствие. Если векторыине коллинеарны, то они линейно независимы.

Теорема 2. Для того чтобы
три вектора были линейно зависимы,
необходимо и достаточно, чтобы они были
компланарны.

Необходимость. Пусть векторы,илинейно зависимы. Покажем, что они
компланарны.

Из определения
линейной зависимости векторов следует
существование чисел
итаких, что линейная комбинация,
и при этом (для определенности).
Тогда из этого равенства можно выразить
вектор:=,
то есть векторравен диагонали параллелограмма,
построенного на векторах, стоящих в
правой части этого равенства (рис.2.6).
Это означает, что векторы,илежат в одной плоскости.

Достаточность. Пусть векторы,икомпланарны. Покажем, что они линейно
зависимы.

Исключим случай
коллинеарности какой либо пары векторов
(ибо тогда эта пара линейно зависима и
по следствию 3 (см.п.1⁰) все три
вектора линейно зависимы). Заметим, что
такое предположение исключает также
существование нулевого вектора среди
указанных трех.

Перенесем три компланарных
вектора в одну плоскость и приведем их
к общему началу. Через конец вектора
проведем прямые, параллельные векторами;
получим при этом векторыи(рис.2.7) – их существование обеспечено
тем, что векторыине коллинеарные по предположению
векторы. Отсюда следует, что вектор=+.
Переписав это равенство в виде
(–1)++=0,
заключаем, что векторы,илинейно зависимы.

Из доказанной теоремы вытекает
два следствия.

Следствие 1. Пустьине коллинеарные векторы, вектор– произвольный, лежащий в плоскости,
определяемой векторамии,
вектор. Существуют тогда числаитакие, что

=+.
(2.10)

Следствие 2. Если векторы,ине компланарны, то они линейно независимы.

Теорема 3. Любые четыре
вектора линейно зависимы.

Доказательство опустим; с
некоторыми изменениями оно копирует
доказательство теоремы 2. Приведем
следствие из этой теоремы.

Следствие. Для любых
некомпланарных векторов,,и любого вектораитакие, что

.
(2.11)

Замечание. Для векторов в
(трехмерном) пространстве понятия
линейной зависимости и независимости
имеют, как это следует из приведенных
выше теорем 1-3, простой геометрический
смысл.

Пусть имеются два линейно
зависимых вектора
и.
В таком случае один из них является
линейной комбинацией второго, то есть
просто отличается от него численным
множителем (например,).
Геометрически это означает, что оба
вектора находятся на общей прямой; они
могут иметь одинаковое или противоположное
направления (рис.2.8 хх ).

Если же два вектора расположены
под углом друг к другу (рис.2.9 хх ), то в
этом случае нельзя получить один из них
умножением другого на число – такие
векторы линейно независимы. Следовательно,
линейная независимость двух векторов
иозначает, что эти векторы не могут быть
уложены на одну прямую.

Выясним геометрический смысл
линейной зависимости и независимости
трех векторов.

Пусть векторы
,илинейно зависимы и пусть (для определенности)
векторявляется линейной комбинацией векторови,
то есть расположен в плоскости, содержащей
векторыи.
Это означает, что векторы,илежат в одной плоскости. Справедливо и
обратное утверждение: если векторы,илежат в одной плоскости, то они линейно
зависимы.

Таким образом,
векторы
,илинейно независимы в том и только в том
случае, если они не лежат в одной
плоскости.

3⁰. Понятие
базиса. Одним из важнейших понятий
линейной и векторной алгебры является
понятие базиса. Введем определения.

Определение 1. Пара векторов
называется упорядоченной, если указано,
какой вектор этой пары считается первым,
а какой вторым.

Определение 2. Упорядоченная
пара,неколлинеарных векторов называется
базисом на плоскости, определяемой
заданными векторами.

Теорема 1. Всякий векторна плоскости может быть представлен
как линейная комбинация базисной системы
векторов,:

(2.12)

и это представление единственно.

Доказательство. Пусть
векторыиобразуют базис. Тогда любой векторможно представить в виде.

Для доказательства единственности
предположим, что имеется еще одно
разложение
.
Имеем тогда=0,
причем хотя бы одна из разностей отлична
от нуля. Последнее означает, что векторыилинейно зависимы, то есть коллинеарны;
это противоречит утверждению, что они
образуют базис.

Но тогда
– разложение единственно.

Определение 3. Тройка
векторов называется упорядоченной,
если указано, какой вектор ее считается
первым, какой вторым, а какой третьим.

Определение 4. Упорядоченная
тройка некомпланарных векторов называется
базисом в пространстве.

Здесь также справедлива теорема
разложения и единственности.

Теорема 2. Любой векторможет быть представлен как линейная
комбинация базисной системы векторов,,:

(2.13)

и это представление единственно
(опустим доказательство теоремы).

В разложениях (2.12) и (2.13) величины
называются координатами векторав заданном базисе (точнее, аффинными
координатами).

При фиксированном базисе
иможно писать.

Например, если задан базис
и дано, что,
то это означает, что имеет место
представление (разложение).

4⁰. Линейные
операции над векторами в координатной
форме. Введение базиса позволяет
линейные операции над векторами заменить
обычными линейными операциями над
числами – координатами этих векторов.

Пусть задан некоторый базис
.
Очевидно, задание координат вектора в
этом базисе полностью определяет сам
вектор. Имеют место следующие предложения:

а) два вектора
иравны тогда и только тогда, когда равны
их соответственные координаты:

;
(2.14)

б) при умножении вектора
на числоего координаты умножаются на это число:

;
(2.15)

в) при сложении векторов
складываются их соответственные
координаты:

.
(2.16)

Доказательства этих свойств
опустим; докажем лишь для примера
свойство б). Имеем

==

==.

Замечание. В пространстве
(на плоскости) можно выбрать бесконечно
много базисов.

Приведем пример перехода от
одного базиса к другому, установим
соотношения между координатами вектора
в различных базисах.

Пример 1. В базисной системезаданы три вектора:,и.
В базисе,,векторимеет разложение.
Найти координаты векторав базисе.

Решение. Имеем разложения:,,;
следовательно,=+2+=
=,
то естьв базисе.

Пример 2. Пусть в некотором
базисечетыре вектора заданы своими координатами:,,и.

Выяснить,
образуют ли векторы
базис; в случае положительного ответа
найти разложение векторав этом базисе.

Решение. 1) векторы образуют
базис, если они линейно независимы.
Составим линейную комбинацию векторов()
и выясним, при какихиона обращается в нуль:=0.
Имеем:

=++=

=.

По определению
равенства векторов в координатной форме
получим следующую систему (линейных
однородных алгебраических) уравнений:
;;,
определитель которой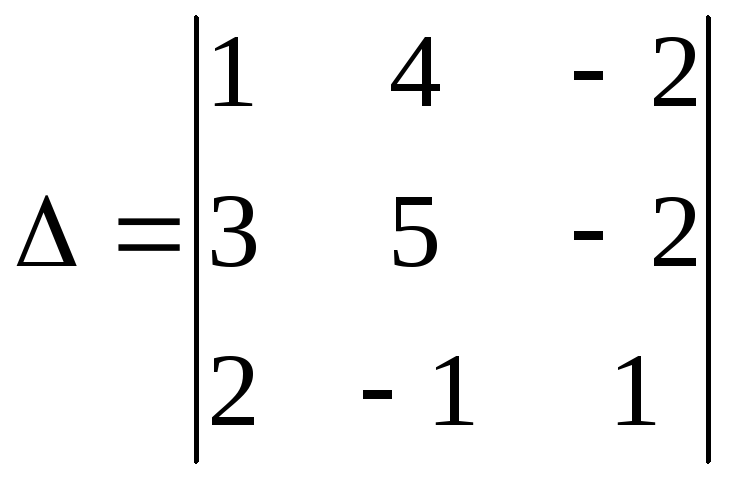=1,
то есть система имеет (лишь) тривиальное
решение.
Это означает линейную независимость
векторови, следовательно, они образуют базис.

2) разложим вектор
в этом базисе. Имеем:=или в координатной форме.

Переходя к
равенству векторов в координатной
форме, получим систему линейных
неоднородных алгебраических уравнений:
;;.
Решая ее (например, по правилу Крамера),
получим:,,и ().
Имеем разложение векторав базисе:=.

5⁰. Проекция
вектора на ось. Свойства проекций. Пусть
имеется некоторая осьl,
то есть прямая с выбранным на ней
направлением и пусть задан некоторый
вектор.Определим
понятие проекции векторана осьl.

Определение. Проекцией
векторана осьlназывается
произведение модуля этого вектора на
косинус угла между осьюlи вектором (рис.2.10):

.
(2.17)

Следствием этого определения
является утверждение о том, что равные
векторы имеют равные проекции (на одну
и ту же ось).

Отметим свойства
проекций.

1) проекция суммы векторов на
некоторую ось lравна
сумме проекций слагаемых векторов на
ту же ось:

.
(2.18)

2) проекция произведения скаляра
на вектор равна произведению этого
скаляра на проекцию вектора на ту же
ось:

=.
(2.19)

Следствие. Проекция линейной
комбинации векторов на ось равна линейной
комбинации их проекций:

.
(2.20)

Доказательства свойств опустим.

6⁰. Прямоугольная
декартова система координат в пространстве.Разложение вектора по ортам осей.
Пусть в качестве базиса выбраны три
взаимно перпендикулярных орта; для них
вводим специальные обозначения.
Поместив их начала в точкуO,
направим по ним (в соответствии с ортами)
координатные осиOx,OyиOz(ось с выбранным на ней положительным
направлением, началом отсчета и единицей
длины называется координатной осью).

Определение. Упорядоченная
система трех взаимно перпендикулярных
координатных осей с общим началом и
общей единицей длины называется
прямоугольной декартовой системой
координат в пространстве.

Ось Ox
называется осью абсцисс,Oy– осью ординат иOz
– осью аппликат.

Займемся
разложением произвольного вектора по
базису
.
Из теоремы (см.§2.2,п.3⁰, (2.13)) следует,
чтоможет быть и единственным образом
разложен по базису(здесь вместо обозначения координатупотребляют):

.
(2.21)

В (2.21)
суть (декартовы прямоугольные) координаты
вектора.
Смысл декартовых координат устанавливает
следующая теорема.

Теорема. Декартовы
прямоугольные координатывектораявляются проекциями этого вектора
соответственно на осиOx,OyиOz.

Доказательство.Поместим
векторв начало системы координат – точкуO.
Тогда его конец будет совпадать с
некоторой точкой.

Проведем через
точку
три плоскости, параллельные координатным
плоскостямOyz,OxzиOxy(рис.2.11 хх ). Получим
тогда:

.
(2.22)

В (2.22) векторы
и
называются составляющими векторапо осямOx,OyиOz.

Пусть через
иобозначены соответственно углы,
образованные векторомс ортами.
Тогда для составляющих получим следующие
формулы:

==,
==,
==(2.23)

Из (2.21), (2.22) (2.23)
находим:

==;==;==(2.23)

– координаты
вектораесть проекции этого вектора на координатные
осиOx,OyиOzсоответственно.

Замечание . Числаназываются направляющими косинусами
вектора.

Модуль вектора
(диагональ прямоугольного параллелепипеда)
вычисляется по формуле:

.
(2.24)

Из формул (2.23) и (2.24) следует,
что направляющие косинусы могут быть
вычислены по формулам:

=;=;=.
(2.25)

Возводя обе части каждого из
равенств в (2.25) и складывая почленно
левые и правые части полученных равенств,
придем к формуле:

(2.26)

– не любые три угла образуют
некоторое направление в пространстве,
но лишь те, косинусы которых связаны
соотношением (2.26).

7⁰. Радиус-вектор
и координаты точки.Определение
вектора по его началу и концу. Введем
определение.

Определение. Радиусом-вектором
(обозначается)
называется вектор, соединяющий начало
координатOс этой
точкой (рис.2.12 хх ):

.
(2.27)

Любой точке пространства
соответствует определенный радиус-вектор
(и обратно). Таким образом, точки
пространства представляются в векторной
алгебре их радиус-векторами.

Очевидно, координаты
точкиMявляются
проекциями ее радиус-векторана координатные оси:

(2.28’)

и, таким образом,

(2.28)

– радиус-вектор точки есть
вектор, проекции которого на оси координат
равны координатам этой точки. Отсюда
следует две записи:
и.

Получим формулы для вычисления
проекций вектора
по координатам его начала – точкеи конца – точке.

Проведем радиус-векторы
и вектор(рис.2.13). Получим, что

==(2.29)

– проекции вектора на координатные
орты равны разностям соответствующих
координат конца и начала вектора.

8⁰. Некоторые
задачи на декартовы координаты.

1) условия коллинеарности
векторов. Из теоремы (см.§2.1,п.2⁰,
формула (2.7)) следует, что для коллинеарности
векторовинеобходимо и достаточно, чтобы выполнялось
соотношение:=.
Из этого векторного равенства получаем
три в координатной форме равенства:,
откуда следует условие коллинеарности
векторов в координатной форме:

(2.30)

– для коллинеарности векторов
инеобходимо и достаточно, чтобы их
соответствующие координаты были
пропорциональны.

2) расстояние между
точками. Из представления (2.29)
следует, что расстояниемежду точкамииопределяется формулой

==.
(2.31)

3) деление отрезка в
данном отношении. Пусть даны точкиии отношение.
Нужно найти– координаты точкиM
(рис.2.14).

Имеем из условия коллинеарности
векторов:
,
откудаи

.
(2.32)

Из (2.32) получим в координатной
форме:

.
(2.32’)

Из формул (2.32’) можно получить
формулы для вычисления координат
середины отрезка
,
полагая:

.
(2.32”)

Замечание. Будем считать
отрезкииположительными или отрицательными в
зависимости от того, совпадает их
направление с направлением от началаотрезка к концу,
или не совпадает. Тогда по формулам
(2.32) – (2.32”) можно находить координат
точки, делящей отрезоквнешним образом, то есть так, что делящая
точкаMнаходится на
продолжении отрезка,
а не внутри его. При этом конечно,.

4) уравнение сферической
поверхности. Составим уравнение
сферической поверхности – геометрического
места точек,
равноудаленных на расстояниеот некоторого фиксированного центра –
точки.
Очевидно, что в данном случаеи с учетом формулы (2.31)

.
(2.33)

Уравнение (2.33) и есть уравнение
искомой сферической поверхности.