Давление жидкости на дно сосуда определяется по формуле Р=ρgh, g — величина постоянная, равна 9,8 Н/кг, но в школе её обычно округляют до 10 Н/кг. ρ у каждой жидкости своя. Для воды ρ=1000 кг/м³, для машинного масла ρ=910 кг/м³. Нам нужно найти давление, которое оказывает машинное масло слоем в 3 см, и давление воды слоем в 1 см, т.к. давление нужно узнать на высоте 2 см от дна сосуда. 3-2=1 см. Ну а потом два давления сложить. Приступим. Высота дана в см, нужно перевести её в метры.
3 см=0,03 м
1 см=0,01 м
Теперь считаем давление по формулам:
Рводы=1000*10*0,01=100 Па
Рмасла=910*10*0,03=273 Па
Складываем оба давления.
Р=100+273=373 Па
Ответ: давление жидкости на расстоянии 2 см от сосуда равно 373 Па.
Как вы уже знаете, согласно закону Паскаля, давление в жидкостях распространяется одинаково во всех направлениях. Что же необходимо знать, чтобы рассчитать это давление? От чего зависит давление жидкости?
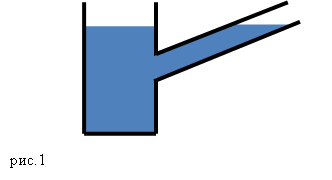
Взгляните на рисунок 1.
Как вы думаете, в каком сосуде больше жидкости? А будет ли одинаково давление, оказываемое на дно сосудов? С этими вопросами нам и предстоит разобраться.
Вывод формулы
Выведем формулу для расчета давления жидкости на дно сосуда, имеющего форму прямоугольного параллелепипеда (рисунок 2).
Давление жидкости $p$ рассчитывается по формуле: $p = frac{F}{S}$, где $F$ — это сила, действующая на дно сосуда, а $S$ — это площадь дна сосуда.
- Сила $F$ в данном случае равна весу $P$ жидкости, которая находится в сосуде;
- Как узнать вес жидкости? Необходимо знать массу $m$ жидкости;
- Массу $m$ мы можем вычислить по известной нам формуле:
$m = rho V$;
- Так как нам известна жидкость, находящаяся в сосуде, мы знаем ее плотность . Остается вычислить объем $V$ жидкости. Обозначим высоту столба жидкости буквой $h$, площадь дна сосуда — $S$. Тогда объем можно вычислить по формуле:
$V = Sh$;
- Итак, подставляем наши данные в формулу для вычисления массы и получаем:
$m = rho Sh$;
- Таким образом, возвращаемся к весу жидкости и получаем, что:
$P = mg$, где $g$ — ускорение свободного падения, или $P = g rho Sh$.
С другой стороны, мы знаем, что вес столба жидкости равен силе, с которой жидкость давит на дно сосуда. Поэтому если мы разделим вес $P$ на площадь $S$, то получим искомое давление жидкости:
$p = frac{P}{S}$,
или $p =frac{g rho Sh}{S}$,
То есть:
$p = rho gh$.
Рассмотрим измерительные величины, которые мы будем использовать в данной формуле: плотность мы будем выражать в килограммах на кубический метр ($frac{кг}{м^3}$), $g = 9.8 frac{H}{кг}$, высоту столба жидкости — в метрах ($м$). Тогда давление $p$ будет выражено в паскалях ($Па$).
Выводы
Так мы с вами вывели формулу для расчета давления жидкости на дно сосуда. Какие выводы мы можем сделать?
От каких величин зависит давление жидкости на дно сосуда?
Давление жидкости не зависит от формы сосуда, оно зависит только от плотности жидкости и высоты ее столба.
Обратите внимание, что во многих случаях, когда говорят о высоте столба жидкости, говорят о глубине.
По какой формуле рассчитывают давление жидкости на стенки сосуда, давление внутри жидкости?
По формуле $p = rho gh$ можно вычислить давление на стенки сосуда или внутри жидкости, так как на одной глубине давление в жидкости будет одинаково во всех направлениях.
Вопросы и пример задачи
Вопрос №1
Как вы думаете, изменится ли давление на дно цилиндрического сосуда, частично заполненного водой, если в него опустить деревянный брусок (рисунок 3)?
Посмотреть ответ
Скрыть
Ответ:
В данном случае уровень воды поднимется и высота столба станет больше, значит и давление увеличится.
Вопрос №2
Какая вода: пресная или соленая оказывает большее давление на дно сосуда при одинаковом объеме?
Посмотреть ответ
Скрыть ответ
Ответ:
Здесь достаточно вспомнить, что в соленой воде нам намного проще плавать и держаться на поверхности, что о говорит о ее большей плотности. А давление прямо пропорционально плотности. Соответственно, большее давление оказывает соленая вода.
Задача
Определите давление керосина на дно цистерны, если высота столба керосина $8 space м$, а его плотность $800 frac{кг}{м^3}$.
Дано:
$rho = 800 frac{кг}{м^3}$
$h = 8 space м$
$p — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Давление рассчитывается по формуле:
$p= rho gh$.
Подставим все величины и рассчитаем его:
$p = 800 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 8 space м = 62 720 space Па approx 63 space кПа$.
Ответ: $p approx 63 space кПа$.
Упражнения
Упражнение №1
Определите давление на глубине $0.6 space м$ в воде, керосине, ртути.
Дано:
$h = 0.6 space м$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 800 frac{кг}{м^3}$
$rho_3 = 13600 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$p_1 — ?$
$p_2 — ?$
$p_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Для расчета давления на заданной глубине будем использовать формулу $p = rho gh$.
Давление в воде:
$p_1 = rho_1 gh$,
$p_1 = 1000 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.6 space м = 5880 space Па approx 5.9 space кПа$.
Давление в керосине:
$p_2 = rho_2 gh$,
$p_2 = 800 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.6 space м = 4704 space Па approx 4.7 space кПа$.
Давление в ртути:
$p_3 = rho_3 gh$,
$p_3 = 13600 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.6 space м = 79 space 968 space Па approx 80 space кПа$.
Ответ: $p_1 approx 5.9 space кПа$, $p_2 approx 4.7 space кПа$, $p_3 approx 80 space кПа$.
Упражнение №2
Вычислите давление воды на дно одной из глубочайших морских впадин — Марианской, глубина которой приблизительно равна $10 space 900 space м$. Плотность морской воды равна $1030 frac{кг}{м^3}$.
Дано:
$h = 10 space 900 space м$
$rho = 1030 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$p — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем давление на дне Марианской впадины по формуле:
$p = rho gh$,
$p = 1030 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 10 space 900 space м = 110 space 024 space 600 space Па approx 110 space МПа$.
Ответ: $p approx 110 space МПа$.
Упражнение №3
На рисунке 3 изображена футбольная камера, соединенная с вертикально расположенной стеклянной трубкой. В камере и трубке находится вода. На камеру положена дощечка, а на нее — гиря массой $5 space кг$. Высота столба воды в трубке равна $1 space м$. Определите площадь соприкосновения дощечки с камерой.
Дано:
$m = 5 space кг$
$h = 1 space м$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Гиря оказывает давление на футбольную камеру:
$p_1 = frac{F}{S}$.
Сила $F$, с которой она давит, будет определяться ее весом:
$F = P = F_{тяж} = mg$.
Тогда формула для давления примет следующий вид:
$p_1 = frac{mg}{S}$.
В то же время вода в трубке и камере давит на нее изнутри снизу вверх:
$p_2 = rho gh$.
Так как гиря и камера находятся в равновесии:
$p_1 = p_2$,
$frac{mg}{S} = rho gh$,
$S = frac{m}{rho h}$.
Рассчитаем эту площадь:
$S = frac{5 space кг}{1000 frac{кг}{м^3} cdot 1 space м} = 0.005 space м^2 = 50 space см^2$.
Ответ: $S = 50 space см^2$.
Задания
Задание №1
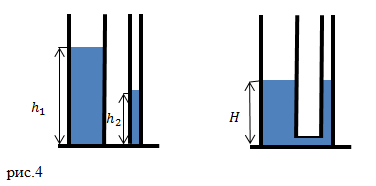
Возьмите высокий сосуд. В боковой поверхности его на разной высоте от дна сделайте три небольших отверстия. Закройте отверстия спичками и наполните сосуд водой. Откройте отверстия и проследите за струйками вытекающей воды (рисунок 4). Почему вода вытекает из отверстий? Из чего следует, что давление увеличивается с глубиной?
Показать ответ
Скрыть
Ответ:
Вода вытекает из отверстий по действием давления самой жидкости. Мы видим, что из самого нижнего отверстия бьет струйка воды с самым сильным напором, а из верхнего отверстия — с самым слабым. Этот момент объясняется тем, что с увеличением глубины давление увеличивается.
Задание №2
Налейте в стеклянный сосуд (стакан или банку) произвольное количество воды. Сделайте необходимые измерения и рассчитайте давление воды на дно сосуда.
Дано:
$h = 0.086 space м$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$p — ?$
Показать решение и овет
Скрыть
Решение:
Рассчитаем давление воды на дно нашего стакана по формуле:
$p = rho gh$,
$p = 1000 frac{кг}{м^3} cdot 9.8 frac{Н}{кг} cdot 0.086 space м = 842.8 space Па approx 843 space Па$.
Ответ: $p approx 843 space Па$.
Давление жидкостей и газов. Закон Паскаля
- Особенности давления жидкостей и газов
- Закон Паскаля
- Давление столба жидкости
- Давление столба газа
- Задачи
п.1. Особенности давления жидкостей и газов
Давление жидкостей и газов отличается от давления твердых тел. Причина – в особенностях поведения частиц вещества в разных агрегатных состояниях (см. §16 данного справочника).
В отличие от твердых тел, молекулы жидкостей и газов подвижны.
Жидкость принимает форму сосуда, который предохраняет её от растекания. Поэтому жидкость в сосуде оказывает давление не только на дно, но и на стенки. Верхние слои жидкости давят на нижние, и давление растет с глубиной (с увеличением столба жидкости).
Газ заполняет весь предоставленный ему объем. В закрытом сосуде хаотически движущиеся молекулы газа будут сталкиваться с дном, стенками и крышкой сосуда. Таким образом, газ будет оказывать давление во все стороны: вниз, по бокам и даже вверх.
Давление газа также растет с увеличением высоты столба. Однако за счет малой плотности газов этот рост менее заметен по сравнению с жидкостями. В небольшом сосуде давление газа можно считать постоянным во всем объеме сосуда.
п.2. Закон Паскаля
При давлении на жидкость или газ в определенной области происходит сжатие; расстояние между молекулами становится меньше, начинают сильнее действовать силы отталкивания. В результате молекулы перемещаются из области сжатия с большим давлением в области с меньшим давлением. Это происходит достаточно быстро; например, у кислорода при 0°С средняя скорость молекул 425 м/с, у паров воды — 570 м/с. Поэтому в течение небольшого времени давление в сосуде выравнивается.
Закон Паскаля
Жидкости и газы передают давление по всем направлениям одинаково.
Для подтверждения закона Паскаля можно провести следующие эксперименты.
п.3. Давление столба жидкости
Как было замечено выше, давление жидкостей заметно увеличивается с глубиной. Это объясняется тем, что верхние слои давят на нижние.
Найдем давление столба жидкости высотой (h)
Согласно закону Паскаля, давление в жидкости передается во всех направлениях одинаково. Поэтому на данной глубине (h) в каждой точке уровня давление будет постоянно.
 |
Рассмотрим сосуд в форме прямоугольного параллелепипеда. Пусть в его основании – прямоугольник с длиной (a) и шириной (b). Нальем в этот сосуд воду до отметки высотой (h). Нас интересует давление воды на дно сосуда. Сила давления на дно направлена вертикально вниз и равна силе тяжести: $$ F=mg=rho Vg $$ Объем воды в сосуде: $$ V=abh $$ |
Получаем: $$ F=rhocdot abhcdot g $$ Давление на дно сосуда равно отношению силы давления к площади дна: $$ p=frac FS=frac{rhocdot abh cdot g}{ab}=rho gh $$
Давление столба жидкости
На глубине (h) давление жидкости равно $$ p=rho gh $$
Давление не зависит от площади дна, и, следовательно, не зависит от его формы.
Полученное выражение будет справедливо для вертикального столба жидкости высотой (h) с любым сечением (квадратным, круглым, треугольным, совершенно фантазийным).
Это интересно
 |
Давление не зависит ни от формы, ни от размеров сечения столба жидкости, зато резко увеличивается с высотой. Это свойство использовал Паскаль, продемонстрировав своим современникам забавный эксперимент. Он взял прочную дубовую бочку, наполнил ее доверху водой, плотно закрыл и вставил очень узкую, но очень длинную трубку (около 4 м). Затем он поднялся на второй этаж и вылил в трубку кружку воды. Бочка тут же …лопнула. Действительно, ведь давление в бочке увеличилось на (p=1000cdot 10cdot 4=40 text{кПа}): её будто «придавило» четырьмя тоннами воды, хотя понадобилась всего лишь кружка. Тем не менее, результат этого фокуса всегда кажется неожиданным. |
п.4. Давление столба газа
Газы, как и жидкости, также имеют некоторую плотность. Поэтому, рассматривая давление столба газа по аналогии с жидкостью, можно прийти к тем же результатам.
Давление столба газа
Давление столба газа высотой (h) равно $$ p=rho gh $$
Понимание того, что газ также оказывает разное давление в разных слоях, возникло не сразу. Это объясняется небольшой плотностью газов по сравнению с жидкостями.
 |
Для иллюстрации рассчитаем давление столба воды и столба воздуха высотой (h=1 text{м}). Плотность воды (rho_text{воды}=1000 text{кг/м}^3), плотность воздуха при 20°C (rho_text{возд}=1,2 text{кг/м}^3). Получаем: begin{gather*} p_text{вода}= rho_text{вода}ghapprox 1000cdot 10cdot 1=10000 (text{Па})\[7pt] p_text{возд}= rho_text{возд}ghapprox 1,2cdot 10cdot 1=12 (text{Па}) end{gather*} Из-за разности в плотности, давление отличается почти в 1000 раз, ведь масса кубометра воды – 1 тонна, а масса кубометра воздуха – всего 1,2 кг. |
Поэтому при изучении процессов в небольших сосудах разность в давлении газа в верхних и нижних слоях практически не заметна.
С другой стороны, если рассматривать значительные по высоте «столбы» газов, например, атмосферу планеты, давление становится существенной величиной. Так, на поверхности Земли атмосферное давление составляет около 100 000 (Па). Подробней этот вопрос будет рассмотрен в §31 данного справочника.
В итоге, для открытого сосуда с жидкостью, где на поверхность дополнительно оказывает давление атмосфера, давление жидкости на глубине h равно сумме: $$ p=p_text{атм}+rho gh $$
п.5. Задачи
Задача 1. Пятый этаж расположен выше первого на 15 м.
На каком этаже давление в трубах водопровода больше и на сколько?
Дано:
(h=15 text{м})
(p=1000 text{кг/м}^3)
(gapprox 10 text{м/с}^2)
__________________
(Delta p-?)
Давление в водопроводе на первом этаже $$ p_1=p_text{внеш}+rho gh, $$ где (p_text{внеш}) – давление, связанное с действием внешних сил (атмосфера, водонапорная башня, насос и т.п.), второе слагаемое – давление вертикального столба жидкости в трубе в доме.
Давление в водопроводе на пятом этаже (p_5=p_text{внеш}).
Давление больше на первом этаже.
Разность давлений $$ Delta p=p_1-p_5= p_text{внеш}+rho gh -p_text{внеш}=rho gh $$ Получаем: $$ Delta p=1000cdot 10cdot 15=150 000 (text{Па})=150 (text{кПа}) $$ Ответ: на первом; на 150 кПа
Задача 2. Давление в трубах водопровода (4cdot 10^5 text{Па}). На какую максимальную высоту можно достать струей воды в случае пожара, если подключить оборудование к пожарному гидранту на поверхности земли? Атмосферное давление примите равным (1cdot 10^5 text{Па})
Дано:
(p=4cdot 10^5 text{Па})
(p_text{атм}=1cdot 10^5 text{Па})
(p=1000 text{кг/м}^3)
(gapprox 10 text{м/с}^2)
__________________
(h-?)
При подключении на струю воды, направленную вертикально вверх, будет действовать снизу давление водопровода, сверху атмосферное давление.
Под действием разности этих давлений вода может подняться на высоту $$ h=frac{p-p_text{атм}}{rho g} $$ Получаем: $$ h=frac{(4-1)cdot 10^5}{1000cdot 10}=30 (text{м}) $$ Ответ: 30 м
Задача 3. Рассчитайте, какую силу давления воды должен выдерживать жесткий водолазный скафандр, предназначенный для глубоководных работ на глубине до 365 м, если общая поверхность скафандра составляет 2,5 м2?
(Плотность морской воды 1010 кг/м3, g=9,8 м/с2). Ответ округлите до меганьютонов.
Дано:
(rho=1010 text{кг/м}^3)
(g=9,8 text{м/с}^2)
(h=365 text{м})
(S=2,5 text{м}^2)
__________________
(F-?)
Давление воды на максимальной глубине $$ p=rho gh $$ Сила давления $$ F=pS=rho ghS $$ Получаем: $$ F=1010cdot 9,8cdot 365cdot 2,5approx 9,03cdot 10^6 (text{Н})=9 (text{МН}) $$ Ответ: ≈9 МН
Задача 4*. В цилиндрический сосуд налиты ртуть и вода. Общая высота столба жидкости 20 см. Чему равно давление, создаваемое жидкостями на дно сосуда, если:
а) объемы жидкостей одинаковы; б массы жидкостей одинаковы?
Дано:
(rho_1=1000 text{кг/м}^3)
(rho_2=13600 text{кг/м}^3)
(H=20 text{см}=0,2 text{м})
(gapprox 10 text{м/с}^2)
(text{а)} V_1=V_2; text{б)} m_1=m_2)
__________________
(p-?)
Ответ: а) 14,6 кПа; б) 3,7 кПа

В жидкостях частицы подвижны, поэтому они не имеют собственной формы, но обладают собственным объемом, сопротивляются сжатию и растяжению; не сопротивляются деформации сдвига (свойство текучести). В покоящейся жидкости существует два вида статического давления: гидростатическое и внешнее. Вследствие притяжения к Земле жидкость оказывает давление на дно и стенки сосуда, а также на тела, находящиеся внутри нее. Давление, обусловленное весом столба жидкости, называется гидростатическим. Давление жидкости на разных высотах различно и не зависит от ориентации площадки, на которую оно производится. Пусть жидкость находится в цилиндрическом сосуде с площадью сечения S; высота столба жидкости h. Тогда
Гидростатическое давление жидкости зависит от плотности р жидкости, от ускорения g свободного падения и от глубины h, на которой находится рассматриваемая точка. Оно не зависит от формы столба жидкости. Глубина h отсчитывается по вертикали от рассматриваемой точки до уровня свободной поверхности жидкости. В условиях невесомости гидростатическое давление в жидкости отсутствует, так как в этих условиях жидкость становится невесомой. Внешнее давление характеризует сжатие жидкости под действием внешней силы. Оно равно:
Пример внешнего давления: атмосферное давление и давление, создаваемое в гидравлических системах. Французский ученый Блез Паскаль (1623-1662) установил: жидкости и газы передают производимое на них давление одинаково по всем направлениям (закон Паскаля). Для измерения давлений используют манометры. Их конструкции весьма разнообразны. В качестве примера рассмотрим устройство жидкостного манометра. Он представляет собой U-образную трубку, один конец которой соединяется с резервуаром, в котором измеряют давление. По разности столбов в коленах манометра можно определять давление.
Возможно вам будет интересно:
Вокруг нас много жидкостей. Одни из них движутся, например, вода в реках или нефть в трубах, другие – покоятся. При этом все жидкости имеют вес и поэтому давят на дно и стенки сосуда, в котором находятся. Подсчёт давления движущейся жидкости – непростая задача, поэтому изучим лишь как рассчитывать давление, создаваемое покоящейся жидкостью, называемое гидростатическим давлением (греч. «статос» – неподвижный). Оно вычисляется по следующей формуле.
| p – давление слоя жидкости, Па. r – плотность жидкости, кг/м3. g – коэффициент силы тяжести, Н/кг.
h – высота слоя жидкости, м. Рассмотрим, как выведена (то есть получена) эта формула. |
Сила F, с которой жидкость давит на дно сосуда, является весом жидкости. Его мы можем подсчитать по формуле W = Fтяж = mg, так как жидкость и её опора (дно сосуда) покоятся. Вспомним также простую формулу m = rV для выражения массы тела через плотность его вещества и формулу V = Sh для подсчёта объёма тела, имеющего форму прямоугольного параллелепипеда. В результате имеем равенство:
Это равенство иллюстрирует не только способ вывода формулы для вычисления гидростатического давления. Оно также показывает, что формула p = rgh является частным случаем формулы p = F/S. Поэтому здесь уместны те же замечания, что и при изучении нами силы Архимеда (см. § 3-е «под чертой»).
Заметим, что при выводе формулы совершенно необязательно предполагать, что слой высотой h и плотностью r образован именно жидкостью. В наших рассуждениях ничего не изменится, если вместо давления жидкости мы рассмотрим давление твёрдого тела прямоугольной формы или даже газа, заключённого в соответствующий сосуд. Создаваемое ими весовое давление будет именно таким, как предсказывает формула p = rghФормула p = rgh показывает, что давление, создаваемое слоем жидкости, не зависит от её массы, а зависит от плотности жидкости, высоты её слоя и места наблюдения. При увеличении толщины слоя жидкости или её плотности гидростатическое давление будет возрастать.
Полученный нами вывод можно проверить опытами. Проделаем их. Справа изображена стеклянная трубка, дно которой затянуто резиновой плёнкой.
Увеличивая высоту слоя налитой жидкости, мы будем наблюдать увеличение растяжения плёнки. Этот опыт подтверждает, что при увеличении высоты слоя жидкости создаваемое ею давление увеличивается.
На следующем рисунке изображены трубки с водой и «крепким» раствором соли. Видно, что уровни жидкостей находятся на одной и той же высоте, но давление на плёнку в правой трубке больше. Это объясняется тем, что плотность раствора соли больше, чем плотность обычной воды.
Иногда вместо слов давление слоя жидкости употребляют выражение давление столба жидкости. Это выражения-синонимы.
Page 2
Давление может создаваться не только твёрдыми или жидкими телами, но и газами. Например, парусный корабль плывёт по морю именно потому, что на его паруса давит ветер – движущийся газ. Однако покоящиеся газы тоже могут создавать давление. Рассмотрим опыт, подтверждающий это.
Слева на рисунке – так называемая тарелка воздушного насоса. На ней лежит завязанный воздушный шарик с небольшим количеством воздуха (рис. «а»). Накроем его стеклянным колоколом и откачаем из-под него воздух. Мы увидим, что шарик «раздулся», будто в него накачали дополнительную порцию воздуха (рис. «б»). Однако это не так: воздуха в шарике не прибавилось, ведь он завязан. В чем же разгадка противоречия?
Воздух в шарике постоянно давит на его оболочку изнутри. Но и воздух вокруг шарика давит на его оболочку – снаружи (см. рисунок). Откачивая воздух из-под колокола, мы уменьшаем наружное давление. В результате внутреннее давление начинает превосходить наружное и тем самым раздувает оболочку сильнее.
Рассмотренный опыт с тарелкой и колоколом воздушного насоса продемонстрировал нам, что покоящиеся газы постоянно оказывают давление на окружающие их тела. В зависимости от внешних условий это давление может проявляться или же быть незаметным.
Накачивая или откачивая газ в каком-либо сосуде (например, баллоне), мы увеличиваем или, наоборот, уменьшаем массу газа. Из-за этого изменяется плотность газа – увеличивается или уменьшается. Одновременно изменяется и давление газа – говорят, что оно «повышается» или «понижается» (иногда говорят, что давление «растёт» или «падает»).
Однако давление газа можно изменить не только изменением его плотности, но и другим путём – изменяя температуру газа. При нагревании газа его давление будет возрастать, а при охлаждении – уменьшаться. Рассмотрим пример.
На рисунке изображён котёл для воды с прочным корпусом и плотно прилегающей крышкой. На котле имеется манометр – прибор, отмечающий повышение или понижение давления пара. При нагревании котла давление пара возрастает, так как мы видим изменившееся положение стрелки манометра и многочисленные струи пара, вырывающиеся из щелей между корпусом и крышкой.
Опыты показывают, что не только водяной пар, но и вообще все газы при нагревании увеличивают свое давление на окружающие тела, а при охлаждении – уменьшают.
Паровая турбина. Она применяется на тепловых электростанциях. Сгорающий природный газ или мазут нагревают воду, которая превращается в пар. Его подвергают дальнейшему сильному нагреванию. В результате давление пара значительно возрастает, и его направляют на лопасти ротора турбины (см. фото).
Чем выше давление пара, тем с большей скоростью будет вращаться ротор, тем больше электроэнергии может быть выработано. В современных турбинах давление пара составляет более 10 000 кПа при температуре 300–500 °С.
Page 3
О том, что все газы имеют массу, мы часто склонны забывать. Помните ли вы, например, что 1 кубический метр воздуха имеет массу более 1 кг ? Если забыли – загляните в таблицу плотностей в § 2-г… Из этого следует, что масса воздуха, находящегося в классе, составляет примерно 200–300 кг!
Проведём опыт, подтверждающий, что воздух действительно имеет массу. Взгляните на рисунок «а». Вы видите, что к левой чаше весов подвешен стеклянный шар, а на самой чаше лежит пробка с трубкой и зажимом. На правой чаше стоит гиря, уравновешивающая вес предметов на чаше слева: пробки, трубки, зажима и шара, в котором есть окружающий нас воздух.
Взгляните на рисунок «б». Шар отцепили от чаши и присоединили к насосу. Некоторое время воздух из шара откачивали.
Затем трубку пережали зажимом, а шар опять подвесили к чаше (рис. «в»). Мы видим, что теперь гиря «перевешивает», следовательно, масса шара стала меньше массы гири. То есть опыт подтвердил, что атмосферный воздух обладает массой. Её можно измерить при помощи весов и гирь. Зная объём шара, можно даже подсчитать плотность воздуха.
Существование массы воздуха – причина того, что воздух, притягиваясь к Земле, имеет вес. Известно, например, что атмосферный воздух, расположенный над площадью поверхности Земли в 1 м, имеет огромный вес – около 100 тысяч ньютонов!
Как известно, воздух окружает всю Землю в виде шарообразного слоя, поэтому воздушную оболочку Земли называют атмосферой (греч. атмос – пар, воздух; сфера – шар). Как и любое тело, она притягивается к Земле. Действуя на тела своим весом, атмосфера создаёт давление, называемое атмосферным давлением. Согласно закону Паскаля оно распространяется в дома, пещеры, шахты и действует на все тела, соприкасающиеся с атмосферным воздухом.
Космические полёты показали, что атмосфера возвышается над поверхностью Земли на несколько сотен километров, становясь всё более разреженной (менее плотной). Постепенно она переходит в безвоздушное пространство – вакуум (лат. «пустота»), в котором отсутствует воздух, а, следовательно, и атмосферное давление.
Существованием атмосферного давления объясняется множество явлений. Рассмотрим одно из них – поднятие жидкости за поршнем, например, водяного насоса. Обратимся к рисунку.
Если резко поднять рукоятку поршня, то между ним и жидкостью образуется безвоздушное пространство, давление в котором практически равно нулю. Поэтому атмосферное давление, воздействуя на поверхность жидкости в сосуде (голубые стрелки), вгонит жидкость вверх по трубке в пространство с меньшим давлением. Но если же поршень поднимать плавно, то внешне всё будет выглядеть так, как будто бы жидкость «сама собой» поднимается за поршнем.
Page 4
До сих пор мы изучали случаи, когда сила, действующая на тело, была приложена к нему в одной точке. Мы так и говорили про неё: «точка приложения силы» . Настало время ситуаций, когда сила приложена к телу во множестве точек, то есть действует на некоторую площадь поверхности. В каждом из таких случаев говорят не только о самой силе, но и о создаваемом ею давлении.
Как приятна зимняя прогулка на лыжах! Однако стоит выйти на снег без них, как ноги будут глубоко проваливаться при каждом шаге, идти будет трудно, и удовольствие будет испорчено.
На этом рисунке вес лыжника примерно равен весу «пешехода». Поэтому силы, с которыми мальчики давят на снег, будем считать равными. Но заметьте: они действуют не на одну точку, а «распределяются» по некоторым поверхностям. У лыжника – по площади касания снега и лыж, а у пешехода – снега и подошв.
Понятно, что Sлыж > Sподошв. Поэтому и результат действия лыжника на снег проявляется в меньшей степени – лыжник проваливается на меньшую глубину.
Распределение силы по площади её приложения характеризуют особой физической величиной – давлением. Отношение силы F к площади поверхности S, при условии, что сила действует перпендикулярно поверхности, называют давлением. Это определение давления, и его можно записать в виде формулы:
| p – давление, Па. F^ – перпендикулярно приложенная сила, Н.
S – площадь поверхности, м2. |
Единица давления – 1 паскаль (обозначается: 1 Па). Из формулы-определения видно, что 1 Па = 1 Н/мЧисловое значение давления показывает силу, приходящуюся на единицу площади её приложения. Например, при давлении 5 паскалей на каждый 1 м2 будет действовать сила 5 ньютонов.
Вернёмся к примеру с мальчиками. На рисунке не указаны числовые значения F и S. Значит, мы не можем количественно сравнить давления, которое оказывают мальчики (с лыжами и без лыж) на снег.
Однако мы можем сравнить их качественно, используя слова «больше» и «меньше». Сделаем это.
Сначала запишем исходные данные: силы, с которыми мальчики давят на снег, равны, и площадь лыж больше площади подошв (см. столбик слева):
После знака «Ю», который значит «следовательно», мы составили две дроби. Обратите внимание: знак «больше», присутствовавший в исходных данных, изменился на знак «меньше». Почему?
Поскольку знаменатель левой дроби больше знаменателя правой, значит, согласно свойству дроби, сама левая дробь меньше правой. Вспомнив, что каждая дробь в этом неравенстве является давлением, получим: давление лыжника меньше давления пешехода. Этим и объясняется то, что лыжник меньше проваливается в снег, чем пешеход.
Формула-определение давления подсказывает нам, как его можно изменять: чтобы увеличить давление, нужно увеличить силу или уменьшать площадь её приложения. И наоборот: чтобы уменьшить давление, нужно уменьшить силу или увеличить площадь, на которую эта сила действует.
Page 5
Познакомимся с необычным законом: он справедлив лишь для покоящихся жидкостей и газов. Для этого проведём опыт – нальём в пакет воды и завяжем. Если на него надавить рукой, то он прорвётся, и вода вытечет. Однако заметим: пакет рвётся не обязательно в том месте, где на него давят. Следовательно, давление, оказываемое нами на одну часть пакета, распространяется в другие его части.
Этим простым опытом мы проиллюстрировали закон Паскаля: давление, производимое на жидкость или газ, передаётся без изменения во все части жидкости или газа.
Согласно этому закону, давление внутри жидкостей и газов распространяется по всевозможным направлениям. Следовательно, жидкости и газы оказывают давление во всех направлениях: влево, вправо и даже вверх! Это подтверждается опытами. Рассмотрим некоторые из них.
Возьмём стеклянную трубку и лёгкий диск на нити (рис. «а»). Натянув нить, мы получим сосуд с отпадающим дном (рис. «б»). Погрузим этот сосуд в широкий стакан с водой. Удивительно, но теперь дно (то есть диск) не отпадет, даже если нить не натягивать (рис. «в»).
Так происходит потому, что верхние слои воды в стакане создают давление на нижележащие слои, в том числе и на слой воды под диском. Согласно закону Паскаля это давление передаётся через слой воды под диском и действует на диск снизу вверх. Сила этого давления и поддерживает диск, прижимает его к краям стеклянной трубки.
Продолжим опыт. Нальём в трубку столько подкрашенной воды, чтобы её уровень оказался ниже, чем у воды в стакане (рис. «г»).
Мы увидим, что диск не отпадает. Так происходит потому, что давление на диск снизу по-прежнему больше, чем сверху. Теперь увеличим высоту слоя подкрашенной воды.
Диск отпадёт (рис. «д»). Значит, давление на диск сверху, созданное подкрашенной водой, превысило давление снизу, созданное водой в стакане при «помощи» закона Паскаля.
Примечание. При описании опыта мы пренебрегаем весом диска.
Согласно закону Паскаля вне зависимости от формы и размеров сосуда давление внутри жидкости на одной и той же глубине одинаково. Докажем это утверждение. Пусть рассматриваемым «сосудом» будет морская бухта с подводной пещерой. Взгляните на рисунок справа. Казалось бы, что давление воды в пещере меньше, чем давление в открытом море.
Однако, если бы это было так, то под действием большего из давлений вода из моря устремилась бы в пещеру, и уровень воды в море стал бы понижаться. Невероятно, да? Итак, поскольку вода у входа в пещеру (и в море тоже) остаётся в покое, значит давление воды в пещере равно давлению воды в море.
Page 6
Про массу или длину говорят, что они большие или маленькие, увеличиваются или уменьшаются. Про атмосферное давление говорят: оно высокое или низкое, повышается или понижается. Такая традиция установилась ещё с тех пор, когда атмосферное давление измеряли барометрами Торричелли, наблюдая за поднятием или опусканием ртутного столба. Сегодня чаще применяют безжидкостные барометры, так называемые анероиды (греч. «а» – отрицание, «нерос» – влажный).
Главная часть барометра-анероида – лёгкая, упругая, полая внутри металлическая коробочка 2 с гофрированной (волнистой) поверхностью. Воздух из коробочки откачан. Её стенки растягивает пружинящая металлическая пластина 5. К ней при помощи специального механизма прикреплена стрелка 6, которая насажена на ось 7 (см. рисунок ниже). Конец стрелки передвигается по шкале 4, размеченной в мм рт. ст. Все детали барометра помещены внутрь корпуса 1, закрытого спереди стеклом 3.
Согласно формуле F=pS, изменение атмосферного давления (то есть величины «p») будет приводить к изменению силы, сдавливающей стенки коробочки. Следовательно, будет изменяться и величина их прогиба. Возникающее движение стенок коробочки при помощи механизма передастся стрелке и вызовет её сдвиг к другому делению шкалы.
На рисунке – упрощённая схема соединения коробочки со стрелкой. В действительности этот механизм гораздо сложнее. В нём есть даже нить, наматывающаяся на колесо с жёлобом, прикреплённое к стрелке.
Барометр-анероид – очень чувствительный прибор. Например, с его помощью можно заметить изменение атмосферного давления даже при подъёме на лифте жилого дома. Наблюдая за барометром, вы легко обнаружите, что его показания меняются при перемене погоды. Замечено, что перед ненастьем атмосферное давление падает, а перед ясной погодой – возрастает. Кроме того, показания барометра зависят от высоты места наблюдения над уровнем моря. Чем выше мы будем подниматься, тем меньшим будет атмосферное давление. При небольших высотах подъёма каждые 12 м атмосферное давление уменьшается на 1 мм рт. ст.
Как барометр-анероид, так и трубку Торричелли можно использовать не только как барометр, но и как вакуумметр. Так называется прибор, измеряющий давления газа, меньшие атмосферного.
На рисунке изогнутая трубка Торричелли помещена на тарелку воздушного насоса. Поскольку высота трубки гораздо меньше 76 см, то при атмосферном давлении ртуть заполняет трубку целиком (рис. «а»).
Накрыв трубку колоколом и откачивая воздух насосом, мы будем понижать давление. Через некоторое время уровень ртути начнёт понижаться, показывая, что под колоколом постепенно создаётся вакуум (рис. «б»).
Page 7
По телевидению или радио мы часто слышим, что атмосферное давление сегодня равно, например, 760 мм рт. ст. (читается: семьсот шестьдесят миллиметров ртутного столба).
Это число бывает и другим – немного больше или меньше. Что оно означает? Для ответа на вопрос рассмотрим опыт итальянского учёного Э.
Стеклянную трубку длиной около метра, запаянную с одного конца, наполняют доверху ртутью. Затем, плотно закрыв отверстие пальцем, трубку переворачивают и опускают в чашу со ртутью, после чего палец убирают. Ртуть из трубки начинает выливаться, но не вся: остаётся «столб» 76 см высотой, считая от уровня в чаше. Примечательно, что эта высота не зависит ни от длины трубки, ни от глубины её погружения.
Объясним этот опыт. Взгляните на нижний рисунок. На нём мы пометили жёлтым цветом небольшой слой ртути внутри трубки вблизи её отверстия. Вес вышележащих слоёв действует вниз, толкая жёлтый слой в чашу. Причина этого – действие сила тяжести.
Ртуть в чаше давит на жёлтый слой с силой, направленной вверх. Причина этого – атмосферное давление, действующее на поверхность ртути в чаше. И действительно, согласно закону Паскаля оно распространяется через ртуть в чаше внутрь трубки (на рисунке – изогнутые стрелки). Так как ртуть покоится, то выделенные курсивом силы (вес и сила давления) уравновешивают друг друга. Обозначим это как F = F.
Из определения давления, формулы p = F/S следует, что F = pS. Так как F = F, получаем равенство pS = pS. Здесь S и S – площади верхней и нижней поверхностей «жёлтого» слоя ртути, равные друг другу. Значит, равны и давления: p = p. То есть давление, создаваемое столбом ртути в трубке, равно атмосферному давлению.
Трубка Торричелли с линейкой является простейшим барометром – прибором для измерения атмосферного давления (см. рисунок).
Измерения показывают, что атмосферное давление в местностях, лежащих на уровне мирового океана, в среднем 760 мм рт.ст. Такое давление при температуре ртути 0 °С называется нормальным атмосферным давлением. Выразим его в более привычных единицах давления – паскалях:
p = r g h = 13600 кг/м · 10 Н/кг · 0,76 м 100 кПаИтак, как же понимать, что атмосферное давление равно, например, 760 мм рт. ст. или 100 кПа? Это значит, что в данный момент атмосферное давление таково, что уравновешивает давление столба ртути высотой 76 см в трубке Торричелли.
В соответствии с законом Паскаля гидростатическое давление на уровне горизонтального дна сосуда при высоте жидкости в сосуде, равной Н, (1.7) Отсюда следует, что абсолютное давление рна горизонтальное дно не зависит от формы сосуда и объема жидкости в нем. При данной плотности жидкости оно определяется лишь высотой столба жидкостиНи внешним давлениемр0.
Сила давления жидкости Ржна дно сосуда зависит от его площадиF:
(1.8) Общая сила давления на дно сосуда (1.9) Внешнее давление р0передается жидкостью каждому элементу поверхности стенки одинаково, поэтому равнодействующая внешнего давления приложена в точке центра тяжести поверхности стенки. Давление веса жидкости на стенку не одинаково по высоте: чем глубже расположен элемент стенки, тем большее давление веса жидкости он испытывает. Поэтому центр давления жидкости на вертикальную стенку расположен всегда ниже центра тяжести смоченной поверхности стенки.
Сила полного гидростатического давления на плоскую стенку равна произведению гидростатического давления в центре тяжести этой стенки и ее площади: (1.10) где – расстояние от верхнего уровня жидкости до центра тяжести смоченной поверхности стенки; оно зависит от геометрической формы стенки.
Сила избыточного давления (собственно жидкости) Ризбна стенку Точка приложения сил РиРизбносит название центра давленияhди может быть определена в соответствии с законами теоретической механики через момент инерции смоченной поверхности стенки (1.11) где Jx– момент инерции стенки относительно осиox.
Для прямоугольной стенки при уровне жидкости в сосуде, равном Н, и ширине стенкиВ Следовательно, Применив закон Паскаля к сообщающимся сосудам, можно прийти к следующим выводам.
Если сосуды (рис. 1.4 а) заполнены однородной жидкостью (одинаковой плотности), то при равновесии давление в точке 0 может быть выражено:
либо, т.е. в сообщающихся сосудах заполняющая их однородная жидкость располагается на одинаковом уровне.
При заполнении сосудов жидкостями с различной плотностью (рис 1.4 б) в условиях равновесия давление в точке О будет либо.
Рисунок 1.4 – Сообщающиеся сосуды, заполненные жидкостью: а– одной плотности;б– разной плотности Следовательно , т.е.
. (1.12) Соотношение (1.12) указывает на то, что высоты уровней жидкости, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.
Этот принцип используется для измерения уровня жидкости в закрытых аппаратах с помощью водомерных стёкол, в жидкостных манометрах.
Если сообщающиеся сосуды заполнены одной и той же жидкостью, но давление над уровнем жидкости в них разное – рир, то при равновесии , , откуда . (1.13) Последнее выражение используется при измерении давления или разности давлений между различными точками с помощью дифференциальных U-образных манометров.
Рисунок 1.5. – К определению высоты гидравлического затвораЭтот же принцип используется для определения высоты гидравлического затвора в аппаратах, заполненных жидкостью (рис. 1.5).
На рисунке представлен сосуд, заполненный двумя жидкостями с плотностями 1и2; уровень их раздела на глубинеz1необходимо поддерживать в процессе работы постоянным с помощью гидрозатвора, представляющего собойU-образную трубку, подсоединённую снизу (на выходе жидкости из аппарата).
В соответствии с уравнением (1.12) высота гидравлического затвора в случае одинакового давления над жидкостью внутри аппарата и на выходе из затвора . (1.14) На использовании данного уравнения гидростатики основана работа таких простейших гидравлических машин, как гидравлический пресс, мультипликатор (для повышения давления), домкрат, подъемник и др.
Рисунок 1.6 – Схема гидравлического прессаНа рис. 1.6 показана схема гидравлического пресса. Если к поршню П
, имеюшему площадь.
F
, приложена сила.
Р
, то эта сила будет передаваться на жидкость; жидкость же будет давить на поршень П.
, имеющий площадь.
F
, с силой.

None (1.16) Из уравнения (1.16) следует, что при помощи пресса сила Р1увеличивается во столько раз, во сколько площадьF2больше площадиF1.
Источники:
- sfiz.ru
- questions-physics.ru
- studfiles.net
Сообщающиеся сосуды, теория и онлайн калькуляторы
Сообщающиеся сосуды
Определение сообщающихся сосудов
Определение
Соединенные между собой сосуды называют сообщающимися.
В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.
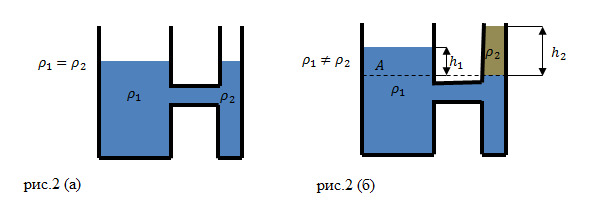
Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:
[p=rho gh left(1right),]
где $rho $ — плотность жидкости; $g$ — ускорение свободного падения; $h$ — высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.
Жидкости разной плотности в сообщающихся сосудах
Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:
[{rho }_1gh_1={rho }_2gh_2left(2right),]
где ${rho }_1$ и ${rho }_2$ — плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:
[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]
Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.
Гидравлический пресс и другие примеры использования сообщающихся сосудов
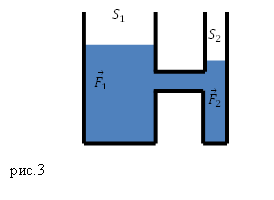
В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:
[p_1=frac{F_1}{S_1}left(4right).]
Второй поршень давит на жидкость:
[p_2=frac{F_2}{S_2}left(5right).]
Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]
Получим:
[F_1=F_2frac{S_1}{S_2}(7)]
величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.
По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана — уровень воды в баке.
Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.
Примеры задач с решением
Пример 1
Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ — площадь сечения правого сосуда. Объемом трубки пренебречь.
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:
[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]
где $S_{1 }$ — площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:
[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]
где $S_{2 }$ — площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:
[Delta V_1=Delta V_2left(1.3right).]
Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:
[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]
Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:
[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=]
[=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]
Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$
Пример 2
Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?
Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):
[F_1=F_2frac{S_1}{S_2}(2.1)]
Ответ. $F_1=F_2frac{S_1}{S_2}$
Читать дальше: условия плавания тел.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!















![[T =-P_0 cdot S_1]](https://fizikinfo.ru/wp-content/uploads/2019/07/Davlenie-zhidkosti-v-raznyh-sosudah14.png)