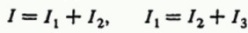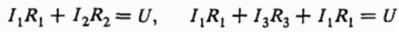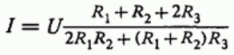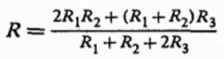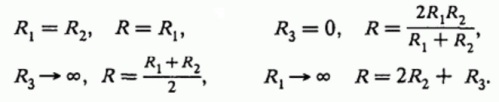Смешанное соединение резисторов. Расчет смешанного соединения
Здравствуйте, уважаемые читатели сайта sesaga.ru. Смешанное соединение резисторов представляет собой сложную электрическую цепь, в которой часть резисторов соединена последовательно, а часть параллельно.
В радиолюбительской практике такое включение резисторов встретить трудно, так как нет смысла подбирать сопротивление таким сложным способом. Достаточно соединить два, ну максимум три резистора последовательно или параллельно, чтобы подобрать нужный номинал.
Смешанное соединение встречается в основном в учебниках физики или электротехники в виде задач. Мне вспоминается такая задачка из школьной программы, но тогда она мне показалась сложной и правильно решить ее не получилось.
И вот, исходя из полученного опыта, хочу рассказать Вам, как вычислить общее сопротивление смешанного соединения резисторов. Вдруг кому-нибудь в жизни да и пригодится.
Расчет смешанного соединения резисторов.
Расчет начинают от дальнего участка цепи по отношению к источнику питания.
Определяют участок с параллельным или последовательным соединением двух резисторов и высчитывают их общее сопротивление Rобщ. Затем полученное сопротивление складывают с рядом стоящим резистором и т.д.
Суть данного метода заключается в уменьшении количества элементов в цепи с целью упрощения схемы и, соответственно, упрощению расчета общего сопротивления.
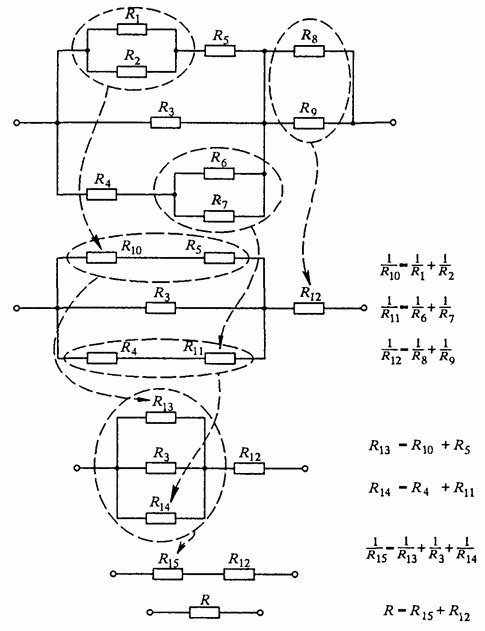
Разберем схему смешанного соединения из семи резисторов:
Самым дальним участком схемы оказались резисторы R6 и R7, соединенные параллельно:
Вычисляем их общее сопротивление используя формулу параллельного соединения:
Теперь если сравнить первоначальную схему с получившейся, то здесь мы видим, что она уменьшилась на один элемент и вместо двух резисторов R6 и R7 остался один R6 с суммарным сопротивлением равным 30, 709 кОм.
Продолжим расчет и следующим дальним участком схемы оказались резисторы R5 и R6, соединенные последовательно:
Вычисляем их общее сопротивление используя формулу последовательного соединения. Сопротивление резистора R5 составляет 27 Ом, а R6 = 30,709 кОм, поэтому для удобства расчета килоомы переводим в Омы (1 кОм = 1000 Ом):
Схема уменьшилась еще на один элемент и приняла вид:
Теперь дальним участком оказались резисторы R4 и R5 соединенные параллельно:
Вычисляем их общее сопротивление:
Первоначальная схема опять изменилась и теперь состоит всего из четырех резисторов соединенных последовательно. Таким образом мы максимально упростили схему и привели ее к удобному расчету.
Теперь все просто. Складываем сопротивления оставшихся четырех резисторов, используя формулу последовательного соединения, и получаем общее сопротивление всей цепи:
Вот в принципе и все, что хотел сказать о смешанном соединении резисторов и расчете смешанного соединения.
Удачи!
Источник
Соединение резисторов — как считать общее сопротивление
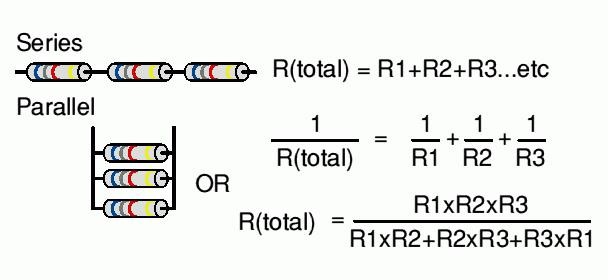
Применяются следующие соединения резисторов: параллельное, последовательное и смешанное.
Последовательное соединение резисторов
Последовательное соединение резисторов — это такое взаимное расположение компонентов, при котором ток движется в одном направлении и имеет общее значение для каждого резистора. При таком соединении напряжение на каждом участке будет пропорционально сопротивлению конкретного резистора в цепи.
Принципиальная схема последовательного соединения:
Для подсчета общего (эквивалентного) сопротивление при последовательном соединении нужно сложить все номинальные сопротивления резисторов входящих в цепь:
В представленной схеме для наглядности приведены напряжения на каждом из трех участков. И падение напряжения происходит в зависимости от сопротивления конкретного резистора. Сила тока в цепи общая для всех резисторов ( I = I1 = I2 = I3 ). Поэтому согласно закону Ома сила тока при известном напряжении источника питания (в данном случае U = 220 В) определяется по формуле:
I = U / R = U / (R1 + R2 + R3 + . + Rn) .
I = 220 / (20 + 70 + 10) = 220 / 100 = 2,2 A.
Формулы нахождения напряжения на участке цепи при известной силе тока (в данном случае I = I1 = I2 = I3 = 2,2 A):
Соответственно U1 = 2,2 × 20 = 44 В; U2 = 2,2 × 70 = 154 В; U3 = 2,2 × 10 = 22 В. В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи (220 В).
Рассмотренные три резистора в последовательной цепи можно заменить одним с сопротивлением 100 Ом:
Если можно несколько резисторов заменить одним, то возникает логичный вопрос, зачем применяется такое комбинирование. Простыми словами можно ответить, что иногда невозможно подобрать резистор с требуемыми параметрами или необходимо создать более сложные электронные схемы. В этом случае прибегают к последовательному, параллельному или смешанному соединению в цепи.
В цепи из последовательно соединенных резисторов главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление. К примеру, если соединить три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате получиться составной с сопротивлением 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом. А если убрать резистор на 10 Ом, то сопротивление незначительно уменьшиться до 101 Ом.
Параллельное соединение резисторов
Параллельное соединение резисторов — это такое взаимное соединение компонентов, при котором оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.
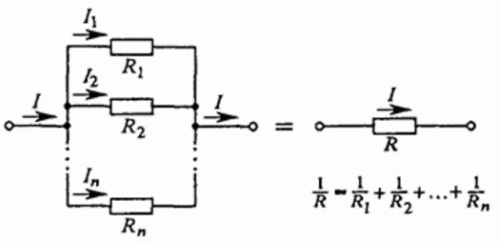
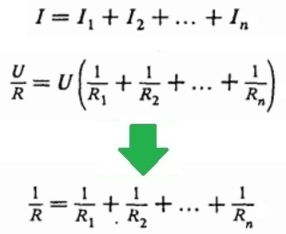
При таком соединении напряжение во всей цепи и на каждом участке одинаково и равно напряжению источника питания U = U1 = U2 = U3 = Un . По каждому резистору течет свой ток. Сумма токов всех резисторов дает общую силу тока цепи: I = I1 + I2 + I3 + . + In . Соответственно общая проводимость параллельной цепи равна сумме ее отдельных проводимостей. Проводимость есть величина, обратная сопротивлению, поэтому эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением:
1 / R = 1 / R1 + 1 / R2 + 1 / R3 + . + 1 / Rn . Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Рассчитаем общее сопротивление для приведенного выше примера с параллельным соединением резисторов:
1 / R = 1 / 20 + 1 / 70 + 1 / 10 ≈ 0,164.
Выделим основные особенности параллельного соединения резисторов:
- Общее сопротивление всегда меньше сопротивления любого параллельно включенного резистора.
- Увеличение числа параллельно соединенных резисторов ведет к уменьшению общего сопротивления и увеличению общей силы тока в цепи.
- Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
- Если в цепи используются резисторы одного номинала, то формула общего сопротивления упрощается и принимает вид R = R1 / N (R1 – номинальное сопротивление резистора; N – количество резисторов с одинаковым номинальным сопротивлением).
Смешанное соединение резисторов
Смешанное соединение резисторов — это комбинация последовательного и параллельного соединения. Иногда такую комбинацию называют последовательно-параллельным соединением.
Пример цепи со смешанным соединением резисторов:
Для расчета эквивалентного сопротивления таких соединений всю цепь разбивают на простейшие участки и придерживаются следующего алгоритма:
Параллельное соединение резисторов используется для получения меньшего сопротивления из имеющихся простейших радиоэлектронных элементов. При таком способе соединения складываются проводимости. Поэтому чем больше параллельно включенных резисторов, тем ниже получается общее сопротивление или выше проводимость соответственного участка электрической цепи – носителям электрических зарядов легче его преодолеть.
Последовательное соединение резисторов используется с целью большего ограничения протеканию электрическому току, то есть приводит к повышению сопротивления соответственного участка электрической цепи или для снижения ее проводимости.
Важнейшим параметром резистора является мощность рассеивания. При любом способе соединения, не важно, при последовательном, при параллельном или при смешанном, происходит сложение мощностей рассеивания отдельных резисторов. Поэтому все вместе они способны рассеять больше тепла, а соответственно и пропустить большие токи не перегреваясь, что широко применяется в радиолюбительской практике.
Источник
Ток и напряжение при параллельном, последовательном и смешанном соединении проводников

Если взглянуть на электрическую цепь, включающую в себя несколько разных проводников, и рассмотреть на ней пару точек (вход и выход), то в принципе остальная часть цепи может быть рассмотрена как одиночный резистор (по ее эквивалентному сопротивлению).
При таком подходе говорят, что если ток I – это ток в цепи, а напряжение U – напряжение на выводах, то есть разность электрических потенциалов между точками «входа» и «выхода», то тогда отношение U/I можно рассмотреть как величину эквивалентного сопротивления R цепи целиком.
Если закон Ома выполняется, то эквивалентное сопротивление можно вычислить довольно легко.
Ток и напряжение при последовательном соединении проводников
В простейшем случае, когда два и более проводников объединены друг с другом в последовательную цепь, ток в каждом проводнике окажется одним и тем же, а напряжение между «выходом» и «входом», то есть на выводах всей цепи, будет равным сумме напряжений на составляющих цепь резисторах. И поскольку закон Ома справедлив для любого из резисторов, то можно записать:
Итак, для последовательного соединения проводников характерны следующие закономерности:
Для нахождения общего сопротивления цепи, сопротивления составляющих цепь проводников складываются;
Ток через цепь равен току через любой из проводников, образующих цепь;
Напряжение на выводах цепи равно сумме напряжений на каждом из проводников, образующих цепь.
Ток и напряжение при параллельном соединении проводников
При параллельном соединении нескольких проводников друг с другом, напряжение на выводах такой цепи — это напряжение на каждом из проводников, составляющих цепь.
Напряжения на всех проводниках равны между собой и равны напряжению приложенному (U). Ток через всю цепь — на «входе» и «выходе» — равен сумме токов в каждой из ветвей цепи, параллельно объединенных и составляющих данную цепь. Зная, что I = U/R, получаем, что:
Итак, для параллельного соединения проводников характерны следующие закономерности:
Для нахождения общего сопротивления цепи — складываются обратные величины сопротивлений составляющих цепь проводников;
Ток через цепь равен сумме токов через каждый из проводников, образующих цепь;
Напряжение на выводах цепи равно напряжению на любом из проводников, образующих цепь.
Эквивалентные схемы простых и сложных (комбинированных) цепей
В большинстве случаев схемы цепей, являясь комбинированным соединением проводников, поддаются пошаговому упрощению.
Группы соединенных последовательно и параллельно частей цепи, заменяют эквивалентными сопротивлениями по приведенному выше принципу, шаг за шагом вычисляя эквивалентные сопротивления кусочков, затем приводя их к одному эквивалентному значению сопротивления всей цепи.
И если сначала схема выглядит довольно запутанной, то будучи упрощенной шаг за шагом, она может быть разбита на меньшие цепочки из последовательно и параллельно соединенных проводников, и так в конце концов сильно упрощена.
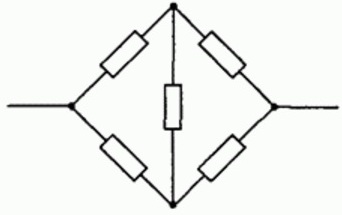
Между тем, не все схемы подаются упрощению таким простым путем. Простая с виду схема «моста» из проводников не может быть исследована таким образом. Здесь нужно применять уже несколько правил:
Для каждого резистора выполняется закон Ома;
В любом узле, то есть в точке схождения двух и более токов, алгебраическая сумма токов равна нулю: сумма токов втекающих в узел, равна сумме токов вытекающих из узла (первое правило Кирхгофа);
Сумма напряжений на участках цепи при обходе по любому пути от «входа» до «выхода» равна приложенному к цепи напряжению (второе правило Кирхгофа).
Мостовое соединение проводников
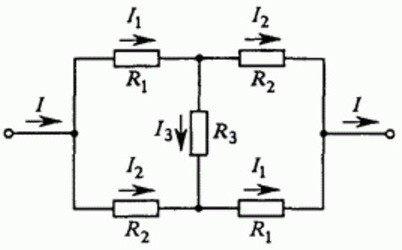
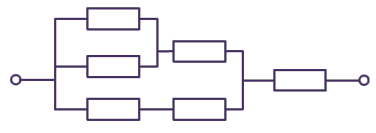
Дабы рассмотреть пример использования приведенных выше правил, рассчитаем цепь, собранную из проводников, объединенных в схему моста. Чтобы вычисления получились не слишком сложными, примем, что некоторые из сопротивлений проводников равны между собой.
Обозначим направления токов I, I1, I2, I3 на пути от «входа» в цепь — к «выходу» из цепи. Видно, что схема симметрична, поэтому токи через одинаковые резисторы одинаковы, поэтому обозначим их одинаковыми символами. В самом деле, если поменять у цепи местами «вход» и «выход», то схема будет неотличима от исходной.
Для каждого узла можно записать уравнения токов, исходя из того, что сумма токов втекающих в узел равна сумме токов вытекающих из узла (закон сохранения электрического заряда), получится два уравнения:
Следующим шагом записывают уравнения сумм напряжений для отдельных участков цепи при обходе цепи от входя к выходу различными путями. Так как схема является в данном примере симметричной, то достаточно двух уравнений:
В процессе решения системы линейных уравнений, получается формула для нахождения величины тока I между зажимами «входным» и «выходным», исходя из заданного приложенного к цепи напряжения U и сопротивлений проводников:
А для общего эквивалентного сопротивления цепи, исходя из того, что R = U/I, следует формула:
Можно даже проверить правильность решения, например приведя к предельным и к частным случаям величины сопротивлений:
Теперь вы знаете, как находить ток и напряжение при параллельном, последовательном, смешанном, и даже при мостовом соединении проводников, применяя закон Ома и правила Кирхгофа. Эти принципы очень просты, и даже самая сложная электрическая цепь с их помощью в конце концов приводится к элементарному виду путем нескольких несложных математических операций.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Конспект урока: Решение задач. Смешанное соединение проводников. Электрические цепи. Измерение токов и напряжений в цепи
Постоянный электрический ток
Решение задач. Смешанное соединение проводников
План урока
- Смешанное соединение проводников. Метод эквивалентных преобразований
- Примеры решения задач
Цели урока
- Знать понятие смешанного соединения проводников; метод эквивалентных преобразований
- Уметь рассчитывать электрические схемы со смешанным соединением проводников
Разминка
- Как найти общее напряжение при последовательном соединении проводников?
- Как найти общее сопротивление при последовательном соединении проводников?
- Как найти общее сопротивление при параллельном соединении проводников?
Смешанное соединение проводников. Метод эквивалентных преобразований
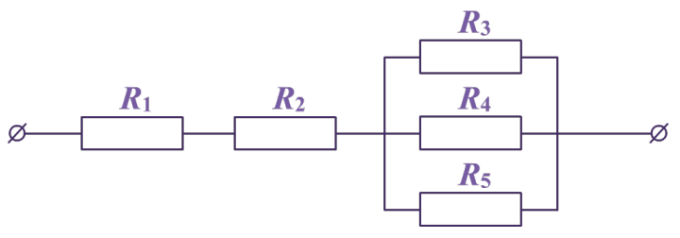
Рис. 1. Смешанное соединение проводников
Рассмотрим схему, представленную на рисунке 1.
Резисторы с сопротивлениями R1 и R2 соединены между собой последовательно, резисторы R3, R4 и R5 – параллельно.
Если в электрической цепи одновременно присутствуют и последовательное, и параллельное соединения проводников, такое соединение называют
смешанным
.
Для расчета электрической цепи, содержащей смешанное соединение, используют метод эквивалентных преобразований. Суть данного метода заключается в том, что исходную электрическую цепь заменяют на более простую электрическую цепь, при этом распределение сил токов и напряжений в непреобразованной части цепи остается прежним.
Например, в изображенной на рисунке 1 схеме проводники с сопротивлениями R3, R4 и R5 можно заменить на один проводник, сопротивление которого R345 равно общему сопротивлению трех данных резисторов:
1R345=1R3+1R4+1R5.
Рис. 2. Эквивалентная схема
Тогда исходную электрическую цепь можно заменить на эквивалентную схему, состоящую из трех последовательно соединенных проводников с сопротивлениями R1, R2 и R345 (рис. 2).
При этом распределение сил токов и напряжений на резисторах R1 и R2 останется таким же, каким было до преобразования электрической цепи.
Примеры решения задач
Пример 1
Рис. 3. Иллюстрация к примеру 1
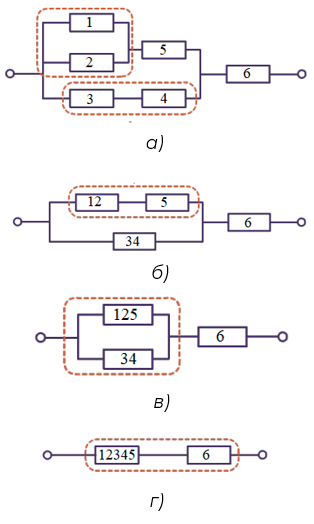
Найти общее сопротивление участка цепи, представленного на рисунке 3, если сопротивления всех резисторов одинаковы и равны R = 2 Ом.
Решение
Рис. 4. Эквивалентные схемы сложной цепи
Пронумеруем резисторы (рис. 4, а). Проводники 1 и 2 соединены параллельно, найдем их общее сопротивление R12:
1R12=1R1+1R2=12+12=1;
R12=1 Ом.
Проводники 3 и 4 соединены последовательно, найдем их общее сопротивление R34:
R34=R3+R4=2+2=4 Ом.
Проводники 1 и 2 можно заменить на один проводник сопротивлением R12, проводники 3 и 4 – на проводник R34. В результате получаем упрощенную, эквивалентную схему, представленную на рисунке 4, б.
Из рисунка 4, б видно, что проводники 12 и 5 соединены последовательно, найдем их общее сопротивление R125:
R125=R12+R5=1+2=3 Ом.
Заменяем два проводника 12 и 5 на один проводник сопротивлением R125, получаем эквивалентную схему, состоящую из трех резисторов (рис. 4, в). Находим общее сопротивление проводников 125 и 34:
1R12345=1R125+1R34=13+14=4+312=712;
R12345=127≈1,7 Ом.
В результате преобразований получаем схему, состоящую из двух последовательно соединенных проводников с сопротивлениями R12345 и R6 (рис. 4. г).
R123456=R12345+R6=1,7+2=3,7 Ом.
Ответ: R123456=3,7 Ом.
Пример 2
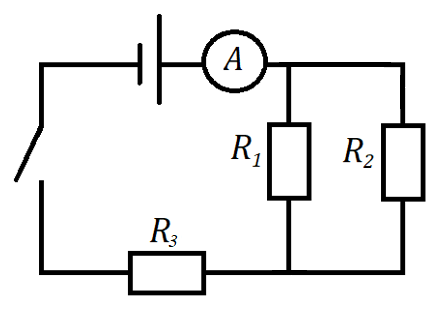
Рис. 5. Иллюстрация к примеру 2
Рассчитайте электрическую цепь, изображенную на рисунке 5. Амперметр показывает силу тока 2 А. Сопротивления первого, второго и третьего резисторов равны 4, 6 и 0,6 Ом соответственно.
Решение
Прежде всего, рассчитаем общее сопротивление цепи. Резисторы 1 и 2 соединены параллельно, найдем их общее сопротивление:
1R12=1R1+1R2=14+16=1024;
R12=2410=2,4 Ом.
Исходной схеме эквивалента схема из двух проводников сопротивлениями R12 и R3, соединенных последовательно. Тогда общее сопротивление данной цепи равно:
R=R12+R3=2,4+0,6=3 Ом.
Амперметр находится в неразветвленной части цепи, следовательно, он показывает общую силу тока в цепи, одинаковую на проводниках, соединенных последовательно:
I=I12=I3=2 А.
Найдем общее напряжение, а также напряжение на проводниках 12 и 3, используя закон Ома:
U=I·R=2·3=6 В;
U12=I12·R12=2·2,4=4,8 В;
U3=I3·R3=2·0,6=1,2 В.
Осталось найти распределение сил токов и напряжений на проводниках 1 и 2. Данные резисторы соединены параллельно, следовательно, напряжения на данных резисторах одинаковы и равны общему напряжению на данном участке цепи:
U1=U2=U12=4,8 В.
Сопротивления резисторов 1 и 2 известны, находим силы токов на данных проводниках по закону Ома:
I1=U1R1=4,84=1,2 А;
I2=U2R2=4,86=0,8 А.
Ответ: I=2 А; I1=1,2 А; I2=0,8 А; U=6 В; U1=4,8 В; U2=4,8 В; U3=1,2 В.
Пример 3
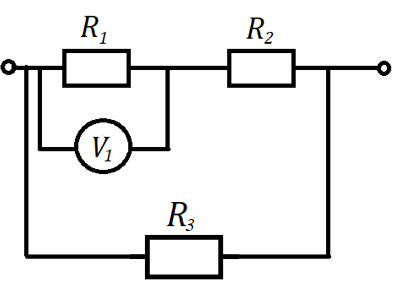
Рис. 6. Иллюстрация к примеру 3
Найти общую силу тока в электрической цепи, изображенной на рисунке 6. Вольтметр показывает напряжение 21 В. Сопротивления первого, второго и третьего резисторов равны 3, 2 и 5 Ом соответственно.
Решение
Из условия задачи известны сопротивление и напряжение на первом резисторе, найдем силу тока на данном проводнике:
I1=U1R1=213=7 А.
Так как проводники 1 и 2 соединены последовательно, сила тока на них одинакова:
I12=I1=I2=7 А.
Используя закон Ома, найдем напряжение на втором резисторе:
U2=I2·R2=7·2=14 В.
Так как проводники 1 и 2 соединены последовательно, общее напряжение на данном участке равно сумме напряжений на данных резисторах:
U12=U1+U2=21+14=35 В.
Участок цепи, изображенный на рисунке 6 можно представить в виде упрощенной схемы, состоящей из двух параллельно соединенных проводников с сопротивлениями R12 и R3. Тогда напряжение на данных резисторах одинаково и равно общему напряжению на данном участке:
U12=U3=U=35 В.
Найдем силу тока на третьем резисторе:
I3=U3R3=355=7 А.
Общая сила тока равна сумме сил тока на проводниках 12 и 3:
I=I12+I3=7+7=14 А.
Ответ: I=14 А.
Упражнение 1
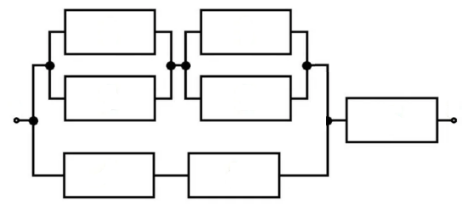
Рис. 7
1. Рассчитайте общее сопротивление участка цепи, представленного на рисунке 7, если сопротивления всех резисторов одинаковы и равны R = 2 Ом.
Рис. 8
2. Рассчитайте электрическую цепь, представленную на рисунке 8, если сопротивления всех резисторов одинаковы и равны 4 Ом. Сила тока в неразветвленной части цепи равна 50 А.
Рис. 9
3. Сопротивления резисторов 1, 2, 3 и 4 равны 2, 3, 7 и 3 Ом соответственно
(рис. 9). Известно, что напряжение на резисторе 1 составляет 20 В. Найти распределение сил токов и напряжений на данном участке цепи.
Ответы
Упражнение 1
1. R = 3,3 Ом.
2. I1 = I2 = I3 = I4 = 25 А; U = 200 В; U1 = U2 = U3 = U4 = 100 В.
3. I = 16,7 А; I1 = 10 А; I2 = 6,7 А; I3 = 5 А; I4 = 11,7 А; U = 55,07 В;
U2 = 20 В; U3 = U4 = 35,07 В.
Предыдущий урок
Расчёт сопротивления проводника. Удельное сопротивление вещества
Постоянный электрический ток
Следующий урок
Источники тока
Постоянный электрический ток
Все разнообразие схем построено на двух типах соединения — параллельном и последовательном. Для разных соединений действуют разные законы, что и дает возможность создания устройств с различными характеристиками. Рассмотрим последовательное и параллельное соединение резисторов.
Содержание статьи
- 1 Что такое резистор и для чего он нужен
- 2 Последовательное соединение сопротивлений
- 2.1 Теоретическая часть
- 2.2 Примеры расчета
- 3 Параллельное соединение резисторов
- 3.1 Теория и законы параллельного соединения
- 3.2 Примеры расчета параллельного соединения сопротивлений
- 4 Смешанное соединение
- 5 Практическое применение параллельного и последовательного соединения резисторов
Что такое резистор и для чего он нужен
Резистор — это радиоэлемент, который увеличивает сопротивление цепи. Ставят его обычно для того, чтобы понизить/ограничить напряжение или ток. Есть сопротивления постоянные и переменные.
Например, светодиоды требуют небольшого тока, иначе перегревается и быстро выходит из строя. Чтобы ограничить ток, перед светодиодом поставьте сопротивление. Ток в цепи станет меньше.
Для чего нужны резисторы: для подстройки параметров питания
Постоянные сопротивления — это те, которые не меняют своего номинала в процессе работы. Если это и происходит, то считается выходом из строя.
Так выглядят переменные и постоянные резисторы
Переменные резисторы, наоборот, отличаются тем, что их сопротивление можно изменять. Они имеют бегунок или поворотную ручку, при помощи которых и изменяется номинал. На основе таких устройств делают регуляторы. Например, регулятор громкости, накала греющего элемента и т.д.
Последовательное соединение сопротивлений
Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.
Лампы накаливания соединенные последовательно, можно рассматривать как сопротивления
Теоретическая часть
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2).
Последовательно соединенные сопротивления. I1 — ток протекающий через резистор R1, I2 — ток протекающий через резистор R2
Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают.
R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых.
Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.
Примеры расчета
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:
- U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
- U2 = R2 * I = 800 Ом * 2А = 1600 В.
Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В.
Так понятнее, что такое последовательное соединение
Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом. Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.
А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В.
Параллельное соединение резисторов
Параллельное соединение — это когда входы нескольких деталей соединяются в одной точке. Точно так же — в одну точку — соединяют их выходы.
Так выглядит параллельное соединение на схеме и в реальности
Теория и законы параллельного соединения
Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение. То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение.
U = U1 = U2 = U3.
Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.
Так выглядит параллельное соединение резисторов на схеме
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле:
1/R = 1/R1 + 1/R + 1/R3+…
Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.
Формулы расчета сопротивления при параллельном подключении двух и трех резисторов
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала.
Примеры расчета параллельного соединения сопротивлений
Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
- Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом.
- Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.
Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
Как высчитывать сопротивление составных резисторов
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом.
Еще один пример с лампочками
При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее. Но картина не отличается:
- Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом.
- Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом.
Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Смешанное соединение
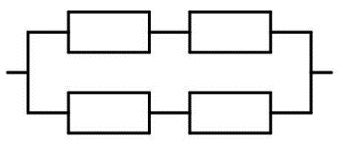
Как быть, если в схеме есть и параллельное, и последовательное соединение резисторов? В таком случае считают общее сопротивление по участкам. Можно при этом перерисовывать схему, заменяя составные сопротивления на один «прямоугольник», но проставляя над ним высчитанный результат.
Пример расчета сопротивления при смешанном соединении резисторов. Рассматриваем исходную схему как совокупность параллельных и последовательных соединений
Шаг 1. Нашли общее сопротивление последовательно соединенных резисторов R3 и R4:
R3-4 = 3 кОм + 3 кОм = 6 кОм;
Шаг 2. Рассчитали сопротивление параллельно соединенных резисторов R2 и R3-4:
R2-4 = 3 кОм * 6 кОм / (3 кОм + 6 кОм) = 18 кОм/9 кОм = 2 кОм;
Шаг 3. Рассчитали общее сопротивление последовательно соединенных резисторов R1 и R2-4:
R1-4 = R1 + R2-4 = 1 кОм + 2 кОм = 3 кОм.
Практическое применение параллельного и последовательного соединения резисторов
Для чего практически можно использовать параллельное и последовательное соединение резисторов? Случается, что при ремонте электронной аппаратуры, не всегда в наличии сопротивление нужного номинала. Ехать в магазин за одним копеечным элементом — накладно. Вот тут и могут пригодиться составные резисторы. Просто надо последовательно или параллельно соединить их, подобрав требуемый номинал.
Последовательное и параллельное соединение резисторов применяют для подбора требуемого номинала. Контролировать точное значение получившегося сопротивления можно при помощи цифрового мультиметра
При соединении резисторов, их ножки первоначально скручивают. Какой стороной разворачивать сопротивление — неважно (в отличие от диодов, резисторы одинаково пропускают ток в обоих направлениях). На концах скрутку слегка обжимают плоскогубцами, затем пропаивают. Следите за тем, чтобы корпуса были друг от друга подальше — так они будут лучше охлаждаться при работе.
Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике. Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов. Соединение резисторов может производиться последовательно, параллельно и смешанно (то есть и последовательно и параллельно), что показано на рисунке 1.
Рисунок 1. Соединение резисторов.
Смешанное соединение резисторов. Расчет смешанного соединения
Здравствуйте, уважаемые читатели сайта sesaga.ru. Смешанное соединение резисторов представляет собой сложную электрическую цепь, в которой часть резисторов соединена последовательно, а часть параллельно.
В радиолюбительской практике такое включение резисторов встретить трудно, так как нет смысла подбирать сопротивление таким сложным способом. Достаточно соединить два, ну максимум три резистора последовательно или параллельно, чтобы подобрать нужный номинал.
Смешанное соединение
встречается в основном в учебниках физики или электротехники в виде задач. Мне вспоминается такая задачка из школьной программы, но тогда она мне показалась сложной и правильно решить ее не получилось.
И вот, исходя из полученного опыта, хочу рассказать Вам, как вычислить общее сопротивление смешанного соединения резисторов. Вдруг кому-нибудь в жизни да и пригодится.
топологические понятия, элементы, схема замещения
2.Законы Ома и Кирхгофа для цепей постоянного тока
3.Последовательное, параллельное и смешанное соединение потребителей
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I. Напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3,
Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
4.Расчёт цепи постоянного тока методами контурных токов и узловых потенциалов
Метод контурных токов. В основе лежит 2-й закон Кирхгофа. Суть метода в ведении фиктивных контурных токов и их расчёт.
1.Определение числа уравнений: у=в-ви.т-(n-1).
В-число ветвей, ви.т-с источником тока,n-число узлов.
2.Составляем уравнения для неизвестных контурных токов в общем виде.
3.Определяем неизвестные коэффициенты левой и правой части (Е и R).
4.Подставив коэффициенты, решаем уравнения, находим токи контуров.
5.Определяем через контурные токи токи в ветвях.
Метод узловых потенциалов. В основе лежит 1-й закон Кирхгофа. Определяем потенциалы узлов цепи с последующим определением токов в ветвях, используя закон Ома для участков цепи.
1.Подготовка схемы. Обозначим узлы. Потенциал одного из них принимаем за 0.
2.Составляем уравнения потенциалов в общем виде:
Фи1*g11 + фи2*g12 = I11 – для первого узла
Фи1g21 + фи*g22 = I22 – для второго узла
3.Определяем неизвестные проводимости gmn –сумма проводимостей ветвей, подходящих к узлу n.
4.Подставив, решаем уравнения, находим фи1 и фи2.
5.Произвольно выбираем направления токов и, используя закон Ома для участка цепи определяем эти токи: In = (фиX-фиY+En)/Rn.
Расчет смешанного соединения резисторов.
Расчет начинают от дальнего участка цепи по отношению к источнику питания. Определяют участок с параллельным или последовательным соединением двух резисторов и высчитывают их общее сопротивление Rобщ
. Затем полученное сопротивление складывают с рядом стоящим резистором и т.д.
Суть данного метода заключается в уменьшении
количества элементов в цепи с целью
упрощения схемы
и, соответственно, упрощению расчета общего сопротивления.
Разберем схему смешанного соединения из семи резисторов
:
Самым дальним участком схемы оказались резисторы R6
и
R7
, соединенные
параллельно
:
Вычисляем их общее сопротивление используя формулу параллельного
соединения:
Теперь если сравнить первоначальную схему с получившейся, то здесь мы видим, что она уменьшилась на один элемент и вместо двух резисторов R6 и R7 остался один R6
с суммарным сопротивлением равным
30, 709 кОм
.
Продолжим расчет и следующим дальним участком схемы оказались резисторы R5
и
R6
, соединенные
последовательно
:
Вычисляем их общее сопротивление используя формулу последовательного
соединения. Сопротивление резистора R5 составляет 27 Ом, а R6 = 30,709 кОм, поэтому для удобства расчета килоомы переводим в Омы (1 кОм = 1000 Ом):
Схема уменьшилась еще на один элемент и приняла вид:
Теперь дальним участком оказались резисторы R4
и
R5
соединенные
параллельно
:
Вычисляем их общее сопротивление:
Первоначальная схема опять изменилась и теперь состоит всего из четырех резисторов соединенных последовательно
. Таким образом мы максимально упростили схему и привели ее к удобному расчету.
Теперь все просто. Складываем сопротивления оставшихся четырех резисторов, используя формулу последовательного
соединения, и получаем общее сопротивление всей цепи:
Вот в принципе и все, что хотел сказать о смешанном соединении резисторов и расчете смешанного соединения. Удачи!
Виды соединений потребителей.
Различают последовательное, параллельное и смешанное соединение потребителей.
Припоследовательном соединении потребителей конец первого потребителя присоединяется к началу второго, конец второго – к началу третьего и т.д.
Рисунок 9 – Схема последовательного соединения потребителей
1) Сила тока на всех потребителях одинаковая
2)
Общее сопротивление равно сумме сопротивлений отдельных потребителей
3) Напряжение на зажимах цепи равно сумме падений напряжений на отдельных её участках .
При необходимости уменьшить U и I приемника последовательно ему подключают резистор.
Вывод: при выходе из работы одного элемента вся цепь обесточивается, и при изменении сопротивления одного из них меняется ток во всей цепи и напряжение на каждом элементе.
При параллельном соединении элементов цепи все начала собираются в одну точку, а концы в другую точку и включаются в электрическую цепь, образуя параллельные ветви.
Рисунок 10 – Схема параллельного соединения потребителей
1) Общий ток равен сумме токов параллельных ветвей
2) Напряжение на всех потребителях включенных параллельно одинаковое
3) Общее сопротивление будет меньше наименьшего из включенных параллельно
Из закона Ома для участка цепи
—
для двух потребителей
Если сопротивление потребителей равны, то
Вывод:
При выходе из строя одного потребителя остальные остаются включенные в цепь.
Все приемники находятся под одним напряжением независимо от их мощности (сопротивления).
Смешанным называется такое соединение потребителей, когда в цепи имеются одновременно и параллельное и последовательное их соединение.
Цепь постепенно упрощают, заменяя эквивалентным (равноценным) сопротивлением, используя формулы для последовательного и параллельного соединения потребителей.
Дата добавления: 2017-11-21; ;
Похожие статьи:
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Общее сопротивление Rобщ
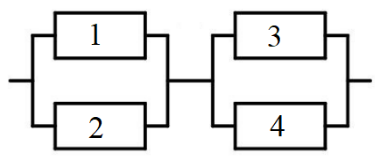
Для того чтобы посчитать общее сопротивление смешанного соединения:
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.
- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
После подстановки формулы параллельного соединения вместо «||»:
Резистор представляет собой устройство, обладающее устойчивым, стабильным значением сопротивления. Это позволяет выполнять регулировку параметров на любых участках электрической цепи. Существуют различные виды соединений, в том числе и смешанное соединение резисторов. От использования того или иного способа в конкретной схеме, напрямую зависит падение напряжений и распределение токов в цепи. Вариант смешанного соединения состоит из последовательного и параллельного подключения активных сопротивлений. Поэтому в первую очередь нужно рассматривать эти два вида соединений, чтобы понять, как работают другие схемы.
Смешанное соединение резисторов. Расчет смешанного соединения
Здравствуйте, уважаемые читатели сайта sesaga.ru. Смешанное соединение резисторов представляет собой сложную электрическую цепь, в которой часть резисторов соединена последовательно, а часть параллельно.
В радиолюбительской практике такое включение резисторов встретить трудно, так как нет смысла подбирать сопротивление таким сложным способом. Достаточно соединить два, ну максимум три резистора последовательно или параллельно, чтобы подобрать нужный номинал.
Смешанное соединение
встречается в основном в учебниках физики или электротехники в виде задач. Мне вспоминается такая задачка из школьной программы, но тогда она мне показалась сложной и правильно решить ее не получилось.
И вот, исходя из полученного опыта, хочу рассказать Вам, как вычислить общее сопротивление смешанного соединения резисторов. Вдруг кому-нибудь в жизни да и пригодится.
Смешанное соединение приемников энергии
Наиболее широко распространено смешанное соединение приемников электрической энергии. Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии
В качестве примера рассчитаем токи и напряжения на всех участках цепи. Для начала определим эквивалентное сопротивление цепи. Выделим два участка с параллельным соединением приемников энергии. Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид
В результате получили цепь из двух последовательных приемников энергии R12R345 эквивалентное сопротивление и ток, протекающий через них, составит
Тогда падение напряжения по участкам составит
Тогда токи, протекающие через каждый приемник энергии, составят
Расчет смешанного соединения резисторов.
Расчет начинают от дальнего участка цепи по отношению к источнику питания. Определяют участок с параллельным или последовательным соединением двух резисторов и высчитывают их общее сопротивление Rобщ
. Затем полученное сопротивление складывают с рядом стоящим резистором и т.д.
Суть данного метода заключается в уменьшении
количества элементов в цепи с целью
упрощения схемы
и, соответственно, упрощению расчета общего сопротивления.
Разберем схему смешанного соединения из семи резисторов
:
Самым дальним участком схемы оказались резисторы R6
и
R7
, соединенные
параллельно
:
Вычисляем их общее сопротивление используя формулу параллельного
соединения:
Теперь если сравнить первоначальную схему с получившейся, то здесь мы видим, что она уменьшилась на один элемент и вместо двух резисторов R6 и R7 остался один R6
с суммарным сопротивлением равным
30, 709 кОм
.
Продолжим расчет и следующим дальним участком схемы оказались резисторы R5
и
R6
, соединенные
последовательно
:
Вычисляем их общее сопротивление используя формулу последовательного
соединения. Сопротивление резистора R5 составляет 27 Ом, а R6 = 30,709 кОм, поэтому для удобства расчета килоомы переводим в Омы (1 кОм = 1000 Ом):
Схема уменьшилась еще на один элемент и приняла вид:
Теперь дальним участком оказались резисторы R4
и
R5
соединенные
параллельно
:
Вычисляем их общее сопротивление:
Первоначальная схема опять изменилась и теперь состоит всего из четырех резисторов соединенных последовательно
. Таким образом мы максимально упростили схему и привели ее к удобному расчету.
Теперь все просто. Складываем сопротивления оставшихся четырех резисторов, используя формулу последовательного
соединения, и получаем общее сопротивление всей цепи:
Вот в принципе и все, что хотел сказать о смешанном соединении резисторов и расчете смешанного соединения. Удачи!
Последовательное соединение
При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.
Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.
Рис. 4. Последовательное соединение
Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.
1. При последовательном соединении проводников сила тока в них одинакова. В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике.
Действительно, напряжение на участке — это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке — это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:
Можно и более формально, без всяких словесных объяснений:
3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.
Пусть — сопротивление участка . По закону Ома имеем:
что и требовалось.
Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .
Сопротивления проводников равны:
Эти два проводника образуют единый проводник длиной и сопротивлением
Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения. Доказательство этого даётся с помощью закона Ома, как показано выше. Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Параметры цепи при параллельном соединении
Параллельное соединение представляет собой включение начальных выходов двух и более резисторов в единой точке, и концов этих же элементов в другой общей точке. Таким образом, фактически происходит соединение каждого резистора непосредственно с источником электроэнергии.
В результате, напряжение каждого резистора будет одинаковым с общим напряжением цепи: Uобщ = U1 = U2. В свою очередь, значение токов будет разным на каждом резисторе, их распределение становится прямо пропорциональным сопротивлению этих резисторов. То есть, при увеличении сопротивления, сила тока уменьшается, а общий ток становится равен сумме токов, проходящих через каждый элемент. Формула для данного положения выглядит следующим образом: Iобщ= I1 + I2.
Для расчетов общего сопротивления используется формула:
. Она используется при наличии в цепи только двух сопротивлений. В тех случаях, когда сопротивлений в цепи подключено три и более, применяется другая формула:
Таким образом, значение общего сопротивления электрической цепи будет меньше, чем самое минимальное сопротивление одного из резисторов, подключенных параллельно в эту цепь. На каждый элемент поступает напряжение, одинаковое с напряжением источника электроэнергии. Распределение тока будет прямо пропорциональным сопротивлению резисторов. Значение общего сопротивления резисторов, соединенных параллельно, не должно превышать минимального сопротивления какого-либо элемента.
Общее сопротивление Rобщ
Для того чтобы посчитать общее сопротивление смешанного соединения:
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.
- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
После подстановки формулы параллельного соединения вместо «||»:
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный амперметр. Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 – силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.