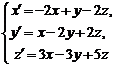Как найти общее решение дифференциального уравнения онлайн - Исправление недочетов и поиск решений вместе с Examum.ru

Дифференциальным уравнением
называется уравнение которое связывает неизвестную функцию и её производные различных порядков:

F(x, y‘, y», … , y⁽ⁿ⁾)=0

Порядком дифференциального уравнения называется порядок его старшей производной. Решить дифференциальное уравнение, значит найти неизвестную функцию
,
которая обращает это уравнение в верное тождество. Этого можно достичь, изучив теоретический материал по дифференциальным уравнениям, или воспользовавшись нашим онлайн калькулятором.

Наш калькулятор может находить как общее решение дифференциального уравнения, так и частное. Для поиска частного решения, необходимо ввести начальные условия в калькулятор. Для поиска общего решения, поле ввода начальных условий необходимо оставить пустым.

Источник

Дифференциальные уравнения по-шагам

Примеры дифференциальных уравнений

Простейшие дифференциальные уравнения 1-порядка
```
y' + y = 0
```
```
y' - 5*y = 0
```
```
x*y' - 3 = 0
```
Дифференциальные уравнения с разделяющимися переменными
```
(x-1)*y' + 2*x*y = 0
```
```
tan(y)*y' = sin(x)
```
Линейные неоднородные дифференциальные уравнения 1-го порядка
```
y' + 7*y = sin(x)
```
Линейные однородные дифференциальные уравнения 2-го порядка
```
3*y'' - 2*y' + 11y = 0
```
Уравнения в полных дифференциалах
```
dx*(x^2 - y^2) - 2*dy*x*y = 0
```
Решение дифференциального уравнения заменой
```
x^2*y' - y^2 = x^2
```
Смена y(x) на x в уравнении
```
x^2*y' - y^2 = x^2
```
Линейные дифференциальные уравнения 3-го порядка
```
y''' + 3*y'' + y' + 3y = 0
```
```
y''' + 2*y'' + y' = exp(-x)
```
```
y''' + 3*y'' + y' + 3y = sin(x) + 2
```
Другие

-6*y - 5*y'' + y' + y''' + y'''' = x*cos(x) + sin(x)

Что умеет калькулятор дифференциальных уравнений?

Детальное решение для:
- Обыкновенное дифференциальное уравнение
- Разделяемые переменные
- Уравнение Бернулли
- Уравнение в полных дифференциалах
- Дифференциальное уравнение первого порядка
- Дифференциальное уравнение второго порядка
- Дифференциальное уравнение третьего порядка
- Однородное дифференциальное уравнение
- Неоднородное дифференциальное уравнение
- Дифференциальные уравнения с заменой
- Система обыкновенных дифференциальных уравнений
Строит графики множества решений
Решает задачу Коши
Классификация дифференциальных уравнений
Примеры численных решений

Подробнее про Дифференциальные уравнения.

Указанные выше примеры содержат также:

модуль или абсолютное значение: absolute(x) или |x|
квадратные корни sqrt(x),
кубические корни cbrt(x)
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
показательные функции и экспоненты exp(x)
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x)
натуральные логарифмы ln(x),
десятичные логарифмы log(x)
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x)
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x)
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x)
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x)
знак числа:
sign(x)
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x)
Факториал от x:
x! или factorial(x)
Гамма-функция gamma(x)
Функция Ламберта LambertW(x)
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)

Правила ввода

Можно делать следующие операции

2*x: — умножение
3/x: — деление
x^2: — возведение в квадрат
x^3: — возведение в куб
x^5: — возведение в степень
x + 7: — сложение
x — 6: — вычитание
Действительные числа: вводить в виде 7.5, не 7,5

Постоянные

pi: — число Пи
e: — основание натурального логарифма
i: — комплексное число
oo: — символ бесконечности

Источник

Решение дифференциальных уравнений

Уравнение, связывающее независимую переменную, искомую функцию и некоторое количество ее производных, т.е. уравнение вида

F(x,y,y') = 0

называется обыкновенным дифференциальным уравнением n-го порядка.

Решение онлайн
Видеоинструкция
Оформление Word

Например, решить дифференциальное уравнение онлайн: y''-2y+1=sinx. Записываем как y''-2*y+1=sin(x). Для отображение хода решения нажмите Show steps или Step-by-step.

Если определить тип дифференциального уравнения, то решение будет доступно в MS Word:

не знаю

Линейное уравнение первого порядка типа y'+2*y=4*x, x*y’-y=3*x^2-3, , , либо задача Коши.

Уравнение в полных дифференциалах типа 2xydx+x²dy=0, 2xydx=(x²-y²)dy или с разделяющимися переменными.

Уравнение Бернулли типа y'+2xy=2xy³, 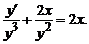, xy’+2y+x⁵y³e^x=0

Уравнение с постоянными коэффициентами типа y''+2*y-8=x, 2*y''-3*y-8=x*cos(x).

Уравнения, допускающие понижение порядка: x³y''+x²y'=1, (y')²+2yy''=0.

Находить частное решение при y() = .

Способы решений дифференциальных уравнений

Уравнения с разделяющимися переменными: y'=e^x+y, xydx+(x+1)dy=0
Однородные уравнения: (y²-2xy)dx+x²dy=0
Постановка задачи о выделении решений.
Калькулятор Линейные уравнения первого порядка: y'+2y=4x
Уравнения Бернулли: y'+2xy=2xy³,
Уравнения в полных дифференциалах: 2xydx+x²dy=0, 2xydx=(x²-y²)dy=0.
Приближенные методы решения дифференциальных уравнений
Уравнения высших порядков
- Уравнения, допускающие понижение порядка: yy'''=y'y'', (y')²+2yy''=0
- Линейные дифференциальные уравнения высших порядков
- Линейные дифференциальные уравнения с постоянными коэффициентами: y''-3y'+2y=0, y''-2y'+5y =e^x
- Метод вариации произвольной постоянной решения линейных неоднородных уравнений
- Уравнения с правой частью специального вида
Системы дифференциальных уравнений:

Однородные системы линейных дифференциальных уравнений с постоянными коэффициентами:

Метод вариации произвольной постоянной

Пример. Найти частное решение дифференциального уравнения y'+xy=x, удовлетворяющего начальному условию y(0)=2.

Решение.

Данное дифференциальное уравнение – уравнение 1-го порядка, линейное относительно неизвестной функции y.

Применяя метод Бернулли для решения этого уравнения, сделаем замену y(x) = u(x)·v(x), где u(x) и v(x) – неизвестные функции, которые мы будем искать поочередно.

Согласно правилу дифференцирования произведения, имеем:

y′ = u′·v+u·v′.

Подставляя выражения для y и y’ в исходное уравнение, получим:

u′·v+u·v′ + x·u·v = x (*)

Отсюда

u′·v + (u·v′ + x·u·v) = x;

u′·v + u(v′ + x·v) = x;

Выражение в скобках зависит только от v(x). Будем искать v(x), исходя из условия:

v′ + x·v = 0.

Рассматривая это равенство как дифференциальное уравнение, найдём частное решение для v(x) методом разделения переменных:

; ;

Переходим к интегралу:

; ; .

Подставим найденную функцию v(x) в уравнение (*):

; .

Найдём теперь общее решение для неизвестной функции u(x):

.

Окончательно, имеем общее решение исходного дифференциального уравнения:

.

Теперь, используем данное начальное условие и найдём частное решение уравнения:

y(0) = c·e⁰+1 = c+1 = 2

Отсюда c=1,

Ответ: частное решение дифференциального уравнения имеет вид: .

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

2y’-y=4sin(3t)
ty’+2y=t^2-t+1
y’=e^{-y}(2x-4)
frac{dr}{dtheta}=frac{r^2}{theta}
y’+frac{4}{x}y=x^3y^2
y’+frac{4}{x}y=x^3y^2, y(2)=-1
Лаплас:y^{prime}+2y=12sin(2t),y(0)=5
Бернулли:frac{dr}{dθ}=frac{r^2}{θ}
Показать больше

Описание

Поэтапное решение обыкновенных дифференциальных уравнений (ОДУ)

ordinary-differential-equation-calculator

Блог-сообщения, имеющие отношение к Symbolab

Advanced Math Solutions – Ordinary Differential Equations Calculator

<div class=»p1″> Differential equations contain derivatives, solving the equation involves integration (to get…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Решение дифференциальных уравнений

Данный онлайн калькулятор позволяет вычислять дифференциальные уравнения практически любого типа и порядка: линейные дифференциальные уравнения, с разделяемыми или неразделяемыми переменными, уравнения Бернулли и т.д. При этом у вас есть возможность решать уравнения в общем виде или получить частное решение соответствующее введенным вами начальным (граничным) условиям.

По умолчанию в уравнении функция y является функцией от переменной x. Однако вы можете задать своё обозначение переменной, если напишете, например, y(t) в уравнении, то калькулятор автоматически распознает, что y есть функция от переменной t. С помощью калькулятора вы сможете решать дифференциальные уравнения любой сложности и вида: однородные и неоднородные, линейные или нелинейные, первого порядка или второго и более высоких порядков, уравнения с разделяющимися или не разделяющимися переменными и т.д. Решение диф. уравнения даётся в аналитическом виде, имеет подробное описание. Дифференциальные уравнения очень часто встречаются в физике и математике. Без их вычисления невозможно решать многие задачи (особенно в математической физике).

Одним из этапов решения дифференциальных уравнений является интегрирование функций. Есть стандартные методы решений дифференциальных уравнений. Необходимо привести уравнения к виду с разделяющимися переменными y и x и отдельно проинтегрировать разделенные функции. Чтобы это сделать иногда следует провести определенную замену.

Синтаксис
основных функций:
x^a: x^a
|x|: abs(x)
√x: Sqrt[x]
ⁿ√x: x^(1/n)
a^x: a^x
log^ax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]

sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]

arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]

areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция «И» ∧: &&
дизъюнкция «ИЛИ» ∨: ||
отрицание «НЕ» ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Источник