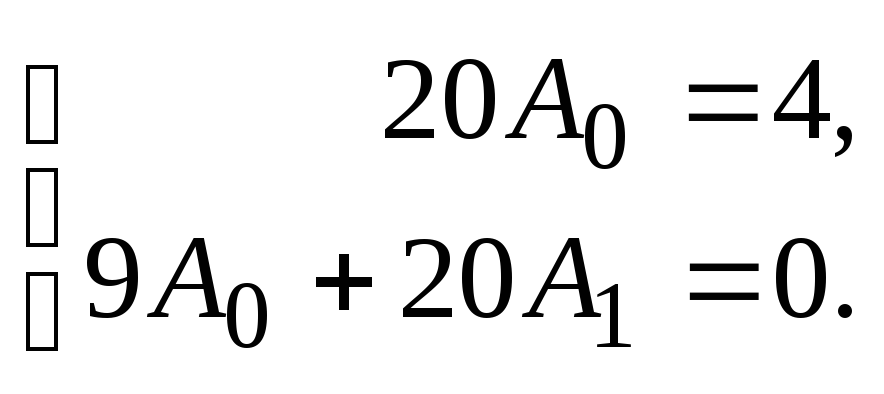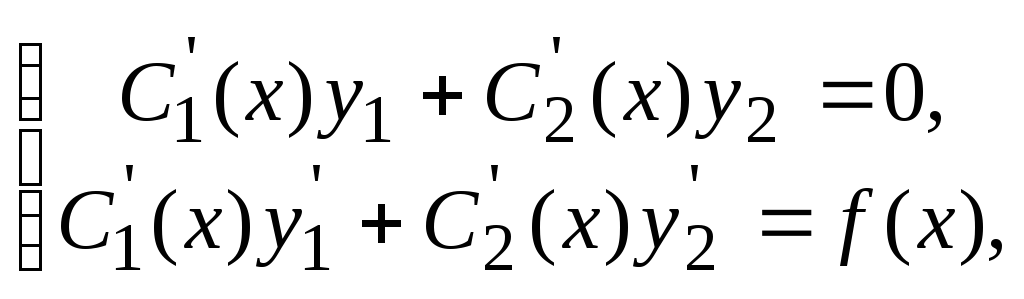(схема 47)
Линейным называется дифференциальное уравнение n-го порядка,
если оно 1-ой степени относительно искомой функции y(x) и ее производных 
, то есть имеет вид:
. (8.42)
Если коэффициент P0(x) ≠ 1, то на
него можно поделить и после соответствующих переобозначений получить:
. (8.43)
Уравнение (8.43) называется уравнением с переменными
коэффициентами. Предположим, что в нем функции 
, непрерывны на интервале 
. Тогда для уравнения (8.43) на данном интервале имеет место задача Коши, сформулированная нами
ранее.
Примечание. Частным случаем (8.43) является линейное
дифференциальное уравнение 2-го порядка с переменными коэффициентами:
(8.44)
Если
в уравнении (8.43) f(x)≡0, то оно
называется однородным, если f(x) ≠ 0, то неоднородным.
Теорема 8.3 (о
структуре общего решения линейного неоднородного ДУ). Общее решение
линейного неоднородного дифференциального уравнения представляет собой сумму
общего решения соответствующего однородного и некоторого частного решения
неоднородного уравнения 
. Запишем коротко:
Однородное дифференциальное уравнение,
соответствующее неоднородному уравнению (8.43), имеет вид:
. (8.45)
Пусть в уравнении (8.45) функции
. Тогда оно принимает вид:
(8.46)
и
называется линейным однородным дифференциальным
уравнением n-го порядка с постоянными коэффициентами, где 
–
функции, n раз дифференцируемые.
Рассмотрим решения уравнений (8.45) и (8.46).
Обозначим полную совокупность их линейно независимых решений через . Тогда, по свойству
решений однородного уравнения, их линейная комбинация также является решением
уравнения (8.45) и (8.46), то есть общее
решение может быть записано в виде:
, (8.47)
где
ci– константы интегрирования.
Перейдем к конструированию функций . Какого они вида? Так как эти функции в уравнениях (8.45) и
(8.46) n раз дифференцируемы, то их конструкция при дифференцировании не
меняется. Это возможно в случае экспоненциального вида функций, то есть при
, (8.48)
где 
, . Отсюда, линейная комбинация функций (8.48):
(8.49)
– также
решение уравнений (8.45) и (8.46).
Рассмотрим одну из функций (8.48) – функцию y=eλx как решение для уравнения (8.46) с постоянными
коэффициентами. Продифференцируем ее n раз:
.
По определению решения
дифференциального уравнения при подстановке y=eλx
и ее производных в (8.46) имеем тождество: 
. После вынесения общего множителя eλx получаем:
.
Так как eλx ≠ 0, то 
(8.50)
–алгебраическое
уравнение n-ой степени относительно λ, называемое характеристическим уравнением для
уравнения (8.46). Известно, что уравнение n-ой степени имеет равно n корней как действительных, так и комплексных, с
учетом их кратности. Значит, характеристическое уравнение (8.50) дает нам n значений
числа λ, ранее обозначенных нами
через 
, которые при подстановке в (8.49) приводит нас к
окончательному виду общего решения линейного однородного дифференциального
уравнения (8.46) с постоянными коэффициентами.
Рассмотрим наиболее распространенный частный случай
уравнения (8.46) – его аналог 2-го порядка:
. (8.51)
Для данного уравнения характеристическое уравнение (8.50)
принимает вид:
. (8.52)
Уравнение (8.52) является квадратным относительно λ. В зависимости от дискриминанта D характеристического
уравнения рассматривают три случая, приведенных в таблице 8.1.
Таблица 8.1
Пример 8.17. Найти общее решение уравнений:
Решение.
а) Составляем характеристическое уравнение λ2+2λ–15 = 0. Корнями этого уравнения
будут λ1= –5 и λ2= 3. Тогда, применяя (8.53), получаем общее решение: y=C1e
–5x+C2e3x.
б) Составляем характеристическое уравнение λ2–16λ+64 = 0.
Решая это уравнение,
получим λ1= λ2= 8. Так как корни равные, то, применяя (8.54), будем иметь:
.
в) Характеристическое уравнение λ2–4λ+13 = 0 имеет комплексные корни λ1= 2+3i и λ2= 2–3i. Положив в (8.55) α=2
и β=3, получим общее
решение: 
.
г) Характеристическое уравнение λ2+9 = 0 имеет корни λ1;2= ±3i. Полагая в (8.55) α=0 и
β=3,
получим общее решение 
Рассмотрим теперь линейное неоднородное дифференциальное
уравнение 2-го порядка с постоянными коэффициентами:
, (8.56)
являющееся частным случаем уравнения (8.44). Функция f(x) может представлять собой функцию специального вида.
Тогда общее решение уравнения находится с помощью следующей теоремы.
Теорема 8.4.
Пусть
задано линейное дифференциальное неоднородное уравнение второго порядка с
постоянными коэффициентами и правой частью специального вида
. (8.57)
1. Если 
не является корнем
характеристического уравнения соответствующего однородного уравнения, то частное
решение уравнения (8.57) имеет вид:
, (8.58)
где 
– многочлены общего
вида (с неопределенными коэффициентами).
2. Если 
– корень
характеристического уравнения кратности s, то частное решение уравнения (8.57) имеет вид:
, (8.59)
– многочлены общего
вида 
Рассмотрим в
таблице 8.2 некоторые случаи составления частного решения линейного
неоднородного дифференциального уравнения (8.57) по специальному виду его правой
части.
Таблица 8.2
Пример 8.18. Найти общее решение уравнения 
.
Решение. Найдем общее решение соответствующего однородного ДУ: 
. Характеристическое
уравнение λ2+2λ+1 = 0 имеет корень λ1= 1 кратности 2 (смотри таблицу 8.1). Значит, yo.o. = c1∙ex+c2∙x∙ex.
Находим частное решение исходного уравнения. В нем правая часть x–4=(x–4)∙e0∙x есть
формула вида P1(x)∙e0∙x,
причем α=0 не является
корнем характеристического уравнения: α ≠ λ. Поэтому согласно формуле (8.58), частное решение yч.н.
ищем в виде yч.н. = Q1(x)∙e0∙x, т.е.
yч.н. = Ax+B, где A и B –
неопределенные коэффициенты. Тогда
. Подставив 
в исходное уравнение,
получим –2A+Ax+B = x–4
или Ax+(–2A+B) = x–4. Приравнивая коэффициенты при
одинаковых степенях x, получим систему уравнений:
. Отсюда A=1, B= –2. Поэтому частное решение данного уравнения имеет вид
yч.н. = x–2. Следовательно, искомое общее решение уравнения 
Пример 8.19. Решить уравнение 
.
Решение. Находим общее решение
yo.o.
соответствующего однородного
уравнения 
. Характеристическое уравнение λ2–4λ+13 = 0 имеет корни λ1= 2+3i, λ2= 2–3i (смотри таблицу 8.1). Следовательно,
.
Находим частное решение yч.н.. Правая часть неоднородного уравнения в нашем случае
имеет вид
. Так как 
не совпадают с корнями характеристического уравнения, то согласно формуле
(8.58), частное решение ищем в виде 
. Дифференцируем частное решение, получаем:
. Подставляя yч.н. и его производные в исходное уравнение, получаем:
Отсюда, сравнивая коэффициенты при косинусе и синусе,
имеем 
. Следовательно, A=1, B= –3. Поэтому 
. И наконец, с учетом теоремы 8.3 получаем общее решение
заданного линейного неоднородного ДУ в виде:
Пример 8.20.
Найти
частное решение уравнения 
, удовлетворяющее
начальным условиям 
.
Решение. Находим общее решение
однородного уравнения
. Характеристическое уравнение λ2 – λ – 2 = 0 имеет два корня λ1= –1 и λ2= 2 (смотри таблицу 8.1); тогда yo.o. = C1∙e–x+C2∙e2x – общее решение
соответствующего однородного ДУ.
В правой части заданного уравнения имеется
показательная функция. Так как в данном случае α=2 совпадает с одним из
корней характеристического уравнения, то частное решение следует искать в виде функции Axe2x. Таким образом, yч.н.= Axe2x. Дифференцируя дважды это равенство, получим: 
. Подставим yч.н. и ее производные в левую часть заданного уравнения
и найдем коэффициент A:
. Следовательно, частное решение yч.н.= 3xe2x, общее решение
. (8.60)
Используя начальные условия, определим значения
произвольных постоянных C1 и C2. Дифференцируя общее
решение (8.60), получим:
.
Подставим в общее решение (8.60) значения x=0
и y=2,
будем иметь 2 = C1+C2. Подставим в выражение для 
значения x=0 и 
, будем иметь: 13 = –C1+2C2+3; 10 = –C1+C2. Из этих уравнений составим
систему
, из которой находим: C1= –2 и C2=4. Таким образом,
есть то частное
решение, которое удовлетворяет заданным начальным условиям
Теорема 8.5
(о наложении решений). Если правая часть
уравнения (8.56) представляет собой сумму двух функций: 
, а y1 ч.н. и y2 ч.н. – частные решения уравнений 
и 
соответственно, то
функция
(8.61)
является частным решением
данного уравнения
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Определение
Уравнение
(*)
где
и
– непрерывные
функция в интервале
называется
неоднородным линейным дифференциальным уравнение второго порядка, функции
и
– его
коэффицинентами. Если
в
этом интервале, то уравнение принимает вид:
(**)
и называется однородным
линейным дифференциальным уравнением второго порядка. Если уравнение (**) имеет
те же коэффициенты
и
, как уравнение (*), то оно называется
однородным уравнением, соответствующим неоднородному уравнению (*).
Однородные дифференциальные линейные уравнения второго порядка
Пусть в линейном уравнении
и
— постоянные
действительные числа.
Частное решение уравнения
будем искать в виде функции
, где
– действительное
или комплексное число, подлежащее определению. Дифференцируя по
, получаем:
Подставляя в исходное дифуравнение, получаем:
Отсюда, учитывая, что
, имеем:
Это уравнение называется
характеристическим уравнением однородного линейного дифуравнения. Характеристическое уравнение и дает
возможность найти
. Это уравнение второй степени, поэтому
имеет два корня. Обозначим их через
и
. Возможны три случая:
Корни действительные и разные
В этом случае общее решение уравнения:
Пример 1
Решение
Характеристическое уравнение имеет вид:
Решение характеристического уравнения:
Общее решение исходного дифуравнения:
Корни действительные и равные
В этом случае общее решение уравнения:
Пример 2
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Характеристическое уравнение имеет вид:
Решение характеристического уравнения:
Общее решение исходного дифуравнения:
Корни комплексные
В этом случае общее решение уравнения:
Пример 3
Решение
Характеристическое уравнение имеет вид:
Решение характеристического уравнения:
Общее решение исходного дифуравнения:
Неоднородные дифференциальные линейные уравнения второго порядка
Рассмотрим теперь решение некоторых
типов линейного неоднородного уравнения второго порядка с постоянными
коэффициентами
где
и
– постоянные
действительные числа,
– известная непрерывная
функция в интервале
. Для нахождения общего решения такого
дифференциального уравнения необходимо знать общее решение соответствующего
однородного дифференциального уравнения
и частное
решение
. Рассмотрим
некоторые случаи:
Правая часть дифференциального уравнения имеет вид:
Частное решение дифференциального
уравнения ищем также в форме квадратного трехчлена:
Подставляя
и
в исходное
дифференциальное уравнение, получим тождество, откуда находим коэффициенты.
Если нуль – однократный корень
характеристического уравнения, то
Если нуль – двухкратный корень
характеристического уравнения, то
Аналогично обстоит дело, если
– многочлен
произвольной степени
Пример 4
Решение
Решим соответствующее однородное уравнение.
Характеристическое уравнение:
Общее решение однородного уравнения:
Найдем частное решение неоднородного
дифуравнения:
Подставляя найденные производные в исходное дифуравнение, получаем:
Искомое частное решение:
Общее решение исходного дифуравнения:
Правая часть дифференциального уравнения имеет вид:
Частное решение ищем в виде
, где
– неопределенный
коэффициент.
Подставляя
и
в исходное
дифференциальное уравнение, получим тождество, откуда находим коэффициент.
Если
– корень
характеристического уравнения, то частное решение исходного дифференциального
уравнения ищем в виде
, когда
– однократный
корень, и
, когда
– двукратный
корень.
Пример 5
Решение
Характеристическое
уравнение:
Общее
решение соответствующего однородного дифференциального уравнения:
Найдем
частное решение соответствующего неоднородного дифференциального уравнения:
Подставляя
в исходное дифуравнение, получаем:
Общее
решение дифуравнения:
Правая часть дифференциального уравнения имеет вид:
В этом случае частное решение
ищем в форме тригонометрического двучлена:
где
и
– неопределенные коэффициенты
Подставляя
и
в исходное
дифференциальное уравнение, получим тождество, откуда находим коэффициенты.
Эти уравнения определяют коэффициенты
и
кроме случая, когда
(или когда
– корни характеристического уравнения). В
последнем случае частное решение дифференциального уравнения ищем в виде:
Пример 6
Решение
Характеристическое
уравнение:
Общее
решение соответствующего однородного дифуравнения:
Найдем
частное решение неоднородного дифуравнения
Подставляя
в исходное дифуравнение, получаем:
Общее
решение исходного дифуравнения:
-
Неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
и
специальной правой частью
Общее
решение линейного неоднородного
уравнения (1) равно сумме общего решения
соответствующего однородного уравнения
и любого частного решения
неоднородного уравнения:
.
В
некоторых случаях частное решение
неоднородного уравнения можно найти
довольно просто по виду правой части
уравнения (1). Рассмотрим случаи, когда
это возможно.
Пусть
неоднородное уравнение имеет вид
,
(7)
т.е.
правая часть неоднородного уравнения
является многочленом степени m.
Если
не является корнем характеристического
уравнения, то частное решение неоднородного
уравнения следует искать в виде многочлена
степени m,
т.е.
.
Коэффициенты
определяются в процессе нахождения
частного решения.
Если
же
является корнем характеристического
уравнения, то частное решение неоднородного
уравнения следует искать в виде
.
Пример
7.
Найти общее решение дифференциального
уравнения
.
Решение.
Соответствующим однородным уравнением
для данного уравнения является
.
Его характеристическое уравнение
имеет корни
и
.
Общее решение однородного уравнения
имеет вид
.
Так
как
не является корнем характеристического
уравнения, то частное решение неоднородного
уравнения будем искать в виде функции
.
Найдём производные этой функции
,
и подставим их в данное уравнение :
или
.
Приравняем коэффициенты при
и свободные члены:
Решив
данную систему , получим
,
.
Тогда частное решение неоднородного
уравнения имеет вид
,
а общим решением данного неоднородного
уравнения будет сумма общего решения
соответствующего однородного уравнения
и частного решения неоднородного:
.
Пусть
неоднородное уравнение имеет вид
(8)
Если
не является корнем характеристического
уравнения, то частное решение неоднородного
уравнения следует искать в виде
.
Если же
есть корень характеристического
уравнения кратности k
(k=1
или k=2),
то в этом случае частное решение
неоднородного уравнения будет иметь
вид
.
Пример
8.
Найти общее решение дифференциального
уравнения
.
Решение.
Характеристическое уравнение для
соответствующего однородного уравнения
имеет вид
.
Его корни
,
.
В этом случае общее решение соответствующего
однородного уравнения записывается в
виде
.
Так
как число 3 не является корнем
характеристического уравнения, то
частное решение неоднородного уравнения
следует искать в виде
.
Найдём производные первого и второго
порядков:
,
.
Подставим в дифференциальное уравнение:
+
+
,
+
,
.
Приравняем
коэффициенты при
и свободные члены:
Отсюда
,
.
Тогда частное решение данного уравнения
имеет вид
,
а общее решение
.
-
Метод Лагранжа вариации произвольных постоянных
Метод
вариации произвольных постоянных можно
применять к любому неоднородному
линейному уравнению с постоянными
коэффициентами независимо от вида
правой части. Этот метод позволяет
всегда найти общее решение неоднородного
уравнения, если известно общее решение
соответствующего однородного уравнения.
Пусть
и
являются линейно независимыми решениями
уравнения (2). Тогда общим решением этого
уравнения является
,
где
и
—
произвольные постоянные. Суть метода
вариации произвольных постоянных
состоит в том, что общее решение уравнения
(1) ищется в виде
,
(9)
где
и
— новые неизвестные функции, которые
необходимо найти. Так как неизвестных
функций две, то для их нахождения
необходимы два уравнения, содержащие
эти функции. Эти два уравнения составляют
систему
которая
является линейной алгебраической
системой уравнений относительно
и
.
Решая данную систему, найдём
и
.
Интегрируя обе части полученных равенств,
найдём
и
.
Подставив
эти выражения в (9), получим общее решение
неоднородного линейного уравнения (1).
Пример
9.
Найти общее решение дифференциального
уравнения
.
Решение.
Характеристическим уравнением для
однородного уравнения, соответствующего
данному дифференциальному уравнению,
является
.
Корни его комплексные
,
.
Так как
и
,
то
,
,
а общее решение однородного уравнения
имеет вид
.
Тогда общее решение данного неоднородного
уравнения будем искать в виде
,
где
и
—
неизвестные функции.
Система
уравнений для нахождения этих неизвестных
функций имеет вид
Решив
эту систему, найдём
,
.
Тогда
,
.
Подставим полученные выражения в формулу
общего решения:
.
Это и есть общее решение данного
дифференциального уравнения, полученное
по методу Лагранжа.
Вопросы
для самоконтроля знаний
-
Какое
дифференциальное уравнение называется
линейным дифференциальным уравнением
второго порядка с постоянными
коэффициентами? -
Какое
линейное дифференциальное уравнение
называется однородным, а какое –
неоднородным? -
Какими
свойствами обладает линейное однородное
уравнение? -
Какое
уравнение называется характеристическим
для линейного дифференциального
уравнения и как оно получается? -
В
каком виде записывается общее решение
линейного однородного дифференциального
уравнения с постоянными коэффициентами
в случае разных корней характеристического
уравнения? -
В
каком виде записывается общее решение
линейного однородного дифференциального
уравнения с постоянными коэффициентами
в случае равных корней характеристического
уравнения? -
В
каком виде записывается общее решение
линейного однородного дифференциального
уравнения с постоянными коэффициентами
в случае комплексных корней
характеристического уравнения? -
Как
записывается общее решение линейного
неоднородного уравнения? -
В
каком виде ищется частное решение
линейного неоднородного уравнения,
если корни характеристического уравнения
различны и не равны нулю, а правая часть
уравнения есть многочлен степени m? -
В
каком виде ищется частное решение
линейного неоднородного уравнения,
если среди корней характеристического
уравнения есть один нуль, а правая часть
уравнения есть многочлен степени m? -
В
чём суть метода Лагранжа?
Задания
для самостоятельной работы
Решить
дифференциальные уравнения второго
порядка с постоянными коэффициентами:
-
; -
; -
; -
; -
.
;
;
;
;
.13
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
29.02.20164.2 Mб13ЛПЗ по гистологии.docx
- #
- #
- #
- #