Как найти общее решение рекуррентных соотношений

Рекуррентные соотношения и уравнения

В этом разделе вы найдете бесплатные примеры решений рекуррентных соотношений методом характеристического уравнения и подбора частного решения по правой части. Также приведены краткие алгоритмы решения для двух методов и пример их использования для последовательности Фибоначчи.

Как решать рекуррентные соотношения?

Для решения рекуррентных соотношений применяют один из двух основных способов:

• Метод производящих функций
• Метод характеристического уравнения

В следующем разделе мы сравним, как выглядит процесс решения для одной и той же последовательности двумя методами.

Метод производящих функций

1. Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен $k$)
   $$a_{0} = …, \ a_{1} = …, \ a_{k-1} = …, \ … \ a_{n} = …, ngeqslant k$$
2. Домножить каждую строчку на $z$ в соответствующей степени $z^{k} cdot a_{k}$ и сложить все выражения для $n ge 0$. В левой части получится сумма $displaystylesum_{n=0}^{infty} a_nz^n$ — это производящая функция, назовем ее $G(z)$. Правую часть преобразовать так, чтобы она превратилась в выражение, включающее $G(z)$.
3. Решить полученное уравнение относительно $G(z)$.
4. Разложить $G(z)$ в степенной ряд, тогда коэффициент при $z_n$ будет искомым выражением для $a_n$.

Метод характеристических функций

Этот метод практически полностью аналогичен методу решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами, кратко алгоритм выглядит так:

1. Записать соответствующее однородное рекуррентное уравнение (РУ):
   $$
   p_{n+k} a_{n+k} + p_{n+k-1}a_{n+k-1} + … + p_n a_n =f to \ to p_{n+k} a_{n+k} + p_{n+k-1}a_{n+k-1} + … + p_n a_n =0.
   $$
2. Выписать для него характеристическое уравнение и найти его корни $lambda_i$
   $$
   p_{n+k} lambda^{k} + p_{n+k-1}lambda^{k-1} + … + p_{n-1}lambda + p_n =0.
   $$
3. Выписать согласно полученным корням $lambda_1, …,lambda_k$ общее решение однородного рекуррентного соотношения (подробнее теорию см. по ссылке [1] ниже).
   $$
   C_1 lambda_1^n +…+C_k lambda_k^n , mbox { для случая различных простых корней},
   $$
   $$
   C_1 lambda_1^n + C_2 nlambda_1^n +…+C_m n^m lambda_1^n+…+C_k lambda_k^n mbox { для случая корня }, lambda_1 , { кратности }, m.
   $$

4. Подобрать частное решение неоднородного рекуррентного соотношения по виду правой части (особенно удобно для правых частей вида $mu^n*P(n)$, $P(n)$ — многочлен от $n$).
5. Представить общее решение неоднородного РУ как сумму общего решения соответствующего однородного РУ и частного решения неоднородного РУ.
6. Подставить начальные условия $a_0, a_1, …, a_{k-1}$ и получить значения констант $C_1, …, C_k$.

Решение для последовательности чисел Фибоначчи

Последовательность чисел Фибоначи — это последовательность, каждый элемент которой (кроме нулевого и первого) равен сумме двух предыдущих:

$$ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 , … $$

Числа Фибоначчи растут быстро: $f_{10}=55$, $f_{20}=6765$, а $f_{100}=354224848179261915075$.

Общая формула данной рекуррентной последовательности имеет вид6

$$begin{array}{rcl}
f_0&{}={}&0,\
f_1&{}={}&1,\
f_n&{}={}&f_{n-1}+f_{n-2}, quad ngeq2.\
end{array}
$$

Способ 1. Производящяя функция

Начинаем с второго шага алгоритма, домножаем на $z^n$:

$$begin{array}{rcl}
1cdot f_0 &= &0cdot 1,\
zcdot f_1 &= &1cdot z,\
zcdot f_n & = &(f_{n-1}+f_{n-2})cdot z^n, quad ngeq2.\
end{array}
$$

Складываем все строчки:

$$f_0 + f_1 z + sum_{n=2}^{infty}f_nz^n =
z + sum_{n=2}^{infty}f_{n-1}z^n+sum_{n=2}^{infty}f_{n-2}z^n.
$$

На третьем шаге алгоритма приводим все суммы к замкнутому виду:

$$begin{array}{rcl}
G(z) &=& z + zsum_{n=2}^{infty}f_{n-1}z^{n-1}+z^2 sum_{n=2}^{infty}f_{n-2}z^{n-2},\
G(z) &=& z + zsum_{n=1}^{infty}f_{n}z^{n}+z^2 sum_{n=0}^{infty}f_{n}z^{n},\
G(z) &=& z + z(G(z)-f_0)+z^2 G(z),\
G(z) &=& z + zG(z)+z^2G(z),\
end{array}
$$

откуда выводим искомое выражение для производящей функции:

$$ G(z) = frac{z}{1-z-z^2}. $$

Теперь разложим ее в степенной ряд. Для этого сначала разложим знаменатель на множители. Найдем корни уравнения:

$$1-z-z^2 = 0,\
z_1=-frac{1-sqrt{5}}{2}, z_2=-frac{1+sqrt{5}}{2}.$$

Таким образом,

$$G(z) = frac{z}{1-z-z^2}=frac{-z}{(z_1-z)(z_2-z)}
= frac{z_1/(z_1-z_2)}{z_1-z} + frac{z_2/(z_2-z_1)}{z_2-z}.
$$

Чтобы разложить данные дроби в ряды, используем известное разложение для дроби:

$$frac{1}{1-z} = sum_{n=0}^{infty}z^n = 1 + z + z^2 + z^3 + cdots.$$

Рассмотрим первую дробь и поделим в ней числитель и знаменатель на $z_1$:

$$ frac{z_1/(z_1-z_2)}{z_1-z} = frac{1}{z_1-z_2} frac{1}{1-frac{z}{z_1}} =
frac1{z_1-z_2}sum_{n=0}^{infty}frac{z^n}{z_1^n}.
$$

Аналогично (но с делением на $z_2$) действуем со второй дробью:

$$frac{z_2/(z_2-z_1)}{z_2-z} = frac{1}{z_2-z_1}frac{1}{1-frac{z}{z_2}} =
frac{1}{z_2-z_1}sum_{n=0}^{infty}frac{z^n}{z_2^n}.
$$

Таким образом,

$$G(z)=sum_{n=0}^{infty} f_nz^n =sum_{n=0}^{infty}biggl (frac{1}{z_1-z_2} frac{1}{z_1^n} + frac{1}{z_2-z_1}frac{1}{z_2^n} biggr)z^n,
$$

и, следовательно,

$$f_n = frac1{z_1-z_2}frac{1}{z_1^n} + frac1{z_2-z_1}frac{1}{z_2^n}.
$$

Преобразуем данное выражение, используя то, что

$$1/z_1=-z_2, quad 1/z_2 = -z_1, quad z_1-z_2=sqrt{5} $$

$$f_n=frac{1}{sqrt{5}}left( biggl( frac{1+sqrt{5}}{2} biggr)^n — biggl( frac{1-sqrt{5}}{2} biggr)^n right).
$$

И окончательно,

$$ f_n = frac1{2^nsqrt{5}} bigl( (1+sqrt{5})^n — (1-sqrt{5})^n bigr). $$

Способ 2. Характеристическое уравнение

Запишем характеристический многочлен для $f_n=f_{n-1}+f_{n-2}$, и найдем его корни:

$$
x^2=x+1,\
D=1+4=5, \
x_{1,2}=frac{1pm sqrt{5}}{2}.
$$

Тогда общее решение однородного рекуррентного уравнения имеет вид:

$$
f_n=C_1 biggl(frac{1- sqrt{5}}{2} biggr)^n+C_2 biggl(frac{1+ sqrt{5}}{2} biggr)^n.
$$

Осталось найти значения произвольных постоянных $C_1, C_2$ из начальных условий $f_0=0, f_1=1$.

$$
f_0=C_1 +C_2 =0,\
f_1=C_1 bigl(frac{1- sqrt{5}}{2} bigr)+C_2 bigl(frac{1+ sqrt{5}}{2} bigr)=1.
$$

Решая систему, найдем

$$
C_1 =-1/sqrt{5},\
C_2 = 1/sqrt{5}.
$$

Итоговое выражение для последовательности чисел Фибоначчи:

$$
f_n= -frac{1}{sqrt{5}} bigl(frac{1- sqrt{5}}{2} bigr)^n +frac{1}{sqrt{5}} bigl(frac{1+ sqrt{5}}{2} bigr)^n = \
=frac1{2^nsqrt{5}} bigl( (1+sqrt{5})^n — (1-sqrt{5})^n bigr).
$$

Результаты обоих методов совпали, решение вторым методом оказалось проще и короче.

Примеры решений

Задача 1. Решить рекуррентное соотношение $f(n+2)=-6f(n+1)+7f(n)+n-3$ с начальными условиями $f(0)=2$ и $f(1)=4$, сделать проверку

Задача 2. Решить рекуррентное соотношение $f(n+2)=-2f(n+1)+3f(n)-3^n$ с начальными условиями $f(0)=1$, $f(1)=3$ и сделать проверку

Задача 3. 1. Решить рекуррентное соотношение $f(n+2) =-5f(n+1) -4f(n) + 3n^2$
с начальными условиями $f(0) = 2$, $f(1) = 3$.
2. Проверить, удовлетворяет ли найденное решение начальным условиям и обращает ли оно рекуррентное соотношение в справедливое тождество.

Задача 4. Найти последовательность ${a_n}$, удовлетворяющую рекуррентному соотношению $a_{n+2} + 4 a_{n+1} + 3 a_{n} = 0$ и начальным условиям $a_1=2$, $a_2=4$.

Полезные ссылки

• Рекуррентные последовательности, ЛОРУ, ЛНРУ Краткое изложений лекций по ДМ для 1 курса МГУ
• Решение рекуррентных соотношений Краткая теория и примеры, метод производящих функций
• Разностное уравнение и рекуррентная последовательность Более продвинутый материал
• Примеры: примитивно-рекурсивные функции
• Примеры: разностные уравнения

1.
Определение
и примеры.
Последовательность

(2.2.1)

называется однородной
линейной рекуррентной последовательностью
порядка,
если существуют натуральное число
и числа(действительные или комплексные, причем)
такие, что для любого

справедливо

.
(2.2.2)

Соотношение (2.2.2) называется
при этом однородным линейным
рекуррентным соотношением порядкаk^.

Из этого
определения следует, что соотношение
(2.1.1), задающее при
,последовательность Фибоначчи, –
однородное линейное рекуррентное
соотношение второго порядка, а сама эта
последовательность – однородная
линейная рекуррентная последовательность
второго порядка.

Задача
2.1. Доказать, что арифметическая
и геометрическая прогрессии являются
однородными линейными последовательностями.

Решение. Пусть
– разность арифметической прогрессии.
Тогда,и, следовательно,.
Отсюда.
Сравнивая полученное рекуррентное
соотношение с (2.2.2), видим, что арифметическая
прогрессия является однородной линейной
рекуррентной последовательностью
второго порядка, для которой,.

Геометрическая
прогрессия может быть задана рекуррентным
соотношением
,
которое получается из (2.2.2) при.
Поэтому геометрическая прогрессия
является однородной линейной рекуррентной
последовательностью первого порядка.

Задача
2.2. Доказать, что последовательность

,
,,
…,,
…

квадратов натуральных чисел
является однородной линейной рекуррентной
последовательностью.

Решение. Представим
члены

и

в виде

,

.

Почленным вычитанием левых
и правых частей записанных равенств
получим

.

Подставим в найденное
соотношение
вместо

.

Вычитая почленно из этого
равенства предыдущее, получим

.

Это соотношение
получается из соотношения (2.2.2) при
,
,.
Поэтому рассматриваемая последовательность
является однородной линейной рекуррентной
последовательностью третьего порядка.

2.
Решение
однородного линейного рекуррентного
соотношения.
Рассмотрим свойства решений
однородного линейного рекуррентного
соотношения k-го
порядка.

Теорема
2.2.1.Пусть– частное решения рекуррентного
соотношения(2.2.2)k-го
порядка,– произвольное число. Тогда– частное решение этого рекуррентного
соотношения.

Доказательство.
По определению решения,

,

– верное
числовое равенство.
Умножая это тождество на ,будем иметь:
.
Полученное равенство означает, что– частное решение рекуррентного
соотношения (2.2.2). ■

Теорема
2.2.2.Пусть,– частное решения рекуррентного
соотношенияk-го порядка
(2.2.2). Тогда– частное решение этого рекуррентного
соотношения.

Доказательство.
Складывая верные равенства

,

,

получим верное
равенство

.

Значит,
– частное
решение рекуррентного соотношения
(2.2.2). ■

Теорема
2.2.3.
Если
– корень алгебраического уравнения

,(2.2.4)

то
функция
является частным решением рекуррентного
соотношения

.

Доказательство.
Пусть
– корень уравнения (2.2.4). Изследует, что

,
…,
,.

Подставив эти
значения в рассматриваемое рекуррентное
соотношение, получим равенство:

.

Поскольку

,
это равенство справедливо для любого

.
Следовательно,
– частное решение однородного линейного
рекуррентного соотношения (2.2.2). ■

Уравнение
(2.2.4) называется характеристическим
уравнением
однородного линейного рекуррентного
соотношения (2.2.2).

Рассмотренные
теоремы позволяют найти общее решение
рекуррентного соотношения (2.2.2).

Теорема
2.2.4. Если
характеристическое уравнение
(2.2.4) однородного
линейного рекуррентного соотношения
(2.2.2) имеет
различных
корней
,то общее
решение этого соотношения имеет вид

.

Задача
2.3.
Найти общее
решение однородного линейного
рекуррентного соотношения
.

Решение.
Составим
характеристическое уравнение данного
рекуррентного соотношения второго
порядка:
или.
Это квадратное уравнение имеет корни,.
Следовательно, общее решение рекуррентного
соотношения имеет вид.

Задача
2.4.
Найти общее
решение однородного линейного соотношения
и частное решение, соответствующее
начальным условиям.

Решение.
Составим
характеристическое уравнение

.

Оно
имеет корни
,.
Поэтому общее решение этого рекуррентного
соотношения имеет вид.

Найдем
частное решение, соответствующее
начальным условиям
.
Для этого необходимо решить систему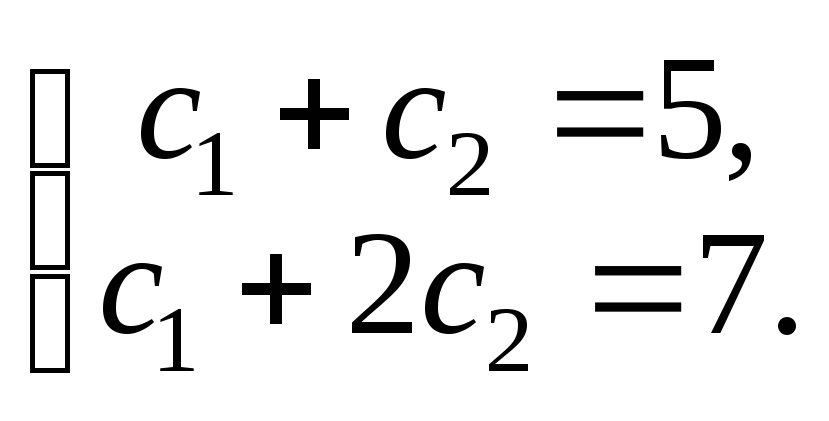Эта система имеет решение.
Поэтому частное решение, соответствующее
заданным начальным условиям, есть.

Пусть
характеристическое уравнение
(2.2.4) имеет два комплексных корня, которые
являются сопряженными числами
.
Из комплексных решений,рекуррентного соотношения (2.2.2) можно
составить его действительные решения.
Для этого комплексные числапредставим в тригонометрической форме:

,
,

где
,.
Тогда

,

.

По теореме 2.2.2

,

– решения
рекуррентного соотношения (2.2.2), а,
значит,

– также решение этого соотношения.
Поэтому в общем решении (2.2.5) слагаемые,
соответствующие комплексным сопряженным
корням характеристического уравнения,
можно заменить полученной суммой.

Задача
2.5.
Найти общее
и одно частное решение однородного
линейного соотношения
второго порядка.

Решение.
Характеристическое
уравнение
имеет корни.
Представим найденные корни в
тригонометрической форме. Так как,,
имеем

,
.

Отсюда
следует, что общее решение рекуррентного
соотношения можно записать в виде

.

Найдем
частное решение этого соотношения с
начальными значениями
,.
Для этого подставим ввместо

последовательно 1 и 2. Тогда получим, что

Отсюда
,,
поэтому искомым частным решением
является

.

В том случае, когда
среди корней характеристического
уравнения имеются кратные корни, формула
(2.2.5) не задает общего решения рекуррентного
соотношения (2.2.2). В этом легко убедиться
на следующем примере.

Рассмотрим
рекуррентное соотношение

.

Его
характеристическое уравнение есть
,
т.е.,
имеющее трехкратный корень:.
Если воспользоваться формулой (2.2.5), то
получим решение, зависящее только от
одной постоянной:

.

Поэтому
очевидно, что не для любых a,
b
и c
можно выбрать начальные значения
,и.

Но
можно проверить, что кроме решения
,
решениями рассматриваемого соотношения
будути.
Действительно,

,

.

Подставляя эти значения
в наше рекуррентное соотношение,
соответственно получим:

,

.

Зная три частных
решения рекуррентного соотношения, его
общее решение можно записать так:

.

Докажем, что в
общем случае имеет место

Теорема
2.2.5. Пусть
характеристическое уравнение
(2.2.4) однородного
линейного рекуррентного соотношения
(2.2.2) имеет
только k-кратный
корень
.
Тогда общее решение рекуррентного
соотношения имеет вид

.

Заметим,
что в случае, когда характеристическое
уравнение имеет комплексный корень
кратности,
сопряженный ему корень
тоже имеет кратность.
Как и в случае простого, т.е. однократного
корня, из соответствующих кратному
корню комплексных решений

,

,

………………………………………………….

можно
получить
действительных решений:

,
,
…,;

,
,
…,.

Это
позволяет записать общее решение в
следующем виде:

.

Задача
2.6.
Найти общее
решение рекуррентного соотношения
четвертого порядка.

Решение.
Характеристическое
уравнение
илиимеет двукратные корнии.
Поскольку,
общее решение рекуррентного соотношения
записывается в виде

.

В
общем случае характеристическое
уравнение может иметь корни –
кратности,кратности,
и т.д.,кратности,.
Тогда в общем решении соответствующего
рекуррентного соотношения каждому
корню отвечает слагаемое вида

,
,

а
само общее решение есть сумма таких
слагаемых.

Доказательство
этого утверждения производится примерно
по такой же схеме, как и доказательство
теоремы 2.2.5. Поэтому по причине большого
объема уже не столь интересных и в
основном аналогичных рассуждений и
преобразований не будем приводить это
доказательство.

Задача
2.7. Найти
общее решение рекуррентного соотношения

.

Решение.
Характеристическое
уравнение имеет вид

или
.

Непосредственной
проверкой (например, подставляя в
уравнение делители свободного члена)
можно убедиться, что это уравнение имеет
два двукратных корня –
,и один простой –.
Поэтому общее решение данного рекуррентного
соотношения имеет вид:

или
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В этой главе мы обсудим, как рекурсивные методы могут выводить последовательности и использоваться для решения задач подсчета. Процедура поиска членов последовательности рекурсивным способом называется рекуррентным отношением . Мы изучаем теорию линейных рекуррентных соотношений и их решения. Наконец, мы вводим производящие функции для решения рекуррентных отношений.

Определение

Рекуррентное отношение – это уравнение, которое рекурсивно определяет последовательность, в которой следующий член является функцией предыдущих членов (выражая Fn как некоторую комбинацию Fi с i<n).

Пример – ряд Фибоначчи – Fn=Fn−1+Fn−2, Ханойская башня – Fn=2Fn−1+1

Линейные рекуррентные отношения

Линейное рекуррентное уравнение степени k или порядка k – это рекуррентное уравнение в формате xn=A1xn−1+A2xn−1+A3xn−1+ dotsAkxnk (An – константа, а Ak neq0) на последовательности чисел как полинома первой степени.

Вот некоторые примеры линейных рекуррентных уравнений –

Рецидив отношений	Начальные значения	Решения
F n = F n-1 + F n-2	a 1 = a 2 = 1	Число Фибоначчи
F n = F n-1 + F n-2	а 1 = 1, а 2 = 3	Номер Лукаса
F n = F n-2 + F n-3	a 1 = a 2 = a 3 = 1	Падовская последовательность
F n = 2F n-1 + F n-2	a 1 = 0, a 2 = 1	Число Пелла

Как решить линейное рекуррентное соотношение

Предположим, что два упорядоченных линейных рекуррентных соотношения имеют вид – Fn=AFn−1+BFn−2, где A и B – действительные числа.

Характеристическое уравнение для вышеуказанного рекуррентного соотношения –

x2−Axe−B=0

Три случая могут возникнуть при поиске корней –

Случай 1 – Если это уравнение учитывается как (x−x1)(x−x1)=0 и оно дает два различных реальных корня x1 и x2, то Fn=axn1+bxn2 является решение. [Здесь a и b являются константами]

Случай 2 – Если это уравнение вычисляется как (x−x1)2=0, и оно порождает один действительный корень x1, то решением является Fn=axn1+bnxn1.

Случай 3 – Если уравнение дает два различных комплексных корня, x1 и x2 в полярной форме x1=r angle theta и x2=r angle(− theta), то Fn=rn(acos(n theta)+bsin(n theta)) является решением.

Проблема 1

Решите рекуррентное соотношение Fn=5Fn−1−6Fn−2, где F0=1 и F1=4.

Решение

Характеристическое уравнение рекуррентного соотношения –

x2−5x+6=0,

Итак, (x−3)(x−2)=0

Следовательно, корни –

x1=3 и x2=2

Корни реальны и различны. Итак, это в форме дела 1

Следовательно, решение –

Fn=axn1+bxn2

Здесь Fn=a3n+b2n (As x1=3 and x2=2)

Следовательно,

1=F0=a30+b20=a+b

4=F1=a31+b21=3a+2b

Решая эти два уравнения, мы получаем a=2 и b=−1

Следовательно, окончательное решение –

$$ F_n = 2,3 ^ n + (-1). 2 ^ n = 2,3 ^ n – 2 ^ n $$

Проблема 2

Решите рекуррентное соотношение – Fn=10Fn−1−25Fn−2, где F0=3 и F1=17.

Решение

Характеристическое уравнение рекуррентного соотношения –

x2−10x−25=0

Итак, (x−5)2=0

Следовательно, существует один действительный корень x1=5

Поскольку существует единый действительный корень, он имеет вид случая 2

Следовательно, решение –

Fn=axn1+bnxn1

3=F0=a.50+b.0.50=a

17=F1=a.51+b.1.51=5a+5b

Решая эти два уравнения, мы получаем a=3 и b=2/5

Следовательно, окончательное решение – Fn=3.5n+(2/5).n.2n

Проблема 3

Решите рекуррентное соотношение Fn=2Fn−1−2Fn−2, где F0=1 и F1=3

Решение

Характеристическое уравнение рекуррентного соотношения –

x2−2x−2=0

Следовательно, корни –

x1=1+i и x2=1−i

В полярной форме,

x1=r angle theta и x2=r angle(− theta), где r= sqrt2 и  theta= frac pi4

Корни воображаемые. Итак, это в форме случая 3.

Следовательно, решение –

Fn=( sqrt2)n(cos(n. Sqcap/4)+bsin(n. Sqcap/4))

1=F0=( sqrt2)0(acos(0. Sqcap/4)+bsin(0. Sqcap/4))=a

3=F1=( sqrt2)1(acos(1. Sqcap/4)+bsin(1. Sqcap/4))= sqrt2(a/ sqrt2+b/ sqrt2)

Решая эти два уравнения, мы получаем a=1 и b=2

Следовательно, окончательное решение –

Fn=( sqrt2)n(cos(n. Pi/4)+2sin(n. Pi/4))

Неоднородное рекуррентное соотношение и частные решения

Рекуррентное отношение называется неоднородным, если оно имеет вид

Fn=AFn−1+BFn−2+f(n), где f(n) ne0

Связанное с ним однородное рекуррентное соотношение равно Fn=AFn–1+BFn−2

Решение (an) неоднородного рекуррентного отношения состоит из двух частей.

Первая часть – это решение (ah) связанного однородного рекуррентного соотношения, а вторая часть – это частное решение (at).

an=AH+at

Решение первой части выполняется с использованием процедур, описанных в предыдущем разделе.

Чтобы найти конкретное решение, мы находим подходящее пробное решение.

Пусть f(n)=cxn; пусть x2=Ax+B – характеристическое уравнение связанного однородного рекуррентного соотношения, а x1 и x2 – его корни.

• Если x nex1 и x nex2, то at=Axn

• Если x=x1, x nex2, то at=Anxn

• Если x=x1=x2, то at=An2xn

Если x nex1 и x nex2, то at=Axn

Если x=x1, x nex2, то at=Anxn

Если x=x1=x2, то at=An2xn

пример

Пусть неоднородное рекуррентное соотношение имеет вид Fn=AFn–1+BFn−2+f(n) с характеристическими корнями x1=2 и x2=5. Пробные решения для различных возможных значений f(n) следующие:

е (п)	Пробные решения
4
5,2 н	An2 n
8,5 n	An5 n
4 н	A4 н
2n 2 + 3n + 1	Ан 2 + Бн + С

проблема

Решите рекуррентное соотношение Fn=3Fn−1+10Fn−2+7.5n, где F0=4 и F1=3

Решение

Это линейное неоднородное отношение, где ассоциированное однородное уравнение имеет вид Fn=3Fn−1+10Fn−2 и f(n)=7,5n.

Характеристическое уравнение его связанного однородного отношения –

x2−3x−10=0

Или (x−5)(x+2)=0

Или x1=5 и x2=−2

Следовательно, ah=a.5n+b.(−2)n, где a и b – постоянные.

Поскольку f(n)=7,5n, то есть в форме cxn, разумным пробным решением at будет Anxn.

at=Anxn=An5n

После помещения решения в рекуррентное соотношение мы получаем –

An5n=3A(n−1)5n−1+10A(n−2)5n−2+7,5n

Разделив обе стороны на 5n−2, получим

An52=3A(n−1)5+10A(n−2)50+7,52

Или 25An=15An−15A+10An−20A+175

Или 35 ​​=175

Или A=5

Итак, Fn=An5n=5n5n=n5n+1

Решение рекуррентного отношения можно записать в виде –

Fn=ah+at

=А.5п+Ь.(−2)п+n5п+1

Положив значения F0=4 и F1=3, в приведенном выше уравнении получим a=−2 и b=6

Следовательно, решение –

Fn=n5n+1+6.(−2)n−2,5n

Генерация функций

Генерирующие функции представляют последовательности, где каждый член последовательности выражается в виде коэффициента переменной x в формальном степенном ряду.

Математически, для бесконечной последовательности, скажем, a0,a1,a2, dots,ak, dots, производящая функция будет –

Gx=a0+a1x+a2x2+ dots+akxk+ dots= sum inftyk=0akxk

Некоторые области применения

Генерирующие функции могут быть использованы для следующих целей –

• Для решения различных задач подсчета. Например, количество способов внести изменения для рупий. 100 примечание с примечаниями достоинств Rs.1, Rs.2, Rs.5, Rs.10, Rs.20 и Rs.50

• Для решения рекуррентных отношений

• Для доказательства некоторых комбинаторных тождеств

• Для нахождения асимптотических формул для членов последовательностей

Для решения различных задач подсчета. Например, количество способов внести изменения для рупий. 100 примечание с примечаниями достоинств Rs.1, Rs.2, Rs.5, Rs.10, Rs.20 и Rs.50

Для решения рекуррентных отношений

Для доказательства некоторых комбинаторных тождеств

Для нахождения асимптотических формул для членов последовательностей

Проблема 1

Каковы производящие функции для последовательностей  lbraceak rbrace с ak=2 и ak=3k?

Решение

Когда ak=2, производящая функция, G(x)= sum inftyk=02xk=2+2x+2x2+2x3+ точки

Когда ak=3k,G(x)= sum inftyk=03kxk=0+3x+6x2+9x3+ dots точки

Проблема 2

Что является производящей функцией бесконечного ряда; 1,1,1,1, dots?

Решение

Здесь ak=1 для 0 lek le infty

Следовательно, G(x)=1+x+x2+x3+ dots dots= frac1(1−x)

Для ak=ak,G(x)= sum inftyk=0akxk=1+ax+a2x2+ dots dots dots=1/(1−топор)

Для ak=(k+1)G(x)= sum inftyk=0(k+1)xk=1+2x+3x2 dots dots dots= frac1(1−x)2

Для ak=cnk,G(x)= sum inftyk=0cnkxk=1+cn1x+cn2x2+ dots dots dots+x2=(1+x)n

Для ak= frac1k!,G(x)= sum inftyk=0 fracxkk!=1+x+ fracx22!+ fracx33! dots dots dots=ex

Определения

Определение:

Рекуррентная формула (англ. recurrence relation) — формула вида , выражающая каждый следующий член последовательности через предыдущих членов и номер члена последовательности , вместе с заданными первыми p членами, где — порядок рекуррентного соотношения.

Для рекуррентного соотношения, которому удовлетворяет последовательность мы часто хотим получить выражение для . Например, для рекуррентного соотношения, задающего числа Фибоначчи:

член может быть записан следующим образом:

Для этого можно использовать метод производящих функций (англ. generating function method).

Метод производящих функций

Алгоритм получения выражения для чисел , удовлетворяющих рекуррентному соотношению, с помощью производящих функций cостоит из шагов.

1. Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен ):

2. Домножить каждую строчку на в соответствующей степени () и сложить все выражения, многоточие надо рассматривать как множество из выражений, где . В левой части получится сумма — это производящая функция, назовем ее . Правую часть преобразовать так, чтобы она превратилась в выражение, включающее .
3. Решить полученное уравнение, получив для выражение в замкнутом виде.
4. Разложить в степенной ряд, коэффициент при будет искомым выражением для .

Примеры

пример

Производящие функции позволяют решать рекуррентные соотношение механически по одному и тому же алгоритму. Рассмотрим общую схему на простом примере, который позволит продемонстрировать базовые приёмы работы.

Задано линейное однородное рекуррентное соотношение порядка с постоянными коэффициентами:

Порядок соотношения — это его «глубина», то есть количество предшествующих элементов, требуемых для вычисления элемента с номером . В данном случае порядок равен , так как для вычисления требуется знать и .

Будем искать производящую функцию последовательности в виде

с этой целью умножим верхнюю строчку в записи рекуррентного соотношения на , следующую — на и последнюю — на :

Теперь сложим все уравнения для всех значений :

Левая часть уравнения в точности равна , а в правой части есть суммы, очень похожие на функцию , но не равные ей. Эти суммы нужно привести к виду . Начнём с первой:

Равенство получатся вынесением в первой степени за знак суммы, это необходимо, чтобы уровнять степень переменной и индекс переменной a внутри суммы. Действие — изменение индекса суммирования, которое позволяет избавиться от . Равенство получается, если прибавить и снова отнять значение , чтобы получить полную сумму от до . Равенство справедливо в силу того, что .

Аналогичные манипуляции со второй суммой дают нам выражение

Теперь наше исходное уравнение для производящей функции принимает вид:

откуда получаем производящую функцию последовательности в замкнутом виде:

Отыскав производящую функцию в замкнутом виде, её нужно снова разложить в ряд. Это можно сделать разными способами, но самый простой из них — разбить всю дробь на простые дроби и применить формулу для разложения . Итак, разложим знаменатель функции на множители:

Теперь разобьём дробь на сумму простых дробей:

Вспомним разложение для простейшей рациональной функции:

Из этого разложения следует, что

Таким образом,

С другой стороны, мы искали в виде

поэтому, в силу равенства рядов, (для ).

пример: числа Фибоначчи

Рассмотрим рекуррентное соотношение для чисел Фибоначчи:

Первый шаг алгоритма мы уже выполнили, записав рекуррентное соотношение. Выполним второй шаг:

Складываем все строчки:

Третий шаг алгоритма требует привести все суммы к замкнутому виду:

откуда получаем замкнутое выражение для производящей функции:

Осталось разложить её в ряд (чего требует четвёртый шаг алгоритма). С этой целью нужно разложить знаменатель на множители. Найдем корни уравнения:

Таким образом,

Нам известно разложение следующей рациональной функции:

Рассмотрим первую дробь и поделим в ней числитель и знаменатель на :

Аналогично (но с делением на ) поступим со второй дробью:

Таким образом,

и, следовательно,

Данное выражение можно упростить, если обратить внимание на то, что , и . Подставим и в предыдущее выражение:

пример

Найдём производящую функцию для последовательности квадратов чисел Фибоначчи: $1, 1, 4, 9, 25, ldots, f_k^2,ldots$.

По определению последовательности Фибоначчи выполняется:

Возведя в квадрат и сложив, получим:

Обозначим рассматриваемую последовательность , а её члены , тогда:

Рекуррентное соотношение:

Приведём суммы к замкнутому виду:

откуда получаем замкнутое выражение для производящей функции:

пример

Рассмотрим следующее рекуррентное соотношение:

Следующие действия аналогичны тем, которые мы делали для чисел Фибоначчи:

Вспомним, что

поэтому

Последняя сумма может быть свёрнута:

Подставив свёрнутое выражение обратно, имеем,

Таким образом, наше последнее уравнение примет вид

Это уравнение для производящей функции. Из него выражаем :

Разложим знаменатель на множители и разобьём дробь на сумму простых дробей:

Дальше мы знаем что делать со всеми этими дробями, кроме, разве лишь, первой. Рассмотрим её (без множителя) подробнее:

Теперь соберём ответ:

Значит,

См. также

• Производящая функция
• Арифметические действия с формальными степенными рядами

Источники информации

• Решение рекуррентных соотношений