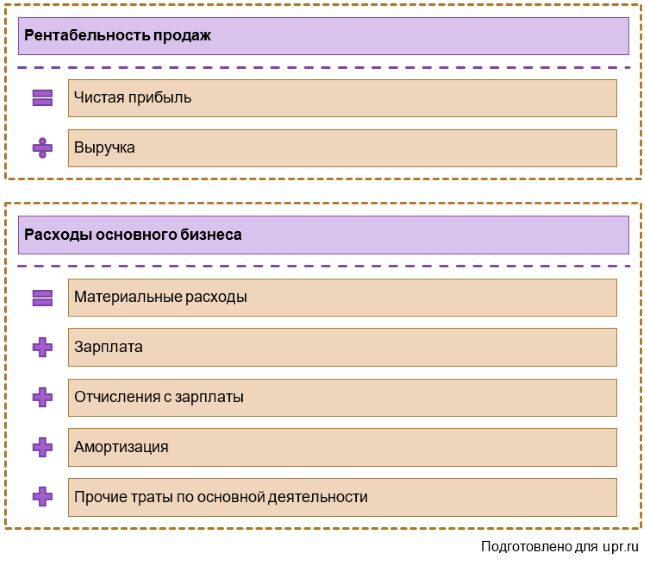
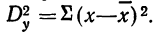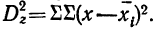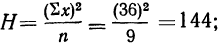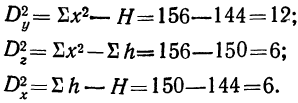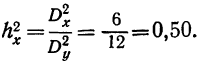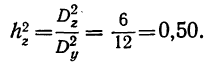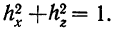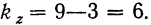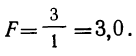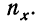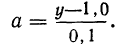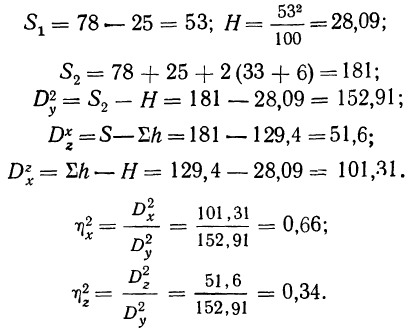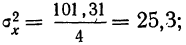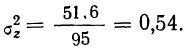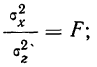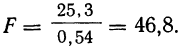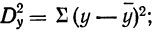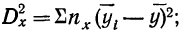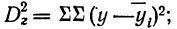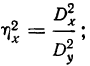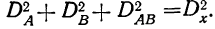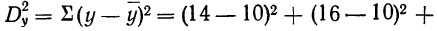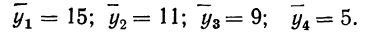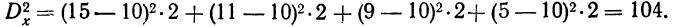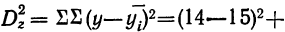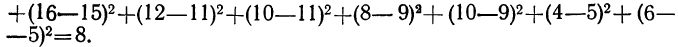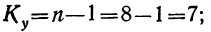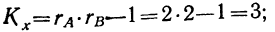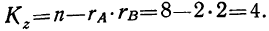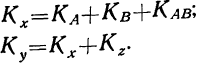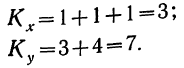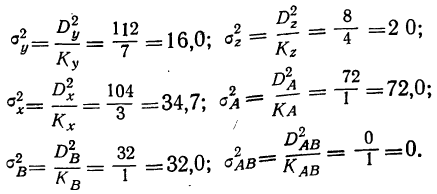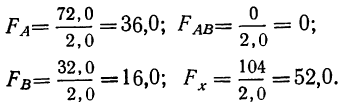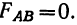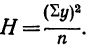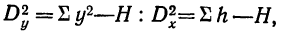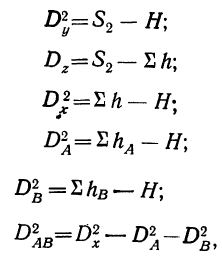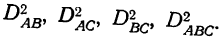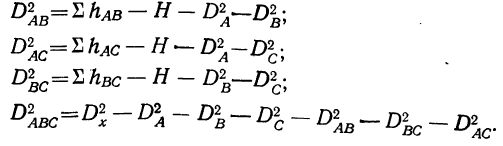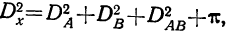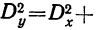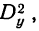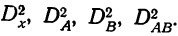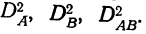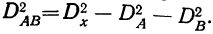Прибыль от продаж компании рассчитывается как разница между выручкой от продаж товаров, работ, услуг (за исключением НДС, акцизов и других обязательных платежей), себестоимостью, коммерческих расходов и управленческих расходов.
Основными факторами, влияющими на величину прибыли от продаж являются:
-
изменение объема продаж;
-
изменение ассортимента реализованной продукции;
-
изменение себестоимости продукции;
-
изменение цены реализации продукции.
Факторный анализ прибыли от продаж необходим для оценки резервов повышения эффективности производства, т.е. основной задачей факторного анализа является поиск путей максимизации прибыли компании. Кроме того, факторный анализ прибыли от продаж является обоснованием для принятия управленческих решений.
С аналитикой также поможет управлеческий учет. Сможете видеть полную картину по финансам в бизнесе и управлять расходами и доходами. Подробнее рассказали про управленку профи на курсе «Клерка».
Управленческий учет: с нуля до настройки в 1С, Excel и Google-таблицах
Уметь настраивать и вести управленку — значит быть полезным для руководителей. Научитесь понимать, откуда приходят и куда уходят деньги компании на курсе повышения квалификации от «Клерка».
Для проведения анализа составим аналитическую таблицу, источником информации служат данные бухгалтерского баланса и отчет о прибылях/убытках компании (1 и 2 форма баланса):
Исходные данные для факторного анализа прибыли от продаж:
|
Показатели |
Предыдущий период, |
Отчетный период, |
Абсолютное изменение, |
Относительное |
|
1 |
2 |
3 |
4 |
5 |
|
Выручка от продажи продукции, работ или услуг |
57 800 |
54 190 |
-3 610 |
-6,2% |
|
Себестоимость |
41 829 |
39 780 |
-2 049 |
-4,9% |
|
Коммерческие расходы |
2 615 |
1 475 |
-1 140 |
-43,6% |
|
Управленческие расходы |
4 816 |
3 765 |
-1 051 |
-21,8% |
|
Прибыль от продаж |
8 540 |
9 170 |
630 |
7,4% |
|
Индекс изменения цен |
1,00 |
1,15 |
0,15 |
15,0% |
|
Объем реализации в сопоставимых ценах |
57 800 |
47 122 |
-10 678 |
-18,5% |
Определим влияние факторов на сумму прибыли компании следующим образом.
1. Для определения влияния объема продаж на прибыль необходимо прибыль предыдущего периода умножить на изменение объема продаж.
Выручка от реализации товаров предприятия в отчетном периоде составила 54 190 тыс. рублей, для начала необходимо определить объем продаж в базисных ценах (54 190/1,15), который составил 47 122 тыс. рублей. С учетом этого изменение объема продаж за анализируемый период составило 81,5% (47 122/57 800*100%), т.е. произошло снижение объема реализованной продукции на 18,5%. За счет снижения объема продажи продукции прибыль от продажи продукции, работ, услуг снизилась: 8 540 * (-0,185) = −1 578 тыс. рублей.
Основная методическая сложность определения влияния объема продаж на прибыль компании связана с трудностями определения изменения физического объема реализованной продукции. Правильнее всего определять изменения в объеме продаж путем сопоставления отчетных и базисных показателей, выраженных в натуральных или условно-натуральных измерителях. Это возможно тогда, когда продукция однородна.
В большинстве же случаев реализованная продукция по своему составу является неоднородной и необходимо производить сопоставления в стоимостном выражении. Для обеспечения сопоставимости данных и исключения влияния других факторов необходимо сопоставлять отчетный и базисный объемы реализации, выраженные в одинаковых ценах (предпочтительно в ценах базисного периода).
Индекс изменения цен на продукцию, работы, услуги рассчитывается путем деления объема реализации отчетного периода на индекс изменения цен реализации. Такой расчет является не совсем точным, так как цены на реализованную продукцию изменяются в течение всего отчетного периода.
2. Влияние ассортимента продаж на величину прибыли организации определяется сопоставлением прибыли отчетного периода, рассчитанной на основе цен и себестоимости базисного периода, с базисной прибылью, пересчитанной на изменение объема реализации.
Прибыль отчетного периода, исходя из себестоимости и цен базисного периода, можно определить с некоторой долей условности следующим образом:
-
выручка от продажи отчетного периода в ценах базисного периода 47 122 тыс. рублей;
-
фактически реализованная продукция, рассчитанная по базисной себестоимости (41 829*0,815) = 34 101 тыс. рублей;
-
коммерческие расходы базисного периода 2 615 тыс. рублей;
-
управленческие расходы базисного периода 4 816 тыс. рублей;
-
прибыль отчетного периода, рассчитанная по базисной себестоимости и базисным ценам (47 122-34 101-2 615-4 816) = 5 590 тыс. рублей.
Таким образом, влияние сдвигов в структуре ассортимента на величину прибыли от продаж равно: 5 590 — (8 540*0,81525) = −1 373 тыс. рублей.
Произведенный расчет показывает, что в составе реализованной продукции увеличился удельный вес продукции с меньшим уровнем доходности.
3. Влияние изменения себестоимости на прибыль можно определить, сопоставляя себестоимость реализации продукции отчетного периода с затратами базисного периода, пересчитанными на изменение объема продаж: (41 829*0,815) — 39780 = −5 679 тыс. рублей. Себестоимость реализованной продукции увеличилась, следовательно, прибыль от продажи продукции снизилась на ту же сумму.
4. Влияние изменения коммерческих и управленческих расходов на прибыль компании определим путем сопоставления их величины в отчетном и базисном периодах. За счет снижения размера коммерческих расходов прибыль выросла на 1 140 тыс. рублей (1 475 — 2 615), а за счет снижения размера управленческих расходов — на 1 051 тыс. рублей (3 765 — 4 816).
5. Для определения влияния цен реализации продукции, работ, услуг на изменение прибыли необходимо сопоставить объем продаж отчетного периода, выраженного в ценах отчетного и базисного периода, т.е.: 54 190 — 47 122 = 7 068 тыс. рублей.
Подводя итог, посчитаем общее влияние всех перечисленных факторов:
1. влияние объема продаж −1 578 тыс. рублей;
2. влияние структуры ассортимента реализованной продукции −1 373 тыс. рублей;
3. влияние себестоимости −5 679 тыс. рублей;
4. влияние величины коммерческих расходов 1 140 тыс. рублей;
5. влияние величины управленческих расходов 1 051 тыс. рублей;
6. влияние цен реализации 7 068 тыс. рублей;
7. общее влияние факторов 630 тыс. рублей.
Значительный рост себестоимости продукции произошел в основном за счет повышения цен на сырье и материалы. Кроме этого, на сумму прибыли оказало отрицательное влияние уменьшение объема продаж и негативные сдвиги в ассортименте продукции.
Отрицательное воздействие перечисленных факторов было компенсировано повышением реализационных цен, а также снижение управленческих и коммерческих расходов. Следовательно, резервами роста прибыли предприятия являются рост объема продаж, увеличение доли более рентабельных видов продукции в общем объеме реализации и снижение себестоимости товаров, работ и услуг.
Оценка влияния фактора
При
изучении и анализе сложных и многообразных
причинно-следственных отношений
между объектами и явлениями биологу
приходится учитывать целый комплекс
внешних и внутренних факторов, от которых
в конечном итоге зависят уровень и ход
наблюдаемых процессов, те или иные
биологические свойства живых
организмов, их динамика и разнообразие.
При этом зачастую важно оценивать не
только роль одного из многочисленных
внешних факторов, но и их взаимодействие
при констелляционном влиянии на популяцию
или организм.
Идейная
база для изучения действия факторов
содержится уже в методе сравнения двух
выборок. Биологическим содержанием
операции сравнения двух выборок, в конце
концов, выступает поиск факторов,
ответственных за смещение средних
арифметических или усиление изменчивости
признаков. Развивая это направление
биометрического исследования, можно
не ограничиваться только двумя «дозами»
фактора, но изучить серию ситуаций, в
которых фактор проявлял разную силу
действия на результативный признак –
от самого слабого до самого сильного.
При этом каждому уровню фактора будет
соответствовать отдельная выборка и
общая задача получит формулировку
«сравнить несколько выборок». В терминах
факториальной биометрии вопрос о влиянии
фактора на признак звучит так: сказывается
ли отличие условий получения разных
выборок на качестве (значениях) вариант?
В терминах статистики вопрос звучит
несколько иначе: из одной ли генеральной
совокупности отобраны все выборки,
оценивают ли выборочные средние
арифметические одну и ту же генеральную
среднюю? Вариантов ответа может быть
только два:
-
Все
выборки отобраны из одной генеральной
совокупности, условия возникновения
вариант одни и те же. -
Выборки
отобраны из разных генеральных
совокупностей, условия возникновения
вариант выборок различаются.
В
постановке вопроса можно уловить
противоречие. Выше было сказано, что по
условию задачи выборки формировались
в разных условиях, и тут же предполагается,
что условия были одинаковые. На самом
деле противоречия нет, поскольку речь
идет об определении чувствительности
признака к действию фактора. Условия
формирования выборок могут отличаться,
но они могут никак и не сказаться на
величине изучаемого признака, не
отразиться на значениях вариант. Смысл
статистического сравнения в том и
состоит, чтобы оценить эффективность
действия фактора на признак, доказать
реальность реакции вариант выборок на
разные условия их формирования. В сферу
исследования можно вовлекать как один,
так и два признака, как количественные,
так и качественные характеристики. В
каждом случае процедура анализа несколько
отличается.
Однофакторный
дисперсионный анализ количественных
признаков
Дисперсионный
анализ позволяет оценить степень и
достоверность отличия нескольких
выборочных средних одновременно, т. е.
изучить влияние одного контролируемого
фактора на результативный признак
путем оценки его относительной роли в
общей изменчивости этого признака,
вызванной влиянием всех факторов.
Сущность дисперсионного анализа
заключается в расчленении общей
вариации (дисперсии) изучаемого
признака, вычисляемой по сумме квадратов
отклонений отдельных вариант (x)
от средней арифметической всего
комплекса наблюдений (М),
на его составные части –дисперсию,
вызванную организованными, учитываемыми
в исследовании факторами (факториальную
дисперсию), оценивающую межгрупповую
изменчивость, и дисперсию, обусловленную
остальными, неорганизованными в данном
исследовании факторами (внутригрупповую,
или случайную, дисперсию) отклонения
отдельных значений от средней в группе.
Общая
вариация (сумма квадратов) признака
рассчитывается как сумма квадратов
отклонений всех вариант (xi)
от общей средней (M):
Собщ.
= Σ
(xi
− M)².
Факториальная
(межгрупповая, межвыборочная) сумма
квадратов рассчитывается как сумма
квадратов отклонений частных средних
(Mi)
для каждой выборки (всего k
выборок) от общей средней:
Сфакт.
= Σ
(Mj
− M)².
Остаточная
(случайная, внутригрупповая) сумма
квадратов есть сумма квадратов отклонений
вариант каждой выборки (xi)
от своей средней (Mj):
Сслуч.
= Σ
(xi
−
Mj)².
Очевидно, что
в общем
комплексе наблюдений должно выполняться
равенство Собщ.
= Сфакт.
+ Сслуч.
Отношение
сумм квадратов к соответствующему числу
степеней свободы дает оценку величины
дисперсии, или средний квадрат, иногда
ее именуют варианса. Влияние изучаемого
фактора отражает факториальная, или
межгрупповая, дисперсия
S²факт.,
а влияние случайных неорганизованных
в данном исследовании причин – случайная
S²случ.,
или внутригрупповая, остаточная дисперсия
S²остат.:
,
где dfфакт.
= k − 1,
j
= 1, 2, …, k,
k
– число сравниваемых средних.
,
где df
случ.
= n − 1,
i
= 1, 2, …, n,
n
– число вариант всех выборок.
Сила
влияния фактора определяется как доля
частной суммы квадратов в общем
варьировании признака. Показатель силы
влияния изучаемого фактора составляет:
η² факт. = Сфакт. / Собщ.,
неорганизованных
(случайных): η² случ. = Сслуч. /
Собщ.;
сумма
этих показателей, естественно, равна
единице: η² факт. +
η² случ.
= 1. Заметим,
что показатель силы влияния дисперсионного
комплекса есть не что иное, как квадрат
пирсоновского корреляционного отношения,
которым и оценивается относительная
доля влияния организованного (изучаемого)
фактора в общем суммарном статистическом
влиянии всех факторов, определяющих
развитие данного результативного
признака.
О достоверности
оценок влияния факторов судят по уже
знакомому нам критерию Фишера:
~ F(α,
df1,
df2),
где
df1
= k − 1,
df2
=
n − k,
k
– число градаций,
n – общий
объем всех выборок.
Проверяется
нулевая гипотеза: «влияние фактора на
признак отсутствует». Влияние считается
доказанным, если величина расчетного
критерия равна или превышает свое
табличное значение с принятым уровнем
значимости (обычно α = 0.05)
(F
определяется по табл. 7П).
Все параметры однофакторного дисперсионного
анализа и порядок их вычислений
представлены в таблице 8.
Таблица 8
|
Составляющие |
Суммы |
Сила влияния, η² |
Степени df |
Дисперсии
(средний S² |
Критерий F |
|
Факториальная |
Сфакт.
Σ |
|
k − 1 |
S²
= |
F = |
|
Случайная |
Сслуч.
Σ |
n − k |
S²случ. =
= |
|
|
|
Общая |
Собщ.
Σ |
Однофакторным
называется анализ, изучающий действие
на результативный признак только одного
организованного фактора А.
Для примера оценим влияние растворенного
в воде вещества на плодовитость
дафний, используемых в качестве
тест-объектов в водно-токсикологических
экспериментах. В ходе предварительного
исследования были получены четыре
выборки, четыре группы значений
плодовитости животных, выращенных в
средах с разным содержанием химической
добавки.
Сначала
необходимо сгруппировать выборочный
материал в комбинативную таблицу
(организовать дисперсионный комплекс).
Для этого варианты каждой выборки
записываются в отдельные графы, именуемые
градациями (табл. 9). Результативным
признаком служит средняя плодовитость
дафний за неделю (для иллюстративности
расчетов она дана в целых числах). В
нашем примере организованы 4
градации – чистая вода (контроль,
градация А1;
значения плодовитости 6, 5, 5, 7),
слабая концентрация вещества (5 мг/л,
А2;
8, 7, 6, 6), средняя (15 мг/л,
А3;
8, 8, 7) и сильная (30 мг/л,
А4;
8, 7, 9). Предлагаемый ниже алгоритм
расчетов позволяет использовать неравное
число вариант в градациях. Расчеты
показаны в таблице 9.
Таблица 9
|
Градации фактора |
||||||||||
|
A1 |
A2 |
A3 |
A4 |
|||||||
|
x |
x2 |
x |
x2 |
x |
x2 |
x |
x2 |
|||
|
6 |
36 |
8 |
64 |
8 |
64 |
8 |
64 |
|||
|
5 |
25 |
7 |
49 |
8 |
64 |
7 |
49 |
|||
|
5 |
25 |
6 |
36 |
7 |
49 |
9 |
81 |
|||
|
7 |
49 |
6 |
36 |
|||||||
|
Σ |
||||||||||
|
Σx² |
135 |
185 |
177 |
194 |
691 |
H1 |
||||
|
Σx |
23 |
27 |
23 |
24 |
97 |
H2 |
||||
|
n |
4 |
4 |
3 |
3 |
14 |
= |
||||
|
Σx²/n |
132 |
182 |
176.3 |
192 |
682.8 |
H3 = 682.8 |
||||
|
M |
5.8 |
6.8 |
7.67 |
8 |
6.93 |
|||||
|
Сфакт. |
||||||||||
|
Сслуч. |
||||||||||
|
Собщ. |
Полученные
значения позволяют вычислить дисперсии,
определить силу влияния фактора и
критерий достоверности Фишера.
|
Составляющие |
Суммы |
Сила η² |
Степени df |
Дисперсии, |
Критерий, |
|
Факториальная |
10.76 |
57% |
3 |
3.59 |
|
|
Случайная |
8.17 |
10 |
0.82 |
4.39 |
|
|
Общая |
18.93 |
4.39 |
Поскольку
полученное значение критерия (F
=
4.39) больше табличного (F(0.05,3,10)
=
3.7) (табл. 7П),
отличие факториальной и случайной
дисперсий достоверно, влияние фактора
значимо.
Отсюда
следует биологический вывод: стимулирующее
влияние изучаемого фактора (вещества)
на плодовитость дафний относительно
велико (57%) и достоверно (с вероятностью
Р > 0.95).
Непараметрический
однофакторный дисперсионный анализ
Рассмотренные
выше схемы дисперсионного анализа
исходили из предположения о нормальном
распределении изучаемого результативного
признака. Когда для какого-либо признака
нет уверенности, что выполняется
предположение о его нормальном
распределении, когда требуется провести
анализ быстро и без особой точности,
когда мало данных или они выражены
качественными
признаками,
можно использовать схему непараметрического
дисперсионного анализа. Этот метод
более неприхотлив, но менее точен, нежели
параметрический анализ. Он исследует
распределения вариант в нескольких
выборках. Нулевая гипотеза состоит в
том, что распределения одинаковы, т. е.
выборки взяты из одной генеральной
совокупности.
Порядок
вычислений состоит в том, что все варианты
ранжируются в порядке возрастания.
Затем суммируются ранги вариант по
каждой выборке отдельно и рассчитывается
критерий:

k − 1),
где n –
число всех вариант,
nj –
объем j—й
градации фактора,
Rj
– сумма рангов для каждой j—й
градации фактора,
k
–
число градаций фактора (j
=
1, 2, …, k).
При
объеме выборок больше 5 вариант статистика
H
имеет распределение хи-квадрат с df
= k − 1
степенями свободы и сравнивается со
значениями из табл. 9П.
Применим
эту схему (табл. 10) к нашим данным из
табл. 9, расположив их в строку.
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
Градация |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
4 |
4 |
4 |
|
Значение |
5 |
5 |
6 |
7 |
6 |
6 |
7 |
8 |
7 |
8 |
8 |
7 |
8 |
9 |
Затем
упорядочим и ранжируем их. Для нескольких
одинаковых значений берется средний
ранг.
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
Градация |
1 |
1 |
1 |
2 |
2 |
1 |
2 |
3 |
4 |
2 |
3 |
3 |
4 |
4 |
|
Значение |
5 |
5 |
6 |
6 |
6 |
7 |
7 |
7 |
7 |
8 |
8 |
8 |
8 |
9 |
|
Ранг |
1.5 |
1.5 |
4 |
4 |
4 |
7.5 |
7.5 |
7.5 |
7.5 |
11.5 |
11.5 |
11.5 |
11.5 |
14 |
Наконец,
разнесем ранги по градациям и подсчитаем
необходимые суммы.
Таблица 10
|
Градация |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
4 |
4 |
4 |
|
Значение |
5 |
5 |
6 |
7 |
6 |
6 |
7 |
8 |
7 |
8 |
8 |
7 |
8 |
9 |
|
Ранг, |
1.5 |
1.5 |
4 |
7.5 |
4 |
4 |
7.5 |
11.5 |
7.5 |
11.5 |
11.5 |
7.5 |
11.5 |
14 |
|
Сумма, |
14.5 |
27 |
30.5 |
33 |
||||||||||
|
n |
4 |
4 |
3 |
3 |
||||||||||
|
R²/n |
52.56 |
182.3 |
310.1 |
363 |
Общий
объем выборки равен n = 14.
Величина критерия H
составит:
=
0.065934∙907.8958 – 45 = 14.86.
По
таблице распределения статистики χ²
для
α = 0.05
и df
=
4 − 1 = 3 находим χ²(0.05, 3)
=
7.81. Полученное значение критерия (14.86)
больше табличного (7.81), значит, отличие
выборочных распределений достоверно.
Химическая добавка действительно
изменяет плодовитость дафний.
Двухфакторный
дисперсионный анализ количественных
признаков
Двухфакторный
дисперсионный анализ исследует влияние
на результативный признак двух факторов
как порознь, так и совместно. Учет эффекта
влияния каждого фактора по отдельности
теоретически ничем не отличается от
описанных выше схем. И там и тут оценивается
изменчивость средних по градациям на
фоне случайной изменчивости вариант
внутри градаций, с помощью критерия
Фишера устанавливается достоверность
отличий межгрупповых дисперсий от
внутригрупповых.
Двухфакторный
дисперсионный
анализ, естественно, требует более
сложных вычислительных операций, чем
однофакторный, но в принципе ничем не
отличается от описанных выше схем.
Однако это относится лишь к ортогональным
(равномерным, или пропорциональным)
комплексам, характеризующимся равной
или по крайней мере пропорциональной
численностью групп (в градациях содержатся
одинаковые или пропорциональные
числа вариант). Что же касается
неортогональных многофакторных
комплексов, то их анализ принципиально
возможен, но имеет свои особенности,
существенно усложняющие технику
вычислений, и в настоящем пособии не
рассматривается.
На практике вполне
допустим и такой способ избегнуть
сложностей обработки неравномерных
комплексов, как искусственное превращение
их в равномерные. Для этого нужно
составить выборки одинаковой или
пропорциональной численности,
используя только часть имеющихся
данных. Следует, однако, помнить, что
такой отбор не должен
быть субъективным. Чтобы не допустить
возможной тенденциозности, лучше
всего прибегнуть к жеребьевке.
Важным
преимуществом
двухфакторного дисперсионного анализа
перед однофакторным служит то, что
с его помощью удается определить
варьирование по сочетанию градаций
Ссочет.
= СAB,
позволяющее получить новый и весьма
ценный в биологическом отношении
показатель – оценку влияния сочетанного
действия (взаимодействия) факторов.
Общая
вариация (сумма квадратов) признака
теперь состоит из четырех компонентов
за счет более детального разложения
факториальной дисперсии.
Правило
разложения вариаций предстает как:
Собщ.
= СA
+
СB
+
СAB
+ Сслуч.,
Сфакт.
= Собщ.
− Сслуч.
= СA
+
СB
+ СAB.
Для расчетов
используются следующие смысловые
формулы:
Собщ.
= Σ(xi
− M)²,
СA.
= Σ(MAj
− M)²,
j
–
число градаций фактора А,
MAj
– групповые средние по градациям фактора
А,
СB
= Σ(MBk
− M)²,
k
–
число градаций фактора В,
MBk
–
групповые средние по градациям фактора
В,
Сслуч.
=
Σ(xi
−
Mxi)²,
СAB
= Собщ.
−
(СA
+
СB
+ Сслуч.).
Сочетанное
действие (взаимодействие) каждого из
двух факторов проявляется в усилении
или ослаблении непосредственного
действия другого фактора на объект
исследования. К примеру, неурожай кормов
усугубляет негативное действие зимнего
холода на численность популяций мелких
млекопитающих.
Рассмотрим
числовой пример – испытания стимулятора
многоплодия при разной полноценности
рационов. Полноценность рациона
(первый фактор) представлена двумя
градациями: A1 –
рацион с недостатком минеральных
веществ, А2 – рацион,
полностью сбалансированный по всем
питательным веществам, включая и
минеральные. Стимулятор (второй фактор)
был испытан в трех дозах: В1 – одинарная,
В2
– двойная, В3
– тройная. Результативный признак –
плодовитость самок, измерявшаяся
числом детенышей в помете. Для каждого
сочетания градаций рациона и стимулятора
были подобраны три одновозрастные
самки.
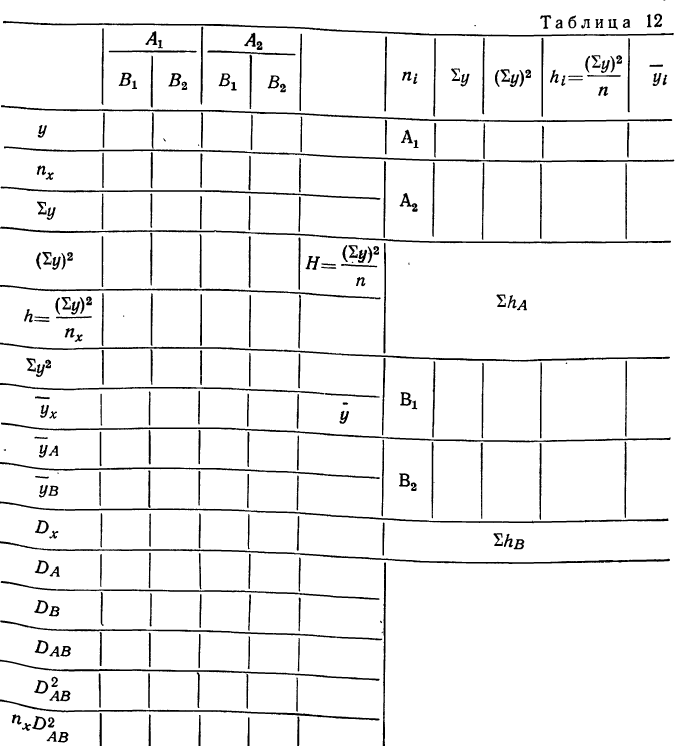
Комбинативная
таблица двухфакторного равномерного
дисперсионного комплекса с трехкратной
повторностью (ni = 3)
включает две градации по фактору А
и три градации по фактору В
(табл. 11).
Варианты размещаются по градациям,
определяется объем градации,
вычисляются суммы вариант, частные
средние, затем вспомогательные величины
(Н1,
Н2,
Н3,
НА,
НВ)
и суммы квадратов отклонений (дисперсий)
по рабочим формулам. В завершение
всего заполняют таблицу дисперсионного
анализа (табл. 12), находят показатель
достоверности влияния Фишера и,
сопоставляя его с табличным для
соответствующих степеней свободы и
принятого уровня значимости, делают
статистический вывод.
Таблица 11
|
Градации факторов |
A1 |
А2 |
Для |
B |
|||||
|
x |
x2 |
x |
x2 |
Σ |
MB |
ΣΣx²/n |
Σ(Σx²/n) |
||
|
В1 |
5 |
25 |
1 |
1 |
|||||
|
6 |
36 |
4 |
16 |
||||||
|
7 |
49 |
1 |
1 |
||||||
|
Σx² |
110 |
18 |
ΣΣx² |
||||||
|
Σx |
18 |
6 |
ΣΣx |
4 |
96 |
||||
|
n |
3 |
3 |
nB1 |
||||||
|
Σx²/n |
108 |
12 |
Σ(Σx²/n) = 120 |
||||||
|
В2 |
4 |
16 |
10 |
100 |
|||||
|
3 |
9 |
9 |
81 |
||||||
|
5 |
25 |
11 |
121 |
HB |
|||||
|
Σx² |
50 |
302 |
ΣΣx² |
Σ(Σx²/n) |
|||||
|
Σx |
12 |
30 |
ΣΣx |
7 |
294 |
= |
|||
|
n |
3 |
3 |
nB2 |
||||||
|
Σx²/n |
48 |
300 |
Σ(Σx²/n) = 348 |
||||||
|
В3 |
2 |
4 |
7 |
49 |
|||||
|
3 |
9 |
4 |
16 |
||||||
|
1 |
1 |
7 |
49 |
||||||
|
Σx² |
14 |
114 |
ΣΣx² |
||||||
|
Σx |
6 |
18 |
ΣΣx |
4 |
96 |
||||
|
n |
3 |
3 |
nB3 |
||||||
|
Σx²/n |
12 |
108 |
Σ(Σx²/n) =120 |
||||||
|
ΣΣx² |
174 |
434 |
H1 |
||||||
|
ΣΣ |
ΣΣx |
36 |
54 |
ΣΣΣx |
H2 |
(ΣΣΣx)²/N |
|||
|
nA = Σn |
9 |
9 |
N |
||||||
|
Σx²/n |
168 |
420 |
H3 |
||||||
|
MA = |
2 |
6 |
j |
||||||
|
Для |
Σx²/n |
144 |
324 |
k = |
|||||
|
A |
HA |
|
Собщ. |
|
Сслуч. |
|
Cфакт. |
|
СA |
|
СB |
|
СAB |
В нашем примере
все факториальные влияния оказались
достоверными с доверительной вероятностью
Р > 0.95
(табл. 12). Это позволяет сделать определенные
выводы относительно действия стимулятора
на плодовитость самок. Влияние каждого
фактора в отдельности (качества рациона
и дозы стимулятора) и их суммарного
эффекта достаточно существенно, но
особенно результативно действие
стимулятора в сочетании с полноценным
рационом (величина η²АВ
выше, чем
η²А
и η²В).
Более того, при недостатке в корме
минеральных веществ двукратные и
трехкратные дозы стимулятора могут
даже снизить плодовитость животных.
Таблица 12
|
Составляющие дисперсии |
Суммы С |
Сила
η² |
Степени свободы, df |
Дис-персии, |
Критерий,
F |
|
Фактор |
18 |
11 |
j |
18 |
10.8 (4.7) |
|
Фактор |
36 |
23 |
k |
18 |
10.8 (3.9) |
|
Взаимодействие |
84 |
53 |
dfA ∙ |
42 |
25.2 (3.9) |
|
Факториальная |
138 |
87 |
j∙k |
27.6 |
16.5 (3.1) |
|
Случайная |
20 |
13 |
N |
1.67 |
|
|
Общая |
158 |
100 |
N |
Таблица двухфакторного
дисперсионного анализа имеет ту же
структуру, что и таблица для однофакторного
анализа, только факториальная дисперсия
разложена на три компоненты (для факторов
А,
В
и их взаимодействия). Для каждой из них
требуется вычислить число степеней
свободы с учетом числа градаций фактора
А
(j,
количество столбцов) и числа градаций
фактора В
(k,
количество рядов),
значения дисперсий, а также критерий
Фишера. Поскольку каждому из расчетных
значений критерия соответствует свое
число степеней свободы, табличные
значения окажутся разными.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Рентабельность активов снизилась. Что повлияло сильнее: недобор по прибыли или снижение эффективности использования имущества? Себестоимость выросла. Что тому виной: увеличение материальных трат, рост зарплаты или иное? Для ответа на такие вопросы проведите факторный анализ. В статье рассказали о его этапах и показали примеры. Сможете скачать Excel-расчетчик, чтобы провести аналогичные вычисления по своим данным.
Факторный анализ: что это и зачем нужен
Факторный анализ – это оценка влияния одних показателей на другие. Например, вы хотите узнать причину снижения финансового результата. Для этого нужно посчитать, какое воздействие на него оказали доходы и расходы. Или вам важно понять, почему просела рентабельность собственного капитала. Тогда исследуйте, какой вклад в процесс внесли прибыль на рубль активов и структура пассивов.
Предлагаем скачать Excel-файл. В него встроили четыре формулы для анализа рентабельности активов, продукции и собственного капитала.
Вот три вопроса, ответы на которые понадобятся, чтобы провести подобные расчеты.
Первый. Что такое факторная модель.
Это формульная взаимосвязь между основным показателем, который вы анализируете, и теми, что на него влияют.
Откуда ее взять? Есть готовые варианты. К примеру, факторные модели DuPont для рентабельности активов и собственного капитала. Вот они:
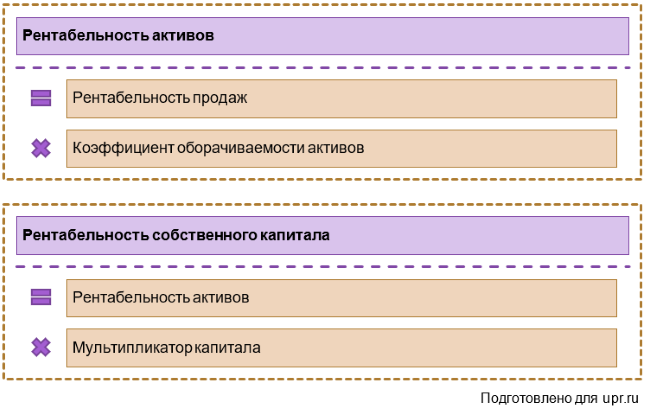
Рисунок 1. Факторные модели DuPont для рентабельности активов и собственного капитала
Можно составить зависимость самим. Иногда это несложно. Особенно, если отталкиваться от базовой формулы расчета показателя. Приведем два простых примера, основанных на таком подходе:
Рисунок 2. Примеры факторный моделей
Условимся называть искомое значение в формулах «результатом», а прочие показатели «факторами».
Второй. Почему иногда универсальной зависимости между результатом и факторами нет.
Потому что есть два типа факторного анализа:
- детерминированный;
- стохастический.
Примеры, которые привели выше, относятся к первому варианту. Их особенность в том, что взаимосвязь между показателями однозначна и работает для любой организации. Допустим, чистая прибыль выросла в два раза при неизменном значении выручки. Значит, рентабельность продаж тоже увеличится в два раза. По-другому не бывает.
Стохастический вариант предполагает: зависимость между результатом и факторами есть, но одинаково определить ее для всех компаний не получится. Например, индексация зарплаты способна поднять производительность труда работников. Но как соотносятся проценты повышения? Если заложим в расходы двукратный рост оплаты труда, то на сколько именно увеличится людская отдача? Для каждой организации ответ свой. Более того, он свой даже для одного и того же предприятия, но в разные месяцы и годы.
Чтобы не усложнять, далее в статье все сведем только к детерминированным зависимостям.
Третий. Как посчитать влияние факторов на результат.
Для этого есть специальные методы. К примеру, метод цепных подстановок, абсолютных и относительных разниц. Это не полный перечень. Но знать все необязательно. В следующих частях материала расскажем теорию про два основных подхода и покажем примеры использования.
Модели и методы факторного анализа
Начнем с видов моделей. Они – это форма взаимосвязи между факторами. Выше приводили примеры, где показатели складывались, перемножались или делились один на другой. Это и определяет вид. Смотрите на схеме четыре возможных варианта.

Рисунок 3. Модели факторного анализа: какие бывают
Теперь расскажем про методы. То есть про то, как посчитать влияние факторных показателей на результирующий. Остановимся на двух подходах:
- цепные подстановки;
- абсолютные разницы.
Первый вариант хорош своей универсальностью. Подойдет для модели любого типа.
Второй отличается чуть большей простотой вычислений, однако используется с ограничениями. Пригодится, когда анализируете мультипликативные модели или смешанные мультипликативно-аддитивные.
Схема действий для цепных подстановок такая:
- сначала подставляете в формулу значения базового периода. Так делаете для факторов и результата. Базовый период обозначим индексом 0. Это тот, что самый ранний по времени. Например, для факторного анализа изменений за 2020-2021 гг. цифры из 2020 г. – базовые;
- затем считаете первое условное значение результата. Для этого у первого фактора базовое значение меняете на отчетное. Индекс поменяется с нуля на единицу. Отчетные цифры – это величины из последнего по времени периода. В примере выше – из 2021-го;
- из полученного первого условного результата вычитаете базовый. Так находите влияние первого фактора;
- вычисляете второй условный результат. Для этого работаете со следующим фактором в модели – меняете его цифру с базовой на отчетную. Заметьте: первый фактор так и остается отчетным, его не трогаем;
- считаем разницу между вторым и первым условными результатами. Она показывает силу воздействия второго фактора;
- повторяем процесс до тех пор, пока все факторы в модели не окажутся с отчетными значениями.
Вот как это выглядит на практике:
Рисунок 4. Факторный анализ методом цепных подстановок: пример
Немного пояснений к схеме:
- значения результата называются условными потому, что в реальности компания их не достигает. Они нужны только для подсчета факторного влияния;
- условных значений на единицу меньше, чем факторов. В примере использовали трехфакторную модель. Условных результатов вышло два;
- главное – не перепутать что из чего вычитать. Сначала из первого условного вычитаем отчетную величину. Затем из второго – первое, из третьего – второе и т.д. Идем словно по цепочке от последнего к предыдущему. Отсюда и название подхода;
- для проверки правильности расчета сложите все факторные влияния. Сумма должна сравняться с изменением результата за анализируемый период. Если не получается, значит, закралась ошибка;
- главный недостаток метода – так называемый неразложимый остаток. Это взаимное влияние факторов друг на друга. Выражается в том, что оценка воздействия последнего фактора в модели всегда завышена. Причем, если поменять порядок смены базовых значений на отчетные, то станет иной и величина влияния. Например, если бы сначала меняли значения З, а не СК, то получили бы другие цифры. Это не ошибка. Это особенность, с которой в рамках цепных подстановок ничего не сделать. Если нужна повышенная точность, тогда используйте интегральный или логарифмический методы факторного анализа.
Но для них выше сложность реализации.
А вот этапы для способа абсолютных разниц:
- рассчитайте влияние первого фактора. Для этого включите в формулу его абсолютное изменение. Обозначим эту величину значком ∆. Считается как разница между отчетным и базовым значениями. Все остальные факторы должны быть с базовыми цифрами;
- определите воздействие второго фактора. Включайте в формулу его абсолютное изменение ∆. Фактор, который стоит слева от него в модели, берется с отчетным значением. Те, что находятся справа, пойдут с базовыми;
- повторите вычисления для третьего и последующих факторов, если они есть. Логика та же. Фактор, чье влияние оцениваем, включается как ∆. Стоящие от него слева как отчетные. Находящиеся справа как базовые.
Чтобы было понятнее, подготовили схему.

Рисунок 5. Факторный анализ показателя методом абсолютных разниц: пример
Согласитесь, этот подход проще, чем цепные подстановки. Все бы с ним хорошо, если бы не упомянутое выше ограничение в применении по типам моделей.
Хотя запутаться в подобных расчетах негде, однако есть смысл сделать проверку. Сложите все факторные влияния и сравните полученное с абсолютным изменением результата за период. Если сходится, значит, все правильно.
Как провести факторный анализ: пример
Теперь закрепим написанное расчетами для реальной компании. Понадобится ее финансовая отчетность. А еще нужно определиться с моделями.
Будем основываться на цифрах из баланса и отчета о финансовых результатах за 2021 г. для ПАО «КАМАЗ». Воспользуемся четырьмя факторными моделями. Их формулы показали на схеме. Первая и последняя – это простая и расширенная формулы DuPont.
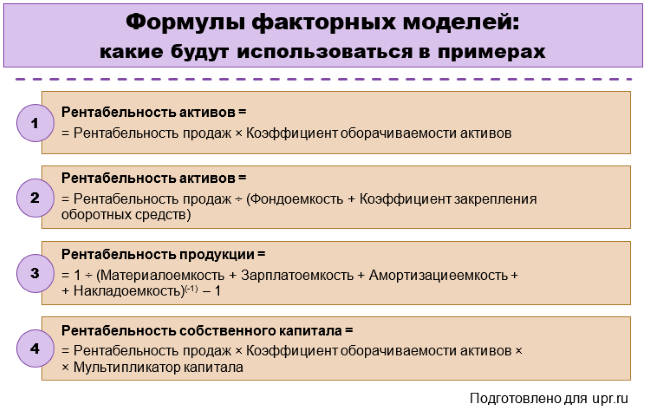
Рисунок 6. Формулы факторный моделей, которые используются в примерах
Анализируем рентабельность активов по двухфакторной модели
Исходные данные и расчетные значения свели в таблицу. Так как модель мультипликативная, то применили способ абсолютных разниц.
|
Показатель, млн руб. (если не указано иное) |
2019 (0) |
2020 (1) |
Абсолютное отклонение (∆) |
|
Исходные данные: |
|||
|
– активы на начало года |
179 083 |
188 522 |
× |
|
– активы на конец года |
188 522 |
212 292 |
× |
|
– выручка |
160 816 |
185 868 |
× |
|
– чистая прибыль (убыток) |
-1 546 |
1 545 |
× |
|
Расчетные значения: |
|||
|
– рентабельность (убыточность) активов (Ра), % |
-0,84 |
0,77 |
1,61 |
|
– рентабельность (убыточность) продаж (Рп), % |
-0,96 |
0,83 |
1,79 |
|
– коэффициент оборачиваемости активов (Коа), ед. |
0,87 |
0,93 |
0,05 |
|
Факторное влияние на рентабельность активов, %: |
|||
|
– рентабельности продаж ∆Ра(Рп) = ∆Рп × Коа0 |
1,57 |
× |
|
|
– оборачиваемости активов ∆Ра(Коа) = Рп1 × ∆Коа |
0,04 |
× |
|
|
– суммарное ∆Ра = ∆Ра(Рп) + ∆Ра(Коа) |
1,61 |
× |
Суммарное влияние факторов 1,61 соответствует абсолютному изменению рентабельности активов за 2019-2020 гг. Значит, ошибки в расчетах нет. Есть смысл перейти к анализу цифр. Вот краткие выводы:
- за год предприятие ушло от убыточности активов к их рентабельности. В чем главная причина? Во влиянии рентабельности продаж. За счет нее показатель прирос на 1,57%. Она характеризует, сколько чистого финансового результата содержится в одном рубле выручки. Когда увеличивается, это означает: доходы компании прирастают быстрее, чем расходы. Так происходит за счет оптимизации последних, грамотной ценовой политики, стабильного спроса на продукцию предприятия;
- оборачиваемость ресурсов тоже внесла положительный вклад в изменение рентабельности активов. Правда, он в разы меньше – 0,04. Выходит, с точки зрения управления имуществом предприятию есть куда расти. В 2020-м прирост выручки с каждого рубля, вложенного в активы, оказался всего 5 копеек. Отлично, что он был. Однако, возможно, стоит поискать резервы для дальнейшего улучшения ситуации.
Анализ по первой модели рассказал о трех особенностях функционирования компании:
- в 2020-м она попала в зону чистой прибыли за счет оптимального соотношения между совокупными доходами и расходами;
- в этом же году немного выросла эффективность управления активами или ресурсоотдача;
- вместе эти факторы определили рост рентабельности активов на 1,57%.
Оцениваем рентабельность активов по трехфакторной модели
По проведенным расчетам заметили: доходная отдача от активов у ПАО «КАМАЗ» не столь велика. Посмотрим, какая их составляющая «проседает» в этом отношении особенно сильно. Поможет трехфакторная модель. Цифры по ней находятся в таблице. Для определения факторного влияния применили способ цепных подстановок, так как абсолютные разницы для модели данного смешанного типа не подходят.
|
Показатель, млн руб. (если не указано иное) |
2019 (0) |
2020 (1) |
Абсолютное отклонение (∆) |
|
|
Исходные данные: |
||||
|
– внеоборотные активы на начало года |
86 445 |
102 759 |
× |
|
|
– внеоборотные активы на конец года |
102 759 |
120 946 |
× |
|
|
– оборотные активы на начало года |
92 638 |
85 763 |
× |
|
|
– оборотные активы на конец года |
85 763 |
91 346 |
× |
|
|
Расчетные значения: |
||||
|
– рентабельность (убыточность) активов (Ра), % |
-0,84 |
0,77 |
1,61 |
|
|
– рентабельность (убыточность) продаж (Рп), % |
-0,96 |
0,83 |
1,79 |
|
|
– фондоемкость (Фе), руб./руб. |
0,59 |
0,60 |
0,01 |
|
|
– коэффициент закрепления оборотных средств (Кз), руб./руб. |
0,55 |
0,48 |
-0,08 |
|
|
Факторное влияние на рентабельность активов, %: |
||||
|
– рентабельности продаж ∆Ра(Рп) = Рп1 ÷ (Фе0 + Кз0) – Рп0 ÷ (Фе0 + Кз0) |
1,57 |
× |
||
|
– фондоемкости ∆Ра(Фе) = Рп1 ÷ (Фе1 + Кз0) – Рп1 ÷ (Фе0 + Кз0) |
-0,01 |
× |
||
|
– коэффициента закрепления оборотных средств ∆Ра(Кз) = Рп1 ÷ (Фе1 + Кз1) – Рп1 ÷ (Фе1 + Кз0) |
0,05 |
× |
||
|
– суммарное ∆Ра = ∆Ра(Рп) + ∆Ра(Фе) + ∆Ра(Кз) |
1,61 |
× |
||
Знаки влияния фондоемкости и закрепления оборотных средств показывают, какая именно часть активов в 2020-м использовалась менее эффективно. Минус у Фе говорит, что это внеоборотные активы. Почему так? Потому что их стоимостное увеличение обогнало прирост выручки. Выходит, чтобы заработать 1 руб. дохода от основной деятельности в 2020-м требовалось больше зданий, оборудования, транспорта и т.п.
В отношении оборотных активов ситуация иная: они тоже увеличились, но выручка приросла значительнее. Выходит, отдача с каждого вложенного в них рубля стала больше.
Мы показываем пример общего анализа, поэтому на частностях не останавливаемся. В реальной же практике они должны быть. Например, разумно посмотреть, какие именно составляющие внеоборотных активов стали использоваться менее эффективно. Для этого рассчитываются значения фондоемкости по отдельным составляющим долгосрочного имущества. Затем принимается решение: насколько разумно сохранять и приумножать объемы подобных активов, если отдача от них падает и тормозит рост бизнеса.
Ответ на такой вопрос нельзя предсказать заранее. В каждой конкретной ситуации он будет свой. К примеру, у ПАО «КАМАЗ» в 2020-м значительно увеличились долгосрочные финансовые вложения. Это предоставленные займы на срок свыше года и участие в уставных капиталах других компаний. Они тоже относятся к внеоборотным активам. Если предприятие планирует получать от них стабильный, причем существенный доход, то их рост оправдан.
Аналогичное мнение относительно суммы вложений в имущество и ожидаемой от него доходности разумно сформулировать по каждому значимому элементу первого раздела баланса.
Выявляем влияние факторов на рентабельность продукции
Данная модель поможет понять структуру себестоимости. А еще, какой ее элемент растет скорее остальных, а потому особенно сильно «съедает» прибыль бизнеса. Расчеты привели в таблице. Влияние факторов оценивали цепными подстановками.
|
Показатель, млн руб. (если не указано иное) |
2019 (0) |
2020 (1) |
Абсолютное отклонение (∆) |
|
|
Исходные данные: |
||||
|
– материальные затраты |
110 628 |
123 404 |
× |
|
|
– расходы на оплату труда |
13 953 |
14 593 |
× |
|
|
– отчисления на социальные нужды |
4 229 |
4 451 |
× |
|
|
– амортизация |
1 471 |
1 739 |
× |
|
|
– прочие затраты |
32 590 |
42 012 |
× |
|
|
Расчетные значения, руб./руб. (если не указано иное): |
||||
|
– рентабельность (убыточность) продукции (Рпрод), ед. |
-0,012 |
0,024 |
0,036 |
|
|
– материалоемкость (Ме) |
0,687 |
0,647 |
-0,040 |
|
|
– зарплатоемкость (Зе) |
0,113 |
0,100 |
-0,013 |
|
|
– амортизациеемкость (Ае) |
0,009 |
0,009 |
0,000 |
|
|
– накладоемкость (Не) |
0,203 |
0,220 |
0,018 |
|
|
Факторное влияние на рентабельность продукции, ед.: |
||||
|
– материалоемкости ∆Рпрод(Ме) = (Ме1 + Зе0 + Ае0 + Не0)-1 – (Ме0 + Зе0 + Ае0 + Не0)-1 |
0,041 |
× |
||
|
– зарплатоемкости ∆Рпрод(Зе) = (Ме1 + Зе1 + Ае0 + Не0)-1 – (Ме1 + Зе0 + Ае0 + Не0)-1 |
0,014 |
× |
||
|
– амортизациеемкости ∆Рпрод(Ае) = (Ме1 + Зе1 + Ае1 + Не0)-1 – (Ме1 + Зе1 + Ае0 + Не0)-1 |
0,000 |
× |
||
|
– накладоемкости ∆Рпрод(Не) = (Ме1 + Зе1 + Ае1 + Не1)-1 – (Ме1 + Зе1 + Ае1 + Не0)-1 |
-0,019 |
× |
||
|
– суммарное ∆Рпрод = ∆Рпрод(Ме) + ∆Рпрод(Зе) + ∆Рпрод(Ае) + ∆Рпрод(Не) |
0,036 |
× |
||
Рентабельность продукции – это отношение операционной прибыли к расходам основного бизнеса. В 2020-м показатель увеличился на 0,036 ед. Причем за год предприятие сумело выйти из минуса в плюс.
Положительную роль в этом сыграло то, что два значимых элемента расходов прирастали медленнее выручки. Речь про материальные траты и оплату труда с отчислениями. Амортизация никак не повлияла на изменение результативного показателя. А накладные расходы его уменьшили на 0,019.
Выходит, накладная составляющая – это то, что предприятию есть смысл изучить подробнее. Проанализировать состав, оценить оправданность отдельных элементов и причины их увеличения. Это так еще и потому, что на накладные траты у ПАО «КАМАЗ» приходится более 20% расходов по обычной деятельности. К ним относятся две группы:
- прочая составляющая расходов основного бизнеса;
- утилизационный сбор.
Первая приросла на 2,3 млрд руб. Целесообразно установить, что именно вызвало такое увеличение. Возможно, часть трат можно оптимизировать.
Второй стал больше на 7,1 млрд руб. Повлиять на эту сумму предприятие вряд ли сможет. Величина такого сбора для производителей транспортных средств определяется законодательно.
Считаем факторное воздействие для рентабельности собственного капитала
Оценим, насколько эффективно используется капитал собственников и что снижает его прибыльную отдачу. Для этого воспользуемся трехфакторной моделью DuPont. Она является мультипликативной. Поэтому для расчета влияния факторов применим способ абсолютных разниц.
|
Показатель, млн руб. (если не указано иное) |
2019 (0) |
2020 (1) |
Абсолютное отклонение (∆) |
|
Исходные данные: |
|||
|
– собственный капитал на начало года |
43 105 |
41 458 |
× |
|
– собственный капитал на конец года |
41 458 |
47 006 |
× |
|
Расчетные значения: |
|||
|
– рентабельность (убыточность) собственного капитала (Рск), % |
-3,66 |
3,49 |
7,15 |
|
– рентабельность (убыточность) продаж (Рп), % |
-0,96 |
0,83 |
1,79 |
|
– коэффициент оборачиваемости активов (Коа), ед. |
0,87 |
0,93 |
0,05 |
|
– мультипликатор капитала (МК), ед. |
4,35 |
4,53 |
0,18 |
|
Факторное влияние на рентабельность собственного капитала, %: |
|||
|
– рентабельности продаж ∆Рск(Рп) = ∆Рп × Коа0 × МК0 |
6,82 |
× |
|
|
– оборачиваемости активов ∆Рск(Коа) = Рп1 × ∆Коа × МК0 |
0,19 |
× |
|
|
– мультипликатора капитала ∆Рск(МК) = Рп1 × Коа1 × ∆МК |
0,14 |
||
|
– суммарное ∆Рск = ∆Рск(Рп) + ∆Рск(Коа) + ∆Рск(МК) |
7,15 |
× |
Чистая прибыль, отнесенная к капиталу собственников, в 2020-м стала выше на 7,15%. Это очень хорошо. Тем более, что годом ранее показатель был минусовым. Как и в случае с рассчитанными выше рентабельностью активов и продукции, главная причина такого – получение положительного финансового результата в 2020 г.
На увеличение рентабельности собственного капитала повлияли все три фактора. В наибольшей мере – рентабельность продаж. Она определила 6,82% увеличения. В наименьшей – мультипликатор капитала.
Последний считается как отношение активов к капиталу собственников. Поэтому его высокие значения и продолжающийся рост стоит рассматривать двояко. С одной стороны, все это увеличивает рентабельность. Но с другой, снижает финансовую устойчивость. Ведь, чтобы величина мультипликатора повышалась, собственный капитал должен расти медленнее, чем активы или – что то же самое по сумме – пассивы компании. При таком раскладе доля заемных источников становится больше, значит, долговая яма глубже.
Ситуация усугубляется тем, что удельный вес капитала собственников у ПАО «КАМАЗ» и так меньше нормы. В среднем составляет 22,5% при рекомендуемом значении 50%.
Итог анализа таков:
- собственные источники в 2020-м стали использоваться в разы эффективнее, так как компания получила чистую прибыль;
- наибольшее влияние на это оказало оптимальное соотношение между совокупными доходами и расходами. Именно оно определило рост рентабельности продаж и связанное с ним увеличение рентабельности собственного капитала;
- настораживает структура пассива, в котором примерно 80% приходится на долги.
Если вам нужны аналогичные расчеты по данным вашей компании, то не забудьте скачать Excel-файл из начала статьи. Он сам вычислит значения рентабельности и сделает оценку факторного влияния. Вам нужно лишь внести исходные цифры из бухгалтерской отчетности. Строки, в которых находятся требуемые значения, мы там указали.
Факторный анализ – это раскладка ситуации на составляющие и поиск ответа на вопрос: «Почему значение конкретного показателя оказалось таким, и на какой рычаг давить, чтобы переломить ситуацию в нужное русло?». Базовые подходы рассмотренного метода просты, а получаемые результаты информативны. Применяйте данный инструмент, если хотите оценить взаимосвязь между разными величинами.
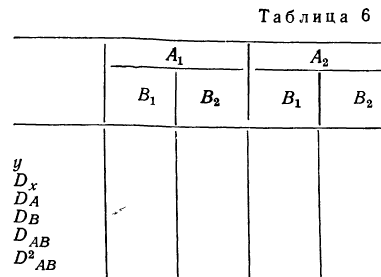
Содержание:
Сущность дисперсионного анализа:
Задачей дисперсионного анализа является изучение влияния одного или нескольких факториальных признаков на результативный признак. При этом имеется в виду, что каждый признак измерен статистически и варьирует в совокупности единиц.
Степень вариации группы единиц обычно измеряется показателями вариации: средним линейным отклонением, дисперсией, средним квадратическим отклонением и коэффициентом вариации. Определенный способ измерения и анализа вариации единиц составляет специфическую особенность дисперсионного анализа как метода изучения влияния факторов.
Применение дисперсионного анализа
При применении дисперсионного анализа требуется расчленить совокупность на группы по факториальному признаку и измерить результативный признак в каждой группе единиц. Отбор единиц в каждую группу может осуществляться методом случайной выборки (или, как ее называют в дисперсионном анализе, по принципу рэндомизации). Можно также использовать материалы проведенных ранее наблюдений. Дисперсионный анализ имеет широкое распространение в экспериментальных работах по технике и биологии. Он может быть с успехом применен и в экономических расчетах.
Дисперсия как мера вариации нам уже известна. Она представляет собой среднюю величину из квадратов отклонений всех вариантов от средней арифметической. В дисперсионном анализе принято не делить сумму квадратов отклонений на число единиц, а находить лишь сумму
Случайная дисперсия находится как сумма квадратов отклонений всех вариантов от частных средних, т. е.
Она аналогична внутригрупповой дисперсии, рассмотренной в разделе I.
Факториальная дисперсия равна сумме квадратов отклонений частных средних от общей средней: 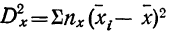
Дисперсия, исчисляемая как сумма квадратов отклонений, зависит от числа единиц в группе. Отношение факториальной дисперсии к дисперсии комплекса показывает долю вариации за счет фактора группировки и называется корреляционным отношением.
В дисперсионном анализе применяется и дисперсия, рассчитанная на одну степень свободы варьирования. В этом случае сумма квадратов отклонений делится на число степеней свободы.
Дисперсия на одну степень свободы в однофакторном комплексе составит:
Для дисперсии комплекса число степеней свободы равно числу значений варьирующего признака без одного: 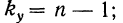
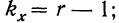
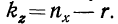
Однофакторный комплекс
Изучение методом дисперсионного анализа действия на результативный признак одного факториального признака требует расчета одного дисперсионного комплекса и называется однофакторным комплексом. Для однофакторных комплексов не требуется пропорциональности групп по их численности, так как они пропорциональны при любом соотношении частот по группам. В однофакторных комплексах вполне применимы свойства дисперсий, которые даны в разделе «Вариационные ряды и их характеристики».
Расчет однофакторного комплекса с малым числом групп может быть иллюстрирован следующим примером.
При изучении действия многих факторов заработной платы выделен один фактор — образование рабочих. Установлены 3 группы этого фактора: начальное образование, семилетнее и среднее образование. Для каждой группы было отобрано с сохранением принципа рандомизации по 3 рабочих. Заработная плата и порядок вычисления дисперсий приведен в следующей таблице:
Факториальная дисперсия 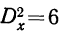
Обработаем данный однофакторный комплекс по-другому и заполним таблицу 2.
Используя свойства дисперсий и имея в виду, что в дисперсионном анализе находится не средний квадрат отклонений, а сумма квадратов отклонений, вычислим:
Влияние образования на вариацию заработной платы рабочих находится из корреляционного отношения:
Влияние прочих факторов определится другим корреляционным отношением:
Сумма этих двух корреляционных отношений должна быть равна 1:
Для определения достоверности влияния данного фактора определяем величину отношения дисперсий 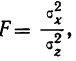
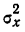
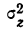
Число степеней свободы по комплексу равно 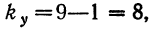
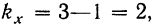
Достоверность влияния данного фактора определяется из сравнения F с некоторой стандартной величиной, исчисляемой по особой формуле, зависящей от числа степеней свободы для факториальной и случайной дисперсий. Таблица стандартных величин дана в приложении IX и определена для вероятностей 0,95 и 0,99. Если F окажется больше стандартного отношения, то вывод о наличии зависимости, основанный на дисперсионном анализе, считается обоснованным; если же F меньше любого стандартного значения, то вывод является необоснованным.
В данном примере дисперсии на одну степень свободы составят:
Определив величину F по эмпирическим данным, найдем по таблице стандартных отношений дисперсий стандартное F, зная, что число степеней свободы по фактору 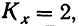
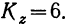
Следовательно, величина F меньше любого из стандартных отношений и вывод о значительном влиянии фактора образования нельзя считать обоснованным.
Для групп, имеющих большое число единиц, расчет дисперсионного однофакторного комплекса производится по корреляционной таблице.
Корреляционная таблица составляется по правилам, применяющимся при расчетах коэффициента корреляции и корреляционного уравнения. Однако обработка корреляционной решетки проводится особым способом, специфичным для дисперсионного анализа. Для этого к корреляционной таблице приписывается четыре строки и три столбца.
В первой приписанной строке, как и в любой корреляционной таблице, записываются суммы по столбцам, во второй строке— суммы произведений частот на отклонения 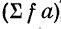
В первом приписанном столбце записываются суммы частот. Во втором и третьем столбцах находятся суммы накопленных частот. Все эти расчеты приведены в следующей таблице, где рассматривается зависимость объема ампул (у) от их диаметра (k). Вместо абсолютных величин у взяты отклонения:
Рассчитываем характеристики:
По величине корреляционного отношения 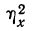
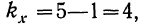
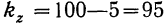
свободы:
Затем вычисляем отношение:
В таблице стандартных значений F при данных числах свободы 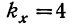
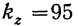
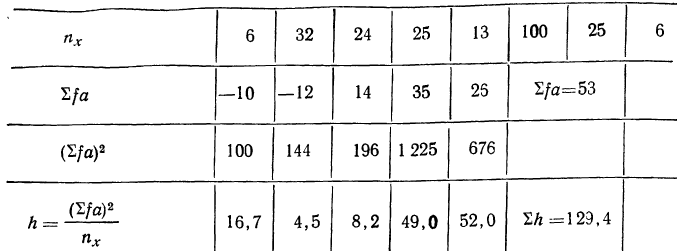
Двухфакторный комплекс
При анализе влияния двух факторов на результативный признак решается двухфакторный комплекс. Решение двухфакторного комплекса отличается от решения однофакторного комплекса. При этом имеется в виду, что факторы независимы друг от друга.
Решение двухфакторного комплекса облегчается при пропорциональной численности единиц в группах.
Если изучается действие двух факторов А и В на результативный признак, то каждый фактор делится на группы по фактору А, которые в свою очередь делятся на подгруппы по фактору В.
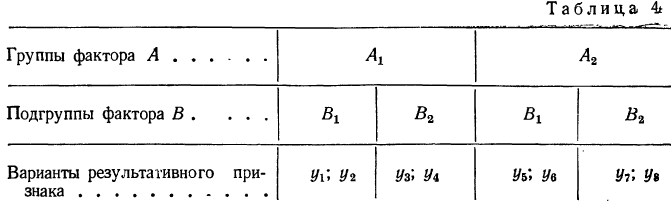
Фактором А, например, является количество внесенных удобрений в почву, а фактором В — глубина вспашки. Оба фактора влияют на результативный признак — урожайность. Пусть даныг две группы фактора А, каждая из которых разбивается на подгруппы по фактору В. Результат группировки дан в таблице.
Каждый результативный признак имеет два значения. Следовательно, для каждой подгруппы было отобрано по 2 единицы изучаемой совокупности.
Анализ двухфакторного комплекса ответит на два вопроса:
- каково суммарное действие обоих факторов;
- как велико значение каждого фактора в отдельности и какова роль сочетания факторов.
Проще всего в этом случае предположить, что действует один фактор, распадающийся по сочетанию признаков на 4 группы (общее число подгрупп).
Тогда расчет будет вестись по схеме однофакторного комплекса. Для этого вычислим:
- общую дисперсию
- факториальную дисперсию
- случайную дисперсию
- степень влияния объединенных факторов А и В:
- определим достоверность влияния объединенных факторов, для чего вычислим:
Однако еще не выяснено действие каждого из факторов и различие их совместного действия в разных комбинациях групп и подгрупп. Для этого решается двухфакторный комплекс, где сначала находятся общая и случайная дисперсии и дисперсии суммарного действия (как и в однофакторном комплексе), а затем частные факториальные дисперсии.
Частные факториальные дисперсии находятся так. Дисперсия по фактору А измеряется вариацией частных средних по
группам фактора A 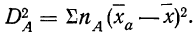
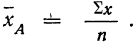
Запишем расчет дисперсии по фактору А в табл. 5.
Аналогично вычисляются дисперсии по фактору В. Дисперсия по сочетаниям признаков 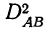
Способы определения 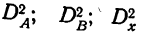
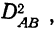
Для определения дисперсии 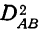
Здесь D является первой степенью отклонений. 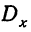
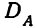
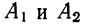
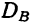
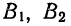
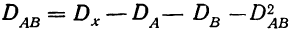
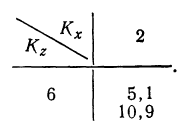
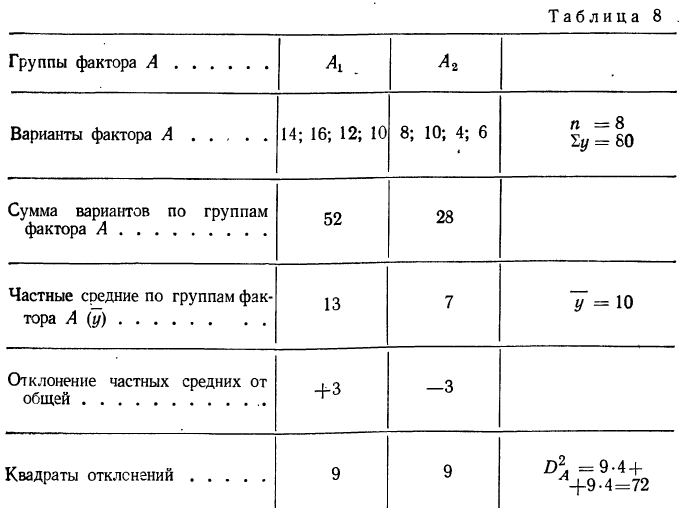
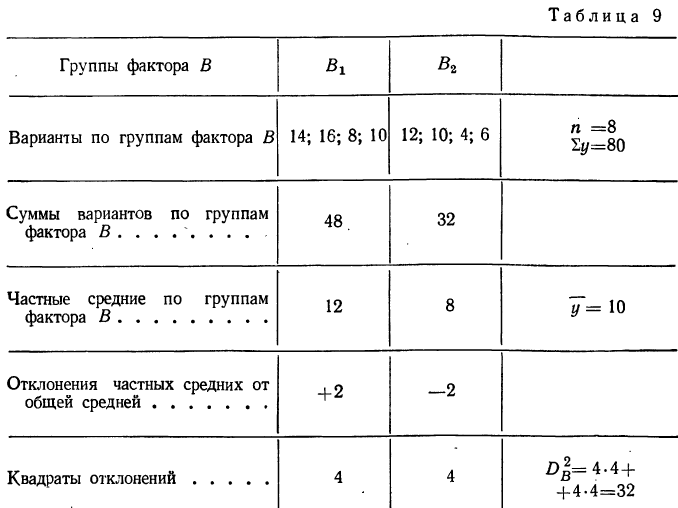
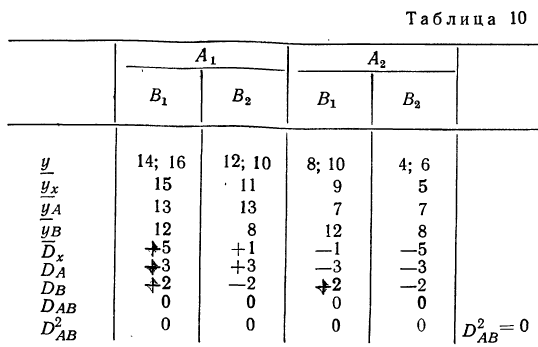
Разберем изложенное на конкретном примере. Методом дисперсионного анализа изучается влияние внесенных удобрений (факторов А) и глубины вспашки (факторов В) на урожай (у) (см. табл. 7). По фактору А взяты 2 группы участков: хорошо удобренные и мало удобренные.
По фактору В также 2 группы: с глубокой вспашкой и с мелкой. В каждую группу отобрали методом рэндомизации (случайной выборки) по 2 участка, которые имели следующую урожайность (у): 14; 16; 12; 10; 8; 10; 4; 6.
Общая дисперсия 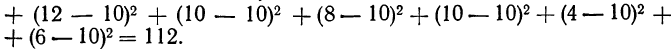
Факториальная дисперсия суммарного действия факторов определяется по формуле: 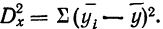
Случайная дисперсия выразится:
Вычислим частную факториальную дисперсию по фактору А.
Отношение 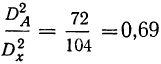
Отношение 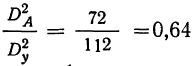
Влияние фактора В в суммарном влиянии факторов А и В составит 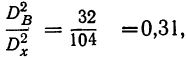
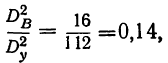
Вычислим дисперсию по сочетанию факторов АВ, т. е. дисперсию 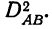
Находим число степеней свободы и определяем дисперсии на одну степень свободы для рассмотрения достоверности влияния факторов.
Для общей дисперсии число степеней свободы равно:
для случайной дисперсии
Проверяем, чтобы
В нашем примере:
Дисперсии на одну степень свободы составят.
Определим величину F для каждой дисперсии. Для этого делим каждую факториальную дисперсию на случайную.
Сравниваем каждое отношение дисперсий F со стандартными величинами, данными в таблице, учитывая число степеней свободы обеих взятых дисперсий.
Для фактора A 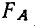
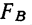
Для суммарного действия факторов сравниваем 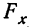
Используя свойства дисперсии, можно составить упрощенную схему расчета двухфакторного комплекса. При этом расчет общей дисперсии 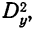
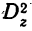
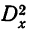
Тогда
где 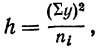
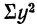
Дисперсии по факторам А и В, а также дисперсию по сочетанию факторов АВ находим по тем же формулам. Так, дисперсия по фактору A 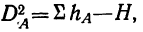
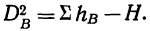
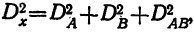
Вычислим дисперсии по факторам А и В для приведенного выше примера.
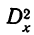
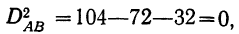
Расчет двухфакторного комплекса при большом числе наблюдений ведется по корреляционной таблице по той же схеме, как и для однофакторного комплекса. Дисперсии можно находить по способу сумм по формулам:
где 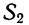
Исследование продолжаем далее по общей схеме дисперсионного анализа.
Анализ дисперсий трехфакторного комплекса ведется по тому же принципу, что и двухфакторного комплекса, только в этом случае будет 3 дисперсии по факторам 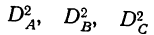
Непропорциональные комплексы
Непропорциональными называются дисперсионные комплексы, в которых не соблюдается пропорциональность численностей вариантов.
В непропорциональных дисперсионных комплексах дисперсия суммарного действия факторов не равна сумме дисперсий по факторам и дисперсии сочетания факторов. Между этими дисперсиями существует следующая связь:
где 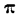
Для пропорциональных комплексов 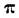
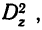
При решении непропорциональных комплексов создаются затруднения не только при отыскании дисперсий, но также при определении степени влияния каждого фактора, так как сумма частных влияний не равна суммарному влиянию. Влияние каждого фактора определяется при помощи соответствующего корреляционного отношения.
В непропорциональных комплексах общее корреляционное отношение не состоит из суммы частных корреляционных отношений, так как имеется еще слагаемое it, которое не имеет реального смысла и носит условный характер.
Чтобы определить, как влияет каждый из факторов в непропорциональном комплексе, необходимо иметь единую структуру комплекса.
Одним из способов приведения непропорционального комплекса к единой структуре является способ его замены пропорциональным комплексом, в котором частоты осереднены по группам. Когда такая замена произведена, комплекс решается по принципам пропорциональных комплексов в отношении 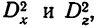
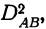
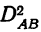
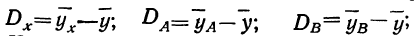
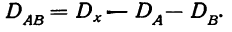
Мы не должны при этом смущаться тем обстоятельством, что сумма составляющих дисперсий 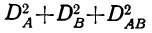
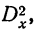
Величину дисперсии 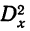
Так получается комплекс, общая часть которого совпадает с пропорциональной частью комплекса, а отношения между частными дисперсиями пропорциональны соотношениям частных дисперсий в исходном комплексе.
Схема расчета непропорционального комплекса дана в таблице 12.
Альтернативный комплекс
Если исследование методом дисперсионного анализа ведется по альтернативному признаку, в котором из n единиц у m единиц имеется данный признак, то расчет ведется несколько по-другому, чем в варьирующих комплексах.
Дисперсия альтернативного комплекса исчисляется по формуле: 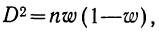
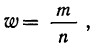
Используя свойства дисперсии приведем их к расчету по сокращенным формулам:
Расчет однофакторного альтернативного комплекса удобно вести, как показано в табл. 13, где в качестве группировочного признака выступают различные показатели одного и того же признака. Например, изучая действие режима работы (хотя бы, например, температуры) на качество продукции, мы выделяем несколько групп по этому признаку.
Определение достоверности вывода ведется исходя из соответствия эмпирического F стандартному. Число степеней свободы определяется по формулам: для общей дисперсии 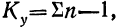
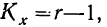
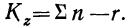
Расчет двухфакторного альтернативного комплекса ведется в общей части по тем же правилам и схемам, что и в однофакторном альтернативном комплексе. Расчет же частных дисперсий 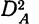
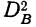

Используя данные табл. 14, будем иметь все необходимое для расчета дисперсий 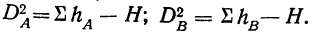
Достоверность вывода определяется методами, известными из предыдущего изложения.
При помощи дисперсионного анализа сравниваются также средние величины по группам комплекса и устанавливается достоверность разности между ними. Однако изложение этих методов не входит в нашу задачу.
- Математическая обработка динамических рядов
- Корреляция — определение и вычисление
- Элементы теории ошибок
- Методы математической статистики
- Теория статистической проверки гипотез
- Линейный регрессионный анализ
- Вариационный ряд
- Законы распределения случайных величин
Ни одна компания не может обойтись без такого аналитического инструмента, как факторный анализ. Не важно, имеет ли бизнес миллионы прибыли или убытки — важно понимать, какие факторы оказали влияние на появления прибыли или убытка. Почему статья называется Факторный анализ простым языком? Почему именно простым?
Например, Википедия определяет факторный анализ как “многомерный метод, применяемый для изучения взаимосвязей между значениями переменных”. Отлично, только что делать, если мы только начинаем постигать азы аналитики в целом и факторного анализа в частности? Именно поэтому в данной статье рассмотрен самый простой пример факторного анализа на примере 3-х магазинов одной сети.
Мы проведем факторный анализ показателей реализации продукции, т.е. товарооборота, валовой прибыли и себестоимости складских запасов в разрезе трех магазинов компании и определим, как каждый из магазина в том или ином случае повлияли на общий результат компании. Таким образом, магазин будет являться фактором, который влияет на общий результат работы компании.
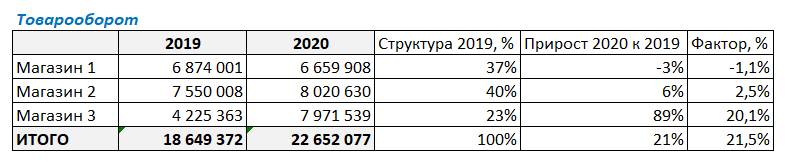
Факторный анализ пример расчета по продажам
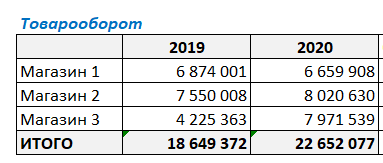
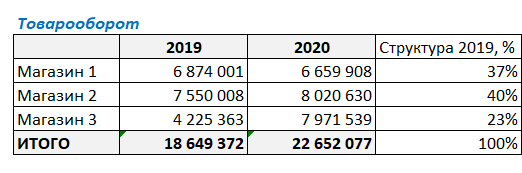
Имеем такую таблицу, в которой показаны суммы продаж за 2019 и 2020 годы по трем магазинам сети.
Как видите, товарооборот в 2020 году изменился по отношению к 2019 г. во всех магазинах. У кого-то уменьшился, у кого-то увеличился. И нужно понять, насколько изменение товарооборота конкретного магазина повлияло на общий результат деятельности компании.
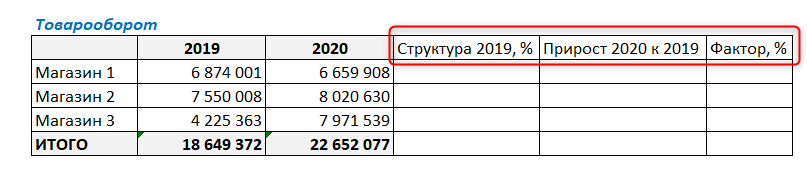
Для этого добавим в таблицу следующие столбцы:
Для начала нашего факторного анализа посчитаем структуру товарооборота в 2019 году. Структура будет показывать долю каждого магазина в суммарных продажах за 2019 год.
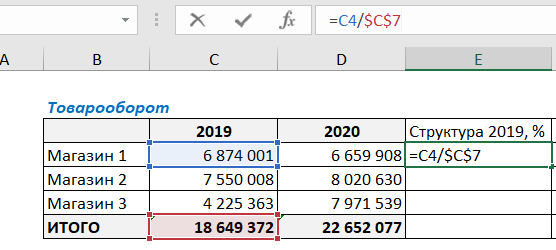
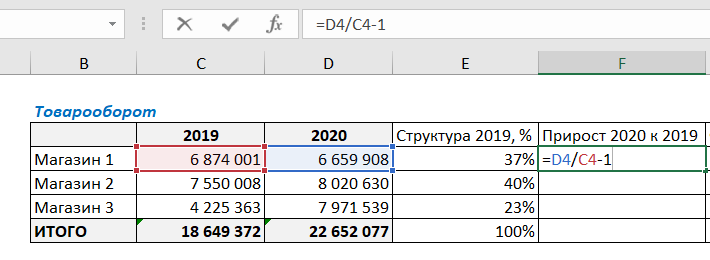
Для этого в ячейку Е4 введем следующую формулу:
Нужно поделить продажи Магазина 1 на общую сумму продаж. Не забудьте закрепить значение итоговой ячейки C7 в формуле знаками $ ($C$7). Закрепить значение ячейки можно, установив курсор на C7 и нажав клавишу F4 (подробнее об абсолютных и относительных ссылках в *статье*). Это нужно для того, чтобы ссылка на итоговую ячейку не съехала при протягивании формулы вниз.
Для полученного результата выберем процентный формат ячейки и протянем формулу вниз:
На данном этапе факторного анализа видим, что наибольший вклад в товарооборот компании за 2019 г. внес Магазин 2 — 40%. В итоговой ячейке нужно просуммировать получившиеся проценты, сумма обязательно должна быть равна 100% — это значит, что все посчитано верно.
Далее в ячейке F4 посчитаем прирост продаж 2020 года к 2019. Для этого разделим сумму продаж за 2020 г на сумму за 2019 и отнимем единицу (стандартная формула для расчета изменения показателя).
Протянем формулу вниз, захватывая итоговую строку, и увидим, что продажи в 2020 г. в целом по компании выросли на 21% по отношению к предыдущему году. Также видим изменение товарооборота в каждом из магазинов.
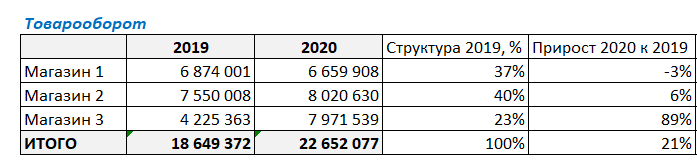
И в завершении данного этапа факторного анализа нужно умножить долю магазина на прирост продаж. Для этого в ячейке G4 напишем следующую формулу:
Протянем формулу вниз до итоговой ячейки.
Что же можно увидеть из итоговых результатов факторного анализа по товарообороту?
В целом товарооборот, вырос на 21,5% (выведем десятые доли для наглядности). И эти 21,5% складываются из следующих составляющих (факторов):
Фактор “Магазин 1” дал -1,1 % прироста в изменении товарооборота компании (т.е. падение товарооборота, т.к. прирост отрицательный)
Фактор “Магазин 2” для 2,5 % прироста из 21%.
А вот Фактор “Магазин 3” дал 20,1% прироста в составе группы магазинов, и аж 89% по отношению к собственным продажам в предыдущем году.
В итоге:
-1,1% + 2,5% + 20,1% = 21,5%
Таким образом, этот простой пример факторного анализа показывает, что максимальный вклад в прирост товарооборота сделал фактор “Магазин 3”.
Но не будем останавливаться на достигнутом, т.к. нам, во-первых, нужно понять, так ли на самом деле успешен Магазин 3 (ведь конечной целью бизнеса является получение прибыли, а не выручки), а во-вторых, понять, чем можно объяснить такой большой прирост продаж по данному магазину и падение продаж по Магазину 1.
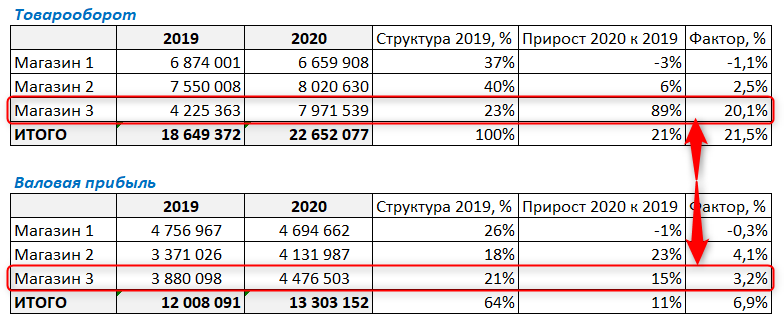
Факторный анализ по операционной прибыли
Что такое операционная прибыль, можно прочитать в статье Что такое прибыль. Виды прибыли
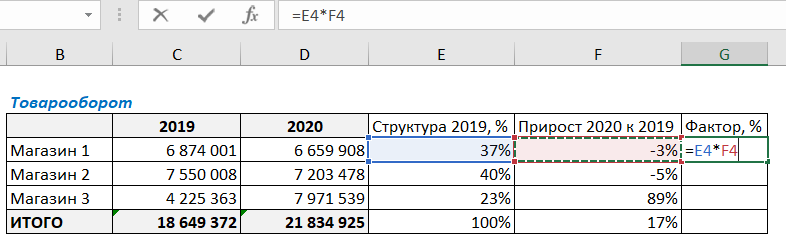
Факторный анализ по операционной прибыли проведем по тем же этапам, что и анализ по продажам. Используем те же дополнительные столбцы и такие же формулы (их можно даже скопировать).
В итоге видим, что Магазин 3, который показывал головокружительный рост выручки, по операционной прибыли уже не такой успешный.
О чем это может говорить? О том, что нужно проводить дополнительный анализ факторов, которые могли повлиять на операционную прибыль. В данном случае в Магазине 3 сильно увеличились издержки (намного сильнее, чем выросла выручка), и при дополнительном анализе нужно понять, какие именно это издержки. Возможно, значительно увеличился штат сотрудников или арендуемая площадь, и т.д.
Магазин 2 показал рост прибыли больше, чем рост выручки. Это может говорить о том, что данный магазин снизил издержки (например, сократился штат сотрудников).
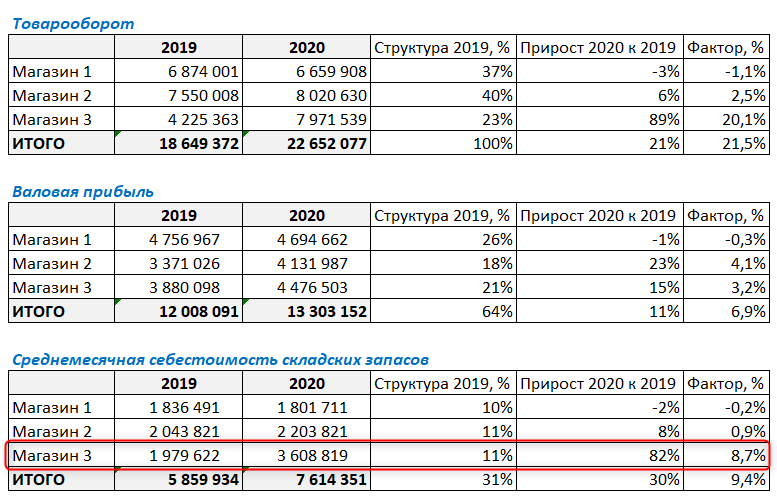
Факторный анализ пример расчета по себестоимости складских запасов
Дополнительно можно провести факторный анализ складских запасов. Это нужно, чтобы понять, за счет чего изменяется выручка.
Проделаем те же шаги, что и на предыдущих двух этапах.
Видим, что у Магазин 3, который показал высокий рост выручки и совсем небольшой рост операционной прибыли, очень сильно выросла сумма складских запасов.
Какой можно сделать предварительный вывод? Например, что Магазин 3, увидев тенденцию к росту продаж, арендовал дополнительную площадь для хранения товарных запасов. А рост выручки хоть и был достаточно высок — но меньше ожидаемого, и в итоге аренда дополнительных площадей для хранения сказалась на прибыли не лучшим образом.
Таким вот нехитрым образом можно провести простой факторный анализ. Конечно, для полноценной аналитики этого может быть недостаточно, нужно учитывать еще множество факторов и составляющих. Но для того, чтобы увидеть общие тенденции, такого простого анализа бывает достаточно.
Более подробно о факторном анализе с примерами расчета можно прочитать в статьях:
Вам может быть интересно: