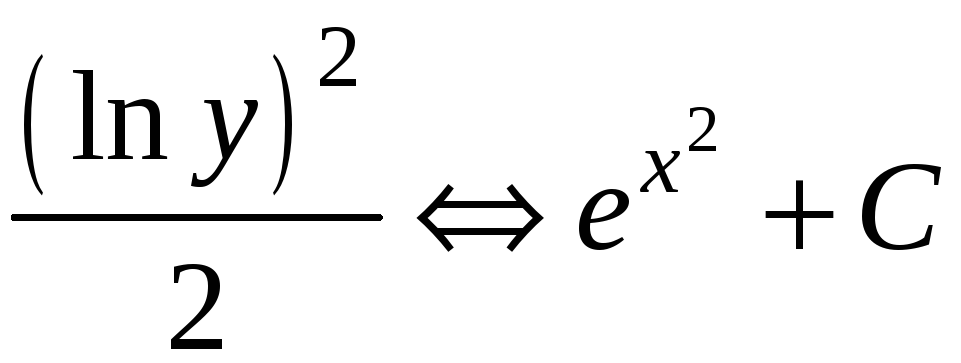Заказать задачи по любым предметам можно здесь от 10 минут
Найти общий интеграл дифференциального уравнения
Общий интеграл дифференциального уравнения записывается следующим образом $$F(x,y)=С.$$
| Пример 1 |
| Найти общий интеграл дифференциального уравнения первого порядка $$(x^2 y + y)dy = sqrt{4+y^2}dx.$$ |
| Решение |
|
Перед нами уравнение с разделяющимися переменными. То есть можно отделить $y$ от $x$ по разные стороны уравнения. Для этого видим, что можно в левой части уравнения вынести за скобку $y$. Затем разделим обе части уравнения на скобку и корень. $$y(x^2+1)dy=sqrt{4+y^2}dx,$$ $$frac{ydy}{sqrt{4+y^2}}=frac{dx}{x^2+1}$$ Теперь нужно проинтегрировать обе части уравнения. Для этого необходимо использовать таблицу интегрирования основных элементарных функций. Для правой части преобразований делать не нужно, можно сразу взять данные из таблицы. А вот левую часть нужно преобразовать в подходящий вид. Для этого выполним подведение под знак дифференциала числитель. $$int frac{d(4+y^2)}{2sqrt{4+y^2}} = arctg x + C$$ Теперь левую часть можно легко проинтегрировать, зная, что $(sqrt{x})’ = frac{1}{2sqrt{x}}$. Получаем $$sqrt{4+y^2} = arctg x + C.$$ И вот теперь мы подошли к самому главному. Вытащить $y$ из под корня или нет? Так как общий интеграл дифференциального уравнения выглядит следующим образом $F(x,y)=С$, то достаточно перенести арктангенс из правой части равенства в левую $$sqrt{4+y^2}-arctg x = C.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$sqrt{4+y^2}-arctg x = C$$ |
| Пример 2 |
| Найти общий интеграл однородного дифференциального уравнения $(x^2+y^2)dx-xydy=0$. |
| Решение |
|
Для начала убеждаемся, что уравнение однородное. Для этого подставляем $lambda$ перед всеми $x$ и $y$. Для подтверждения однородности все $lambda$ должны сократиться и уравнение примет исходный вид. $$((lambda x)^2 + (lambda y)^2) dx — lambda x lambda y dy = 0,$$ $$lambda^2 (x^2 + y^2) dx — lambda^2 xy dy = 0,$$ $$(x^2+y^2)dx — xydy = 0.$$ Далее начинаем решение уравнения с подстановки $y = tx$, $y’ = t’x+t$. Но заметим, что $y’ = frac{dy}{dx}$. Получаем $$(x^2+t^2x^2)-x^2 t (t’x+t)=0,$$ $$x^2 + t^2 x^2 — t’tx^3 — t^2 x^2=0,$$ $$x^2 — t’tx^3=0.$$ После раскрытия скобок и сокращения подобных получили дифференциальное уравнение с разделяющимися переменными. Выполняем разделение переменных $t$ и $x$ по левой и правой частям уравнения. $$t’tx^3 = x^2,$$ $$t’t = frac{1}{x},$$ $$tfrac{dt}{dx} = frac{1}{x}, $$ $$tdt = frac{dx}{x}.$$ Далее теперь можно проинтегрировать обе части уравнения. Для этого используем таблицу интегралов. $$int t dt = int frac{dx}{x},$$ $$frac{t^2}{2} = ln|x| + C,$$ $$t^2 = 2ln|x|+C.$$ Выполняем обратную замену $t = frac{y}{x}$ $$frac{y^2}{x^2} = 2ln|x|+C.$$ Так как достаточно по условию задания найти общий интеграл дифференциального уравнения, то запишем ответ в виде $$frac{y^2}{x^2} — 2ln|x| = C.$$ |
| Ответ |
| $$frac{y^2}{x^2} — 2ln|x| = C$$ |
1. Уравнения с разделяющимися переменными
Общий вид уравнений

С учетом равенства

уравнение (8.10) может быть записано в виде 
Разделим обе части на произведение функций M(x)∙Q(y) (при условии 

почленно:
исходного ДУ. Предполагая, что
подстановкой M(x)=0, Q(y)=0 в исходное уравнение сделать проверку. В том
случае, когда данные функции удовлетворяют уравнению, они также являются его решениями.
Пример 8.2. Проинтегрировать уравнение 
Решение. Представим уравнение в виде


После
применения теоремы о сумме логарифмов и потенцирования получаем

2.
Однородные дифференциальные уравнения первого порядка
Общий вид уравнений

где M(x;y) и N(x;y)– однородные функции аргументов x и y одного и
того же измерения m, то есть
имеют место равенства

Метод решения уравнения (8.12) – деление на переменную
x в
степени измерения m: 

Однородное уравнение (8.12) принимает вид: 
разделяющимися переменными. Следовательно, дальнейшее решение – по пункту 1.
Пример 8.3. Проинтегрировать уравнение 
Решение. Поделим уравнение на x2, получим
вид 



интеграл
Пример 8.4. Найти общее решение
(общий интеграл) дифференциального уравнения 
Решение. Правая часть уравнения 

уравнение является однородным дифференциальным уравнением первого порядка.
Совершим замену 
функция от аргумента x. Отсюда



После
интегрирования обеих частей уравнения получаем


Потенцируя,
находим 
Итак,
общий интеграл исходного уравнения приобретает вид cy=x2+y2, где c – произвольная
постоянная
3. Дифференциальные уравнения первого порядка, приводящиеся к однородным или к уравнениям с разделяющимися переменными
Общий вид уравнений

где
При c1=c2=0 уравнение
является однородным. Рассмотрим два случая при c1 и c2 не равных нулю одновременно.
1) Определитель

В результате данной подстановки уравнение (8.15)
становится однородным.
Пример 8.5. Найти общее решение
(общий интеграл) дифференциального уравнения 
Решение. Определитель 
решаем систему уравнений 
использованием которых осуществляем
замену x=u–1;y=v+2, при этом 
ДУ принимает вид:

Обозначим 


С помощью формул
интегрирования (4.8) и (4.17) получаем:

Осуществим обратную
подстановку

2) Определитель




уравнению с разделяющимися переменными вида 
Пример 8.6. Найти общее решение
(общий интеграл) дифференциального уравнения

Решение. Определитель 

Исходное
уравнение принимает вид:


Далее 



После обратной замены получим: 
исходного уравнения
4.
Линейные дифференциальные уравнения первого порядка
Общий вид уравнений

где
P(x) и Q(x) –
заданные функции (могут быть постоянными).
Уравнение (8.16) может быть решено двумя способами.
1) Метод Бернулли-Фурье состоит в том,
что решение ищется в виде произведения двух неизвестных функций y(x)=u(x)∙v(x) или коротко y=u∙v, при этом 
содержать константу интегрирования c, другая функция может быть взята в частном виде при
конкретном значении константы (общее решение ДУ первого порядка должно содержать
одну константу интегрирования). Подставим выражения y и 
оно принимает вид:

Функцию v(x) подберем в частном виде так, чтобы выражение в
скобках обратилось в ноль. Для этого решим уравнение с разделяющимися
переменными 



разделяющимися переменными 


Пример 8.7. Проинтегрировать уравнение 
Бернулли.
Решение. Данное уравнение является линейным ДУ первого порядка с
функциями 
y=u∙v, где u и v – некоторые функции аргумента x. Так
как y=u∙v, 

(**)
Выберем функцию u так, чтобы выражение, стоящее в скобках, обращалось в ноль, то есть 

Полагая c=1, получим
u=cos x.
При таком выборе функции u уравнение
(**) примет вид:


заданного уравнения.
Общее решение заданного ДУ можно также получить,
пользуясь непосредственно формулой (8.18):

По условию задачи имеем: P(x)=tg x, 


получаем:

Таким образом, 
уравнения
2) Метод Лагранжа иначе называют методом вариации произвольной постоянной.
Рассмотрим сначала соответствующее линейное однородное ДУ первого порядка, то есть
исходное уравнение без правой части 
полагают постоянную c функцией c(x). После этого функцию y дифференцируют и вместе с 
уравнение. При этом получают уравнение относительно неизвестной функции c(x), отыскав
которую, подставляют ее в y – общее решение заданного линейного неоднородного
уравнения (с правой частью).
Пример 8.8. Проинтегрировать уравнение 
Лагранжа (сравни с примером 8.7).
Решение. Решим сначала соответствующее линейное однородное ДУ
первого порядка 



соответствующего однородного уравнения. Применим метод варьирования константы,
то есть предположим c=c(x). Тогда общее решение исходного линейного
неоднородного уравнения будет иметь вид: 




Подставляя найденное c(x) в y, имеем общее решение линейного неоднородного
уравнения:
5.
Уравнения Бернулли
Общий вид уравнений

При n=1 (8.19)– уравнение с разделяющимися переменными. При n=0 (8.19)– линейное ДУ.
Рассмотрим 


С помощью замены z=y–n+1
исходное уравнение становится линейным относительно функции z(x):

то есть его решение находится аналогично пункту 4. На
практике искать решение уравнения (8.17) удобнее методом Бернулли в виде
произведения неизвестных функций y=u∙v. Заметим, что y=0 – всегда является решением исходного уравнения
(8.17).
Пример 8.9. Проинтегрировать уравнение 
Решение. Заданное
уравнение является уравнением Бернулли. Положим y=u∙v, тогда 
вид:

Выберем функцию u так, чтобы выполнялось равенство:
проинтегрируем:


Тогда заданное уравнение после сокращения на u примет
вид: 

с разделяющимися переменными. Находим его общее решение:
получим:
6. Уравнения
в полных дифференциалах
6.1. Общий вид уравнений

где
левая часть есть полный дифференциал некоторой функции F(x;y), то есть 

Условие, по которому можно судить, что выражение 
дифференциалом, можно сформулировать в виде следующей теоремы.
Теорема 8.2.
Для того чтобы выражение 
производные 

области D плоскости x0y, было
полным дифференциалом, необходимо и
достаточно выполнение условия

Таким образом, согласно определению полного
дифференциала (6.6) должны выполняться равенства:

Формула (8.22) представляет собой теорему Шварца,
согласно которой смешанные производные второго порядка функции F(x;y) равны.
Зафиксируем переменную y и проинтегрируем первое уравнение из (8.23) по x, получим:

Здесь
мы применили метод вариации произвольной постоянной, так как предположили, что
константа c зависит от y (либо
является числом). Продифференцировав (8.24) по переменной y
и приравняв производную к функции N(x;y), мы получим уравнение для нахождения неизвестной c(y).
Подставив c(y) в (8.24), находим функцию F(x;y) такую, что
Пример 8.10. Решить
уравнение 
Решение. Здесь функция 
Проверим условие (8.22): 
некоторой функции F(x;y). Для ее
отыскания проинтегрируем функцию M(x;y) по
переменной x, считая y=const:

Пусть c=c(y),
тогда 
получим 

Найденное c(y) подставляем в функцию F(x;y), получаем
решение заданного ДУ:
Если условие (8.22) не выполняется, то ДУ (8.21) не
является уравнением в полных дифференциалах.
Однако это уравнение иногда можно привести к уравнению
в полных дифференциалах умножением его на некоторую функцию μ(x;y), называемую интегрирующим множителем.
Чтобы уравнение 
дифференциалах, должно выполняться условие

Выполнив дифференцирование 
слагаемые, получим: 
проинтегрировать полученное ДУ в частных производных. Решение этой задачи не
простое. Нахождение интегрирующего множителя может быть упрощено, если
допустить существование μ как функции только одного аргумента x либо
только y.
6.2. Пусть μ = μ(x). Тогда уравнение (8.25) принимает вид:

При этом подынтегральное выражение должно зависеть только от x.
6.3. Пусть
μ = μ(y). Тогда
аналогично можно получить

где подынтегральное выражение должно зависеть только
от y.
Пример 8.11. Решить
уравнение 
Решение. Здесь 

формуле (8.26) составляем подынтегральное выражение:

переменной x. Следовательно, уравнение имеет интегрирующий
множитель μ(x). В нашем
случае он имеет вид 
μ=x, получаем: 

интеграл исходного уравнения имеет вид
7. Дифференциальные уравнения, неразрешенные относительно производной
К уравнениям данного вида относятся уравнения Лагранжа и Клеро, которые образуют достаточно большой класс ДУ, решаемых методом введения параметра 
7.1.
Уравнение Лагранжа
Общий вид уравнений

где
φ
и ψ– известные функции от 

принимает вид

Продифференцируем его по x:

Полученное уравнение (8.30) является линейным уравнением относительно
неизвестной функции x = x(p). Решив
его, найдем:
x = λ(p;c). (8.31)
Исключая параметр p из уравнений
(8.29) и (8.31), получаем общий
интеграл уравнения (8.28) в
виде y = γ(x;c).
Примечание. При переходе к уравнению (8.30) мы делили на 

означает, что p0 является
корнем уравнения p = φ(p)=0 (смотри уравнение (8.30)). Тогда
решение 
является особым
7.2. Уравнение
Клеро представляет собой частный случай уравнения Лагранжа
при 

Вводим
параметр 

Продифференцируем уравнение (8.33) по переменной x:

то согласно (8.33), уравнение (8.32) имеет общее решение

При 
в параметрической форме:

(8.35)
Это – особое решение уравнения Клеро, так как оно не
содержится в формуле общего решения уравнения.
Пример 8.12.
Решить уравнение Клеро 
Решение. Согласно формуле (8.32) общее решение имеет вид y=cx+c2. Особое решение уравнения получим по (8.33) в виде

Вопросы для самопроверки
Начальные
условия
,
будучи набором из
чисел, задают точку пространства
.
Множество всех рассматриваемых вариантов
начальных условий образует некоторую
область
.
Для
различных видов ограничений на функцию
и на область
имеет место существование и единственность
решения задачи Коши для начальных
условий из
.
Приведем примеры соответствующих
теорем.
I.
Пусть уравнение 1-го порядка является
разрешённым относительно производной
:
.
Теорема 1. Если
функция
и ее частная производная
непрерывны в области
плоскости
,
то решение задачи Коши для любых начальных
условий
существует и единственно в некоторой
окрестности точки
.
II.
Пусть
уравнение
-го
порядка является разрешённым относительно
старшей производной
:
.
Теорема 2. Если
функция
и ее частные производные
непрерывны в области
-мерного
пространства
,
то решение задачи Коши для любых начальных
условий
существует и единственно в некоторой
окрестности точки
.
В дальнейшем будем
предполагать, что дифференциальные
уравнения рассматриваются в области
существования и единственности решения.
Определение.
Общим решением
дифференциального уравнения
-го
порядка называется функция
,
зависящая от аргумента
и от
произвольных постоянных
,
которая удовлетворяет двум условиям:
1) при любых значениях
произвольных постоянных эта функция
является решением;
2) за счет выбора
значений произвольных постоянных можно
получить решение задачи Коши для любых
начальных условий из области существования
и единственности решения.
Заметим, что
количество
произвольных постоянных равно порядку
уравнения.
Определение.
Частным
решением
дифференциального уравнения называется
функция, которая получается из общего
решения, если произвольным постоянным
придать определенные значения.
Напомним определение
неявной функции: функция
в окрестности
точки
,
задана неявно
уравнением
,
если при всех
из этой окрестности справедливо равенство
.
Обычное, «явное»
задание функции можно рассматривать
как частный случай неявного:
;
здесь
.
Определение.
Общим
интегралом
дифференциального уравнения
-го
порядка называется уравнение
,
(3)
зависящее от
произвольных постоянных
,
которое задает общее решение
как неявную функцию.
Определение.
Частным
интегралом
называется уравнение, которое получается
из общего интеграла (3), если произвольным
постоянным придать определенные
значения.
Замечание.
В тех случаях, когда удается найти
решение дифференциального уравнения,
оно имеет, как правило, вид общего
интеграла (3). Если при этом можно
явно выразить через
(«разрешить уравнение относительно
»),
то приходим к общему решению.
4. Метод разделения переменных
Определение.
Уравнением
с разделенными переменными называется
дифференциальное
уравнение первого порядка вида
,
(4)
с
непрерывными функциями
и
Смысл
этого термина заключается в том, что
переменные
и
разделены по разным частям равенства
(4).
Напомним,
что, согласно определению, дифференциал
функции
есть произведение производной на
дифференциал независимой переменной:
.
Если умножить обе части равенства (4) на
,
получим:
.
(5)
Это
другой, более традиционный способ записи
уравнения с разделенными переменными.
Теорема.
Если в уравнении (5) функции
и
имеют первообразные
и
,
то общий интеграл уравнения имеет вид:
,
(6)
где
—
произвольная постоянная.
Замечание.
Если для обозначения первообразных
использовать символ неопределенного
интеграла, то общий интеграл записывается
в виде:
.
(7)
Доказательство.
Опуская доказательство того, что
уравнение (6) действительно задает
неявную функцию
,
убедимся, что
удовлетворяет уравнению (4). Для этого
продифференцируем по
равенство (6), применяя для левой части
правило производной сложной функции с
промежуточной переменной
:
,
или,
учитывая, что
и
первообразные для
и
:
.
Остается
убедиться, что за счет выбора значения
произвольной постоянной
можно обеспечить выполнение любых
начальных условий
.
Подставляя начальные условия в (6),
получаем:
.
▄
Примеры.
1. Для уравнения
найдем общий интеграл и частный интеграл
для начальных условий

Имеем:
—
это
общий интеграл.
Подставим
теперь в общий интеграл начальные
условия и найдем соответствующее
значение константы
:

Следовательно,
частный интеграл, дающий решение задачи
Коши, имеет вид:
.
2.
Рассмотрим уравнение
с начальными условиями
.
Умножая обе части уравнения на
и затем интегрируя, получаем:
– это
общий интеграл. Выражая отсюда явно
через
и
,
получаем общее решение:

Подстановка начальных условий в общее
решение дает:

так что
.
Следовательно, функция
является решением задачи Коши.
Определение.
Уравнением
с разделяющимися переменными называется
дифференциальное
уравнение первого порядка вида
,
(8)
с
непрерывными функциями
.
В
этом уравнении каждая из частей является
произведением двух множителей, один из
которых зависит только от
,
а другой – только от
.
От
этого уравнения легко перейти к уравнению
с разделенными переменными, деля обе
части на произведение
(«разделяя переменные»):

Примеры.
1.

Обе части разделим на
и умножим на
:

Интегрируем:
—
общий
интеграл.
2.
;
начальные условия:

Записываем производную
как отношение дифференциалов:

Обе
части умножим на
,
разделим на
и проинтегрируем:
—
общий
интеграл. Найдем теперь частный интеграл,
удовлетворяющий начальным условиям.
Подставляя начальные условия в полученное
уравнение, имеем:
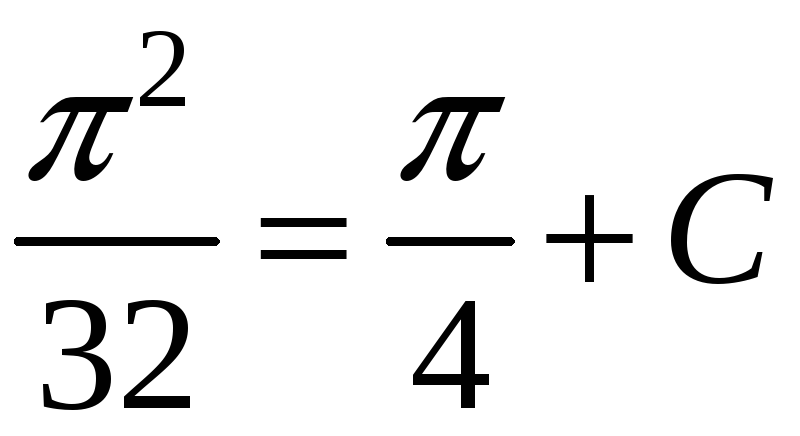

Следовательно,
частный интеграл, дающий решение задачи
Коши, имеет вид:
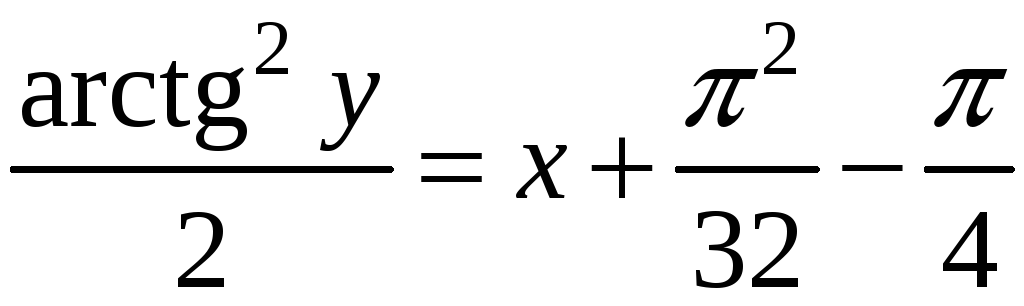
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #