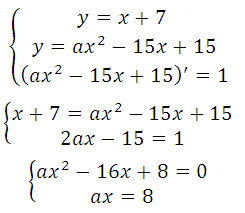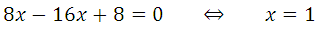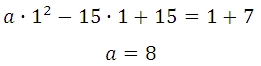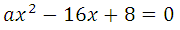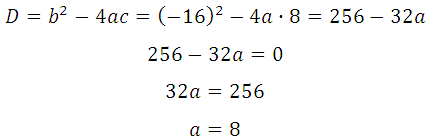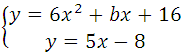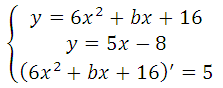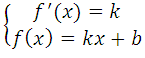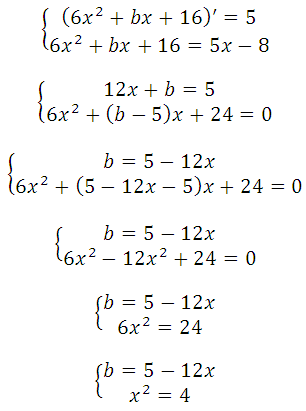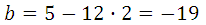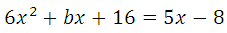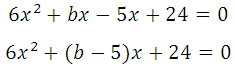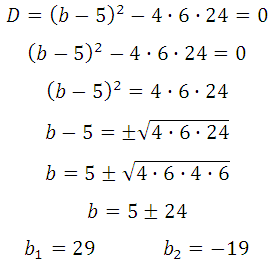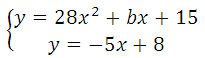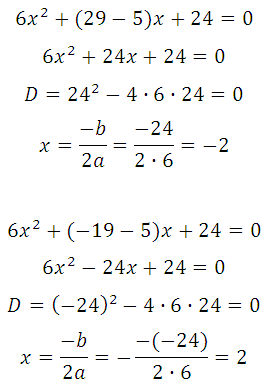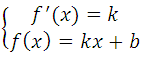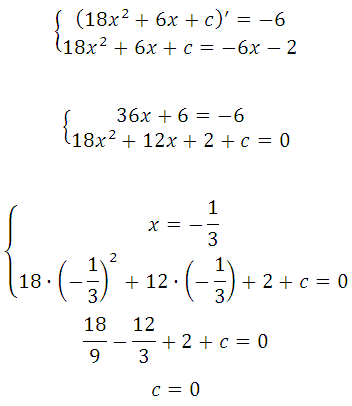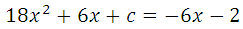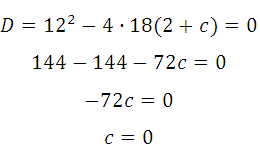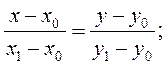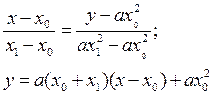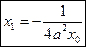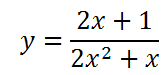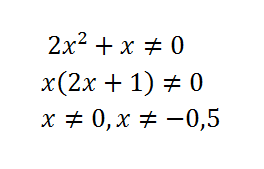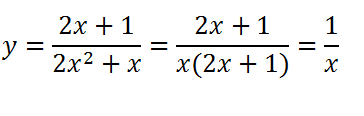Как найти общие точки прямой с графиком - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти точку пересечения прямой и параболы

Задачи по поиску точек пересечения каких-нибудь фигур идеологически просты. Сложности в них бывают только из-за арифметики, так как именно в ней допускаются различные опечатки и ошибки.

Инструкция

Данная задача решается аналитически, поэтому можно вовсе не рисовать графики прямой и параболы. Часто это дает большой плюс в решении примера, так как в задаче могут быть даны такие функции, что их проще и быстрее не нарисовать.

Согласно учебникам по алгебре парабола задается функцией вида f(x)=ax^2+bx+c, где a,b,c – это вещественные числа, притом коэффициент a отличен он нуля. Функция g(x)=kx+h, где k,h – это вещественные числа, определяет прямую на плоскости.

Точка пересечения прямой и параболы – это общая точка обеих кривых, поэтому в ней функции примут одинаковые значение, то есть f(x)=g(x). Данное утверждение позволяет записать уравнение: ax^2+bx+c=kx+h, которое даст возможность найти множество точек пересечения.

В уравнении ax^2+bx+c=kx+h необходимо перенести все слагаемые в левую часть и привести подобные: ax^2+(b-k)x+c-h=0. Теперь остается решить полученное квадратное уравнение.

Все найденные «иксы» – это еще не ответ на задачу, так как точку на плоскости характеризуют два вещественных числа (x,y). Для полного завершения решения необходимо вычислить соответствующие «игрики». Для этого нужно подставить «иксы» либо в функцию f(x), либо в функцию g(x), ведь для точки пересечения верно: y=f(x)=g(x). После этого вы найдете все общие точки параболы и прямой.

Для закрепления материала очень важно рассмотреть решение на примере. Пусть парабола задается функцией f(x)=x^2-3x+3, а прямая – g(x)=2x-3. Составьте уравнение f(x)=g(x), то есть x^2-3x+3=2x-3. Перенося все слагаемые в левую часть, и приводя подобные, получите: x^2-5x+6=0. Корни данного квадратного уравнения: x1=2, x2=3. Теперь найдите соответствующие «игрики»: y1=g(x1)=1, y2=g(x2)=3. Таким образом, найдены все точки пересечения: (2,1) и (3,3).

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Существует определенный класс задач по дисциплине «Алгебра и начало анализа», в которых нужно найти точки пересечения графиков функций без их построения. Решать такие задания довольно просто, когда известна определенная методика нахождения координат по оси абсцисс и ординат. Однако для этого необходимо научиться правильно находить корни уравнений различных типов.

Функция — некоторое выражение, описывающее зависимость между двумя величинами. Следует отметить, что последних может быть несколько. Параметр, который не зависит от других элементов, называется аргументом, а зависимое тождество — значением функции.

Точка пересечения графиков означает, что у системы уравнений существует общее решение. Следует отметить, что для их нахождения можно воспользоваться графическим и аналитическим методом. Первый подразумевает построение графического представления выражения с переменной.

Чтобы найти пересечение графиков функций аналитическим способом, необходимо решить уравнение, корни которого являются искомыми точками. Для их нахождения специалисты рекомендуют получить базовые понятия о равенствах с переменными, а также о методах их решения.

Уравнение — тождество, содержащее неизвестные величины (переменные), которые следует найти при помощи определенного алгоритма. Последний зависит от типа выражений. Тождества классифицируются на несколько типов:

По теореме Виета.

Первый способ применяется довольно часто, поскольку с его помощью можно понижать степень при неизвестной величине. Второй подразумевает выделение квадрата по одной из формул сокращенного умножения. Чтобы воспользоваться одним из двух методов, необходимо знать соответствующие тождества (правила разложения на множители).

Однако не всегда можно быстро решить квадратное уравнение при помощи первых двух методов. Еще один вариант — нахождение корней через дискриминант (Д), т. е. дополнительный параметр, позволяющий сразу находить решения. Он находится по следующей формуле: Д=(-S)^2 -4PU.

Следует отметить, что при Д>0 переменная принимает два значения, которые превращают равенство в истину. Если Д=0, то корень только один. Когда Д

Учитель физики, информатики и вычислительной техники. Победитель конкурса лучших учителей Российской Федерации в рамках Приоритетного Национального Проекта «Образование».

Построение графиков функций

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ — наглядно.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Исследование функции

Важные точки графика функции y = f(x):

стационарные и критические точки;
точки экстремума;
нули функции;
точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

Найти область определения функции.
Найти область допустимых значений функции.
Проверить не является ли функция четной или нечетной.
Проверить не является ли функция периодической.
Найти нули функции.
Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
Найти асимптоты графика функции.
Найти производную функции.
Найти критические точки в промежутках возрастания и убывания функции.
На основании проведенного исследования построить график функции.

У нас есть отличные курсы по математике для учеников с 1 по 11 классы!

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Упростим формулу функции:

при х ≠ -1.

График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).

Задача 2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

Вспомним, как параметры a, b и c определяют положение параболы.

Ветви вниз, следовательно, a 0.

Точка пересечения с осью Oy — c = 0.

Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a 0.

Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

б)

г)

д)

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)

Преобразование в одно действие типа f(x — a).

Сдвигаем график вправо на 1:

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г)

Преобразование в одно действие типа

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

Как найти координаты точек пересечения графика функции: примеры решения

Вы будете перенаправлены на Автор24

В практике и в учебниках наиболее распространены нижеперечисленные способы нахождения точки пересечения различных графиков функций.

Первый способ

Первый и самый простой – это воспользоваться тем, что в этой точке координаты будут равны и приравнять графики, а из того что получится можно найти $x$. Затем найденный $x$ подставить в любое из двух уравнений и найти координату игрек.

Найдём точку пересечения двух прямых $y=5x + 3$ и $y=x-2$, приравняв функции:

Теперь подставим полученный нами икс в любой график, например, выберем тот, что попроще — $y=x-2$:

$y=-frac<1> <2>– 2 = — 2frac12$.

Точка пересечения будет $(-frac<1><2>;- 2frac12)$.

Второй способ

Второй способ заключается в том, что составляется система из имеющихся уравнений, путём преобразований одну из координат делают явной, то есть, выражают через другую. После это выражение в приведённой форме подставляется в другое.

Узнайте, в каких точках пересекаются графики параболы $y=2x^2-2x-1$ и пересекающей её прямой $y=x+1$.

Решение:

Второе уравнение проще первого, поэтому подставим его вместо $y$:

Вычислим, чему равен x, для этого найдём корни, превращающие равенство в верное, и запишем полученные ответы:

Подставим наши результаты по оси абсцисс по очереди во второе уравнение системы:

$y_1= 2 + 1 = 3; y_2=1 — frac<1> <2>= frac<1><2>$.

Точки пересечения будут $(2;3)$ и $(-frac<1><2>; frac<1><2>)$.

Третий способ

Готовые работы на аналогичную тему

Перейдём к третьему способу — графическому, но имейте в виду, что результат, который он даёт, не является достаточно точным.

Для применения метода оба графика функций строятся в одном масштабе на одном чертеже, и затем выполняется визуальный поиск точки пересечения.

Данный способ хорош лишь в том случае, когда достаточно приблизительного результата, а также если нет каких-либо данных о закономерностях рассматриваемых зависимостей.

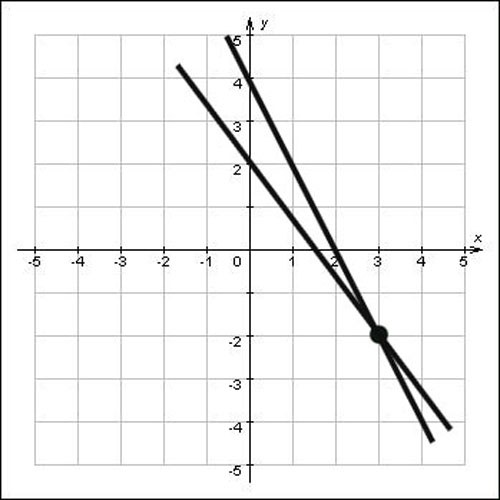
Найдите точку пересечения графиков на общем рисунке.

Рисунок 1. Точка пересечения двух функций. Автор24 — интернет-биржа студенческих работ

Решение:

Тут всё просто: ищем точки пересечения пунктиров, опущенных с графиков с осями абсцисс и ординат и записываем по порядку. Здесь точка пересечения равна $(2;3)$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 07 05 2021

источники:

http://skysmart.ru/articles/mathematic/postroenie-grafikov-funkcij

http://spravochnick.ru/matematika/kak_nayti_koordinaty_tochek_peresecheniya_grafika_funkcii_primery_resheniya/

Источник

Как найти точку касания параболы и прямой

Здравствуйте! Продолжаем рассматривать задачи входящие в состав экзамена по математике. Задания, которые мы рассмотрим ниже, по-большому счёту, никаких глубоких знаний теории не требуют. Для их решения необходимо понимание геометрического смысла производной , умение решать квадратное уравнение и немного логики.

Суть заданий следующая: дана парабола вида у = ах 2 +bх+c и касательная к этой параболе у=kх b. Один из коэффициентов (a, b или c) неизвестен и его необходимо найти.

Как решать такие задачи? Что необходимо вспомнить?

1. Если даны уравнения двух функций, то точка (точки) пересечения их графиков находится путём решения системы этих уравнений. Пара (х;у) являющаяся решением системы есть точка пересечения графиков (или пары, если точек пересечения больше).

2. Если к графику функции проведена касательная, то производная этой функции в точке касания равна угловому коэффициенту этой касательной (см. ссылку выше).

Рассмотрим задачи (показаны два способа решения):

Прямая у=х+7 является касательной к графику функции ах 2 –15х+15. Найдите a.

Прямая и график данной функции имеют одну общую точку, это значит, что данные уравнения можно внести для решения в одну систему, но этих уравнений будет недостаточно для решения (кроме неизвестных х и у имеется ещё параметр а).

Известно, что производная функции в данной точке равна угловому коэффициенту касательной у = kх + b (где k это угловой коэффициент), то есть f′(x_o) = k. Это третье уравнение, запишем систему:

Подставим из второго уравнения в первое:

Найдём а, подставим х = 1 в ах 2 – 15х + 15 = х + 7 или в 2ах – 15 = 1

По смыслу задачи параметр a ≠ 0, график заданной функции — парабола. Прямая с параболой имеет единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение ах 2 – 15х + 15 = х + 7 имело единственно решение:

Квадратное уравнение будет иметь единственное решение тогда, когда дискриминант будет равен нулю:

Прямая у=3х+1 является касательной к графику функции ах 2 +2х+3. Найдите a.

Прямая у=5х–8 является касательной к графику функции 6х 2 + bх + 16

Найдите b, учитывая, что абсцисса точки касания больше 0.

Прямая и парабола пересекаются в одной точке, поэтому оба уравнения можно внести в систему, но она не решаема, так как имеем три неизвестных:

Известно, что производная функции в данной точке равна угловому коэффициенту касательной у = kх + b (где k это угловой коэффициент), то есть f′(x o ) = k. Это третье уравнение, запишем систему:

Кратко можно сказать так:

Условия касания графика функции f (x) = k и прямой у = kх + b задаётся системой требований:

По условию, абсцисса точки касания положительна, значит х = 2.

График заданной функции — парабола. Прямая с параболой имеет единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение

имело единственно решение. Преобразуем:

Квадратное уравнение будет иметь единственное решение тогда, когда дискриминант будет равен нулю:

Теперь определим, при каком значении b абсцисса точки касания будет больше нуля. Можно подставить поочерёдно полученные значения в систему:

Далее решить её и сдать вывод. Верным решением будет то значение b, при котором получим положительную абсциссу.

Но мы сразу подставим их (поочерёдно) в 28х 2 + (b – 5) + 24 = 0.

Таким образом, b = – 19 (при этом значении абсцисса точки касания положительна).

Прямая у = –5х+8 является касательной к графику функции 28х 2 + bх + 15.

Найдите b, учитывая, что абсцисса точки касания больше 0.

Прямая у=–6х–2 является касательной к графику ф-ии 18х 2 +6х+с. Найдите c.

Условия касания графика функции у = f (x) и прямой у = kx + b задаётся системой требований:

имело единственное решение, преобразуем:

Квадратное уравнение будет иметь единственное решение тогда, когда дискриминант будет равен нулю, значит:

Прямая у=3х+4 является касательной к графику функции 3х 2 –3х+с. Найдите c.

Как видим, понимание способа нахождения точки пересечения графиков функций, заключающееся в решении системы, пригодилось при решении указанных задач (на ЕГЭ могут быть и другие). Но какие бы они не были, если чётко уясните геометрический смысл производной, проблем с подобными у вас не будет.

В данной рубрике продолжим рассматривать задачи, не пропустите!

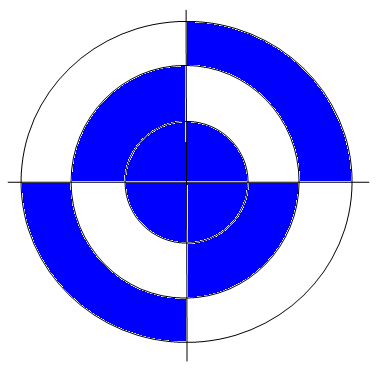
Имеется круглая мишень радиуса R. На ней отмечены две окружности, радиусы которых равны 1/3 и 2/3 от радиуса мишени. Какова вероятность того, что кинутый в мишень дротик попадёт в закрашенную часть мишени? Результат округлите до тысячных.

*Учесть, что дротик мимо мишени попасть не может.

Тот учащийся, который первый напишет верный ответ, получит поощрительный приз в размере 150 рублей 😉

Надеюсь материал был вам полезен. Успехов Вам!

Наука: Математика

Секция: Геометрия

Условия публикаций
Все статьи конференции

КАСАТЕЛЬНЫЕ К ПАРАБОЛЕ

Паршева Валентина Васильевна

научный руководитель, заслуженный учитель РФ, учитель математики, школа № 24, г. Северодвинск

150%;background:»>
Понятие касательной — одно из важнейших в математическом анализе. «Изучение прямых, касательных к кривым линиям, во многом определили пути развития математики» [2, с. 229]. Но касательную можно провести к различным кривым, в том и числе и к параболе, интерес к которой проявляли древние математики, такие как Апполоний Пергский, Архимед, Папп, Исидор Милетский. Интерес к касательным не ослабевал и у математиков последующих поколений. Исследования, связанные с построением касательных с помощью аналитических методов, проводили Р. Декарт, Г.В. Лейбниц, И. Ньютон.

150%;background:»>
С помощью циркуля и линейки нетрудно построить касательную к окружности в данной ее точке. В Древней Греции умели строить с помощью циркуля и линейки касательные ко всем коническим сечениям: эллипсам, гиперболам и параболам, что свидетельствует о высоком уровне развития геометрии в то время.

150%;background:»>
Актуальность работы в том, что понятия касательной к параболе, ее уравнение изучается только в 11 классе, и ее свойства не рассматриваются. В то же время исследование вопроса о касательной к параболе расширяет знания о параболе и круг решаемых задач. Одновременно актуальной является идея применения ИГС GeoGebra для проведения компьютерного моделирования исследуемого вопроса.

150%»>
Проблемный вопрос: Понятие касательной к кривым вводится в школьном курсе математики только в 11 классе с помощью производной функции. Понятие производной функции возникло на много позже (XVII век) понятий параболы и касательной к ней. Можно ли без понятия производной функции дать определение параболы, сделать вывод ее уравнения и полученные знания применить для построения касательной к параболе?

150%;background:»>
Цель исследования: применить имеющиеся знания о касательной для исследования новых свойств функции y=x 2 и попытаться использовать эти свойства для построения касательных к параболе y=x 2 без вычисления производной.

line-height:150%;background:»>
1.Установить геометрическое место точек, являющихся точками пересечения взаимно-перпендикулярных касательных к параболе у=ах 2 .

line-height:150%;background:»>
2.Установить, что касательная к параболе, проходящая через точку А параболы, является прямой, содержащей биссектрису угла, образованного лучом AF, где А — фокус параболы, и перпендикуляром, опущенном из точки А на директрису параболы.

line-height:150%;background:»>
3.Установить, что точки, симметричные фокусу параболы относительно всевозможных ее касательных, расположены на директрисе параболы.

line-height:150%;background:»>
4.Установить, что касательные в концах фокальной хорды параболы пересекаются на директрисе параболы.

line-height:150%;background:»>
5.На основании установленных свойств касательной к параболе выявить способы построения касательной.

line-height:150%»>
·Анализ школьных учебников математики, математической, справочной литературы, литературы по истории математики.

line-height:150%»>
·Компьютерное моделирование математических объектов с помощью ИГС GeoGebra (компьютерный эксперимент).

line-height:150%»>
·Анализ полученных с помощью компьютерного эксперимента данных.

line-height:150%»>
·Обобщение найденных с помощью компьютерного эксперимента закономерностей.

line-height:150%;background:»>
·Аналитические рассуждения.

150%»>
Объект исследования: парабола

150%»>
Предмет исследования: касательные к параболе.

150%»>
Гипотеза исследования Видимо, касательная к параболе, как любой геометрический объект, имеет свои свойства, которые расширят наши знания о параболе.

150%;background:»>
В учебной литературе даются такие определения касательной к параболе:

150%;background:»>
Определение 1. Прямая, имеющая с параболой только одну общую точку и не параллельная ее оси, называется касательной к параболе.

150%;background:»>
В математическом анализе касательная к кривой в точке М определяется как предельное положение секущей МN при приближении точки N по кривой к точке М.

150%;background:»>
Определение 2. Касательной к кривой в данной точке МО называется предельное положение секущей ММ₁ при условии, что точка М₁ стремится к точке М по данной кривой [1, с. 21].

Вывод уравнения касательной к параболе у = ах 2 в точке М (х; ах 2 )

150%;background:»>
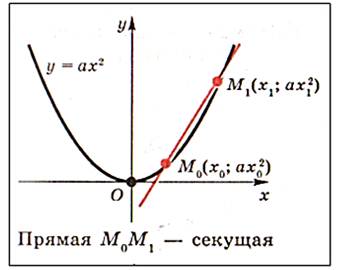
•Точки М(х; ах 2 ) и М₁(х₁; ах₁ 2 ) принадлежат параболе у=ах2. Уравнение секущей М0М1 имеет вид:

Пусть точка М₁ стремится к точке М. Тогда х₁ стремится к х и в пределе уравнение секущей переходит в уравнение касательной в точке М(х; ах 2 )

150%;background:»>
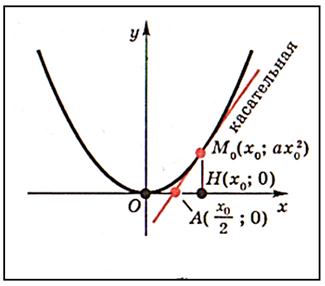
Касательная пересекает ось абсцисс в точке А (х/2; 0), что следует из уравнения касательной при у=0. Этот факт дает возможность построить касательную к параболе в данной точке М с помощью циркуля и линейки. Для этого нужно провести перпендикуляр МН из данной точки М к оси абсцисс, а затем построить середину отрезка ОН. Это точка А. Проведем прямую через точки А и М.

line-height:150%;background:»>
• Прямая АМО является касательной к параболе в данной точке М0.

Построение касательной в ИГС GeoGebra

Алгоритм построения с помощь. ИГС аналогичен, только выполняется с помощью инструментов программы:

line-height:150%;background:»>
• перпендикулярная прямая;

line-height:150%;background:»>
• середина или центр;

line-height:150%;background:»>
• прямая по двум точка.

150%;background:»>
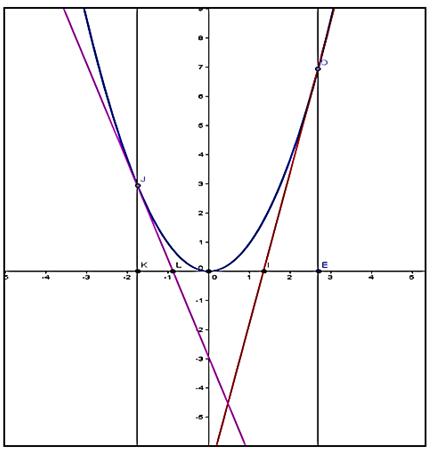
Задача. К параболе y = x 2 составить уравнения взаимно-перпендикулярных касательных. Найти точку их пересечения.

150%;background:»>
Решение. Уравнение касательной к параболе y = ax 2 в точке с абсциссой х. Угловой коэффициент этой касательной k = 2ax. Уравнение касательной к параболе y = ax 2 в точке с абсциссой х₁. Угловой коэффициент этой касательной k₁ = 2ax₁.

150%;background:»>
Найдем соотношение между абсциссами х и х₁. k·k₁=-1 — условие перпендикулярности двух прямых. Тогда: 2ax∙2ax1 = -1; 4a 2 xx₁ = -1;

150%;background:»>
Искомое уравнение

background:»>

150%;background:»>
Составим уравнения взаимно-перпендикулярных касательных к параболе у = х 2 в различных точках, найдем их точки пересечения и сделаем сравнение

150%;background:»>
Выполнив аналогичные рассуждения для параболы у = ах 2 и сравним координаты точек пересечения взаимно-перпендикулярных касательных к параболе у = ах 2 можно сделать вывод: абсциссы этих точек разные, а ординаты равны -1/4а, т. е. все такие точки находятся на прямой у = -1/4а, т. е. взаимно-перпендикулярные касательные пересекаются на директрисе параболы.

150%;background:»>
Возникает вопрос: всегда ли к параболе можно провести две взаимно-перпендикулярных касательных. Ответ очевиден — исключением является вершина параболы.

150%;background:»>
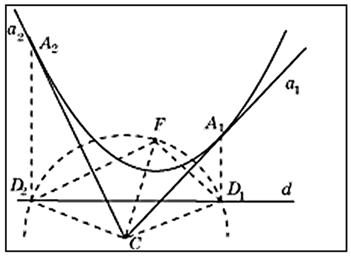
Теорема параболы. Пусть A — точка на параболе с фокусом F, директриса d, АD — перпендикуляр, опущенный на директрису. Тогда касательной к параболе, проходящей через точку A, будет прямая, содержащая биссектрису угла FAD.

150%;background:»>
Доказательство. Пусть касательная t в точке M параболы пересекает ее директрису в точке Q и пусть P — основание перпендикуляра, опущенного из точки M на директрису.

150%;background:»>
В четырехугольнике MFQP два противолежащих угла — прямые и стороны MP и MF равны.

150%;background:»>
Следовательно, ΔPMQ = ΔQMF и касательная t является биссектрисой угла, образованного фокальным радиусом и прямой, проходящей через данную точку параллельно оси x.

150%;background:»>
Если MP — перпендикуляр, опущенный из точки M параболы на директрису, то биссектриса угла FMP есть касательная к параболе в точке M.

150%;background:»>
Вывод. Отсюда, далее, следует, что основания перпендикуляров, опущенных из фокуса параболы на ее касательные, принадлежат касательной к параболе в ее вершине.

150%;background:»>
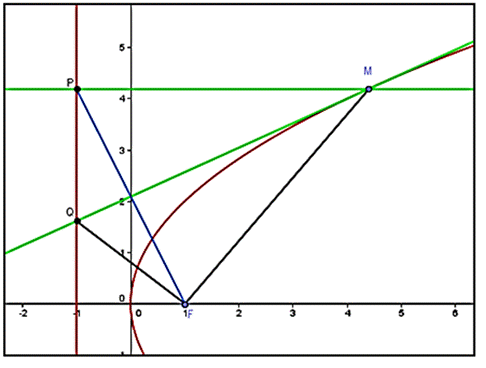
На основании свойств касательной можно выполнить построение касательных к параболе, проведенных из точки P. Пусть парабола задана фокусом F и директрисой d. Используя циркуль и линейку, построим касательную к параболе, проходящую через данную точку C. С центром в точке C и радиусом CF проведем окружность и найдем ее точки пересечения с директрисой d. Если расстояние от точки C до фокуса больше, чем расстояние до директрисы, то таких точек две. Обозначим их D₁ и D₂. Проведем биссектрисы углов FCD₁ и FCD₂соответственно. Прямые a₁ и a₂, содержащие эти биссектрисы являются серединными перпендикулярами к отрезкам FD₁ и FD2 и, значит, будут искомыми касательными к параболе. Для построения точек касания через точки D₁ и D₂ проведем прямые, перпендикулярные директрисе и найдем их точки пересечения

150%;background:»>
A₁ и A₂ с прямыми a₁ и a₂. Они и будут искомыми точками касания. Через точку C проходят две касательные к параболе.

150%;background:»>
Построение касательных, проходящих через точку С выполнено в ИГС GeoGebra с помощью инструментов: Окружность по центру и радиусу, Отрезок по двум точкам, Пересечение двух объектов, Серединный перпендикуляр.

150%;background:»>
В результате выполнения работы установлено, что:

line-height:150%;background:»>
•геометрическое место точек, являющихся точками пересечения взаимно-перпендикулярных касательных к параболе у = ах 2 .

line-height:150%;background:»>
•касательная к параболе, проходящая через точку А параболы, является прямой, содержащей биссектрису угла, образованного лучом AF, где А — фокус параболы, и перпендикуляром, опущенном из точки А на директрису параболы.

line-height:150%;background:»>
•точки, симметричные фокусу параболы относительно всевозможных ее касательных, расположены на директрисе параболы.

line-height:150%;background:»>
•На основании установленных свойств касательной к параболе выявлены способы построения касательной

150%;background:»>
При выполнении работы были продемонстрированы возможности применения ИГС GeoGebra, что явилось новизной в исследовании поставленной проблемы.

-1.0cm;line-height:150%;background:»>
1.Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия. Дополнительные главы к учебнику 9 класса — М.: Вита — Пресс, 2003. — 176 с.;

-1.0cm;line-height:150%;background:»>
2.Энциклопедический словарь юного математика. Сост. Савин А.П. — М.: Педагогика, 1985. — 352 с.;

План занятий

Парабола. Фокус. Директриса. У равнение параболы.

Уравнение касательной к параболе.

Условие касания прямой и параболы.

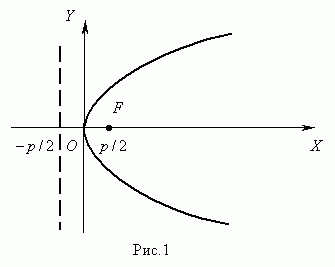
Параболой ( рис.1 ) называется геометрическое место точек, равноудалённых от заданной точки F , называемой фокусом параболы, и данной прямой, не проходящей через эту точку и называемой директрисой параболы.

Уравнение параболы ( рис.1 ) :

Здесь ось ОХ является осью симметрии параболы.

Пусть Р ( х ₁ , у ₁ ) – точка параболы, тогда уравнение касательной к параболе в данной точке имеет вид:

Источник

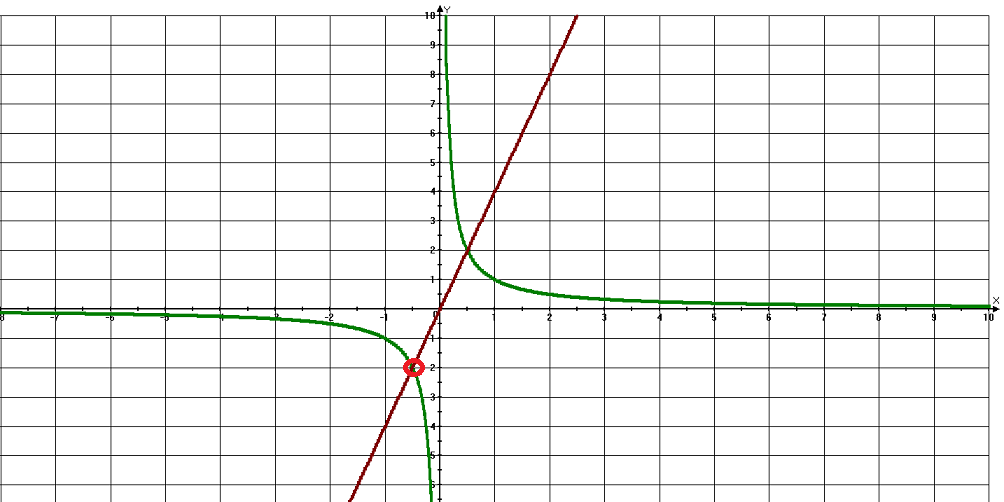
Прямая и гипербола имеют одну общую точку

Постройте график функции и определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.

Так как функция содержит дробное выражение, обязательно нужно найти область допустимых значений переменной.

ОДЗ:

Упростим функцию.
Для этого разложим на множители знаменатель, затем сократим дробь.

Функция приобрела вид y = 1/x.

Это функция обратной пропорциональности. Ее графиком является гипербола, состоящая из двух ветвей.

Заполним таблицу значений, чтобы по точка построить график функции.

Прямая y = kx будет иметь с гиперболой y = 1/x одну общую точку только в том случае, если она пройдет через выколотую точку (-0,5; -2).

Подставив координаты этой точки в формулу функции y = kx, определим значение параметра k.

k = 4

Теперь осталось построить графики функций и записать ответ.

Ответ: 4

Смотрите видеоурок с подробным решением задачи.

В комментариях пишите, какие темы вызывают у вас затруднения.

Если вам понравился материал, не поленитесь — нажмите на кнопочки любимой социальной сети, чтобы поделиться с друзьями.

Интересная статья? Поделитесь ею пожалуйста с другими:

Источник

Совет 1: Как обнаружить точку пересечения прямой и параболы

Задачи по поиску точек пересечения каких-либо фигур идеологически примитивны. Трудности в них бывают только из-за арифметики, потому что именно в ней допускаются разные опечатки и ошибки.

Инструкция

1. Данная задача решается аналитически, следственно дозволено совсем не рисовать графики прямой и параболы. Зачастую это дает огромный плюс в решении примера, потому что в задаче могут быть даны такие функции, что их проще и стремительней не нарисовать.

2. Согласно учебникам по алгебре парабола задается функцией вида f(x)=ax^2+bx+c, где a,b,c – это вещественные числа, притом показатель a хорош он нуля. Функция g(x)=kx+h, где k,h – это вещественные числа, определяет прямую на плоскости.

3. Точка пересечения прямой и параболы – это всеобщая точка обеих кривых, следственно в ней функции примут идентичные значение, то есть f(x)=g(x). Данное заявление разрешает записать уравнение: ax^2+bx+c=kx+h, которое даст вероятность обнаружить уйма точек пересечения .

4. В уравнении ax^2+bx+c=kx+h нужно перенести все слагаемые в левую часть и привести сходственные: ax^2+(b-k)x+c-h=0. Сейчас остается решить полученное квадратное уравнение.

5. Все обнаруженные “иксы” – это еще не результат на задачу, потому что точку на плоскости характеризуют два вещественных числа (x,y). Для полного заключения решения нужно вычислить соответствующие “игрики”. Для этого необходимо подставить “иксы” либо в функцию f(x), либо в функцию g(x), чай для точки пересечения правильно: y=f(x)=g(x). Позже этого вы обнаружите все всеобщие точки параболы и прямой .

6. Для закрепления материала дюже главно разглядеть решение на примере. Пускай парабола задается функцией f(x)=x^2-3x+3, а прямая – g(x)=2x-3. Составьте уравнение f(x)=g(x), то есть x^2-3x+3=2x-3. Перенося все слагаемые в левую часть, и приводя сходственные, получите: x^2-5x+6=0. Корни данного квадратного уравнения: x1=2, x2=3. Сейчас обнаружьте соответствующие “игрики”: y1=g(x1)=1, y2=g(x2)=3. Таким образом, обнаружены все точки пересечения : (2,1) и (3,3).

Совет 2: Как обнаружить точку пересечения прямых

Точку пересечения прямых дозволено приблизительно определить по графику. Впрочем частенько необходимы точные координаты этой точки либо график строить не требуется, тогда дозволено обнаружить точку пересечения , зная только уравнения прямых.

Инструкция

1. Пускай две прямые заданы всеобщими уравнениями прямой: A1*x + B1*y + C1 = 0 и A2*x + B2*y + C2 = 0. Точка пересечения принадлежит и одной прямой, и иной. Выразим из первого уравнения прямой x, получим: x = -(B1*y + C1)/A1. Подставим полученное значение во второе уравнение: -A2*(B1*y + C1)/A1 + B2*y + C2 = 0. Либо -A2B1*y – A2C1 + A1B2*y + A1C2 = 0, отсель y = (A2C1 – A1C2)/(A1B2 – A2B1). Подставим обнаруженное значение в уравнение первой прямой: A1*x + B1(A2C1 – A1C2)/(A1B2 – A2B1) + C1 = 0.A1(A1B2 – A2B1)*x + A2B1C1 – A1B1C2 + A1B2C1 – A2B1C1 = 0(A1B2 – A2B1)*x – B1C2 + B2C1 = 0Тогда x = (B1C2 – B2C1)/(A1B2 – A2B1).

2. В школьном курсе математики прямые зачастую задаются уравнением с угловым показателем, разглядим данный случай. Пускай две прямые заданы таким образом: y1 = k1*x + b1 и y2 = k2*x + b2. Видимо, что в точке пересечения y1 = y2, тогда k1*x + b1 = k2*x + b2. Получаем, что ордината точки пересечения x = (b2 – b1)/(k1 – k2). Подставим x в всякое уравнение прямой и получим y = k1(b2 – b1)/(k1 – k2) + b1 = (k1b2 – b1k2)/(k1 – k2).

Видео по теме

Совет 3: Как составить уравнение параболы

Уравнение параболы является квадратичной функцией. Существует несколько вариантов составления этого уравнения. Все зависит от того, какие параметры представлены в условии задачи.

Инструкция

1. Парабола представляет собой кривую, которая по своей форме напоминает дугу и является графиком степенной функции. Самостоятельно от того, какие колляции имеет парабола, эта функция является четной. Четной именуется такая функция, у которой при всех значениях довода из области определения при изменении знака довода значение не изменяется:f(-x)=f(x)Начните с самой примитивную функции: y=x^2. Из ее вида дозволено сделать итог, что она нарастает как при правильных, так и при негативных значениях довода x. Точка, в которой x=0, и при этом, y =0 считается точкой минимума функции.

2. Ниже приведены все основные варианты построения этой функции и ее уравнение. В качестве первого примера ниже рассмотрена функция вида:f(x)=x^2+a, где a – целое числоДля того, дабы возвести график данной функции, нужно сдвинуть график функции f(x) на a единиц. Примером может служить функция y=x^2+3, где по оси y сдвигают функцию вверх на две единицы. Если дана функция с противоположным знаком, скажем y=x^2-3, то ее график сдвигают вниз по оси y.

3. Еще один вид функции, которой может быть задана парабола – f(x)=(x +a)^2. В таких случаях график, напротив, сдвигается по оси абсцисс (оси x) на a единиц. Для примера дозволено разглядеть функции: y=(x +4)^2 и y=(x-4)^2. В первом случае, где имеется функция со знаком плюс, график сдвигают по оси x налево, а во втором случае – вправо. Все эти случаи показаны на рисунке.

4. Существуют также параболические зависимости вида y=x^4. При таких случаях x=const, а y круто повышается. Впрочем, это касается только четных функций.Графики параболы зачастую присутствуют и в физических задачах, скажем, полет тела описывает линию, схожую именно на параболу. Также вид параболы имеет продольное сечение рефлектора фары, фонаря. В различие от синусоиды, данный график является непериодическим и нарастающим.

Совет 4: Как определить точку пересечения прямой с плоскостью

Данная задача на построение точки пересечения прямой с плоскостью является классической в курсе инженерной графики и выполняется способами начертательной геометрии и их графического решения на чертеже.

Инструкция

1. Разглядим определение точки пересечения прямой с плоскостью частного расположения (рисунок 1).Прямая l пересекает фронтально-проектирующую плоскость ?. Точка их пересечения K принадлежит и прямой и плоскости, значит, общая проекция K2 лежит на ?2 и l2. То есть, K2= l2??2, а ее горизонтальная проекция K1 определяется на l1 при помощи линии проекционной связи.Таким образом, желанная точка пересечения K(K2K1) строится непринужденно без использования вспомогательных плоскостей.Подобно определяются точки пересечения прямой с всякими плоскостями частного расположения.

2. Разглядим определение точки пересечения прямой с плоскостью всеобщего расположения. На рисунке 2 в пространстве заданы произвольно расположенные плоскость ? и прямая l . Для определения точки пересечения прямой с плоскостью всеобщего расположения используется способ вспомогательных секущих плоскостей в дальнейшем порядке:

3. Через прямую l проводится вспомогательная секущая плоскость ?.Для облегчения построений это будет проектирующая плоскость.

4. Дальше строится линия пересечения MN вспомогательной плоскости с заданной: MN=???.

5. Отмечается точка K пересечения прямой l и построенной линии пересечения MN. Она и является желанной точкой пересечения прямой и плоскости.

6. Применим это правило для решения определенной задачи на комплексном чертеже.Пример. Определить точку пересечения прямой l с плоскостью всеобщего расположения, заданной треугольником ABC (рисунок 3).

7. Через прямую l проводится вспомогательная секущая плоскость ?, перпендикулярная плоскости проекции ?2. Ее проекция ?2 совпадает с проекцией прямой l2.

8. Строится линия MN. Плоскость ? пересекает AB в точке M. Отмечается ее общая проекция M2= ?2?A2B2 и горизонтальная M1 на A1B1 по линии проекционной связи.Плоскость ? пересекает сторону AC в точке N. Ее общая проекция N2=?2?A2C2, горизонтальная проекция N1 на A1C1.Прямая MN принадлежит единовременно обеим плоскостям, а, значит, является линией их пересечения .

9. Определяется точка K1 пересечения l1 и M1N1, после этого с поддержкой линии связи строится точка K2. Выходит, K1 и K2 – проекции желанной точки пересечения K прямой l и плоскости ? ABC:K(K1K2)= l(l1l2)? ? ABC(A1B1C1, A2B2C2).При помощи конкурирующих точек М,1 и 2,3 определяется видимость прямой l касательно данной плоскости ? ABC.

Видео по теме

Обратите внимание!
Применяйте вспомогательную плоскость при решении задачи.

Полезный совет
Исполняйте вычисления, применяя подробные чертежи, соответствующие условиям задачи. Это поможет стремительней сориентироваться в решении.

Совет 5: Как вычислить точки пересечения прямых

Две прямые, если они непараллельны и не совпадают, неукоснительно пересекаются в одной точке. Обнаружить координаты этого места – значит вычислить точки пересечения прямых. Две пересекающиеся прямые неизменно лежат в одной плоскости, следственно довольно разглядеть их в декартовой плоскости. Разберем на примере, как обнаружить всеобщую точку прямых.

Инструкция

1. Возьмите уравнения 2-х прямых, помня о том, что уравнение прямой в декартовой системе координат уравнение прямой выглядит как ах+ву+с=0, причем а, в, с – обыкновенные числа, а х и у – координаты точек. Для примера обнаружьте точки пересечения прямых 4х+3у-6=0 и 2х+у-4=0. Для этого обнаружьте решение системы этих 2-х уравнений.

2. Для решения системы уравнений измените всякое из уравнений так, дабы перед y стоял идентичный показатель. Потому что в одном уравнении показатель перед у равен 1, то примитивно умножьте это уравнение на число 3 (показатель перед у в ином уравнении). Для этого всякий элемент уравнения умножьте на 3: (2х*3)+(у*3)-(4*3)=(0*3) и получите обыкновенное уравнение 6х+3у-12=0. Если бы показатели перед у были чудесны от единицы в обоих уравнениях, умножать нужно было бы оба равенства.

3. Вычтите из одного уравнения другое. Для этого вычтите из левой части одного левую часть иного и верно также поступите с правой. Получите такое выражение: (4х+3у-6) – (6х+3у-12)=0-0. Потому что перед скобкой стоит знак «-», все знаки в скобках поменяйте на противоположные. Получите такое выражение: 4х+3у-6 – 6х-3у+12=0. Упростите выражение и вы увидите, что переменная у исчезла. Новое уравнение выглядит так: -2х+6=0. Перенесите число 6 в иную часть уравнения, и из получившегося равенства -2х=-6 выразите х: х=(-6)/(-2). Таким образом, вы получили х=3.

4. Подставьте значение х=3 в всякое уравнение, скажем, во второе и получите такое выражение: (2*3)+у-4=0. Упростите и выразите у: у=4-6=-2.

5. Запишите полученные значения х и у в виде координат точки (3;-2). Эти и будет решение задачи. Проверьте полученное значение способом подстановки в оба уравнения.

6. Если прямые не даны в виде уравнений, а даны примитивно на плоскости, обнаружьте координаты точки пересечения графически. Для этого продлите прямые так, дабы они пересеклись, после этого опустите на оси ох и оу перпендикуляры. Пересечение перпендикуляров с осями ох и оу, будет координатами этой точки , посмотрите на рисунок и вы увидите, что координаты точки пересечения х=3 и у=-2, то есть точка (3;-2) и есть решение задачи.

Видео по теме

Совет 6: Как нарисовать параболу

Парабола – это плоская кривая второго порядка, каноническое уравнение которой в декартовой системе координат имеет вид y?=2px. Где р – это фокальный параметр параболы, равный расстоянию от фиксированной точки F, называемой фокусом, до фиксированной прямой D в этой же плоскости, носящей имя – директриса. Вершина такой параболы проходит через предисловие координат, а сама кривая симметрична касательно оси абсцисс Ох. В школьном курсе алгебры принято рассматривать параболу, ось симметрии которой совпадает с осью ординат Оу: x?=2py. А уравнение при этом записывается несколько напротив: y=ax?+bx+c, а=1/(2p). Нарисовать параболу дозволено несколькими методами, условно которые дозволено назвать алгебраическим и геометрическим.

Инструкция

1. Алгебраическое построение параболы.Узнаете координаты вершины параболы. Координату по оси Ох вычислите по формуле: x0=-b/(2a), а по оси Оy: y0=-(b?-4ac)/4a либо подставьте полученное значение х0 в уравнение параболы y0=ax0?+bx0+c и вычислите значение.

2. На координатной плоскости постройте ось симметрии параболы. Ее формула совпадает с формулой координаты х0 вершины параболы: x=-b/(2a). Определите, куда направлены ветви параболы. Если а>0, то оси направлены вверх, если а

3. Возьмите произвольно 2-3 значения для параметра х так, дабы: х0

4. Поставьте точки 1′, 2′, и 3′ так, дабы они были симметричны точкам 1, 2, 3 касательно оси симметрии.

5. Объедините точки 1′, 2′, 3′, 0, 1, 2, 3 плавной косой линией. Продолжите линию вверх либо вниз, в зависимости от направления параболы. Парабола построена.

6. Геометрическое построение параболы. Данный способ основан на определении параболы, как общности точек, равноудаленных как от фокуса F, так и от директрисы D.Следственно вначале обнаружьте фокальный параметр заданной параболы р=1/(2а).

7. Постройте ось симметрии параболы, как описано во 2 шаге. На ней поставьте точку F с координатой по оси Оу равной у=р/2 и точку D с координатой у=-р/2.

8. При помощи угольника постройте линию, проходящую через точку D, перпендикулярную оси симметрии параболы. Эта линия – директриса параболы.

9. Возьмите нить по длине равной одному из катетов угольника. Один конец нити кнопкой закрепите на вершине угольника, к которому прилегает данный катет, а 2-й конец – в фокусе параболы в точке F. Линейку положите так, дабы ее верхний край совпадал с директрисой D. На линейку поставьте угольник, свободным от кнопки катетом.

10. Карандаш установите так, дабы он своим острием прижимал нить к катету угольника. Двигайте угольник по линейки. Карандаш вычертит необходимую вам параболу.

Видео по теме

Обратите внимание!
Не рисуйте вершину параболы в виде угла. Ее ветви сходятся друг с ином, плавно закругляясь.

Полезный совет
При построении параболы геометрическим методом следите, дабы нить неизменно была натянута.

Совет 7: Как обнаружить точки пересечения функции

Раньше чем приступить к изысканию поведения функции, нужно определить область метаморфозы рассматриваемых величин. Примем допущение, что переменные относятся к множеству действительных чисел.

Инструкция

1. Функция – это переменная величина, зависящая от значения довода. Довод – переменная самостоятельная. Пределы изменений довода именуются областью возможных значений (ОДЗ). Поведение функции рассматривается в рамках ОДЗ потому, что в этих пределах связанность между двумя переменными не хаотическая, а подчиняется определенным правилам и может быть записана в виде математического выражения.

2. Разглядим произвольную функциональную связанность F=?(x), где ? – математическое выражение. Функция может иметь точки пересечения с осями координат либо с другими функциями.

3. В точках пересечения функции с осью абсцисс функция становится равной нулю:F(x)=0.Решите это уравнение. Вы получите координаты точек пересечения заданной функции с осью ОХ. Таких точек будет столько, сколько найдется корней уравнения на заданном участке метаморфозы довода.

4. В точках пересечения функции с осью ординат значение довода равно нулю. Следственно, задача превращается в нахождение значения функции при х=0. Точек пересечения функции с осью OY будет столько, сколько найдется значений заданной функции при нулевом доводе.

5. Для нахождения точек пересечения заданной функции с иной функцией нужно решить систему уравнений:F=?(x)W=?(x).Тут ?(x) — выражение, описывающее заданную функцию F, ?(x) — выражение, описывающее функцию W, точки пересечения с которой заданной функции надобно обнаружить. Видимо, что в точках пересечения обе функции принимают равные значения при равных значениях доводов. Всеобщих точек у 2-х функций будет столько, сколько решений у системы уравнений на заданном участке изменений довода.

Видео по теме

Совет 8: Как обнаружить точки пересечения функций

В точках пересечения функции имеют равные значения при идентичном значении довода. Обнаружить точки пересечения функций — значит определить координаты всеобщих для пересекающихся функций точек.

Инструкция

1. В всеобщем виде задача нахождения точек пересечения функций одного довода Y=F(x) и Y?=F?(x) на плоскости XOY сводится к решению уравнения Y= Y?, от того что в всеобщей точке функции имеют равные значения. Значения х, удовлетворяющие равенству F(x)=F?(x), (если они существуют) являются абсциссами точек пересечения заданных функций.

2. Если функции заданы несложным математическим выражением и зависят от одного довода х, то задачу нахождения точек пересечения дозволено решить графически. Постройте графики функций. Определите точки пересечения с осями координат (х=0, y=0). Задайте еще несколько значений довода, обнаружьте соответствующие значения функций, добавьте полученные точки на графики. Чем огромнее точек будет использовано для построения, тем вернее будет график.

3. Если графики функций пересекутся, определите по чертежу координаты точек пересечения. Для проверки подставьте эти координаты в формулы, которыми заданы функции. Если математические выражения окажутся объективными, точки пересечения обнаружены положительно. Если графики функций не пересекаются, испробуйте изменить масштаб. Сделайте шаг между точками построения огромнее, дабы определить, на каком участке числовой плоскости линии графиков сближаются. После этого на выявленном участке пересечения постройте больше подробнейший график с мелким шагом для точного определения координат точек пересечения.

4. Если необходимо обнаружить точки пересечения функций не на плоскости, а в трехмерном пространстве, доводится разглядеть функции 2-х переменных: Z=F(x,y) и Z?=F?(x,y). Для определения координат точек пересечения функций необходимо решить систему уравнений с двумя незнакомыми х и y при Z= Z?.

Видео по теме

Источник