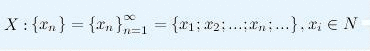Как найти общий член числовой последовательности - Исправление недочетов и поиск решений вместе с Examum.ru

Нахождение общего члена ряда по заданным первым членам. Первая часть.

Числовой ряд можно задать по-разному. Чаще всего просто используют запись вида $sumlimits_{n=1}^{infty}u_n$. Однако изредка указывают несколько первых членов ряда, по которым нужно восстановить общий член ряда. Честно говоря, подобные задачи не имеют единственного решения, и это будет продемонстрировано в примере №1. Впрочем, есть некие общие приёмы, которые применяют в стандартных случаях.

Для начала стоит запомнить несколько последовательностей. Например, квадраты натуральных чисел, т.е. последовательность $u_n=n^2$. Вот несколько первых членов этой последовательности:

$$
begin{equation}
1;; 4;; 9;; 16;; 25;; 36;; 49;; 64; ;81; ldots
end{equation}
$$

Как мы получили эти числа? показатьскрыть

Также стоит иметь в виду члены последовательности $u_n=n^3$. Вот несколько первых её членов:

$$
begin{equation}
1;; 8;; 27;; 64;; 125;; 216;; 343;; 512;;729; ldots
end{equation}
$$

Кроме того, для формирования общего члена ряда частенько используется последовательность $u_n=n!$, несколько первых членов которой таковы:

$$
begin{equation}
1;; 2;; 6;; 24;; 120;; 720;; 5040; ldots
end{equation}
$$

Что обозначает «n!»? показатьскрыть

Часто используются также арифметическая и геометрическая прогрессии. Если первый член арифметической прогрессии равен $a_1$, а разность равна $d$, то общий член арифметической прогрессии записывается с помощью такой формулы:

$$
begin{equation}
a_n=a_1+dcdot (n-1)
end{equation}
$$

Что такое арифметическая прогрессия? показатьскрыть

Стоит также отметить геометрическую прогрессию. Если первый член прогрессии равен $b_1$, а знаменатель равен $q$, то общий член геометрической прогрессии задаётся такой формулой:

$$
begin{equation}
b_n=b_1cdot q^{n-1}
end{equation}
$$

Что такое геометрическая прогрессия? показатьскрыть

Во всех изложенных ниже примерах члены рядов будем обозначать буквами $u_1$ (первый член ряда), $u_2$ (второй член ряда) и так далее. Запись $u_n$ будет обозначать общий член ряда.

Пример №1

Найти общий член ряда $frac{1}{7}+frac{2}{9}+frac{3}{11}+frac{4}{13}+ldots$.

Решение

Суть таких задач состоит в том, чтобы заметить закономерность, которая присуща первым членам ряда. И на основании этой закономерности сделать вывод о виде общего члена. Что означает фраза «найти общий член»? Она означает, что необходимо найти такое выражение, подставляя в которое $n=1$ получим первый член ряда, т.е. $frac{1}{7}$; подставляя $n=2$ получим второй член ряда, т.е. $frac{2}{9}$; подставляя $n=3$ получим третий член ряда, т.е. $frac{3}{11}$ и так далее. Нам известны первые четыре члена ряда:

$$
u_1=frac{1}{7};; u_2=frac{2}{9};; u_3=frac{3}{11};; u_4=frac{4}{13}.
$$

Давайте двигаться постепенно. Все известные нам члены ряда – дроби, поэтому резонно предположить, что и общий член ряда тоже представлен дробью:

$$
u_n=frac{?}{?}
$$

Наша задача – выяснить, что же скрывается под знаками вопроса в числителе и знаменателе. Сначала обратимся к числителю. В числителях известных нам членов ряда стоят числа 1, 2, 3 и 4. Заметьте, что номер каждого члена ряда равен числителю. У первого члена в числителе стоит единица, у второго – двойка, у третьего – тройка, у четвёртого – четвёрка.

Ряд

Логично предположить, что у n-го члена в числителе будет стоять $n$:

$$
u_n=frac{n}{?}
$$

Кстати сказать, к этому выводу мы можем прийти и иным путём, более формальным. Что представляет собой последовательность 1, 2, 3, 4? Отметим, что каждый последующий член этой последовательности на 1 больше, чем предыдущий. Мы имеем дело с четырьмя членами арифметической прогрессии, первый член которой $a_1=1$, а разность $d=1$. Используя формулу (4), получим выражение общего члена прогрессии:

$$
a_n=1+1cdot (n-1)=1+n-1=n.
$$

Итак, угадывание или формальный расчёт – дело вкуса. Главное – мы записали числитель общего члена ряда. Перейдём к знаменателю.

В знаменателях мы имеем последовательность 7, 9, 11, 13. Это четыре члена арифметической прогрессии, первый член которой равен $b_1=7$, а разность $d=2$. Общий член прогрессии найдем, используя формулу (4):

$$
b_n=7+2cdot (n-1)=7+2n-2=2n+5.
$$

Полученное выражение, т.е. $2n+5$, и будет знаменателем общего члена ряда. Итак:

$$
u_n=frac{n}{2n+5}.
$$

Общий член ряда получен. Давайте проверим, подходит ли найденная нами формула $u_n=frac{n}{2n+5}$ для вычисления уже известных членов ряда. Найдём члены $u_1$, $u_2$, $u_3$ и $u_4$ по формуле $u_n=frac{n}{2n+5}$. Результаты, естественно, должны совпасть с заданными нам по условию первыми четырьмя членами ряда.

$$
u_1=frac{1}{2cdot 1+5}=frac{1}{7};; u_2=frac{2}{2cdot 2+5}=frac{2}{9};; u_3=frac{3}{2cdot 3+5}=frac{3}{11};; u_4=frac{4}{2cdot 4+5}=frac{4}{13}.
$$

Всё верно, результаты совпадают. Заданный в условии ряд можно записать теперь в такой форме: $sumlimits_{n=1}^{infty}frac{n}{2n+5}$. Общий член ряда имеет вид $u_n=frac{n}{2n+5}$.

В принципе, если речь идёт о стандартном примере, то можно считать, что ответ получен. Однако если вам интересно поисследовать вопрос более детально, то прошу читать далее. Вопрос вот в чём: является ли найденное выше представление общего члена единственным? Ответ на этот вопрос далеко не столь очевидный, как кажется на первый взгляд. Например, давайте продолжим заданный в условии ряд таким образом:

$$
frac{1}{7}+frac{2}{9}+frac{3}{11}+frac{4}{13}+0+0+0+0+0+0+0+ldots
$$

Разве такой ряд не имеет право на существование? Ещё как имеет. И для этого ряда можно записать, что

$$
u_1=frac{1}{7};; u_2=frac{2}{9};; u_3=frac{3}{11};; u_4=frac{4}{13}; ; u_n=0; (n≥ 5).
$$

Можно записать и иное продолжение. Например, такое:

$$
frac{1}{7}+frac{2}{9}+frac{3}{11}+frac{4}{13}+frac{1}{5}+frac{1}{6}+frac{1}{7}+frac{1}{8}+frac{1}{9}+frac{1}{10}+ldots
$$

И такое продолжение ничему не противоречит. При этом можно записать, что

$$
u_1=frac{1}{7};; u_2=frac{2}{9};; u_3=frac{3}{11};; u_4=frac{4}{13}; ; u_n=frac{1}{n}; (n≥ 5).
$$

Если первые два варианта показались вам чересчур формальными, то предложу третий. Давайте запишем общий член в таком виде:

$$
u_n=frac{n}{n^4-10n^3+35n^2-48n+29}.
$$

Вычислим первые четыре члена ряда, используя предложенную формулу общего члена:

begin{aligned}
& u_1=frac{1}{1^4-10cdot 1^3+35cdot 1^2-48cdot 1+29}=frac{1}{7};\
& u_2=frac{2}{2^4-10cdot 2^3+35cdot 2^2-48cdot 2+29}=frac{2}{9};\
& u_3=frac{3}{3^4-10cdot 3^3+35cdot 3^2-48cdot 3+29}=frac{3}{11};\
& u_4=frac{4}{4^4-10cdot 4^3+35cdot 4^2-48cdot 4+29}=frac{4}{13}.
end{aligned}

Как видите, предложенная формула общего члена вполне корректна. И таких вариаций можно придумать бесконечно много, их количество ничем не ограничено. В стандартных примерах, конечно, используется стандартный набор неких известных последовательностей (прогрессии, степени, факториалы и т.д.). Однако в таких задачах всегда присутствует неопределённость, и об этом желательно помнить.

Во всех последующих примерах эта неоднозначность оговариваться не будет. Решать станем стандартными способами, которые приняты в большинстве задачников.

Ответ: общий член ряда: $u_n=frac{n}{2n+5}$.

Пример №2

Записать общий член ряда $frac{1}{1cdot 5}+frac{1}{3cdot 8}+frac{1}{5cdot 11}+frac{1}{7cdot 14}+frac{1}{9cdot 17}+ldots$.

Решение

Нам известны первые пять членов ряда:

$$
u_1=frac{1}{1cdot 5};; u_2=frac{1}{3cdot 8}; ; u_3=frac{1}{5cdot 11}; ; u_4=frac{1}{7cdot 14}; ; u_5=frac{1}{9cdot 17}.
$$

Все известные нам члены ряда – дроби, значит и общий член ряда будем искать в виде дроби:

$$
u_n=frac{?}{?}.
$$

Сразу обратим внимание на числитель. Во всех числителях стоят единицы, поэтому и в числителе общего члена ряда будет единица, т.е.

$$
u_n=frac{1}{?}.
$$

Теперь обратимся к знаменателю. В знаменателях известных нам первых членов ряда расположены произведения чисел: $1cdot 5$, $3cdot 8$, $5cdot 11$, $7cdot 14$, $9cdot 17$. Первые из этих чисел таковы: 1, 3, 5, 7, 9. Данная последовательность имеет первый член $a_1=1$, а каждый последующий получается из предыдущего прибавлением числа $d=2$. Иными словами, это первые пять членов арифметической прогрессии, общий член которой можно записать с помощью формулы (4):

$$
a_n=1+2cdot (n-1)=1+2n-2=2n-1.
$$

В произведениях $1cdot 5$, $3cdot 8$, $5cdot 11$, $7cdot 14$, $9cdot 17$ вторые числа таковы: 5, 8, 11, 14, 17. Это элементы арифметической прогрессии, первый член которой $b_1=5$, а знаменатель $d=3$. Общий член этой прогрессии запишем с помощью всё той же формулы (4):

$$
b_n=5+3cdot (n-1)=5+3n-3=3n+2.
$$

Сведём результаты воедино. Произведение в знаменателе общего члена ряда таково: $(2n-1)(3n+2)$. А сам общий член ряда имеет следующий вид:

$$
u_n=frac{1}{(2n-1)(3n+2)}.
$$

Для проверки полученного результата найдём по формуле $u_n=frac{1}{(2n-1)(3n+2)}$ те четыре первых члена ряда, которые нам известны:

begin{aligned}
& u_1=frac{1}{(2cdot 1-1)(3cdot 1+2)}=frac{1}{1cdot 5};\
& u_2=frac{1}{(2cdot 2-1)(3cdot 2+2)}=frac{1}{3cdot 8};\
& u_3=frac{1}{(2cdot 3-1)(3cdot 3+2)}=frac{1}{5cdot 11};\
& u_4=frac{1}{(2cdot 4-1)(3cdot 4+2)}=frac{1}{7cdot 14};\
& u_5=frac{1}{(2cdot 5-1)(3cdot 5+2)}=frac{1}{9cdot 17}.
end{aligned}

Итак, формула $u_n=frac{1}{(2n-1)(3n+2)}$ позволяет точно вычислить члены ряда, известные из условия. При желании заданный ряд можно записать так:

$$
sumlimits_{n=1}^{infty}frac{1}{(2n-1)(3n+2)}=frac{1}{1cdot 5}+frac{1}{3cdot 8}+frac{1}{5cdot 11}+frac{1}{7cdot 14}+frac{1}{9cdot 17}+ldots
$$

Ответ: общий член ряда: $u_n=frac{1}{(2n-1)(3n+2)}$.

Продолжение этой темы рассмотрим в второй и третьей частях.

Источник

Содержание:

Основные понятия и определения
Задание последовательности формулой ее общего члена
Рекуррентный способ задания последовательности

Основные понятия и определения

Определение

Последовательностью называется функция, которая переводит множество
натуральных
чисел $N$ в некоторое множество
$X$ :
$left{x_{n}right}=left{x_{n}right}_{n=1}^{infty}=left{x_{1} ; x_{2} ; ldots ; x_{n} ; ldotsright}, x_{i} in N$

Элемент $x_{1}$ называется первым членом
последовательности, $x_{2}$ — вторым, … ,
$x_{n}$ —
$n$-ым или общим членом последовательности.

Пример

Задание. Для последовательности $x_{n}={-1 ; 2 ; 5 ; 8 ;-3 ; 0 ; ldots}$
определить, чему равен третий член $x_{3}$

Решение. Третьим элементом последовательности будет элемент, идущий третьим по счету, то есть для
заданной последовательности имеем, что $x_{3}=5$

Ответ. $x_{3}=5$

Задание последовательности формулой ее общего члена

Обычно последовательность целесообразнее задавать формулой ее общего члена, которая позволяет найти любой член
последовательности, зная его номер.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти формулу общего члена последовательности
$x_{n}={6 ; 20 ; 56 ; 144 ; 352 ; ldots}$

Решение. Запишем каждый член последовательности в следующем виде:

$n=1 : x_{1}=6=2 cdot 3=2^{1} cdot 3=2^{1} cdot(2 cdot 1+1)$

$n=2 : x_{2}=20=4 cdot 5=2^{2} cdot 5=2^{2} cdot(2 cdot 2+1)$

$n=3 : x_{3}=56=8 cdot 7=2^{3} cdot 7=2^{3} cdot(2 cdot 3+1)$

Как видим, члены последовательности представляют собой произведение степени двойки, умноженной на
последовательные нечетные числа, причем два возводится в степень, которая равна номеру рассматриваемого элемента.

Таким образом, делаем вывод, что

$x_{n}=2^{n} cdot(2 n+1)$

Ответ. Формула общего члена: $x_{n}=2^{n} cdot(2 n+1)$

Пример

Задание. Найти 15 член последовательности, заданной формулой
$n$-го члена:
$x_{n}=frac{(-1)^{n}}{n}, n in N$

Решение. Для того чтобы найти $x_{15}$ ,
подставим в формулу общего члена значение $n=15$ . Получим:

$x_{15}=frac{(-1)^{15}}{15}=-frac{1}{15}$

Ответ. $x_{15}=frac{(-1)^{15}}{15}=-frac{1}{15}$

Пример

Задание. Проверить, являются ли числа
$a=6$ и
$b=1$ членами последовательности
$left{x_{n}right}=left{frac{n^{2}+11}{n+1}right}$

Решение. Число $a=6$ является
членом последовательности $left{x_{n}right}, n in N$ , если существует
такой номер $n_{0} in N$ , что
$x_{n_{0}}=a=6$ :

$6=x_{n o}=frac{n_{0}^{2}+11}{n_{0}+1} Rightarrow frac{n_{0}^{2}+11}{n_{0}+1}=6 Rightarrow$

$Rightarrow n_{0}^{2}-6 n_{0}+5=0 Rightarrow=left{begin{array}{l}{n_{0}=1} \ {n_{0}=5}end{array}right.$

Таким образом, число $a=6$ является первым и
пятым членами заданной последовательности.

Проверим теперь, является ли число $b=1$ членом указанной
последовательности $left{x_{n}right}=left{frac{n^{2}+11}{n+1}right}$ . Рассуждая аналогично,
как и для $a=6$ , получаем:

$frac{n_{0}^{2}+11}{n_{0}+1}=1 Rightarrow n_{0}^{2}-n_{0}+10=0 Rightarrow D=1-40=-39 lt 0$

Таким образом, уравнение $n_{0}^{2}-n_{0}+10=0$ не имеет
решение в натуральных числах, а значит, $b=1$ не
является членом последовательности $left{x_{n}right}$

Ответ. Число $a=6$ является
первым и пятым членами заданной последовательности, а
$b=1$ не является членом последовательности
$left{x_{n}right}=left{frac{n^{2}+11}{n+1}right}$

Рекуррентный способ задания последовательности

Другим способом задания последовательности является задание последовательности с помощью рекуррентного соотношения.
В этом случае задается один или несколько первых элементов последовательности, а остальные определяются по некоторому
правилу. Например, известен первый член $x_{1}$
последовательности и известно, что $x_{n+1}=fleft(x_{n}right)$ , то
есть $x_{2}=fleft(x_{1}right), x_{3}=fleft(x_{2}right)$ и так далее до нужного члена.

Пример

Примером рекуррентно заданной последовательности является последовательность чисел
Фибоначчи — 1, 1, 2, 3, 5, 8, 13, … , в которой каждое последующее число, начиная с третьего, является суммой
двух предыдущих: 2 = 1 + 1; 3 = 2 + 1 и так далее. Данную последовательность можно задать рекуррентно:

$x_{n+2}=x_{n+1}+x_{n}, n in N, x_{1}=x_{2}=1$

Пример

Задание. Последовательность $left{x_{n}right}$
задана при помощи рекуррентного соотношения $x_{n+2}=frac{1}{2}left(x_{n+1}+x_{n}right), x_{1}=2, x_{2}=4$ .
Выписать несколько первых членов этой последовательности.

Решение. Найдем третий член заданной последовательности:

$x_{3}=frac{1}{2}left(x_{2}+x_{1}right)=frac{4+2}{2}=frac{6}{2}=3$

Аналогично находим далее, что

$x_{4}=frac{1}{2}left(x_{3}+x_{2}right)=frac{3+4}{2}=frac{7}{2}=3,5$

$x_{5}=frac{1}{2}left(x_{4}+x_{3}right)=frac{3+3,5}{2}=frac{6,5}{2}=3,25$

и так далее.

При рекуррентном задании последовательностей, получаются очень громоздкими выкладки, так как, чтобы найти элементы с
большими номерами, необходимо найти все предыдущие члены указанной последовательности, например, для
нахождения $x_{500}$ надо найти все предыдущие 499 членов.

Читать дальше: ограниченные последовательности.

Источник

Онлайн калькулятор для нахождения формулы общего члена последовательности.

Скачать калькулятор

Рейтинг: 2.7 (Голосов 311)

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Сообщить об ошибке

Смотрите также

Решение прогрессии	Графические построения	Математический анализ	Решение интегралов	Решение неравенств
Решение функций	Решение комплексных чисел	Производные функции	Решение логарифмов	Решение уравнений

Источник

17:22

формула последовательности

Формула общего члена последовательности

Определение. Последовательностью называется функция, которая переводит множество натуральных чисел N в некоторое множество X:

Как найти общую формулу

Пример 1. Найти формулу общего члена последовательности { 2, 3/2, 5/4, 9/8,…}

Решение. В калькулятор вводим первые четыре члена последовательности 2, 3/2, 5/4, 9/8, получаем формулу общего члена

Пример 2. Найти общий член ряда

Решение. Не всегда калькулятор сам справляется с задачей найти общий член последовательности. Тогда проявляем математическую смекалку: находим по отдельности общую формулу числителя и знаменателя.В калькулятор вводим первые четыре члена последовательности числителей 3, 8, 15, 24 — получаем формулу числителя n²+2n. Далее вводим в калькулятор четыре первые знаменателя: 13,103,1003,10003 — получаем 3+10ⁿ

Следовательно, общий член

Пример 3. Найти общий член ряда

Решение. Нетрудно заметить, что четвертый член ряда выбивается из закономерности числителей √n. Выполним замену

Следовательно общая формула числителя √n. В калькулятор вводим четыре первых знаменателя 1,2,6,24 — получаем n!

Можем записать формулу общего члена (учитываем знак)

Категория: Найти предел | Просмотров: 28374 | | Теги: найти предел | Рейтинг: 2.0/3

Источник

Что такое последовательность?

Последовательность — это функция, домен которой представляет собой упорядоченный список чисел. Эти числа представляют собой положительные целые числа, начинающиеся с 1. Иногда люди по ошибке используют термины «серия» и «последовательность». Последовательность — это набор положительных целых чисел, а серия — это сумма этих положительных целых чисел. Обозначение терминов в последовательности:

₁, A ₂, A ₃, A ₄, A _н,…

Найти n-й член последовательности легко с помощью общего уравнения. Но делать наоборот — борьба. Поиск общего уравнения для заданной последовательности требует много размышлений и практики, но изучение конкретного правила поможет вам найти общее уравнение. В этой статье вы узнаете, как вызвать закономерности последовательностей и написать общий термин, когда даны первые несколько терминов. Существует пошаговое руководство, которое поможет вам понять процесс и дать вам четкие и правильные вычисления.

Общий термин арифметических и геометрических рядов

Джон Рэй Куэвас

Что такое арифметическая последовательность?

Арифметический ряд — это последовательность упорядоченных чисел с постоянной разницей. В арифметической последовательности вы заметите, что каждая пара следующих друг за другом членов отличается на одинаковую величину. Например, вот первые пять членов серии.

3, 8, 13, 18, 23

Вы замечаете особый узор? Очевидно, что каждое число после первого на пять больше, чем предыдущее. То есть общая разница в последовательности — пять. Обычно формула для n-го члена арифметической последовательности, первый член которой равен _1, а общая разность — d, отображается ниже.

а _п = а ₁ + (п — 1) г

Этапы нахождения общей формулы арифметических и геометрических последовательностей

1. Создайте таблицу с заголовками n и a _n, где n обозначает набор последовательных положительных целых чисел, а _n обозначает термин, соответствующий положительным целым числам. Вы можете выбрать только первые пять членов последовательности. Например, сведите в таблицу ряды 5, 10, 15, 20, 25,…


п	ан
1	5
2	10
3	15
4	20
5	25

2. Решите первое общее различие a. Рассмотрим решение как древовидную диаграмму. Для этого шага есть два условия. Этот процесс применяется только к последовательностям, имеющим линейный или квадратичный характер.

Условие 1: Если первая общая разность является константой, используйте линейное уравнение ax + b = 0 при нахождении общего члена последовательности.

а. Выберите две пары чисел из таблицы и составьте два уравнения. Значение n из таблицы соответствует x в линейном уравнении, а значение a _n соответствует 0 в линейном уравнении.

а (п) + Ь = а _п

б. Сформировав два уравнения, вычислите a и b методом вычитания.

c. Подставим вместо общего члена a и b.

d. Проверьте правильность общего члена, подставив значения в общее уравнение. Если общий термин не соответствует последовательности, в ваших расчетах есть ошибка.

Условие 2: Если первая разность непостоянна, а вторая разность постоянна, используйте квадратное уравнение ax ² + b (x) + c = 0.

а. Выберите из таблицы три пары чисел и составьте три уравнения. Значение n из таблицы соответствует x в линейном уравнении, а значение an соответствует 0 в линейном уравнении.

an ² + b (n) + c = a _n

б. Сформировав три уравнения, вычислите a, b и c методом вычитания.

c. Замените a, b и c на общий термин.

Нахождение общего члена последовательности

Джон Рэй Куэвас

Проблема 1: общий термин арифметической последовательности с использованием условия 1

Найдите общий член последовательности 7, 9, 11, 13, 15, 17,…

Решение

а. Создайте таблицу значений _n и n.


п	ан
1	7
2	9
3	11
4	13
5	15
6	17

б. Возьмите первое отличие _n.

Первая разность арифметического ряда

Джон Рэй Куэвас

c. Постоянная разница равна 2. Поскольку первая разность постоянна, общий член данной последовательности является линейным. Выберите два набора значений из таблицы и составьте два уравнения.

Общее уравнение:

an + b = a _n

Уравнение 1:

при n = 1, a ₁ = 7

а (1) + Ь = 7

а + Ь = 7

Уравнение 2:

при n = 2, a ₂ = 9

а (2) + Ь = 9

2a + b = 9

d. Вычтите два уравнения.

(2a + b = 9) — (a + b = 7)

а = 2

е. Подставьте значение a = 2 в уравнение 1.

а + Ь = 7

2 + Ь = 7

б = 7 — 2

b = 5

f. Подставьте значения a = 2 и b = 5 в общее уравнение.

an + b = a _n

2n + 5 = a _n

г. Проверьте общий член, подставив значения в уравнение.

а _п = 2 _п + 5

а ₁ = 2 (1) + 5 = 7

а ₂ = 2 (2) + 5 = 9

а ₃ = 2 (3) + 5 = 11

а ₄ = 2 (4) + 5 = 13

а ₅ = 2 (5) + 5 = 15

а ₆ = 2 (6) + 5 = 17

Следовательно, общий член последовательности:

а _п = 2 _п + 5

Проблема 2: общий термин арифметической последовательности с использованием условия 2

Найдите общий член последовательности 2, 3, 5, 8, 12, 17, 23, 30,…

Решение

а. Создайте таблицу значений _n и n.


п	ан
1	2
2	3
3	5
4	8
5	12
6	17
7	23
8	30

б. Возьмите первое отличие _n. Если первая разность _n непостоянна, возьмите вторую.

Первая и вторая разность арифметического ряда

Джон Рэй Куэвас

c. Вторая разница равна 1. Поскольку вторая разность постоянна, общий член данной последовательности квадратичен. Выберите три набора значений из таблицы и составьте три уравнения.

Общее уравнение:

an ² + b (n) + c = a _n

Уравнение 1:

при n = 1, a ₁ = 2

а (1) + Ь (1) + с = 2

а + б + с = 2

Уравнение 2:

при n = 2, a ₂ = 3

а (2) ² + Ь (2) + с = 3

4a + 2b + c = 3

Уравнение 3:

при n = 3, a ₂ = 5

а (3) ² + Ь (3) + с = 5

9a + 3b + c = 5

d. Вычтите три уравнения.

Уравнение 2 — Уравнение 1: (4a + 2b + c = 3) — (a + b + c = 2)

Уравнение 2 — Уравнение 1: 3a + b = 1

Уравнение 3 — Уравнение 2: (9a + 3b + c = 5) — (4a + 2b + c = 3)

Уравнение 3 — Уравнение 2: 5a + b = 2

(5a + b = 2) — (3a + b = 1)

2а = 1

а = 1/2

е. Подставьте значение a = 1/2 в любое из двух последних уравнений.

3а + Ь = 1

3 (1/2) + Ь = 1

б = 1 — 3/2

б = — 1/2

а + б + с = 2

1/2 — 1/2 + c = 2

с = 2

f. Подставьте значения a = 1/2, b = -1/2 и c = 2 в общее уравнение.

an ² + b (n) + c = a _n

(1/2) n ² — (1/2) (n) + 2 = a _n

г. Проверьте общий член, подставив значения в уравнение.

(1/2) n ² — (1/2) (n) + 2 = a _n

а _{п =} 1/2 (п ² — п + 4)

а ₁ = 1/2 (1 ² — 1 + 4) = 2

а ₂ = 1/2 (2 ² — 2 + 4) = 3

а ₃ = 1/2 (3 ² — 3 + 4) = 5

а ₄ = 1/2 (4 ² — 4 + 4) = 8

а ₅ = 1/2 (5 ² — 5 + 4) = 12

а ₆ = 1/2 (6 ² — 6 + 4) = 17

₇ = 1/2 (7 ² — 7 + 4) = 23

Следовательно, общий член последовательности:

а _{п =} 1/2 (п ² — п + 4)

Проблема 3: общий термин арифметической последовательности с использованием условия 2

Найдите общий член для последовательности 2, 4, 8, 14, 22,…

Решение

а. Создайте таблицу значений _n и n.


п	ан
1	2
2	4
3	8
4	14
5	22

б. Возьмите первую и вторую разность _n.

Первая и вторая разность арифметической последовательности

Джон Рэй Куэвас

c. Вторая разность равна 2. Поскольку вторая разность является константой, общий член данной последовательности квадратичен. Выберите три набора значений из таблицы и составьте три уравнения.

Общее уравнение:

an ² + b (n) + c = a _n

Уравнение 1:

при n = 1, a ₁ = 2

а (1) + Ь (1) + с = 2

а + б + с = 2

Уравнение 2:

при n = 2, a ₂ = 4

а (2) ² + Ь (2) + с = 4

4a + 2b + c = 4

Уравнение 3:

при n = 3, a ₂ = 8

а (3) ² + Ь (3) + с = 8

9a + 3b + c = 8

d. Вычтите три уравнения.

Уравнение 2 — Уравнение 1: (4a + 2b + c = 4) — (a + b + c = 2)

Уравнение 2 — Уравнение 1: 3a + b = 2

Уравнение 3 — Уравнение 2: (9a + 3b + c = — (4a + 2b + c = 4)

Уравнение 3 — Уравнение 2: 5a + b = 4

(5a + b = 4) — (3a + b = 2)

2а = 2

а = 1

е. Подставьте значение a = 1 в любое из двух последних уравнений.

3а + Ь = 2

3 (1) + Ь = 2

б = 2-3

б = — 1

а + б + с = 2

1-1 + с = 2

с = 2

f. Подставьте значения a = 1, b = -1 и c = 2 в общее уравнение.

an ² + b (n) + c = a _n

(1) n ² — (1) (n) + 2 = a _n

п ² — п + 2 = а _п

г. Проверьте общий член, подставив значения в уравнение.

п ² — п + 2 = а _п

а _{1 =} 1 ² — 1 + 2 = 2

а _{2 =} 2 ² — 2 + 2 = 4

а _{3 =} 3 ² — 3 + 2 = 8

а _{4 =} 4 ² — 4 + 2 = 14

а _{5 =} 5 ² — 5 + 2 = 22

Следовательно, общий член последовательности:

а _{п =} п ² — п + 2

Самооценка

Для каждого вопроса выберите лучший ответ. Ключ ответа ниже.

Найдите общий член последовательности 25, 50, 75, 100, 125, 150,...
- ан = п + 25
- an = 25n
- an = 25n ^ 2
Найдите общий член последовательности 7/2, 13/2, 19/2, 25/2, 31/2,...
- an = 3 + n / 2
- ан = п + 3/2
- ан = 3n + 1/2

Ключ ответа

an = 25n
ан = 3n + 1/2

Интерпретация вашей оценки

Если вы получили 0 правильных ответов: извините, попробуйте еще раз!

Если вы получили 2 правильных ответа: Хорошая работа!

Изучите другие статьи по математике

Полное руководство по треугольнику 30-60-90 (с формулами и примерами)
Эта статья представляет собой полное руководство по решению задач для треугольников 30-60-90. Он включает формулы паттернов и правила, необходимые для понимания концепции треугольников 30-60-90. Также приведены примеры, показывающие пошаговую процедуру, как это сделать.
Как использовать правило знаков Декарта (с примерами)
Научитесь использовать правило знаков Декарта для определения количества положительных и отрицательных нулей в полиномиальном уравнении. Эта статья представляет собой полное руководство, которое определяет Правило знаков Декарта, процедуру его использования, а также подробные примеры и решения.
Решение проблем связанных ставок в исчислении
Научитесь решать различные виды задач связанных ставок в исчислении. Эта статья представляет собой полное руководство, которое показывает пошаговую процедуру решения проблем, связанных со связанными / связанными ставками.
Односторонние внутренние углы: теорема, доказательство и примеры
В этой статье вы можете изучить концепцию теоремы об односторонних внутренних углах в геометрии, решая различные приведенные примеры. В статье также содержится обращение к теореме о односторонних внутренних углах и ее доказательство.
Предельные законы и оценка пределов
Эта статья поможет вам научиться оценивать пределы, решая различные задачи в исчислении, которые требуют применения предельных законов.
Формулы уменьшения мощности и их использование (с примерами)
В этой статье вы можете узнать, как использовать формулы уменьшения мощности для упрощения и оценки тригонометрических функций различных степеней.

Вопросы и Ответы

Вопрос: Как найти общий член последовательности 0, 3, 8, 15, 24?

Ответ: Общий термин для последовательности — an = a (n-1) + 2 (n + 1) + 1

Вопрос: каков общий термин набора {1,4,9,16,25}?

Ответ: Общий член последовательности {1,4,9,16,25} равен n ^ 2.

Вопрос: Как получить формулу, если общая разница приходится на третью строку?

Ответ: Если постоянная разность приходится на третье, уравнение кубическое. Попробуйте решить его по образцу квадратных уравнений. Если это не применимо, вы можете решить эту проблему, используя логику и метод проб и ошибок.

Вопрос: Как найти общий член последовательности 4, 12, 26, 72, 104, 142, 186?

Ответ: Общий член последовательности равен an = 3n ^ 2 — n + 2. Последовательность квадратична со второй разностью 6. Общий член имеет вид an = αn ^ 2 + βn + γ. Чтобы найти α, β, Вставные значения γ для n = 1, 2, 3:

4 = α + β + γ

12 = 4α + 2β + γ

26 = 9α + 3β + γ

и решаем, получая α = 3, β = −1, γ = 2

Вопрос: Каков общий член последовательности 6,1, -4, -9?

Ответ: Это простая арифметическая последовательность. Он следует формуле an = a1 + d (n-1). Но в этом случае второй член должен быть отрицательным an = a1 — d (n-1).

При n = 1, 6 — 5 (1-1) = 6

При n = 2, 6 — 5 (2-1) = 1

При n = 3,6 — 5 (3-1) = -4

При n = 4, 6 — 5 (4-1) = -9

Вопрос: Каким будет n-й член последовательности 4, 12, 28, 46, 72, 104, 142…?

Ответ: К сожалению, такой последовательности не существует. Но если вы замените 28 на 26. Общий член последовательности будет an = 3n ^ 2 — n + 2

Вопрос: Как найти общий член для последовательности 1/2, 2/3, 3/4, 4/5…?

Ответ: Для данной последовательности общий термин можно определить как n / (n + 1), где «n» явно натуральное число.

Вопрос: Есть ли более быстрый способ вычислить общий член последовательности?

Ответ: К сожалению, это самый простой способ найти общий член базовых последовательностей. Вы можете обратиться к своим учебникам или подождать, пока я напишу еще одну статью о вашей проблеме.

Вопрос: Какова явная формула для n-го члена последовательности 1,0,1,0?

Ответ: Явная формула для n-го члена последовательности 1,0,1,0: an = 1/2 + 1/2 (−1) ^ n, где индекс начинается с 0.

Вопрос: Что такое обозначение пустого множества в построителе множеств?

Ответ: обозначение пустого множества — «Ø».

Вопрос: Какова общая формула последовательности 3,6,12, 24..?

Ответ: Общий член данной последовательности равен an = 3 ^ r ^ (n-1).

Вопрос: Что делать, если для всех строк нет общей разницы?

Ответ: если для всех строк нет общей разницы, попробуйте определить ход последовательности методом проб и ошибок. Вы должны сначала идентифицировать шаблон, прежде чем заключать уравнение.

Вопрос: Каков общий вид последовательности 5,9,13,17,21,25,29,33?

Ответ: Общий член последовательности равен 4n + 1.

Вопрос: Есть ли другой способ найти общий член последовательностей, используя условие 2?

Ответ: Есть много способов решить общий член последовательностей, один — методом проб и ошибок. Главное, что нужно сделать, это записать их общие черты и вывести из них уравнения.

Вопрос: Как найти общий член последовательности 9,9,7,3?

Ответ: Если это правильная последовательность, то единственная картина, которую я вижу, — это когда вы начинаете с числа 9.

9 — 0 = 9

9 — 2 = 7

9–6 = 3

Следовательно.. 9 — (n (n-1)), где n начинается с 1.

Если нет, то я считаю, что указанная вами последовательность ошибочна. Пожалуйста, попробуйте перепроверить.

Вопрос: Как найти выражение для общего члена ряда 1 + 1 • 3 + 1 • 3 • 5 + 1 • 3 • 5 • 7 +…?

Ответ: Общий член серии (2n-1) !.

Вопрос: Общий термин для последовательности {1,4,13,40,121}?

Ответ: 1

1 + 3 = 4

1 + 3 + 3 ^ 2 = 13

1 + 3 + 3 ^ 2 + 3 ^ 3 = 40

1 + 3 + 3 ^ 2 + 3 ^ 3 + 3 ^ 4 = 121

Итак, общий член последовательности — (под) n = a (под) n-1 + 3 ^ (n-1)

Вопрос: Как найти общий член для последовательности, заданной как an = 3 + 4a (n-1), заданной a1 = 4?

Ответ: То есть вы имеете в виду, как найти последовательность с учетом общего термина. Учитывая общий термин, просто начните подставлять значение a1 в уравнение и пусть n = 1. Сделайте это для a2, где n = 2, и так далее и так далее.

Вопрос: Как найти общую схему 3/7, 5/10, 7/13,…?

Ответ: Для дробей можно отдельно анализировать закономерность в числителе и знаменателе.

Для числителя мы видим, что образец складывается из 2.

3 + 2 = 5

5 + 2 = 7

или добавив число, кратное 2

3 + 2 = 5

3 + 4 = 7

Следовательно, общий член числителя равен 2n + 1.

Что касается знаменателя, мы можем заметить, что образец складывается из 3.

7 + 3 = 10

10 + 3 = 13

Или добавив число, кратное 3

7 + 3 = 10

7 + 6 = 13

Следовательно, знаменатель равен 3n + 4.

Объедините два шаблона, и вы получите (2n + 1) / (3n + 4), который является окончательным ответом.

Вопрос: Каков общий член последовательности {7,3, -1, -5}?

Ответ: Шаблон для данной последовательности:

7 — 4 = 3

3–4 = -1

-1-4 = -5

Все последующие члены вычитаются на 4.

Вопрос: Как найти общий член последовательности 8,13,18,23,…?

Ответ: Первое, что нужно сделать, это попытаться найти общее различие.

13 — 8 = 5

18–13 = 5

23–18 = 5

Таким образом, общее различие — 5. Последовательность достигается добавлением 5 к предыдущему члену. Напомним, что формула арифметической прогрессии имеет вид an = a1 + (n — 1) d. Если a1 = 8 и d = 5, подставьте значения в общую формулу.

an = a1 + (n — 1) d

an = 8 + (n — 1) (5)

ан = 8 + 5n — 5

an = 3 + 5n

Следовательно, общий член арифметической последовательности равен an = 3 + 5n

Вопрос: Как найти общий член последовательности -1, 1, 5, 9, 11?

Ответ: На самом деле я не очень хорошо понимаю последовательность. Но мой инстинкт подсказывает, что это так…

-1 + 2 = 1

1 + 4 = 5

5 +4 = 9

9 + 2 = 11

+2, +4, +4, +2, +4, +4, +2, +4, +4

Вопрос: Как найти общий член 32,16,8,4,2,…?

Ответ: Я считаю, что каждый термин (кроме первого) находится путем деления предыдущего члена на 2.

Вопрос: Как найти общий член последовательности 1/2, 1/3, 1/4, 1/5?

Ответ: Вы можете заметить, что единственная изменяющаяся часть — это знаменатель. Итак, мы можем установить числитель равным 1. Тогда общая разница знаменателя равна 1. Итак, выражение равно n + 1.

Общий член последовательности равен 1 / (n + 1)

Вопрос: Как найти общий член последовательности 1,6,15,28?

Ответ: Общий член последовательности равен n (2n-1).

Вопрос: Как найти общий член последовательности 1, 5, 12, 22?

Ответ: Общий член последовательности 1, 5, 12, 22 равен / 2.

Источник