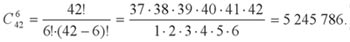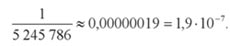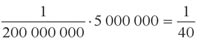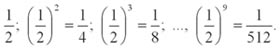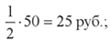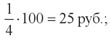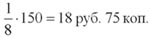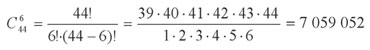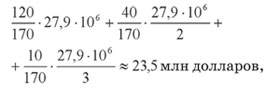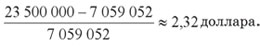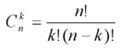Как найти общий выигрыш

Теперь нас интересует
вопрос, кто и в какой степени выигрывает
от рыночного обмена. Начнем анализ с
потребителей.

А. Выигрыш
потребителей

Любой
потребитель хотел бы купить товар как
можно дешевле, но для каждого из них
существует максимальная цена, которую
он согласен заплатить за данную единицу
товара, прежде чем откажется от ее
покупки. Такая цена называется ценой
спроса.
Совокупность цен спроса всех потребителей
образует кривую рыночного спроса.

Вместе
с тем, все потребители независимо от их
цен спроса покупают товар по единой
рыночной цене. Разница между индивидуальной
ценой спроса и рыночной ценой составляет
выигрыш
потребителя
(потребительский излишек) при покупке
данной единицы товара. Это своего рода
прибыль потребителя.

Поясним это
примером. Пусть перед нами три любителя
пива, каждый из которых желает выпить
одну бутылку в день. Доходы, однако, у
них разные, а потому первый любитель
мог бы максимально заплатить за пиво
15 руб. Второй чуть беднее, и он не заплатит
больше 12 руб. А доходы третьего не
позволяют ему покупать пиво дороже, чем
за 10 руб. Допустим, рыночная цена пива
10 руб. Тогда первый любитель выигрывает
5 руб. (10-5) на каждой бутылке, второй — 2
руб., а третий выигрыша не получает, ибо
он реально платит ту максимальную сумму,
которую в состоянии заплатить.

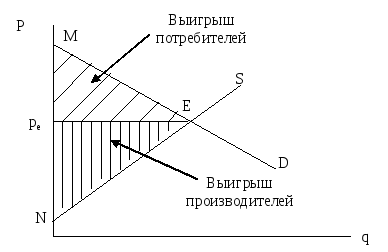
Предположим
теперь, что потребителей очень много.
Тогда геометрически выигрыш всех
потребителей равен площади треугольника,
ограниченного кривой спроса, линией
рыночной цены и осью цен. В нашем примере
это треугольник P^*EM,
где P^*
— рыночная цена (рис. 4-16):

Рис.
4-16. Выигрыш потребителей

Б. Выигрыш
производителей

Поговорим
теперь о производителях. Любой
производитель хотел бы продать товар
как можно дороже, но для каждого из них
существует минимальная цена, по которой
он еще согласится продавать данную
единицу товара, прежде чем откажется
от ее производства и продажи. Такая цена
называется ценой
предложения.
Совокупность цен предложения всех
производителей образует кривую рыночного
предложения.

Вместе
с тем все производители независимо от
их цен предложения продают товар по
единой рыночной цене. Разница между
рыночной ценой и индивидуальной ценой
предложения и составляет выигрыш
производителя
(излишек производителя) при продаже
данной единицы товара. Предупреждение:
выигрыш производителя обычно не равен
его прибыли, но для объяснения этого
необходим более скрупулезный анализ.

Расчет выигрыша
производителей производится по той же
схеме, что и расчет выигрыша потребителей.
Пусть три фирмы производят по одной
единице однородного товара, но с разными
затратами. Затраты первой составляют
2 руб., второй — 3 руб. и третьей – 4 руб.
Допустим также, что на рынке этот товар
стоит 4 руб. Тогда, продавая по данной
цене свои товары, первая фирма выигрывает
2 руб., вторая — 1 руб., а третья выигрыша
не получает.

Предположим
теперь, что товаров производится очень
много. Тогда геометрически выигрыш всех
производителей равен площади треугольника,
ограниченного кривой предложения,
линией рыночной цены и осью цен. В нашем
примере это треугольник P^*EN,
где P^*
— рыночная цена (рис. 4-17):

Рис.
4-17. Выигрыш производителей

Выигрыш
потребителей и выигрыш производителей
можно показать на одном рисунке (рис.
4-18):

Рис.
4-18. Выигрыш потребителей и выигрыш
производителей

Отсюда вывод:
добровольный рыночный обмен по равновесной
цене выгоден как покупателям, так и
продавцам.

Соседние файлы в папке микро

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В пределах поля возможностей, ограниченного бюджетной линией, потребитель свободен осуществить любой выбор, предпочесть любую комбинацию товаров А и В. При этом потребитель основывается на субъективной оценке того удовлетворения, которое он получит от потребления товара. В экономической теории такое удовлетворение называется полезностью.

Каждый потребитель заинтересован максимизировать общее количество полезности, которое он получает. В этом состоит его выигрыш. В своем стремлении к максимизации полезного эффекта потребитель наращивает потребление. С потреблением каждой дополнительной единицы одноименного товара совокупная полезность прирастает на некоторую величину, именуемую предельной полезностью.

Предельная полезность есть полезность от потребления дополнительной единицы продукта или услуги.

Таким образом, совокупная полезность данного количества одноименного товара равна сумме предельных полезностей всех единиц этого товара.

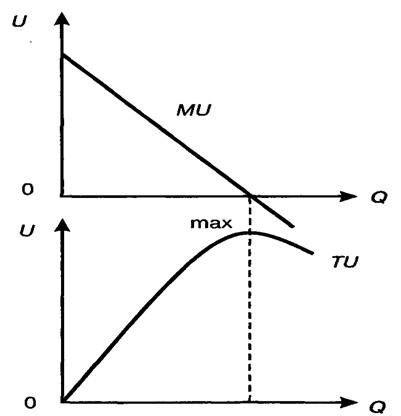
Нехитрый житейский опыт подсказывает, что по мере увеличения количества потребляемого в заданное время одноименного продукта предельная полезность каждой последующей его единицы будет снижаться. Другими словами, чем больше пирожных вы съедаете за один присест, тем меньше хочется съесть еще одно, тем меньше удовольствия оно вам принесет. Этот феномен был охарактеризован известным английским экономистом А. Маршаллом как закон убывания предельной полезности (1890).

Графики на рис. 1 иллюстрируют поведение совокупной и предельной полезностей. Можно заметить, что совокупная полезность растет по мере увеличения единиц потребляемого продукта, но растет все медленнее и медленнее, поскольку предельная полезность неуклонно сокращается. Когда предельная полезность становится равной нулю, совокупная полезность достигает своего максимума. Если продолжать потребление далее этой точки, предельная полезность станет отрицательной величиной, а совокупная полезность начнет уменьшаться.

Рис. 1. Соотношение предельной (MU) и совокупной (TU) полезности

Прослеживается и такая взаимосвязь совокупной и предельной полезности: предельная полезность есть отношение изменения совокупной полезности к изменению потребляемого количества продукта:

MU = изменение TU / изменение Q.

При бесконечно малых изменениях данный показатель представляет собой не что иное, как первую производную от совокупной полезности, если последняя представлена как функция от потребляемого количества продукта

MU = dTU/dQ.

До сих пор стремление потребителя максимизировать совокупную полезность рассматривалось вне всяческих ограничений. При этих условиях совокупная полезность максимизируется в точке, где предельная полезность равна нулю. Однако задача усложняется, если учитывать бюджетные ограничения и цены. Рациональный покупатель обязательно сопоставит свой выигрыш (предельную полезность) с предельными издержками.

Предельными издержками потребителя будут затраты на приобретение дополнительной единицы товара. При совершенной конкуренции предельные издержки равны цене этого товара. Покупка и потребление очередной единицы одноименного товара имеет смысл только в том случае, если предельная полезность будет больше, чем предельные издержки.

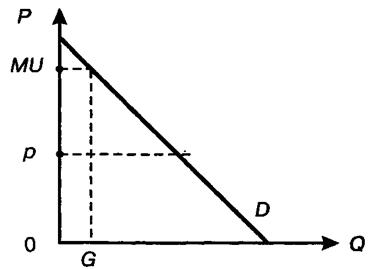
Положительная разница между предельной полезностью и предельными издержками (ценой товара) составляет предельный выигрыш потребителя. Этот показатель означает, что потребитель оценивает данную единицу товара выше уровня рыночной цены (рис. 2). Потребитель был готов заплатить в соответствии со своей субъективной оценкой предельной полезности продукта. Однако рыночная цена оказалась ниже, и покупатель остался в выигрыше.

Рис. 2. Предельный выигрыш потребителя (MU — Р) в точке Q

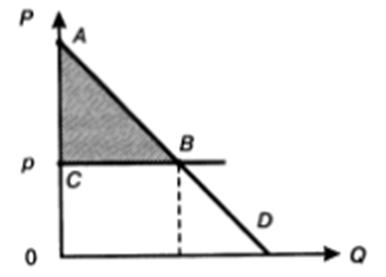
Общий выигрыш потребителя равен разнице между совокупной полезностью потребленных одноименных товаров и общими расходами на их приобретение (рис. 3). Графически совокупный потребительский выигрыш представлен площадью треугольника ABC и достигает максимума в точке, где предельная полезность товара равна его цене. Другим словами, полезность потребителя максимизируется, если MU = МС, или MU = Р.

Рис. 3. Общий выигрыш потребителя  (площадь треугольника ABC)

Введение в оборот категории «выигрыш потребителя» позволяет конкретизировать понятие рационального поведения. Поведение потребителя является рациональным, если максимизируется его совокупный выигрыш.

< Предыдущая		Следующая >

— В жизни ведь ещё лотерея есть. Я вот всегда лотерейный билет покупаю!
— Ну и как, выиграла что-нибудь?
— А как же! Два раза по рублю!
Из разговора героев фильма «Москва слезам не верит»

«Лотерея — организованная игра на счастье, при которой распределение выгод и убытков зависит от случайного извлечения того или иного билета или номера» (Энциклопедический словарь Брокгауза и Ефрона).

Игра эта давно приобрела массовый характер и стала неотъемлемой частью современной жизни. И хотя лотерея всё больше расширяет свои возможности, многие люди по-прежнему видят в ней лишь способ обогащения. Пусть и не бесплатный и не надёжный. С другой стороны, как заметил один из героев Джека Лондона, в азартной игре нельзя не считаться с фактами — людям иногда везёт. История лотерей знает и удивительные случаи выигрышей, и примеры необъяснимых совпадений, и образчики сообразительности участников и устроителей игры. С некоторыми из них непременно стоит познакомиться — хотя бы ради любопытства.

Любимчики Фортуны

Известный «способ» быстро разбогатеть — выиграть в мгновенной лотерее. Как правило, шансы приобрести счастливый билет очень малы. Тем более невероятной выглядит история работницы нью-йоркского гастронома Валери Вильсон, которая получила главный приз дважды. В 2002 году она выиграла миллион долларов в лотерее Cool Million, имея шансы 1 : 5 200 000. А четыре года спустя, приняв участие в лотерее Jubilee, стала обладательницей второго миллиона. На этот раз шансы на выигрыш оценивались как 1 : 705 600. Каков же был её шанс выиграть главный приз в обеих лотереях? Их нетрудно подсчитать: 1 : (5 200 000 • 705 600) = 1 : 3 669 120 000 000, или примерно один из 3,7 триллиона. Шанс и в самом деле ничтожно мал, в чём можно убедиться, если представить себе другую лотерею.

Допустим, что в ней участвуют все жители Земли — 7 млрд человек. Выпущенные по такому случаю 3,7 триллиона билетов со стираемым защитным слоем, из которых лишь один выигрышный, распределены между ними поровну. По правилам лотереи в регулярном еженедельном розыгрыше каждый участник использует один билет. Конечно, первый же открытый билет может оказаться выигравшим. Однако в самом неблагоприятном случае ожидание выпадения счастливого билета растянется на 10 лет!

Надо сказать, в истории американских лотерей (коих множество, и проводятся они постоянно) было всего несколько случаев с повторным выигрышем призов, превышающих миллион долларов. Правда, все они касались обычных лотерей, в которых джекпот, как правило, куда больше главного приза в мгновенной лотерее. Примечательно также, что один из самых крупных выигрышей — 254 млн долларов — достался в 2007 году 84-летнему пенсионеру, чья фамилия оказалась… Вильсон. Вот и не верь после этого в совпадения.

А рекордсменкой по количеству крупных выигрышей стала Джоан Гинтер из Лас-Вегаса. За 17 лет она побеждала в различных лотереях четыре раза — последний в 2010 году — и «заработала» таким образом более 20 млн долларов. Согласно расчётам, учтя имевшиеся каждый раз шансы выиграть, подобное достижение возможно лишь в одном случае из 36 • 10²⁴, или 36 септиллионов, на фоне которых меркнут даже 3,7 триллиона, или 3,7 • 10¹²!

Как остроумно и верно заметил по этому поводу один американский профессор математики, специалист в области теории вероятностей, случай сей поразительный, однако у вероятности нет памяти! И что характерно, шансы Джоан выиграть в очередной лотерее точно такие же, как и у любого другого игрока. Иными словами, они есть всегда, пусть и крошечные. Должно быть, перед покупкой очередного билета подобные мысли посещают (более того — обнадёживают) многих любителей лотерей.

Заветная шестёрка

«Случилось невероятное!» — так прокомментировал директор болгарской лотереи «6 из 42» выпадение в двух тиражах подряд одинаковых выигрышных чисел: 4, 15, 23, 24, 35 и 42. Произошли эти события в сентябре 2009 года, с разницей всего в четыре дня. В простое совпадение никто, включая очевидцев, тогда не поверил. Однако тщательная проверка, проведённая под личным контролем министра спорта, в чьём ведении находится лотерея, фактов махинаций не выявила. Почему же все усомнились в том, что одна и та же выигрышная комбинация чисел выпала два раза подряд случайно?

Сделаем простой расчёт. Всего способов выбрать шесть из сорока двух различных чисел имеется

Значит, вероятность выпадения единственно возможного выигрышного набора чисел в любом тираже равна

А серьёзные сомнения в случайности выпадения одной и той же числовой комбинации в двух тиражах подряд возникли из-за того, что вероятность этого события крайне мала, всего

(1,9 • 10⁻⁷)² = 3,61 • 10⁻¹⁴.

Заметим, что в подобных лотереях повторное выпадение выигрышного набора чисел изредка всё же происходит (в той же Болгарии такое было два-три раза), правда, не в двух тиражах кряду. А вот интересно, что предприняли бы организаторы лотереи, если бы числа выпали дважды, да ещё в одном и том же порядке? И, кстати, чему равна вероятность такого двойного совпадения? Между тем если в первый раз шесть чисел не угадал никто, то во второй на них поставили сразу 18 человек! Надежды тех, кто рассчитывал на крупный выигрыш, не оправдались: призовую сумму пришлось делить на всех. Словно желая опровергнуть законы теории вероятностей, накануне следующего тиража многие всерьёз обсуждали, не поставить ли на те же числа снова, ведь не исключено, что они выпадут и в третий раз!

Если одни игроки в лотерею рассчитывают победить благодаря якобы придуманной ими системе угадывания чисел (рано или поздно она, возможно, и даст результат — по законам всё той же теории вероятностей), то другие придерживаются примитивных стратегий. Ставишь, например, всегда на один и тот же набор чисел и ждёшь, когда он выпадет (если вообще выпадет). Поступавшему так американцу Крису Хоффману, любителю лотереи «5 из 39», можно сказать, крупно повезло: ждать пришлось всего-то 15 лет! О том, сколько средств он потратил за это время на покупку билетов, а главное, покрыл ли все расходы выигрыш в размере 150 тысяч долларов, история умалчивает.

«Бесплатная» лотерея

Кстати, о потраченных деньгах. В середине 1990-х годах в США проводилась «почтовая лотерея». В ней разыгрывался денежный приз в 5 млн долларов, а шанс получить его составлял 1 из 200 млн. От участников требовалось всего ничего: сделать ставку и отправить её по почте. Разрешалось делать сколько угодно ставок, но с условием — высылать их по одной. Стоит ли участвовать в такой «бесплатной» лотерее?

При таких условиях, конечно, не стоит. И вот почему. Зная вероятность выигрыша и его сумму, легко подсчитать ожидаемый выигрыш игрока^*:

доллара,

или 2,5 цента.

Однако расходы на отправку письма куда больше! Иначе говоря, ожидаемый выигрыш во много раз меньше вложенной игроком суммы, и их разность выражается числом отрицательным. Так что если тратиться на пересылку многократно, очень скоро придётся подсчитывать убытки.

Как тут не вспомнить рассказ Антона Павловича Чехова «Житейские невзгоды»? Если бы его герой сразу прикинул, во сколько ему обойдётся покупка выигрышного билета внутреннего займа, участвовавшего в денежной лотерее, то всерьёз призадумался, нужен ли он ему вообще.

Кому же выгодна «почтовая лотерея»? Ответ очевиден: почтовой службе США. По самым скромным подсчётам, при благоприятном развитии событий доход с отправленных писем должен был превзойти заявленный приз как минимум в десять раз.

Народные лотереи

И в России имеется свой любопытный опыт. Так, у нас прижились лотереи с вещевыми призами. Недаром их часто называют «народными». Вот лишь один из примеров. Чего только не придумывают транспортники, чтобы заставить пассажиров платить за проезд! Весной 2010 года в Барнауле проводилась стимулирующая лотерея «Счастливый билет». В ней разыгрывались номер и серия разовых проездных билетов на трамвай и троллейбус. Призы выдавались «натурой»: подарочными картами гипермаркета электроники, месячными проездными на городской транспорт и тому подобным. Стоит ли говорить, что за три недели проведения лотереи число «зайцев» резко сократилось, а доходы транспортников (при скромных в общем-то затратах) ощутимо возросли!

Бывает, сам процесс игры захватывает не меньше, чем желание получить приз, особенно когда возможность выигрыша заложена в каждый билет. Об этом заявляют, например, организаторы моментальной «Всероссийской жилищной лотереи». А дальше, как и положено в рекламе: «Не верите? Не хотите рисковать? Всё ещё сомневаетесь? Тогда мы идём к вам!» И не просто так, а с разумным предложением потренироваться для начала на виртуальных лотерейных билетах.

Правила игры просты. В билете девять строк (этажей), по два игровых окна в каждой; в одном из них спрятано «счастливое число», равное сумме выигрыша (она указана на защитном слое). Задача проста — угадать это число, открыв только одно окно в строке. Таким образом, двигаясь построчно снизу вверх, можно по желанию открыть от одного до девяти окон. При первой же неудаче игра прекращается, билет считается невыигрышным. Так насколько справедливо заявление организаторов? Ясно, что вероятность выбора «счастливого числа» на каждом шаге одна и та же — она равна одной второй — и по ходу игры убывает в геометрической прогрессии:

А какова средняя сумма выигрыша, приходящаяся на один билет? Если сделать всего один шаг из девяти, то она составит

если два шага, то

если три, то

и далее будет только уменьшаться (из-за того, что вероятность выигрыша убывает значительно быстрее, нежели растёт призовая сумма), а проигрыш, напротив, будет увеличиваться.

Сколько ни тренируйся, а предугадать исход игры в каждом конкретном случае невозможно. А вот сесть за компьютер всё же стоит. Если достаточно долго экспериментировать с виртуальными билетами и фиксировать результаты, можно заметить, как проявит себя «закон больших чисел» — с увеличением числа испытаний частота появления события (выпадения крупного денежного приза) приближается к его вероятности, а последняя, как мы убедились, невелика.

Имея билет на руках, благоразумно ограничиться угадыванием чисел во второй-третьей строках и скромным выигрышем. Очевидно, так же рассудили многие участники лотереи. А на что всегда рассчитывают её устроители? Как и в любой азартной игре — на человеческие слабости и неумение вовремя остановиться. Поэтому уже на билетах следующей партии «по многочисленным просьбам игроков» была выделена строка с несгораемой суммой (на седьмом этаже), а также добавилось новое правило: если на пятой или шестой строке окажется открытым окно с символом «+», игра закончится, а вы получите утешительный приз — 50 рублей. Устроителям лотереи в изобретательности не откажешь, не так ли? Как думаете, стали ли правила честнее и возросла ли после этих нововведений продажа билетов?

Непростительный промах

Допускают ли организаторы лотерей просчёты? Не поверите, но и такое случается. Следующая история произошла в одном американском штате 20 лет назад. Карточки очередного тиража лотереи «6 из 44» продавались по 1 доллару, в то время как призовой фонд составлял на тот момент 27,9 млн долларов, и почти все они приходились на джекпот.

Несколько инвесторов сообразили, что смогут хорошо заработать, выкупив и заполнив карточки всеми возможными комбинациями шести из сорока четырёх чисел. Они учли дополнительные расходы и риски (в частности, изучив статистику предыдущих розыгрышей, выяснили: в 120 случаях победителей не оказалось, в 40 был один победитель, ещё в 10 — два) и заодно оценили прибыль. Для осуществления задуманного привлекли 2,5 тысячи мелких инвесторов из разных стран, а также группу людей для работы с карточками. В итоге из-за нехватки времени удалось использовать всего 70% карточек от запланированного числа, но и этого хватило, чтобы выиграть главный приз. А ведь повезло!

В чём заключался финансовый просчёт организаторов лотереи, побудивший инвесторов пойти на сговор? И каковы были, по их подсчётам, общий ожидаемый выигрыш и прибыль с одного вложенного доллара? (Второстепенными расходами можно пренебречь.) Просчёт был в том, что организаторы лотереи продавали лотерейные карточки по невыгодной для себя цене. На самом деле её следовало увеличить в четыре раза. Действительно, для гарантированной победы нужно заполнить

карточек. Призовой фонд — 27,9 млн долларов. Значит, карточка должна стоить хотя бы

27 900 000 : 7 059 052 ≈ 3,95 доллара**.

Неудивительно, что цена 1 доллар показалась инвесторам очень привлекательной. В идеале доход с неё составляет 2,95 доллара.

Как показывают расчёты, общий ожидаемый выигрыш равен

а прибыль с одного вложенного доллара

Даже с учётом всех затрат доход оказался бы огромным!

Нетрудно догадаться, чем закончилась эта история. Узнав, что главный приз достался группе инвесторов, устроители лотереи поначалу не хотели выплачивать выигрыш. Но после непродолжительных юридических пререканий были вынуждены признать, что причин для отказа нет. В итоге им пришлось дорого заплатить за собственный промах. Случай исключительный и довольно поучительный.

Доводы рассудка

Так стоит ли участвовать в лотереях в надежде быстро разбогатеть? Стоит ли полагаться на случай в погоне за лёгкими деньгами? Повезёт или нет — большой вопрос. В лотереи регулярно играют миллионы людей по всему миру, а побеждают единицы. Но в одном можно не сомневаться — в любой лотерее всегда выигрывают организаторы.

Никаких надёжных стратегий угадывания чисел в лото или выявления счастливого билета в мгновенной лотерее не существует, кроме как заполнить все карточки или скупить все билеты. Но это возможно лишь при условии, что игроки объединят усилия, и имеет смысл делать, только если призовой фонд значительно превышает стоимость всех билетов, на что рассчитывать не приходится.

В лотерее типа «почтовой» устроители и игроки решают две обратные задачи: первые подбирают комбинацию, которую не угадает никто, а вторые её старательно отгадывают, — и наблюдать за этим «состязанием» всё же интереснее, чем за случайным выпадением чисел в лото. Каковы шансы на успех у тех и других в теории? А на практике? Как ни странно, разные: не секрет, что никак не связанные между собой участники нередко ставят на одни и те же комбинации, а любого рода совпадения и повторы на руку организаторам: почти всегда можно просчитать наиболее вероятный «круг» таких комбинаций.

Устроители лотереи заинтересованы в том, чтобы в ней участвовало как можно больше народа. При подходящем ожидаемом выигрыше и приемлемой цене на билеты любой призовой фонд быстро окупится за счёт проданного количества билетов (о том, какая их доля приходится на тот или иной выигрыш, игрокам, конечно, неведомо). На продажу влияют и размер приза, и вероятность выигрыша, а её можно варьировать, изменяя правила игры. Так, если эта вероятность довольно велика (а в таком случае выигрыш всегда маловат) или, напротив, слишком мала, продажа лотерейных билетов падает. Одним словом, успех лотереи во многом зависит от умения устроителей отыскать ту «золотую середину» между величиной призов и шансом выиграть, которая обеспечила бы им крупный доход. И этим искусством они прекрасно владеют, будучи знакомы и с психологией любителей азартных игр, и с основами теории вероятностей.

И, наконец, главный довод рассудка, не только подтверждённый многовековым опытом, но и научно обоснованный: во всякой азартной игре каждый раз всё решают везение и случай, но чем больше играешь, тем больше проигрываешь.

Словарикк статье

Сочетание — выборка k элементов из n имеющихся (k ≤ n), при которой их порядок неважен. Число всевозможных сочетаний из n элементов по k обозначается и вычисляется по формуле

(по определению n! = 1 × 2 × 3 × … × n).

Случайное событие — событие (результат, исход испытания), которое объективно может произойти или не произойти в данном испытании.

Вероятность события A — число, выражающее меру объективной возможности наступления случайного события A; определяется как отношение числа m исходов испытания, благоприятствующих этому событию (влекущих за собой его наступление), к числу n всех равновозможных исходов, то есть равно .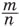

Случайная величина — переменная величина X, которая может принимать то или иное значение в зависимости от случая.

Математическое ожидание (или среднее значение) случайной величины X, принимающей конечное число значений x₁, x₂, … , x_n, — число, равное сумме произведений этих значений на соответствующие им вероятности p₁, p₂, … , p_n, то есть

x₁p₁ + x₂p₂ + … + x_np_n.

Комментарии к статье

* Средняя сумма выигрыша, которая приходится на один билет. Определяется как сумма произведений возможных выигрышей на вероятности их выпадения.

** Минимальная цена лотерейного билета равна математическому ожиданию выигрыша игрока. В данном примере «мелкие» выигрыши, по сути не влияющие на результат, в расчёт не принимались.

***

От редакции. Вы можете приобрести новую книгу автора статьи в нашем интернет-магазине.

Решение задач про билеты лотереи

После разобранных вероятностных задач на выбор шаров из урны и деталей из ящика, перейдем к еще одной популярной задаче на гипергеометрическую вероятность — задаче о покупке лотерейных билетов. Общая постановка задачи следующая:

В лотерее из $N$ билетов $K$ выигрышные и $N-K$ — билеты без выигрыша. Куплено $n$ лотерейных билетов. Найти вероятность того, что из них ровно $k$ выигрышных (соответственно, $n-k$ безвыигрышных) билетов.

Сначала найдем общее число исходов — это число всех различных способов выбрать любые $n$ билетов из общего числа $N$ продающихся билетов (без учета порядка), то есть число сочетаний $C_N^n$ (см. подробнее про сочетания).

Теперь найдем число всех способов выбрать $k$ выигрышных билетов из $K$ возможных — это сочетания $C_K^k$, и одновременно число всех способов выбрать $n-k$ невыигрышных билетов из $N-K$ возможных — $C_{N-K}^{n-k}$. По правилу произведения перемножая эти числа, получим число исходов, благоприятствующих нашему событию — $C_K^k cdot C_{N-K}^{n-k}$.

Применяя классическое определение вероятности, то есть поделив число благоприятствующих событию исходов на общее число исходов испытания (покупки билетов), придем к искомой формуле:

$$
P=frac{C_K^k cdot C_{N-K}^{n-k}}{C_N^n}. qquad (1)
$$

Видеоурок и шаблон Excel

Посмотрите наш ролик о решении задач про лотерейные билеты в схеме гипергеометрической вероятности, узнайте, как использовать Excel для решения типовых задач.

Расчетный файл Эксель из видео можно бесплатно скачать и использовать для решения своих задач.

Примеры решений задач о покупке лотерейных билетов

Пример 1. Среди 100 лотерейных билетов 2 выигрышных. Вы покупаете 3 билета. Какова вероятность, что вы ничего не выиграете?

Начинаем решение задачи с ввода события $A = $ (Из купленных 3 билетов ни один не выиграет) и общей формулы для нахождения вероятности. Так как речь идет о выборе элементов из некоторого множества, используем классическое определение вероятности $P(A)=m/n$, где $n$ — общее число всех равновозможных элементарных исходов, а $m$ — число исходов, благоприятствующих событию $A$.

Сначала найдем общее число исходов — это число способов выбрать любые 3 билета из 100 возможных. Так как порядок выбора несущественнен, используем формулу сочетаний из 100 элементов по 3: $n=C_{100}^3$.

Теперь переходим к числу благоприятствующих нашему событию исходов. Для этого нужно, чтобы из все 3 билета были без выигрыша. Всего таких билетов $100-2=98$, значит способов выбора $m = C_{98}^3$.

Искомая вероятность:

$$
P(A)=frac{m}{n}=frac{C_{98}^3}{C_{100}^3} = frac{152096}{161700} = 0.941.
$$

Вероятность остаться без выигрыша велика — 94,1% (при этом куплен не один, а целых 3 билета). Впрочем, любая лотерея заведома проигрышна для участника, помните об этом. Не стоит искать схемы и правила выигрыша в лотерею. Их не существует.

Пример 2. Среди 8 лотерейных билетов 4 выигрышных. Наудачу взяли 5 билетов. Определить вероятность того что среди них 2 выигрышных.

Подставляем в формулу (1) значения: $K=4$ выигрышных билета, $N-K=8-4=4$ невыигрышных билета, всего $N=8$ билетов. Выбираем $n=5$ билетов, из них должно быть $k=2$ выигрышных и соответственно, $n-k=5-2=3$ без выигрыша. Получаем нужную вероятность:

$$
P=frac{C_{4}^2 cdot C_{4}^{3}}{C_{8}^5} = frac{6 cdot 4}{56} = 0.429.
$$

Пример 3. В лотерее 24 билета, из них 10 выигрышных и 14 пустых. Найти вероятность того, что из трех вынутых билетов, по крайней мере, один окажется выигрышным.

Введем исходное событие:
$A = $ (Среди 3 вынутых билетов, по крайней мере, один окажется выигрышным),
а также противоположное ему событие, которое можно записать как:
$overline{A} = $ (Все три выбранные билеты будут без выигрыша).

Будем искать вероятность события $overline{A}$. Выпишем значения параметров: $K=10$ выигрышных билетов, $N-K=14$ невыигрышных (пустых) билета, всего $N=24$ билета. Выбираем $n=3$ билета, из них должно быть $k=0$ выигрышных и соответственно, $n-k=3$ без выигрыша. Подставляем в формулу (1) и получаем:

$$
P(overline{A})=frac{C_{10}^0 cdot C_{14}^{3}}{C_{24}^3} = frac{1 cdot 364}{2024}= 0.18.
$$

Тогда вероятность искомого события (что будет хотя бы один выигрышных билет), равна:

$$
P(A)= 1 — P(overline{A})= 1- 0.18 = 0.82.
$$

Пример 4. В розыгрыше лотереи участвуют 100 билетов, среди которых 25 выигрышных. Какова вероятность остаться без выигрыша, приобретя 3 билета лотереи?

Подставляем в формулу (1) значения: $K=25$ выигрышных билетов, $N-K=100-25=75$ невыигрышных билета, всего $N=100$ билетов участвует в розыгрыше лотереи. Выбираем $n=3$ билета, из них должно быть $k=0$ выигрышных и соответственно, $n-k=3$ без выигрыша. Приходим к ответу:

$$
P=frac{C_{25}^0 cdot C_{75}^{3}}{C_{100}^3} = frac{1 cdot 67525}{161700} = 0.418.
$$

Полезные ссылки

• Задачи о лотерейных билетах в схеме Бернулли
• Онлайн учебник по теории вероятностей
• Решенные контрольные по теории вероятностей
• Заказать работу по теории вероятностей

Поищите готовые задачи в решебнике: