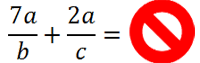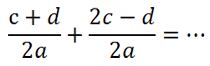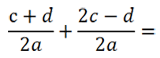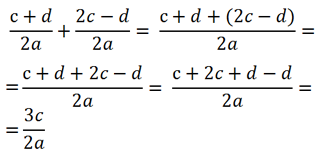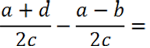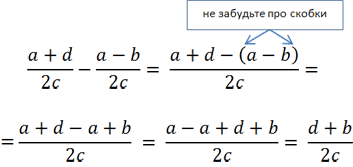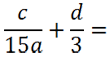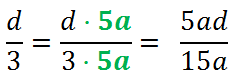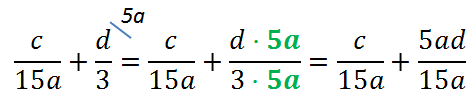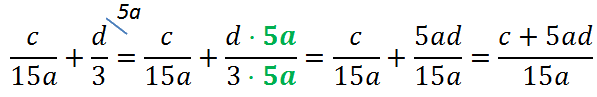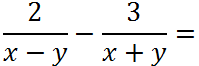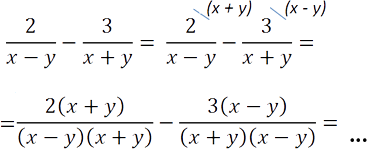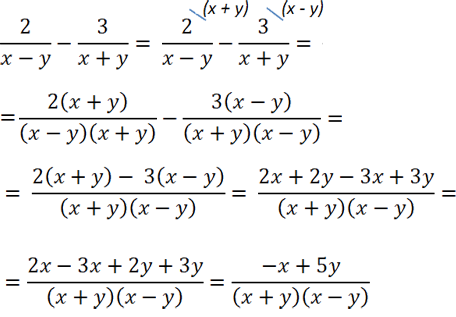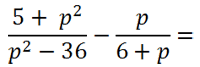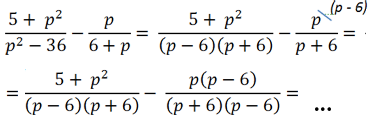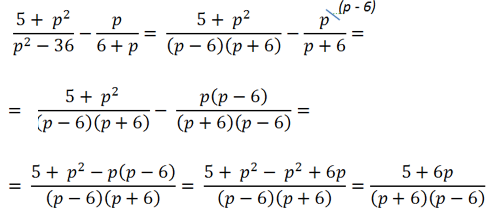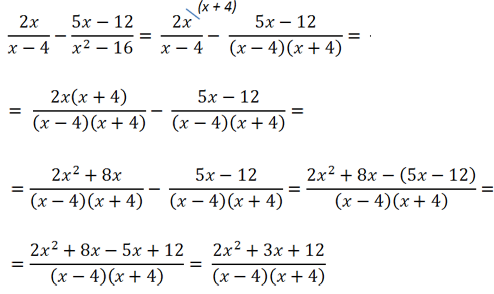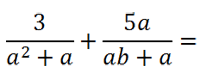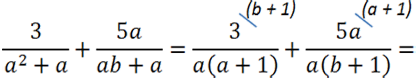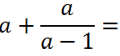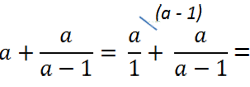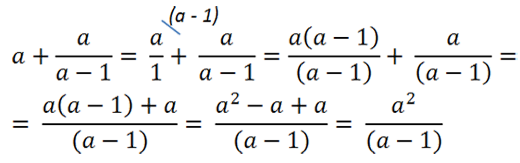Как найти общий знаменатель рациональных дробей - Исправление недочетов и поиск решений вместе с Examum.ru

Приведение рациональных дробей к общему знаменателю

Общим знаменателем двух или нескольких рациональных Дробей называется целое рациональное выражение, которое делится на знаменатель каждой дроби.
Например, общим знаменателем дробей

является многочлен (x — 1)(2х + 1), однако не только он, но и многочлены 2(х-1)(2х + 1), 7х(х — 1)(2х + 1), 9х²(х-1)³(2х+1)² и Т. Д. Предпочтительнее взять наименьший общий знаменатель — такой простейший общий знаменатель, что любой другой общий знаменатель делится на этот простейший. Наименьшим общим
знаменателем дробей

является (х — 1)(2х + 1).
Можно записать:

Приведение исходных дробей к наименьшему общему знаменателю (в дальнейшем будем называть его просто общим знаменателем) было достигнуто умножением числителя и знаменателя первой дроби на (2х +1), а числителя и знаменателя второй дроби на (х-1). Многочлены (2х + 1) и (х-1) называют дополнительными множителями для первой и второй дробей соответственно. Таким образом, дополнительный множитель для данной дроби равен частному от деления общего знаменателя на знаменатель данной дроби.
Для того чтобы несколько рациональных дробей привести к общему знаменателю, необходимо:
1) разложить знаменатель каждой дроби на множители, если это возможно;
2) составить общий знаменатель, включив в него в качестве сомножителей все различные множители, полученные в пункте 1); если некоторый множитель имеется в нескольких разложениях, то он берется с показателем степени, равным наибольшему из имеющихся;
3) определить дополнительные множители для каждой из дробей, для чего общий знаменатель разделить на знаменатель каждой дроби;
4) умножить числитель и знаменатель каждой дроби на дополнительный множитель.
Пример. Привести дроби к общему знаменателю.

Решение.

Наименьшее общее кратное чисел 9, 36, 20 есть число 180. Отсюда общий знаменатель имеет вид 180·а³(а- 2b)(а + 2b). Дополнительные множители: 20а², 5(а + 2b), 9а(а — 2b),— для первой, второй и третьей дробей соответственно.
Окончательно получаем:

Источник

Например, для дробей (frac{1}{5a}) и (frac{3}{b}) общим знаменателем будет (5ab), потому что именно это выражение содержит в себе все множители первого знаменателя (то есть, пятерку и (a)), а также все множители второго (это (b)).

Получается, что для нахождения общего знаменателя достаточно просто перемножить знаменатели всех дробей? Да, вообще говоря, это так. Однако на практике такой способ часто бывает неудобен, так как приводит к громоздким вычислениям в дальнейшем. Поэтому обычно находят наименьший общий знаменатель.

Например, для дробей (frac{1}{ab}) и (frac{3}{abc}) наименьшим общим знаменателем будет выражение (abc), но не (a^2 b^2c) (которое мы получим, если просто перемножим (ab) и (abc)).

Как искать наименьший общий знаменатель?

В приведенном выше примере наименьший общий знаменатель был очевиден. Однако в более сложных случаях его вот так сходу не напишешь.

Чтобы найти наименьший общий знаменатель нескольких дробей нужно все знаменатели разложить на множители, а потом собрать из этих множителей наименьший общий знаменатель.

Пример. Найдите общий знаменатель для дробей (frac{3}{x^2-5x}) и (frac{x}{x^2-25}).

Решение.

Пример. Найдите общий знаменатель для дробей (frac{a+1}{5a^2}), (frac{11-b}{a^3-9a}) и (frac{7}{(a-3)^2}).

Решение. И вновь раскладываем на множители знаменатели всех трех дробей, а потом собираем нашего «Франкенштейна»:

Общий знаменатель зависит только от знаменателей дробей, числители же на него не влияют вообще никак!

Поиск общего знаменателя важный этап при работе с алгебраическими дробями, а также при решении дробно-рациональных уравнений.

Скачать статью

Источник

Как привести дроби к общему знаменателю

Как привести алгебраические (рациональные) дроби к общему знаменателю?

1) Если в знаменателях дробей стоят многочлены, нужно попытаться разложить эти многочлены на множители одним из известных способов.

2) Наименьший общий знаменатель (НОЗ) состоит из всех множителей, взятых в наибольшей степени.

Наименьший общий знаменатель для чисел устно ищем как наименьшее число, которое делится на остальные числа.

3) Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый.

4) Числитель и знаменатель первоначальной дроби умножаем на дополнительный множитель.

Рассмотрим примеры приведения алгебраических дробей к общему знаменателю.

$[1)frac{{2a}}{{15b}}ufrac{{7b}}{{9c}}]$

Чтобы найти общий знаменатель для чисел, выбираем большее число и проверяем, делится ли оно на меньшее. 15 на 9 не делится. Умножаем 15 на 2 и проверяем, делится ли полученное число на 9. 30 на 9 не делится. Умножаем 15 на 3 и проверяем, делится ли полученное число на 9. 45 на 9 делится, значит, общий знаменатель для чисел равен 45.

Наименьший общий знаменатель состоит из всех множителей, взятых в наибольшей степени. Таким образом, общий знаменатель данных дробей равен 45 bc (буквы принято записывать в алфавитном порядке).

Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый. 45bc:(15b)=3c, 45bc:(9c)=5b. Умножаем числитель и знаменатель каждой дроби на дополнительный множитель:

$[frac{{2{a^{backslash 3c}}}}{{15b}} = frac{{6ac}}{{45bc}};frac{{7{b^{backslash 5b}}}}{{9c}} = frac{{35{b^2}}}{{45bc}};]$

$[2)frac{b}{{6{a^3}c}}ufrac{7}{{8{a^2}bc}}]$

Сначала ищем общий знаменатель для чисел: 8 на 6 не делится, 8∙2=16 на 6 не делится, 8∙3=24 на 6 делится. Каждую из переменных нужно включить в общий знаменатель один раз. Из степеней берем степень с большим показателем.

Таким образом, общий знаменатель данных дробей равен 24a³bc.

Чтобы найти дополнительный множитель к каждой дроби, нужно новый знаменатель разделить на старый: 24a³bc:(6a³c)=4b, 24a³bc:(8a²bc)=3a.

Дополнительный множитель умножаем на числитель и знаменатель:

$[frac{{{b^{backslash 4b}}}}{{6{a^3}c}} = frac{{4{b^2}}}{{24{a^3}bc}};frac{{{7^{backslash 3a}}}}{{8{a^2}bc}} = frac{{21a}}{{24{a^3}bc}};]$

$[3)frac{{2x + 1}}{{{x^2} - 18x + 81}}ufrac{3}{{{x^2} - 81}}]$

Многочлены, стоящие в знаменателях данных дробей, нужно разложить на множители. В знаменателе первой дроби — полный квадрат разности: x²-18x+81=(x-9)²; в знаменателе второй — разность квадратов: x²-81=(x-9)(x+9):

$[frac{{2x + 1}}{{{x^2} - 18x + 81}} = frac{{2x + 1}}{{{{(x - 9)}^2}}},]$

$[frac{3}{{{x^2} - 81}} = frac{3}{{(x - 9)(x + 9)}}.]$

Общий знаменатель состоит из всех множителей, взятых в наибольшей степени, то есть равен (x-9)²(x+9). Находим дополнительные множители и умножаем их на числитель и знаменатель каждой дроби:

$[frac{{2x + {1^{backslash (x + 9)}}}}{{{{(x - 9)}^2}}} = frac{{(2x + 1)(x + 9)}}{{{{(x - 9)}^2}(x + 9)}} = ]$

$[ = frac{{2{x^2} + 18x + x + 9}}{{{{(x - 9)}^2}(x + 9)}} = frac{{2{x^2} + 19x + 9}}{{{{(x - 9)}^2}(x + 9)}},]$

$[frac{{{3^{backslash (x - 9)}}}}{{(x - 9)(x + 9)}} = frac{{3(x - 9)}}{{{{(x - 9)}^2}(x + 9)}} = ]$

$[ = frac{{3x - 27}}{{{{(x - 9)}^2}(x + 9)}};]$

$[4)frac{5}{{{x^2} - 5x}}ufrac{{3x}}{{4x - 20}}]$

Многочлены, стоящие в знаменателях, раскладываем на множители. В знаменателе первой дроби выносим за скобки общий множитель x, из второй — 4:

$[frac{5}{{{x^2} - 5x}} = frac{5}{{x(x - 5)}},]$

$[frac{{3x}}{{4x - 20}} = frac{{3x}}{{4(x - 5)}}.]$

Общий знаменатель состоит из всех множителей, взятых в наибольшей степени, а значит, равен 4x(x-5).

Находим дополнительные множители и умножаем их на числитель и знаменатель:

$[frac{{{5^{backslash 4}}}}{{x(x - 5)}} = frac{{20}}{{4x(x - 5)}},]$

$[frac{{3{x^{backslash x}}}}{{4(x - 5)}} = frac{{3{x^2}}}{{4x(x - 5)}}.]$

Необходимость в приведении рациональных дробей к общему знаменателю в алгебре возникает при сложении и вычитании дробей. Как складывать и как вычитать дроби с разными знаменателями, рассмотрим в следующий раз.

Источник

Приведение алгебраических дробей к общему знаменателю

Приведение алгебраических дробей к общему знаменателю выполняется по тем же правилам, что и приведение обыкновенных дробей к общему знаменателю. Следовательно, чтобы привести алгебраические дроби к общему знаменателю, нужно:

найти общий знаменатель для данных дробей;
найти дополнительный множитель для каждой дроби;
умножить числитель каждой дроби на её дополнительный множитель;
записать дроби с найденными новыми числителями и общим знаменателем.

Чтобы найти наименьший общий знаменатель для дробей, надо разложить знаменатель каждой дроби на множители и взять каждый множитель в наибольшей встречающейся степени.

Пример 1. Привести дроби к общему знаменателю:

2b	,	c	и	a	.
3a²	2b	6ab

Решение: Разложим знаменатели дробей на множители:

3a² = 3 · a²;

2b = 2 · b;

6ab = 2 · 3 · a · b.

Выпишем множители первого знаменателя и добавим к ним недостающие множители из второго и третьего знаменателя:

3 · a² · 2 · b = 6a²b.

Мы нашли наименьший общий знаменатель для данных дробей. Теперь, чтобы привести дроби к общему знаменателю, нам надо найти для каждой дроби дополнительный множитель. Для этого нужно разделить общий знаменатель на знаменатель каждой дроби:

6a²b : 3a² = 2b;

6a²b : 2b = 3a²;

6a²b : 6ab = a.

Умножаем числитель каждой дроби на её дополнительный множитель:

2b · 2b = 4b²;

c · 3a² = 3a²c;

a · a = a².

Осталось записать дроби с найденными новыми числителями и их общим знаменателем:

4b²	,	3a²c	и	a²	.
6a²b	6a²b	6a²b

Пример 2. Привести дроби к общему знаменателю:

Решение: Разложим на множители знаменатель второй дроби, используя формулу разности квадратов:

a² — 4 = a² — 2² = (a + 2)(a — 2).

Получившееся произведение и будет общим знаменателем для данных дробей. Значит, для приведения дробей к общему знаменателю, нам нужно только умножить числитель первой дроби на сумму чисел (a + 2).

3a · (a + 2) = 3a² + 6a.

В результате у нас получилось:

3a² + 6a	и	4	.
(a + 2)(a — 2)	(a + 2)(a — 2)

Произведение суммы и разности чисел a и 2 можно обратно свернуть в квадрат разности для более краткой записи дробей:

3a² + 6a	и	4	.
a² — 4	a² — 4

Источник

Алгебраические дроби складывают и вычитают по
правилам сложения и вычитания
обыкновенных дробей.

Сложение алгебраических дробей

Запомните!

Складывать можно только дроби с одинаковыми знаменателями!

Нельзя складывать дроби без преобразований

Можно складывать дроби

При сложении алгебраических дробей с одинаковыми знаменателями:

числитель первой дроби складывается с числителем второй дроби;
знаменатель остаётся прежним.

Рассмотрим пример сложения алгебраических дробей.

Так как знаменатель у обеих дробей «2а», значит, дроби можно сложить.

Сложим числитель первой дроби с числителем второй дроби, а знаменатель оставим прежним.
При сложении дробей в полученном числителе
приведем подобные.

Вычитание алгебраических дробей

Запомните!

Вычитать можно только дроби с одинаковыми знаменателями!

При вычитании алгебраических дробей с одинаковыми знаменателями:

из числителя первой дроби вычитается числитель второй дроби.
знаменатель остаётся прежним.

Важно!

Обязательно заключите в скобки весь числитель вычитаемой дроби.

Иначе вы сделаете ошибку в знаках при раскрытии скобок вычитаемой дроби.

Рассмотрим пример вычитания алгебраических дробей.

Так как у обеих алгебраических дробей знаменатель «2с», значит, эти дроби можно вычитать.

Вычтем из числителя первой дроби «(a + d)» числитель второй дроби
«(a − b)».
Не забудем заключить числитель вычитаемой дроби в скобки. При раскрытии скобок используем
правило раскрытия скобок.

Приведение алгебраических дробей к общему знаменателю

Рассмотрим другой пример. Требуется сложить алгебраические дроби.

В таком виде сложить дроби нельзя, так как у них разные знаменатели.

Прежде чем складывать алгебраические дроби их необходимо привести к общему знаменателю.

Правила приведения алгебраических дробей к общему знаменателю очень похожи на
правила приведения к общему знаменателю
обыкновенных дробей.
.

В итоге мы должны получить многочлен, который без остатка разделится на каждый прежний знаменатель дробей.

Чтобы привести алгебраические дроби к общему знаменателю необходимо сделать следующее.

Работаем с числовыми коэффициентами. Определяем
НОК
(наименьшее общее кратное) для всех числовых коэффициентов.
Работаем с многочленами. Определяем все различные многочлены в наибольших степенях.
Произведение числового коэффициента и всех различных многочленов в наибольших степенях и будет общим знаменателем.
Определяем, на что нужно умножить каждую алгебраическую дробь, чтобы получить общий знаменатель.

Вернемся к нашему примеру.

Рассмотрим знаменатели «15a» и «3» обеих дробей и найдем для них общий знаменатель.

Работаем с числовыми коэффициентами. Находим НОК (наименьшее общее кратное — это число, которое без остатка
делится на каждый числовый коэффициент).
Для «15» и «3» — это «15».
Работаем с многочленами. Необходимо перечислить все многочлены в наибольших степенях.
В знаменателях «15a» и «5» есть только
один одночлен — «а».
Перемножим НОК из п.1 «15» и одночлен «а» из п.2. У нас получится «15a». Это и будет общим знаменателем.
Для каждой дроби зададим себе вопрос: «На что нужно умножить знаменатель этой дроби, чтобы получить «15a»?».

Рассмотрим первую дробь. В этой дроби и так знаменатель «15a», значит, ее не требуется ни на что умножать.

Рассмотрим вторую дробь. Зададим вопрос: «На что нужно умножить «3», чтобы получить «15a»?»
Ответ — на «5a».

При приведении к общему знаменателю дроби умножаем на «5a»
и числитель, и знаменатель.

Сокращенную запись приведения алгебраической дроби к общему знаменателю можно записать через
«домики».

Для этого держим в уме общий знаменатель. Над каждой дробью сверху «в домике» пишем, на что умножаем каждую из дробей.

Теперь, когда у дробей одинаковые знаменатели, дроби можно сложить.

Рассмотрим пример вычитания дробей с разными знаменателями.

В таком виде вычитать дроби нельзя, так как у них разные знаменатели. Чтобы вычесть дроби, необходимо привести их к общему знаменателю.

Рассмотрим знаменатели «(x − y)» и «(x + y)» обеих дробей и найдем для них общий знаменатель.

Работаем с числовыми коэффициентами. Числовых коэффициентов в знаменателях нет, поэтому переходим к многочленам.
Работаем с многочленами. Находим все различные многочлены из знаменателей в наибольших степенях и перемножаем их.

Важно!

Многочлены необходимо рассматривать целиком!
Для удобства заключайте целый многочлен в скобки.

У нас есть два различных многочлена в знаменателях «(x − y)» и «(x + y)».
Их произведение будет общим знаменателем, т.е. «(x − y)(x + y)» — общий знаменатель.

Теперь дроби можно вычитать, т.к. у них одинаковый знаменатель.

Сложение и вычитание алгебраических дробей с помощью формул сокращенного умножения

В некоторых примерах, чтобы привести алгебраические дроби к общему знаменателю, нужно использовать
формулы сокращенного умножения.

Рассмотрим пример сложения алгебраических дробей, где нам потребуется использовать формулу разности квадратов.

В первой алгебраической дроби знаменатель «(p² − 36)». Очевидно, что к нему можно
применить формулу разности квадратов.

После разложения многочлена «(p² − 36)» на произведение
многочленов
«(p + 6)(p − 6)»
видно, что в дробях повторяется многочлен «(p + 6)».
Значит, общим знаменателем дробей будет произведение многочленов «(p + 6)(p − 6)».

Важно!

Прежде чем приводить многочлены к общему знаменателю, попытайтесь
использовать формулы сокращённого умножения или вынесение общего множителя за скобки.

Примеры сложения и вычитания дробей с разными знаменателями с использованием формул сокращенного умножения.

Сложение и вычитание алгебраических дробей с вынесением общего множителя за скобки

На первый взгляд одинаковых многочленов в обеих дробях нет.

Вынесем общий множитель
«а» за скобки в обоих знаменателях.

После вынесения общего множителя «а» за скобки, в
обоих знаменателях появился одинаковый одночлен «а».
Значит, общий знаменатель для обеих дробей будет выглядеть так: «а(а + 1)(b + 1)».

Сложение алгебраической дроби с одночленом или числом

Рассмотрим пример. Требуется сложить алгебраическую дробь с одночленом (буквой).

Чтобы сложить одночлен или число с алгебраической дробью,
нужно представить одночлен в виде дроби со знаменателем «1».

Представим одночлен «а» как алгебраическую дробь со знаменателем «1».

Подобное действие можно сделать, так как при делении на единицу получается тот же самый одночлен.

Теперь приведем алгебраические дроби к общему знаменателю «(а − 1)» и решим пример.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник