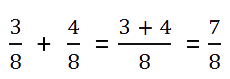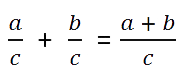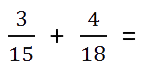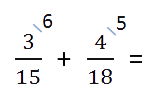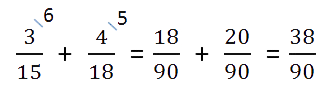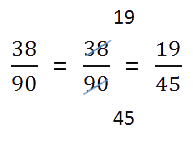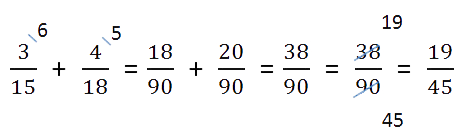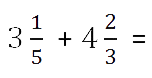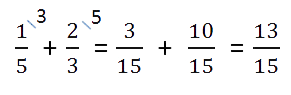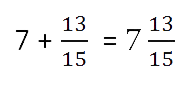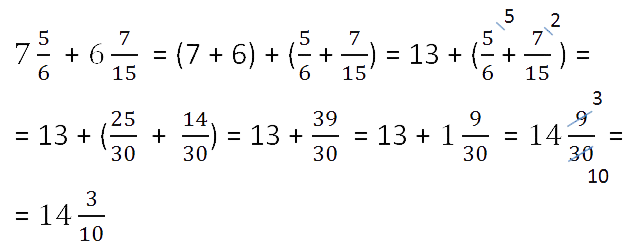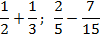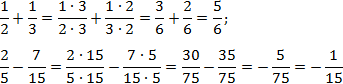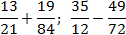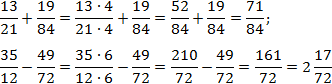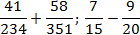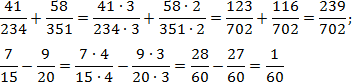Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Сложение дробей
Поддержать сайт
При сложении дробей могут встретиться разные случаи.
Сложение дробей с одинаковыми знаменателями
Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают
числители, а знаменатель оставляют тот же.
Пример.
C помощью букв это правило сложения можно записать так:
Запомните!
Записывая ответ, проверьте нельзя ли полученную дробь сократить.
Сложение дробей с разными знаменателями
Чтобы сложить дроби с разными знаменателями нужно воспользоваться
следующими правилами.
- Привести данные дроби к наименьшему общему знаменателю (НОЗ). Для этого найти
наименьшее общее кратное знаменателей.
Пример. Сложить дроби.
Как найти общий знаменатель
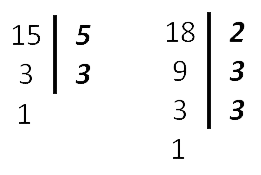
Находим НОК (15, 18).
НОК (15, 18) = 3 · 2 · 3 · 5 = 90
- Найти дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель (НОК из пункта 1)
делим по очереди на знаменатель каждой дроби.Полученные числа и будут дополнительными множителями
для каждой из дробей. Множители записываем над числителем дроби справа сверху.90 : 15 = 6 — дополнительный множитель для дроби
.
90 : 18 = 5 — дополнительный множитель для дроби
.
- Числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель, пользуясь
основным свойством дроби.После умножения в знаменателях
обеих дробей должен получиться наименьший общий знаменатель.
Затем складываем дроби как дроби с одинаковыми знаменателями.
- Проверяем полученную дробь.
- Eсли в результате получилась
неправильная дробь,
результат записываем в виде смешанного числа. Проверим нашу
дробь.38 < 90
У нас дробь правильная.
- Если в результате получилась сократимая дробь, необходимо выполнить сокращение.
- Eсли в результате получилась
- Ещё раз весь пример целиком.
Сложение смешанных чисел
Сочетательное и переместитительное свойства сложения позволяют привести
сложение смешанных чисел к сложению их целых частей и к сложению их дробных частей.
Чтобы сложить смешанные числа нужно.
- Отдельно сложить их целые части.
Пример.
Складываем целые части.
- Отдельно сложить дробные части.
Если у дробных частей знаменатели разные, то
сначала приводим их к общему знаменателю, а затем складываем. - Сложить полученные результаты из пунктов 1 и 2.
- Если при сложении дробных частей получилась неправильная дробь, то нужно
выделить целую часть из этой дроби и прибавить к полученной
в пункте 1 целой части.
Ещё один пример на сложение смешанных чисел.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
24 декабря 2018 в 11:19
Baur Nurgazinov
Профиль
Благодарили: 0
Сообщений: 1
Baur Nurgazinov
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
2 января 2019 в 14:18
Ответ для Baur Nurgazinov
Лина Аникеева
Профиль
Благодарили: 0
Сообщений: 2
Лина Аникеева
Профиль
Благодарили: 0
Сообщений: 2
1) приводим все дроби к общему знаменателю
(2 -1 ) · х=
2) Вычислаем разность в скобках
( — ) · х=
· х=
сократим дроби на 3
· х=
3) вычисляем х
х= :
По правилу деления дробей делитель переворачиваем
x= · =
4 — сокращаем
х=3
Проверка:
(2 -1 ) · 3=( — ) · 3= · 3= · 3 = · = =
Ответ верный
0
Спасибо
Ответить
24 января 2017 в 19:44
Фанис Газизов
Профиль
Благодарили: 0
Сообщений: 1
Фанис Газизов
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
24 января 2017 в 21:12
Ответ для Фанис Газизов
Marina Kazakova
Профиль
Благодарили: 0
Сообщений: 1
Marina Kazakova
Профиль
Благодарили: 0
Сообщений: 1
?
0
Спасибо
Ответить
1 марта 2016 в 18:39
Денис Демидов
Профиль
Благодарили: 0
Сообщений: 1
Денис Демидов
Профиль
Благодарили: 0
Сообщений: 1
спасибо сайт класс тему не понял
| было очень непонятно |
| теперь понятно + + |
+ + + + · + + + + +
0
Спасибо
Ответить
19 сентября 2016 в 13:05
Ответ для Денис Демидов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
0
Спасибо
Ответить
6 февраля 2016 в 18:54
Денис Бочин
Профиль
Благодарили: 0
Сообщений: 1
Денис Бочин
Профиль
Благодарили: 0
Сообщений: 1
Сложи
числа 30 и
числа 14.
0
Спасибо
Ответить
10 февраля 2016 в 19:03
Ответ для Денис Бочин
Алексей Пешков
Профиль
Благодарили: 0
Сообщений: 2
Алексей Пешков
Профиль
Благодарили: 0
Сообщений: 2
1) от 30=;
2)
от 14=
2)
+ ===24=24
0
Спасибо
Ответить
14 января 2016 в 15:31
Анжела Волк
Профиль
Благодарили: 0
Сообщений: 1
Анжела Волк
Профиль
Благодарили: 0
Сообщений: 1
2/6 или1/2 сравнение дробей
0
Спасибо
Ответить
14 января 2016 в 18:05
Ответ для Анжела Волк
Александр Хан
Профиль
Благодарили: 0
Сообщений: 1
Александр Хан
Профиль
Благодарили: 0
Сообщений: 1
больше
0
Спасибо
Ответить
19 сентября 2016 в 10:33
Ответ для Анжела Волк
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Отрицательное число всегда меньше положительного =)
0
Спасибо
Ответить
27 декабря 2015 в 20:00
Надежда Егина
Профиль
Благодарили: 0
Сообщений: 2
Надежда Егина
Профиль
Благодарили: 0
Сообщений: 2
0
Спасибо
Ответить
19 сентября 2016 в 10:07
Ответ для Надежда Егина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
· a12· b4 · · a8· b5 = · a20 · b9=125· a20 · b9При раскрытии скобок отбросил знак ?, т.к. степень чётная, а значит получится +.
0
Спасибо
Ответить
21 апреля 2015 в 15:17
Алина Гимадеева
Профиль
Благодарили: 0
Сообщений: 2
Алина Гимадеева
Профиль
Благодарили: 0
Сообщений: 2
1) 15 — 7
4/7= 2) 20
4/5 — 1
5/6 *
1/3
3) 5
1/3 + 4
1/3 +
2/5
0
Спасибо
Ответить
14 апреля 2016 в 12:32
Ответ для Алина Гимадеева
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Судя по всему, не разобрались с использованием кнопки дробь. Интерпретирую задачу следующим образом:
1) 15 ? 7
=8
2) 20
? 1 · = ? = = = =9 — похоже ошибка в примере, он гораздо сложнее двух других.
3) 5
+4 + = 9 + = + = = =10
0
Спасибо
Ответить
7 апреля 2015 в 20:06
Александр Гридюшко
Профиль
Благодарили: 0
Сообщений: 1
Александр Гридюшко
Профиль
Благодарили: 0
Сообщений: 1
как решить?4
+
0
Спасибо
Ответить
7 апреля 2015 в 21:13
Ответ для Александр Гридюшко
Анастасия Власова
Профиль
Благодарили: 0
Сообщений: 1
Анастасия Власова
Профиль
Благодарили: 0
Сообщений: 1
4+ = + = + = = = = 6
0
Спасибо
Ответить
14 апреля 2015 в 16:55
Ответ для Александр Гридюшко
Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
4 + = + = = =16:3=1
0
Спасибо
Ответить
16 апреля 2015 в 19:06
Ответ для Александр Гридюшко
Мирон Федоров
Профиль
Благодарили: 0
Сообщений: 1
Мирон Федоров
Профиль
Благодарили: 0
Сообщений: 1
Asel не правильно
0
Спасибо
Ответить
Загрузить PDF
Загрузить PDF
Для сложения или вычитания дробей с разными знаменателями (числа, стоящие под дробной чертой) сначала необходимо найти их наименьший общий знаменатель (НОЗ). Таким числом будет наименьшее кратное, которое встречается в списке кратных каждого знаменателя, то есть число, делящееся нацело на каждый знаменатель.[1]
Также вы можете вычислить наименьшее общее кратное (НОК) двух или более знаменателей. В любом случае речь идет о целых числах, методы нахождения которых весьма схожи. Определив НОЗ, вы сможете привести дроби к общему знаменателю, что в свою очередь позволит вам складывать и вычитать их.
-
1
Перечислите кратные каждого знаменателя. Составьте список из нескольких кратных для каждого знаменателя в уравнении. Каждый список должен состоять из произведения знаменателя на 1, 2, 3, 4 и так далее.
- Пример: 1/2 + 1/3 + 1/5
- Кратные 2: 2 * 1 = 2; 2 * 2 = 4; 2 * 3 = 6; 2 * 4 = 8; 2 * 5 = 10; 2 * 6 = 12; 2 * 7 = 14; и так далее.
- Кратные 3: 3 * 1 = 3; 3 * 2 = 6; 3 *3 = 9; 3 * 4 = 12; 3 * 5 = 15; 3 * 6 = 18; 3 * 7 = 21; и так далее.
- Кратные 5: 5 * 1 = 5; 5 * 2 = 10; 5 * 3 = 15; 5 * 4 = 20; 5 * 5 = 25; 5 * 6 = 30; 5 * 7 = 35; и так далее.
-
2
Определите наименьшее общее кратное. Просмотрите каждый список и отметьте любые кратные числа, которые являются общими для всех знаменателей. После выявления общих кратных определите наименьший знаменатель.
- Обратите внимание, что если общий знаменатель не найден, возможно, потребуется продолжить выписывать кратные до тех пор, пока не появится общее кратное число.
- Лучше (и легче) пользоваться этим методом в том случае, когда в знаменателях стоят небольшие числа.
- В нашем примере общим кратным всех знаменателей является число 30: 2 * 15 = 30; 3 * 10 = 30; 5 * 6 = 30
- НОЗ = 30
-
3
Перепишите исходное уравнение. Для того чтобы привести дроби к общему знаменателю, при этом не изменив их значения, умножьте каждый числитель (число, стоящее над дробной чертой) на число, равное частному от деления НОЗ на соответствующий знаменатель.
- Пример: (15/15) * (1/2); (10/10) * (1/3); (6/6) * (1/5)
- Новое уравнение: 15/30 + 10/30 + 6/30
-
4
Решите полученное уравнение. После нахождения НОЗ и изменения соответствующих дробей, просто решите полученное уравнение. Не забудьте упростить полученный ответ (если это возможно).
- Пример: 15/30 + 10/30 + 6/30 = 31/30 = 1 1/30
Реклама
-
1
Перечислите делители каждого знаменателя. Делитель – это целое число, которое делит нацело данное число.[4]
Например, делителями числа 6 являются числа 6, 3, 2, 1. Делителем любого числа является 1, потому что любое число делится на единицу.- Пример: 3/8 + 5/12
- Делители 8: 1, 2, 4, 8
- Делители 12: 1, 2, 3, 4, 6, 12
-
2
Найдите наибольший общий делитель (НОД) обоих знаменателей. Перечислив делители каждого знаменателя, отметьте все общие делители. Самый большой общий делитель является наибольшим общим делителем, который понадобится вам для решения задачи.
- В нашем примере общими делителями для знаменателей 8 и 12 являются числа 1, 2, 4.
- НОД = 4.
-
3
Перемножьте знаменатели между собой. Если вы хотите использовать НОД для решения задачи, сначала перемножьте знаменатели между собой.
- Пример: 8 * 12 = 96
-
4
Разделите полученное значение на НОД. Получив результат перемножения знаменателей, разделите его на вычисленный вами НОД. Полученное число будет наименьшим общим знаменателем (НОЗ).
- Пример: 96 / 4 = 24
-
5
Разделите НОЗ на исходный знаменатель. Для вычисления множителя, который требуется для приведения дробей к общему знаменателю, разделите найденный вами НОЗ на исходный знаменатель. Умножьте числитель и знаменатель каждой дроби на этот множитель. Вы получите дроби с общим знаменателем.
- Пример: 24 / 8 = 3; 24 / 12 = 2
- (3/3) * (3/8) = 9/24; (2/2) * (5/12) = 10/24
- 9/24 + 10/24
-
6
Решите полученное уравнение. НОЗ найден; теперь вы можете сложить или вычесть дроби. Не забудьте упростить полученный ответ (если это возможно).
- Пример: 9/24 + 10/24 = 19/24
Реклама
-
1
Разложите каждый знаменатель на простые множители. Разложите каждый знаменатель на простые множители, то есть простые числа, которые при перемножении дают исходный знаменатель. Напомним, что простые множители – это числа, которые делятся только на 1 или самих себя.[6]
- Пример: 1/4 + 1/5 + 1/12
- Простые множители 4: 2 * 2
- Простые множители 5: 5
- Простые множители 12: 2 * 2 * 3
-
2
Подсчитайте число раз каждый простой множитель есть у каждого знаменателя. То есть определите, сколько раз каждый простой множитель появляется в списке множителей каждого знаменателя.
- Пример: Есть две 2 для знаменателя 4; нуль 2 для 5; две 2 для 12
- Есть нуль 3 для 4 и 5; одна 3 для 12
- Есть нуль 5 для 4 и 12; одна 5 для 5
-
3
Возьмите только наибольшее число раз для каждого простого множителя. Определите наибольшее число раз наличия каждого простого множителя в любом знаменателе.
- Например: наибольшее число раз для множителя 2 — 2 раза; для 3 – 1 раз; для 5 – 1 раз.
-
4
Запишите по порядку найденные в предыдущем шаге простые множители. Не записывайте число раз наличия каждого простого множителя во всех исходных знаменателях – делайте это с учетом наибольшего числа раз (как описано в предыдущем шаге).
- Пример: 2, 2, 3, 5
-
5
Перемножьте эти числа. Результат произведения этих чисел равен НОЗ.
- Пример: 2 * 2 * 3 * 5 = 60
- НОЗ = 60
-
6
Разделите НОЗ на исходный знаменатель. Для вычисления множителя, который требуется для приведения дробей к общему знаменателю, разделите найденный вами НОЗ на исходный знаменатель. Умножьте числитель и знаменатель каждой дроби на этот множитель. Вы получите дроби с общим знаменателем.
- Пример: 60/4 = 15; 60/5 = 12; 60/12 = 5
- 15 * (1/4) = 15/60; 12 * (1/5) = 12/60; 5 * (1/12) = 5/60
- 15/60 + 12/60 + 5/60
-
7
Решите полученное уравнение. НОЗ найден; теперь вы можете сложить или вычесть дроби. Не забудьте упростить полученный ответ (если это возможно).
- Пример: 15/60 + 12/60 + 5/60 = 32/60 = 8/15
Реклама
-
1
Преобразуйте каждое смешанное число в неправильную дробь. Для этого умножьте целую часть смешанного числа на знаменатель и сложите с числителем – это будет числитель неправильной дроби. Целое число тоже превратите в дробь (просто поставьте 1 в знаменателе).
- Пример: 8 + 2 1/4 + 2/3
- 8 = 8/1
- 2 1/4, 2 * 4 + 1 = 8 + 1 = 9; 9/4
- Переписанное уравнение: 8/1 + 9/4 + 2/3
-
2
Найти наименьший общий знаменатель. Вычислите НОЗ любым способом, описанным в предыдущих разделах. Для этого примера мы будем использовать метод «перечисление кратных», в котором выписываются кратные каждого знаменателя и на их основе вычисляется НОЗ.
- Обратите внимание, что вам не нужно перечислять кратные для 1, так как любое число, умноженное на 1, равно самому себе; иными словами, каждое число является кратным 1.
- Пример: 4 * 1 = 4; 4 * 2 = 8; 4 * 3 = 12; 4 * 4 = 16; т.д.
- 3 * 1 = 3; 3 * 2 = 6; 3 * 3 = 9; 3 * 4 = 12; т.д.
- НОЗ = 12
-
3
Перепишите исходное уравнение. Числители и знаменатели исходных дробей умножьте на число, равное частному от деления НОЗ на соответствующий знаменатель.
- Например: (12/12) * (8/1) = 96/12; (3/3) * (9/4) = 27/12; (4/4) * (2/3) = 8/12
- 96/12 + 27/12 + 8/12
-
4
Решите уравнение. НОЗ найден; теперь вы можете сложить или вычесть дроби. Не забудьте упростить полученный ответ (если это возможно).
- Пример: 96/12 + 27/12 + 8/12 = 131/12 = 10 11/12
Реклама
Что вам понадобится
- Карандаш
- Бумага
- Калькулятор (по желанию)
Об этой статье
Эту страницу просматривали 223 547 раз.
Была ли эта статья полезной?
Содержание
- как найти общий знаменатель
- Находим общий знаменатель
- Что такое общий знаменатель?
- Но что такое общий знаменатель простыми словами ?
- Пример общего знаменателя :
- В каком случае ноз двух дробей будет являться произведением знаменателей?
- Когда ноз двух дробей равен произведению знаменателей?
- Формула общего знаменателя
- Нахождение общего знаменателя с помощью нок.
- Пример нахождения общего знаменателя методом разложения на множители
- Пример номер 2 подбора общего знаменателя
- Как найти общий знаменатель дробей онлайн
- Переходим к нахождению общего знаменателя онлайн
- Что такое наименьший общий знаменатель?
- Но, что же такое «наименьший общий знаменатель»
- Определение, что же такое «наименьший общий знаменатель»
- Формула наименьшего общего кратного
- Как найти наименьший общий знаменатель на калькуляторе
- Как найти общий знаменатель трех дробей
- Задача/пример найдите общий знаменатель для трех дробей.
- Найдем общий знаменатель для трех дробей на калькуляторе через НОК.
- Как найти общий знаменатель дробей с разными знаменателями
- Приведение дробей к общему знаменателю
- Умножение «крест-накрест»
- Метод общих делителей
- Метод наименьшего общего кратного
как найти общий знаменатель
Как найти общий знаменатель, что такое общий знаменатель и конечно же нахождение общего знаменателя онлайн на нашем калькуляторе. И если вам требуется наименьший общий знаменатель, то он тут.
И! Вне зависимости от класса — общий знаменатель находят одинаково!
Находим общий знаменатель
Что такое общий знаменатель?
Кроме понятия «общий знаменатель«, есть еще такое понятие как — «Наименьший общий знаменатель (НОЗ)» — это. тоже самое, что и «НОК». Поэтому, мы не будем это разбирать здесь второй раз.
Но что такое общий знаменатель простыми словами ?
Общий знаменатель — это любое целое число, которое делится без остатка на первый и второй знаменатель.
Количество чисел, которые могут быть общим знаменателем стремится к бесконечности, но обычно общим знаменателем принимают НОЗ
Пример общего знаменателя :
Для того, чтобы понять, «что такое общий знаменатель» нам нужен пример двух дробей и какое-то действие(иначе смысла в этом нет), пусть это будут две дроби 1/2 и 1/3 и действие сложение — «+».
Для таких маленьких чисел, как 2 и 3 — «нок» будет равен 6. Для этого нам никакие инструменты не понадобятся, наверняка вы это тоже смогли посчитать в уме.
Т.е. 6 делится на 2 без остатка 6 : 2 = 3, и 6 делится на 3 без остатка 6 : 3 = 2.
Мы получили два числа, первую дробь 1/2 надо умножить на 3, чтобы привести её к общему знаменателю 6 — 1*3/2*3 = 3/6.
А вторую дробь нужно умножить на 2, чтобы привести и её к общему знаменатель 6, 1*2/3*2 = 2/6.
После того, как мы нашли общий знаменатель, мы можем произвести действие, в нашем случае — «+» — 3/6 + 2/6 = (3 + 2)/6 = 5/6.
Когда мы нашли «общий знаменатель» мы смогли выполнить необходимое действие с дробями.
В каком случае ноз двух дробей будет являться произведением знаменателей?
Отличный поисковый запрос — «в каком случае ноз двух дробей будет являться произведением знаменателей?«, что выше не было озвучено.
Когда ноз двух дробей равен произведению знаменателей?
Как минимум, когда знаменатели будут простыми числами, т.е. в качестве примера, это выше приведенные дроби со знаменателями 2 и 3. Эти числа являются простыми, т.е. делятся на себя и на 1.
И общий знаменатель двух чисел 2 и 3 будет равен произведению 2 * 3 = 6.
Формула общего знаменателя
Как вы знаете. что если умножить и числитель и знаменатель на одно число, то результат дроби не изменится! Поэтому мы можем вывести формулу общего знаменателя буквами :
Первую дробь умножаем на знаменатель второй дроби.
А вторую дробь умножаем на знаменатель первой дроби
Нахождение общего знаменателя с помощью нок.
Для того чтобы найти общий знаменатель, можно воспользоваться правилом «НОК» для двух чисел, которые здесь — знаменатели.
Если вы не сходили по ссылке, то давайте вкратце попробуем разобраться в формуле подбора общего знаменателя.
Пример нахождения общего знаменателя методом разложения на множители
Это тоже самое. что и выше приведенный «НОК» — только может называться по другому.
Этот способ может называться как «нахождение общего знаменателя методом разложения на множители»
Либо «метод нахождения наименьшего общего знаменателя» или просто «НОЗ»
Рассмотрим два знаменателя 8 и 6, к примеру это могут быть две дроби 1/8 и 1/6 и нам нужно найти их общий знаменатель.
Надо расположить в первую строчку наибольший знаменатель — это 8 и разложить его на множители:
Ниже раскладываем меньший знаменатель :
Далее нам нужно исключить все множители, которые повторяются в меньшем знаменателе. это 2 и у нас остается 3. далее эту тройку надо умножить на больший знаменатель :
Итого получаем общий знаменатель = 24.
Пример номер 2 подбора общего знаменателя
Чтобы у вас не возникало сомнений, давайте разберем второй пример подбора общего знаменателя, пусть это будут 4 и 10.
Берем больший знаменатель раскладываем его на множители :
Раскладываем меньший знаменатель :
Виртуально исключаем повторяющиеся множители из второго знаменателя — это 2. И во втором знаменателе остается вторая 2. Умножаем больший знаменатель на 2 :
Итого получаем общий знаменатель 20, двух чисел 4 и 10.
Как найти общий знаменатель дробей онлайн
У нас есть калькулятор, который в том числе умеет находить общий знаменатель дробей онлайн!
Прежде чем приступать к поиску общего знаменателя, давайте найдем общий знаменатель для двух знаменателей, а потом проверим данное решение на калькуляторе.
Пусть это будут два знаменателя 20 и 6.
Раскладываем больший знаменатель на множители :
Раскладываем на множители второй знаменатель :
Исключаем повторяющиеся множители во втором знаменателе и у нас остается одна двойка.
Умножаем больший знаменатель на 2 :
Итого получаем их общий знаменатель 40.
Переходим к нахождению общего знаменателя онлайн
Вводим первый знаменатель 20.
Набираем второй знаменатель 8.
Получаем результат нахождения общего знаменателя онлайн :
Далее вы можете сравнить два результата нахождения общего знаменателя.
Что такое наименьший общий знаменатель?
Разница между «общим знаменателем«(1) и «наименьшим общим знаменателем«(2) в том, что первое может быть бесконечное количество. а второе «НОЗ», только один!
Но, что же такое «наименьший общий знаменатель»
НОЗ — это абсолютно тоже самое, что и «НОК».
Определение, что же такое «наименьший общий знаменатель»
Наименьший общий знаменатель двух знаменателей — это самое маленькое целое число, которое делится без остатка на первый и второй знаменатель.
Формула наименьшего общего кратного
Для нахождения «наименьшего общего знаменателя» двух знаменателей, нужно эти два знаменателя разложить на множители. Больший знаменатель записываем в первую строчку, второй знаменатель раскладываем на множители и записываем во вторую строчку.
Сравниваем две строки и удаляем из второй все цифры, которые повторяются в первой строчке.
То число(если больше 1, то перемножаем между собой) умножаем на большее число.
Для понимания формулы наименьшего общего кратного нам нужен пример!
Предположим, что у нас есть два знаменателя 10 и 6 и нужно найти наименьший общий знаменатель :
Разложим больший знаменатель на множители :
Разложим второй знаменатель на множители :
Теперь, нам нужно исключить повторяющеюся цифру 2 из второй строчки, остается цифра 3.
Умножаем больший знаменатель на 3.
Итого получаем, что наименьший общий знаменатель двух знаменателей 10 и 5 равно 30.
Как найти наименьший общий знаменатель на калькуляторе
Для понимания процесса получения наименьшего общего знаменателя на калькуляторе нам потребуются два знаменателя, например 18 и 12 из дробей 1/18 и 1/12
Прежде чем приступать к нахождению «нок» двух чисел на калькуляторе, давайте найдем наименьшее общее кратное, как мы делали это выше :
Раскладываем большее число на множители :
Раскладываем меньшее число на множители :
Исключаем повторяющиеся цифры — это одна 2 и 3, остается 2.
Умножаем большее число на 2.
Итого получаем, что наименьшее общее кратное двух чисел 18 и 12 = 36.
Теперь проверим правильность нахождения «нок» на калькуляторе.
Набираем первое число – пусть это будет число 12
Нажимаем «нок» на калькуляторе – для этого есть специальная кнопка.
После нажатия на кнопку нок – нам нужно добавить втрое число –пусть это будет 18.
И нам отсеется нажать кнопку равно!
И видим результат нахождения наименьшего общего кратного на калькуляторе…
Как найти общий знаменатель трех дробей
Для того чтобы найти общий знаменатель сразу трех дробей нужно подряд найти нок между этими тремя знаменателями!
Для подтверждения данного тезиса — давайте решим задачку/пример.
Задача/пример найдите общий знаменатель для трех дробей.
У нас даны три дроби и у них у всех три разных знаменателя :
Для такой простой задачи можно в уме посчитать. перебором. а потом подтвердим наше решение через «НОК».
5 — не подходит — не делится на 3.
10 — не подходит — не делится на 3.
15 — не подходит, не делится на 2.
20 — не подходит, не делится на 3.
25 — не подходит, не делится на 2.
30 — подходит , делится на все без остатка. мы нашли общий знаменатель для трех дробей, методом перебора
Найдем общий знаменатель для трех дробей на калькуляторе через НОК.
Набираем первый знаменатель — 2.
Нажимаем кнопку — «НОК».
Набираем второй знаменатель — 3.
Далее опять нажимаем — «НОК».
Набираем третий знаменатель — 6.
Получаем общий знаменатель для трех дробей посчитанный онлайн на калькуляторе.
Как найти общий знаменатель дробей с разными знаменателями
Если говориться о том, чтобы найти общий знаменатель, то логично предположить, что у дробей изначально разные знаменатели — иначе, зачем искать общий знаменатель — ведь знаменатели одинаковые.
Выше были рассмотрены варианты нахождения общего знаменателя дробей с разными знаменателями .
Вариант разложения знаменателей на множители.
Вариант нахождения общего знаменателя с помощью НОК и т.д
Источник
Приведение дробей к общему знаменателю
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется . А искомые числа, «выравнивающие» знаменатели, называются .
Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:
- Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
- Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
- Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
Задача. Найдите значения выражений:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:
- Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
- Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
- При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.
Задача. Найдите значения выражений:
Заметим, что . Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.
Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку . Это число намного меньше произведения .
Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).
Обозначение: наименьшее общее кратное чисел обозначается . Например, ; .
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:
Задача. Найдите значения выражений:
Заметим, что . Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий.
Аналогично, . Множители 3 и 4 взаимно просты, а множитель 5 — общий.
Теперь приведем дроби к общим знаменателям:
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
- Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
- Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, , следовательно, для первой дроби дополнительный множитель равен 3.
Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!
Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Источник
Как найти общий знаменатель, что такое общий знаменатель и конечно же нахождение общего знаменателя онлайн на нашем калькуляторе. И если вам требуется наименьший общий знаменатель, то он тут.
Что такое общий знаменатель?
Кроме понятия «общий знаменатель«, есть еще такое понятие как — «Наименьший общий знаменатель (НОЗ)» — это… тоже самое, что и «НОК». Поэтому, мы не будем это разбирать здесь второй раз.
Но что такое общий знаменатель простыми словами?
Общий знаменатель — это любое целое число, которое делится без остатка на первый и второй знаменатель.
Количество чисел, которые могут быть общим знаменателем стремится к бесконечности, но обычно общим знаменателем принимают НОЗ
Пример общего знаменателя :
Для того, чтобы понять, «что такое общий знаменатель» нам нужен пример двух дробей и какое-то действие(иначе смысла в этом нет), пусть это будут две дроби 1/2 и 1/3 и действие сложение — «+».
Для таких маленьких чисел, как 2 и 3 — «нок» будет равен 6. Для этого нам никакие инструменты не понадобятся, наверняка вы это тоже смогли посчитать в уме.
Т.е. 6 делится на 2 без остатка 6 : 2 = 3, и 6 делится на 3 без остатка 6 : 3 = 2.
Мы получили два числа, первую дробь 1/2 надо умножить на 3, чтобы привести её к общему знаменателю 6 — 1*3/2*3 = 3/6.
А вторую дробь нужно умножить на 2, чтобы привести и её к общему знаменатель 6, 1*2/3*2 = 2/6.
После того, как мы нашли общий знаменатель, мы можем произвести действие, в нашем случае — «+» — 3/6 + 2/6 = (3 + 2)/6 = 5/6.
Когда мы нашли «общий знаменатель» мы смогли выполнить необходимое действие с дробями.
1 2 + 1 3 =
1*3 2*3 + 1*2 3*2 =
3 6 + 2 6 =
3 + 2 6 =
5 6
В каком случае ноз двух дробей будет являться произведением знаменателей?
Отличный поисковый запрос — «в каком случае ноз двух дробей будет являться произведением знаменателей?«, что выше не было озвучено.
Когда ноз двух дробей равен произведению знаменателей?
Как минимум, когда знаменатели будут простыми числами, т.е. в качестве примера, это выше приведенные дроби со знаменателями 2 и 3. Эти числа являются простыми, т.е. делятся на себя и на 1.
И общий знаменатель двух чисел 2 и 3 будет равен произведению 2 * 3 = 6.
Формула общего знаменателя
Как вы знаете. что если умножить и числитель и знаменатель на одно число, то результат дроби не изменится! Поэтому мы можем вывести формулу общего знаменателя буквами :
Первую дробь умножаем на знаменатель второй дроби.
А вторую дробь умножаем на знаменатель первой дроби
A B + C D =
A*D B*D + C*B D*B =
A*D + C*B DB
Нахождение общего знаменателя с помощью нок.
Для того чтобы найти общий знаменатель, можно воспользоваться правилом «НОК» для двух чисел, которые здесь — знаменатели.
Если вы не сходили по ссылке, то давайте вкратце попробуем разобраться в формуле подбора общего знаменателя.
Пример нахождения общего знаменателя методом разложения на множители
Это тоже самое. что и выше приведенный «НОК» — только может называться по другому…
смайлы
Этот способ может называться как «нахождение общего знаменателя методом разложения на множители»
Либо «метод нахождения наименьшего общего знаменателя» или просто «НОЗ»
Рассмотрим два знаменателя 8 и 6, к примеру это могут быть две дроби 1/8 и 1/6 и нам нужно найти их общий знаменатель.
Надо расположить в первую строчку наибольший знаменатель — это 8 и разложить его на множители:
8 = 2 * 2 * 2
Ниже раскладываем меньший знаменатель :
6 = 2 * 3
Далее нам нужно исключить все множители, которые повторяются в меньшем знаменателе… это 2 и у нас остается 3. далее эту тройку надо умножить на больший знаменатель :
8 * 3 = 24
Итого получаем общий знаменатель = 24.
Пример номер 2 подбора общего знаменателя
Чтобы у вас не возникало сомнений, давайте разберем второй пример подбора общего знаменателя, пусть это будут 4 и 10.
Берем больший знаменатель раскладываем его на множители :
10 = 2 * 5
Раскладываем меньший знаменатель :
4 = 2 * 2
Виртуально исключаем повторяющиеся множители из второго знаменателя — это 2. И во втором знаменателе остается вторая 2. Умножаем больший знаменатель на 2 :
10 * 2 = 20
Итого получаем общий знаменатель 20, двух чисел 4 и 10.
Как найти общий знаменатель дробей онлайн
У нас есть калькулятор, который в том числе умеет находить общий знаменатель дробей онлайн!
Прежде чем приступать к поиску общего знаменателя, давайте найдем общий знаменатель для двух знаменателей, а потом проверим данное решение на калькуляторе.
Пусть это будут два знаменателя 20 и 6.
Раскладываем больший знаменатель на множители :
20 = 2 * 2 * 5
Раскладываем на множители второй знаменатель :
8 = 2 * 2 * 2
Исключаем повторяющиеся множители во втором знаменателе и у нас остается одна двойка.
Умножаем больший знаменатель на 2 :
20 * 2 = 40
Итого получаем их общий знаменатель 40.
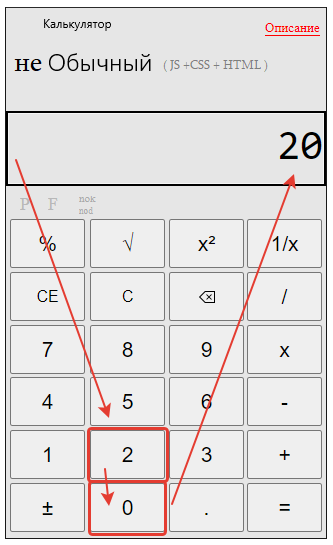
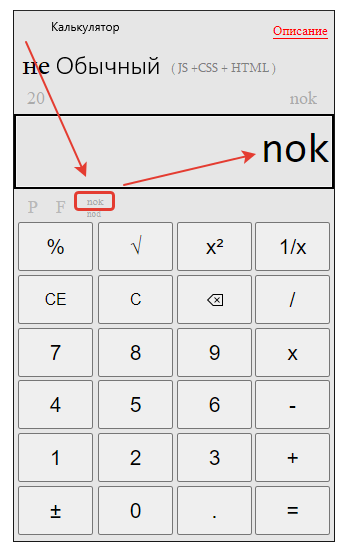
Переходим к нахождению общего знаменателя онлайн
Открываем наш калькулятор.
Вводим первый знаменатель 20.
Нажимаем кнопку «НОК»
Набираем второй знаменатель 8.
Нажимаем равно — «=»
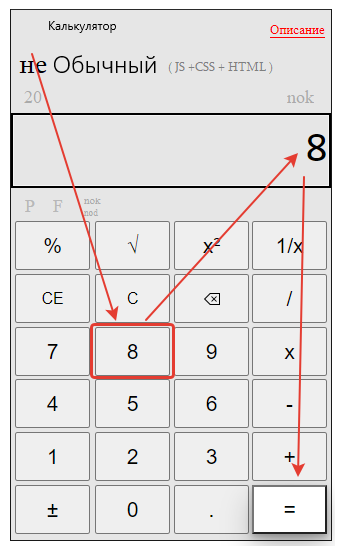
Получаем результат нахождения общего знаменателя онлайн :

Далее вы можете сравнить два результата нахождения общего знаменателя.
Что такое наименьший общий знаменатель?
Разница между «общим знаменателем«(1) и «наименьшим общим знаменателем«(2) в том, что первое может быть бесконечное количество… а второе «НОЗ», только один!
Но, что же такое «наименьший общий знаменатель»
НОЗ — это абсолютно тоже самое, что и «НОК».
Определение, что же такое «наименьший общий знаменатель»
Наименьший общий знаменатель двух знаменателей — это самое маленькое целое число, которое делится без остатка на первый и второй знаменатель.
Формула наименьшего общего кратного
Для нахождения «наименьшего общего знаменателя» двух знаменателей, нужно эти два знаменателя разложить на множители. Больший знаменатель записываем в первую строчку, второй знаменатель раскладываем на множители и записываем во вторую строчку.
Сравниваем две строки и удаляем из второй все цифры, которые повторяются в первой строчке.
То число(если больше 1, то перемножаем между собой) умножаем на большее число.
Для понимания формулы наименьшего общего кратного нам нужен пример!
Предположим, что у нас есть два знаменателя 10 и 6 и нужно найти наименьший общий знаменатель :
Разложим больший знаменатель на множители :
10 = 2 * 5
Разложим второй знаменатель на множители :
6 = 2 * 3
Теперь, нам нужно исключить повторяющеюся цифру 2 из второй строчки, остается цифра 3.
Умножаем больший знаменатель на 3.
10 * 3 = 30
Итого получаем, что наименьший общий знаменатель двух знаменателей 10 и 5 равно 30.
Как найти наименьший общий знаменатель на калькуляторе
Для понимания процесса получения наименьшего общего знаменателя на калькуляторе нам потребуются два знаменателя, например 18 и 12 из дробей 1/18 и 1/12
Прежде чем приступать к нахождению «нок» двух чисел на калькуляторе, давайте найдем наименьшее общее кратное, как мы делали это выше :
Раскладываем большее число на множители :
18 = 2 * 3 * 3
Раскладываем меньшее число на множители :
12 = 2 * 2 * 3
Исключаем повторяющиеся цифры — это одна 2 и 3, остается 2.
Умножаем большее число на 2.
18 * 2 = 36
Итого получаем, что наименьшее общее кратное двух чисел 18 и 12 = 36.
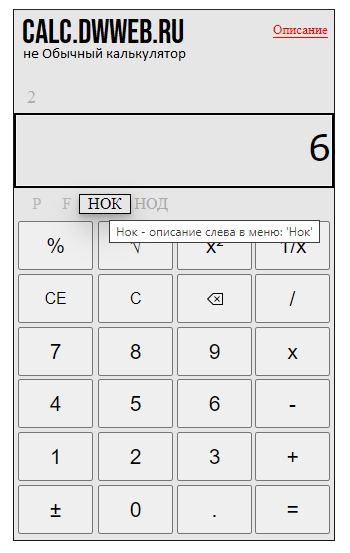
Теперь проверим правильность нахождения «нок» на калькуляторе.
Открываем калькулятор.
Набираем первое число – пусть это будет число 12
Нажимаем «нок» на калькуляторе – для этого есть специальная кнопка.
После нажатия на кнопку нок – нам нужно добавить втрое число –пусть это будет 18.
И нам отсеется нажать кнопку равно!
И видим результат нахождения наименьшего общего кратного на калькуляторе…
Как найти общий знаменатель трех дробей
Для того чтобы найти общий знаменатель сразу трех дробей нужно подряд найти нок между этими тремя знаменателями!
Для подтверждения данного тезиса — давайте решим задачку/пример.
Задача/пример найдите общий знаменатель для трех дробей.
У нас даны три дроби и у них у всех три разных знаменателя :
Для такой простой задачи можно в уме посчитать… перебором…, а потом подтвердим наше решение через «НОК».
5 — не подходит — не делится на 3.
10 — не подходит — не делится на 3.
15 — не подходит, не делится на 2.
20 — не подходит, не делится на 3.
25 — не подходит, не делится на 2.
30 — подходит
, делится на все без остатка… мы нашли общий знаменатель для трех дробей, методом перебора
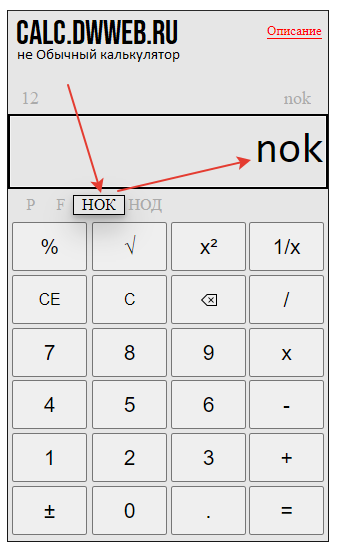
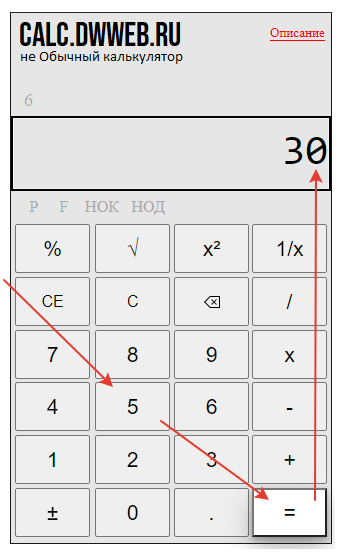
Найдем общий знаменатель для трех дробей на калькуляторе через НОК.
Набираем первый знаменатель — 2.
Нажимаем кнопку — «НОК».
Набираем второй знаменатель — 3.
Нажимаем равно — «=».
Далее опять нажимаем — «НОК».
Набираем третий знаменатель — 6.
Нажимаем равно — «=».
Получаем общий знаменатель для трех дробей посчитанный онлайн на калькуляторе.
Как найти общий знаменатель дробей с разными знаменателями
Если говориться о том, чтобы найти общий знаменатель, то логично предположить, что у дробей изначально разные знаменатели — иначе, зачем искать общий знаменатель — ведь знаменатели одинаковые.
Выше были рассмотрены варианты нахождения общего знаменателя дробей с разными знаменателями.
Вариант разложения знаменателей на множители.
Вариант нахождения общего знаменателя с помощью НОК и т.д
Нахождение наименьшего общего знаменателя бывает нужно для сложения, вычитания и сравнения дробей.
Наименьший общий знаменатель – это наименьшее число, которое нацело делится и на первый, и на второй знаменатель двух дробей.
Правило нахождения наименьшего знаменателя следующее:
Для того, чтобы найти наименьший общий знаменатель двух дробей, нужно найти методом подбора наименьшее общее число, которое бы делилось и на первый, и на второй знаменатель. После этого нужно умножить каждую дробь на такое число, чтобы в знаменателе этих дробей получилось найденное нами наименьшее общее число.
Найти наименьший общий знаменатель двух дробей: 56frac{5}{6} и 34frac{3}{4}.
Решение
Находим методом подбора такое наименьшее число, которое нацело делилось бы и на 6, и на 4. Это число 12. Далее умножаем каждую дробь на такие числа, чтобы в знаменателе получилось 12. Первую дробь умножаем на 2, а вторую на 3:
56=5⋅26⋅2=1012frac{5}{6}=frac{5cdot2}{6cdot2}=frac{10}{12}
34=3⋅34⋅3=912frac{3}{4}=frac{3cdot3}{4cdot3}=frac{9}{12}
Дроби приведены к наименьшему общему знаменателю: 12.
Ответ
12
Найти наименьший общий знаменатель двух дробей: 521frac{5}{21} и 27frac{2}{7}.
Решение
Находим методом подбора такое наименьшее число, которое нацело делилось бы и на 21, и на 7. В этом случае это – один из знаменателей, число 21. Далее нужно умножить вторую дробь на такое число, чтобы в знаменателе получилось 21. Умножаем вторую дробь на 3:
27=2⋅37⋅3=621frac{2}{7}=frac{2cdot3}{7cdot3}=frac{6}{21}
Дроби приведены к наименьшему общему знаменателю: 21.
Ответ
21
Решение задач по алгебре онлайн от экспертов Студворк!
Тест по теме “Наименьший общий знаменатель”