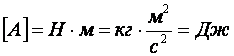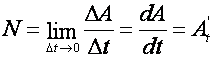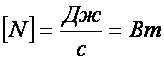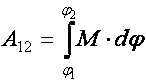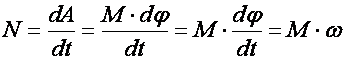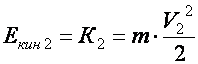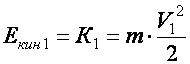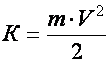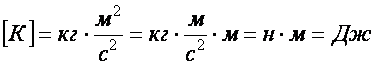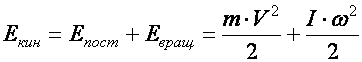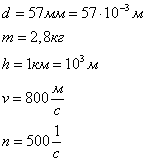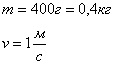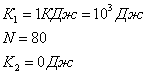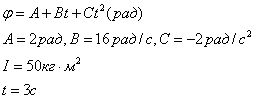Как рассчитать полную энергию
Полная механическая энергия тела – это сумма потенциальной и кинетической энергий, которые свойственны любому физическому телу в каждый момент времени. Их соотношение может изменяться, но сумма двух этих видов энергии всегда остается постоянной.

Инструкция
Вначале нужно посчитать потенциальную энергию тела, ее еще называют энергия покоя. Она вычисляется по формуле: P=m*g*h (произведение массы, высоты и ускорения свободного падения), где m – масса тела, g – ускорение свободного падения, равное 9,8Н/м, h – высота, на которую тело поднято над Землей. Если его удаленность от поверхности Земли, как точки опоры, равна 0, то потенциальная энергия тоже равна 0. Таким образом, если тело подвешено над поверхностью на определенной высоте, то оно имеет положительную потенциальную энергию. Если оно находится ниже поверхности, то есть, под Землей, то его потенциальная энергия отрицательна (ведь на его подъем на нулевую высоте потребуется дополнительные затраты энергии).
Кинетическая – это энергия движения тела, то есть, она есть только у перемещающихся объектов (имеющих скорость). Формула вычисления следующая: E=m*V^2/2 (произведение массы тела на квадрат его скорости, деленное на 2), где m – масса тела, V – скорость, которую имеет тело в момент вычисления. Если тело неподвижно закреплено на подвесе, или оно покоится на опоре, то кинетическая энергия равна 0, так как скорость отсутствует. Чем больше скорость и масса тела, тем больше его кинетическая энергия.
Чтобы найти полную энергию, нужно сложить кинетическую и потенциальную. Формула следующая: Eп=P+E=m*g*h + m*V^2/2. Обычно физическое тело находится в состоянии покоя, но удалено от Земли, так что оно имеет только потенциальную энергию, кинетическая равна 0 (например, подвешенный груз). Движущееся по поверхности Земли тело имеет только кинетическую энергию, потенциальная равна 0 (например, едущий автомобиль). Но если тело находится в полете, то значение обоих видов энергии – ненулевое.
Полезный совет
Энергия – это скалярная физическая величина, которая характеризует всевозможные формы движения материи, а также ее переход из одной формы в другую. Для замкнутой механической системы работает закон сохранения энергии. Формула вычисления полного ее значение как раз является одним из свойств этого закона. Единица измерения энергии – Джоуль. Дж = кг*м^2*с^2 (килограмм на метр в квадрате на секунду в квадрате) = Н*м (Ньютон на метр).
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Полная механическая энергия тела равна сумме его кинетической и потенциальной энергии.
Полную механическую энергию рассматривают в тех случаях, когда действует закон сохранения энергии и она остаётся постоянной.
Если на движение тела не оказывают влияния внешние силы, например, нет взаимодействия с другими телами, нет силы трения или силы сопротивления движению, тогда полная механическая энергия тела остаётся неизменной во времени.
Eпот+Eкин=const
Разумеется, что в повседневной жизни не существует идеальной ситуации, в которой тело полностью сохраняло бы свою энергию, так как любое тело вокруг нас взаимодействует хотя бы с молекулами воздуха и сталкивается с сопротивлением воздуха. Но, если сила сопротивления очень мала и движение рассматривается в относительно коротком промежутке времени, тогда такую ситуацию можно приближённо считать теоретически идеальной.
Закон сохранения полной механической энергии обычно применяют при рассмотрении свободного падения тела, при его вертикальном подбрасывании или в случае колебаний тела.
Пример:
При вертикальном подбрасывании тела его полная механическая энергия не меняется, а кинетическая энергия тела переходит в потенциальную и наоборот.
Преобразование энергии отображено на рисунке и в таблице.
|
Точка нахождения тела |
Потенциальная энергия |
Кинетическая энергия |
Полная механическая энергия |
|
3) Самая верхняя (h = max) |
Eпот
= m⋅g⋅h (max) |
Eкин
= 0 |
Eполная
= m⋅g⋅h |
|
2) Средняя (h = средняя) |
Eпот
= m⋅g⋅h |
Eкин
= m⋅v22 |
Eполная
= m⋅v22 + m⋅g⋅h |
|
1) Самая нижняя (h = 0) |
Eпот
= 0 |
Eкин
= m⋅v22 (max) |
Eполная
= m⋅v22 |
Исходя из того, что в начале движения величина кинетической энергии тела одинакова с величиной его потенциальной энергии в верхней точке траектории движения, для расчётов могут быть использованы ещё две формулы.
Если известна максимальная высота, на которую поднимается тело, тогда можно определить максимальную скорость движения по формуле:
Если известна максимальная скорость движения тела, тогда можно определить максимальную высоту, на которую поднимается тело, брошенное вверх, по такой формуле:
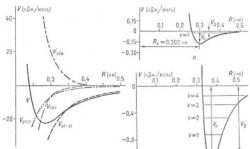
Чтобы отобразить преобразование энергии графически, можно использовать имитацию «Энергия в скейт-парке», в которой человек, катающийся на роликовой доске (скейтер) перемещается по рампе. Чтобы изобразить идеальный случай, предполагается, что не происходит потерь энергии в связи с трением. На рисунке показана рампа со скейтером, и далее на графике показана зависимость механической энергии от места положения скейтера на траектории.
На графике синей пунктирной линией показано изменение потенциальной энергии. В средней точке рампы потенциальная энергия равна (нулю). Зелёной пунктирной линией показано изменение кинетической энергии. В верхних точках рампы кинетическая энергия равна (нулю). Жёлто-зелёная линия изображает полную механическую энергию — сумму потенциальной и кинетической — в каждый момент движения и в каждой точке траектории. Как видно, она остаётся (неизменной) во всё время движения. Частота точек характеризует скорость движения — чем дальше точки расположены друг от друга, тем больше скорость движения.
На графике видно, что значение потенциальной энергии в начальной точке совпадает со значением кинетической энергии в середине рампы.
В реальной ситуации всегда происходят потери энергии, так как часть энергии выделяется в виде тепла под влиянием сил трения и сопротивления.
Поэтому для того, чтобы автомобиль двигался с равномерной и неизменной скоростью, необходимо постоянно подводить дополнительную энергию, которая компенсировала бы энергетические потери.
Как найти полную энергию
В одном и том же теле энергия может храниться одновременно в нескольких формах. Форма всех его энергий, выраженных во всех формах, называется полной энергией. Некоторые процессы протекают таким образом, что в их ходе полная энергия тела почти не изменяется, а изменяется лишь соотношение видов энергии в нем.
Энергией называется величина, характеризующая движения тел и их совместное взаимодействие. В зависимости от вида движения энергия принимает различные формы: кинетическую, потенциальную, внутреннюю, электромагнитную, и т.д. Однако, в большинстве задач по динамике и кинематике рассматривают кинетическую и потенциальную энергии. Сумма этих двух величин составляет полную энергию, которую и требуется найти во многих таких задачах.
Для того чтобы найти полную энергию, как указано выше, необходимо вначале вычислить отдельно как кинетическую, так и потенциальную энергию. Кинетическая энергия — это энергия механического движения системы. Скорость движения при этом является основополагающей величиной, и чем она больше, тем больше кинетическая энергия тела. Ниже указана формула для вычисления кинетической энергии:E=mv^2 /2, где m- масса тела, кг, v — скорость движущегося тела, м/с.Из данной формулы можно сделать вывод, что значение кинетической энергии зависит не только от скорости, но и от массы. Груз большей массы при той же скорости обладает большей энергией.
Потенциальную энергию также называют энергией покоя. Это механическая энергия нескольких тел, характеризующаяся взаимодействием их сил. Величина потенциальной энергии находится исходя из массы тела, однако, в отличие от предыдущего случая, оно никуда не перемещается, то есть, его скорость равна нулю. Наиболее распространен случай, когда тело висит над поверхностью Земли в состоянии покоя. При этом формула потенциальной энергии будет иметь вид:P=mgh, где m — масса тела кг, а h — высота, на которой находится тело, м.Следует также обратить внимание, что потенциальная энергия не всегда имеет положительное значение. Если, например, необходимо определить узнать потенциальную энергию тела, находящегося под землей, тоона примет отрицательное значение:P=-mgh
Полная энергия является результатом суммирования кинетической и потнециальной. Поэтому формулу для ее вычисления можно записать следующим образом: Eo=E+P=mv^2/2+mgh.В частности, обоими видами энергии одновременно обладает летящее тело, причем, соотношение между ними в ходе разных фаз полета изменяется. В нулевой точке отсчета преобладает кинетическая энергия, затем по мере полета часть ее преобразуется в потенциальную, а в конце полета снова начинает преобладать кинетическая.
ЛЕКЦИЯ № 3. РАБОТА. МОЩНОСТЬ. ЭНЕРГИЯ
1. РАБОТА И
МОЩНОСТЬ ПРИ ПОСТУПАТЕЛЬНОМ И ВРАЩТЕЛЬНОМ ДВИЖЕНИИ
Работа силы
– скалярная
физическая величина, характеризующая меру действия силы на материальное тело.
Работа силы зависит от величины силы, направления вектора силы и от перемещения
точки приложения силы.
Если сила, действующая на тело
постоянна по величине и направлению , а перемещение
тела происходит по прямолинейной
траектории (рис.1), то в этом случае работа силы вычисляется по простой
формуле:
где – угол между вектором силы и вектором перемещения : .
В Интернациональной системе
единиц работа измеряется в джоулях:
Как видно из формулы, работа силы
может быть как положительной величиной, так и отрицательной.
Если угол между вектором силы и
вектором перемещения острый (рис.1) , то сила совершает положительную работу:
Если угол между вектором силы и
вектором перемещения тупой , то сила совершает отрицательную работу, в этом случае говорят,
что работа совершается против силы:
Если вектор силы перпендикулярен
вектору перемещения и , то в этом случае сила не совершает работу:
В общем случае, если вектор силы
изменяется по величине или по направлению , а перемещение тела происходит по криволинейной траектории
(рис.2), вводится понятие элементарной работы :
где – вектор элементарного перемещения тела, – угол между вектором силы и вектором
элементарного перемещения , то есть: . Величина элементарного перемещения определяется тем, что
сила, действующая на тело на этом перемещении, остается постоянной как по
величине, так и по направлению.
Полная работа силы на конечном
перемещении материального тела из точки в точку по криволинейной
траектории равна сумме элементарных
работ, то есть интегралу вида:
Если тело под действием силы перемещается по
замкнутой траектории , то в этом случае работа силы будет вычисляться по формуле:
В природе существуют силы, работа
которых по любой замкнутой траектории всегда (тождественно)
равна нулю, такие силы называются консервативными или потенциальными:
Примерами консервативных сил может служить
сила тяжести, сила упругости, сила Кулона и некоторые другие силы.
Силы, работа которых по любой
замкнутой траектории не равна тождественно нулю, называются неконсервативными
или непотенциальными
:
Примерами неконсервативных сил
является сила трения скольжения, сила сопротивления.
Чтобы охарактеризовать скорость
совершения работы, вводят понятие мощности.
Средняя мощность это скалярная
физическая величина, равная отношению работы, совершенной за некоторый
промежуток времени, к величине этого промежутка времени:
Если уменьшать промежуток времени
, то отношение будет стремиться к
некоторому пределу. Этот предел называется мгновенной мощностью силы:
Таким образом, мощность силы
является производной работы, совершаемой силой, по времени.
Используя определение
механической работы, можно получить удобную для решения задач формулу:
где – угол между направлением вектора силы и вектора скорости , то есть . Итак, мгновенная мощность, развиваемая силой , равна скалярному произведению вектора силы на вектор
скорости, с которой движется точка приложения этой силы.
Единицы измерения мощности в
Интернациональной системе единиц – ватт:
Рассмотрим теперь вращательное
движение. Пусть тело вращается по окружности радиусом под действием силы,
которая направлена перпендикулярно к траектории движения тела (то есть
перпендикулярно к окружности) в любой точке (рис.3). В этом случае сила и элементарное перемещение
тела будут всегда коллинеарны
,тоесть , следовательно, угол между этими векторами всегда будет
равен нулю. Поэтому элементарная работа силы выразится формулой:
С другой стороны нам известно из
геометрии, что длина дуги окружности радиуса равна , где – угол, на который опирается эта дуга.
Таким образом, можно записать для
элементарной работы следующее выражение:
Легко заметить, что в нашем
случае произведение величины силы на радиус окружности равно величине момента
силы относительно оси вращения, проходящей через центр окружности:
Окончательно можно записать
выражение для элементарной работы:
Чтобы найти полную работу,
которая совершается силой при повороте тела по
окружности на угол , необходимо проинтегрировать указанное выше выражение:
Если момент силы есть величина
постоянная (что совсем необязательно), то формула для работы силы при
вращательном движении принимает простой вид:
Используя полученные формулы,
легко видеть, что мощность при вращательном движении равна произведению момента
силы на угловую скорость точки приложения силы:
2. МЕХАНИЧЕСКАЯ
ЭНЕРГИЯ
Понятие механической работы тесно
связано с понятием механической энергии. Энергия, как известно, это единая
количественная мера движения материи во всех проявлениях этого движения. А
работа есть мера изменения энергии системы. Если механическая система совершает
положительную работу над внешними телами, то неизбежно энергия системы уменьшается.
В этом случае говорят, что работа совершается за счет убыли энергии системы, а
работу совершают внутренние силы системы:
То есть
И, наоборот, если внешние тела совершают
над механической системой работу, то ее энергия увеличивается:
То есть
Механическая энергия бывает двух
типов – кинетической и потенциальной. Кинетическая энергия системы обусловлена механическим
движением этой системы, то есть кинетическая энергия является мерой
механического движения данной системы.
Выведем формулу, описывающую
кинетическую энергию системы при поступательном движении. Пусть на тело
действует постоянная по величине и направлению сила .
Под действием этой силы, как
известно, тело будет двигаться прямолинейно и равноускоренно. Ускорение тела определяется вторым
законом Ньютона:
Пусть начальная скорость тела
была равна нулю, тогда через некоторый момент времени от начала движения скорость тела будет равна , где – перемещение тела или, что тоже самое
,
– перемещение точки приложения силы. Выразим перемещение через скорость, получим: .
Теперь можно записать выражение
для элементарной работы, которую совершила сила при перемещении тела
на бесконечно малое расстояние :
Где – угол между вектором скорости и вектором , при поступательном движении этот угол всегда равен нулю
градусов, следовательно .
Таким образом, элементарная
работа при поступательном движении выражается формулой:
Чтобы найти полную работу,
которую совершает сила при разгоне тела из состояния покоя до некоторой скорости , необходимо проинтегрировать полученное выражение от
значения начальной скорости до конечного значения
скорости :
Как было сказано выше, если
работу совершает внешняя сила, то энергия системы увеличивается, более того
работа внешней сила равна изменению кинетической энергии системы, то есть:
Сравнивая два выражения для одной
и той же величины, можно прийти к выводу, что кинетическая энергия тела во
втором его состоянии равна:
Соответственно, кинетическая
энергия в первом состоянии описывается аналогичной формулой:
Если тело находится в состоянии
покоя , то его кинетическая энергиятождественно равна нулю.
В общем случае кинетическая
энергия тела, движущегося со скоростью , равна:
Как видно из полученной формулы
кинетическая энергия зависит только от массы тела (постоянной величины в
классической физике) и мгновенной скорости тела, следовательно, кинетическая
энергия является функцией состояния системы и не зависит от того, каким образом
система попала в это состояние.
Проверим размерность полученной
формулы:
Так как скорость системы в
различных инерциальных системах отсчета различна, следовательно, кинетическая
энергия системы так же зависит от выбора системы отсчета.
Если тело участвует во вращательном
движении, то оно так же обладает кинетической энергией. Получим формулу для
кинетической энергии вращающегося тела.
Пусть материальная точка, имеющая
массу , вращается по окружности радиусом с угловой скоростью . Как известно, линейная скорость материальной точки связана с угловой
скоростью следующим соотношением:
Подставим это соотношение в формулу
для кинетической энергии, получим:
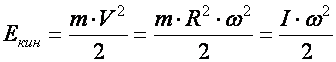
где – момент инерции материальной точки относительно оси
вращения.
Полученная формула для
кинетической энергии справедлива не только для материальной точки, но и для любого
вращающегося абсолютно твердого тела, обладающего моментом инерции относительно оси
вращения.
Если же тело участвует
одновременно и в поступательном и во вращательном движении, то его кинетическая
энергия складывается из кинетической энергии поступательного движения и
кинетической энергии вращательного движения:
Примером может служить летящий
снаряд (пуля), выпущенный из нарезного оружия. За счет наличия вращательного
движения, кинетическая энергия, а значит, убойная сила снаряда увеличивается по
сравнению с кинетической энергией такого же снаряда, выпущенного из
гладкоствольного оружия.
Потенциальная энергия системы –
энергия, обусловленная взаимным расположением тел, составляющих систему, и
характером взаимодействия между ними.
Понятие потенциальная энергия
имеет смысл только для систем, где действуют консервативные силы, о которых
говорилось выше. Потенциальная энергия в такихсистемах равна работе, которую совершают внутренние (консервативные)
силы системы при переходе системы из данного положения в положение, где
потенциальная энергия системы по договоренности равна нулю.
Таким образом, одной
универсальной формулы для вычисления потенциальной энергии произвольной
системыне существует, ее необходимо получать
для каждой конкретной системы определенным образом.
Выведем формулу потенциальной
энергии, например для тела, поднятого над поверхностью Земли. Прежде всего,
необходимо доказать, что силы, действующие в такой системе консервативны, и
понятие потенциальной энергии действительно имеет смысл. Итак, между любым
телом, поднятым над поверхностью Земли, и Землей действует сила тяжести равная , где – вектор ускорения
свободного падения, который направлен к центру Земли вертикально вниз. Найдем,
какую работу совершает сила тяжести при перемещении тела из одной точки над
поверхностью Земли в другую. Пусть первая точка находится над поверхностью
Земли на высоте , а вторая точка находится соответственно на высоте , причем . Траектория движения тела из первого состояния во второе представляет
собой линию .
Прежде всего, запишем выражение
для элементарной работы, которую совершает сила тяжести при бесконечно малом
перемещении тела :
Где – угол между вектором элементарного перемещения и вектором ускорения свободного
падения , а – бесконечно малое перемещение тела по вертикали.
Чтобы найти полную работу силы
тяжести при перемещении тела из первого состояния во второе состояние,
необходимо проинтегрировать выражение для элементарной работы:
Проанализируем полученный
результат – полная работа силы тяжести определяется только положением тела над
уровнем Земли и совершенно не зависит от вида траектории тела. Этот факт
является доказательством того, что сила тяжести этоконсервативная сила, значит для системы
«тело-Земля» имеет смысл понятие потенциальная энергия, Область пространства,
где действует консервативная сила тяжести, называется потенциальным полем силы
тяжести.
Так как работу совершает
внутренняя сила системы – сила тяжести, то энергия системы уменьшается. Другими
словами работа совершается за счет убыли потенциальной энергии системы, то есть
Сравнивая два выражения для
работы силы тяжести можно прийти к выводу, что тело в первом состоянии, то есть
на высоте над Землей, обладало потенциальной
энергией равной , во втором состоянии потенциальная энергия тела равна
соответственно . Потенциальная энергия тела, находящегося на поверхности
Земли равна нулю.
Итак, в общем случае,
потенциальная энергия тела поднятого на высоту над поверхностью
Земли, равна:
.
Как мы видим, потенциальная энергия
так же зависит только от массы тела и его высоты над поверхностью Земли, то
есть потенциальная энергия является функцией состояния системы и не зависит от
того, каким способом система пришла в это состояние.
Аналогичные рассуждения приводят
нас к выводу, что сила упругости пружины так же является консервативной силой.
Сила упругости, как известно,
описывается законом Гука: ,
где – коэффициент жесткости пружины,характеристика данной пружины, имеющая размерность
, – деформация пружины, то есть изменение размеров пружины.
Знак минус в законе Гука
указывает на то, что направление силы, возникающей в деформированной пружине,
всегда противоположно деформации пружины. Действительно, если растянуть
пружину, то в ней возникает сила, стремящаяся возвратить пружину в исходное
состояние, и наоборот.
Таким образом, упруго
деформированная пружина обладает запасом потенциальной энергии, то есть может
совершить некоторую механическую работу, точнее, работу совершает сила
упругости, возникающая в пружине.
Величина потенциальной энергии,
запасенной в деформированной пружине,равна:
Потенциальная энергия не
деформированной пружины ()
тождественно равна нулю.
Полная механическая энергия
системы равна сумме кинетической и потенциальной энергии: или
Если механическая система замкнута и в системе действуют
только консервативные силы, то полная механическая энергия всей системы остается
неизменной при любых взаимодействиях между телами, составляющими эту систему.
Это утверждение выражает суть закона сохранения механической энергии.
Необходимо заметить, что энергия каждого тела системы может изменяться,
неизменной остается только суммарная механическая энергия всей системы.
Математически закон сохранения
механической энергии можно записать несколькими способами:
где – потенциальная и кинетическая энергия всей системы до
взаимодействия, а – потенциальная и кинетическая энергия всей системы после
взаимодействия.
Если же в системе действуют
неконсервативные силы (сила трения и т.п.)или система незамкнута, то есть в ней действуют внешние силы, то в этом
случае суммарная механическая энергия не остается постоянной – закон сохранения
энергии не выполняется. При этом изменение суммарной механической энергии будет
равно работе, произведенной неконсервативными силами или внешними силами при
переходе системе из одного состояния в другое.
Математически этот факт
записывается следующим образом:
или ,
где – количество теплоты, выделяющееся в системе.
Примером взаимодействий, при
котором выполняется закон сохранения полной механической энергии системы,
является абсолютно упругий
удар или столкновение.
Столкновение (удар) – это взаимодействие двух или более тел, которое длится
очень короткое время, при сближении этих тел на малыерасстояния. Абсолютно упругий удар –
столкновение тел, при котором тела не деформируются (фо
рма
тел не изменяется), и суммарная кинетическая энергия системы тел остается
постоянной. При абсолютно упругом
ударе выполняется
как закон сохранения механической энергии системы, так и закон сохранения
импульса системы.
Полной противоположностью абсолютно упругого
удара является столкновение тел, при
котором сталкивающиеся тела объединяются и в дальнейшем двигаются как одно целое.
Такое взаимодействие называется абсолютно неупругим ударом. При абсолютно
неупругом ударе закон сохранения энергии системы не выполняется, однако закон
сохранения импульса системы остается справедливым.
3. ПРИМЕРЫ
РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ «РАБОТА, МОЩНОСТЬ, ЭНЕРГИЯ»
ЗАДАЧА № 1. Снаряд автоматической зенитной пушки
АЗП-57, масса которого 2,8 кг,
летит на высоте 1 км
со скоростью 800 метров
в секунду и вращается, делая 500 оборотов в секунду. Найти полную механическую
энергию снаряда, считая его сплошным однородным цилиндром.
Начинаем решение этой задачи с того, что запишем
данные в условии задачи величины под заголовок «Дано», учитывая, что калибр
снаряда равняется его диаметру.
ДАНО:
Найти:
Е
Решение: как известно полная механическая энергия
системы равна сумме потенциальной и кинетической энергии. В нашей задаче
рассматривается система «снаряд-земля». Потенциальная энергия снаряда в этой системе
равна . Кинетическая энергия снаряда складывается из кинетической
энергии его поступательного движения и кинетической энергии его вращательного
движения: . Кинетическую энергию поступательного движения можно вычислить
сразу, так как все необходимые величины нам известны. Для тогочтобы вычислить кинетическую энергию
вращательного движения нам необходимо знать момент инерции снаряда и его
угловую скорость. Так как снаряд, рассматривается как сплошной однородный
цилиндр, его момент инерции будет равен . Угловую скорость так же легко найти, так как нам известна
частота вращения снаряда: .
Таким
образом, полная механическая энергия снаряда в системе «снаряд-земля» будет
равна следующему выражению: — мы получили рабочую формулу, так как она отвечает на вопрос
задачи и в нее входят только известные величины. Проверим размерность рабочей
формулы: — размерность правильная, значит можно подставлять числовые
значения. .
Задача
решена, однако надо заметить, что кинетическая энергия вращательного движения
снаряда в данном случае намного меньше кинетической энергии его поступательного
движения. Вращение снарядапридает
устойчивость снаряду, повышая точность попадания. В данной задаче надо
напомнить, что вращательное и поступательное движение снаряда никак не связано
друг с другом ипроисходят независимо
друг от друга.
Задача № 2.Сплошной цилиндр массой 4 00 грамм катится без
проскальзывания по горизонтальной поверхности. Линейная скорость осицилиндра 1 метр в секунду. Определить
полную кинетическую энергию цилиндра.
ДАНО:
НАЙТИ:
К
РЕШЕНИЕ:
Данная задача очень похожа на предыдущую задачу. Так как цилиндручаствует одновременно в двух движениях, его
кинетическая энергия будет равна сумме кинетической энергии поступательного
движения и кинетической энергии вращательного движения, Однако эти движения не
являются независимыми, линейная скорость оси цилиндра будет определять и
угловую скорость вращения цилиндра по формуле . Далее, момент инерции цилиндра считается известным: . На данном этапе у курсантов обязательно возникают
затруднения, так как в условии задачи ничего не говорится о радиусе цилиндра.
Поэтому преподавателю целесообразно еще раз подчеркнуть важность решения задачи
в общем буквенномвиде, так при
подстановке перечисленных выше выражений в формулу для кинетической энергии радиус
сократится и не будет присутствовать в конечной формуле: — мы получили рабочую
формулу, в ней присутствуют только величины заданные в условии задачи: масса и
скорость .
Размерность рабочей формулы очевидна и не
требует проверки. Числовое значение кинетической энергии равно: 
Задача № 3.Кинетическая энергиявращающегося
маховика 1 Килоджоуль. Под действием постоянного тормозящего момента маховик
начал вращаться равнозамедленно и, сделав 80 оборотов, остановился. Определить
момент силы торможения.
Запишем
известные величины под заголовок «Дано», учитывая при этом, что в конечном
состоянии система покоится, значит, его энергия в этом состоянии равна нулю.
ДАНО:
Найти:
М
Решение:
для того, чтобы найти момент силы торможения нам необходимо записать формулу
вычисления работы при вращательном движении: — здесь мы учли тот факт, что работа совершается равномерно.
Угловое перемещение можно вычислить, зная- размерность
соответствует действительности, следовательно, можно подставлять числовые
значения известных величин: . Знак минус в полученном результате говорит о том, работа
совершается телом, маховиком против внешней силы, в результате чего энергия маховика
уменьшается до нуля.
Задача
№ 4 Маховик вращается по закону, выражаемому уравнением , где А
=2 рад, В=16 рад/с, С=-2
рад/с 2 . Момент инерции маховика 50 кгм 2
.
Найти кинетическую энергию маховика и его мощность через 3 секунды после начала
движения.
Дано:
Найти:
К,
N
Решение:
сначала найдем кинетическую энергию вращательного движения маховика, как
известно, она равна . Угловую скорость маховика найдем как первую производную
углового перемещения: , подставим полученное выражение в формулу для кинетической
энергии маховика, получим:
— все величины,
входящие в эту формулу нам известны из условия задачи. Проверим размерность
полученной формулы: — размерность правильная, подставим числовые значения
известных величин:
. Угловое ускорение можно найтикак производную угловой скорости по времени: . Подставим все эти выражения в формулу, которую мы получили
выше для мощности силы:
Это рабочая формула,
она отвечает на вопрос задачи и в нее входят только известные из условия задачи
величины. Проверим размерность этой формулы: -р
азмерность рабочей формулы
соответствует размерности мощности, значит рабочая формула правильная,
следовательно мы можем приступить к вычислению числового значения этой величины: .
Проанализируем
полученный результат, знак минус говорит о том, что маховик тормозится, и он
совершает работу против внешних сил.
3.4. Механическая энергия
3.4.1. Кинетическая энергия
Кинетическая энергия поступательного движения
тела определяется формулой
где m
— масса движущегося тела; v
— модуль его скорости.
Для расчета кинетической энергии при поступательном движении тела существует еще одна формула:
где P
= mv
— модуль импульса движущегося тела.
Кинетическая энергия вращательного движения
тела определяется формулой
W k = m ω 2 R 2 2 ,
где m
— масса движущегося тела; ω — величина угловой скорости (циклическая частота); R
— радиус окружности, по которой движется тело.
Для расчета кинетической энергии при вращательном движении тела существует еще одна формула:
W k = 2 m π 2 ν 2 R 2 ,
где ν — частота вращения тела.
При решении задач на расчет кинетической энергии системы тел
полезно помнить, что она складывается из кинетических энергий каждого из тел:
W k сис = W k 1 + W k 2 + … + W k N ,
где W
k
1 , W
k
2 , …, W
kN
— кинетические энергии каждого тела.
При решении задач на расчет кинетической энергии вращательного движения могут оказаться полезными
следующие формулы:
- связь между линейной v
и угловой ω скоростями:
v
= ωR
,
где R
— радиус окружности по которой движется тело;
- связь между циклической частотой ω и частотой ν:
- связь между циклической частотой ω (или частотой ν) и периодом обращения тела по окружности T
:
ωT
= 2π или ν = 1 T .
Пример 24.
Координата тела, движущегося вдоль оси Ox
, зависит от времени по закону x
(t
) = 8,0 − 2,0t
+ t
2 , где координата задана в метрах, время — в секундах. Определить изменение кинетической энергии тела с начала третьей до конца четвертой секунды движения. Масса тела составляет 3,0 кг.
Решение.
Кинетическая энергия тела определяется формулами:
W k 1 = m v 2 (t 1) 2 ;
W k 2 = m v 2 (t 2) 2 ,
где v
(t
1) — модуль скорости тела в начале третьей секунды; v
(t
2) — модуль скорости тела в конце четвертой секунды.
Уравнение движения тела
x (t) = 8,0 − 2,0 t + t 2
позволяет установить закон изменения проекции скорости на ось Ox
с течением времени в виде:
v x (t) = v 0 x + a x t ,
где v
0 x
= −2,0 м/с — проекция начальной скорости на ось Ox
; a
x
= = 2,0 м/с 2 — проекция ускорения на указанную ось.
Таким образом, зависимость проекции скорости от времени, записанная в явном виде
v x (t) = − 2,0 + 2,0 t ,
позволяет получить соответствующие проекции скоростей:
- в начале третьей секунды движения (t
1 = 2 c)
v x (t 1) = − 2,0 + 2,0 t 1 = − 2,0 + 2,0 ⋅ 2 = 2,0 м/с;
- в конце четвертой секунды движения (t
2 = 4 c)
v x (t 2) = − 2,0 + 2,0 t 2 = − 2,0 + 2,0 ⋅ 4 = 6,0 м/с.
Значения кинетической энергии тела в указанные моменты времени:
- в начале третьей секунды движения (t
1 = 2 c)
W k 1 = 3,0 ⋅ (2,0) 2 2 = 6,0 Дж,
- в конце четвертой секунды движения (t
2 = 4 c)
W k 2 = 3,0 ⋅ (6,0) 2 2 = 54 Дж.
Искомая разность кинетических энергий составляет
Δ W k = W k 2 − W k 1 = 54 − 6,0 = 48 Дж.
Таким образом, кинетическая энергия тела за указанный интервал времени возросла на 48 Дж.
Пример 25.
Тело движется в плоскости xOy
по траектории вида x
2 + y
2 = 25 под действием центростремительной силы, величина которой равна 50 Н. Масса тела составляет 2,0 кг. Координаты x
и y
заданы в метрах. Найти кинетическую энергию тела.
Решение.
Траектория движения тела представляет собой окружность радиусом 5,0 м. Согласно условию задачи, на тело действует только одна сила, направленная к центру этой окружности.
Модуль указанной силы является постоянной величиной, поэтому тело обладает постоянным центростремительным ускорением, не влияющим на величину скорости тела; следовательно, тело движется по окружности с постоянной скоростью.
Рисунок иллюстрирует данное обстоятельство.
Величина центростремительной силы определяется формулой
F ц. с = m v 2 R ,
где m
— масса тела; v
— модуль скорости тела; R
— радиус окружности, по которой движется тело.
Выражение для кинетической энергии тела имеет вид:
Отношение уравнений
F ц. с W k = m v 2 R 2 m v 2 = 2 R
позволяет получить формулу для расчета искомой кинетической энергии:
Кинетическая
энергия
механической системы — это энергия
механического движения этой системы.
Сила
F
,
действуя на покоящееся тело и вызывая
его движение, совершает работу, а энергия
движущегося тела возрастает на величину
затраченной работы. Таким образом,
работа dA
силы F
на пути, который тело прошло за время
возрастания скорости от 0 до
,
идёт на увеличение кинетической энергии
dE
к
тела, т. е.
Используя
второй закон Ньютона
и умножая на перемещениеdr
,
получаем:
Так
как
,
то
Таким
образом, тело массой m
,
движущееся со скоростью
,
обладает кинетической энергией
Потенциальная
энергия
– механическая энергия системы тел,
определяемая их взаимным
расположением и характером сил
взаимодействия между ними.
При
перемещении тела из одного положения
в
другое,
работа, совершаемая
действующими силами при перемещении
тела из одного положения в
другое, не зависит от того, по какой
траектории это перемещение произошло,
а
зависит только от начального и конечного
положения. Такие поля называются
потенциальными
,
а силы, действующие в них, – консервативными
.
Работа
консервативных сил на замкнутой
траектории равна нулю
.
Это утверждение поясняет рис. 2.1.
Свойством
консервативности обладают сила тяжести
и сила упругости. Для этих сил можно
ввести понятие потенциальной энергии.
Работа
консервативной силы A
12a = A
12b .
Работа на замкнутой траектории
A
= A
12a + A
21b = A
12a – A
12b = 0.
Тело,
находясь в потенциальном поле сил,
обладает потенциальной энергией
E
п
.
Работа консервативных сил при элементарном
(бесконечно малом) изменении кон
фигурации
системы равна приращению потенциальной
энергии, взятому со знаком
минус,
так как работа совершается за счет убыли
потенциальной энергии
:
Работа
dA
выражается
как скалярное произведение силы F
на перемещение dr
и
выражение (2.2) можно записать в виде
Следовательно,
если известна функция Е
п
(r
),
то из формулы (2.3) можно найти силу F
по модулю и направлению.
Потенциальная энергия может быть определена исходя из (2.3) как
где
C
–
постоянная интегрирования.
Если
тело перемещается вблизи поверхности
Земли, то на него действует постоянная
по величине и направлению сила тяжести
.
Работа этой силы зависит только от
вертикального перемещения тела. На
любом участке пути работу силы тяжести
можно записать в проекциях вектора
перемещенияна ось
OY
:
где
– проекция силы тяжести,
Δ
S
y
– проекция вектора перемещения. Если
тело переместилось из точки, расположенной
на высоте
h
1
,
в точку, расположенную на высоте
h
2
от начала координатной оси
OY
(рис
. 2.2.),
то сила тяжести совершила работу
:
Эта
работа равна изменению некоторой
физической величины
,
взятому с противоположным знаком. Эту
физическую величину называютпотенциальной
энергией
тела в поле силы тяжести
E
p
=
mgh
.
Она
равна работе, которую совершает сила
тяжести при опускании тела на нулевой
уровень.
Работа
силы тяжести равна изменению потенциальной
энергии тела, взятому с противоположным
знаком.
A
= –(E
p 2 – E
p 1).
Найдём
потенциальную энергию упругодеформированного
тела (пружины). Сила
упругости пропорциональна деформации:
где
F
упр
—
проекция силы упругости на ось х
,
k
—
коэффициент упругости (для пружины
– жёсткость),
знак
минус указывает, что
F
упр
направлена
в сторону,
противоположную
деформации х.
По
третьему закону Ньютона, деформирующая
сила равна по модулю силе уп
ругости
и противоположно ей направлена, т. е.
Элементарная
работа dA
,
совершаемая
силой F
x
при
бесконечно малой деформации dx
,
равна:
а
полная работа
.
идет
на увеличение потенциальной энергии
пружины. Таким образом, потенциальная
энергия упругодеформированного тела
:
Полная
механическая энергия системы:
т.е.
равна сумме кинетической и потенциальной
энергий.
Пусть произвольная механическая система
состоит из
частиц;
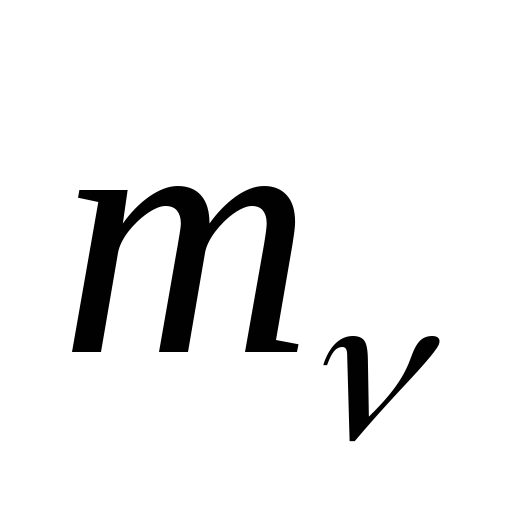

скорость

из них. Тогда:
величину
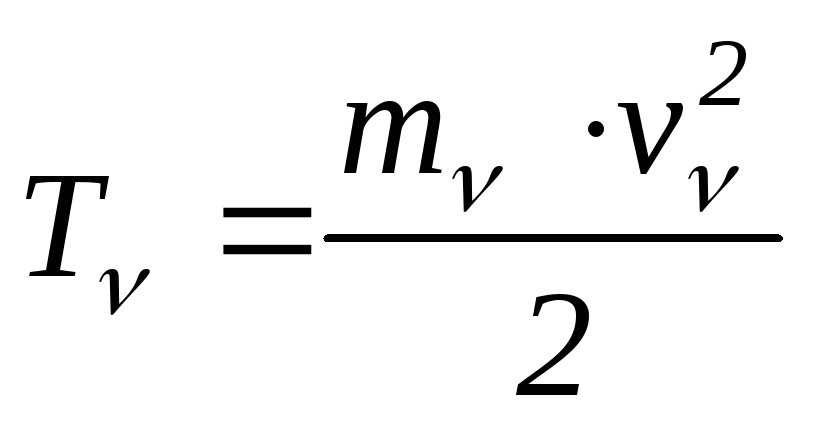
энергией

частицы, а
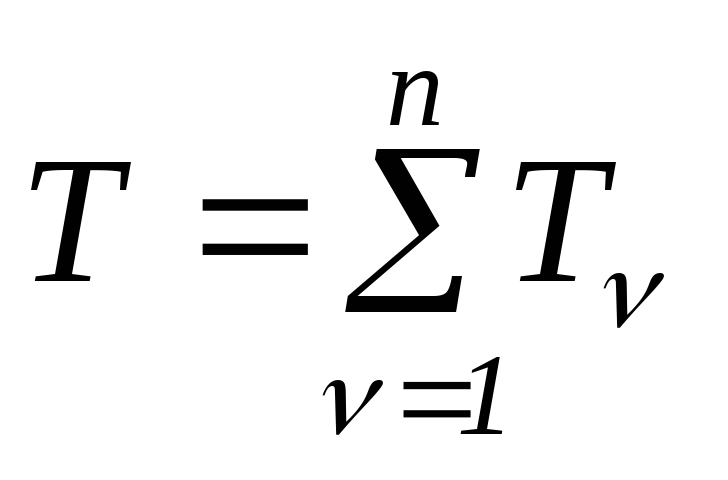
кинетической энергией рассматриваемой
механической системы.
По причине одинаковости скоростей всех
точек
кинетическая энергия поступательно
движущегося тела определяется формулой
,
где
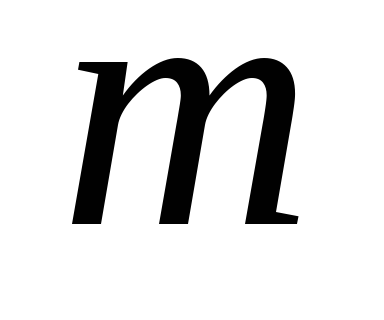
его масса, а

Для вращательно движущегося тела:
кинетическая
энергия пврщательно движущегося тела
определяется формулой
30.20, Где
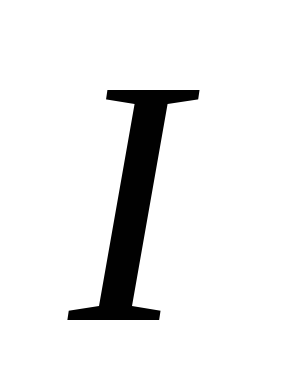
момент инерции тела относительно оси
вращения и

30.6*. Формула для вычисления кинетической энергии сферически движущегося тела
Пусть
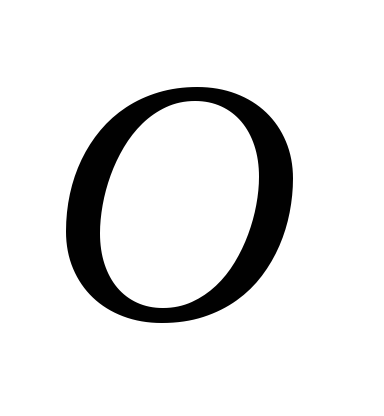
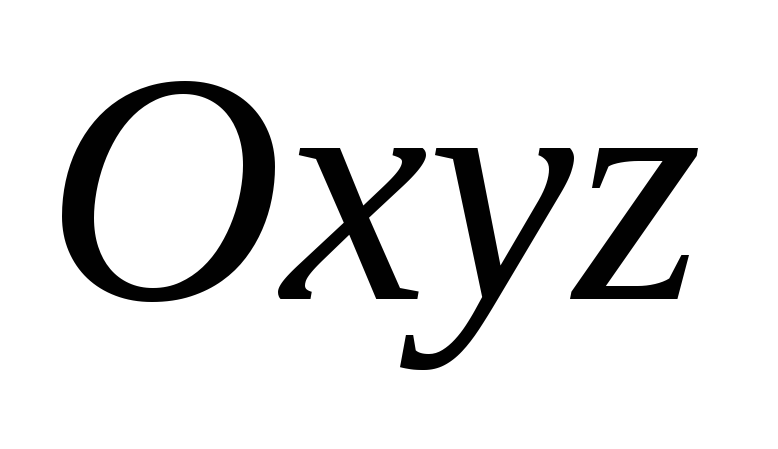
причём, её оси являются главными осями
инерции тела.
В общей формуле —
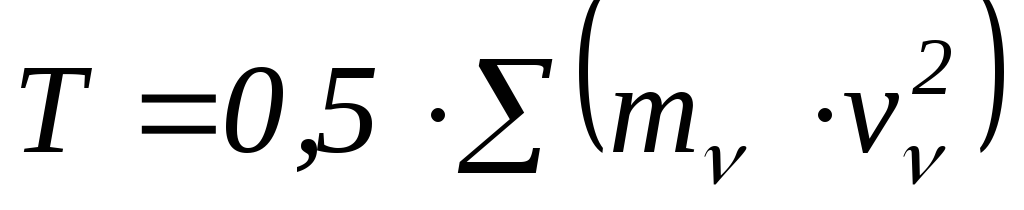
выразим

характеристики тела:
Т.к.
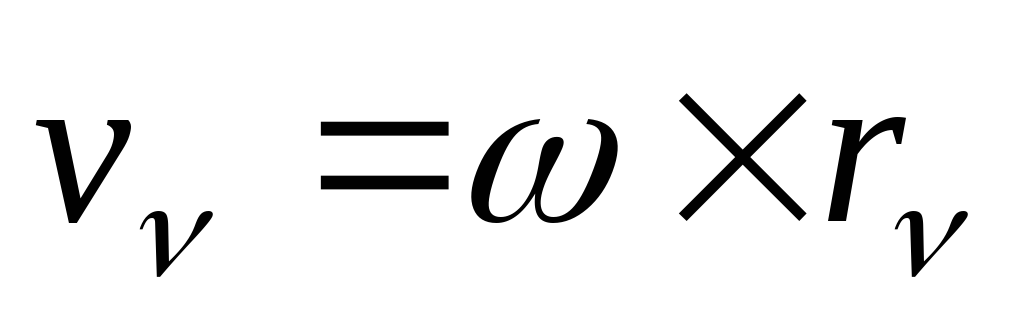
то по способу перестановки индексов
имеем:
Но

т.е. вектор
Учитываем, что скалярные произведения
ортогональных векторов равны нулю и
получаем:
При возведениях в квадраты средние
члены будут содержать попарные
произведения различных координат. При
подстановке в формулу (а
)
они дадут центробежные моменты инерции.
Принятые оси главные и, поэтому, все
центробежные моменты инерции тела равны
нулям. Таким образом, от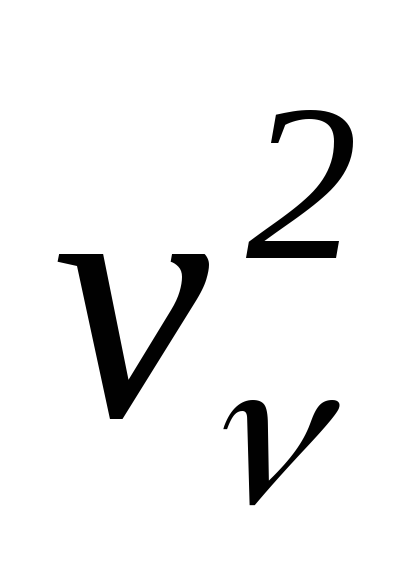
После подстановки в формулу (а
)
выражения (б
),
получаем:
Выражения в круглых скобках приводят
к появлению осевых моментов инерции —
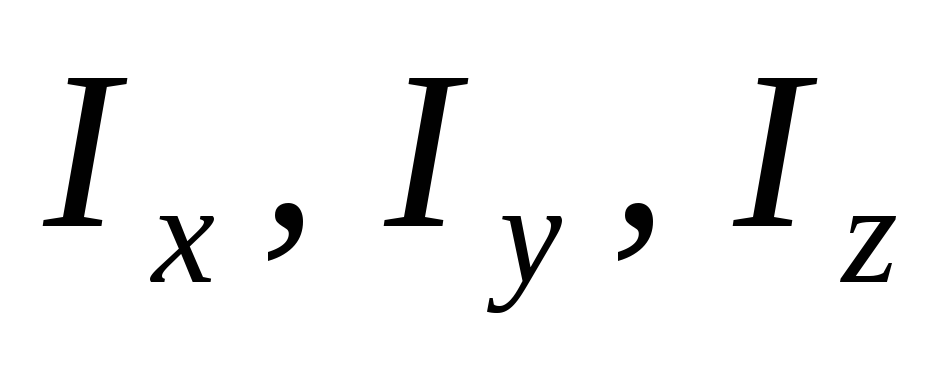
Таким образом и получается
формула
для вычисления кинетической энергии
сферически движущегося тела:
30.7*. Формулы для вычисления кинетической энергии свободно и плоско движущихся тел
Пользуясь
законом сложения скорость

частицы представляем суммой двух
составляющих –

где

отсчёта (относительно инерциальной);
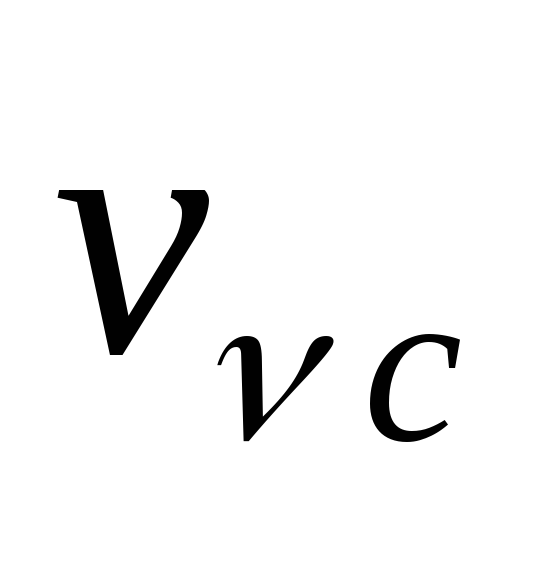

частицы относительно центромассовой
системы.
Из предыдущих двух подразделов видно,
что первые две составляющие (
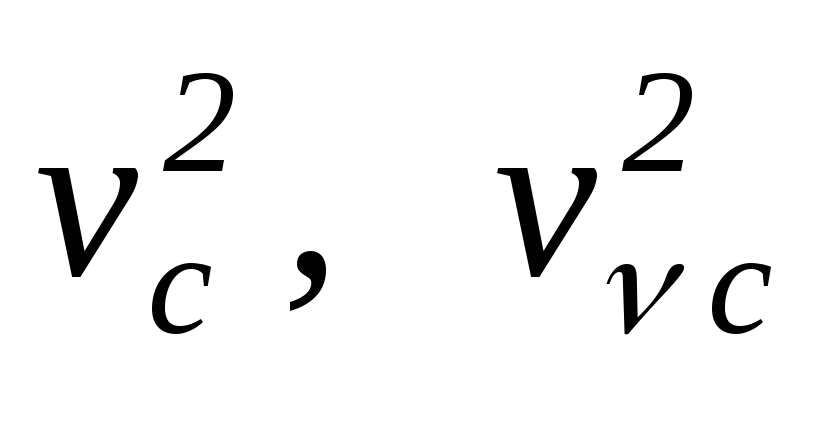
выражения (б
)
при подстановке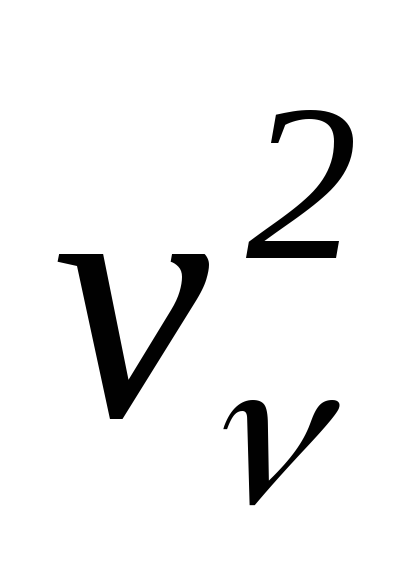
кинетической энергии дадут поступательную
и сферическую составляющие полной
кинетической энергии —
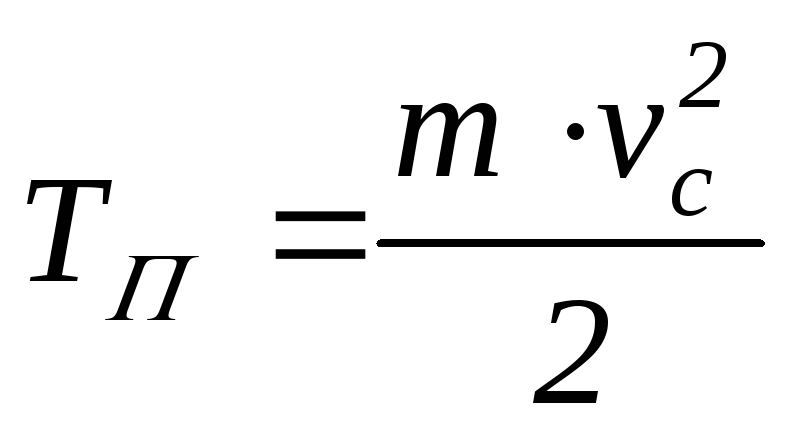
,
где
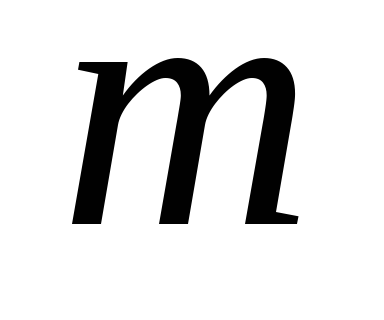
масса тела;
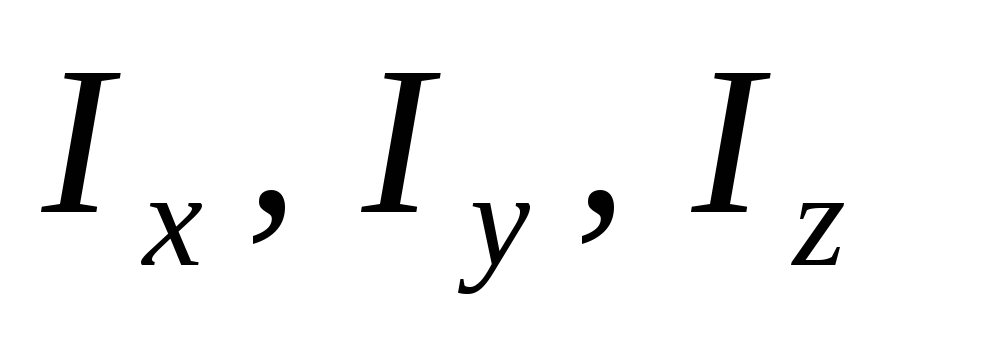
моменты инерции тела относительно его
главных центральных осей инерции;

проекции угловой скорости тела в
сферическом его движении относительно
центромассовой системы отсчёта.
Выясним, что даст третья составляющая
выражения (б
)
при подстановке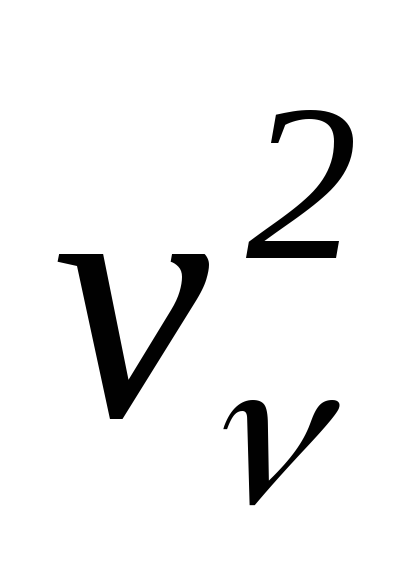
кинетической энергии.-
на
основании понятия центра масс =
кинетическую энергию свободно
движущегося тела можно вычислять как
сумму двух слагаемых – кинетической
энергии поступательного движения
(вычисляемую как для материальной точки,
движущейся со скоростью центра масс
тела и обладающей его массой) и кинетической
энергии тела в его сферическом движении
относительно центромассовой системы
отсчёта:
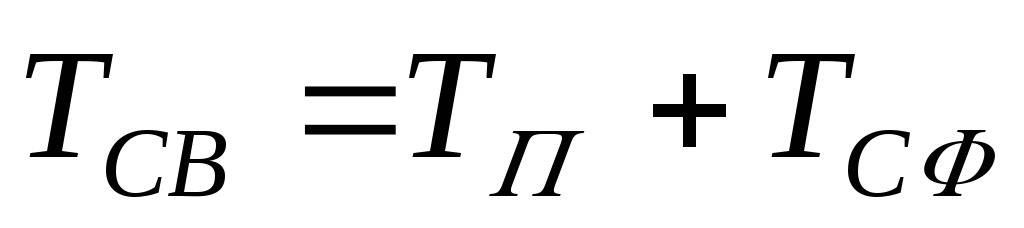
Самостоятельно предлагаем получить
результат:
кинетическую энергию плоско движущегося
тела можно вычислять как сумму двух
слагаемых – кинетической энергии
поступательного его движения со скоростью
центра масс и кинетической энергии во
вращательном движении этого тела
относительно центромассовой системы
отсчёта:

Полная механическая энергия
Энергия тела — физическая величина, которая показывает работу, совершаемую рассматриваемым телом в течение любого, в том числе неограниченного периода времени.
Объект, который совершает положительную работу, расходует частично энергию. В случае, когда положительную работу совершают над телом, его энергия возрастает. Если рассматривается отрицательная работа, то эффект будет противоположным. Таким образом, энергия выражается через физическую величину, характеризующую способность тела или системы взаимодействующих объектов совершать работу. Единицей измерения энергии в СИ является Джоуль (Дж).
Кинетическая энергия — это энергия тел, находящихся в движении.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В качестве движущихся тел рассматриваются не только перемещающиеся тела, но и объекты, которые вращаются. Кинетическая энергия возрастает по мере увеличения массы тела и скорости, с которой оно движется, то есть перемещается, либо вращается в пространстве. Кинетическая энергия определяется телом, по отношению к которому проводят измерения скорости рассматриваемого объекта. Для расчета кинетической энергии Ек тела, масса которого составляет m, движущегося со скоростью v, используют следующую формулу:
Потенциальная энергия — энергия тел или их частей, которые взаимодействуют друг с другом.
Потенциальная энергия тел отличается в зависимости от силы, которая на них воздействует:
- сила тяжести;
- сила упругости;
- архимедова сила.
Любая потенциальная энергия определяется силой взаимодействия и расстоянием между взаимодействующими телами или их частями. Для расчета потенциальной энергии выбирают какой-то условный нулевой уровень. В качестве примера потенциальной энергии можно рассмотреть энергию, которой будет обладать груз, поднятый на определенную высоту над поверхностью Земли, или сжатая пружина. Потенциальная энергия рассчитывается по формуле:
Энергия может трансформироваться из одного вида в другой. Так кинетическая энергия объекта может преобразоваться в его потенциальную энергию, и наоборот.
Механическая энергия тела — это сумма его кинетической и потенциальной энергий.
Механическая энергия любого тела определяется несколькими факторами:
- Объект, относительно которого выполняют измерение скорости рассматриваемого тела.
- Условные нулевые уровни, присущие всем разновидностям имеющихся у тела потенциальных энергий.
Данная величина является одной из основных характеристик тела. С помощью механической энергии определяют способность тела или системы объектов совершать работу по причине изменений скорости тела, либо взаимного положения тел, находящихся во взаимодействии.
Закон изменения и сохранения полной механической энергии
Закон сохранения и превращения энергии: энергия не может возникать ниоткуда, либо исчезать бесследно. Можно лишь наблюдать переход одного вида энергии в другой, либо от одного тела к другому.
Закон сохранения механической энергии: когда тела системы испытывают на себе воздействие силы тяжести или силы упругости, сумма кинетической и потенциальной энергии не будет изменяться, таким образом, механическая энергия сохраняется.
Изменение механической энергии системы тел определяется, как сумма работы внешних по отношению к системе тел и работы внутренних сил трения и сопротивления. Формула для расчета имеет следующий вид:
В случае замкнутой системы тел ее полная механическая энергия будет изменена только в том случае, когда совершается работа внутренних диссипативных сил системы таких, как сила трения:
Aвнешн = 0, то ΔW = Адиссип
Когда рассматривают консервативную систему тел, то есть при отсутствии сил трения и сопротивления, полная механическая энергия системы тел изменяется при работе внешних, относительно системы тел, сил:
Чему равна полная энергия, как изменяется по времени
Полная механическая энергия тела определяется суммой его кинетической и потенциальной энергии. Определение полной механической энергии справедливо в случае действия закона сохранения энергии, и ее постоянном значении.
В ситуации, когда тело движется без влияния внешних сил, включая отсутствие взаимодействия с другими телами, силы трения и силы сопротивления, полная механическая энергия тела не меняется со временем. С помощью формулы это утверждение можно записать следующим образом:
В реальном мире нельзя смоделировать таких идеальных ситуаций, в условиях которых объект полностью сохраняет свою энергию. Причиной этому является постоянное взаимодействие тела с другими телами, к примеру с молекулами воздуха или сопротивлением воздуха.
В случаях, когда сила сопротивления минимальна, и поступательное или другое движение наблюдают в относительно короткое время, подобную систему можно принять за теоретически идеальную. Как правило, закон сохранения полной механической энергии справедлив для тела, совершающего свободное падение, при вертикальном подбрасывании объекта или в случае колебательного движения тела такого, как маятник.
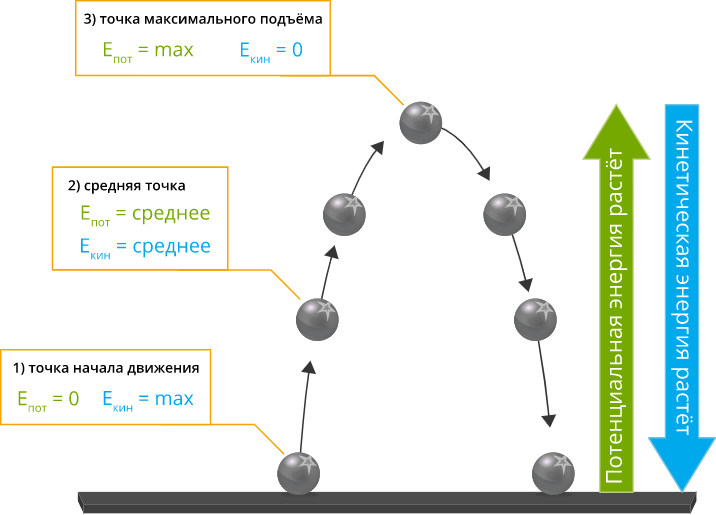
К примеру, во время вертикального подбрасывания тела наблюдают сохранение его полной механической энергии. Кинетическая энергия объекта при этом трансформируется в потенциальную, и наоборот. Амплитуда изменений энергий представлена на графике.
В зависимости от точки нахождения тела энергия будет рассчитываться следующим образом:
- самая верхняя точка при (h = max) , (Eпот = mgh) , (Eкин = 0) , (Eполная = mgh) ;
- средняя точка при (h = средняя) , (Eпот = mgh) , (Eкин = mv2/2) , (Eполная = mgh + mv2/2) ;
- самая нижняя точка при (h = 0) , (Eпот = 0) , (Eкин = mv2/2) , (Eполная = mv2/2) .
В начале пути тело обладает кинетической энергией, которая будет равна его потенциальной энергии в верхней точке траектории движения. Исходя из этого, можно использовать еще несколько полезных формул. При известном значении максимальной высоты, на которую поднимется тело, максимальная скорость движения будет определена следующим образом:
При известном значении максимальной скорости, с которой движется тело, можно рассчитать максимальную высоту подъема тела, брошенного вверх. Формула будет иметь такой вид:
Механическая энергия
Энергия – скалярная величина. Любую энергию в системе СИ измеряют в Джоулях.
В механике рассматривают два вида энергии тел – кинетическую энергию и потенциальную энергию.
Сумма кинетической и потенциальной энергии называется полной механической энергией
Кинетическая энергия
Кинетическая энергия – это энергия движения. Любое тело, находящееся в движении, обладает кинетической энергией.
В русском языке есть глагол «кинуть». Бросим (кинем) камень – он будет находиться в движении, то есть, будет обладать кинетической энергией.
Когда тело изменяет свою скорость, изменяется его кинетическая энергия.
Скорость увеличивается – кинетическая энергия тоже растет, скорость падает – кинетическая энергия уменьшается.
Если тело покоится, кинетической энергии нет. Математики в таком случае запишут: (E_=0 ).
Рассмотрим тело, движущееся по поверхности с какой-либо скоростью (рис 1а).
Зная массу и скорость тела, можно рассчитать его кинетическую энергию с помощью формулы:
( E_ left( textright) ) – кинетическая энергия;
( m left( textright) ) – масса тела;
( v left( frac>right) ) – cскорость, с которой тело движется.
Потенциальная энергия
Любое тело, поднятое над поверхностью, обладает потенциальной возможностью упасть и совершить работу. Например, потенциальная энергия поднятого над гвоздем молотка переходит в работу по забиванию гвоздя в доску.
Физики говорят: поднятое на высоту тело обладает потенциальной энергией.
Примечание: Потенциальная энергия возникает у тела из-за притяжения Земли.
Вообще, потенциальная энергия – это энергия взаимодействия (притяжения, или отталкивания). В нашем примере – энергия притяжения тела и Земли.
Если тело изменит высоту, на которой оно находится, будет изменяться его потенциальная энергия.
Тело опускается вниз – потенциальная энергия уменьшается.
Тело поднимается выше – потенциальная энергия растет.
Когда тело находится на поверхности земли, потенциальной энергии у него нет (E_
=0).
Рассмотрим тело, находящееся на какой-либо высоте над поверхностью земли (рис 1б).
Можно рассчитать потенциальную энергию тела, зная его массу и высоту тела над поверхностью земли, с помощью формулы:
[ large boxed = m cdot g cdot h>]
( E_
left( textright) ) – потенциальная энергия;
( m left( textright) ) – масса тела;
( h left( textright) ) – высота, на которую тело подняли над поверхностью земли.
Полная механическая энергия тела
Если сложить кинетическую энергию тела с его потенциальной энергией в какой-либо момент времени, мы получим полную механическую энергию, которой тело обладало в этот момент времени.
Летящий в небе самолет (рис. 3) одновременно будет обладать и кинетической энергией – он движется, и потенциальной энергией – он находится на высоте.
Любая энергия – это скаляр (просто число). Значит, энергия направления не имеет и ее можно складывать алгебраически.
( E_
left( textright) ) – потенциальная энергия тела;
( E_ left( textright) ) – кинетическая энергия, которой обладает тело;
( E_> left( textright) ) – полная механическая энергия этого тела;
Закон сохранения механической энергии
Если мы погуглим определение слова «Энергия», то скорее всего найдем что-то про формы взаимодействия материи. Это верно, но совершенно непонятно.
Поэтому давайте условимся здесь и сейчас, что энергия — это запас, который пойдет на совершение работы.
Энергия бывает разных видов: механическая, электрическая, внутренняя, гравитационная и так далее. Измеряется она в Джоулях (Дж) и чаще всего обозначается буквой E.
Механическая энергия
Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.
Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия.
Представьте, что вы взяли в руки канцелярскую резинку, растянули ее и отпустили. Из растянутого положения резинка просто «полетит», как только вы ей позволите это сделать. В этом процессе в момент натяжения резинка обладает потенциальной энергией, а в момент полета — кинетической.
Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим ), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия.
Кинетическая энергия
Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость.
Кинетическая энергия
Ек — кинетическая энергия [Дж]
m — масса тела [кг]
Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия.
Задачка раз
Определить кинетическую энергию собаченьки массой 10 кг, если она бежала за мячом с постоянной скоростью 2 м/с.
Решение:
Формула кинетической энергии
Ответ: кинетическая энергия пёсы равна 20 Дж.
Задачка два
Найти скорость бегущего по опушке гнома, если его масса равна 20 кг, а его кинетическая энергия — 40 Дж
Решение:
Формула кинетической энергии
Ответ: гном бежал со скоростью 2 м/с.
Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!
Потенциальная энергия
В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия.
Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия.
Потенциальная энергия деформированной пружины
Еп — потенциальная энергия [Дж]
k — жесткость [Н/м]
x — удлинение пружины [м]
Потенциальная энергия в поле тяжести
Еп = mgh
Еп — потенциальная энергия [Дж]
m — масса тела [кг]
g — ускорение свободного падения [м/с 2 ]
На планете Земля g ≃ 9,8 м/с 2
Задачка раз
Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с 2 .
Решение:
Формула потенциальной энергии Еп = mgh
Eп = 0,1 · 9,8 · 2500 = 2450 Дж
Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж.
Задачка два
Найти высоту горки, с которой собирается скатиться лыжник массой 65 кг, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с 2 .
Решение:
Формула потенциальной энергии Еп = mgh
Переведем 637 кДж в Джоули.
637 кДж = 637000 Дж
Ответ: высота горы равна 1000 метров.
Задачка три
Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E1 и E2. Считать, что потенциальная энергия отсчитывается от уровня крышки стола.
Решение:
Потенциальная энергия вычисляется по формуле: E = mgh
По условию задачи
Таким образом, получим, что
Закон сохранения энергии
В физике и правда ничего не исчезает бесследно. Чтобы это как-то выразить, используют законы сохранения. В случае с энергией — Закон сохранения энергии.
Закон сохранения энергии
Полная механическая энергия замкнутой системы остается постоянной.
Полная механическая энергия — это сумма кинетической и потенциальной энергий. Математически этот закон описывается так:
Закон сохранения энергии
Еполн. мех. — полная механическая энергия системы [Дж]
Еп — потенциальная энергия [Дж]
Ек — кинетическая энергия [Дж]
const — постоянная величина
Задачка раз
Мяч бросают вертикально вверх с поверхности Земли. Сопротивление воздуха пренебрежимо мало. Как изменится высота подъёма мяча при увеличении начальной скорости мяча в 2 раза?
Решение:
Должен выполняться закон сохранения энергии:
В начальный момент времени высота равна нулю, значит Еп = 0. В этот же момент времени Ек максимальна.
В конечный момент времени все наоборот — кинетическая энергия равна нулю, так как мяч уже не может лететь выше, а вот потенциальная максимальна, так как мяч докинули до максимальной высоты.
Это можно описать соотношением:
Разделим на массу левую и правую часть
Из соотношения видно, что высота прямо пропорциональна квадрату начальной скорости, значит при увеличении начальной скорости мяча в два раза, высота должна увеличиться в 4 раза.
Ответ: высота увеличится в 4 раза
Задачка два
Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью v0, поднялось на максимальную высоту h0. Сопротивление воздуха пренебрежимо мало. Чему будет равна полная механическая энергия тела на некоторой промежуточной высоте h?
Решение
По закону сохранения энергии полная механическая энергия изолированной системы остаётся постоянной. В максимальной точке подъёма скорость тела равна нулю, а значит, оно будет обладать исключительно потенциальной энергией Емех = Еп = mgh0.
Таким образом, на некоторой промежуточной высоте h, тело будет обладать и кинетической и потенциальной энергией, но их сумма будет иметь значение Емех = mgh0.
Задачка три
Мяч массой 100 г бросили вертикально вверх с поверхности земли с начальной скоростью 6 м/с. На какой высоте относительно земли мяч имел скорость 2 м/с? Сопротивлением воздуха пренебречь.
Решение:
Переведем массу из граммов в килограммы:
m = 100 г = 0,1 кг
У поверхности земли полная механическая энергия мяча равна его кинетической энергии:
На высоте h потенциальная энергия мяча есть разность полной механической энергии и кинетической энергии:
Ответ: мяч имел скорость 2 м/с на высоте 1,6 м
Переход механической энергии во внутреннюю
Внутренняя энергия — это сумма кинетической энергии хаотичного теплового движения молекул и потенциальной энергии их взаимодействия. То есть та энергия, которая запасена у тела за счет его собственных параметров.
Часто механическая энергия переходит во внутреннюю. Происходит этот процесс путем совершения механической работы над телом. Например, если сгибать и разгибать проволоку — она будет нагреваться.
Или если кинуть мяч в стену, часть энергии при ударе перейдет во внутреннюю.
Задачка
Какая часть начальной кинетической энергии мяча при ударе о стену перейдет во внутреннюю, если полная механическая энергия вначале в два раза больше, чем в конце?
Решение:
В самом начале у мяча есть только кинетическая энергия, то есть Емех = Ек.
В конце механическая энергия равна половине начальной, то есть Емех/2 = Ек/2
Часть энергии уходит во внутреннюю, значит Еполн = Емех/2 + Евнутр
Ответ: во внутреннюю перейдет половина начальной кинетической энергии
Закон сохранения энергии в тепловых процессах
Чтобы закон сохранения энергии для тепловых процессов был сформулирован, было сделано два важных шага. Сначала французский математик и физик Жан Батист Фурье установил один из основных законов теплопроводности. А потом Сади Карно определил, что тепловую энергию можно превратить в механическую.
Вот что сформулировал Фурье:
При переходе теплоты от более горячего тела к более холодному температуры тел постепенно выравниваются и становятся едиными для обоих тел — наступает состояние термодинамического равновесия.
Таким образом, первым важным открытием было открытие того факта, что все протекающие без участия внешних сил тепловые процессы необратимы.
Дальше Карно установил, что тепловую энергию, которой обладает нагретое тело, непосредственно невозможно превратить в механическую энергию для производства работы. Это можно сделать, только если часть тепловой энергии тела с большей температурой передать другому телу с меньшей температурой и, следовательно, нагреть его до более высокой температуры.
Закон сохранения энергии в тепловых процессах
При теплообмене двух или нескольких тел абсолютное количество теплоты, которое отдано более нагретым телом, равно количеству теплоты, которое получено менее нагретым телом.
Математически его можно описать так:
Уравнение теплового баланса
Qотд — отданное системой количество теплоты [Дж]
Qпол — полученное системой количество теплоты [Дж]
Данное равенство называется уравнением теплового баланса. В реальных опытах обычно получается, что отданное более нагретым телом количество теплоты больше количества теплоты, полученного менее нагретым телом:
Это объясняется тем, что некоторое количество теплоты при теплообмене передаётся окружающему воздуху, а ещё часть — сосуду, в котором происходит теплообмен.
Чтобы разобраться в задачках, читайте нашу статью про агрегатные состояния вещества.
Задачка раз
Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С, если учесть, что на нагревание пошло 20% затраченной энергии.
Удельная теплота сгорания спирта 2,9 · 107 Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг · °С).
Решение:
При нагревании тело получает количество теплоты
где c — удельная теплоемкость вещества
При сгорании тела выделяется энергия
где q — удельная теплота сгорания топлива
По условию задачи нам известно, что на нагревание воды пошло 20% энергии, полученной при горении спирта.
Ответ: масса сгоревшего топлива равна 33,6 г.
Задачка два
Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь. Удельная теплоемкость льда равна 2100 Дж/кг · ℃, удельная теплота плавления льда равна 3,3 · 10 5 Дж/кг.
Решение:
Для нагревания льда до температуры плавления необходимо:
Qнагрев = 2100 · 0,5 · (10 − 0) = 10 500 Дж
Для превращения льда в воду:
Qпл = 3,3 · 10 5 · 0,5 = 165 000 Дж
Таким образом, для превращения необходимо затратить:
Q = Qнагрев + Qпл = 10 500 + 165 000 = 175 500 Дж = 175,5 кДж
Ответ: чтобы превратить 0,5 кг льда в воду при заданных условиях необходимо 175,5 кДж тепла.