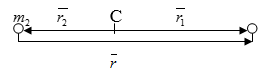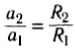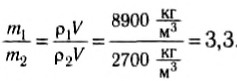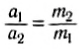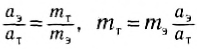Как найти общую массу двух тел

Математика, 3 класс

Урок №9. Связь между величинами: масса одного предмета, количество предметов, масса всех предметов

Перечень вопросов, рассматриваемых в теме:

— Что такое масса?

— Как найти массу одного предмета?

— Как найти общую массу?

Глоссарий по теме:

Масса предмета – величина, характеризующая вес предмета.

Чтобы найти массу одного предмета, нужно массу всех предметов разделить на количество предметов.

Чтобы найти массу всех предметов, нужно массу одного предмета умножить на количество предметов.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с.23.
2. Волкова С. И. Математика. Проверочные работы 3 класс. М.; Просвещение, 2014. – с.20.

Теоретический материал для самостоятельного изучения.

Рассмотрим задачу в картинках.

В задаче нужно определить массу каждого животного, т.е. вес.

Слово масса пришло к нам из латинского языка. Обозначает большое количество чего-нибудь или кого-нибудь. Измеряется масса килограммами, граммами. Вес очень больших предметов (машин, вагонов) измеряют тоннами. Прибор, с помощью которого измеряют массу — весы. Существуют разного вида и типа весы.

Решим задачу.

Масса пакета с мукой 2 кг. Узнай массу 4 таких пакетов.
К задаче можно составить схему, но удобнее будет заполнить таблицу.

В таблицу записываем названия величины и числовые данные.

Чтобы узнать массу 4 пакетов, мы должны 2 кг взять 4 раза. Массу всех пакетов узнаем действием умножением.

2 ∙ 4 = 8 (кг)

Вывод: Чтобы узнать массу всех предметов (пакетов, мешков, ящиков), нужно массу одного предмета умножить на количество.

Составим обратную задачу.

Масса 4 одинаковых пакетов с мукой 8 кг. Узнай массу одного пакета.

Заполняем таблицу.

Массу всех пакетов поровну распределим на 4 пакета.

8 : 4 = 2 (кг) – масса одного пакета.

Вывод: Чтобы узнать массу одного пакета, нужно массу всех пакетов разделить на количество.

Составим и решим следующую обратную задачу.

Масса одного пакета с мукой 2 кг. Сколько пакетов понадобится для 8 кг муки?

Заполняем таблицу.

Чтобы узнать количество пакетов, общую массу будем поровну раскладывать по 2 кг.

8 : 2 = 4 (п.)

Вывод: Чтобы узнать количество (пакетов, мешков, ящиков), нужно массу всех предметов разделить на массу одного предмета.

Тренировочные задания:

1. Выберите правильный ответ к задаче.

В одном пакете 2 кг яблок. Сколько килограммов в пяти пакетах?

7 кг; 10 кг; 5кг;

Правильный вариант: 10 кг.

2. Вставьте в таблицу пропущенные числа.

Правильный вариант:

Приведенная масса

Решение уравнений динамики системы материальных точек встречает непреодолимые математические трудности, т.к. точного решения этих уравнений для произвольных сил не найдено уже в случае трех материальных точек.

В связи с этим важна задача о замкнутой системе двух точек, называемая задачей двух тел. Она имеет простое и исчерпывающее решение — сводится к основной задаче динамики одной материальной точки. Решение задачи двух тел используется в небесной механике, описывающей движение планет и их спутников в Солнечной системе, в задачах на столкновение частиц, в статистической физике и других вопросах.

Обозначим массы частиц через $m_{1} $ и $m_{2} $ и их радиус-векторы, проведенные от центра масс, соответственно $overline{r_{1} }$ и $overline{r_{2} }$. Пусть $overline{r}$- вектор, проведенный от точки $m_{2} $ к $m_{1} $. Из определения радиус-вектора центра масс имеем:

Непосредственно из рисунка следует соотношение между радиус-векторами:

$overline{r}_{1} =overline{r}_{2} +overline{r}$. (1)

Два последних равенства позволяют выразить радиус-векторы $overline{r_{1} }$ и $overline{r_{2} }$ через вектор $overline{r}$, соединяющий точки $m_{2} $ и $m_{1} $. Имеем:

$overline{r}_{1} =frac{m_{2} }{m_{1} +m_{2} } overline{r}$, $overline{r}_{2} =frac{m_{1} }{m_{1} +m_{2} } overline{r}$. (2)

Запишем основные уравнения для движения обеих точек в Ц-системе:

$begin{array}{l} {m_{1} overline{ddot{r}_{1} }=overline{F}_{2,1} (r)} \ {m_{2} overline{ddot{r}_{2} }=overline{F}_{1,2} (r)} end{array}$ (3)

Силы в уравнениях (3) зависят от расстояния между точками, а не от расстояния до центра масс, т.е. решать уравнения (1) отдельно для каждой точки нельзя.

«Задача двух тел» 👇

Пользуясь выражениями для радиус-векторов (2), исключим из основных уравнений (3) $overline{r_{1} }$ и $overline{r_{2} }$. Тогда получаем уравнения движения:

Так как по третьему закону Ньютона $overline{F}_{2,1} (r)=-overline{F}_{1,2} (r)$, оба уравнения становятся тождественными, и движение системы двух точек, в результате их взаимодействия эквивалентно движению одной точки в соответствии с уравнением:

$frac{m_{1} B_{2} }{m_{1} +m_{2} } overline{ddot{r}}=overline{F}(r)$. (4)

Уравнение (4) отличается от известного уравнения движения материальной точки в поле заданной силы только тем, что вместо массы $m$здесь выступает комбинация масс двух точек:

$m’=frac{m_{1} B_{2} }{m_{1} +m_{2} } $ (5)

Величина $m’$ называется приведенной массой.

Итак, задача двух тел свелась к задаче о движении одной материальной точки с приведенной массой в Ц-системе под действием центральной силы; уравнение движения имеет обычный вид:

$m’overline{ddot{r}}=overline{F}(r)$ (6)

Но при использовании результатов решения уравнения (6) необходимо помнить, что точка $m’$, движущаяся на конце радиус-вектора $overline{r}$под действием силового центра в начале координат Ц-системы, является не реальной, а изображающей движение системы. От ее движения, после того как уравнение (6) проинтегрировано, следует переходить к реальному движению двух материальных точек $m_{2} $ и $m_{1} $.

Движение двух материальных точек в системе центра масс

Движение изображающей точки в соответствии с уравнением (6) будет плоским. Пусть кинематическое уравнение движения найдено: $overline{r}=overline{r}(t)$.

В таком случае с помощью формулы (2) находим кинематическое уравнение движения обеих материальных точек в Ц-системе:

$overline{r}_{1} =frac{m_{2} }{m_{1} +m_{2} } overline{r}(t),$ $overline{r}_{2} =frac{m_{1} }{m_{1} +m_{2} } overline{r}(t)$. (7)

Очевидно, что траектория движения изображающей точки и точек $m_{2} $ и $m_{1} $ будут подобными кривыми относительно центра масс, а отношение подобия есть обратное отношение масс, т.е.:

$frac{r_{1} }{r_{2} } =frac{m_{2} }{m_{1} } $ (8)

Нетрудно найти и скорости движения точек. Дифференцируя (7) по времени, имеем:

$overline{v}_{1} =frac{m_{2} }{m_{1} +m_{2} } overline{v},$ $overline{v}_{2} =frac{m_{1} }{m_{1} +m_{2} } overline{v}$. (9)

Задача двух тел решена.

Многие из нас в школьное время задавались вопросом: «Как найти массу тела»? Сейчас мы попытаемся ответить на этот вопрос.

Нахождение массы через его объем

Допустим, в вашем распоряжении есть бочка на двести литров. Вы намерены целиком заполнить ее дизельным топливом, используемом вами для отопления своей небольшой котельной. Как найти массу этой бочки, наполненной соляркой? Давайте попробуем решить эту простейшую на первый взгляд задачу вместе с вами.

Решить задачу, как найти массу вещества через его объем, довольно легко. Для этого следует применить формулу удельной плотности вещества

p = m/v,

где p является удельной плотностью вещества;

m — его массой;

v — занимаемым объемом.

В качестве меры массы будут использоваться граммы, килограммы и тонны. Меры объёмов: сантиметры кубические, дециметры и метры. Удельная плотность будет вычисляться в кг/дм³, кг/м³, г/см³, т/м³.

Таким образом, в соответствии с условиями задачи в нашем распоряжении есть бочка объемом двести литров. Это значит, что ее объем равняется 2 м³.

Но вы хотите узнать, как найти массу. Из вышеназванной формулы она выводится так:

m = p*v

Сначала нам требуется найти значение р – удельной плотности дизельного топлива. Найти данное значение можно, используя справочник.

В книге мы находим, что р = 860,0 кг/м³.

Затем полученные значения мы подставляем в формулу:

m = 860*2 = 1720,0 (кг)

Таким образом, ответ на вопрос, как найти массу, был найден. Одна тонна и семьсот двадцать килограммов – это вес двухсот литров летнего дизтоплива. Затем вы можете точно так же сделать приблизительный расчет общего веса бочки и мощности стеллажа под бочку с соляром.

Нахождение массы через плотность и объем

Очень часто в практических заданиях по физике можно встретить такие величины, как масса, плотность и объем. Для того чтобы решить задачу, как найти массу тела, вам требуется знать его объем и плотность.

Предметы, которые вам будут нужны:

1) Рулетка.

2) Калькулятор (компьютер).

3) Емкость для измерения.

4) Линейка.

Известно, что у предметов с равным объемом, но изготовленных из различных материалов, будет разная масса (например, металл и дерево). Массы тел, которые изготовлены из определенного материала (без пустот), прямо пропорциональны объему рассматриваемых предметов. В противном случае, константа – это отношение массы к объему предметы. Этот показатель называется «плотностью вещества». Мы будем его обозначать буквой d.

Теперь требуется решить задачу, как найти массу в соответствии с формулой d = m/V, где

m является массой предмета (в килограммах),

V является его объемом (в метрах кубических).

Таким образом, плотность вещества является массой единицы его объема.

Если вам необходимо найти плотность материала, из которого создан предмет, то следует воспользоваться таблицей плотностей, которую можно найти в стандартном учебнике по физике.

Объем предмета вычисляется по формуле V = h * S, где

V – объем (м³),

H – высота предмета (м),

S – площадь основания предмета (м²).

В том случае, если вы не можете четко измерить геометрические параметры тела, то вам следует прибегнуть к помощи законов Архимеда. Для этого вам понадобится сосуд, у которого есть шкала, служащая для измерений объема жидкостей и опустить предмет в воду, то есть в сосуд, на котором есть деления. Тот объем, на который будет увеличено содержимое сосуда, является объемом тела, которое погружено в него.

Зная объем V и плотность d предмета, вы можете легко найти его массу по формуле m = d * V. Перед тем, как вычислить массу, требуется привести все измерительные единицы в единую систему, например, в систему СИ, являющуюся интернациональной измерительной системой.

В соответствии с вышеназванными формулами можно сделать следующий вывод: для нахождения требуемой величины массы с известным объемом и известной плотностью требуется умножить значение плотности материала, из которого изготовлено тело, на объем тела.

Содержание:

Масса тела:

Согласно первому закону Ньютона в инерциальных системах отсчета скорость тела не изменяется при условии, что воздействие других тел скомпенсировано. А если это условие не выполняется?

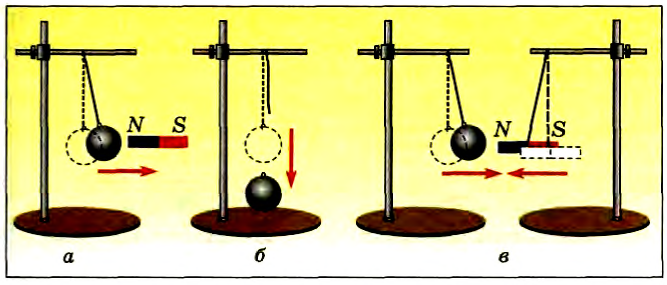
Проведем опыт с железным шариком, подвешенным на нити, прикрепленной к неподвижному штативу. Шарик покоится, так как воздействие нити компенсирует притяжение Земли. Если поднести сбоку к шарику магнит, то под его действием шарик начнет двигаться (рис. 29, а).

Если убрать магнит, а нить, на которой подвешен шарик, перерезать, то воздействие Земли не будет уравновешено, и, как вы уже хорошо знаете, шарик начнет двигаться ускоренно вниз (рис. 29. б).

Эти опыты и многочисленные наблюдения за различными телами в окружающем мире позволяют сделать вывод, что ускоренное движение тела — результат нескомпенсированного воздействия на него других тел.

А возможно ли какое-либо воздействие на конкретное тело без того, чтобы это тело также оказывало свое действие (противодействие)?

Если в нашем опыте с шариком мы подвесим рядом магнит на нити, то сможем наблюдать одновременное движение шарика и магнита друг к другу (рис. 29, в).

Ударяя по мячу (рис. 30), человек ощущает воздействие мяча во время удара. Если подержать за ручку тяжелый портфель некоторое время, то на ладони останутся вмятины из-за действия на нее этого груза.

Чтобы исследовать, как происходит взаимодействие тел и от чего зависят их ускорения при этом, проведем несколько экспериментов. Возьмем два одинаковых по размеру шара — один из алюминия, а второй из железа — и рассмотрим их столкновение при движении по неподвижному горизонтальному металлическому желобу.

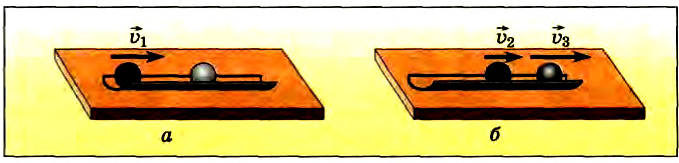
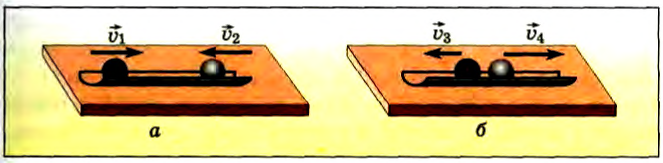
Пусть железный шар катится по желобу к покоящемуся алюминиевому шару (рис. 31, а). Мы увидим, что во время взаимодействия (столкновения) оба шара изменят свою скорость, т. е. будут иметь ускорения (рис. 31, б). Если оба шара движутся навстречу друг другу, то при столкновении их скорости также изменяются (рис. 32, а, б).

Рис. 31

Рис. 32

Значит, при взаимодействии оба шара изменяют свою скорость, но измерить и сравнить полученные ими при ударе ускорения в таком опыте сложно. Поэтому проведем опыт, в котором ускорения взаимодействующих тел можно достаточно просто определить.

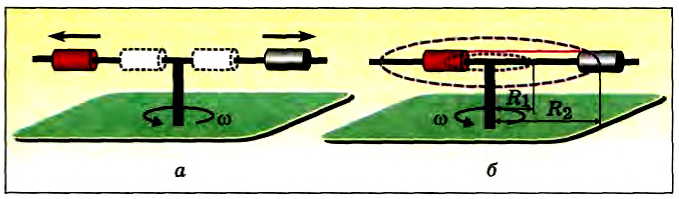
Для опыта используем два одинаковых по размеру цилиндра из алюминия и меди с просверленными вдоль их осей отверстиями. Вставим в отверстия цилиндров гладкий стержень, вдоль которого цилиндры могут легко скользить. Закрепим стержень с цилиндрами в установке, которая может вращать стержень с постоянной угловой скоростью в горизонтальной плоскости.

Если стержень вращать, то можно наблюдать скольжение цилиндров к концам стержня (рис. 33, а). Остановим вращение, свяжем цилиндры нитью и вновь приведем во вращение стержень.
Так как теперь цилиндры взаимодействуют друг с другом с помощью нити, то они будут вращаться вместе со стержнем, находясь на определенных расстояниях от оси вращения (рис. 33, б). Рассчитаем и сравним центростремительные ускорения цилиндров.

Рис. 33

Таким образом, модули ускорений относятся как радиусы окружностей, по которым вращаются центры цилиндров, и в нашем опыте это отношение равно 3,3.

Если провести этот опыт при другой угловой скорости вращения или связав цилиндры нитью другой длины, то радиусы окружностей изменятся, но их отношение, а значит, и отношение модулей ускорений останется тем же. Как объяснить постоянство отношений модулей ускорений для двух взаимодействующих цилиндров?

Ускорение характеризует быстроту изменения скорости тела. В 7-м классе вы познакомились с физической величиной — массой тела, от которой также зависела величина изменения скорости тела. Вы знаете, что, чем больше масса тела, тем труднее изменить его скорость.

Сравним массы медного и алюминиевого цилиндров. Так как их размеры одинаковы, то одинаковы и объемы, и отношение масс равно отношению плотностей меди и алюминия, т. е.:

Таким образом, сравнение отношений модулей ускорений и масс цилиндров показывает, что ускорения цилиндров обратно пропорциональны их массам:

Многочисленные эксперименты, проведенные учеными по исследованию самых разнообразных взаимодействий тел, показывают, что всегда выполняется полученная нами закономерность.

Отношение модулей ускорений двух взаимодействующих тел равно обратному отношению их масс.

Что же такое масса тела? Ответ на этот вопрос в полном объеме требует знания более сложных разделов физики.

Поэтому рассмотрим упрощенное представление о массе тела. В 8-м классе вы узнали, что все тела состоят из атомов и молекул, которые имеют массу. Тогда масса тела — это суммарная масса всех его частиц. На основании опытных данных упрощенное понятие «масса» можно охарактеризовать следующим образом:

1. масса тела — физическая скалярная величина, равная сумме масс всех частиц (или материальных точек), из которых оно состоит (свойство аддитивности);
2. для данной системы тел выполняется закон сохранения массы — при любых процессах в системе ее масса остается неизменной;
3. масса тела не зависит ни от взаимодействий, в которых тело участвует, ни от скорости движения тела;
4. масса тела при его взаимодействии с другими телами определяет модуль полученного телом ускорения.

Вы уже знаете, что единицей массы в СИ является 1 кг. Это масса специально изготовленного эталона (образца). Как, используя эталон массы, измерить массу определенного тела?

Если привести во взаимодействие эталон и тело неизвестной массы, а затем измерить их ускорения, то можно определить неизвестную массу тела:

Конечно, для обычных тел такой способ менее удобен, чем обычное взвешивание. Зато определение масс космических тел, например планет по ускорению их спутников или мельчайших частиц вещества (атомов, молекул и т. п.) по ускорению при их взаимодействии, производится практически всегда.

Главные выводы:

1. Тело движется ускоренно в инерциальной системе отсчета, если воздействие других тел на него нескомпенсировано.
2. При взаимодействии двух тел воздействие испытывают оба тела, а отношение модулей ускорений двух взаимодействующих тел равно обратному отношению их масс.
3. Масса тела — физическая скалярная аддитивная величина, не зависящая от взаимодействий, в которых участвует тело, и от его скорости.

Что такое масса тела

Наблюдение 1. Мяч падает на поверхность Земли, а потом отскакивает от неё -это пример взаимодействия двух тел. Мы уже знаем, что результатом взаимодействия тел является изменение их скорости и направления движения. Мяч после столкновения отскакивает почти с той же скоростью, что и падал, но в обратном направлении. В состоянии Земли практически не заметно никаких изменений, хотя на самом деле они есть, но бесконечно малые. В приведённом примере наглядно видно, что результаты взаимодействия тел для каждого из них будут разными и зависят от свойств этих тел. Ежедневный опыт и специальные исследования свидетельствуют, что в результате взаимодействия разные тела получают определённое изменение скорости за неодинаковые интервалы времени: одни за большие, другие — за меньшие. Движение того тела, которое в результате взаимодействия медленнее изменяет собственную скорость, более напоминает движение по инерции, поэтому говорят, что оно более инертно.

Инертность — это свойство тела, заключающееся в том, что для изменения его скорости при взаимодействии с любыми другими телами нужно определённое время.

Свойством инертности обладают все тела. Количественной мерой инертности тела является масса тела.

Масса тела — это физическая величина, характеризующая инертность тела. Чем больше масса тела, тем более оно инертно.

Существуют разные методы определения массы тела. Все они базируются на использовании свойств, присущих всем без исключения телам, например на свойстве инертности тел. На практике наиболее удобным оказался метод измерения массы, связанный с хорошо известным явлением взаимодействия всех тел с Землей.

• Заказать решение задач по физике

Наблюдение 2. Вы, наверное, неоднократно наблюдали, как падают капли дождя, снежинки, как оседают мелкие пылинки, как любое тело, поднятое над Землей и отпущенное, стремительно летит к Земле. Эти явления объясняются тем, что все физические тела притягиваются Землей, т. е. взаимодействуют с ней. Опыты показывают, что значение этого взаимодействия тем больше, чем больше масса тела.

Опыт. Возьмём в одну руку спичечный коробок, а в другую — кусок дерева (рис. 56).

Оба тела вследствие притяжения их Землёй давят на удерживающие их руки. Большую нагрузку ощущаем в руке, держащей кусок дерева, т. е. он тяжелее спичечного коробка и соответственно его масса больше, чем у коробки.

Если массы тел близки по значению, если тела очень малы или слишком велики, то сравнить их массу на руках уже невозможно. Как можно измерить массу тела с достаточной точностью?

Для определения массы тела используют специальные приборы — весы. В магазинах, аптеках, на почте с помощью весов разных конструкций взвешивают продукты, лекарства, посылки и пр. Определение массы тела с помощью весов называют взвешиванием.

Массу тела обозначают малой латинской буквой 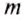. За единицу массы в СИ принят один килограмм (1 кг). Международный образец (эталон) (рис. 57, а) килограмма сохраняется во Франции (г. Севр близ Парижа). Он изготовлен из платиноиридиевого сплава и имеет форму цилиндра диаметром и высотой 39 мм (рис. 57, б). По этому образцу с большой точностью изготовлены копии для всех стран мира.

На практике применяют также кратные и дольные единицы массы: тонну (т), грамм (г), миллиграмм (мг):

Основной частью учебных весов (рис. 58) является стержень (коромысло весов), который может свободно поворачиваться вокруг оси, размещённой посреди стержня (в следующей главе вы узнаете, что такой механизм называют рычагом). К его концам подвешены чашки весов. Определение массы тела с помощью весов основано на том, что коромысло находится в равновесии при условии, что массы тел, лежащих на разных чашках, одинаковы. При этом коромысло весов располагается горизонтально, а стрелка прибора указывает на нулевую отметку. Таким образом, взвешивая тело на весах, сравнивают его массу с массой эталона.

Пример:

На одну чашку весов положим тело, массу которого нужно измерить, а на другую — гири с известными массами (рис. 59).

Гири подбираем такие, чтобы установилось равновесие. Определяем общую массу гирь, уравновесивших тело. Масса тела равна сумме масс гирь, т. е. 370 г. Результат записывают так:

= 370 г = 0,370 кг.

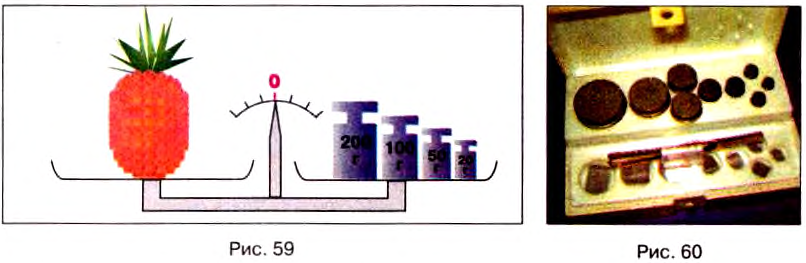
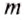
Для взвешивания используют специальный набор гирь разной массы. На рисунке 60 изображён набор гирь к учебным весам. В нём есть 9 гирь массой 100, 50, 20, 20, 10, 5, 2, 2 и 1 г. С их помощью можно подобрать любую массу от 1 до 210 г. Гири, масса которых меньше 1 г, изготавливают из алюминия в виде пластинок массой 500, 200, 200, 100, 50, 20, 20, 10 мг.

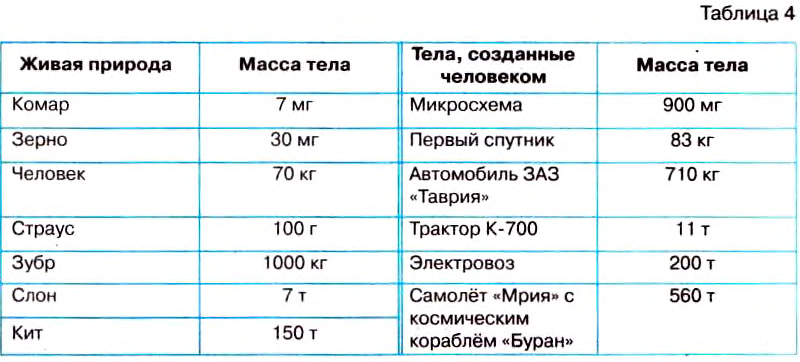
С помощью специальных весов можно измерять как большие, так и малые массы. В таблице 4 приведены массы тел живой природы, а также массы тел, созданных человеком.

Кстати:

Кроме системных существуют и другие единицы массы. Например, массу драгоценных камней измеряют в каратах: 1 карат = 0,2 г. В Киевской Руси единицей массы была 1 гривна, которая составляла приблизительно 410 г. Позднее эта единицу стали называть фунтом: 1 фунт = 0,025 пуда = 32 лота = 96 золотников = 9216 долей = 0,4 кг. Распространённой была и такая единица массы, как пуд (около 16 кг). Для взвешивания лекарств используются граны: 1 гран = 0,6 г. По традиции ещё применяют унцию, значение которой в зависимости от области применения лежит в пределах 28-31 г.

Пример №1

На столе лежит книжка. Вследствие взаимодействия с какими телами книжка находится в состоянии покоя?

Ответ: книжка взаимодействует с Землёй, а также со столом.

Пример №2

Почему с разбега можно прыгнуть на большее расстояние, чем без разбега?

Ответ: за счёт инерции.

Пример №3

На рисунке 61, а, б, в изображён процесс измерения массы воды с помощью весов. Какова масса сосуда с водой? Какова масса пустого сосуда? Какова масса воды в сосуде?

Ответ:

а)весы были уравновешены;

б)масса сосуда с водой составляла 70 г 200 мг = 70,2 г = 0,0702 кг;

в)масса пустого сосуда — 15 г 600 мг = 15,6 г = 0,0156 кг; масса воды в сосуде — 54 г 600 мг = 54,6 г = 0,0546 кг.

Определение массы

Для количественного выражения инертности тел пользуются физической величиной, которую называют массой.

Масса — это физическая величина, которая характеризует инертные свойства тела.

Очевидно, что масса стального шарика в предыдущем опыте была большей, чем алюминиевого, поэтому они и приобрели различную скорость.

Единицы массы

Как и всякая физическая величина, масса имеет единицу измерения. Основной единицей массы является килограмм (кг).

Килограмм равен массе международного прототипа килограмма.

Килограмм принадлежит к основным единицам Международной системы единиц (СИ). За единицу массы килограмм взята масса специально изготовленного образца (эталона) (рис. 43). Он сделан из сплава платины и иридия и имеет форму цилиндра. Сохраняется эталон массы в Международном бюро мер и весов в г. Севре, который находится вблизи Парижа.

Если тело имеет массу 1 кг, то под действием силы 1 Н его скорость каждую секунду изменяется на 1м/с.

Как и для других единиц измерения, для килограмма используют производные единицы:

• 1 г = 0,001 кг — 10^-3 кг;
• 1 мг = 0,000001 кг = 10^-6 кг;
• 1 т = 1000 кг = 10³ кг;
• 1 ц = 100 кг = 10² кг.

Для прямого измерения массы используют различные весы. Среди них самые распространенные и самые простые — рычажные (рис. 44). На этих весах сравнивают взаимодействие с Землей тела и эталонных грузов, положенных на чашки весов. На практике используют также и другие весы, которые приспособлены к различным условиям работы и имеют различную конструкцию.