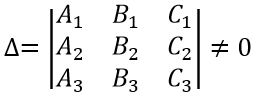Л
пересечения двух плоскостей – прямая
линия. Рассмотрим сначала частный случай
(рис. 3.9), когда одна из пересекающихся
плоскостей параллельна горизонтальной
плоскости проекций (α ׀׀
π1,
f0α
׀׀Х).
В этом случае линия пересечения а,
принадлежащая плоскости α,
будет также параллельна плоскости π1,
(рис. 3.9. а) т.
е. будет совпадать с горизонталью
пересекающихся плоскостей (а ≡ h).
Если одна из
плоскостей параллельна фронтальной
плоскости проекций (рис. 3.9. б), то линия
пересечения а, принадлежащая этой
плоскости, будет параллельна плоскости
π2
и будет совпадать с фронталью
пересекающихся
плоскостей (а ≡ f).
а)
б)
Рис. 3.9. Частный
случай пересечения плоскости общего
положения с плоскостями: а) горизонтального
уровня; б) фронтального уровня
Пример построения
точки пересечения (К) прямой а (АВ) с
плоскостью α (DEF)
показан на рис. 3.10. Для этого прямая а
заключена в произвольную плоскость β
и определена линия пересечения плоскостей
α и β.
В рассматриваемом
примере прямые АВ и MN
принадлежат одной плоскости β и
пересекаются в точке К, а т. к. прямая MN
принадлежит заданной плоскости α (DEF),
то точка К является и точкой пересечения
прямой а (АВ) с плоскостью α. (рис. 11).
Рис. 3.10. Построение
точки пересечения прямой с плоскостью
Для решения подобной
задачи на комплексном чертеже необходимо
уметь находить точку пересечения прямой
общего положения с плоскостью общего
положения.
Рассмотрим пример
нахождения точки пересечения прямой
АВ c
плоскостью треугольника DEF
представленный на рис. 3.11.
Для нахождения
точки пересечения через фронтальную
проекцию прямой А2В2
проведена фронтально-проецирующая
плоскость β которая пересекла треугольник
в точках M
и N.
На фронтальной плоскости проекций (π2)
эти точки представлены проекциями M2,
N2.
Из условия принадлежности прямой
плоскости на горизонтальной плоскости
проекций (π1)
находятся горизонтальные проекции
полученных точек M1
N1.
В пересечении горизонтальных проекций
прямых А1В1
и M1N1
образуется горизонтальная проекция
точки их пересечения (К1).
По линии связи и условиям принадлежности
на фронтальной плоскости проекций
находится фронтальная проекция точки
пересечения (К2).
В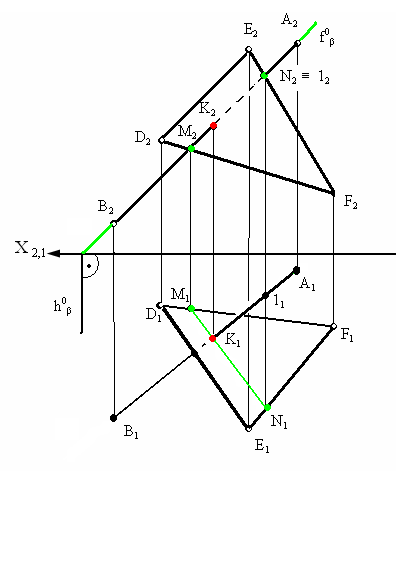
отрезка АВ относительно треугольника
DEF
определена методом конкурирующих
точек.
На плоскости π2
рассмо- трены две точки NEF
и
Рис. 3.11. Пример
определения точки
пересечения прямой
и плоскости
1АВ.
По горизонтальным проекциям этих
точек можно установить, что точка N
рас- положена ближе к наблюда-
телю (YN>Y1
), чем точка 1 (направление луча
зрения параллельно S).
Следовательно, прямая АВ, т. е. часть
прямой АВ (К1)
закрыта плоскостью DEF
на плоскости π2
(ее проекция К212
показана штриховой линией). Аналогично
установлена видимость на плоскости
π1.
Вопросы для
самоконтроля
-
В чем заключается
сущность метода конкурирующих точек
? -
Свойства прямой.
-
Каков алгоритм
определения точки пересечения прямой
и плоскости ? -
Каков алгоритм
определения линии пересечения плоскостей
? -
Какие задачи
называются позиционными ? -
Сформулируйте
условия принадлежности прямой плоскости.
Соседние файлы в папке Лекции нг
- #
- #
- #
- #
- #
- #
- #
- #
Чтобы найти координаты точки пересечения трех плоскостей, необходимо решить эти уравнения относительно х, у и z, при этом координаты точки пересечения должны удовлетворять уравнениям всех трех плоскостей.
Система уравнений трёх плоскостей имеет вид:
A1x + B1y + C1z + D1 = 0
A2x + B2y + C2z + D2 = 0
A3x + B3y + C3z + D3 = 0
Если определитель этой системы не равен нулю,
то система имеет единственное решение и тогда три плоскости пересекаются в одной точке.
Замечания
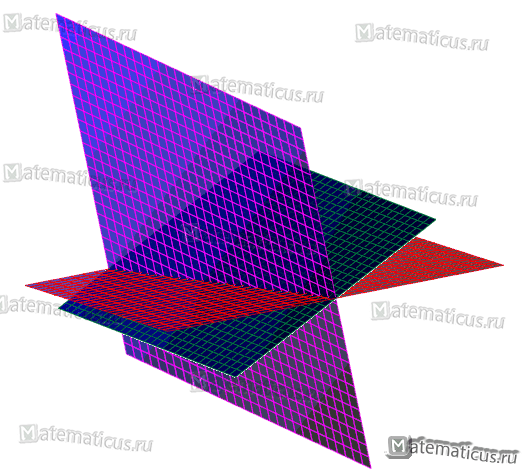
1. Если три плоскости не имеют ни одной общей точки ( или хотя бы две из них параллельны) — система уравнений не имеет решений.
2.Если плоскости имеют бесчисленное множество общих точек ( все они проходят через одну прямую), то система уравнений имеет бесчисленное множество решений.
3.Если система имеет одну общую точку, то система уравнений имеет только одно решение.
Пример 1
Исследовать, есть ли общие точки у плоскостей
x+y+z=1, x-2y-3z=5, 2x-y-2z=6
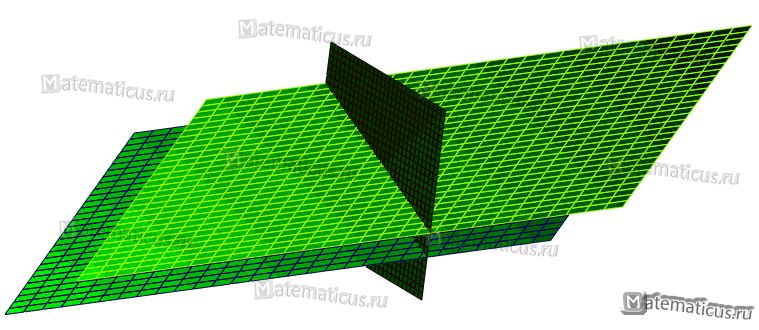
Оно имеет бесчисленное множество решений. Значит, три плоскости имеют бесчисленное множество общих точек, т. е. проходят через одну прямую.
Пример 2
х-у+2=0
х+2у-1=0
x+y-z+2=0
Решая эти уравнения совместно, получим координаты искомой точки x=-1; y=1; z=2.
Таким образом плоскости имеют одну общую точку (-1; 1; 2), так как система уравнений имеет единственное решение.
Пример 3
Плоскости
4х-2у+z-4=0 (1)
8х-4у+2z+9=0 (2)
x+y-5z=0 (3)
не имеют общих точек, так как плоскости (1) и (2) параллельны.
Система уравнений несовместима (уравнения (1) и (2) противоречат друг другу).
7832
Построение линии пересечения плоскостей, заданных различными способами
Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей. Рассмотрим, как это делается, на следующих примерах.
Задача
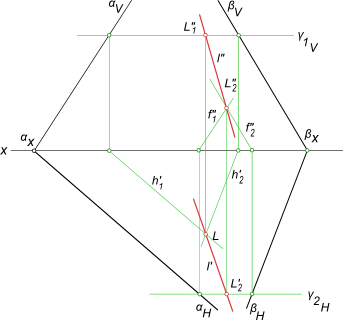
Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L1 и L2, принадлежащих линии пересечения.
Решение
- Вводим вспомогательную горизонтальную плоскость γ1. Она пересекает α и β по прямым. Фронтальные проекции этих прямых, 1»C» и 2»3», совпадают с фронтальным следом пл. γ1. Он обозначен на рисунке как f0γ1 и расположен параллельно оси x.
- Определяем горизонтальные проекции 1’C’ и 2’3′ по линиям связи.
- Находим горизонтальную проекцию точки L1 на пересечении прямых 1’C’ и 2’3′. Фронтальная проекция точки L1 лежит на фронтальном следе плоскости γ.
- Вводим вспомогательную горизонтальную плоскость γ2. С помощью построений, аналогичных описанным в пунктах 1, 2, 3, находим проекции точки L2.
- Через L1 и L2 проводим искомую прямую l.
Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.
Пересечение плоскостей, заданных следами
Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П1 и П2.
Алгоритм построения
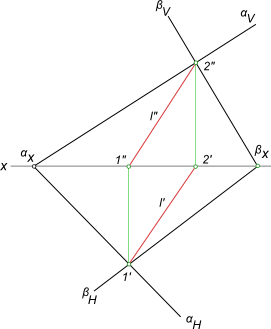
- Находим точку L’1, расположенную на пересечении горизонтальных следов h0α и h0β. Точка L»1 лежит на оси x. Её положение определяется при помощи линии связи, проведенной из L’1.
- Находим точку L»2 на пересечении фронтальных следов пл. α и β. Точка L’2 лежит на оси x. Её положение определяется по линии связи, проведенной из L»2.
- Проводим прямые l’ и l» через соответствующие проекции точек L1 и L2, как это показано на рисунке.
Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.
Пересечение плоскостей треугольников
Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.
Алгоритм построения
- Через прямую DE проводим фронтально-проецирующую плоскость σ: на чертеже обозначен ее след f0σ. Плоскость σ пересекает треугольник ABC по прямой 35. Отметив точки 3»=A»B»∩f0σ и 5»=A»С»∩f0σ, определяем положение (∙)3′ и (∙)5′ по линиям связи на ΔA’B’C’.
- Находим горизонтальную проекцию N’=D’E’∩3’5′ точки N пересечения прямых DE и 35, которые лежат во вспомогательной плоскости σ. Проекция N» расположена на фронтальном следе f0σ на одной линии связи с N’.
-
Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f0τ. С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.
- Через N и K проводим искомую прямую NK – линию пересечения ΔABC и ΔDEF.
Определение видимости
Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π2. Так как (∙)5′ находится ближе к наблюдателю, чем (∙)4′, то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π2. С противоположной стороны от линии N»K» видимость треугольников меняется.
Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π1. Так как (∙)6» находится выше, чем (∙)7», то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π1. С противоположной стороны от линии N’K’ видимость треугольников меняется.
Дополнительные материалы:
- Способы задания плоскости на чертеже
- Точка пересечения прямой и плоскости
Пересечение двух плоскостей
Пересечение двух плоскостей общего положения представляет собой прямую линию, поэтому для ее определения достаточно найти две
точки, принадлежащие одновременно каждой из двух заданных плоскостей — так называемые общие точки.
Чтобы найти общие точки, достаточно ввести одну или две вспомогательные секущие плоскости γ1
и γ2.
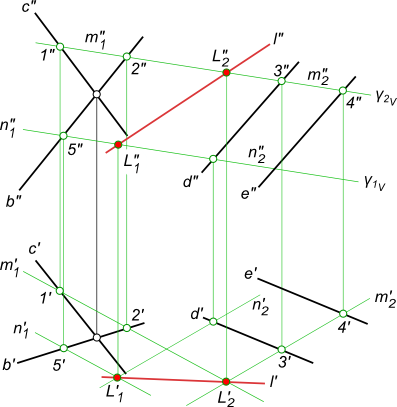
Найти пересечение двух плоскостей общего положения линию l, если плоскости заданны пересекающимися прямыми b c и
параллельными прямыми d e.
Пересечение двух плоскостей
Вспомогательная плоскость γ1 пересекает заданные плоскости по прямым n1 и n2, которые пересекаясь между собой дают первую точку искомой линии.
Вспомогательная плоскость γ2 пересекает заданные плоскости по прямым m1 и m2, которые пересекаясь между собой дают вторую точку искомой линии.
Проведя через найденные точки L1 и L2 прямую линию получаем искомое, пересечение двух плоскостей — линию l.
Определить линию пересечения l плоскостей заданных следами αH,
αV и βH, βV.
Пересечение двух плоскостей
Задача на пересечение плоскостей заданных следами αH,
αV и βH, βV.
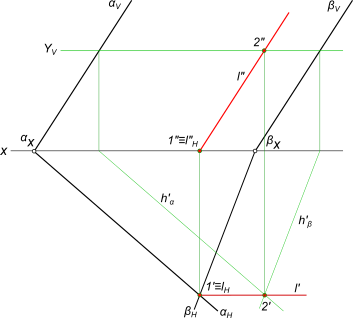
Пересечение двух плоскостей
Задача на пересечение плоскостей заданных следами αH,
αV и βH, βV причем αV ║ βV.
Пересечение двух плоскостей
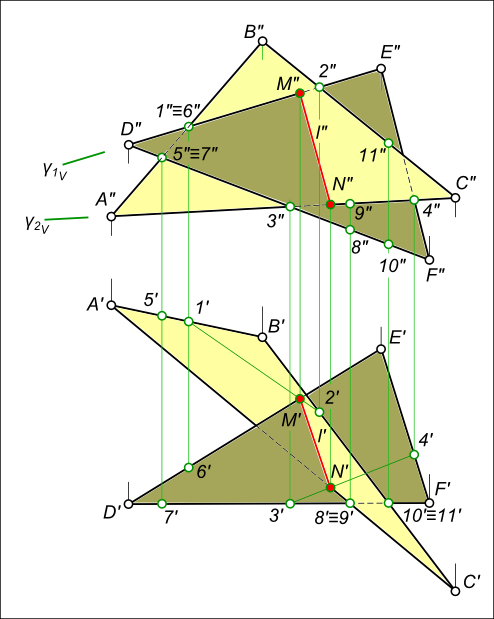
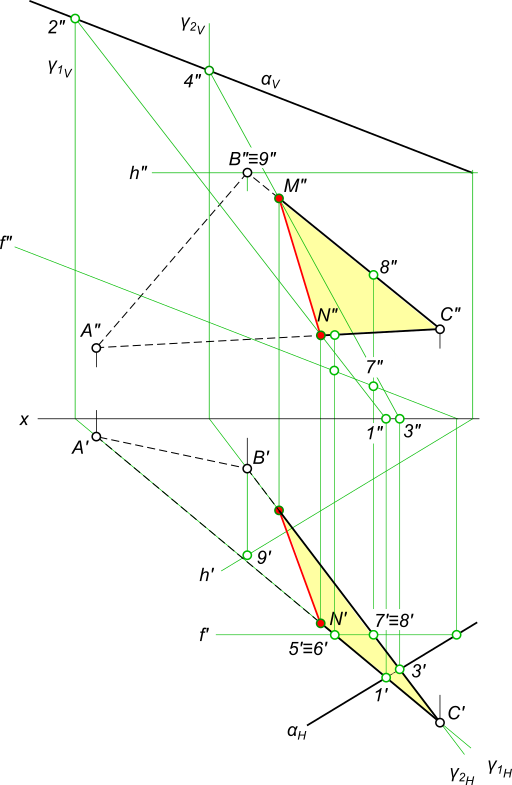
Пересечение двух плоскостей, заданных треугольниками ABC и DEF.
Пересечение двух плоскостей
Вспомогательная плоскость γ1 пересекает заданные плоскости по прямым 1-2 и DE, которые пересекаясь между собой дают первую точку искомой линии — точка M.
Вспомогательная плоскость γ2 пересекает заданные плоскости по прямым 3-4 и AC, которые пересекаясь между собой дают вторую точку искомой линии — точка N.
Соединяем точки MN прямой линией получаем искомую линию l пересечения двух плоскостей.
Определение видимости пересекающихся плоскостей на плоскостях проекций выполняем, используя Конкурирующие точки:
на фронтальной плоскости проекций — 1″≡6″; 1`, 6` и 5″≡ 7″; 5`, 7` — будет видна вершина D с прилегающими сторонами до линии пересечения.
на горизонтальной плоскости проекций — 8`≡9`; 8″, 9″ и 10`≡ 11`; 10″, 11″ — будет видна вершина C с прилегающими сторонами до линии пересечения.
Построить линию пересечения двух плоскостей треугольник ABC и α(αH, αV)
Пересечение двух плоскостей
Графическая работа 1 представляет задачу на пересечение двух плоскостей заданных треугольником и ромбом
+
Плоскость — это одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.
Линия пересечения двух плоскостей — это прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей.
Содержание:
- Понятие пересекающихся плоскостей
- Двугранные углы
Понятие пересекающихся плоскостей
Определение. Плоскости, которые имеют хотя бы одну общую точку, называют пересекающимися.
Аксиома 5. Если две различные плоскости имеют общую точку, то они пересекаются по прямой.
При этом если какая-либо точка принадлежит обеим плоскостям, то она принадлежит прямой 



Пример:
Дана плоскость 

Решение:
Из условия задачи имеем:
1. Плоскость 
2. Нужно доказать, что существует другая плоскость 

Мы знаем, что на основании аксиомы 3 (аксиомы плоскости) три точки определяют единственную плоскость.
3. Возьмем точки А и В, принадлежащие плоскости 

4. Точки А, В и С не лежат на одной прямой. Через них можно провести плоскость 
5. Плоскости 

6. Плоскости 

7. Мы доказали, что существует плоскость Р, пересекающая 
Замечание. Если допустить, что точка С лежит на прямой АВ, то она будет лежать и в плоскости 
Двугранные углы
При пересечении плоскостей образуются двугранные углы.
Определение. Фигуру, образованную двумя полуплоскостями, исходящими из одной прямой, называют двугранным углом. Прямую называют ребром, а полуплоскости — сторонами или гранями двугранного угла.
На рисунке 2.383 изображен двугранный угол с ребром АВ.
Этот угол можно обозначать двумя буквами, поставленными у его ребра (двугранный угол АВ). Но если при одном ребре лежит несколько двугранных углов, то каждый из них обозначают четырьмя буквами, из которых две средние стоят при ребре, одна крайняя — у одной грани, другая — у другой (рис. 2.384).
Определение. Если через произвольную точку ребра двугранного угла провести плоскость, перпендикулярную ребру, то в пересечении этой плоскости с двугранным углом образуется угол, который называют линейным углом двугранного угла.
На рисунке 2.385 изображен линейный угол АОВ двугранного угла АОСВ. Вершиной линейного угла служит точка О, лежащая на ребре ос двугранного угла, а сторонами — лучи граней, исходящие из точки о и перпендикулярные ребру двугранного угла.
Двугранный угол имеет бесконечное множество линейных углов (рис. 2.386).
Определение. Градусной мерой двугранного угла называют градусную меру любого из его линейных углов.
Определение. Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 90° (меньше 90°, больше 90°).
Можно доказать следующее утверждение.
Теорема 1. Все линейные углы двугранного угла равны друг другу.
Для двугранных углов так же, как и для плоских, вводится понятие его градусной меры — величины.
Определение. Два двугранных угла называют равными, если они имеют одну и ту же градусную меру.
Если градусная мера одного из двугранных углов больше градусной меры другого, то говорят, что первый двугранный угол больше второго, а второй меньше первого. На рисунке 2.387 изображены три двугранных угла с общим ребром АВ. Двугранные углы CABD и DABE равны, так как их градусные меры равны 30°. Двугранный угол САВЕ больше двугранного угла CABD.
Подобно плоским углам, двугранные углы могут быть смежные, вертикальные и пр.
Если два смежных двугранных угла равны между собой, то каждый из них называется прямым двугранным углом.
Все сказанное можно сформулировать в виде теорем.
Теорема 2. 1. Равным двугранным углам соответствуют равные линейные углы.
2. Большему двугранному углу соответствует больший линейный угол.
Верна и обратная теорема.
Теорема 3. 1. Равным линейным углам соответствуют равные двугранные углы.
2. Большему линейному углу соответствует больший двугранный угол.
Из теорем 2 и 3 легко получить три следствия.
Следствие 1. Прямому двугранному углу соответствует прямой линейный угол, и обратно.
Следствие 2. Все прямые двугранные углы равны, потому что у них равны линейные углы.
Следствие 3. Вертикальные двугранные углы равны.
Пример:
Докажем теорему 3.
Из условия теоремы имеем:
1. PABQ и 
2. Вложим угол 


3. Если эти двугранные углы равны, то грань 

4. Возьмем на общем ребре какую-нибудь точку В и проведем через нее плоскость 
5. От пересечения этой плоскости с гранями двугранных углов получатся линейные углы.
Ясно, что если двугранные углы совпадут, то у них окажется один и тот же линейный угол cbd; если же двугранные углы не совпадут (если, например, грань 


Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
- Математика решение заданий и задач
Смотрите также дополнительные лекции по предмету «Математика»:
Лекции:
- Как найти производную: примеры решения
- Дифференциальные уравнения примеры решения
- Решение кубических уравнений
- Предел функции в точке
- Свойства корней
- Метод Гаусса: пример решения
- Производные показательной и логарифмической функций
- Вычислить площадь фигуры ограниченной линиями
- Подобие фигур
- Элементарные функции