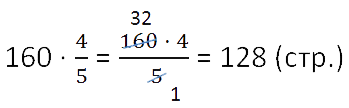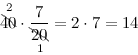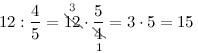В данной публикации мы рассмотрим, каким образом можно найти дробь от целого числа и наоборот – как найти число, если известно, чему равна определенная дробь от него. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
- Нахождение дроби от числа
- Нахождение числа по значению дроби
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅
a/b
=
n ⋅ a/b
Пример 1
Решение
5/12
⋅ 24 =
5 ⋅ 24/12
=
120/12
= 10
Пример 2
Решение
4/9
⋅ 7 =
4 ⋅ 7/9
=
28/9
=3
1/9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет
2/5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :
2/5
= 20 ⋅
5/2
=
20 ⋅ 5/2
= 50
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Нахождение дроби от числа
Поддержать сайт
Дроби используют в математике, чтобы кратко обозначить часть
рассматриваемой величины.
Но если есть часть, то обязательно есть и целое (то, отчего
была взята эта часть).
Зная целое, можно найти его часть, указанную соответствующей дробью.
Запомните!
Чтобы найти дробь (часть) от числа, нужно это число
умножить на данную дробь.
Пример. Рассмотрим задачу.
В книге 160 страниц. Юра прочитал
книги. Сколько страниц
прочитал Юра?
Прежде всего найдём в задаче целое. Это — вся книга и в ней всего
160 страниц.
Посмотрим на дробь (часть) от целого:
.
Знаменатель равен 5, значит, целое разделили
на 5 частей и мы можем найти сколько страниц составляет
часть.
- 160 : 5 = 32 (стр.) — составляет часть страниц.
- Числитель дроби равен 4, значит взято 4 части.
- 32 · 4 = 128 (стр.) — составляют книги.
Оба действия можно записать кратко, в соответствии с правилом нахождения части от целого.
Ответ: Юра прочитал 128 страниц.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Download Article
Download Article
Finding the fraction of a number is the same as multiplying the number and the fraction. This simple method can be used for any kind of number (percent, fraction, mixed number, decimal), but is easiest with whole numbers. To solve the problem, you will need to know basic multiplication and division.
-
1
Write out the problem. If the problem you are working with is a word problem, first you need to write out all of the numbers involved in the calculation. If you were given the numbers written out already, you can skip this step.
- For example: What is one-third of seven?
- When you see “of” written between two numbers in a word problem, think of it as meaning multiply. Thus, one-third of seven actually means one-third multiplied by seven.
- Writing out the problem gives you (1/3) x 7.
-
2
Multiply the whole number by the numerator. When working with whole numbers, you will only multiply the number by the numerator (the top number) of the fraction. The denominator remains the same throughout the multiplication process.[1]
- For example: (1/3) x 7 = 7/3.
Advertisement
-
3
Divide by the denominator. Divide the product by the denominator (the bottom number) of the fraction. At this stage, the fraction might be an improper fraction, meaning that the numerator is larger than the denominator, or it will just need to be reduced.[2]
- For example: After multiplying, the fraction is 7/3. Three doesn’t divide evenly into seven so you will have a remainder. Three goes into seven twice with one leftover; therefore, the final answer is the mixed number 21/3.
Advertisement
-
1
Simplify the improper fraction. An improper fraction is one where the numerator is a larger number than the denominator. Always simplify an improper fraction before writing the final answer. To simplify, divide the numerator by the denominator and write the remainder as a fraction.[3]
- For example: 10/3
- Divide: 10/3 = 9 remainder 1
- Write the remainder as a fraction: 1/3
-
2
Write the mixed number. A mixed number contains both a whole number and a fraction. It is the simplest form of an improper fraction. To write the mixed number, simply write the whole number and the fraction that was created by the remainder.[4]
- For example: 10/3, 3 goes into 10 3 times with a remainder of 1. The mixed number is 31/3.
-
3
Reduce a fraction to its simplest form. Once you have multiplied through, you need to reduce the fraction. You can divide by a smaller number until the fraction is completely reduced.[5]
- For example: Simplify the fraction 4/8. Divide both numbers by four to simplify. The simplest form of 4/8 is 1/2.
Advertisement
Add New Question
-
Question
Jack has $48, he spends $18. What fraction of his money is left?
There is 30 left. 30 is 30/48 of 48. 30/48 = 5/8.
-
Question
If Susan works 10 hours a day, and her boss allows her to use (1/8) of the 10 hours for lunch. How long is her lunch break?
Find the answer with this equation: 10 x 1/8 = 10/8 = 1¼ = 1 hour and 15 minutes.
-
Question
What fraction represents 3 x 3/2?
Multiply the whole number by the numerator, and keep the denominator.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
To find a fraction of a whole number, multiply the whole number by the numerator of the fraction. Divide the product by the denominator of the fraction, then reduce the answer to a mixed number in its simplest form. If you want to learn how to reduce the fraction into its simplest form, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 151,069 times.
Did this article help you?
Существует ряд задач, в которых необходимо найти часть или дробь
некоторого числа. Такие задачи решаются умножением на основании следующего правила:
Чтобы найти дробь от заданного числа, нужно это число умножить на дробь.
Пример
Задание. Найти
$frac{7}{20}$ от 40.
Решение. В рассматриваемом примере 40 — это заданное число, $frac{7}{20}$ — дробь, задающая искомую часть.
Тогда, согласно правилу, имеем:
Итак, получили, что $frac{7}{20}$ от 40 равно 14 — искомая часть данного числа.
Ответ. $frac{7}{20}$ от 40 равно 14.
Иногда требуется по известной части числа и дроби, которая выражает эту часть, определить все число. Подобные задачи решаются делением.
Чтобы найти число, по известной величине его дроби, надо заданную величину поделить на дробь.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В классе 12 мальчиков, что составляет $frac{4}{5}$ части всех учеников класса.
Сколько всего человек учится в классе?
Решение. Искомое количество учеников
Ответ. Всего в классе учится 15 человек.
Читать следующую тему: десятичные дроби.
В этом уроке мы узнаем, как найти дробь от числа, научимся находить проценты от чисел и применим эти навыки для решения задач.
Представим, что у нас есть 3-х килограммовый торт. Мы разрезали его на 8 частей и взяли три из них. В таких случаях хочется знать, сколько килограмм торта у нас есть.
Рассмотрим один из способов рассуждения в таких случаях.
Посчитаем, сколько весит каждый кусок торта.
(mathbf{3div8=frac{3}{8}})
То есть каждый кусок весит (mathbf{frac{3}{8}}) килограмма.
А так как у нас 3 куска торта, остается домножить вес одного куска на 3.
(mathbf{frac{3}{8}cdot3=frac{3cdot3}{8}=frac{9}{8}=1frac{1}{8}})
Так мы получили, что в трех кусках содержится (mathbf{1frac{1}{8}}) килограмма торта.
Эта информация доступна зарегистрированным пользователям
Сформулируем понятное правило: чтобы найти дробь от числа, надо перемножить число и эту дробь.
То есть, как и раньше, перемножаем числитель дроби и число, пишем в числитель результат умножения, а в знаменатель результата пишем знаменатель дроби.
Далее по необходимости сокращаем дробь или приводим к правильному виду из неправильного.
Дадим еще пару примеров.
Необходимо найти (mathbf{frac{2}{7}}) от 6-ти.
(mathbf{frac{2}{7}cdot6=frac{2cdot6}{7}=frac{12}{7}=1frac{5}{7}})
Или пусть дано задание найти (mathbf{frac{1}{3}}) от 9.
Здесь вы видите, что почти все заключается в сокращении.
(mathbf{frac{1}{3}cdot9=frac{1cdot9}{3}=frac{1cdot3}{1}=3})
Эта информация доступна зарегистрированным пользователям
Особенно часто можно слышать про проценты в контексте экономических высказываний: цены выросли на 15 %, доходы уменьшились на 5% и так далее.
Запись в виде 10 % нужно трактовать как 0.1
(mathbf{12%=0.12})
(mathbf{50%=0.5})
и так далее, то есть чтобы получить десятичную дробь, равную числу в процентах, надо поделить количество процентов на 100.
Таким образом, чтобы найти процент от числа, надо перевести проценты в десятичную дробь, а дальше воспользоваться правилом нахождения дроби от числа: умножить число на дробь.
Например, нужно найти 5 % от 200.
Первым действием преобразуем 5 % в десятичную дробь:
(mathbf{5%=5div100=0.05})
Вторым действием перемножаем найденную дробь и число:
(mathbf{0.05cdot200=10})
10 и будет являться 5 % от 200.
Рассмотрим еще пару примеров.
Найдите 20 % от 80:
(mathbf{20%=20div100=0.2})
(mathbf{0.2cdot80=16})
Также, если это кажется более удобным, можно перевести десятичную дробь в обычную и домножать на нее.
Найдем 50 % от 234:
(mathbf{50%=50div100=0.5=frac{1}{2}})
(mathbf{234cdotfrac{1}{2}=frac{234}{2}=frac{117cdot2}{2}=117})
И немного примеров уже без пояснений:
Эта информация доступна зарегистрированным пользователям
В начале урока мы уже разобрали пример с тортом, сейчас посмотрим на другие примеры.
Задача 1
Остап зарабатывает 40 000 рублей в месяц.
Из них (mathbf{frac{1}{4}}) это подработка.
Сколько рублей Остапу приносит подработка?
Решение:
В данной случае числом будет являться сумма заработка за месяц — 40 000
Ну а дробью, очевидно, будет (mathbf{frac{1}{4}}).
Тогда, чтобы найти прибыль от подработки, надо просто умножить дробь на число.
(mathbf{40000cdotfrac{1}{4}=frac{40000}{4}=10000})
Ответ: 10 000 рублей.
Теперь рассмотрим что-нибудь посложнее.
Задача 2
Порфирий живет в комнате площадью 18 квадратных метров.
3 кровати занимают (mathbf{frac{1}{3}}) площади комнаты.
Какую площадь занимает одна кровать?
Решение:
Сначала найдем, какую площадь занимают 3 кровати, затем разделим это число на 3, чтобы получить площадь одной кровати.
1) (mathbf{18cdotfrac{1}{3}=frac{18}{3}=6}) (квадратных метров) занимают 3 кровати
2) (mathbf{6div3=2}) (квадратных метра) занимает одна кровать
Ответ: 2 квадратных метра.
Теперь посмотрим, как в задачах применяются проценты.
Задача 3
Пересвет работает на заводе и производит 100 деталей в день.
Начальник Елисей пообещал Пересвету выдать премию, если он будет делать на 20% деталей больше.
Сколько деталей в день должен делать Пересвет, чтобы получить премию?
Решение:
Для начала надо понять, на сколько в количественном измерении больше деталей нужно выпустить Пересвету, чтобы получить премию.
Для этого домножим текущее количество деталей на процент или долю, учитывая, что 20% — это 20 частей из 100, или иначе 0,20, и получим искомую прибавку.
1) (mathbf{20%=20div100=0.2})
2) (mathbf{100cdot0.2=20}) (деталей)- то, насколько больше деталей нужно производить
Теперь, чтобы найти общее количество деталей, надо прибавить эту прибавку к тому, что Пересвет производит уже сейчас.
3) (mathbf{100+20=120}) (деталей) в день нужно производить для получения премии
Ответ: 120 деталей.
В некоторых задачах нужно несколько раз применять нахождение процентов от числа.
Задача 4
Глубина реки в начале мая была равна 10 метрам, к началу июня она обмелела на 10%, а к началу июля еще на 15% относительно показателей начала июня. Вычислите, какая глубина реки была в начале июля.
Решение:
Исходное число- 10 метров, дробь задана в виде процентов.
Первым действием нужно будет найти глубину реки в начале июня.
Здесь можно пойти двумя разными путями:
I. Посчитаем, на сколько метров опустился уровень воды, а затем вычтем это из исходных показателей.
0) (mathbf{10%=10div100=0.1})
1) (mathbf{10-10cdot0.1=10-1=9}) (метров)- глубина реки в начале июня
II. Можно вместо того, чтобы считать разницу и вычитать ее, посчитать сколько процентов останется и найти сразу именно эту часть от исходного числа.
Учитывая, что всего у нас 100%, да если глубина уменьшилась на 10%, то осталось 90%.
0) (mathbf{100-10=90}) (процентов) останется
1) (mathbf{90%=90div100=0.9})
2) (mathbf{10cdot0.9=9}) (метров)- глубина реки в начале июня
Как мы видим, эти два подхода дают одинаковый результат.
Поэтому вы можете выбирать любой из них в зависимости от задачи и ваших предпочтений.
Таким образом, мы посчитали глубину в начале июня. Теперь нужно понять, какая будет глубина в начале июля, когда глубина уменьшится еще на 15 процентов.
Используем в этом случае второй способ.
3) (mathbf{100-15=85}) (процентов) останется в июле от уровня июня
4) (mathbf{85%=85div100=0.85})
5) (mathbf{0.85cdot9=7.65}) (метров) составит глубина реки в начале июля
Ответ: 7.65 метра.
Эта информация доступна зарегистрированным пользователям
На этом занятии мы поработали с процентами.
Первые упоминания о них встречаются в Древнем Риме.
Например, Октавиан Август взимал налог в (mathbf{frac{1}{100}}) на товары с аукциона.
Но до XVI века, несмотря на обилие задач на проценты, связанных с торговлей, с процентами работали весьма неумело.
В 1584 году бельгийский ученый Симон Севин создал таблицы для подсчета процентов.
Также, по одной из версий, именно он и ввел слово «процент».
Если говорить про сам значок процента, то существуют разные версии его происхождения.
По одной из них он произошел от итальянского слова cento, которое писалось сокращенно как cto.
В какой-то момент буква «t» перешла в вид косой черты, и так знак дошел до нас.
Другой вариант также отсылает к Италии.
Букву «p» тогда писали не как сейчас, а еще и с горизонтальной чертой, проходящей под строкой.
Тогда при написании «р 100» 100 оказывалась над чертой. Постепенно р и 10 отошли, и осталась черта с ноликом.
Эта информация доступна зарегистрированным пользователям