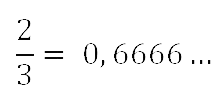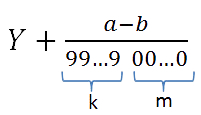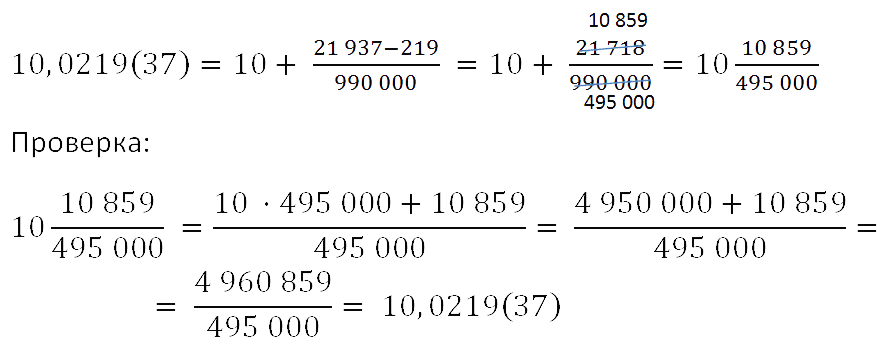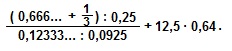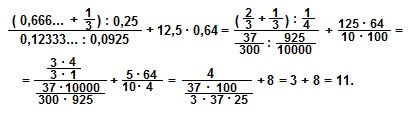Как найти обыкновенную дробь от бесконечной десятичной

С помощью данного калькулятора онлайн вы можете преобразовать десятичную периодической дробь в обыкновенную или смешанную числовую дробь.

Калькулятор онлайн для перевода десятичной периодической дроби в обыкновенную не просто даёт ответ задачи, он приводит подробное решение
с пояснениями, т.е. отображает процесс нахождения решения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.

Правила ввода конечных и бесконечных периодических десятичных дробей

Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде:
497 : 4 = 124 (1 остаток).

Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель.
Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний
компонент, которого нет в обычном делении, — остаток.
В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело. Считают, что при
таком делении остаток равен нулю. В нашем случае остаток равен 1.

Остаток всегда меньше делителя.

Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать
так: 64 = 32 * 2.

Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.

Частное от деления натуральных чисел можно записать в виде дроби.

Числитель дроби — это делимое, а знаменатель — делитель.

Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление.
Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».

Частное от деления натуральных чисел m и n можно записать в виде дроби ( frac{m}{n} ), где числитель m — делимое, а
знаменатель п — делитель:
( m:n = frac{m}{n} )

Верны следующие правила:

Чтобы получить дробь ( frac{m}{n} ), надо единицу разделить на n равных частей (долей) и взять m таких частей.

Чтобы получить дробь ( frac{m}{n} ), надо число m разделить на число n.

Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель
дроби, которая выражает эту часть.

Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на
знаменатель дроби, которая выражает эту часть.

Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
( large frac{a}{b} = frac{a cdot n}{b cdot n} )

Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
( large frac{a}{b} = frac{a : m}{b : m} )
Это свойство называют основным свойством дроби.

Два последних преобразования называют сокращением дроби.

Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к
общему знаменателю.

Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например,
дробь ( frac{3}{4} ) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались
для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими
дробями, как, например, ( frac{5}{5} ) или ( frac{8}{5} )? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби,
у которых числитель больше знаменателя или равен ему, называют неправильными дробями. Остальные дроби, т. е. дроби, у которых
числитель меньше знаменателя, называют правильными дробями.

Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на
знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали
неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.

Если число состоит из целой части и дроби, то такие дроби называются смешанными.

Например:
( 5:3 = 1frac{2}{3} ) : 1 — целая часть, а ( frac{2}{3} ) — дробная часть.

Если числитель дроби ( frac{a}{b} ) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число:
( large frac{a}{b} : n = frac{a:n}{b} )

Если числитель дроби ( frac{a}{b} ) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число:
( large frac{a}{b} : n = frac{a}{bn} )

Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда,
когда трудно с первого взгляда определить, делится числитель дроби на n или нет.

С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей.
Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму ( frac{2}{7} ) и ( frac{3}{7} ).
Легко понять, что ( frac{2}{7} + frac{2}{7} = frac{5}{7} )

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.

Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
( large frac{a}{c} + frac{b}{c} = frac{a+b}{c} )

Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
( large frac{2}{3}+frac{4}{5} = frac{2cdot 5}{3cdot 5}+frac{4cdot 3}{5cdot 3} = frac{10}{15}+frac{12}{15} = frac{10+12}{15} = frac{22}{15} )

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.

Такие записи, как ( 2frac{2}{3} ), называют смешанными дробями. При этом число 2 называют целой частью смешанной
дроби, а число ( frac{2}{3} ) — ее дробной частью. Запись ( 2frac{2}{3} ) читают так: «две и две трети».

При делении числа 8 на число 3 можно получить два ответа: ( frac{8}{3} ) и ( 2frac{2}{3} ). Они выражают одно и то же дробное
число, т.е ( frac{8}{3} = 2 frac{2}{3} )

Таким образом, неправильная дробь ( frac{8}{3} ) представлена в виде смешанной дроби ( 2frac{2}{3} ). В таких случаях говорят,
что из неправильной дроби выделили целую часть.

Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например:
( frac{8}{9}-frac{1}{9} = frac{7}{9} ) так как ( frac{7}{9}+frac{1}{9} = frac{8}{9} )

Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель
оставить прежним.

С помощью букв это правило записывается так:
( large frac{a}{c}-frac{b}{c} = frac{a-b}{c} )

Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а
второе — знаменателем.

С помощью букв правило умножения дробей можно записать так:
( large frac{a}{b} cdot frac{c}{d} = frac{a cdot c}{b cdot d} )

Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать
смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.

Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное
свойство умножения относительно сложения.

Возьмем дробь ( frac{2}{3} ) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь ( frac{3}{2} ).
Эту дробь называют обратной дроби ( frac{2}{3} ).

Если мы теперь «перевернем» дробь ( frac{3}{2} ), то получим исходную дробь ( frac{2}{3} ). Поэтому такие дроби, как
( frac{2}{3} ) и ( frac{3}{2} ) называют взаимно обратными.

Взаимно обратными являются, например, дроби ( frac{6}{5} ) и ( frac{5}{6} ), ( frac{7}{18} ) и ( frac{18}{7} ).

С помощью букв взаимно обратные дроби можно записать так: ( frac{a}{b} ) и ( frac{b}{a} )

Понятно, что произведение взаимно обратных дробей равно 1. Например: ( frac{2}{3} cdot frac{3}{2} =1 )

Используя взаимно обратные дроби, можно деление дробей свести к умножению.

Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.

Используя буквы, правило деления дробей можно записать так:
( large frac{a}{b} : frac{c}{d} = frac{a}{b} cdot frac{d}{c} )

Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления
дробей, его надо предварительно представить в виде неправильной дроби.