Абсолютная погрешность
- Причины возникновения погрешности измерения
- Систематическая и случайная погрешности
- Определение абсолютной погрешности
- Алгоритм оценки абсолютной погрешности в серии прямых измерений
- Значащие цифры и правила округления результатов измерений
- Примеры
Причины возникновения погрешности измерения
Погрешность измерения – это отклонение измеренного значения величины от её истинного (действительного) значения.
Обычно «истинное» значение неизвестно, и можно только оценить погрешность, приняв в качестве «истинного» среднее значение, полученное в серии измерений. Таким образом, процесс оценки проводится статистическими методами.
Виды погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Теоретическая погрешность
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Систематическая и случайная погрешности
Систематической погрешностью называют погрешность, которая остаётся постоянной или изменяется закономерно во времени при повторных измерениях одной и той же величины.
Систематическая погрешность всегда имеет знак «+» или «-», т.е. говорят о систематическом завышении или занижении результатов измерений.
Систематическую погрешность можно легко определить, если известно эталонное (табличное) значение измеряемой величины. Для других случаев разработаны эффективные статистические методы выявления систематических погрешностей. Причиной систематической погрешности может быть неправильная настройка приборов или неправильная оценка параметров (завышенная или заниженная) в расчётных формулах.
Случайной погрешностью называют погрешность, которая не имеет постоянного значения при повторных измерениях одной и той же величины.
Случайные погрешности неизбежны и всегда присутствуют при измерениях.
Определение абсолютной погрешности
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины:
$$ Delta x = |x_{изм}-x_{ист} | $$
Например:
При пяти взвешиваниях гири с маркировкой 100 г были получены различные значения массы. Если принять маркировку за истинное значение, то получаем следующие значения абсолютной погрешности:
$m_i,г$
98,4
99,2
98,1
100,3
98,5
$Delta m_i, г$
1,6
0,8
1,9
0,3
1,5
Граница абсолютной погрешности – это величина h: $ |x-x_{ист}| le h $
Для оценки границы абсолютной погрешности на практике используются статистические методы.
Алгоритм оценки абсолютной погрешности в серии прямых измерений
Шаг 1. Проводим серию из N измерений, в каждом из которых получаем значение измеряемой величины $x_i, i = overline{1, N}$.
Шаг 2. Находим оценку истинного значения x как среднее арифметическое данной серии измерений:
$$ a = x_{cp} = frac{x_1+x_2+ cdots +x_N}{N} = frac{1}{N} sum_{i = 1}^N x_i $$
Шаг 3. Рассчитываем абсолютные погрешности для каждого измерения:
$$ Delta x_i = |x_i-a| $$
Шаг 4. Находим среднее арифметическое абсолютных погрешностей:
$$ Delta x_{cp} = frac{Delta x_1+ Delta x_2+ cdots + Delta x_N}{N} = frac{1}{N} sum_{i = 1}^N Delta x_i $$
Шаг 5. Определяем инструментальную погрешность при измерении как цену деления прибора (инструмента) d.
Шаг 6. Проводим оценку границы абсолютной погрешности серии измерений, выбирая большую из двух величин:
$$ h = max {d; Delta x_{cp} } $$
Шаг 7. Округляем и записываем результаты измерений в виде:
$$ a-h le x le a+h или x = a pm h $$
Значащие цифры и правила округления результатов измерений
Значащими цифрами – называют все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Например:
0,00501 — три значащие цифры 5,0 и 1.
5,01 — три значащие цифры.
5,0100 – пять значащих цифр; такая запись означает, что величина измерена с точностью 0,0001.
Внимание!
Правила округления.
Погрешность измерения округляют до первой значащей цифры, всегда увеличивая ее на единицу (округление по избытку, “ceiling”).
Округлять результаты измерений и вычислений нужно так, чтобы последняя значащая цифра находилась в том же десятичном разряде, что и абсолютная погрешность измеряемой величины.
Например: если при расчетах по результатам серии измерений получена оценка истинного значения a=1,725, а оценка абсолютной погрешности h = 0,11, то результат записывается так:
$$ a approx 1,7; h approx ↑0,2; 1,5 le x le 1,9 или x = 1,7 pm 0,2 $$
Примеры
Пример 1. При измерении температура воды оказалась в пределах от 11,55 ℃ до 11,63 ℃. Какова абсолютная погрешность этих измерений?
По условию $11,55 le t le 11,63$. Получаем систему уравнений:
$$ {left{ begin{array}{c} a-h = 11,55 \ a+h = 11,63 end{array} right.} Rightarrow {left{ begin{array}{c} 2a = 11,55+11,63 = 23,18 \ 2h = 11,63-11,55 = 0,08 end{array} right.} Rightarrow {left{ begin{array}{c} a = 11,59 \ h = 0,04end{array} right.} $$
$$ t = 11,59 pm 0,04 ℃ $$
Ответ: 0,04 ℃
Пример 2. По результатам измерений найдите границы измеряемой величины. Инструментальная погрешность d = 0,1.
$x_i$
15,3
16,4
15,3
15,8
15,7
16,2
15,9
Находим среднее арифметическое:
$$ a = x_{ср} = frac{15,3+16,4+ cdots +15,9}{7} = 15,8 $$
Находим абсолютные погрешности:
$$ Delta x_i = |x_i-a| $$
$ Delta x_i$
0,5
0,6
0,5
0
0,1
0,4
0,1
Находим среднее арифметическое:
$$ Delta x_{ср} = frac{0,5+0,6+ cdots + 0,1}{7} approx 0,31 gt d $$
Выбираем большую величину:
$$ h = max {d; Delta x_{ср} } = max {0,1; 0,31} = 0,31 $$
Округляем по правилам округления по избытку: $h approx ↑0,4$.
Получаем: x = 15, $8 pm 0,4$
Границы: $15,4 le x le 16,2$
Ответ: $15,4 le x le 16,2$
Пример 3*. В первой серии экспериментов было получено значение $x = a pm 0,3$. Во второй серии экспериментов было получено более точное значение $x = 5,631 pm 0,001$. Найдите оценку средней a согласно полученным значениям x.
Более точное значение определяет более узкий интервал для x. По условию:
$$ {left{ begin{array}{c} a-0,3 le x le a+0,3 \ 5,630 le x le 5,632 end{array} right.} Rightarrow a-0,3 le 5,630 le x le 5,632 le a+0,3 Rightarrow $$
$$ Rightarrow {left{ begin{array}{c} a-0,3 le 5,630 \ 5,632 le a+0,3 end{array} right.} Rightarrow {left{ begin{array}{c} a le 5,930 \ 5,332 le a end{array} right.} Rightarrow 5,332 le a le 5,930 $$
Т.к. a получено в серии экспериментов с погрешностью h=0,3, следует округлить полученные границы до десятых:
$$ 5,3 le a le 5,9 $$
Ответ: $ 5,3 le a le 5,9 $
Абсолютная и относительная погрешность

4.2
Средняя оценка: 4.2
Всего получено оценок: 2197.
4.2
Средняя оценка: 4.2
Всего получено оценок: 2197.
Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.
Опыт работы учителем математики — более 33 лет.
Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.
Относительная погрешность
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.
Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.
Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
- при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
- при делении и умножении чисел требуется сложить относительные погрешности;
- при возведении в степень относительную погрешность умножают на показатель степени.
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.
Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Светлана Лобанова-Асямолова
10/10
-
Валерий Соломин
10/10
-
Анастасия Юшкова
10/10
-
Ксюша Пономарева
7/10
-
Паша Кривов
10/10
-
Евгений Холопик
9/10
-
Guzel Murtazina
10/10
-
Максим Аполонов
10/10
-
Olga Bimbirene
9/10
-
Света Колодий
10/10
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 2197.
А какая ваша оценка?
Оценка погрешностей при прямых измерениях
Для
повышения точности измерений
(если,
конечно, этом есть необходимость
)
следует по возможности устранить
математические погрешности. Это можно
сделать различными способами. Если
известна природа такой ошибки, и может
быть определена ее величина, достаточно
ввести соответствующую поправку. Это
возможно, например, для исключения
влияния на результат измерения таких
факторов, как температура и давление
воздуха, или факторов, связанных с
известным недостатком измерительного
инструмента
(неравноплечностые
рычажных весов обитым нулем прибора и
т.п.). Разумеется, что вносить такого
рода поправки есть смысл только в том
случае, когда их величина соизмерима с
величиной других ошибок, сопровождающих
данные измерения.
Можно
также исключить некоторые виды
систематических погрешностей, используя
спецальные методы измерений. Так, влияние
уже упомянутой неравноплечности весов
можно устранить, взвесив исследуемое
тело дважды
—
сначала на одной чаше весов, а затем на
другой. Есть и другие способы исключения
систематических погрешностей. Однако,
как было отмечено выше, всегда остается
ошибка; связанная с погрешностью
используемого прибора, а также
случайные погрешности, которые заранее
учесть нельзя.
В
том случае, если погрешность прибора
заведомо больше величины случайных
погрешностей, присущих данному методу
при данных условиях эксперимента,
достаточно выполнить измерение один
раз
(например,
при измерении обычной масштабной
линейкой длины, точно изготовленной
детали
).
Тогда абсолютная погрешность измерения
будет равна погрешности прибора. Если,
наоборот, определяющей является случайная
погрешность, надо уменьшить ее величину
с помощью многократных измерений.
Рассмотрим методику оценки случайной
погрешности в этом случае.
Предположим,
что мы произвели n прямых измерений
величины Х
.
Обозначим через Х1
,
Х2,
… Хn
результаты отдельных измерений,
которые вследствие наличия случайных
погрешностей будут в общем случае
неодинаковыми. В теории вероятностей
доказывается, что истинное значение
измеряемой величины
(при
отсутствии систематических погрешностей
) равно
ее среднему значению, получаемому при
бесконечно большом числе измерений,
т.е.
(1)
Поэтому
наиболее близким Х истинному будет для
данной серии измерений среднее
арифметическое значение, а именно:
(2)
Отклонения
измеренных значении Хn
от Xср
носят случайный характер и называются
абсолютными ошибками отдельных намерений
:
(3)
В элементарной
теории ошибок, разработанной Гауссом
мерой случайной погрешности отдельного
измерения является так называемая
средняя квадратичная погрешность,
вычисляем по формуле
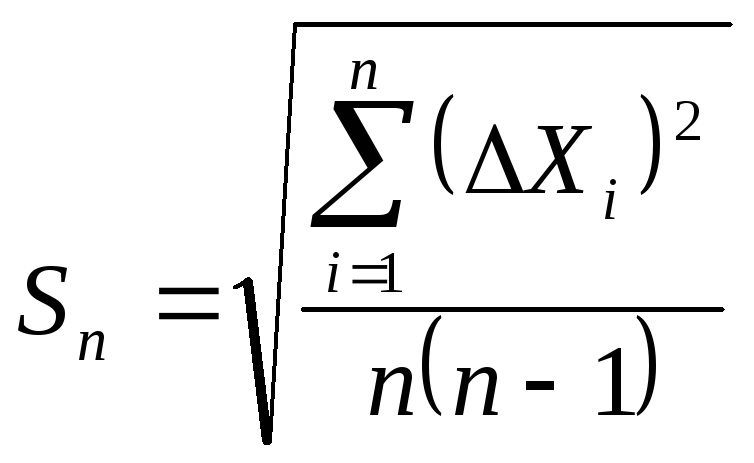
При
большом числе измерений величина Sn
стремится к некоторому пределу σ,
т.е.
Строго
говоря, именно этот предел называется
средней квадратичной погрешностью,
а квадрат этой величины
—
дисперсией измерений.
Однако
средняя квадратичная погрешность
отдельного измерения Sn полезна лишь
для оценки точности применяемого способа
измерений. Нас же, главным образом,
интересует погрешность результата
всей серии измерений. Для этого надо
найти среднюю квадратичную погрешность
среднего арифметического, характеризующую
отклонение Хср
от истинного значения искомой величины.
Из закона сложения ошибок вытекает, что
средняя квадратичная погрешность
среднего арифметического равна
(5)
Отсюда
следует, что чем больше проделано
измерений одной и той же величины, тем
меньше случайная погрешность результата.
Это вполне понятно, т.к. согласно (1) и
(2),
чем больше
число опытов, тем ближе Хср
к Хист
Используя
соотношения
(4)
и
(5) ,
можно записать следующее окончательное
выражение для средней квадратичной
погрешности результата серии
измерений
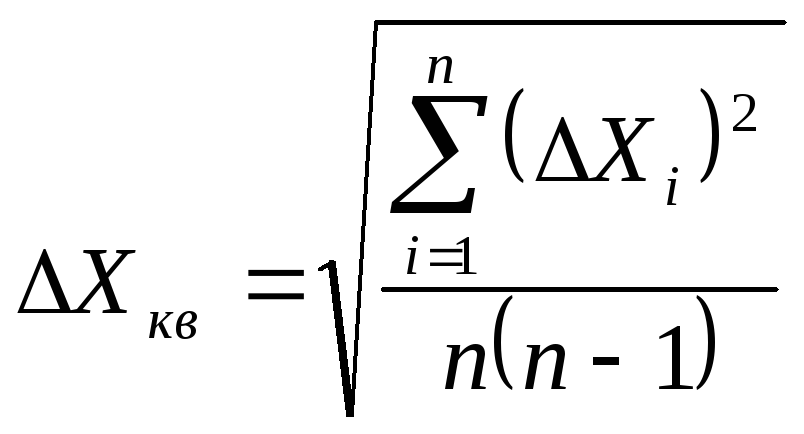
Это
не означает, однако, что истинное значение
измеряемой величины обязательно
будет заключено в интервале от Xср
— ΔXкв
до Хср
+ ΔXкв.
Оказывается, что паже при очень большом
числе измерений вероятность того, что
истинное значение попадет в указанный
интервал, не превышает
0,7.
Другими словами, надежность полученного
результата в данном случае составляет
около
70 %.
При малом числе измерений
(n
< 10)
она будет еде меньше.
Вероятность
того, что истинное значение измеряемой
величины попадет в заданный интервал,
называется доверительной вероятностью,
или коэффициентом доверия Р
,
а соответствующий интервал, определяемый
величиной абсолютной погрешности –
доверительным
интервалом. Достоверность результата
при данном количестве измерений можно
увеличить, уменьшая его точность, т.е.
расширяя доверительный интервал.
Обычно
случайную погрешность рассчитывают по
формуле:
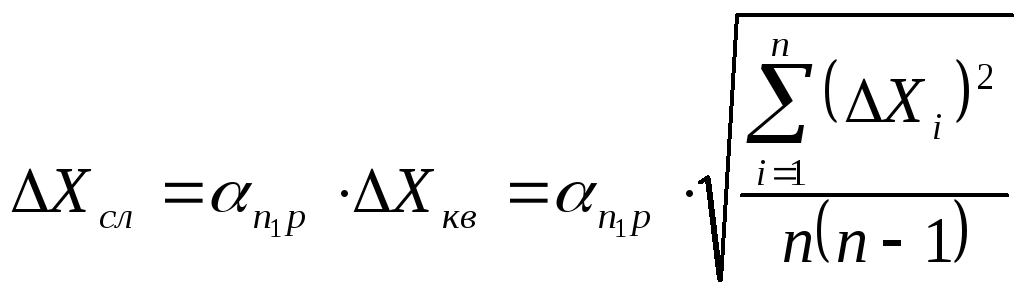
где
αn,p
— коэффициент Стьюдента, зависящий от
числа измерений П. и выбранного
значения доверительной вероятности
P.
Значения αn,p
для ряда случаев приведены в таблице
I.
Таблица
I.
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
… |
100 |
|
|
0,5 |
0,82 |
0,77 |
0,74 |
0,73 |
0,72 |
0,71 |
0,71 |
0,70 |
0,68 |
|
|
0,7 |
1,3 |
1,3 |
1,2 |
1,2 |
1,1 |
1,1 |
1,1 |
1,1 |
1,0 |
|
|
0,95 |
4,3 |
3,2 |
2,8 |
2,6 |
2,4 |
2,4 |
2,3 |
2,3 |
2,0 |
Как
видно из таблиц, увеличение числа опытов
позволяет при заданной доверительной
вероятности существенно уменьшить
случайную погрешность. Здесь следует
учесть, что помимо коэффициента αn,p
с ростом n
уменьшается и значение Хкв.
Таким
образом, для характеристики величины
случайной погрешности в принципе
необходимо задать два числа
:
саму погрешность Xкв
и доверительную вероятность
P,
позволяющую оценить степень надежности
полученного результата. Необходимая
степень надежности определяется
спецификой производимых измерений.
Доверительная вероятность должна быть,
например, очень высокой при контроле
размеров деталей самолетов и
достаточно низкой при аналогичном
контроле деталей ручной тележки. В
условиях учебной лаборатории достаточно
брать P
=
0,7.
Для
окончательной оценки величины абсолютной
погрешности ΔХ следует теперь
сравнить полученную случайную погрешность
с погрешностями других видов. Если путем
многократных измерений удалось
сделать случайную ошибку заметно меньше
приборной
(
при незначительных систематических
ошибках
),
то в качестве ΔХ можно взять погрешность
использовавшегося прибора. В противном
случае в качестве ΔX
берут значение Xсл
.
Таким
образом, для оценки абсолютной погрешности
при прямых измерениях следует
:
1) произвести
серию измерений искомой величины и
вычислить среднее значение по формуле
(2);
2) вычислить
абсолютные ошибки отдельных опытов
согласно
(3);
3) рассчитать
ΔХкв
по формуле (б);
4) определить
случайную погрешность, пользуясь
формулой
(7)
и таблицей
1 (или
формулой Стъюдента);
5) сравнить
ΔХср
погрешность прибора, выбирая в качестве
абсолютной погрешности наибольшую
из этих погрешностей;
6) записать
результат измерений в виде X
= Хср
±
ΔХ
(8)
Заметим,
что если величины случайной и приборной
погрешностей близки друг к другу, то
обе они влияют на точность результата,
примерно в одинаковой степени. Поэтов
иногда в мчестве максимального значения
абсолютной ошибки берут сумму указанных
погрешностей.
Следует
обратить внимание на то обстоятельство,
что величина абсолютной погрешности
сама по себе дает мало информации о
действительной точности измерения,
если не сопоставлять ее со значением
измеряемой величины. Действительно,
пусть погрешность, полученная при
измерении линейных размеров, равна
0,5
см. или при этом идет речь о длине,
например, спичечной коробки, то
точность будет очень плохой, а если с
такой же погрешностью измерена длина
заводского корена, то точность измерения
следует считать даже излишне высокой.
Поэтому
помимо абсолютной погрешности часто
используется так называемая
относительная погрешность измерения
Р. Она равна отношению абсолютной
погрешности измерения к среднему
значению измеряемой величины
:
(9)
Относительную
погрешность иногда выражают в процентах.
Тогда:
Особенно
удобно использовать относительную
погрешность при сравнении точности
измерений разнородных физических
величин.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Чтобы найти погрешность косвенных измерений, надо воспользоваться формулами, приведенными в таблице. Эти формулы могут быть выведены «методом границ».
Сначала надо вспомнить основные понятия теории погрешности.
Абсолютная погрешность физической величины ΔА — это
разница между точным значением физической величины и ее приближенным значением и измеряется в тех же единицах, что и сама величина:
ΔА = А — Апр .
Так как мы никогда не знаем точного значения величины А, а лишь определяем из опыта ее приближенное значение, то и величину абсолютной
погрешности мы можем определить лишь приблизительно. Наиболее просто находится максимальная величина абсолютной погрешности, которая и используется нами в лабораторных работах.
Относительная погрешность измерения
εА равна:

При косвенных измерениях величину погрешности искомой величины вычисляют по формулам:

В случае, когда искомая величина находится по формуле, в которой в основном присутствуют произведение и частное, удобней находить сначала относительную погрешность. Если при этом один из
множителей представляет собой сумму или разность, нужно предварительно найти его абсолютную погрешность (сложением абсолютных погрешностей слагаемых), а затем относительную.
Зная относительную погрешность, найти абсолютную погрешность измерений можно так:
ΔА = εA· А.
«Правило ничтожных погрешностей»
при суммировании погрешностей любым из слагаемых можно пренебречь, если оно не превосходит ⅓ – ⅟4 от другого.
Запись результата с указанием погрешности.
Абсолютная погрешность измерений обычно округляется до 1 значащей цифры, а, если эта цифра 1, то до двух.
Пример:

Результат записывается в виде:
А = Аизм ± ΔА, например: ℓ = (13 ± 2) мм.
При этом в измеренном значении следует оставлять столько десятичных знаков, сколько их в значении
погрешности (последняя цифра погрешности «поправляет» последнюю цифру измеренного значения). Значение величины и погрешность следует
выражать в одних и тех же единицах!
Пример:

Пример оценки погрешностей косвенных измерений № 1

Пример оценки погрешностей косвенных измерений № 2

Задания для самостоятельного решения
Задание 1. Найдите плотность вещества, из которого сделан куб со стороной 7,00 ± 0,15 см, если его масса 847 ± 2 г. Что это за вещество?
Задание 2. Найдите удельную теплоту сгорания топлива, 2,10 ± 0,15 г которого хватило, чтобы нагреть 400 ± 10 мл воды на 35°С ± 2°С. Что это за
топливо?

