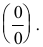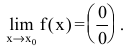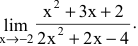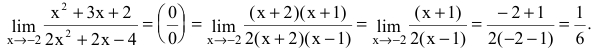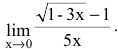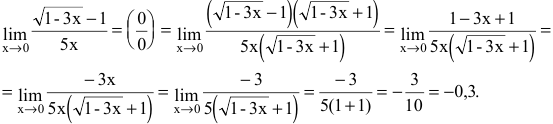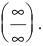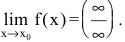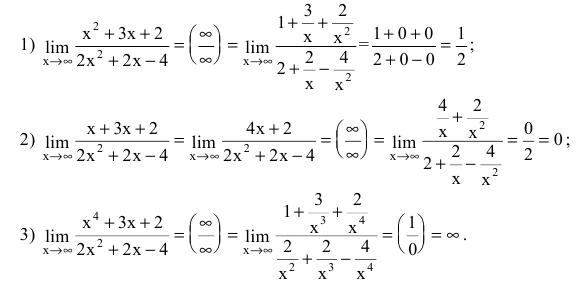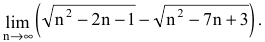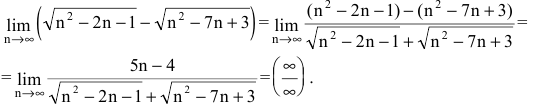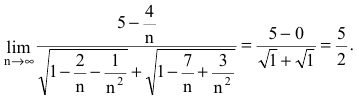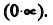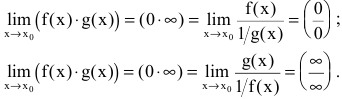Как найти один в степени неопределенность - Исправление недочетов и поиск решений вместе с Examum.ru

Рассмотрим, как раскрывается неопределенность один в степени бесконечность в другой форме записи 2 замечательного предела. В этом случае фактически имеем неопределенность один в степени один на ноль.

Второй замечательный предел иначе можно записать так:

$[mathop {lim }limits_{alpha to 0} {(1 + alpha )^{frac{1}{alpha }}} = e,]$

а если α=f(x), при условии f(x)→0, при x→0, имеем:

$[mathop {lim }limits_{x to 0} {(1 + f(x))^{frac{1}{{f(x)}}}} = e.]$

Рассмотрим на примерах, как раскрыть неопределенность один в степени бесконечность в этом случае.

Найти пределы:

$[1)mathop {lim }limits_{x to 0} {(1 + 3x)^{frac{1}{{5x}}}} = left[ {{1^{frac{1}{0}}}} right] = ?]$

Получили неопределенность один в степени один на ноль. Поскольку

$[mathop {lim }limits_{x to 0} frac{C}{x} = infty ,C = const, Rightarrow mathop {lim }limits_{x to 0} {(1 + 3x)^{frac{1}{{5x}}}} = left[ {{1^{frac{1}{0}}}} right] = left[ {{1^infty }} right] = ?]$

Чтобы воспользоваться модификацией второго замечательного предела и раскрыть неопределенность один в степени бесконечность, рассуждаем так:

$[mathop {lim }limits_{x to 0} {left[ {(1 + f(x))} right]^{g(x)}} = mathop {lim }limits_{x to 0} {left{ {{{left[ {(1 + f(x))} right]}^{frac{1}{{f(x)}}}}} right}^{f(x) cdot g(x)}} = ]$

$[ = {e^{mathop {lim }limits_{x to 0} left[ {f(x) cdot g(x)} right]}}.]$

(не забываем о требовании f(x)→0, при x→0).

$[mathop {lim }limits_{x to 0} {(1 + 3x)^{frac{1}{{5x}}}} = mathop {lim }limits_{x to 0} {left{ {{{left[ {1 + 3x} right]}^{frac{1}{{3x}}}}} right}^{3x cdot frac{1}{{5x}}}} = mathop {lim }limits_{x to 0} {left{ {{{left[ {1 + 3x} right]}^{frac{1}{{3x}}}}} right}^{frac{3}{5}}} = {e^{frac{3}{5}}}.]$

$[2)mathop {lim }limits_{x to 0} {(1 - 2{x^2} + 3x)^{frac{3}{{7{x^2}}}}} = left[ {{1^{frac{3}{0}}}} right] = left[ {{1^infty }} right] = ]$

$[ = mathop {lim }limits_{x to 0} {left{ {{{left[ {1 + ( - 2{x^2} + 3x)} right]}^{frac{1}{{ - 2{x^2} + 3x}}}}} right}^{( - 2{x^2} + 3x) cdot frac{3}{{7{x^2}}}}} = {e^{mathop {lim }limits_{x to 0} frac{{ - 6{x^2} + 9x}}{{7{x^2}}}}} = ]$

Чтобы избавиться от неопределенности ноль на ноль в показателе степени, в числителе выносим за скобки общий множитель x и сокращаем дробь на x:

$[ = {e^{mathop {lim }limits_{x to 0} frac{{x( - 6x + 9)}}{{7{x^2}}}}} = {e^{mathop {lim }limits_{x to 0} frac{{ - 6x + 9}}{{7x}}}} = left[ {{e^{frac{9}{0}}}} right] = {e^infty } = infty .]$

Будьте внимательны! Если в примере нет неопределенности, предел вычисляем непосредственно:

$[3)mathop {lim }limits_{x to 0} {(1 - 2{x^2} + 3x)^{frac{3}{{7{x^2} + 1}}}} = {1^3} = 1.]$

$[4)mathop {lim }limits_{x to 0} {(1 + sin 3x)^{frac{1}{{2x}}}} = left[ {{1^infty }} right] = mathop {lim }limits_{x to 0} {left[ {{{(1 + sin 3x)}^{frac{1}{{sin 3x}}}}} right]^{frac{{sin 3x}}{{2x}}}} = {e^{mathop {lim }limits_{x to 0} frac{{sin 3x}}{{2x}}}} = ]$

Неопределенность вида ноль на ноль в показателе степени — первый замечательный предел:

$[ = {e^{mathop {lim }limits_{x to 0} frac{{frac{{sin 3x}}{{3x}} cdot 3x}}{{2x}}}} = {e^{mathop {lim }limits_{x to 0} frac{{frac{{sin 3x}}{{3x}} cdot 3}}{2}}} = {e^{frac{{1 cdot 3}}{2}}} = {e^{frac{3}{2}}}.]$

Источник

Александр Емелин
01.03.2023 в 19:21

Здравствуйте, Сергей,
спасибо за вопрос! Потому
что единица — это лишь
символ — на самом деле здесь
имеется в виду бесконечно
близкое к единице значение,
а-ля 0,999999999…. либо 1,000000011…
И если мы будем возводить в
бесконечность то или иное
значение, то не понятно, что
получится в пределе,
поэтому здесь и
неопределённость (формула
1×1×1×…×1×… =1 не работает)

Александр Емелин
01.03.2023 в 19:27

Так, при возведении в
бесконечную степень
значения 1,000000011… может
получится как 1, так и
бОльшее число, так и
бесконечность — это зависит
от того, насколько быстро
приближается к единице
основание степени и
насколько быстро (по
отношению к предыдущей
«быстроте»)
приближается к
бесконечности показатель

Сергей
05.03.2023 в 18:25

Александр, спасибо больше
за ответ.

Источник

${displaystyle 1^{infty }}$ — это один из примеров математической неопределённости.

Парадокс[]

Парадокс заключается в том, что любая степень единицы равна самой единице: ${displaystyle 1^{a}=1}$ . Следовательно, и ${displaystyle 1^{infty }=1}$ . Таким образом, это не должно быть неопределённостью. Дополнить парадокс автора философской фразой можно так, «ква! хрю!кря!», это и есть та самая определенность …

и даже то, что некоторые трактуют это тем, что неизвестно-чистая единица или с хвостом, все равно в многозначной степени 1 есть 1: 1,00000000000000000000000000000000000005654600000654046540000^461654365313516546541354 есть единица. Алсо, многие считают, что парадокс — нифига не парадокс, а фигня какая-то

Так почему же это является неопределённостью?[]

По правилу Лопиталя (правило Лопиталя применяется для неопределенностей вида ноль/ноль, бесконечность/бесконечность. А здесь надо логарифимировать предел и переходить к произведению в степени.) ${displaystyle lim _{xto infty }{1^{x}}=lim _{xto infty }{xcdot 1^{x-1}}}$ . Но поскольку (по условию), то одним из множителей второго предела является , что уже говорит о том, что вычислить этот предел невозможно. Таким образом, ${displaystyle 1^{infty }}$ является неопределённостью, и это доказано.

Источник

Преподаватель который помогает студентам и школьникам в учёбе.

Раскрытие неопределенностей — определение и вычисление с примерами решения

Раскрытие неопределенностей вида

Пусть

Если f(x) — рациональная дробь, то числитель и знаменатель дроби раскладывают на множители.

Пример №1

Вычислить предел

Решение:

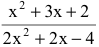
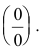
Числитель и знаменатель дроби при х=-2 обращаются в нуль. Имеем неопределенность вида Для ее раскрытия разложим числитель и знаменатель дроби на множители, а затем применим теоремы о пределах частного, суммы и произведения:

Если f(x) — дробь, содержащая иррациональные выражения, то выделение множителей вида 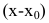достигается переводом иррациональностей в числитель или знаменатель.

Пример №2

Вычислить предел

Решение:

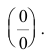
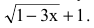
Имеем неопределенность вида Избавимся от иррациональности в числителе, умножив и разделив дробь на сопряженное к числителю выражение Получим:

В остальных случаях для раскрытия неопределенности вида 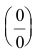используют первый замечательный предел или эквивалентные бесконечно малые функции.

Раскрытие неопределенностей вида

Пусть

Если f(x) — рациональная дробь или дробь, содержащая иррациональности, то числитель и знаменатель делят на х в старшей степени.

Пример №3

Вычислить предел 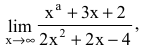если 1) а=2; 2) а=1; 3) а=4.

Решение:

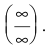
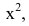
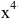
Числитель и знаменатель дроби конечного предела не имеют. Имеем неопределенность вида Для ее раскрытия разделим числитель и знаменатель дроби на высшую степень х (в первом и втором случаях на во третьем — на ), а затем воспользуемся теоремами о пределах функций:

Вывод. Предел рациональной дроби на бесконечности равен отношению коэффициентов при старших степенях, если эти степени совпадают, нулю — если показатель степени числителя меньше показателя степени знаменателя и бесконечности в противном случае.

Замечание. Для раскрытия неопределенностей вида 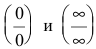используют также правило Лопиталя.

Заказать решение задач по высшей математике

Раскрытие неопределенностей вида

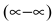
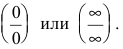
Неопределенное выражение вида преобразуется к неопределенности вида Методику раскрытия такой неопределенности покажем на примерах.

Пример №4

Вычислить предел

Решение:

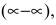
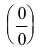
Имеем неопределенность вида которая преобразуется к неопределенности вида приведением функции к общему знаменателю:

Пример №5

Вычислить предел последовательности

Решение:

Для раскрытия неопределенности вида 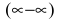умножим и разделим выражение в скобках на сопряженное:

Получили неопределенность вида 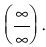Раскроем ее, разделив все члены полученного выражения на n:

Раскрытие неопределенностей вида

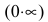
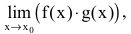
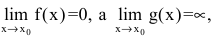
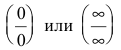
Неопределенное выражение вида получается при нахождении пределов вида где и сводится к неопределенности вида следующим образом:

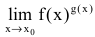
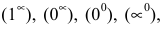
Замечание. При вычислении пределов показательно-степенных функций могут получиться неопределенности вида для раскрытия которых используют второй замечательный предел или правило Лопиталя.

Дробно-рациональные уравнения
Дробно-рациональные неравенства
Прогрессии в математике — арифметическая, геометрическая
Единичная окружность — в тригонометрии
Рациональная дробь
Функция в математике
Наибольшее и наименьшее значения функции
Вычисления в Mathematica с примерами

Источник