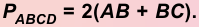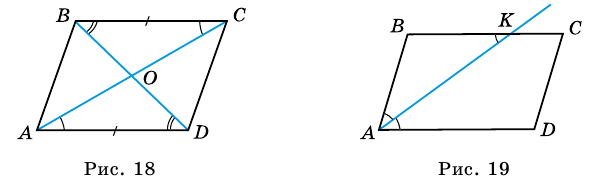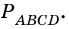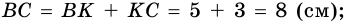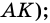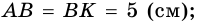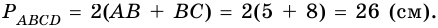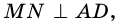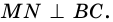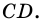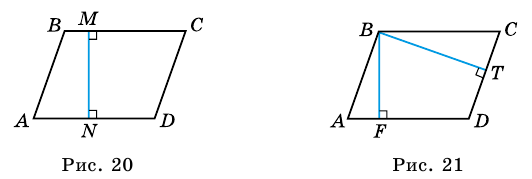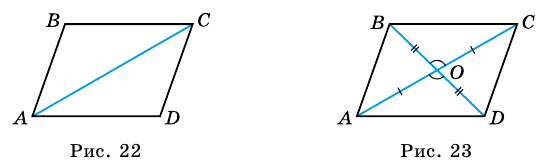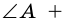Как найти односторонние углы параллелограмма

Углы параллелограмма

Параллелограмм — это геометрическая фигура,
у которой четыре угла и противоположные
стороны попарно параллельны и равны.

Так, как противоположные стороны параллельны,
значит они лежат на параллельных прямых.

Градусные меры противолежащих углов равны.

Сумма двух углов параллелограмма прилежащих к одной
из сторон равна 180 градусам. Внутренние односторонние
углы при параллельных прямых. Это одно из свойств
параллельных прямых для параллелограмма.

Сумма четырех углов параллелограмма — 360 градусов,
как у любого другого четырехугольника.

Формула нахождение углов параллелограмма, если известен только один угол:

Где x, y — два угла при какой-либо стороне.

Частными случаями параллелограмма являются ромб, прямоугольник, квадрат.

Параллелограмм можно условно разделить на два треугольника.
А как мы знаем сумма углов одного треугольника — 180 градусов,
двух — 360 градусов, поэтому сумма углов параллелограмма — 360 градусов.

Свойства сторон и углов параллелограмма

(Свойства сторон и углов параллелограмма)

В параллелограмме противолежащие стороны равны и противолежащие углы равны.

Проведем в параллелограмме ABCD диагональ BD.

Рассмотрим треугольники ABD и CDB.

1) сторона BD — общая

2) ∠ ABD= ∠ CDB (как внутренние накрест лежащие при AB∥CD и секущей BD)

3) ∠ ADB= ∠ CBD (как внутренние накрест лежащие при AD∥BC и секущей BD)

Из равенства треугольников следует равенство соответствующих сторон:

и равенство соответствующих углов:

В пунктах 2) и 3) обосновано, что ∠ ABD= ∠ CDB и ∠ ADB= ∠ CB.

∠ ABC= ∠ ABD+ ∠ CBD= ∠ CDB+ ∠ ADB= ∠ ADC,

Что и требовалось доказать.

II. Свойство углов параллелограмма, прилежащих к одной стороне.

Сумма углов параллелограмма, прилежащих к одной стороне, равна 180º.

Это свойство непосредственно вытекает из того, что углы, прилежащие к одной стороне параллелограмма, являются внутренними односторонними углами при параллельных прямых.

Для параллелограмма ABCD:

∠ A+ ∠ B=180º (как внутренние односторонние при AD∥BC и секущей AB;

∠ C+ ∠ D=180º (как внутренние односторонние при AD∥BC и секущей CD;

∠ A+ ∠ D=180º (как внутренние односторонние при AB∥CD и секущей AD;

∠ B+ ∠ C=180º (как внутренние односторонние при AB∥CD и секущей BC.

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Пусть прямая с пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы и , и — тоже вертикальные.

Углы и — смежные, это мы уже знаем. Сумма смежных углов равна .

Углы и (а также и , и , и ) — накрест лежащие. Накрест лежащие углы равны.

Углы и — односторонние. Они лежат по одну сторону от всей «конструкции». Углы и — тоже односторонние. Сумма односторонних углов равна , то есть

Углы и (а также и , и , и ) называются соответственными.

Соответственные углы равны, то есть

Углы и (а также и , и , и ) называют накрест лежащими.

Накрест лежащие углы равны, то есть

Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.

Ты нашел то, что искал? Поделись с друзьями!

1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .

Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.

Пусть — биссектриса тупого угла . По условию, отрезки и равны и соответственно.

Рассмотрим углы и . Поскольку и параллельны, — секущая, углы и являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник — равнобедренный, следовательно, .

Периметр параллелограмма — это сумма всех его сторон, то есть

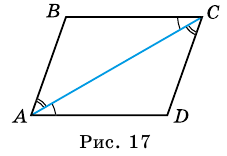
2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.

Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .

3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на чертеж. По условию, , то есть .

Углы и — односторонние при параллельных прямых и секущей, следовательно,

I. Теорема

(Свойства сторон и углов параллелограмма)

В параллелограмме противолежащие стороны равны и противолежащие углы равны.

Дано:

ABCD — параллелограмм.

Доказать:

AB=CD, AD=BC,

∠A=∠C, ∠B=∠D.

Доказательство:

Проведем в параллелограмме ABCD диагональ BD.

Рассмотрим треугольники ABD и CDB.

(Важно правильно назвать треугольники!)

1) сторона BD — общая

2) ∠ABD=∠CDB (как внутренние накрест лежащие при AB∥CD и секущей BD)

3) ∠ADB=∠CBD (как внутренние накрест лежащие при AD∥BC и секущей BD)

Значит,  ∆ABD= ∆CDB (по стороне и двум прилежащим к ней углам).

Из равенства треугольников следует равенство соответствующих сторон:

AB=CD, AD=BC

и равенство соответствующих углов:

∠A=∠C.

В пунктах 2) и 3) обосновано, что ∠ABD=∠CDB и ∠ADB=∠CB.

Следовательно,

∠ABC=∠ABD+∠CBD=∠CDB+∠ADB=∠ADC,

то есть, ∠B=∠D.

Что и требовалось доказать.

II. Свойство углов параллелограмма, прилежащих к одной стороне.

Сумма углов параллелограмма, прилежащих к одной стороне, равна 180º.

Это свойство непосредственно вытекает из того, что углы, прилежащие к одной стороне параллелограмма, являются внутренними односторонними углами при параллельных прямых.

Для параллелограмма ABCD:

∠A+∠B=180º (как внутренние односторонние при AD∥BC и секущей AB;

∠C+∠D=180º (как внутренние односторонние при AD∥BC и секущей CD;

∠A+∠D=180º (как внутренние односторонние при AB∥CD и секущей AD;

∠B+∠C=180º (как внутренние односторонние при AB∥CD и секущей BC.

У параллелограмма 4 угла, это частный случай четырехугольника, у которого противоположные стороны
попарно параллельны. Из этого свойства вытекает равенство противоположных сторон, равенство
противоположных углов и равенство суммы смежных углов двум прямым. Свойства параллелограмма широко
используются в быту и технике.

Острый угол параллелограмма через боковую сторону и высоту

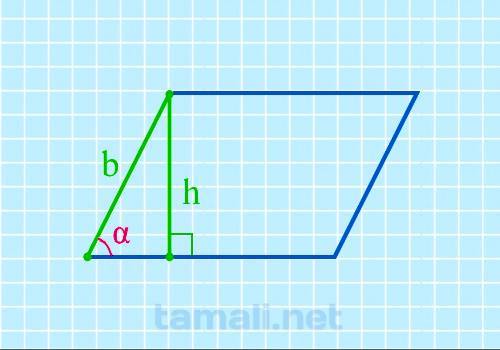
Если известна боковая сторона и высота, то можно найти острый угол параллелограмма по формуле:

sin α = h / b

где α – острый угол, h – высота, b – боковая сторона.

Пример. Пусть h = 4 см, b = 8 см. sin α = h / b = 8 / 4 = 2. α = 90°.

Острый угол параллелограмма через площадь и две стороны

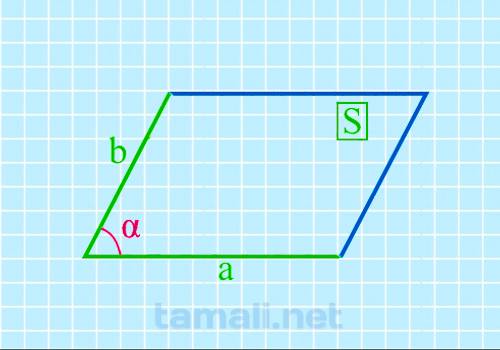
Если известна площадь и две стороны, то можно найти острый угол параллелограмма по формуле:

sin α= S / ab

где α – острый угол, S — площадь параллелограмма, a и b – его стороны.

Пример.  Пусть S=50 м², a=10 м, b=5 м. sin α= S / ab = 50 / (10 * 5) = 1. α = 90°.
Угол прямой, смежные стороны не равны, имеем дело с прямоугольником.

Острый угол параллелограмма через высоту, сторону и периметр

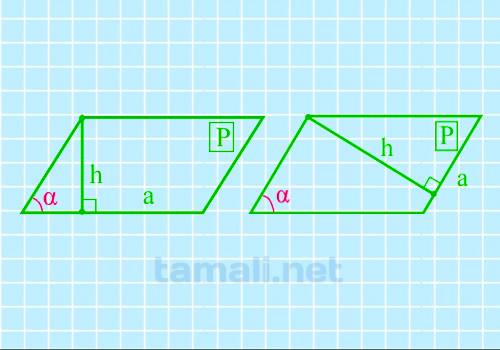
Если известна высота, сторона и периметр, то можно найти острый угол параллелограмма по формуле:

sin α = (2h + a) / P

где α – острый угол, h — высота, a — сторона, P — периметр.

Высота опускается на известную и подставляемую в формулу сторону a. Параллелограмм с заданным
периметром приходится строить, если, например, периметр определен длиной веревки, которую требуется
растянуть на местности в форме параллелограмма.

Пример. Пусть h=10 м, a=15 м, P=70 м. sin α=(2h + a) / P= (2 * 10 + 15) / 70 = 0,5. α = 30°.

Острый угол параллелограмма через две стороны и короткую диагональ

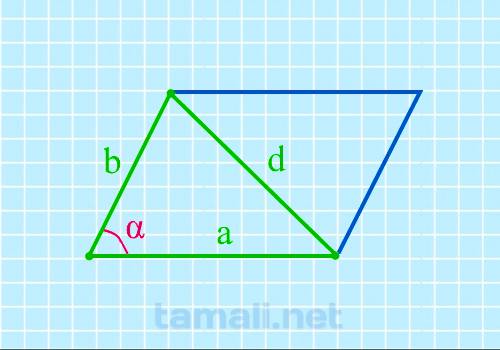
Если известны две стороны и короткая диагональ, то можно найти острый угол параллелограмма по
формуле:

cos α = (a² + b² — d²) / 2ab

где α – острый угол, a и b – стороны параллелограмма, d – его короткая диагональ.

Пример расчета: в данном частном случае 2 прилежащие стороны и короткая диагональ
равны, а именно: a = b = d = 26 мм. cos α=(a² + b² — d²) / 2ab = (26² + 26² — 26²) / (2 * 26 * 26) = 0,5. α=60°.

Из равенства прилежащих сторон следует, что это ромб, а результат расчета показывает, что острый угол
в ромбе равен 60°. Знаете, что это за ромб с подобными размерами? Это нагрудный академический знак
для лиц, окончивших советские высшие учебные заведения, установленный с 1961 года.

Тупой угол параллелограмма через две стороны и длинную диагональ

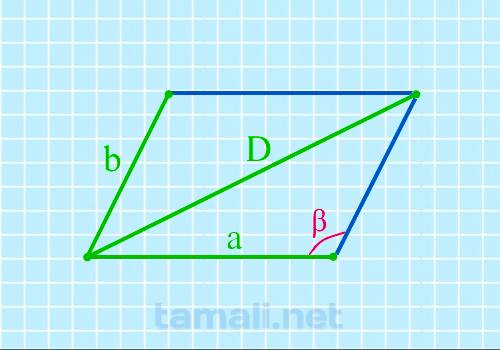
Если известны две стороны и длинная диагональ, то можно найти тупой угол параллелограмма по
формуле:

cos β = (a² + b² — D²) / 2ab

где α – тупой угол, a и b – стороны параллелограмма, D – его длинная диагональ.

Пример расчета: вновь ромб со сторонами a = b = 26 мм и длинной диагональю D=43 мм.
cos β = (a² + b² — D²) / 2ab = (26² + 26² — 43²) / (2 * 26 * 26) = -0,368. α = 112°.
Это опять-таки нагрудный академический знак из предыдущего примера, небольшое отличие полученного
результата от 120° (при остром угле 60° по предыдущему примеру) объясняется округлением исходных
данных до целого числа миллиметров.

Свойства параллелограмма

У любого выпуклого четырехугольника сумма всех внутренних углов равна 360°, исходя из общей формулы
суммы внутренних углов выпуклого многоугольника в градусах s = 180 (n — 2), где n – количество
сторон. Следовательно, если хотя-бы 1 угол параллелограмма равен прямому (90°), остальные 3 угла
также являются прямыми, и параллелограмм вырождается в свой частный вид – прямоугольник.

Если 2 смежные стороны параллелограмма равны, то равны все его 4 стороны, и параллелограмм
вырождается в ромб. И, наконец, если у параллелограмма равны 2 смежные стороны, а угол между ними
прямой, параллелограмм является одновременно и прямоугольником, и ромбом, и вырождается в квадрат.
Зачастую возникает необходимость определения неизвестных характеристик параллелограмма через
известные. Выше ряд примеров подобного рода.

Самый наглядный пример параллелограмма – пантограф электропоезда. При подключении опущенного
пантографа к контактной сети железной дороги изменяется конфигурация пантографа при сохранении длин
сторон, в результате изменяется вертикальная диагональ и происходит касание с подачей электрического
тока.
Форму параллелограмма имеет автомобильный реечный домкрат, велосипедная рама (с
диагональю для увеличения жесткости). Ведь параллелограмм — фигура нежесткая, в отличие от
треугольника. Из нежесткости параллелограмма следует, что знания одних длин сторон недостаточно для
вычисления площади фигуры. Так, пантограф электропоезда можно «сложить» до нулевой площади.
Стеклоочиститель лобового стекла автобуса также представляет собой параллелограмм, и именно
нежесткость фигуры позволяет стеклоочистителю «ометать» при движении стекло.

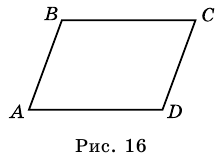
Параллелограммом называют четырехугольник, у которого противолежащие стороны попарно параллельны.

На рисунке 16 изображен параллелограмм

Рассмотрим свойства параллелограмма.

1. Сумма двух любых соседних углов параллелограмма равна 180°.

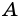
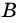
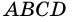
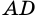
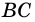
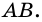
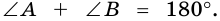
Действительно, углы  и параллелограмма (рис. 16) являются внутренними односторонними углами для параллельных прямых и и секущей Поэтому Аналогично это свойство можно доказать для любой другой пары соседних углов параллелограмма. 

2. Параллелограмм является выпуклым четырехугольником.

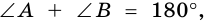
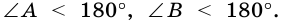
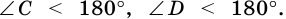
Так как то Аналогично  Поэтому параллелограмм — выпуклый четырехугольник. 

3. В параллелограмме противолежащие стороны равны и противолежащие углы равны.

Доказательство:

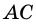
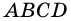
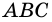
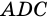
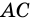
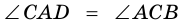
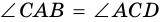
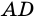
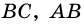
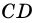
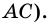
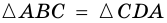
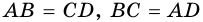
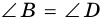
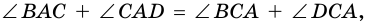
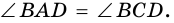
Диагональ разбивает параллелограмм на два треугольника и (рис. 17). -их общая сторона, и (как внутренние накрест лежащие углы для каждой из пар параллельных прямых  и и и секущей Тогда (по стороне и двум прилежащим углам). Откуда, и (как соответственные элементы равных треугольников). Так как то  

4. Периметр параллелограмма

5. Диагонали параллелограмма точкой пересечения делятся пополам.

Доказательство:

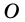
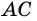
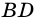
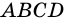
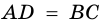
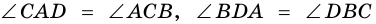
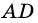
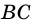
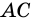
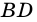
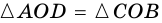
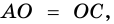
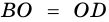
Пусть — точка пересечения диагоналей и параллелограмма (рис. 18). (как противолежащие стороны параллелограмма), (как внутренние накрест лежащие углы для параллельных прямых и и секущих и соответственно). Следовательно, (по стороне и двум прилежащим углам). Тогда   (как соответственные стороны равных треугольников). 

Пример:

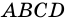
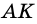
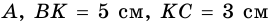
Дано: параллелограмм, — биссектриса угла (рис. 19). Найдите:

Решение:

1)

2)  (как внутренние накрест лежащие углы для параллельных прямых и и секущей

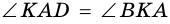
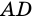
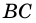
3)  (по условию), тогда Тогда — равнобедренный (по признаку равнобедренного треугольника),

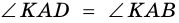
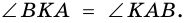
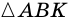
4) 

Ответ. 26 см.

Высотой параллелограмма называют перпендикуляр, проведенный из любой точки стороны параллелограмма к прямой, содержащей противолежащую сторону.

На рисунке 20 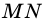— высота параллелограмма,

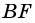
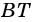
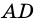
Из каждой вершины параллелограмма можно провести две высоты. Например, на рисунке 21 и — высоты параллелограмма, проведенные соответственно к сторонам и

Рассмотрим признаки параллелограмма.

Теорема (признаки параллелограмма). Если в четырехугольнике: 1) две стороны параллельны и равны, или 2) противолежащие стороны попарно равны, или 3) диагонали точкой пересечения делятся пополам, или 4) противолежащие углы попарно равны, — то четырехугольник является параллелограммом.

Доказательство:

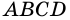
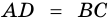
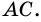
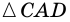
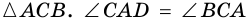
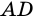
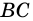
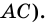
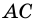
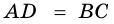
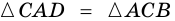
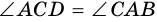
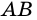
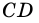
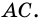
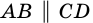
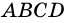
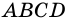
1) Пусть в четырехугольнике   и (рис. 22). Проведем диагональ Рассмотрим и  (как внутренние накрест лежащие при параллельных прямых  и и секущей — общая сторона, (по условию). Следовательно, (по двум сторонам и углу между ними). Тогда (как соответственные). Но это накрест лежащие углы при пересечении прямых и секущей Поэтому (по признаку параллельности прямых). Следовательно, в четырехугольнике противолежащие стороны попарно параллельны. Поэтому -параллелограмм.

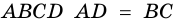
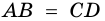
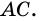
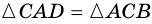
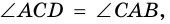
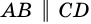
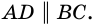
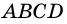
2) Пусть в четырехугольнике и (рис. 22). Проведем диагональ Тогда (по трем сторонам). Поэтому и следовательно, (по признаку параллельности прямых). Аналогично доказываем, что Следовательно, — параллелограмм.

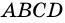
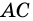
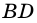
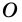
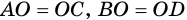
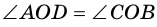
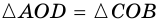
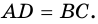
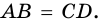
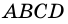
3) Пусть в четырехугольнике диагонали и пересекаются в точке и (рис. 23). (как вертикальные). Поэтому (по двум сторонам и углу между ними). Отсюда Аналогично доказываем, что Принимая во внимание п. 2) этой теоремы, приходим к выводу, что — параллелограмм.

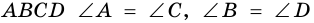
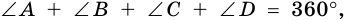
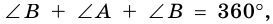
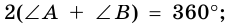
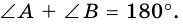
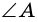
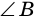
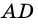
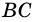
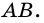
4) Пусть в параллелограмме (рис. 16). Так как  то  т. е.  откуда Но и — внутренние накрест лежащие углы для прямых и и секущей Поэтому

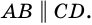
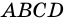
по признаку параллельности прямых). Аналогично доказываем, что Следовательно,  — параллелограмм. 

Пример:

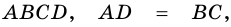
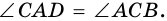
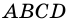
В четырехугольнике  Докажите, что — параллелограмм.

Доказательство:

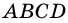
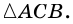
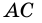
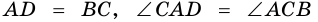
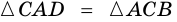
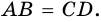
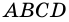
Пусть — данный четырехугольник (рис. 22). Рассмотрим  и — их общая сторона, (по условию). Тогда, (по двум сторонам и углу между ними). Следовательно, Но тогда в четырехугольнике противолежащие стороны попарно равны, поэтому он является параллелограммом. 

A еще раньше…

О некоторых видах четырехугольников (квадраты, прямоугольники, равнобокие и прямоугольные трапеции) знали еще древнеегипетские и вавилонские математики.

Термин «параллелограмм» греческого происхождения, считают, что он был введен Евклидом (около 300 г. до н. э.). Также известно, что еще раньше о параллелограмме и некоторых его свойствах уже знали ученики школы Пифагора («пифагорейцы»).

В «Началах» Евклида доказана следующая теорема: в параллелограмме противолежащие стороны равны и противолежащие углы равны, а диагональ делит его пополам, но не упоминается о том, что точка пересечения диагоналей параллелограмма делит каждую из них пополам.

Евклид также не упоминает ни о прямоугольнике, ни о ромбе.

Полная теория параллелограммов была разработана лишь в конце Средневековья, а в учебниках она появилась в XVII в. Все теоремы и свойства параллелограмма в этих учебниках основывались на аксиоме параллельности Евклида.

Термин «диагональ» — греческого происхождения; «диа» означает «через», а «гониос» — «угол», что можно понимать как отрезок, соединяющий вершины углов.

Следует отметить, что Евклид, как и большинство математиков того времени, для названия отрезка, соединяющего противолежащие вершины четырехугольника, в частности прямоугольника, употреблял другой термин — «диаметр». Это можно объяснить тем, что первые геометры свои рассуждения основывали на вписанных в окружность прямоугольниках. В Средние века для названия упомянутого отрезка использовали оба термина. Лишь в XVIII в. термин «диагональ» стал общепринятым.