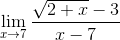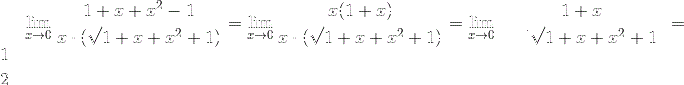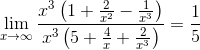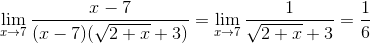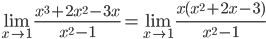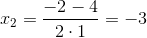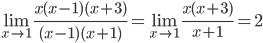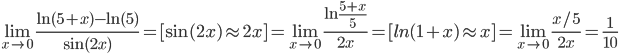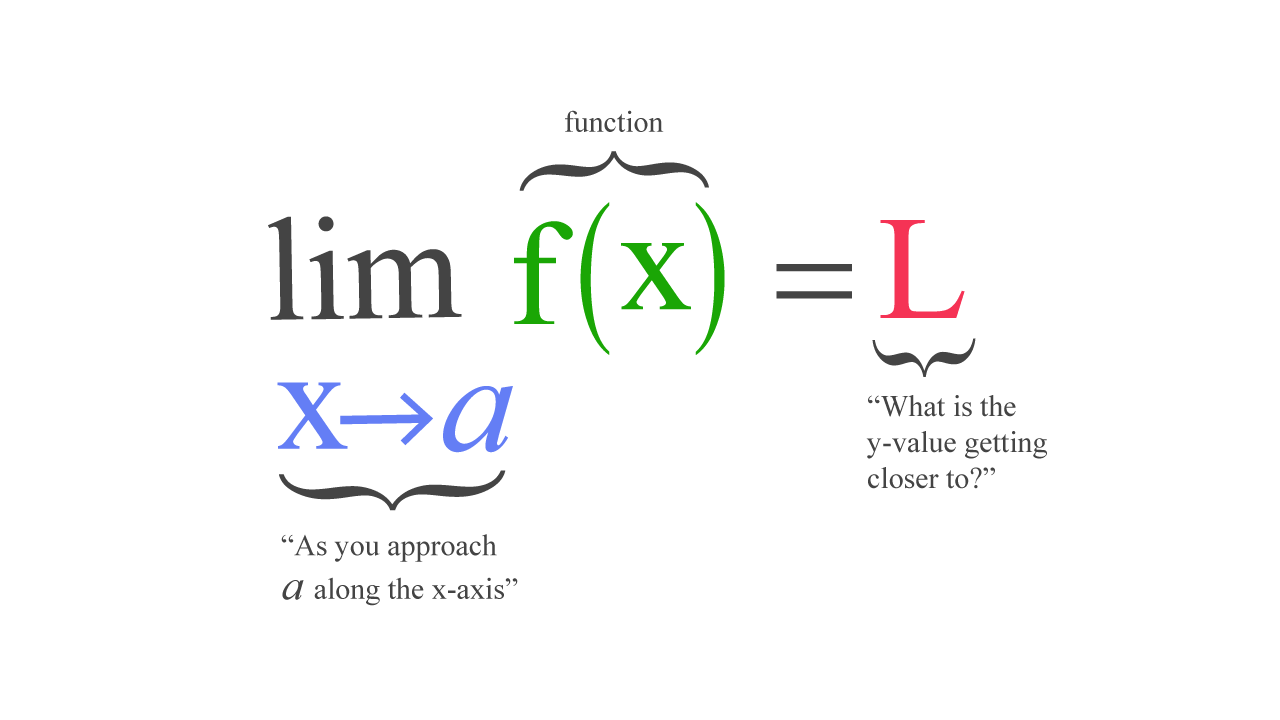| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
lim _{xto 0+}(frac{1}{x})
-
lim _{xto 5-}(frac{10}{x-5})
-
lim _{xto 1-}(frac{x}{x-1})
-
lim _{xto -2+}(frac{1}{x+2})
- Показать больше
Описание
Пошаговое решение односторонних лимитов
one-sided-limit-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Advanced Math Solutions – Limits Calculator, Functions with Square Roots
In the previous post, we talked about using factoring to simplify a function and find the limit. Now, things get…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Предел функции при ( x to x_0 )
Пусть функция ( f(x) ) определена на некотором множестве (X) и пусть точка ( x_0 in X ) или ( x_0 notin X )
Возьмем из (X) последовательность точек, отличных от (x_0) :
(x_1 ;, ; x_2 ;, ; x_3 ;, …, ; x_n ; , ; … tag{1} )
сходящуюся к (x^*).
Значения функции в точках этой последовательности также образуют числовую последовательность
( f(x_1) ;, ; f(x_2) ;, ; f(x_3) ;, …, ; f(x_n) ; , ; … tag{2} )
и можно ставить вопрос о существовании ее предела.
Определение. Число (A) называется пределом функции (f(x)) в точке ( x = x_0 ) (или при ( x to x_0 ) ), если для
любой сходящейся к (x_0) последовательности (1) значений аргумента (x), отличных от (x_0) соответствующая
последовательность (2) значений функции сходится к числу (A).
Символически это записывается так:
$$ lim_{xto x_0}{ f(x)} = A $$
Функция (f(x)) может иметь в точке (x_0) только один предел. Это следует из того, что последовательность ( left{ f(x_n) right} )
имеет только один предел.
Существует другое определение предела функции.
Определение Число (A) называется пределом функции (f(x)) в точке (x_0), если для любого числа ( varepsilon > 0 )
существует число ( delta > 0 ) такое, что для всех ( x in X, ; x neq x_0 ), удовлетворяющих неравенству ( |x-x_0| < delta ),
выполняется неравенство ( |f(x)-A| < varepsilon )
Используя логические символы, это определение можно записать в виде
( (forall varepsilon > 0) (exists delta > 0) (forall x in X, ; x neq x_0, ; |x-x_0| < delta): |f(x)-A| < varepsilon )
Отметим, что неравенства ( x neq x_0, ; |x-x_0| < delta ) можно записать в виде ( 0 < |x-x_0| < delta )
<>Первое определение основано на понятии предела числовой последовательности, поэтому его часто называют определением
«на языке последовательностей».
Второе определение называют определением «на языке ( varepsilon — delta )».
Эти два определения предела функции эквивалентны и можно использовать любое из них в зависимости от того, какое более
удобно при решении той или иной задачи.
Заметим, что определение предела функции «на языке последовательностей» называют также определением предела функции по Гейне,
а определение предела функции «на языке ( varepsilon — delta )» — определением предела функции по Коши.
Предел функции при ( x to x_{0-} ) и при ( x to x_{0+} )
В дальнейшем будут использованы понятия односторонних пределов функции, которые определяются следующим образом.
Определение Число (A) называется правым (левым) пределом функции (f(x)) в точке (x_0), если для любой сходящейся
к (x_0) последовательности (1), элементы (x_n) которой больше (меньше) (x_0), соответствующая
последовательность (2) сходится к (A).
Символически это записывается так:
$$ lim_{x to x_{0+}} f(x) = A ; left( lim_{x to x_{0-}} f(x) = A right) $$
Можно дать равносильное определение односторонних пределов функции «на языке ( varepsilon — delta )»:
Определение число (A) называется правым (левым) пределом функции (f(x)) в точке (x_0), если для любого
( varepsilon > 0 ) существует ( delta > 0 ) такое, что для всех (x), удовлетворяющих неравенствам
( x_0 < x < x_0 + delta ; (x_0 -delta < x < x_0 ) ) , выполняется неравенство ( |f(x)-A| < varepsilon ).
Символические записи:
( (forall varepsilon > 0) (exists delta > 0) (forall x, ; x_0 < x < x_0 + delta ): |f(x)-A| < varepsilon )
( (forall varepsilon > 0) (exists delta > 0) (forall x, ; x_0 -delta < x < x_0 ): |f(x)-A| < varepsilon )
Связь между односторонними пределами и пределом функции устанавливает следующая теорема.
Теорема
Функция (f(x)) имеет в точке (x_0) предел тогда и только тогда, когда в этой точке существуют как правый, так и левый пределы,
и они равны. В этом случае предел функции равен односторонним пределам.
Предел функции при ( x to infty ), при ( x to -infty ) и при ( x to +infty )
Кроме рассмотренных понятий предела функции при ( x to x_0 ) и односторонних пределов существует также понятие предела функции
при стремлении аргумента к бесконечности.
Определение. Число (A) называется пределом функции (f(x)) при ( x to infty ), если для любой бесконечно большой
последовательности (1) значений аргумента соответствующая последовательность (2) значений функции сходится к (A).
Символическая запись:
$$ lim_{x to infty} f(x) = A $$
Определение. Число (A) называется пределом функции (f(x)) при ( x to +infty ; (x to -infty) ) , если для любой бесконечно
большой последовательности значений аргумента, элементы (x_n) которой положительны (отрицательны), соответствующая
последовательность значений функции сходится к (A).
Символическая запись:
$$ lim_{x to +infty} f(x) = A ; left( lim_{x to -infty} f(x) = A right) $$
Теоремы о пределах функций
Определение предела функции «на языке последовательностей» дает возможность перенести доказанные выше теоремы о пределах
последовательностей на функции. Покажем это на примере двух теорем.
Теорема. Пусть функции (f(x)) и (g(x)) имеют в точке (x_0) пределы (B) и (C). Тогда функции ( f(x) pm g(x) ; , ; f(x) cdot g(x) ) и
( frac{f(x)}{g(x)} ) (при ( C neq 0 ) ) имеют в точке (x_0) пределы, равные соответственно ( B pm C ; , ; B cdot C ), и ( frac{B}{C} ).
Теорема. Пусть функции ( f(x) ; , ; g(x) ) и ( h(x) ) определены в некоторой окрестности точки (x_0), за исключением, быть
может, самой точки (x_0), и функции ( f(x) ; , ; h(x) ) имеют в точке (x_0) предел, равный (A), т.е.
$$ lim_{x to x_0} f(x) = lim_{x to x_0} h(x) = A $$
Пусть, кроме того, выполняются неравенства ( f(x) leqslant g(x) leqslant h(x) ).
Тогда $$ lim_{x to x_0} g(x) = A $$
Теорема Лопиталя. Если $$ lim_{x to x_0} f(x) = lim_{x to x_0} g(x) = 0 $$ или (infty ), (f(x)) и (g(x))
дифференцируемы в окрестности (x_0) , и ( g'(x) neq 0 ) в окрестности (x_0) ,
и существует $$ lim_{x to x_0} frac{f'(x)}{g'(x)} $$ то существует $$ lim_{x to x_0} frac{f(x)}{g(x)} = lim_{x to x_0} frac{f'(x)}{g'(x)} $$
Т.е. теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Теорема Лопиталя позволяет раскрывать неопределённости вида ( frac{0}{0} ) и ( frac{infty}{infty} ).
Первый замечательный предел
$$ lim_{x to 0} frac{sin x}{x} = 1 $$
Второй замечательный предел
$$ lim_{x to infty} left( 1+ frac{1}{x} right)^x = e $$
Решение пределов
Число A называется пределом функции y=f(x) в точке x0, если для любой последовательности точек из области определения функции, отличных от x0, сходящейся к точке x0(lim xn = x0), последовательность соответствующих значений функции сходится к числу A.
- Решение онлайн
- Видеоинструкция
- Оформление Word
- Также решают
Если выбрать вид предела, то подробное решение по шагам будет доступно в MS Word:
1. Не знаю
2. Пределы вида 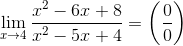
3. Вычислить предел, используя правило Лопиталя.
4. Пределы простейших иррациональности вида
5. Нахождение пределов, используя свойства первого замечательного предела ,
6. Нахождение пределов, используя свойства второго замечательного предела ,
,
Для нахождения предела слева
используйте знак -, справа
: +. Например, 0-, 1+
Примечание: число «пи» (π) записывается как pi, знак ∞ как infinity
Некоторые виды записи пределов
Например, найти предел 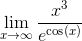
см. также нахождение пределов, используя свойства первого замечательного предела и второго замечательного предела.
Примеры.
Вычислить указанные пределы:
1. 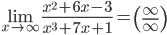
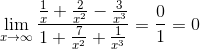
2. 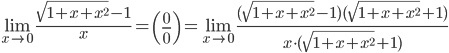
3. 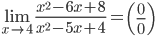
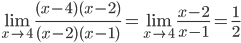
4. 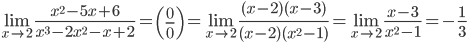
5. 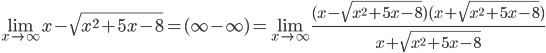
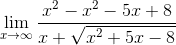
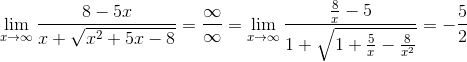
6. 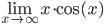
7. 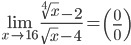
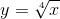
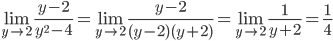
8. 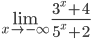
9. 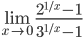
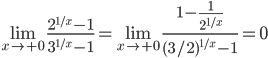
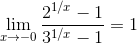
Следовательно, 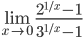
Найти пределы функции, не применяя правило Лопиталя.
а)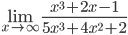
Ответ: 1/5
б) 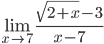
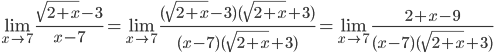
Ответ: 1/6
в) 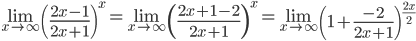
e-2/2 = e-1
Ответ: 1/e
г)
Так как числитель и знаменатель обратились в нуль при x=1, то 1 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x-1).
Найдем корни первого многочлена: x2+2x-3=0
D=22-4•1•(-3)=16
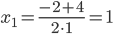
Найдем корни второго многочлена: x2-1=(x-1)(x+1)
Получаем:
Ответ: 2
д) 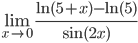
Ответ: 1/10
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Калькулятор лимита с шагами
онлайн калькулятор пределов поможет вам найти предел функции по отношению к переменной. Это онлайн-инструмент, который помогает вам вычислять значение функции, когда вход приближается к определенному значению.
Калькулятор пределов с шагами показывает пошаговое решение пределов вместе с графиком и расширением ряда. Он использует все предельные правила, такие как сумма, произведение, частное и правило Лопиталя, для расчета точного значения.
Вы можете оценить пределы относительно (text{x, y, z, v, u, t}) и (w) с помощью этого калькулятора пределов.
Это не то. С помощью этого инструмента вы также можете найти,
- Правый предел (+)
- Левый предел (-)
- двусторонний предел
Как работает калькулятор лимитов?
Чтобы оценить предел с помощью этого решателя пределов, выполните следующие шаги.
- Введите функцию в данное поле ввода.
- Выберите соответствующую переменную.
- Введите предельное значение.
- Выберите сторону ограничения. т. е. левое, правое или двустороннее.
- Нажмите кнопку «Рассчитать», чтобы получить результат.
- Используйте кнопку «Сброс», чтобы ввести новые значения, и значок клавиатуры , чтобы ввести дополнительные значения.
Вы найдете ответ под инструментом. Нажмите «Показать шаги», чтобы просмотреть пошаговое решение.
Что такое предел в исчислении?
Предел функции — это значение, к которому f(x) приближается по мере приближения x к некоторому числу. Пределы можно использовать для определения производных, интегралов и непрерывности, находя предел данной функции. Это написано как:
Если f — функция с действительным знаком, а a — действительное число, то приведенное выше выражение читается как
предел f x, когда x приближается к a, равен L.
Как найти предел? – со ступеньками
Пределы могут применяться в виде чисел, постоянных значений (π, G, k), бесконечности и т. д. Давайте рассмотрим несколько примеров, чтобы узнать, как оценивать пределы.
Пример — правый предел
(lim _{xto :2^+}frac{left(x^2+2right)}{left(x-1right)})
Решение:
Правый предел – это предел функции по мере ее приближения с правой стороны.
Шаг 1: Примените ограничение x➜2 к приведенной выше функции. Поместите предельное значение вместо x.
(lim :_{xto 2^+}frac{left(x^2+2right)}{left(x-1right)})
(=frac{left(2^2+2right)}{left(2-1right)})
Шаг 2: Решите уравнение, чтобы получить результат.
(=frac{left(4+2right)}{left(2-1right)} =frac{6}{1} =6 )
Шаг 3: Запишите выражение с его ответом.
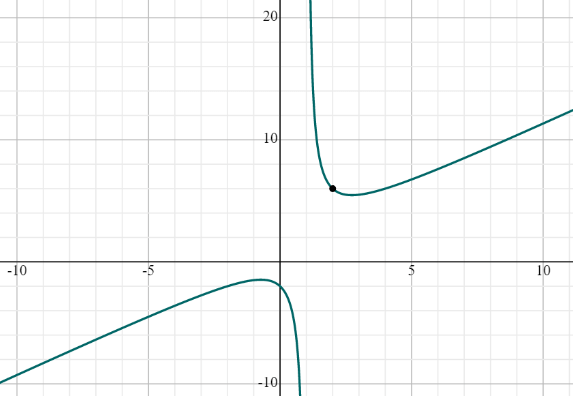
(lim :_{xto ::2^+}frac{left(x^2+2right)}{left(x-1right)}=6)
График
Пример — левосторонний предел
(lim _{xto 3^-}left(frac{x^2-3x+4}{5-3x}right))
Решение:
Левый предел означает предел функции по мере ее приближения с левой стороны.
Шаг 1: Поместите предельное значение в функцию.
(lim _{xto 3^-}left(frac{x^2-3x+4}{5-3x}right))
(=frac{left(3^2-3left(3right)+4right)}{left(5-3left(3right)right)})
Шаг 2: Решите уравнение дальше.
(=frac{left(9-9+4right)}{left(5-9right)})
(=frac{left(0+4right)}{left(-4right)} =frac{4}{-4} =-1 )
Шаг 3: Запишите функцию, как написано ниже.
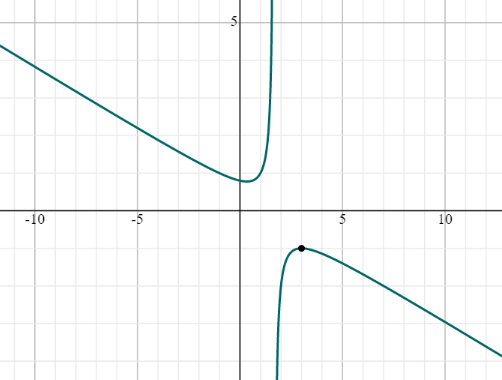
(lim :_{xto :3^-}left(frac{x^2-3x+4}{5-3x}right)=-1)
График
Пример — двусторонний лимит
( lim _{xto 5}left(cos^3left(xright)cdot sinleft(xright)right) )
Решение:
Двусторонний предел существует, если предел, идущий с обоих направлений (положительного и отрицательного), одинаков. Это то же самое, что лимит.
Шаг 1: Подставьте значение limit в функцию.
(lim _{xto 5}left(cos^3left(xright)cdot sinleft(xright)right))
(=cos^3left(5right)cdot :sinleft(5right))
Шаг 2: Упростите уравнение, как мы это делали в предыдущих примерах.
( lim _{xto 5}left(cos^3left(xright)cdot sinleft(xright)right) )
( =cos^3left(5right):sinleft(5right))
Шаг 3: Приведенное выше уравнение можно рассматривать как окончательный ответ. Однако, если вы хотите решить его дальше, решите тригонометрические значения в уравнении.
(=frac{1141}{50000}cdot :-frac{23973}{25000} =-frac{10941}{500000} )
(lim ::_{xto ::5}left(cos^3left(xright)cdot ::sinleft(xright)right))
(=-0.021882 )
График
Часто задаваемые вопросы
Есть ли у sin x предел?
Грех x не имеет предела. Это связано с тем, что по мере приближения x к бесконечности значение y колеблется между 1 и −1.
Каков предел e до бесконечности?
Предел e до бесконечности (∞) равен e.
Каков предел, когда e^x приближается к 0?
Предел, когда e^x приближается к 0, равен 1.
Каков предел, когда x приближается к бесконечности ln(x)?
Предел ln(x) при стремлении x к бесконечности равен +∞. Предел этого натурального логарифма может быть доказан доведением до абсурда.
- Если x >1ln(x) > 0, предел должен быть положительным.
- Поскольку ln(x2) − ln(x1) = ln(x2/x1). Если x2>x1, разность положительна, поэтому ln(x) всегда возрастает.
- Если lim x→∞ ln(x) = M ∈ R, мы имеем ln(x) < M ⇒ x < eM, но x→∞, поэтому M не может находиться в R, и предел должен быть +∞.
Предел по-шагам

Примеры пределов
- Пределы от рациональных дробей на бесконечности
-
(x - 1)/(x + 1)
-
(x^3 + 2*x - 1)/(-7*x^3 - 4*x^2)
- Пределы от рациональных дробей в конечной точке
-
(x - 1)/(sqrt(x) - 1)
- Пределы от дроби в нуле
-
log(x)/x
- Первый замечательный предел
-
sin(7*x)/x
-
(1 - cos(x)^2)/x^2
- Второй замечательный предел
-
(1 - 7/x)^x
-
(1 + x/2)^((5*x + 3)/x)
- Пределы с квадратными корнями
-
sqrt(x + 5) - sqrt(x + 2)
-
x - sqrt(x^2 - 7)
- Правило Лопиталя
-
(e^(x) - x^e)/(x - e)
-
log(1+2*x^2)/x
Что умеет калькулятор пределов?
- Детальное решение для указанных методов:
- Правило Лопиталя
- Теорема о двух милиционерах
- Второй замечательный предел
- Разложение функции на множители
- Использование замены
- Первый замечательный предел
- Типы пределов:
- От одной переменной
- На бесконечности
- Односторонние пределы
- Строит график функции и её предела
- Предлагает другие пределы
Подробнее про Предел функции
.
Указанные выше примеры содержат также:
- модуль или абсолютное значение: absolute(x) или |x|
-
квадратные корни sqrt(x),
кубические корни cbrt(x) -
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
-
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x) -
натуральные логарифмы ln(x),
десятичные логарифмы log(x) -
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x) -
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x) -
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x) -
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x) -
знак числа:
sign(x) -
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x) -
Факториал от x:
x! или factorial(x) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
-
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)
Правила ввода
Можно делать следующие операции
- 2*x
- — умножение
- 3/x
- — деление
- x^2
- — возведение в квадрат
- x^3
- — возведение в куб
- x^5
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- Действительные числа
- вводить в виде 7.5, не 7,5
Постоянные
- pi
- — число Пи
- e
- — основание натурального логарифма
- i
- — комплексное число
- oo
- — символ бесконечности