4.4
Средняя оценка: 4.4
Всего получено оценок: 202.
4.4
Средняя оценка: 4.4
Всего получено оценок: 202.
В этой статье мы разберем в подробностях, как найти каждую из сторон прямоугольника. Посмотрим, какие ситуации возможны в задачах и разберем самые трудные и интересные из задач.
Длины прямоугольника
Очень часто понятия длины и ширины путаются. Некоторые источники утверждают, что вертикальные стороны прямоугольника – это ширина. Но это редкость, обычно длиной называется большая сторона прямоугольника, а шириной меньшая.
Для лучшего восприятия стоит располагать фигуру так, чтобы длина находилась в основании, а боковые стороны имели размеры ширины. Так будет проще решать задачи.
Перед тем, как перейти непосредственно к решению задач, нужно повторить несколько фактов, которые облегчат решение:
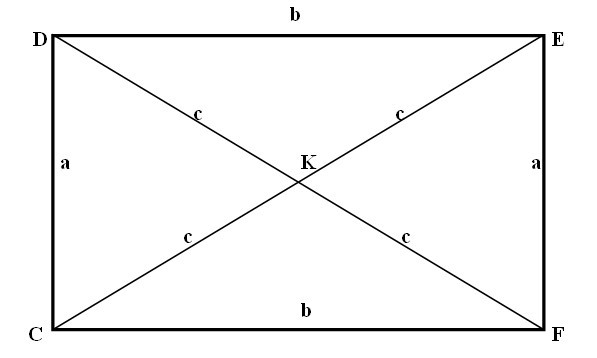
- Диагонали прямоугольника равны.
- Диагонали точкой пересечения делятся пополам.
- Диагонали прямоугольника делят прямоугольник на 4 равнобедренных треугольника, которые равны между собой.
Примеры решения задач
Решим задачу, связанную с формулами вычисления сторон прямоугольника. Рассмотрим несколько вариантов нахождения длин сторон при различных известных параметрах.
Задача 1
- Известно, что площадь прямоугольника равна 21, а периметр 20. Найти стороны прямоугольника.
Такая задача содержит две неизвестных. Величины сторон a и b. Чтобы найти оба значения необходимо составить систему уравнений:
$(a+b)*2=P$ (уравнение нахождения периметра как суммы сторон фигуры)
$a*b=S$ (уравнение для нахождения площади)
При наличии двух неизвестных для решения системы необходимо наличие двух уравнений. Поэтому невозможно найти стороны прямоугольника, зная только площадь или только периметр.
Продолжим решение. Выразим значение a из первого выражения системы.
- $(а+b)*2=Р$
- $а+b={Рover{2}}$
- $а={Рover{2}}-b$
- Подставим значение периметра: $а={20over{2}}-b=10-b$
Подставим получившееся выражение в уравнение нахождения площади:
$a*b=S$
$(10-b)*b=21$
$b^2-10b-21=0$
Это квадратное уравнение. Решим его с помощью теоремы Виета. Такое уравнение будет иметь два корня. Сумма корней будет равна 10, а произведение 21. Такое возможно при значении корней 3 и 7, так как это единственные числа, подходящие под данные условия.
$а=10-b$
Значит, при $b=3$, $а=10-3=7$
При $b=7$, $a=10-7=3$. То есть в любом случае, стороны будут равны 7 и 3. Это и есть ответ задачи.
Задача 2
- Известно, что сторона прямоугольника равна 16, а диагональ 20. Найти другую сторону прямоугольника.
Задача решается теоремой Пифагора. Диагональ делит прямоугольник на два равных прямоугольных треугольника. В таком треугольнике нам известна гипотенуза (20) и катет (16).
Сумма квадратов катетов равняется квадрату гипотенузы. Искать будем сторону а, предположив, что известная нам сторона это сторона b.
$D^2=a^2+b^2$
$A^2=d^2-b^2$
$а^2=400-256=144$
Корень квадратный из 144 равен 12. Это и есть ответ к задаче.
Задача 3
- Известно, что прямоугольник представляет собой ромб. Площадь ромба равна 25, необходимо найти все стороны четырехугольника.
У прямоугольника все углы прямые, а у ромба все стороны между собой равны. Значит, четырехугольник, который одновременно является и ромбом, и прямоугольником это фигура с 4 прямыми углами и сторонами, равными между собой. Такой фигурой может быть только квадрат.
Стороны квадрата равны, значит нас интересует одно значение. Площадь квадрата это значение стороны, возведенное в квадрат.
$а^2=S$
$а^2=25$
$а=5$
Что мы узнали?
Мы узнали, как найти длины прямоугольника. Рассмотрели различные типовые ситуации и научились решать задачи, связанные с нахождением длин прямоугольника.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 202.
А какая ваша оценка?
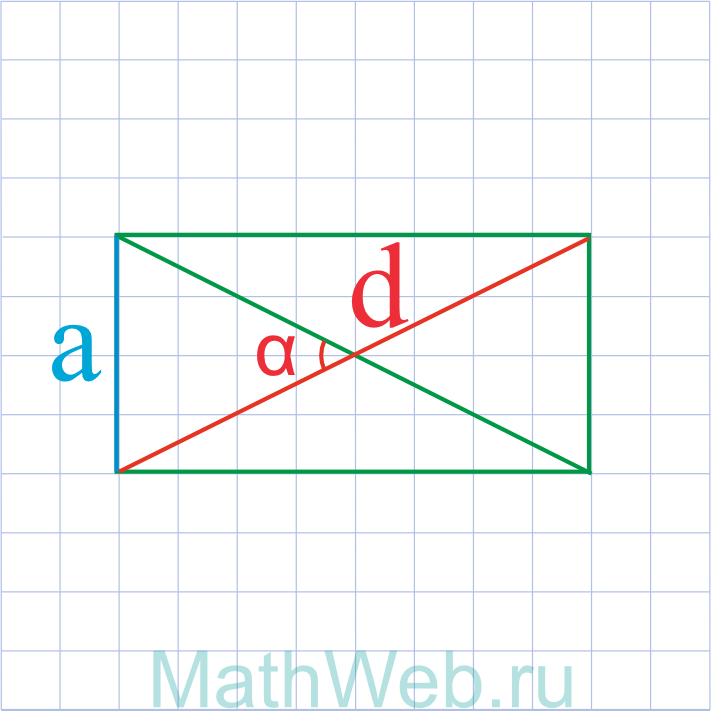
Где d — диагональ,b — сторона.
Где d — диагональ,α — угол между диагональю и искомой стороной.
Где d — диагональ,α — угол между диагональю и другой стороной.
Где S — площадь, b— известная сторона.
Где P — периметр, b — известная сторона.
Где d — диагональ, α — угол между диагоналями.
- Прямоугольник — это четырехугольник у которого противоположные стороны равны и параллельны AB = CD и BC = DA.
- Стороны прямоугольника являются его высотами.
- Между прилегающими сторонами угол всегда 90°.
Как найти длину стороны прямоугольника?
Сторона прямоугольника может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
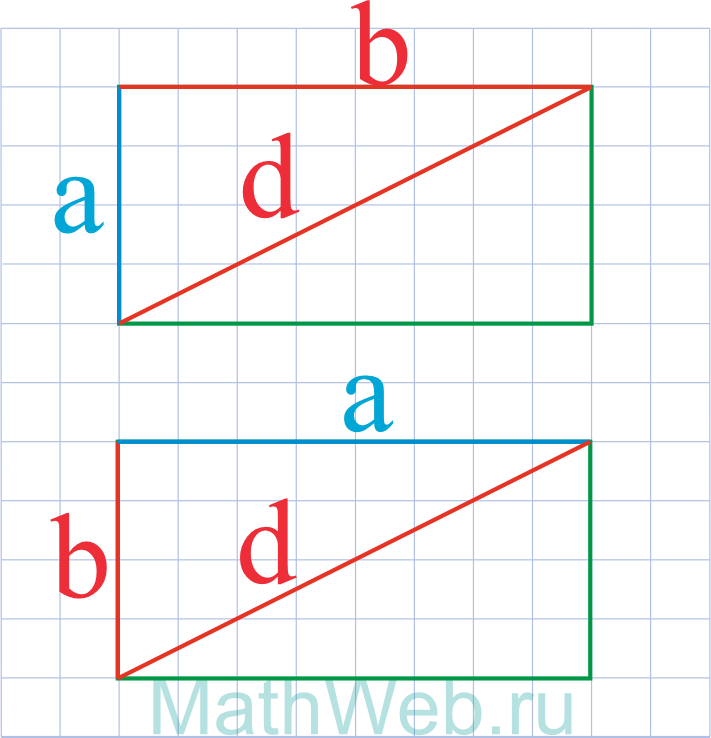 |
a = √d2 ― b2 |
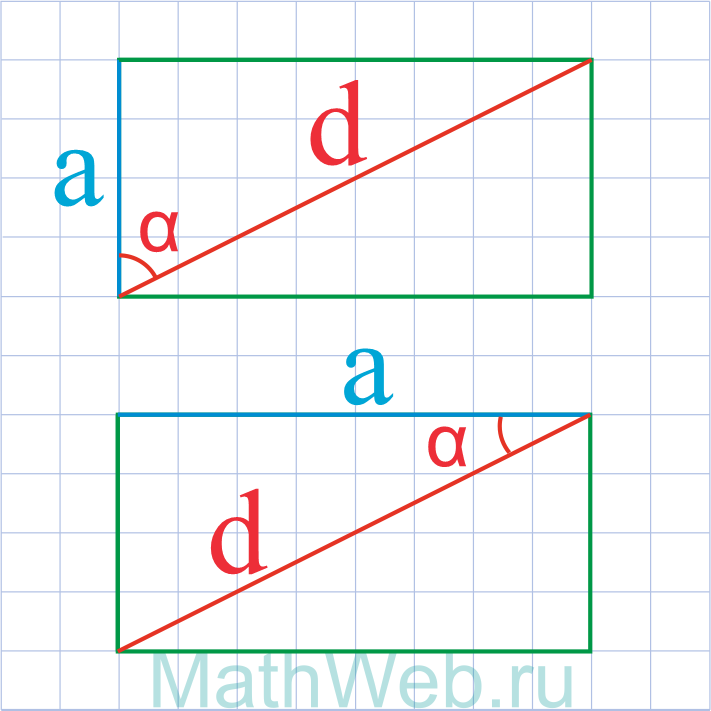 |
a = d·cos(α) |
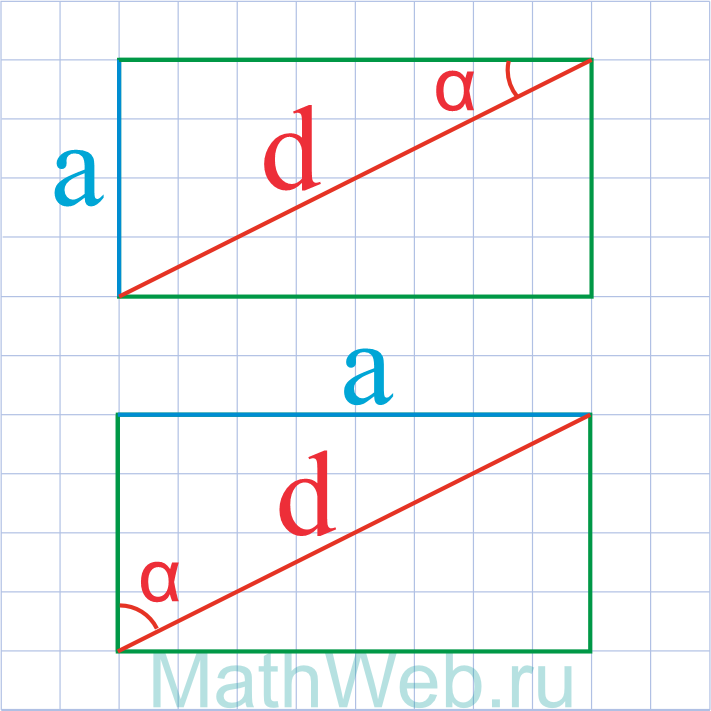 |
a = d·sin(α) |
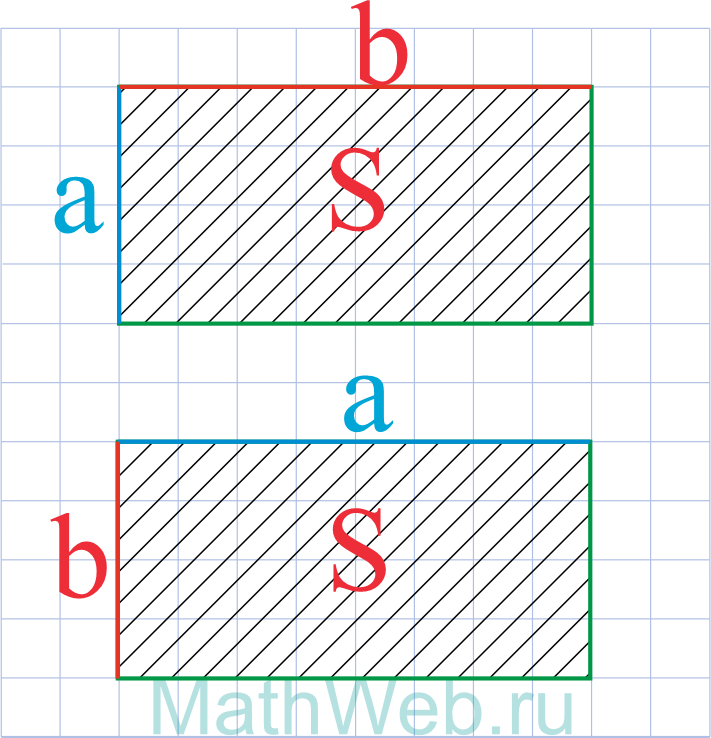 |
a = S b |
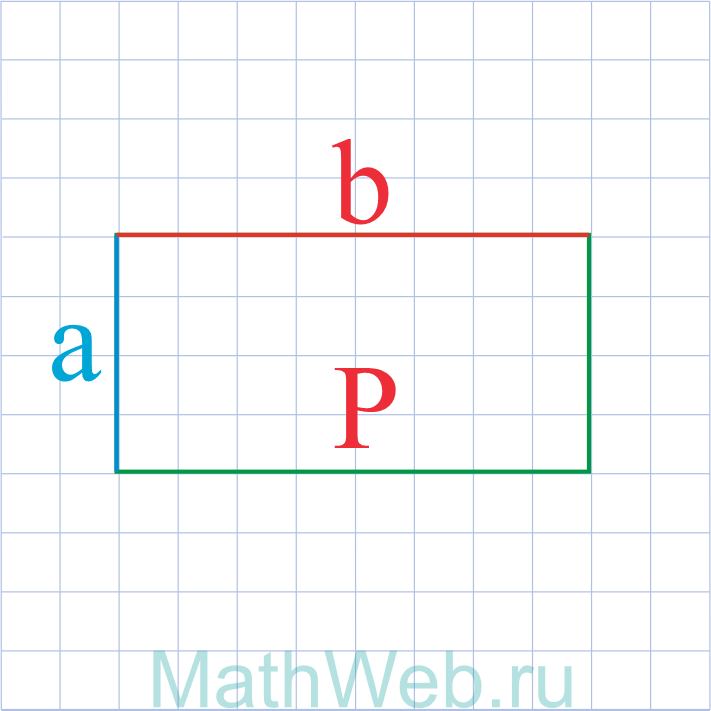 |
a = P — 2b 2 |
 |
a = d·sin(0.5·α) |
Периметр любого прямоугольника составляет 2а+2с. То есть сумме удвоенных произведений противоположных сторон. Кроме того, по свойствам прямоугольника известно, что у него противоположные стороны попарно равны. То есть а=а, с=с. Отсюда имеем: 2а, 2с.
По условию задачи, 2а=1/5*400. то есть 2а=80.
Подставляем 2а в формулу периметра прямоугольника: 2а+2с. Получаем 80+2с=200. Отсюда находим с: с=(200-80):2. с=60. Вот мы нашли одну сторону прямоугольника (с).
Теперь находим сторону а. При этом снова используем формулу периметра прямоугольника, подставив туда найденное значение с. Получаем:
2а+2с=200
2а+120=200
2а=200-120
2а=80
а=40
Вот мы нашли вторую сторону (а).
Итак, стороны прямоугольника равны: а=40, с=60.
Проверка:
Находим периметр, имея заданные стороны (а и с)
Р=2а+2с. Подставляем известные нам а и с. Получаем:
Р=2*40+2*60
Р=80+120
Р=200
Итак, у нас периметр получился равным 200 см., что соответсвует условиям задачи. Значит, найденные значения а и с у нас правильные. а=40, с=60
Четырехугольник, у которого все углы прямые, противоположные стороны равны и параллельны друг другу, называется прямоугольником. Стороной прямоугольника является отрезок, соединяющий две вершины фигуры. Длинная сторона считается длиной, короткая сторона — шириной прямоугольника, прилегающие стороны перпендикулярны, они являются его высотами.
Расчет длины стороны прямоугольника через диагональ и сторону
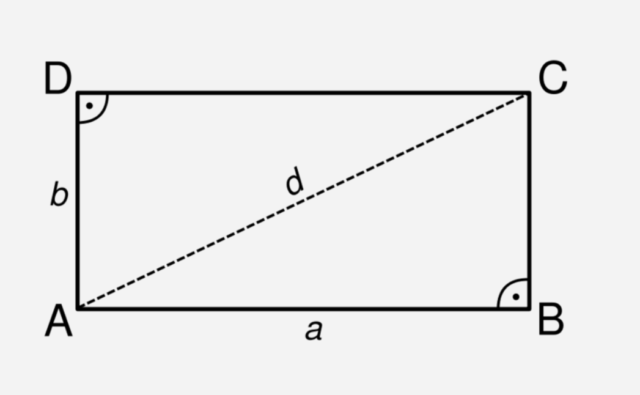
Отрезок, соединяющий 2 противолежащие вершины прямоугольника, является его диагональю. В прямоугольнике две диагонали одинаковой длины. Каждая из них делит прямоугольник на два прямоугольных треугольника, гипотенузой которых является диагональ, а катетами — стороны прямоугольника. Соответственно, квадрат диагонали можно вычислить через теорему Пифагора: d2 = a2 + b2, а сумма квадратов диагоналей прямоугольника равна сумме квадратов его сторон:
2d2 = 2a2 + 2b2
где d — диагональ, а, b — стороны прямоугольника.
Если дана диагональ прямоугольника и одна из его сторон, находим длину другой стороны, как корень из разности: квадрат диагонали минус квадрат известной стороны:
a = √d2 — b2
b = √d2 — a2
где d — диагональ, а, b — стороны прямоугольника.
Расчет стороны прямоугольника через периметр и сорону
Периметр прямоугольника равняется сумме всех его сторон. Если известны длина (а) и ширина (b) прямоугольника, его периметр (Р) будет равен удвоенной сумме сторон, т.к. его противоположные стороны равны:
Р = 2a + 2b = 2 (а + b)
Если известны периметр и одна из сторон прямоугольника, другую находим по формуле:
a = (P — 2b) / 2
b = (P — 2a) / 2
Р — периметр, a — длина, b — ширина прямоугольника
Т.е. сторона прямоугольника равняется половине разности между периметром и удвоенной другой стороной.
Расчет стороны прямоугольника через площадь и сторону
Чтобы рассчитать площадь прямоугольника (S), необходимо его длину а умножить на ширину b:
S = аb
Если известна площадь прямоугольника и одна из его сторон, длину другой находим путем деления площади на длину известной стороны:
a = S / b
b = S / a
где S — площадь прямоугольника, a, b — его стороны.
Пример:
измеряя с помощью линейки длины сторон прямоугольника, получим (2) см и (4) см. Противолежащие им стороны имеют такую же длину — (2) см и (4) см.
Найдём сумму длин всех сторон этого прямоугольника.
Для этого сложим все эти длины.
Получим:
(2) см (+) (4) см (+) (2) см (+) (4) см (=) (12) см.
Периметр — это сумма длин всех сторон фигуры.
Значит,
складывая длины всех сторон прямоугольника, получаем периметр прямоугольника.
Периметр обозначается заглавной латинской буквой (Р).
Итак,
периметр прямоугольника (Р = 12) см.
Найдём периметр треугольника.
Сначала измерим стороны треугольника.
Длины сторон треугольника равны (4) см, (3) см, (6) см.
Значит,
сумма длин всех сторон треугольника, т. е. периметр треугольника
равен:
(Р) (=) (3) см (+) (4) см (+) (6) см (=) (13) см.
Дан квадрат, длина стороны которого равна (4) см.
У квадрата все стороны равны.
Периметр квадрата равен сумме длин всех сторон квадрата.
Получим:
(Р) (=) (4) см (+) (4) см (+) (4) см (+) (4) см (=) (16) см.
Если у треугольника все стороны равны, такой треугольник называется равносторонний.
Для определения периметра данного треугольника найдём сумму длин всех его сторон.
Получим:
(Р) (=) (5) см (+) (5) см (+) (5) см (=) (15) см.
Источники:
Рис. 1. Прямоугольник. © ЯКласс
Рис. 2. Треугольник. © ЯКласс
Рис. 3. Квадрат. © ЯКласс
Рис. 4. Равносторонний треугольник. © ЯКласс